Predictive Model as Screening Tool for Early Warning of Corporate Insolvency in Risk Management: Case Study from Slovak Republic
Abstract
1. Introduction
- ▪
- Identifying five statistically significant predictors of bankruptcy through backwards binary logistic regression.
- ▪
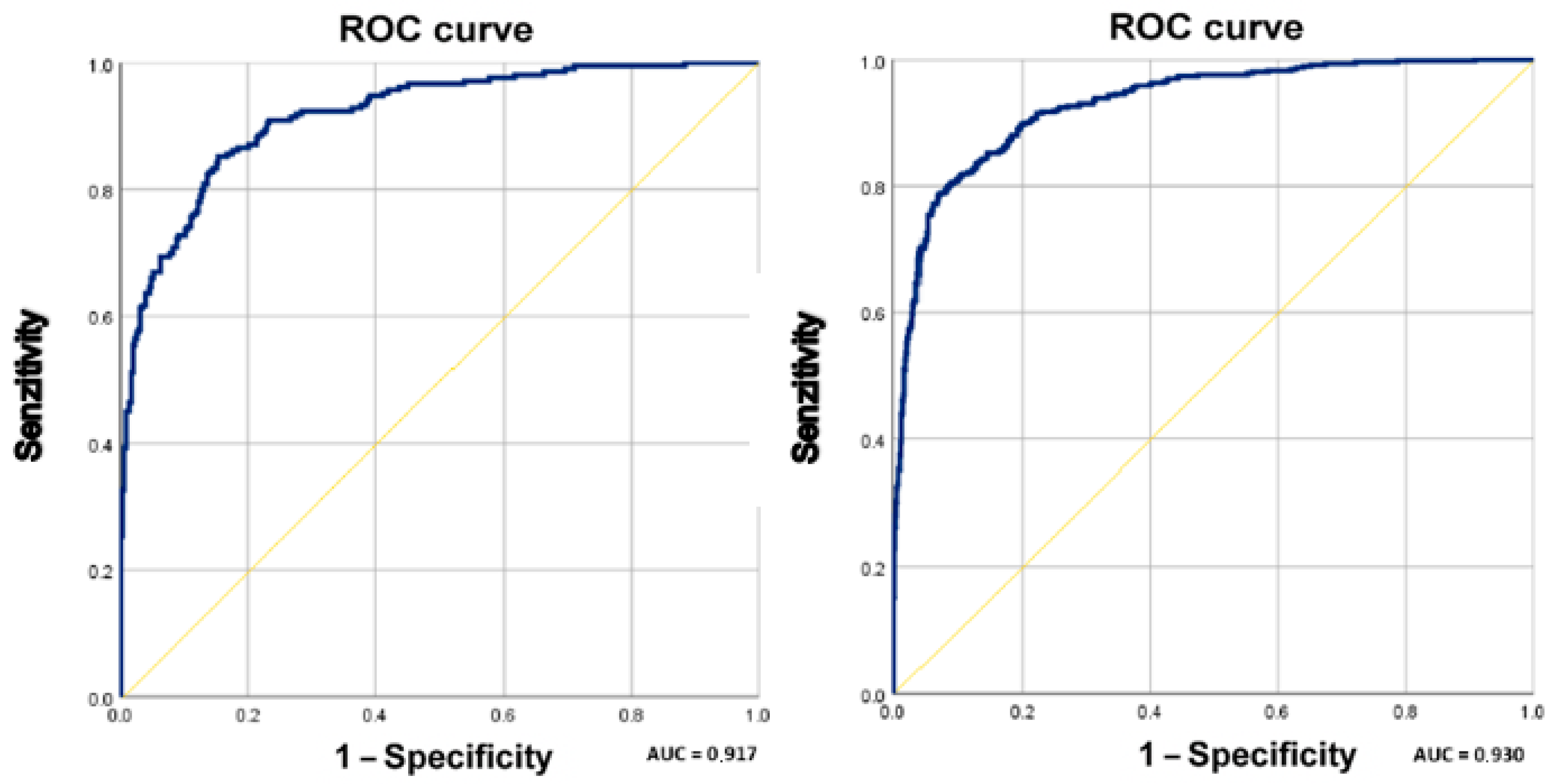
- Demonstrating strong predictive performance with an overall accuracy of 83.78% and an AUC of 91.7%, confirming the model’s discriminative power.
- ▪
- Providing a practical decision-support tool for managers, investors, creditors, and other stakeholders to assess financial health and anticipate potential corporate distress.
- ▪
- Offering insights into financial distress dynamics during the COVID-19 crisis, a period of exceptional economic conditions, thereby extending the applicability of classical insolvency prediction models to crisis contexts.
2. Literature Review
3. Materials and Methods
3.1. Input Data
3.2. Sample
3.3. Dependent Variable
3.4. Independent Variables
3.5. Hypothesis
3.6. Methods
- ▪
- Binary dependent variable. The outcome variable must be dichotomous, meaning it takes on two categorical values (e.g., success/failure, yes/no).
- ▪
- Independence of Observations. The observations should be mutually independent, implying that the outcome of one observation does not influence the outcome or prediction of another. For instance, one respondent’s answer should not affect another’s. Ensuring independence is crucial for the predictive accuracy of the model.
- ▪
- No or minimal multicollinearity. There should be no strong multicollinearity among the independent variables. In other words, the predictors should not be highly correlated with each other. High multicollinearity can distort the estimation of regression coefficients and reduce model interpretability.
- ▪
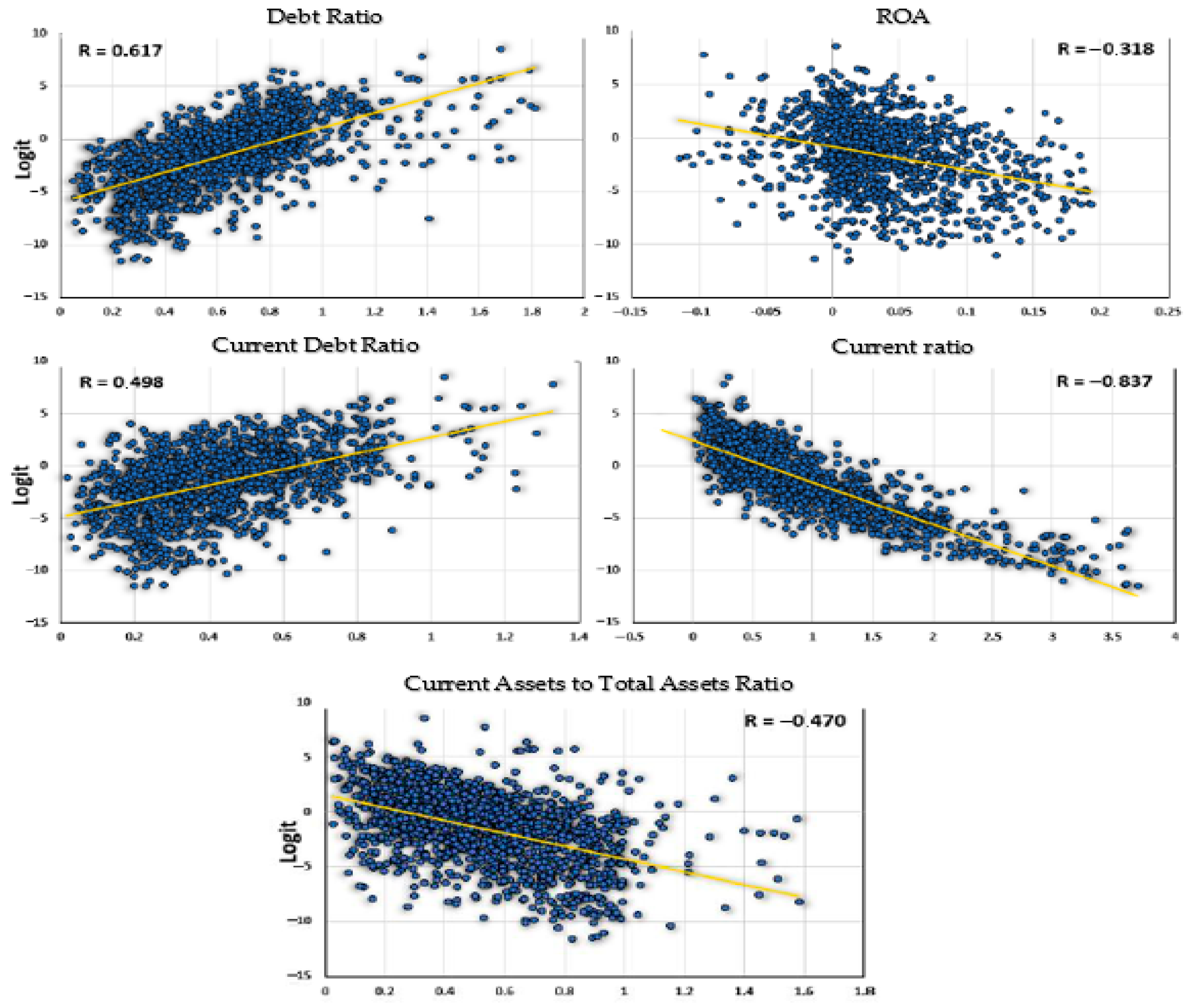
- Linearity of independent variables with the logit. There should be a linear relationship between the continuous independent variables and the logit transformation of the dependent variable. This assumption can be evaluated using graphical methods, such as plotting individual predictors against the logit. However, this approach has limitations, particularly in models with multiple predictors, and should be interpreted cautiously.
- ▪
- Absence of strong outliers. Logistic regression models are sensitive to outliers. Tools such as boxplots and histograms are commonly used to detect the presence of extreme or influential data points, which can adversely affect model performance. Before model estimation, outliers were removed to prevent distortion of the results, and companies with missing financial data were excluded from the analysis. This preprocessing ensured that the dataset used for model estimation was complete and reliable, supporting the robustness and validity of the predictive model. All outliers identified using the standard IQR method (values below Q1 − 1.5 × IQR or above Q3 + 1.5 × IQR) were removed from the dataset to ensure the robustness of the results.
- ▪
- Large sample size. A sufficiently large dataset is necessary to ensure the stability and generalizability of the model. Several rules exist for determining the minimum sample size, most of which are based on the ratio of observations to explanatory variables. One widely used guideline is the Events per Variable (EPV) rule, which recommends a minimum of 10 events (i.e., occurrences of the outcome of interest) for each independent variable included in the model.
4. Results
5. Discussion
6. Conclusions
- ▪
- The company management can monitor financial health and identify early warning signs of financial distress, enabling timely corrective actions such as cost optimization or debt restructuring.
- ▪
- The investors can evaluate the financial stability of potential investment targets and support risk-adjusted decision-making.
- ▪
- The banks and creditors assess the creditworthiness of clients and predict default risk when evaluating loan applications.
- ▪
- The auditors and consultants can incorporate the model into financial risk assessment tools for regular company evaluations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable | Debt Ratio | Current Ratio | Working Capital to Total Assets Ratio | ROA | ROTA | Equity Ratio | Assets Turnover | ROE | Current Assets to Total Assets Ratio | Current Debt Ratio | Quick Ratio | EAT and Depreciation to Total Assets | Financial Leverage | Profit Margin | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Debt Ratio | Pearson r | 1 | −0.406 ** | −0.326 ** | −0.106 ** | −0.043 | −0.697 ** | 0.173 ** | 0.016 | 0.158 ** | 0.604 ** | −0.346 ** | −0.450 ** | 0.216 ** | −0.140 ** |
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | 0.066 | 0.000 | 0.000 | 0.499 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Current Ratio | Pearson r | 1 | 0.844 ** | 0.16 | 0.149 ** | 0.608 ** | 0.055* | −0.001 | 0.422 ** | −0.537 ** | 0.648 ** | 0.281 ** | −0.354 ** | 0.144 ** | |
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | 0.000 | 0.018 | 0.965 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||
| Working Capital to Total Assets Ratio | Pearson r | 1 | 0.227 ** | 0.216 ** | 0.494 ** | 0.206 ** | 0.037 | 0.678 ** | −0.417 ** | 0.582 ** | 0.215 ** | −0.427 ** | 0.143 ** | ||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | 0.000 | 0.113 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| ROA | Pearson r | 1 | 0.972 ** | 0.153 ** | 0.269 ** | 0.826 ** | 0.159 ** | −0.089 ** | 0.233 ** | 0.660 ** | −0.207 ** | 0.829 ** | |||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| ROTA | Pearson r | 1 | 0.114 ** | 0.315 ** | 0.806 ** | 0.176 ** | −0.054 * | 0.220 ** | 0.633 ** | −0.205 ** | 0.786 ** | ||||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.000 | 0.000 | 0.000 | 0.000 | ||||||
| Equity Ratio | Pearson r | 1 | −0.022 | −0.082 ** | 0.090 ** | −0.509 ** | 0.460 ** | 0.541 ** | −0.515 ** | 0.155 ** | |||||
| Sig. (2-tailed) | 0.346 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||||||
| Assets Turnover | Pearson r | 1 | 0.202 ** | 0.430 ** | 0.273 ** | 0.019 | 0.151 ** | −0.172 | 0.034 | ||||||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | 0.408 | 0.000 | 0.000 | 0.140 | ||||||||
| ROE | Pearson r | 1 | 0.041 | 0.004 | 0.089 ** | 0.439* | 0.071 ** | 0.744 ** | |||||||
| Sig. (2-tailed) | 0.079 | 0.857 | 0.000 | 0.000 | 0.002 | 0.000 | |||||||||
| Current Assets to Total Assets Ratio | Pearson r | 1 | 0.385 ** | 0.280 ** | −0.052* | −0.272 | 0.014 | ||||||||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.025 | 0.000 | 0.557 | ||||||||||
| Current Debt Ratio | Pearson r | 1 | −0.385 ** | −0.334 ** | 0.200 ** | −0.163 ** | |||||||||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | 0.000 | |||||||||||
| Quick Ratio | Pearson r | 1 | 0.351 ** | −0.273 ** | 0.221 ** | ||||||||||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | ||||||||||||
| EAT and Depreciation to Total Assets | Pearson r | 1 | −0.303 ** | 0.587 ** | |||||||||||
| Sig. (2-tailed) | 0.000 | 0.000 | |||||||||||||
| Financial Leverage | Pearson r | 1 | −0.130 ** | ||||||||||||
| Sig. (2-tailed) | 0.000 | ||||||||||||||
| Profit Margin | Pearson r | 1 | |||||||||||||
| Sig. (2-tailed) | |||||||||||||||
| Variable | Debt Ratio | Current Ratio | ROA | Equity Ratio | Assets Turnover | Current Assets to Total Assets Ratio | Current Debt Ratio | Quick Ratio | EAT and Depreciation to Total Assets | Financial Leverage | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Debt Ratio | Pearsonovo r | 1 | −0.406 ** | −0.106 ** | −0.697 ** | 0.173 ** | 0.158 ** | 0.604 ** | −0.346 ** | −0.450 ** | 0.216 ** |
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Current Ratio | Pearsonovo r | 1 | 0.166 ** | 0.608 ** | 0.055* | 0.422 ** | −0.537 ** | 0.648 ** | 0.281 ** | −0.354 ** | |
| Sig. (2-tailed) | 0.000 | 0.000 | 0.018 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||
| ROA | Pearsonovo r | 1 | 0.153 ** | 0.269 ** | 0.159 ** | −0.089 ** | 0.233 ** | 0.660 ** | −0.207 ** | ||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||||
| Equity Ratio | Pearsonovo r | 1 | −0.022 ** | 0.090 ** | −0.509 ** | 0.460 ** | 0.541 ** | −0.515 ** | |||
| Sig.(2-tailed) | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||||
| Assets Turnover | Pearsonovo r | 1 | 0.430 ** | 0.273 ** | 0.019 | 0.151 ** | −0.172 ** | ||||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.408 | 0.000 | 0.000 | ||||||
| Current Assets to Total Assets Ratio | Pearsonovo r | 1 | 0.385 ** | 0.280 * | −0.052 * | −0.272 ** | |||||
| Sig. (2-tailed) | 0.000 | 0.025 | 0.000 | 0.000 | |||||||
| Current Debt Ratio | Pearsonovo r | 1 | −0.385 ** | −0.334 ** | 0.200 ** | ||||||
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | ||||||||
| Quick Ratio | Pearsonovo r | 1 | 0.351 ** | −0.273 ** | |||||||
| Sig. (2-tailed) | 0.000 | 0.000 | |||||||||
| EAT and Depreciation to Total Assets | Pearsonovo r | 1 | −0.303 ** | ||||||||
| Sig. (2-tailed) | 0.000 | ||||||||||
| Financial Leverage | Pearsonovo r | 1 | |||||||||
| Sig. (2-tailed) | |||||||||||
Appendix B
| Dimension | Eigenvalue | Variance Proportions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Condition Index | Debt Ratio | ROA | Equity Ratio | Assets Turnover | Current Assets to Total Assets Ratio | Current Debt Ratio | Quick Ratio | EAT and Depreciation to Total Liabilities | Financial Leverage | Current Ratio | ||
| 1 | 8.161 | 1.000 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 2.662 | 1.753 | 0.01 | 0.26 | 0.00 | 0.00 | 0.03 | 0.00 | 0.02 | 0.00 | 0.01 | 0.00 |
| 3 | 1.566 | 2.293 | 0.00 | 0.25 | 0.00 | 0.03 | 0.00 | 0.03 | 0.00 | 0.00 | 0.01 | 0.01 |
| 4 | 1.434 | 2.378 | 0.00 | 0.00 | 0.05 | 0.00 | 0.00 | 0.00 | 0.03 | 0.00 | 0.00 | 0.00 |
| 5 | 0.733 | 3.321 | 0.00 | 0.04 | 0.67 | 0.00 | 0.05 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 |
| 6 | 0.605 | 3.677 | 0.04 | 0.00 | 0.00 | 0.05 | 0.00 | 0.00 | 0.03 | 0.01 | 0.00 | 0.00 |
| 7 | 0.334 | 4.942 | 0.00 | 0.00 | 0.00 | 0.67 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 8 | 0.163 | 7.048 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 |
| 9 | 0.069 | 10.966 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 10 | 0.065 | 11.206 | 0.42 | 0.00 | 0.00 | 0.00 | 0.46 | 0.04 | 0.16 | 0.39 | 0.27 | 0.01 |
| 11 | 0.018 | 21.544 | 0.53 | 0.00 | 0.03 | 0.00 | 0.65 | 0.86 | 0.76 | 0.59 | 0.70 | 0.95 |
Appendix C
| Variable | VIF |
|---|---|
| Debt Ratio | 3.076 |
| ROA | 1.067 |
| Current Assets to Total Assets Ratio | 1.758 |
| Current Debt Ratio | 3.568 |
| Current Ratio | 2.288 |
References
- Hopkin, P. Fundamentals of Risk Management: Understanding, Evaluating and Implementing Effective Risk Management, 4th ed.; Kogan Page: London, UK, 2017. [Google Scholar]
- Ashraf, S.; GSFélix, E.; Serrasqueiro, Z. Do Traditional Financial Distress Prediction Models Predict the Early Warning Signs of Financial Distress? J. Risk Financ. Manag. 2019, 12, 55. [Google Scholar] [CrossRef]
- Herman, S. Industry Specifics of Joint-Stock Companies in Poland and Their Bankruptcy Prediction; ResearchGate: Berlin, Germany, 2017; Available online: https://www.researchgate.net/publication/336216773_Industry_specifics_of_joint-stock_companies_in_Poland_and_their_bankruptcy_prediction (accessed on 20 February 2025).
- Ježovita, A. Designing the model for evaluating business quality in Croatia. Manag. J. Contemp. Manag. Issues 2015, 20, 101–129. [Google Scholar]
- Voda, A.D.; Dobrotă, G.; Țîrcă, D.M.; Dumitrașcu, D.D.; Dobrotă, D. Corporate Bankruptcy and Insolvency Prediction Model. Technol. Econ. Dev. Econ. 2021, 27, 1039–1056. [Google Scholar] [CrossRef]
- Svabova, L.; Michalkova, L.; Durica, M.; Nica, E. Business Failure Prediction for Slovak Small and Medium-Sized Companies. Sustainability 2020, 12, 4572. [Google Scholar] [CrossRef]
- Durica, M.; Adamko, P. Verification of MDA bankruptcy prediction models for enterprises in Slovak Republic. 2016. Available online: https://msed.vse.cz/msed_2016/article/253-Durica-Marek-paper.pdf (accessed on 20 February 2025).
- Němec, D.; Pavlík, M. Predicting Insolvency Risk of the Czech Companies. 2016. Available online: https://www.muni.cz/vyzkum/publikace/1346624 (accessed on 20 February 2025).
- Durica, M.; Valaskova, K.; Janoskova, K. Logit business failure prediction in V4 countries. Eng. Manag. Prod. Serv. 2019, 11, 54–64. [Google Scholar] [CrossRef]
- Střelec, L.; Staňková, M. On the appropriate thresholds in the logistic regression bankruptcy model. AIP Conf. Proc. 2024, 3094, 100003. [Google Scholar] [CrossRef]
- Vukčević, M.; Lakićević, M.; Melović, B.; Backović, T.; Dudić, B. Modern models for predicting bankruptcy to detect early signals of business failure: Evidence from Montenegro. PLoS ONE 2024, 19, e0303793. [Google Scholar] [CrossRef] [PubMed]
- Kuster, D.; Majstorovic, A.; Dmitrovic, V. A logistic regression approach to long-term bankruptcy prediction: The role of financial and non-financial indicators. E+M Ekon. A Manag. 2025, 28, 165–179. [Google Scholar] [CrossRef]
- Pavličko, M.; Mazanec, J. Minimalistic Logit Model as an Effective Tool for Predicting the Risk of Financial Distress in the Visegrad Group. Mathematics 2022, 10, 1302. [Google Scholar] [CrossRef]
- Ohlson, J.A. Financial Ratios and the Probabilistic Prediction of Bankruptcy. J. Account. Res. 1980, 18, 109. [Google Scholar] [CrossRef]
- Zmijewski, M.E. Methodological Issues Related to the Estimation of Financial Distress Prediction Models. J. Account. Res. 1984, 22, 59. [Google Scholar] [CrossRef]
- Adamko, P.; Klieštik, T.; Kováčová, M. A Glm Model for Prediction of Crisis in Slovak Companies; ResearchGate: Berlin, Germany, 2018; Available online: https://www.researchgate.net/publication/326558608_AN_GLM_MODEL_FOR_PREDICTION_OF_CRISIS_IN_SLOVAK_COMPANIES (accessed on 20 February 2025).
- Klieštik, T.; Vrbka, J.; Rowland, Z. Bankruptcy prediction in Visegrad group countries using multiple discriminant analysis. Equilib. Q. J. Econ. Econ. Policy 2018, 13, 569–593. [Google Scholar] [CrossRef]
- Alaminos, D.; Del Castillo, A.; Fernández, M.Á. A Global Model for Bankruptcy Prediction. PLoS ONE 2016, 11, e0166693. [Google Scholar] [CrossRef]
- Ekes, K.S.; Koloszar, L. The Efficiency of Bankruptcy Forecast Models in the Hungarian SME Sector. J. Compet. 2014, 6, 56–73. [Google Scholar] [CrossRef]
- Shirinkina, E.V.; Valiullina, L.A. Formalization of the Model of the Enterprise Insolvency Risk Prediction. Actual Probl. Econ. Law 2015, 2015, 169. [Google Scholar] [CrossRef]
- Mihalovic, M. Performance Comparison of Multiple Discriminant Analysis and Logit Models in Bankruptcy Prediction. Econ. Sociol. 2016, 9, 101–118. Available online: https://www.researchgate.net/publication/316475250_Performance_Comparison_of_Multiple_Discriminant_Analysis_and_Logit_Models_in_Bankruptcy_Prediction (accessed on 20 February 2025).
- Adamowicz, K.; Noga, T. Identification of financial ratios applicable in the construction of a prediction model for bankruptcy of wood industry enterprises. Folia For. Pol. 2018, 60, 61–72. [Google Scholar] [CrossRef]
- Altman, E.I. Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. J. Financ. 1968, 23, 589–609. [Google Scholar] [CrossRef]
- Almamy, J.; Aston, J.; Ngwa, L.N. An evaluation of Altman’s Z-score using cash flow ratio to predict corporate failure amid the recent financial crisis: Evidence from the UK. J. Corp. Financ. 2016, 36, 278–285. [Google Scholar] [CrossRef]
- Jenčová, S.; Štefko, R.; Vašaničová, P. Scoring Model of the Financial Health of the Electrical Engineering Industry’s Non-Financial Corporations. Energies 2020, 13, 4364. [Google Scholar] [CrossRef]
- Jakubík, P.; Teplý, P. The JT Index as an Indicator of Financial Stability of Corporate Sector. Prague Econ. Pap. 2011, 20, 157–176. [Google Scholar] [CrossRef]
- Butkus, M.; Žakarė, S.; Cibulskienė, D. Bankroto diagnostikos modelis ir jo pritaikymas bankroto tikimybei Lietuvos įmonėse prognozuoti. Appl. Econ. Syst. Res. 2014, 8.1, 111–132. [Google Scholar] [CrossRef]
- Blums, M.; College, M. D-Score: Bankruptcy Prediction Model for Middle Market Public Firms. 2003. Available online: https://minneapolisfed.org/-/media/files/mea/contest/2004papers/blums.pdf (accessed on 20 February 2025).
- Horváthová, J.; Mokrišová, M.; Petruška, I. Selected Methods of Predicting Financial Health of Companies: Neural Networks Versus Discriminant Analysis. Information 2021, 12, 505. [Google Scholar] [CrossRef]
- Grünberg, M.; Lukason, O. Predicting Bankruptcy of Manufacturing Firms. Int. J. Trade Econ. Financ. 2014, 5, 93–97. [Google Scholar] [CrossRef]
- Sfakianakis, E. Bankruptcy prediction model for listed companies in Greece. Invest. Manag. Financ. Innov. 2021, 18, 166–180. [Google Scholar] [CrossRef]
- Moody’s. 2021. Available online: https://www.moodys.com/web/en/us/capabilities/company-reference-data/orbis.html (accessed on 20 February 2025).
- Durica, M.; Frnda, J. Využitie Dataminingových Metód pri Predikcii Finančných Ťažkostí. 2021. Available online: https://edis.uniza.sk/produkt/6904/Vyuzitie-dataminingovych-metod-pri-predikcii-financnych--tazkosti/ (accessed on 20 February 2025).
- Tranmer, M.; Vanchugova, D.; Elliot, J.M. Binary Logistic Regression, 2nd ed; ResearchGate: Berlin, Germany, 2024; Available online: https://www.researchgate.net/publication/387665025_Binary_Logistic_Regression_2nd_edition (accessed on 20 February 2025).
- Costea, C.D.; Hostiuc, F. The Liquidity Ratios and Their Significance in the Financial Equilibrium of the Firms. Ann. “Stefan Cel Mare” Univ. Suceava. Fascicle Fac. Econ. Public Adm. 2009, 9, 252–261. [Google Scholar]
- Daoud, J.I. Multicollinearity and Regression Analysis. J. Phys. Conf. Ser. 2017, 949, 012009. [Google Scholar] [CrossRef]
- Alin, A. Multicollinearity. WIREs Comput. Stat. 2010, 2, 370–374. [Google Scholar] [CrossRef]
- Yoo, W.; Mayberry, R.; Bae, S.; Singh, K.; Peter He, Q.; Lillard, J.W. A Study of Effects of Multicollinearity in the Multivariable Analysis. Int. J. Appl. Sci. Technol. 2014, 4, 9–19. [Google Scholar]
- Bewick, V.; Cheek, L.; Ball, J. Statistics review 14: Logistic regression. Crit. Care 2005, 9, 112. [Google Scholar] [CrossRef]
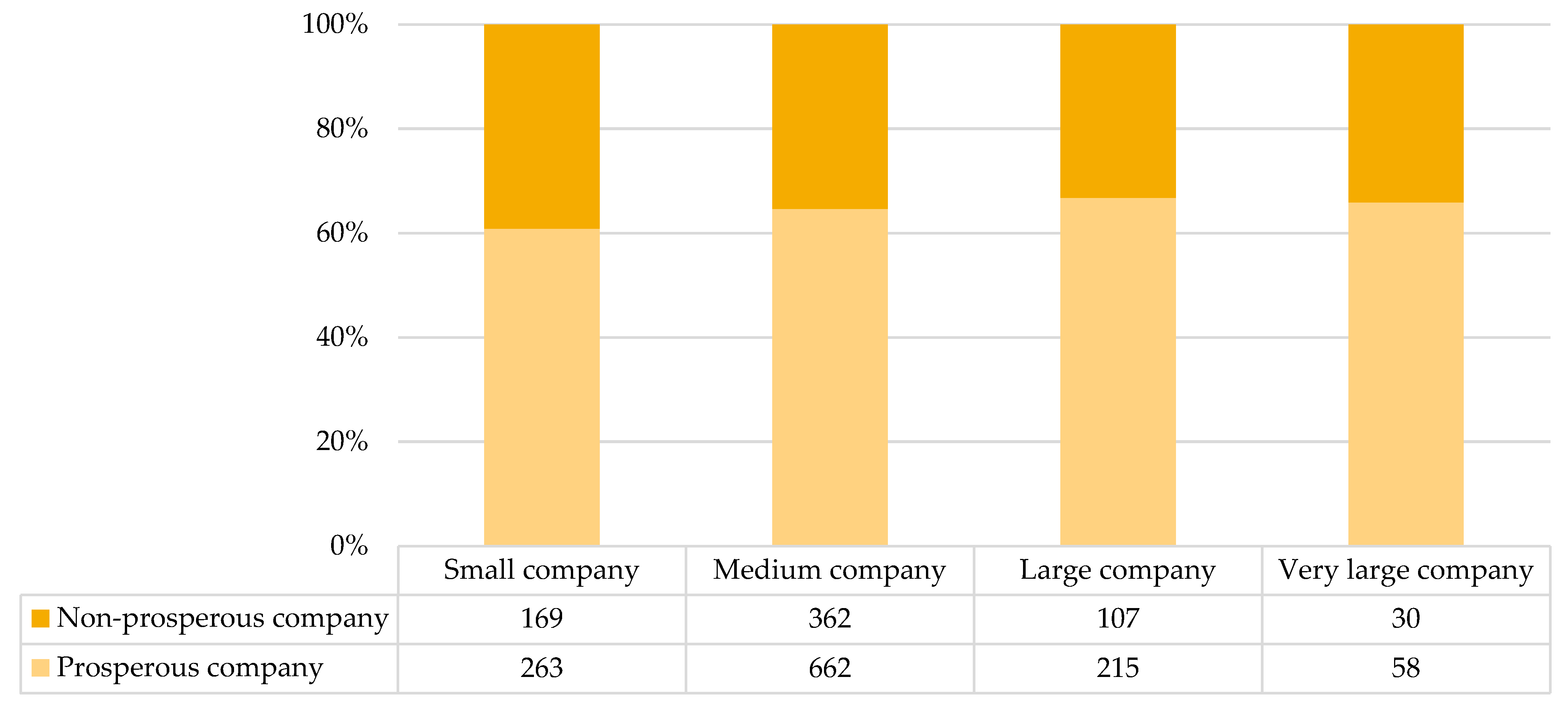

| Variable | Formula | Category | Authors | Number |
|---|---|---|---|---|
| Debt Ratio | Total Liabilities/Total Assets | Indebtedness | Ohlson (1980) [14], Zmijewski (1984) [15], Němec and Pavlík (2016) [8], Herman (2017) [3], Adamko, Klieštik, and Kováčová (2018) [16], Klieštik, Vrbka a Rowland (2018) [17], Alaminos, Del Castillo, and Fernández (2016) [18], Voda et al. (2021) [5], Svabova et al. (2020) [6], Pavličko a Mazanec (2022) [13], Ekes and Koloszar (2014) [19], Durica, Valaskova, and Janoskova (2019) [9] | 12 |
| Current Ratio | Current Assets/Current Liabilities | Liquidity | Zmijewski (1984) [15], Shirinkina a Valiullina (2015) [20], Ježovita (2015) [4], Mihalovič (2016) [21], Alaminos, Del Castillo and Fernández (2016) [18], Klieštik, Vrbka and Rowland (2018) [17], Voda et al. (2021) [5], Adamowicz and Noga (2018) [22], Němec and Pavlík (2016) [8], Ďurica and Adamko (2016) [7], Svabova et al. (2020) [6], Durica, Valaskova, and Janoskova (2019) [9] | 12 |
| Working Capital to Total Assets Ratio | Working Capital/Total Assets | Liquidity | Altman (1968) [23], Ohlson (1980) [14], Durica and Adamko (2016) [7], Almamy, Aston and Ngwa (2016) [24], Mihalovič (2016) [21], Adamko, Klieštik, and Kováčová (2018) [16], Jenčová, Štefko and Vašaničová (2020) [25], Jakubík and Teplý (2011) [26], Butkus, Žakarė, and Cibulskienė (2014) [27], Durica, Valaskova and Janoskova (2019) [9] | 10 |
| ROA (based on EAT) | EAT/Total Assets | Profitability | Ohlson (1980) [14], Zmijewski (1984) [15], Blums and College (2004) [28], Shirinkina and Valiullina (2015) [20], Alaminos, Del Castillo and Fernández (2016) [18], Mihalovič (2016) [21], Klieštik, Vrbka and Rowland (2018) [17], Pavličko and Mazanec (2022) [13], Butkus, Žakarė, and Cibulskienė (2014) [27], Durica, Valaskova and Janoskova (2019) [9] | 10 |
| ROTA (based on EBIT) | EBIT/Total Assets | Profitability | Altman (1968) [23], Ďurica and Adamko (2016) [7], Almamy, Aston, and Ngwa (2016) [24], Alaminos, Del Castillo, and Fernández (2016) [18], Klieštik, Vrbka, and Rowland (2018) [17], Voda et al. (2021) [5], Horváthová, Mokrišová, and Petruška (2021) [29], Adamko, Klieštik, and Kováčová (2018) [16] | 8 |
| Equity Ratio | Equity/Total Liabilities | Indebtedness | Němec and Pavlík (2016) [8], Valiullina (2015) [20] and Adamko (2016) [7], Almamy, Aston and Ngwa (2016) [24], Herman (2017) [3], Altman (1968) [23], Adamowicz and Noga (2018) [22], Ekes and Koloszar (2014) [19], Horváthová, Mokrišová, and Petruška (2021) [29], Butkus, Žakarė, and Cibulskienė (2014) [27] | 8 |
| Asset Turnover | Sales/Total Assets | Activity | Altman (1968) [23], Shirinkina a Valiullina (2015), Almamy, Aston, and Ngwa (2016) [24], Horváthová, Mokrišová, and Petruška (2021) [29], Svabova et al. (2020) [6], Jakubík and Teplý (2011) [26], Durica, Valaskova, and Janoskova (2019) [9] | 7 |
| ROE (based on EAT) | EAT/Equity | Profitability | Shirinkina and Valiullina (2015) [20], Ježovita (2015) [4], Klieštik, Vrbka, and Rowland (2018) [17], Svabova et al. (2020) [6], Jakubík and Teplý (2011) [26], Durica, Valaskova, and Janoskova (2019) [9] | 6 |
| Current Assets to Total Assets Ratio | Current Assets/Total Assets | Asset Structure | Shirinkina and Valiullina (2015) [20], Mihalovič (2016) [21], Alaminos, Del Castillo, and Fernández (2016) [18], Klieštik, Vrbka, and Rowland (2018) [17], Grünberg and Lukason (2014) [30] | 5 |
| Current Debt Ratio | Current Liabilities/Total Assets | Indebtedness | Blums and College (2003) [28], Mihalovič (2016) [21], Klieštik, Vrbka, and Rowland (2018) [17] | 3 |
| Quick Ratio | (Current Assets–Inventory)/Current Liabilities | Liquidity | Jenčová, Štefko, and Vašaničová (2020) [25], Sfakianakis (2021) [31], Durica, Valaskova, and Janoskova (2019) [9] | 3 |
| Retained Earnings to Total Assets Ratio | Retained Earnings/Total Assets | Indebtedness | Altman (1968) [23], Almamy, Aston and Ngwa (2016) [24] | 2 |
| EAT and Depreciation to Total Liabilities Ratio | (EAT + Depreciation)/Total Liabilities | Indebtedness | Adamko, Klieštik, and Kováčová (2018) [16], Voda et al. (2021) [5] | 2 |
| Financial Leverage | Total Assets/Equity | Indebtedness | Jenčová, Štefko, and Vašaničová (2020) [25], Němec and Pavlík (2016) [8] | 2 |
| Cash and Cash Equivalents to Total Assets | Cash and Cash Equivalents/Total Assets | Liquidity | Durica, Valaskova, and Janoskova (2019) [9], Klieštik, Vrbka, and Rowland (2018) [17] | 2 |
| Profit Margin | EAT/Sales | Profitability | Durica, Valaskova, and Janoskova (2019) [9], Svabova et al. (2020) [6] | 2 |
| Company Size | Sales (Million Euros) | Total Assets (Million Euros) | Number of Employees |
|---|---|---|---|
| Very large company | ≥100 | ≥200 | ≥1000 |
| Large company | ≥10 | ≥20 | ≥150 |
| Medium company | ≥1 | ≥2 | ≥15 |
| Small company | Other companies are not included in the remaining three categories. | ||
| Variables | Formula | Category |
|---|---|---|
| Debt Ratio | Total Liabilities/Total Assets | Indebtedness |
| Current Ratio | Current Assets/Current Liabilities | Liquidity |
| Working Capital to Total Assets Ratio | Working Capital/Total Assets | Liquidity |
| ROA (based on EAT) | EAT/Total Assets | Profitability |
| ROTA (based on EBIT) | EBIT/Total Assets | Profitability |
| Equity Ratio | Equity/Total Liabilities | Indebtedness |
| Asset Turnover | Sales/Total Assets | Activity |
| ROE (based on EAT) | EAT/Equity | Profitability |
| Current Assets to Total Assets Ratio | Current Asset/Total Assets | Asset Structure |
| Current Debt Ratio | Current Liabilities/Total Assets | Indebtedness |
| Quick Ratio | (Current Assets–Inventory)/Current Liabilities | Liquidity |
| EAT and Depreciation to Total Liabilities | (EAT + Depreciation)/Total Liabilities | Indebtedness |
| Financial Leverage | Total Assets/Equity | Indebtedness |
| Profit Margin | EAT/Sales | Profitability |
| Mean | Median | Standard Deviation | Kurtosis | Skewness | Interquartile Range | Variance | Min | Max | |
|---|---|---|---|---|---|---|---|---|---|
| Debt Ratio | 0.81 | 0.60 | 1.39 | 1.93 | 234.7 | 12.2 | 36.9 | −0.2 | 36.7 |
| Current Ratio | 2.56 | 1.34 | 4.60 | 21.14 | 116.9 | 8.2 | 122.3 | −14.3 | 108.0 |
| Working Capital to Total Assets Ratio | 0.15 | 0.11 | 0.86 | 0.74 | 181.8 | 1.1 | 40.3 | −18.8 | 21.5 |
| ROA | 0.03 | 0.02 | 0.21 | 0.04 | 159.7 | 0.7 | 9.4 | −4.2 | 5.2 |
| ROTA | 0.05 | 0.04 | 0.21 | 0.05 | 77.1 | −2.9 | 6.4 | −4.1 | 2.3 |
| Equity Ratio | 2.22 | 0.66 | 7.77 | 60.39 | 688.9 | 21.0 | 336.6 | −30.0 | 306.6 |
| Asset Turnover | 1.60 | 1.25 | 1.55 | 2.40 | 37.0 | 4.5 | 23.3 | 0.0 | 23.3 |
| ROE | −0.08 | 0.07 | 5.88 | 34.53 | 787.5 | −21.5 | 307.4 | −202.7 | 104.6 |
| Current Assets to Total Assets Ratio | 0.70 | 0.57 | 0.94 | 0.88 | 245.2 | 12.0 | 25.7 | 0.0 | 25.7 |
| Current Debt Ratio | 0.55 | 0.38 | 0.90 | 0.81 | 336.0 | 13.4 | 30.4 | −0.2 | 30.1 |
| Quick Ratio | 2.14 | 0.89 | 7.35 | 54.03 | 872.5 | 24.0 | 314.6 | −2.2 | 312.4 |
| EAT and Depreciation to Total Liabilities Ratio | 0.35 | 0.15 | 1.00 | 1.01 | 279.8 | 12.6 | 35.9 | −6.1 | 29.8 |
| Financial Leverage | 10.36 | 2.19 | 150.11 | 22,532.04 | 1777.1 | 38.0 | 9354.9 | −1834.3 | 7520.6 |
| Profit Margin | −0.31 | 0.02 | 15.17 | 230.20 | 3385.9 | −57.0 | 920.0 | −912.5 | 7.5 |
| Mean | Median | Standard Deviation | Kurtosis | Skewness | Interquartile Range | Variance | Min | Max | |
|---|---|---|---|---|---|---|---|---|---|
| Debt Ratio | 0.62 | 0.60 | 0.30 | 0.09 | 1.07 | 0.76 | 1.76 | 0.05 | 1.81 |
| Current Ratio | 1.50 | 1.28 | 0.90 | 0.81 | 1.29 | 1.16 | 4.99 | 0.00 | 4.99 |
| Working Capital to Total Assets Ratio | 0.11 | 0.11 | 0.27 | 0.08 | 0.14 | −0.12 | 1.85 | −0.79 | 1.05 |
| ROA | 0.03 | 0.02 | 0.05 | 0.00 | 0.94 | 0.65 | 0.31 | −0.11 | 0.19 |
| ROTA | 0.05 | 0.04 | 0.06 | 0.00 | 0.84 | 0.80 | 0.36 | −0.11 | 0.25 |
| Equity Ratio | 0.97 | 0.67 | 0.84 | 0.70 | 1.57 | 1.40 | 4.75 | −0.60 | 4.15 |
| Asset Turnover | 1.42 | 1.29 | 0.76 | 0.58 | 0.28 | 0.77 | 3.86 | 0.03 | 3.89 |
| ROE | 0.08 | 0.06 | 0.12 | 0.02 | 0.84 | 0.47 | 0.78 | −0.29 | 0.49 |
| Current Assets to Total Assets Ratio | 0.54 | 0.53 | 0.27 | 0.07 | 0.19 | 0.49 | 1.58 | 0.00 | 1.58 |
| Current Debt Ratio | 0.43 | 0.40 | 0.22 | 0.05 | 0.58 | 0.74 | 1.31 | 0.02 | 1.33 |
| Quick Ratio | 1.00 | 0.81 | 0.71 | 0.50 | 1.75 | 1.33 | 3.97 | 0.02 | 3.72 |
| EAT and Depreciation to Total Liabilities Ratio | 0.20 | 0.15 | 0.17 | 0.03 | 1.39 | 1.16 | 1.08 | −0.26 | 0.82 |
| Financial Leverage | 3.14 | 2.49 | 1.98 | 3.93 | 1.12 | 1.13 | 12.83 | −3.31 | 9.52 |
| Profit Margin | 0.02 | 0.02 | 0.04 | 0.00 | 1.07 | 0.28 | 0.24 | −0.09 | 0.15 |
| Variable | VIF |
|---|---|
| Debt Ratio | 2.596 |
| ROA | 2.279 |
| Equity Ratio | 3.935 |
| Asset Turnover | 1.403 |
| Current Assets to Total Assets Ratio | 4.288 |
| Current Debt Ratio | 4.738 |
| Quick Ratio | 1.858 |
| EAT and Depreciation to Total Liabilities | 3.232 |
| Financial Leverage | 1.618 |
| Current Ratio | 5.223 |
| Variables | B | S.E. | Wald | df | Sig. | Exp(B) | 95% C.I. for EXP(B) | |
|---|---|---|---|---|---|---|---|---|
| Lower | Upper | |||||||
| Debt Ratio | 4.226 | 0.410 | 106.306 | 1 | 0.000 | 68.462 | 30.658 | 152.882 |
| ROA | −4.180 | 2.001 | 4.365 | 1 | 0.037 | 0.015 | 0.000 | 0.772 |
| Current Assets to Total Assets Ratio | −6.414 | 0.548 | 136.891 | 1 | 0.000 | 0.002 | 0.001 | 0.005 |
| Current Debt Ratio | 4.499 | 0.622 | 52.251 | 1 | 0.000 | 89.939 | 26.555 | 304.614 |
| Current Ratio | −2.088 | 0.257 | 65.785 | 1 | 0.000 | 0.124 | 0.075 | 0.205 |
| Constant | −0.462 | 0.309 | 2.231 | 1 | 0.135 | 0.630 | ||
| Initial −2 Log Likelihood | Final −2 Log Likelihood | Cox & Snell R Square | Nagelkerke R Square |
|---|---|---|---|
| 1692.604 | 838.752 | 0.480 | 0.661 |
| Threshold = 0.5 | Predicted | Accuracy (%) | ||
|---|---|---|---|---|
| Yes (1) | No (0) | |||
| Observed | Yes (1) | 154 | 55 | 73.68% |
| No (0) | 36 | 316 | 89.77% | |
| Total Accuracy | 83.78% | |||
| Probability Threshold | Youden’s Index (J) | F1 Score | Overall Accuracy |
|---|---|---|---|
| 0.1 | 0.551 | 0.724 | 0.733 |
| 0.2 | 0.645 | 0.772 | 0.800 |
| 0.3 | 0.685 | 0.798 | 0.838 |
| 0.4 | 0.682 | 0.800 | 0.847 |
| 0.5 | 0.635 | 0.772 | 0.838 |
| 0.6 | 0.610 | 0.757 | 0.840 |
| 0.7 | 0.581 | 0.736 | 0.836 |
| 0.8 | 0.471 | 0.644 | 0.799 |
| 0.9 | 0.318 | 0.484 | 0.745 |
| Threshold = 0.4 | Predicted | Accuracy (%) | ||
|---|---|---|---|---|
| Yes (1) | No (0) | |||
| Observed | Yes (1) | 157 | 52 | 75.12% |
| No (0) | 33 | 319 | 90.63% | |
| Total accuracy | 84.75% | |||
| Threshold = 0.5 | Predicted | Accuracy (%) | ||
|---|---|---|---|---|
| Yes (1) | No (0) | |||
| Observed | Yes (1) | 369 | 90 | 80.40% |
| No (0) | 76 | 770 | 91.00% | |
| Total accuracy | 87.30% | |||
| Authors | Country | Industry | AUC (%) | Overall Accuracy (%) | Common Variables |
|---|---|---|---|---|---|
| Mihalovič (2016) [21] | SK | Various | 77.20 | 93.90 | ROA, Current Debt Ratio, Current Assets to Total Assets Ratio |
| Adamko, Klieštik, and Kováčová (2018) [16] | SK | Various | 73.73 | 88.85 | Debt Ratio |
| Jenčová, Štefko, and Vašaničová (2020) [25] | SK | Electrotechnical and Mechanical Industry | 92.02 | 94.00 | Debt ratio, Current Ratio, ROA |
| Svabova et al. (2020) [6] | SK | Various | 95.35 | 93.80 | - |
| Durica, Valaskova, and Janoskova (2019) [9] | SK | Various | 93.40 | 88.10 | - |
| Pavličko and Mazanec (2022) [13] | V4 | Various | 95.07 | 93.91 | Debt Ratio, ROA |
| Horváthová, Mokrišová, and Petruška (2021) [29] | SK | Heating Industry | n/a | 84.00 | - |
| Durica and Adamko (2016) [7] | SK | Industrial Sector | n/a | 82.20 | - |
| New model | SK | Industrial Sector | 91.70 | 83.78 | Debt Ratio, ROA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazanec, J.; Filip, M. Predictive Model as Screening Tool for Early Warning of Corporate Insolvency in Risk Management: Case Study from Slovak Republic. Systems 2025, 13, 1014. https://doi.org/10.3390/systems13111014
Mazanec J, Filip M. Predictive Model as Screening Tool for Early Warning of Corporate Insolvency in Risk Management: Case Study from Slovak Republic. Systems. 2025; 13(11):1014. https://doi.org/10.3390/systems13111014
Chicago/Turabian StyleMazanec, Jaroslav, and Marián Filip. 2025. "Predictive Model as Screening Tool for Early Warning of Corporate Insolvency in Risk Management: Case Study from Slovak Republic" Systems 13, no. 11: 1014. https://doi.org/10.3390/systems13111014
APA StyleMazanec, J., & Filip, M. (2025). Predictive Model as Screening Tool for Early Warning of Corporate Insolvency in Risk Management: Case Study from Slovak Republic. Systems, 13(11), 1014. https://doi.org/10.3390/systems13111014








