Multidimensional Effectiveness Evaluation of Weapon System-of-Systems Based on Hypernetwork Under Communication Constraints

Abstract

A weapon system-of-systems (WSoS) is a higher-level system comprising various functional weapon equipment systems interconnected via mutual relationships, forming a hierarchical structure that can generate overall combat effectiveness. A critical factor in assessing WSoS performance is the kill chain, and quantifying the combat effectiveness of a WSoS based on the kill chain is crucial for optimizing the system’s structure and improving the understanding of the battlefield situation, holding significant military value. Scenarios involving restricted communication (e.g., limitations in weapon system capabilities, terrain obstructions, or enemy interference) make analyzing WSoS performance challenging, so proposed here is a kill chain-based method for analyzing WSoS capability in order to address the impact of communication restrictions. Specifically, a generalized multilayer network model with information relays is used to network the WSoS, then based on this, a capability-matrix-based method for generating and analyzing the kill chain is designed. Experiments show that the proposed model and method enable effective generation and analysis of the kill chain in communication-denial situations. Furthermore, a framework for evaluating WSoS performance is established from the dimensions of mission tasks and network structure, and combat effectiveness is assessed by quantifying performance indicators based on kill chain information. Finally, case studies are used to validate the proposed algorithm and show its reliability.

1. Introduction

The new form of confrontation in modern warfare under informatized conditions involves defense and offense among multiple weapon systems on both sides, unfolding in the integrated five domains of sea, land, air, space, and cyber, and key to achieving victory is situational control of the operational system [1,2,3]. The main steps in the process for designing a weapon system-of-systems (WSoS) are system modeling, evaluation, and optimization. The basic approach is to build a networked model of the WSoS, using the kill chain (KC) as the fundamental element for measuring the system’s effectiveness, and then constructing a multi-objective optimization problem for the system structure design [4,5,6]. Therefore, key components of WSoS design are KC generation and combat-effectiveness evaluation. However, communication-restricted combat situations create a more complex WSoS structure [7,8], therefore requiring more-effective methods for analyzing system capability.

Because of the complexity of real-world combat scenarios, the strong interconnections therein, and the varying information elements among different combat stages, a networked WSoS representation is effective for quantifying the relationships among these stages and capturing KC information from the operational environment. However, the redundancy and constraints in path search within the kill web make obtaining an effective KC very challenging. Cares [9] categorized combat forces into enemy targets, decision entities, sensor entities, and influence entities, thereby creating the Information Age Combat Model (IACM) to represent the complex information flow among these four types of entities. Dekker [10] described the heterogeneity of combat networks and constructed the FINC (force, intelligence, networking, and C2) model that divides combat entities into force nodes, intelligence nodes, and command-and-control nodes, with the information flow among entities represented by lines or arcs. To simulate the real battlefield more accurately, networked WSoS models were developed sequentially [11,12,13], based on which Chen et al. [14] and Tan et al. [15] integrated reconnaissance equipment, decision-making equipment, strike equipment, and enemy targets into a closed loop to form the KC. Qi et al. [16] proposed a combat-network construction algorithm to generate a distributed combat-system network topology model; the constructed combat network model includes the condition of information relays but does not specify the constraints or implementation details of these relays, focusing solely on building the distributed combat-system network topology. Based on the standard KC form, various types of KCs were studied primarily, such as those considering coordination and information sharing [17,18]; however, those models ignored the fact that a single combat stage could be performed by multiple entities working together, limiting the KC acquisition to a simplified form. Furthermore, using higher-order adjacency matrix methods provides only the KC quantity, leaving insufficient the quantification of the KC information of the WSoS. Graph path searching [19] can reveal the KC’s structure, thereby quantifying its effectiveness, but a lack of structural constraints can lead to many redundant chains, thus impacting the evaluation of WSoS effectiveness. However, in real-world combat scenarios, alongside inherent limitations in equipment capabilities and uncontrollable factors such as weather, there are also random variables such as enemy interference and terrain obstructions, which restrict the transmission of both perception and decision-making information. Therefore, the primary motivation herein is to construct a networked model of a WSoS under communication constraints and to acquire all KCs that are both sufficient and meet the necessary constraints.

The KC is the basic unit that forms combat events and is also a fundamental component of evaluating WSoS combat effectiveness. Generating the KCs of a WSoS can quickly capture key information in the battlefield situation, providing data support for networked effectiveness evaluation. Li et al. [12] extended the concept of natural connectivity to directed combat networks and proposed directed natural connectivity to measure the robustness of the CNWSOS (combat network of WSoS) network model. Many studies have addressed the robustness analysis of complex networks by introducing various evaluation metrics, such as vertex (edge) connectivity, fault diameter, isoperimetric number, scattering number, toughness, expansion parameters, algebraic connectivity, and natural connectivity [10,20,21,22,23,24]. However, most of these measures are focused on the structural connectivity of complex networks, with few studies addressing robustness from a functional perspective [25,26]. Furthermore, based on the IACM model, Cares [9] calculated the Perron–Frobenius eigenvalue of the combat network’s adjacency matrix to measure combat efficiency. Similarly, Deller [27] validated the effectiveness of the Perron–Frobenius eigenvalue in assessing the robustness of forces within the combat network by establishing an agent-based simulation model. However, most of those studies considered only the topological structure of the combat network, neglecting the capabilities and cooperation of functional entities when evaluating robustness [28,29]. Di et al. [30] analyzed the robustness of heterogeneous military organizations by quantifying the combat loops within combat networks. Nevertheless, the proposed metrics have high computational complexity and are ill suited for large-scale network applications. Because modern warfare involves offensive and defensive confrontation between the systems on both sides, evaluating the effectiveness of a WSoS based solely on its own capabilities is not sufficiently comprehensive. Therefore, the second motivation herein is to establish an evaluation framework for WSoS effectiveness by considering both sides’ strategies from multiple dimensions, particularly using networked models and KC information for effective assessment.

The aim herein is to provide a solution for the generation and effectiveness evaluation of WSoS KCs under communication constraints. Based on the above theoretical background, the main contributions of this research are as follows.

(1)

A generalized multilayer network model that includes information relays is proposed, and based on combat characteristics, a directed multilayer network model is designed to construct a capability matrix for quantifying a WSoS. Unlike existing relay-less network models and adjacency-matrix quantification methods [11,13], under communication-constrained conditions, this approach integrates combat segment capability information by compensating for missing information relay relationships, thereby providing strong data support for networked effectiveness evaluation.

(2)

Considering time and probability constraints, a KC generation and analysis method is proposed. Based on this, an effectiveness-evaluation index framework for a WSoS is constructed from the two dimensions of mission tasks and network structure. It includes the effectiveness of both the red force’s (explained later) own structure and its execution of combat tasks. Unlike other methods [15,17,19], KCGA simultaneously considers the time and probability constraints of combat loops and individual combat segments, thereby simplifying the KC generation process. The resulting KC information is more accurate and complete, providing support for the networked effectiveness evaluation of the WSoS.

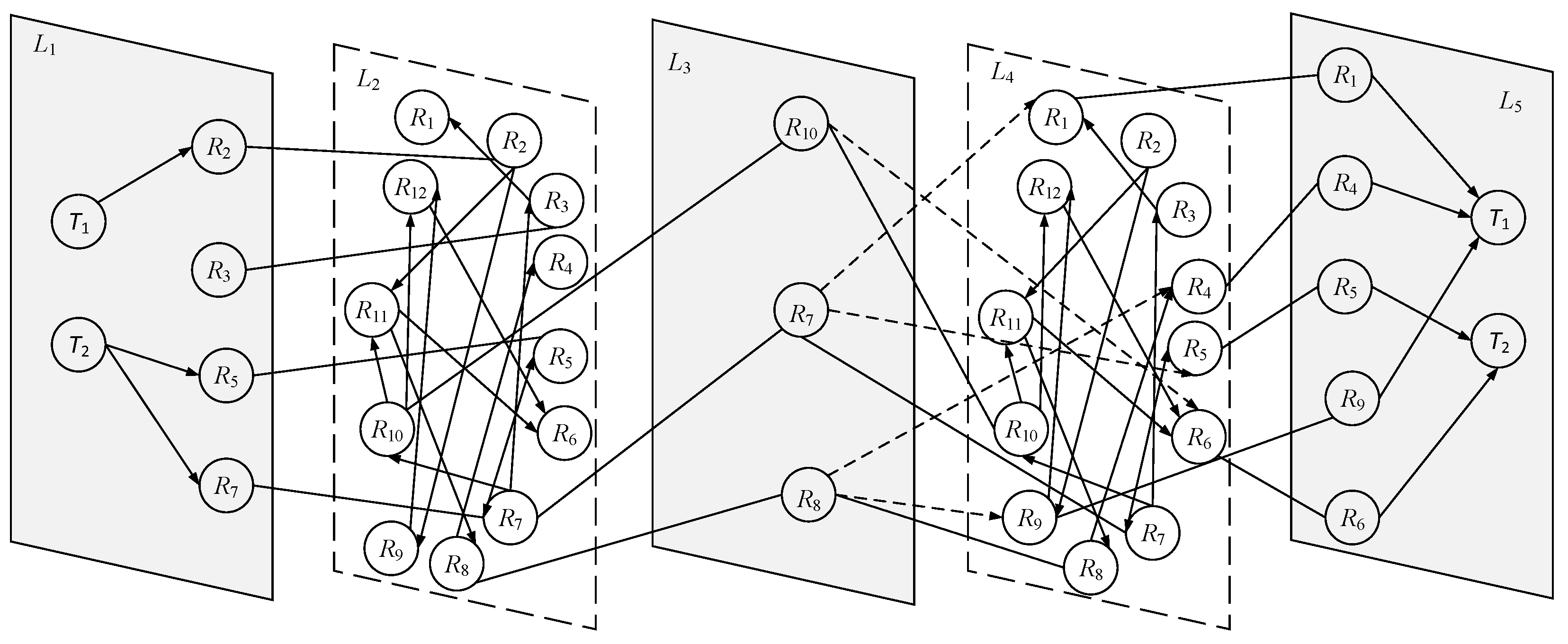
2. Construction of Networked Model for WSoS

2.1. Construction of Supernetwork Model with Information Relays

The primary form of warfare in the information age is system-of-systems warfare, where systems comprise numerous independent units with specific functions interacting with each other, creating a large and complex system with defined capabilities. From a topological perspective, this forms a complex network in which single-function entities or multifunctional integrated entities serve as nodes, while energy, information, and cognitive interactions among entities form the edges. These nodes themselves are also complex networks, characterized by multilevel, multidimensional, multitiered, multi-attribute, and multi-objective features. As a result, complex networks are essentially networks of networks that self-organize and integrate various types of networks, also referred to as a system’s supernetwork. By transforming the system structure into a supernetwork, graph-theory characterization of complex networks can be used to represent the system, thereby enabling the system model to be matrixed and its entity elements digitized.

A supernetwork [31] is a multi-edge heterogeneous network that connects various types of nodes according to the direction of information transmission, emphasizing overall functionality. This network can be divided into multiple interacting complex networks based on the attributes of its nodes or links, and it can be represented as

$$M=(E,L),$$

(1)

where M represents the supernetwork graph model, as shown in Figure 1a; $L={\left\{L_{\alpha }\right\}}_{\alpha =1}^d$ is the set of d complex networks $L_{\alpha }$ in the supernetwork, with complex network layer $\alpha$ consisting of nodes $R_i^{\alpha }$ and the edges among them. Each complex network can represent a specific link of information transmission based on the actual problem’s requirements, and they are formed sequentially according to the order of information transmission. E represents the set of edges within all complex networks in the supernetwork and among different complex networks. The interlayer relationships are divided into two types: Solid lines represent the interactions between adjacent complex network layers, while dashed lines represent the interactions between the current complex network and non-adjacent complex networks. Therefore, the supernetwork requires the construction of models for nodes and edges within each complex network layer, as well as the interaction relationships among the layers of different complex networks. A single-layer complex network $L_{\alpha }$ refers to a network comprising nodes of the same type and their interactions, which can be represented as

$$G_{\alpha }=\left(V_{\alpha },E_{\alpha }\right),$$

(2)

where $V_{\alpha }=\left\{\left(R_i^{\alpha },L_{\alpha }\right)\mid L_{\alpha }\in L,i\in [1,2,\cdots ,n]\right\}$ is the set of nodes in the complex network $L_{\alpha }$, $R_i^{\alpha }$ is the set of nodes in $L_{\alpha }$, $\left|V_{\alpha }\right|=n$ is the number of nodes in the network, and $E_{\alpha }=\left\{\left(R_i^{\alpha },R_j^{\alpha }\right)\mid i,j\in [1,2,\cdots ,n],i\ne j\right\}$ represents the interaction edges among the nodes in the network, with corresponding values as the link weights.

The interlayer relationships of the supernetwork refer to the cross-layer transmission of information. This mode of information transmission requires that the starting nodes in the upper-layer network and the terminal nodes in the lower-layer network can exchange information directly. If communication is restricted, then this will affect the interaction of information between adjacent layers, resulting in the loss of information transmission paths. To enhance the resilience of the supernetwork, a relay complex network $L_{relay}$ is designed to indirectly transmit information between adjacent layers, as shown in Figure 1b. $L_{relay}$ contains all nodes with information transmission functions, and its definition is the same as that of $L_{\alpha }$. At this point, the interlayer relationships represent the mapping of the same equipment across different layers, i.e., the starting nodes are $R_3^{\beta }=R_3^{relay},R_4^{\beta }=R_4^{relay},R_5^{\beta }=R_5^{relay}$, and the terminal nodes are $R_{14}^{\beta +1}=R_{14}^{relay},R_{13}^{\beta +1}=R_{13}^{relay},R_{12}^{\beta +1}=R_{12}^{relay}$. If direct information transmission between adjacent layers is restricted, then relay links in the relay layer can be used to transmit information indirectly, thereby compensating for the link loss caused by communication constraints.

2.2. Construction of Directed Multilayer Network Model for WSoS

The functional combat network of a WSoS is a network aimed at specific combat tasks, where during operations various functional units within the WSoS transmit information through various material, energy, and information flows (functional edges) to form combat power against enemy targets. These units cooperate and work together to complete the corresponding combat tasks, forming a supernetwork interwoven with the enemy’s targets through interconnected links. According to the OODA loop (observe–orient–decide–act) combat theory [32], information-based combat is a target-oriented, directed operational activity that follows the cycle of observe–orient–decide–act, with the target as the source node and ending the cycle with the target as the sink node. Specifically, the target’s information is gathered by reconnaissance equipment, decision-making equipment issues instructions, and impact equipment takes action on the target. Therefore, the combat process is divided into three stages, i.e., reconnaissance–decision–impact, with each stage being directed and essential. Thus, the combat process can be viewed as a directed flow of information (target) from reconnaissance to strike, which is represented in the supernetwork as a directed multilayer network with layers for reconnaissance, decision-making, and impact.

In actual combat scenarios, because of equipment limitations or obstacles such as weather, terrain, or enemy interference, communication may be obstructed between reconnaissance equipment and decision-making equipment or between decision-making equipment and impact equipment. To ensure that the combat process remains complete and closed, information transmission must go through other relay equipment for indirect communication. Therefore, relay entities (C) are introduced to assist in information transmission, compensating for the loss of operational situation information. These relay entities include not only combat equipment with relay capabilities but also other multifunctional equipment with relay capabilities, such as reconnaissance entities, strike entities, and decision-making entities. The WSoS combat entities are classified in

Table 1. Classification of weapon system-of-systems (WSoS) combat entities.

Type	Name	Description	Entity Capabilities
T	Target type node	Enemy combat entity	Anti damage; counter reconnaissance; threat
S	Reconnaissance type node	Our equipment with reconnaissance, surveillance, and other functions	Communication; reconnaissance; identification
C	Communication type node	Responsible for relaying and transmitting information	Communication
D	Command type node	Our command platforms, command posts, or command centers responsible for war command	Communication; information processing
I	Influence type node	A weapon platform or weapon system that causes damage or severe disruption to enemy targets	Communication; firepower strike

.

The WSoS is described using two factions, red and blue. The blue side has m pieces of equipment, while the red side has n pieces: The equipment of the blue side is represented by the set $T=\left\{T_1,T_2,\cdots T_m\right\}$, and that of the red side is represented by the set $R=\left\{R_1,R_2,\cdots R_n\right\}$. If the red side’s equipment $R_i$ has reconnaissance capability, then it is represented by $S_i$; similarly, if $R_i$ has communication, command, or strike capability, then it is represented by $C_i$, $D_i$, or $I_i$, respectively. The difference in the importance of enemy targets affects the WSoS capability analysis. Let $w_t\in [0,1],0\le t\le m$ represent the importance level of target t, and it satisfies ${\sum }_{t=1}^m{w}_t=1$.

From the above discussion, it can be seen that under communication-constrained conditions, the transmission of combat information not only relies on the basic reconnaissance, command, and strike layer networks but also depends on necessary information relays. Therefore, the WSoS directed multi-layer complex network is divided into five interacting networks based on the actual direction of information transmission in combat: the reconnaissance network ($L_1$), relay network ($L_2$), command network ($L_3$), relay network ($L_4$), and strike network ($L_5$). $L_2$ and $L_4$ serve as the media for transmitting reconnaissance and decision-making information, respectively. The quantification of the WSoS’s directed multi-layer network includes the construction of both intra-layer and inter-layer relationships. Intra-layer relationships can be quantified using the adjacency matrix concept in graph theory, while inter-layer relationships can be described based on the construction mechanism of the relay layer in the hypernetwork model and the characteristics of combat information.

2.3. Directed Multilayer Network Model Capability Matrix Representation

In a multilayer network, the intra-network relationship refers to the interactions and connections among nodes within $L_{\alpha }$, including connectivity probability and time metrics. Using the adjacency matrix to represent intra-network relationships not only allows for easy retrieval of connectivity characteristics between any two nodes in the network but also enables the study of various properties of complex networks via matrix analysis. However, traditional 0–1 matrices (0 indicating no connectivity and 1 indicating connectivity) no longer fully meet the requirements for representing multiple attributes among nodes. Therefore, constructing the complex network capability matrices $A^p$ and $A^t$ quantifies the connectivity probability and time attributes of equipment in the WSoS, providing data support for evaluating its effectiveness.

2.3.1. Reconnaissance Layer $L_1$

The reconnaissance layer comprises red-side entities and enemy targets, performed primarily by sensor entities tasked with reconnaissance and surveillance of enemy targets. We define the effective reconnaissance probability threshold $P_{inv}$. The closure probability capability matrix for the reconnaissance layer is $A_{L_1}^p={\left[p_{ij}^{L_1}\right]}_{m\times n}$, where $p_{ij}^{L_1}$ represents the probability of reconnaissance equipment $R_j$ detecting target $T_i$:

$$p_{ij}^{L_1}=\left\{\begin{array}{cc}\hfill p_{ij}^{L_1}& p_{ij}^{L_1}\ge P_{inv}\\ \hfill 0& \mathrm{others}\end{array}\right.$$

(3)

We define the effective reconnaissance time threshold $T_{inv}$. The closure time capability matrix for the reconnaissance layer is $A_{L_1}^t={\left[t_{ij}^{L_1}\right]}_{m\times n}$, where $t_{ij}^{L_1}$ represents the time required for reconnaissance equipment $R_j$ to detect target $T_i$:

$$t_{ij}^{L_L}=\left\{\begin{array}{c}{t}_{ij}^{L_1}{t}_{ij}^{L_1}\le T_{inv}\\ \mathrm{null}\mathrm{others}\end{array}\right.$$

(4)

If $t_{ij}^{L_1}$ does not meet the threshold requirement, it indicates that the reconnaissance time is meaningless and is represented as null. If we consider only whether the entities in the reconnaissance layer can be connected, then the adjacency matrix for the reconnaissance layer is $A_{L_1}={\left[q_{ij}^{L_1}\right]}_{m\times n}$, where $q_{ij}^{L_1}=1$ indicates connectivity, and 0 indicates no connectivity:

$$q_{ij}^{L_1}=\left\{\begin{array}{cc}1& p_{ij}^{L_1}\ge P_{inv},t_{ij}^{L_1}\le T_{inv}\\ 0& \mathrm{others}\end{array}\right.$$

(5)

2.3.2. Relay Layers $L_2$ and $L_4$

The relay network is composed of Red team entities and is primarily responsible for information transmission tasks carried out by Red team equipment with communication capabilities. Define the node effective communication probability judgment threshold $P_{com}$, then the relay layer closure probability adjacency matrix is $A_{L_2}^p=A_{L_4}^p={\left[p_{ij}^{L_2}\right]}_{n\times n}$, where $p_{ij}^{L_2}$ represents the stability of communication between equipment $R_i$ and equipment $R_j$.

$$p_{ij}^{L_2}=\left\{\begin{array}{cc}{p}_{ij}^{L_2}& p_{ij}^{L_2}\ge P_{com}\\ 0& \mathrm{others}\end{array}\right.$$

(6)

Define the node effective communication time judgment threshold $T_{com}$, then the relay layer closure time adjacency matrix is $A_{L_2}^t=A_{L_4}^t={\left[t_{ij}^{L_2}\right]}_{n\times n}$, where $t_{ij}^{L_2}$ represents the time required for equipment $R_i$ and equipment $R_j$ to establish communication. If the threshold requirement is not met, it is represented as null, meaning it is meaningless.

$$t_{ij}^{L_2}=\left\{\begin{array}{cc}{t}_{ij}^{L_2}\hfill & t_{ij}^{L_2}\le T_{com}\\ \mathrm{null}\hfill & \mathrm{others}\end{array}\right.$$

(7)

If only the ability of equipment to establish communication is considered, the relay layer link count adjacency matrix is $A_{L_2}=A_{L_4}={\left[q_{ij}^{L_2}\right]}_{n\times n}$, where $q_{ij}^{L_2}$ = 1 indicates that communication can be established, and $q_{ij}^{L_2}$ = 0 indicates that communication cannot be established.

$$Q_{ij}^{L_2}=\left\{\begin{array}{cc}1& p_{ij}^{L_2}\ge P_{com},t_{ij}^{L_2}\le T_{com}\\ 0& \mathrm{others}\end{array}\right.$$

(8)

The interactive edge between the reconnaissance network and the relay network is denoted as $E_{L_1-L_2}=\left\{\left(S_j\to C_j\right)\mid q_{ij}^{L_1}=1\right\}$, which represents the different mappings of the red side’s equipment $R_j$ that detects enemy entities in the reconnaissance and relay networks, at which point $R_j=S_j=C_j$.

2.3.3. Command Layer $L_3$

The command network is composed of Red team entities and is primarily responsible for the tasks of command and control carried out by decision-making entities. Define the effective command probability judgment threshold $P_{cc}$, then the command layer closure probability capability matrix is $A_{L_3}^p={\left[p_{ij}^{L_3}\right]}_{n\times n}$, where $p_{ij}^{L_3}$ represents the accuracy of the command equipment $R_i$ issuing command information to the strike equipment $R_j$.

$$p_{ij}^{L_3}=\left\{\begin{array}{cc}\hfill p_{ij}^{L_3}& p_{ij}^{L_3}\ge P_{cc}\\ \hfill 0& \mathrm{others}\end{array}\right.$$

(9)

Define the effective command time judgment threshold $T_{cc}$, then the command layer closure time capability matrix is $A_{L_3}^t={\left[t_{ij}^{L_3}\right]}_{n\times n}$, where $t_{ij}^{L_3}$ represents the time required for command equipment $R_i$ to issue command information to strike equipment $R_j$. If the threshold requirement is not met, it is represented as null, meaning it is meaningless.

$$t_{ij}^{L_3}=\left\{\begin{array}{cc}{t}_{ij}^{L_3}\hfill & t_{ij}^{L_3}\le T_{cc}\hfill \\ \mathrm{null}\hfill & \mathrm{others}\hfill \end{array}\right.$$

(10)

If only the accuracy of the command information is considered, the link count capability matrix is $A_{L_3}={\left[q_{ij}^{L_3}\right]}_{n\times n}$, where $q_{ij}^{L_3}$ = 1 indicates that the command information is accurate, and $q_{ij}^{L_3}$ = 0 indicates that the information is unavailable.

$$q_{ij}^{L_3}=\left\{\begin{array}{cc}1& p_{ij}^{L_3}\ge P_{cc},t_{ij}^{L_3}\le T_{cc}\\ 0& \mathrm{others}\end{array}\right.$$

(11)

The interaction edge between the relay network and the command network is $E_{L_2-L_3}=\left\{\left(C_i\to D_i\right)\mid a_{ij}^{L_3}=1\right\}$, representing the different mappings of the Red team equipment $R_i$ that received the perception information in the relay network and the command network, with $R_i=C_i=D_i$ at this time.

2.3.4. Strike Layer $L_5$

The strike network is composed of Red team entities and enemy targets, and is primarily responsible for the tasks of striking enemy targets and performing electromagnetic interference carried out by influencing entities. Define the effective strike probability judgment threshold $P_{act}$, then the strike layer closure probability capability matrix is $A_{L_5}^p={\left[p_{ij}^{L_5}\right]}_{n\times m}$, where $p_{ij}^{L_5}$ represents the probability of strike equipment $R_i$ hitting target $T_j$.

$$p_{ij}^{L_5}=\left\{\begin{array}{cc}{p}_{ij}^{L_5}& p_{ij}^{L_5}\ge P_{act}\\ 0& \mathrm{others}\end{array}\right.$$

(12)

Define the effective strike time judgment threshold $T_{act}$, then the strike layer closure time capability matrix is $A_{L_5}^t={\left[t_{ij}^{L_5}\right]}_{n\times m}$, where $t_{ij}^{L_5}$ represents the time required for strike equipment $R_i$ to hit target $T_j$. If the threshold requirement is not met, it is represented as null, meaning it is meaningless.

$$t_{ij}^{L_5}=\left\{\begin{array}{cc}{t}_{ij}^{L_5}& t_{ij}^{L_5}\le T_{act}\\ \mathrm{null}& \mathrm{others}\end{array}\right.$$

(13)

If only the connectivity between entities in the strike layer is considered, the link count capability matrix is $A_{L_5}={\left[q_{ij}^{L_5}\right]}_{n\times m}$, where $q_{ij}^{L_5}$ = 1 indicates a successful strike, and $q_{ij}^{L_5}$ = 0 indicates a strike failure.

$$q_{ij}^{L_5}=\left\{\begin{array}{cc}1& p_{ij}^{L_5}\ge P_{act},t_{ij}^{L_5}\le T_{act}\\ 0& \mathrm{others}\end{array}\right.$$

(14)

According to the command rules, the command information needs to be transmitted to the strike equipment in order to complete the actual command. The transmission of command information involves a source node (the command node) and a destination node (the accused node), with the information being relayed between the two. Therefore, the interactive edge between the command and relay networks includes not only the command relationship $E_{L_3-L_4}^D$, where command information is transmitted to strike equipment, but also the relay relationship $E_{L_3-L_4}^C$ for command information. Thus, according to the command relationship, $E_{L_3-L_4}^D=\left\{\left(D_i\to I_j\right)\mid q_{ij}^{L_3}=1\right\}$ is used to specify the source and destination nodes of the command link, representing a virtual interlayer interaction relationship. $E_{L_3-L_4}^C=\left\{\left(D_i\to C_i\right)\mid q_{ij}^{L_3}=1\right\}$ is used to define the relay relationship of the command link, transmitting command information to the accused equipment. Therefore, the same equipment in different layers is used to represent interlayer relationships, which constitute the actual interlayer interaction relationship. The interaction edge between the relay network and the strike network is $E_{L_4-L_5}=\left\{\left(C_i\to I_i\right)\mid q_{ij}^{L_5}=1\right\}$, representing the different mappings of the Red team equipment $R_i$ that received the decision information in the relay network and the strike network, with $R_i=C_i=I_i$ at this time.

3. Networked Effectiveness Evaluation Based on Kill Chains

3.1. Kill Chain and Constraint Construction

The KC is a product of information warfare, typically referring to the closed-loop process of detecting a target, targeting the target, engaging the enemy, and assessing the results of the engagement. Based on the OODA loop operational theory, the WSoS’s ability to strike enemy targets effectively is due to the continuous directed combat activities performed by our side’s nodes on the target nodes within the combat network, following the sequence of detect–perceive–decide–strike. The continuous path of the target nodes and combat activities involved in this process is defined as the KC within the WSoS network. If each combat activity is completed by a single node, i.e., the continuous path $T\to S\to D\to I\to T$ from the target node via reconnaissance–decision–impact pointing to the target node, then this type of KC is defined as one of standard form as shown in Figure 2.

For equipment entities with communication limitations, the standard KC model no longer fully meets the requirements in a directed multilayer network. The KC should be a continuous path starting from the target node and passing through the operational activities of reconnaissance–relay–decision–relay–impact leading to the target node, which can be represented as $T\to S\to C^{S-D}\to D\to C^{D-I}\to I\to T$. Here, $C^{S-D}$ and $C^{D-I}$ represent the sets of red-side nodes required for the perception information and decision information relays, respectively.

Multiple relays of information may lead to an explosive growth in the number of KCs, resulting in many redundant chains during network searches. Closing the KC requires the efficient transmission of situational information, necessitating further constraints on the KC structure. When acquiring KCs, those that do not meet the constraint conditions should be filtered out. The completeness constraint is that the KC must simultaneously include nodes of types S, D, I, and T, otherwise the link cannot form a closed loop. The redundancy constraint is that the communication link between S and D cannot use S or D as relay nodes, and similarly neither can the communication link between D and I. If any two nodes on the KC are directly connected in the relay adjacency matrix, then they must also be directly connected in the relay link, otherwise it will cause a “communication detour,” affecting the closure of the KC. The capability constraint is that the KC and each combat segment of which it consists should satisfy time and probability constraints.

3.2. Constraint-Based Kill Chain Generation Algorithm

To address the issue of complex connectivity relationships and redundant information relays in a WSoS, we propose a capability-constrained KC generation algorithm (KCGA) to obtain all chains that satisfy the KC constraints, as shown in Algorithm 1. To increase the KC search efficiency, we consider the special structure of the WSoS supernetwork model, which is split into upper (reconnaissance and command networks) and lower (command and strike networks) layers with the command network $L_3$ acting as the watershed. The KC structure that satisfies the constraints is searched for separately for each layer based on the connectivity relationships in the adjacency matrix of the equipment. Finally, the links between the upper and lower layers are established based on link characteristics, and all the KCs that meet the requirements are obtained.

Algorithm 1: KCGA

KCGA uses the WSoS’s capability matrix as input and ultimately obtains all the KCs that meet the constraint requirements. First, the current network state is checked to see whether it meets the conditions for generating a KC (line 1), i.e., whether there is an intersection between the target set $T_S$ detected by reconnaissance nodes and the target set $T_I$ struck by impact nodes. If there is an intersection, then the WSoS may have a KC; otherwise, KCGA returns an empty list of $KC$. After the condition is satisfied, the upper and lower layers of the network are simultaneously searched for links, and the reconnaissance nodes and strike nodes are connected via command relationships (line 2). The perception and decision information intermediaries are the same command node, initializing two link dictionaries $C^{S-D}$ (upper layer) and $C^{D-I}$ (lower layer) (line 4). The relay link generation algorithm (RCGA) is then executed for both perception information relay (line 7) and decision information relay (line 12) to obtain the links $C^{S-D}$ and $C^{D-I}$ that satisfy the time and probability constraints (lines 5–13). Only when the tail node of the link in $C^{S-D}$ and the head node of the link in $C^{D-I}$ are the same command node can the links be connected to form a KC. All links in $C^{S-D}$ and $C^{D-I}$ are traversed (lines 14–24). For all links in $C^{S-D}$ starting from $node2$, the common target set $T_{common}$ with links in $C^{D-I}$ ending at $node3$ is obtained (line 16). For each target in $T_{common}$, the connection among segment links is established. Specifically, for the target that can be detected by $node2$ and struck by $node3$ (line 17), the link $C^{S-D}$[$node2$] starting from $node2$ and the link $C^{D-I}$[$node3$] ending at $node3$ are concatenated to form a KC $K{C}_c$ (line 18). If this link satisfies the time constraint $T_{thre}$ and the probability constraint $P_{thre}$ (line 19), then it is added to $KC$ (line 20). The same approach is used to concatenate links in $C^{S-D}$ and $C^{D-I}$, and finally, all the KCs that meet the requirements are returned (line 25). Relay links are an important component of the KC. Considering the redundancy constraints and capability constraints related to the KC set for specific targets, the KC constraint conditions are combined with the layer search algorithm [19] to design RCGA, as shown in Algorithm 2.

Algorithm 2: RCGA

RCGA can perform a search for all nonredundant paths in any connectivity matrix. The algorithm takes as input the capability matrix of the relay network, a layer list $layer$, a layer path list $layerPath$, and a set of visited nodes $existList$, ultimately obtaining all paths from the start node S to the end node E that satisfy the requirements. $layer$ records the nodes present at each layer during the search process, $layerPath$ records the paths after traversing each layer, and $existList$ records the nodes that have already been processed by the algorithm. Intermediate variable sets $next$-$existed$, $next$-$path$, and $next$-$layer$ are established to record the elements of $existList$, $layerPath$, and $layer$, respectively (line 1), and the start node E is added to $layer$ (line 2). For each node $node$ in the current layer $layer$ (line 5), the directly connected node set $node$-$set$ is found based on the connectivity matrix $A_{L_2}$ (line 6). If the start node s is in $node$-$set$ and the composed path satisfies the time constraint $T_{thre}$ and probability constraint $P_{thre}$ (line 7), then the path search ends at the current layer and the path [S, $layer$-$path$] is returned (line 8). Otherwise, it is checked whether $node$ has been visited in $existed$-$list$; if it has not been visited and the composed path satisfies the time constraint $T_{thre}$ and probability constraint $P_{thre}$ (line 10), then $node$ is added to $next$-$existed$ and $next$-$layer$ as a visited node and as a starting node for the next layer search, and $node$ is added to the path $layer$-$path$ (line 11). $existList$, $layerPath$, and $layer$ are updated according to the search method described above (line 15) until no elements remain in $layer$ for visitation, at which point the relay link set $RC$ is returned (line 17). For KC i, i.e., $K{C}_i[R_1\to R_2\to \cdots \to R_n]$, its closure time $KC{T}_i$ and closure probability $KC{P}_i$ can be obtained via the time capability matrix and probability capability matrix as follows:

$$KC{T}_i=\sum _{j=1}^{n-1}{t}_{j,j+1}^{L_{\alpha }},\alpha \in \{1,2,3,4,5\},$$

(15)

$$KC{P}_i=\prod _j^{n-1}{p}_{j,j}^{L_{\alpha }},\alpha \in \{1,2,3,4,5\}.$$

(16)

The outer loop of Algorithm 2 requires traversing up to n layers in the worst case, where n is the number of red-side nodes. The inner loop processes n nodes per iteration, which is the maximum number of red-side nodes per layer. The time complexity of a single inner loop operation is $O\left(1\right)$. Therefore, the time complexity of the basic traversal part is $O\left(n^2\right)$. When considering the additional overhead of concatenating relay link paths, in the worst case, all possible paths need to be recorded, resulting in a time complexity of $O(n^2+P\times L)$, where P is the total number of paths and L is the average path length. However, RCGA focuses more on finding valid relay chains rather than recording all paths, so the core complexity is $O\left(n^2\right)$.

Algorithm 1 consists of Part 1 (lines 5–8), Part 2 (lines 9–13), and Part 3 (lines 14–24), where Part 1 and Part 2 have the same structure and thus the same time complexity. In the worst case, Part 1 needs to traverse n nodes, which are all the red-side nodes. The time complexity of RCGA is $O\left(n^2\right)$, so the time complexity of Part 1 is $O\left(n^3\right)$. In Part 3, lines 14 and 15, in the worst case, the number of nodes to be traversed is n, and in line 17, the number of common targets to be traversed is m. Let $q_1$ and $q_2$ be the sizes of $C^{D-I}.keys\left(\right)$ and $C^{S-D}.keys\left(\right)$, respectively, then the time complexity of Part 3 is $O(n^2\times q_1\times q_2\times m)$. Considering that the outer loop needs to traverse n nodes in the worst case, the time complexity of Algorithm 1 is $O(n^3\times m\times q_1\times q_2+n^4)$. Since the time complexity is dominated by the term with the fastest-growing rate, the time complexity of Algorithm 1 can be approximated as $O\left(n^4\right)$.

3.3. Construction of Multidimensional Performance Evaluation Index System

We construct and analyze the WSoS to maintain the stability of its own operational system structure while effectively striking the enemy, meaning that the operational system must maintain the stability of its structure as well as the accuracy and speed of performing combat tasks. For the quantitative supernetwork performance evaluation of the WSoS, on one hand, it is necessary to fully describe and reflect the characteristics of the system structure, and on the other hand, it is crucial to focus on the system’s ability to carry out tasks. The WSoS performance evaluation index framework is constructed from two aspects, i.e., mission task performance and network structure performance, as shown in

Table 2. WSoS effectiveness evaluation indicator framework.

Indicator Type	Indicator Decomposition	Key Quantitative Parameters	Indicator Explanation
Network structure performance	Survivability	N	Number of KCs
		$N_{R_i}$	Number of KCs after $R_i$ is destroyed
	Redundancy	N	Number of KCs
	Communication efficiency	$A_{L_2}$	Adjacency matrix of relay layer
Mission task performance	Task kill chain matching degree	$KCP$	Closure probability of each kill chain
		$w_i$	Importance of each target
	Task completion time	$KCT$	Closure time of each kill chain
	Task completion probability	$KCP$	Closure probability of each kill chain

. Mission task performance is measured by task KC matching degree, task completion time, and task completion probability to assess the accuracy and speed of task execution during operations. Network structure performance is measured by survivability, redundancy, and communication efficiency to evaluate the stability of the operational system. In practical applications, the effectiveness of a kill web could be quantified at different granularities based on varying needs. [33] defines the effectiveness of the WSoS as its ability to complete predetermined combat tasks. This is achieved by considering the probability of a connected loop existing within the kill web under conditions of random failure of edges and nodes, thus converting the effectiveness of the WSoS into network reliability for analysis. This paper analyzes the effectiveness of the WSoS from different granularities, dividing it into mission task performance and network structure performance. This approach provides evaluation information from different levels, allowing for comprehensive analysis of the WSoS. Therefore, the mission task performance evaluation index proposed in this paper is suitable for combat scenarios in red–blue adversarial games, where it measures the accuracy and speed of task execution during combat, using information about the closure of kill chains as fundamental elements. The network structure performance index is used to assess the stability of the own combat system. These two indices together measure the effectiveness of the WSoS, providing strong data support for the capability analysis and design of the kill web.

3.3.1. Mission Task Performance

(1)

The task completion time ($TCT$) represents the average time required for any of the KCs in the WSoS to successfully strike any enemy target; the smaller this value, the faster the average strike speed on a target. Suppose that there are N KCs for all targets and that target j, i.e., $T_j$ (where $j=1,2,\dots ,m$), has $N{T}_j$ KCs: $K{C}_i^{T_j}\left(i=1,2,\dots ,{\mathrm{NT}}_j\right)$. Then, we have $N=N_{T_1}+N_{T_2}+\cdots +N_{T_m}$, and $TCT$ is given as

$$TCT={\displaystyle \frac{{\sum }_{j=1}^m\left({\sum }_{i=1}^{N_{T_j}}KC{T}_{K{C}_i^{T_j}}/N_{T_j}\right)}{m}},$$

(17)

where ${\sum }_{i=1}^{N_{T_j}}KC{T}_{K{C}_i^{T_j}}$ represents the total closure time of the $N{T}_j$ KCs for a single target $T_j$, and ${\sum }_{i=1}^{N_{T_j}}KC{T}_{K{C}_i^{T_j}}/N_{T_j}$ represents the average time required to execute task $T_j$ by selecting any one of the $N{T}_j$ KCs. Using the same method, the average task completion time for all targets can be calculated, and by taking the average of all targets, the average time required for selecting any KC to execute any task across all links is obtained.

(2)

The task completion probability ($TCP$) represents the average reliability with which any of the KCs in the WSoS can successfully strike any enemy target; the larger this value, the greater the probability of successfully striking a target. We have

$$TCP={\displaystyle \frac{{\sum }_{j=1}^m\left({\sum }_{i=1}^{N_{T_j}}KC{P}_{K{C}_i^{T_j}}/N_{T_j}\right)}{m}},$$

(18)

where ${\sum }_{i=1}^{N_{T_j}}KC{P}_{K{C}_i^{T_j}}$ represents the sum of the closure probabilities of the $N{T}_j$ KCs for a single target $T_j$, and ${\sum }_{i=1}^{N_{T_j}}KC{P}_{K{C}_i^{T_j}}/N_{T_j}$ represents the average reliability of completing task $T_j$ using any one of the $N{T}_j$ KCs. Using the same method, the average reliability for all targets can be calculated, and by taking the average of all targets, the average reliability for selecting any KC to execute any task across all links is obtained.

(3)

The KC task matching degree (TMD) describes the matching relationship between the average quality of KCs assigned to each target and the importance of the target. If the target node being struck is considered more important and the probability of successfully striking the target is greater, then the KC TMD is higher; conversely, the TMD is lower. We have

$$TMD=\sum _{t=1}^m\left(1-\left|{\displaystyle \frac{{\sum }_{i=1}^{N_{T_t}}KC{P}_{K{C}_i^{I_t}}}{{\sum }_{j=1}^m{\sum }_{i=1}^{N_{T_j}}KC{P}_{K{C}_i^{{\tau }_j}}}}-{\displaystyle \frac{w_t}{{\sum }_{i=1}^m{w}_i}}\right|\right)/m,$$

(19)

where ${\sum }_{i=1}^{N_{T_t}}KC{P}_{K{C}_i^{T_t}}$ represents the sum of the closure probabilities of all KCs assigned to target $T_t$, and ${\sum }_{j=1}^m{\sum }_{i=1}^{N_{T_j}}KC{P}_{K{C}_i^{{\tau }_j}}$ represents the sum of the closure probabilities of all KCs in the WSoS; the ratio of these two values gives the average quality of KCs assigned to the target. Meanwhile, $w_t$ represents the importance weight of target $T_t$, and ${\sum }_{i=1}^m{w}_i$ represents the sum of the importance weights of all targets in the WSoS; the ratio of these two values gives the average importance of target $T_t$. The smaller the difference between these two values, the more balanced the KC allocation, and the higher the KC TMD for task $T_t$. The average of all targets gives the overall average matching degree between the KC average quality and the target importance for all targets.

3.3.2. Network Structure Performance

(1)

Survivability. The risk $NRK$ of the WSoS represents mainly the impact on the entire kill web after a friendly node is attacked; the fewer the KCs lost by the targets when a friendly node is destroyed and unable to participate in the WSoS’s interaction, the lower the risk. We have

$$NRK={\displaystyle \frac{{\sum }_{i=1}^n\left(N-N_{R_i}\right)}{n}},$$

(20)

where N represents the number of KCs before destruction, and $N_{R_i}$ represents the number of remaining KCs after equipment $R_i$ is destroyed; the difference between these two values is the number of KCs lost. Using the same method, the number of KCs lost after the destruction of all equipment can be calculated, and the average of these values gives the average number of KCs lost when a particular piece of equipment is destroyed in the supernetwork.

(2)

Redundancy. Given by $NRD$, this characterizes mainly the degree of diversification of available strike means for a target in the WSoS, as given by

$$NRD={\displaystyle \frac{N}{m}}.$$

(21)

The specific evaluation approach is to calculate the average number N of KCs that can be formed by a multilayer network for m targets. The more KCs that there are, the stronger the redundancy; conversely, the fewer the KCs, the weaker the redundancy.

(3)

Communication efficiency. The network communication efficiency $NCE$ of the WSoS refers to the ability of various constituent systems within the operational system to seek, acquire, and provide information and services to other systems based on combat needs. The more elements in the communication adjacency matrix $A_{L_2}$ that have the value 1, the greater the communication efficiency. Therefore, the spectral norm ${∥A_{L_2}∥}_2$ can be chosen as the evaluation matrix norm for the connectivity matrix, as given by

$$NCE={\displaystyle \frac{{∥A_{L_2}∥}_2}{{∥A_{L_2}^{*}∥}_2}}.$$

(22)

Here, ${∥A_{L_2}^{*}∥}_2$ represents the spectral norm when $A_{L_2}$ is a fully connected matrix (all elements are 1), and the ratio of these two values represents the degree of connectivity in the current state compared to the optimal connectivity state.

4. Experimental Study

4.1. Scenarios

In this section, we compare two WSoS example scenarios in which the types and quantities of equipment are the same. The scenario includes 12 pieces of Red team equipment and 2 pieces of Blue team equipment. The Red team equipment includes Bombers ($R_1$, $R_6$), Drones ($R_2,R_3,R_5$), Fighters ($R_4,R_9$), Reconnaissance Aircraft ($R_7,R_{10}$), Command Ship ($R_8$), and Satellites ($R_{11},R_{12}$). The Blue team equipment consists of Destroyers ($T_1,T_2$). The interaction relationships between the pieces of equipment can be formed based on factors such as their own capabilities, position, and other constraints in the operational scenario. This paper focuses on solving the generation of the weapon system-of-systems (WSoS) kill chain and performance evaluation after determining the interaction relationships between the pieces of equipment, analyzing the impact of communication constraints on performance evaluation. Figure 3 shows the equipment connectivity relationships of the WSoS at time 1 (scenario I) and time 2 (scenario II). The arrows between pieces of equipment indicate possible connections, and the 2D vector $(p,t)$ above an arrow represents the connection characteristics, with p and t referring to the closure probability and closure time of the operational link, respectively. In scenario I, reconnaissance node $R_2$ can send perception information directly to command node $R_8$ without needing an information relay. In scenario II, because of its own limitations, $R_2$ cannot communicate directly with command node $R_8$, but the connectivity of the other pieces of equipment remains unchanged from that in scenario I. Based on the connectivity relationships of the equipment in the current scenario, a multilayer network model of the WSoS is constructed, and the capability matrix is used to quantify the situational information in the operational scenario, which is then used to evaluate the impact of communication constraints on WSoS KC generation and combat effectiveness.

4.2. Basic Experimental Results

For scenario II, the WSoS multilayer network is constructed by hierarchical node connectivity relationships, as shown in Figure 4. The intra-layer connectivity relationship is denoted by “→”, while the inter-layer connectivity relationship is denoted by “—”. Specifically, “⤏” represents the virtual interaction relationship between the command layer $L_3$ and the relay layer $L_4$, that is, the relationship where command nodes point to the commanded nodes. The capability matrices of the WSoS multilayer network are calculated as shown in

Table 3. WSoS multilayer network capability matrices.

		a Reconnaissance layer’s adjacency matrix ${\mathit{A}}_{{\mathit{L}}_1}$															b Reconnaissance layer’s closure probability capability matrix ${\mathit{A}}_{{\mathit{L}}_1}^{\mathit{p}}$
			$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$				$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$
		$T_1$	0	1	0	0	0	0	0	0	0	0	0	0			$T_1$	0	0.95	0	0	0	0	0	0	0	0	0	0
		$T_2$	0	0	0	0	1	0	1	0	0	0	0	0			$T_2$	0	0	0	0	0.75	0	0.92	0	0	0	0	0
		c Reconnaissance layer’s closure time capability matrix $A_{L_1}^t$															d Strike layer’s adjacency matrix $A_{L_5}$
			$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$				$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$
		$T_1$	null	7	null	null	null	null	null	null	null	null	null	null			$T_1$	1	0	0	1	0	0	0	0	1	0	0	0
		$T_2$	null	null	null	null	8	null	9	null	null	null	null	null			$T_2$	0	0	0	0	1	1	0	0	0	0	0	0
		e Strike layer’s closure probability capability matrix $A_{L_5}^p$															f Strike layer’s closure time capability matrix $A_{L_5}^t$
			$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$				$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$
		$T_1$	0.84	0	0	0.92	0	0	0	0	0.88	0	0	0			$T_1$	20	null	null	35	null	null	null	null	51	null	null	null
		$T_2$	0	0	0	0	0.79	0.85	0	0	0	0	0	0			$T_2$	null	null	null	null	28	42	null	null	null	null	null	null
		g Command layer’s adjacency matrix $A_{L_3}$															h Command layer’s closure probability capability matrix $A_{L_3}^p$
			$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$				$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$
		$R_1$	0	0	0	0	0	0	0	0	0	0	0	0			$R_1$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_2$	0	0	0	0	0	0	0	0	0	0	0	0			$R_2$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_3$	0	0	0	0	0	0	0	0	0	0	0	0			$R_3$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_4$	0	0	0	0	0	0	0	0	0	0	0	0			$R_4$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_5$	0	0	0	0	0	0	0	0	0	0	0	0			$R_5$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_6$	0	0	0	0	0	0	0	0	0	0	0	0			$R_6$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_7$	1	0	0	0	1	0	0	0	0	0	0	0			$R_7$	0.82	0	0	0	0.87	0	0	0	0	0	0	0
		$R_8$	0	0	0	1	0	0	0	0	1	0	0	0			$R_8$	0	0	0	0.94	0	0	0	0	0.92	0	0	0
		$R_9$	0	0	0	0	0	0	0	0	0	0	0	0			$R_9$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_{10}$	0	0	0	0	0	1	0	0	0	0	0	0			$R_{10}$	0	0	0	0	0	0.98	0	0	0	0	0	0
		$R_{11}$	0	0	0	0	0	0	0	0	0	0	0	0			$R_{11}$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_{12}$	0	0	0	0	0	0	0	0	0	0	0	0			$R_{12}$	0	0	0	0	0	0	0	0	0	0	0	0
		i Command layer’s closure time capability matrix $A_{L_3}^t$															j Relay layer’s adjacency matrix $A_{L_2}=A_{L_4}$
			$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$				$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$
		$R_1$	null	null	null	null	null	null	null	null	null	null	null	null			$R_1$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_2$	null	null	null	null	null	null	null	null	null	null	null	null			$R_2$	0	0	0	0	0	0	0	0	1	0	1	0
		$R_3$	null	null	null	null	null	null	null	null	null	null	null	null			$R_3$	1	0	0	0	0	0	0	0	0	0	0	0
		$R_4$	null	null	null	null	null	null	null	null	null	null	null	null			$R_4$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_5$	null	null	null	null	null	null	null	null	null	null	null	null			$R_5$	0	0	0	0	0	0	1	0	0	0	0	0
		$R_6$	null	null	null	null	null	null	null	null	null	null	null	null			$R_6$	0	0	0	0	0	0	0	0	0	0	0	0
		$R_7$	8	null	null	null	7	null	null	null	null	null	null	null			$R_7$	0	0	1	0	1	0	0	0	0	1	0	0
		$R_8$	null	null	null	9	null	null	null	null	10	null	null	null			$R_8$	0	0	0	1	0	0	0	0	1	0	0	0
		$R_9$	null	null	null	null	null	null	null	null	null	null	null	null			$R_9$	0	0	0	0	0	0	0	0	0	0	0	1
		$R_{10}$	null	null	null	null	null	7	null	null	null	null	null	null			$R_{10}$	0	0	0	0	0	0	0	0	0	0	1	1
		$R_{11}$	null	null	null	null	null	null	null	null	null	null	null	null			$R_{11}$	0	0	0	0	0	1	0	1	0	0	0	0
		$R_{12}$	null	null	null	null	null	null	null	null	null	null	null	null			$R_{12}$	0	0	0	0	0	1	0	1	0	0	0	0
		k Relay layer’s closure probability capability matrix $A_{L_2}^p=A_{L_4}^p$															l Relay layer’s closure time capability matrix $A_{L_2}^t=A_{L_4}^t$
			$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$				$R_1$	$R_2$	$R_3$	$R_4$	$R_5$	$R_6$	$R_7$	$R_8$	$R_9$	$R_{10}$	$R_{11}$	$R_{12}$
		$R_1$	0	0	0	0	0	0	0	0	0	0	0	0			$R_1$	null	null	null	null	null	null	null	null	null	null	null	null
		$R_2$	0	0	0	0	0	0	0	0	0.84	0	0.82	0			$R_2$	null	null	null	null	null	null	null	null	8	null	5	null
		$R_3$	0.91	0	0	0	0	0	0	0	0	0	0	0			$R_3$	7	null	null	null	null	null	null	null	null	null	null	null
		$R_4$	0	0	0	0	0	0	0	0	0	0	0	0			$R_4$	null	null	null	null	null	null	null	null	null	null	null	null
		$R_5$	0	0	0	0	0	0	0.85	0	0	0	0	0			$R_5$	null	null	null	null	null	null	6	null	null	null	null	null
		$R_6$	0	0	0	0	0	0	0	0	0	0	0	0			$R_6$	null	null	null	null	null	null	null	null	null	null	null	null
		$R_7$	0	0	0.77	0	0.87	0	0	0	0	0.79	0	0			$R_7$	null	null	3	null	4	null	null	null	null	7	null	null
		$R_8$	0	0	0	0.84	0	0	0	0	0.91	0	0	0			$R_8$	null	null	null	6	null	null	null	null	7	null	null	null
		$R_9$	0	0	0	0	0	0	0	0	0	0	0	0.89			$R_9$	null	null	null	null	null	null	null	null	null	null	null	4
		$R_{10}$	0	0	0	0	0	0	0	0	0	0	0.92	0.78			$R_{10}$	null	null	null	null	null	null	null	null	null	null	10	8
		$R_{11}$	0	0	0	0	0	0.95	0	0.88	0	0	0	0			$R_{11}$	null	null	null	null	null	11	null	9	null	null	null	null
		$R_{12}$	0	0	0	0	0	0.73	0	0.82	0	0	0	0			$R_{12}$	null	null	null	null	null	8	null	8	null	null	null	null

.

Based on the adjacency matrix of each functional layer, the supernetwork is divided into two layers, and KCGA search is performed simultaneously to generate KCs. Scenario I is similar to scenario II except that during the RCGA second-layer search, the termination node is found and the search stops, thus obtaining the desired KCs.

Table 4. KC information for scenarios I and II.

Scenario	${\mathit{T}}_1$			${\mathit{T}}_2$
I	Kill Chain	Time [s]	Probability	Kill Chain	Time [s]	Probability
				$T_2$→$S_5$→$D_7$→$I_5$→$T_2$	53	0.38
				$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{11}$→$I_6$→$T_2$	91	0.37
	$T_1$→$S_2$→$D_8$→$I_4$→$T_1$	61	0.5	$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{12}$→$I_6$→$T_2$	86	0.24
	$T_1$→$S_2$→$D_8$→$I_9$→$T_1$	79	0.5	$T_2$→$\left(S_7\right)$→$D_7$→$I_5$→$T_2$	48	0.55
				$T_2$→$S_7$→$D_{10}$→$C_{11}$→$I_5$→$T_2$	86	0.53
				$T_2$→$S_7$→$D_{10}$→$C_{12}$→$I_5$→$T_2$	81	0.34
II	$T_1$→$S_2$→$C_{11}$→$D_8$→$I_4$→$T_1$	71	0.5	$T_2$→$S_5$→$D_7$→$I_5$→$T_2$	53	0.38
				$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{11}$→$I_6$→$T_2$	91	0.37
	$T_1$→$S_2$→$C_9$→$C_{12}$→$D_8$→$I_4$→$T_1$	77	0.42	$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{12}$→$I_6$→$T_2$	86	0.24
	$T_1$→$S_2$→$C_{11}$→$D_8$→$I_9$→$T_1$	89	0.51	$T_2$→$\left(S_7\right)$→$D_7$→$I_5$→$T_2$	48	0.55
	$T_1$→$S_2$→$C_9$→$C_{12}$→$D_8$→$I_9$→$T_1$	95	0.43	$T_2$→$S_7$→$D_{10}$→$C_{11}$→$I_5$→$T_2$	86	0.53
				$T_2$→$S_7$→$D_{10}$→$C_{12}$→$I_5$→$T_2$	81	0.34

compares the KC information between scenarios I and II.

Table 4 shows the KC structures, along with the corresponding time and probability information, obtained by KCGA under two scenarios: one where information transfer between $R_2$ and $R_8$ is normal, and one where it is restricted. For target $T_2$, the KC information in both scenarios is the same because the closure of the operational link related to $T_2$ does not require the participation of $R_2$’s perception information. In contrast, the closure of the operational link for $T_1$ does require $R_2$’s perception information, and the information transfer from $R_2$ has a significant impact on both scenarios. For $T_1$, when $R_2$ and $R_8$ can communicate normally (scenario I), two KCs are obtained in total, with no need for relay nodes in the communication between $R_2$ and $R_8$. When communication between $R_2$ and $R_8$ is restricted (scenario 2), four KCs are obtained in total. At this point, the direct link between $R_2$ and $R_8$ is lost, resulting in the loss of the two standard KCs from scenario I. However, four additional KCs involving indirect information transfer through $R_9$, $R_{11}$, and $R_{12}$ are acquired, compensating for the loss caused by the communication restrictions. Furthermore, in the KC $T_2\to S_7\to \left(D_7\right)\to I_5\to T_2$, $S_7$ acts as both the reconnaissance and command equipment.

Based on the capability information of each KC in Table 4 and the multilayer network capability matrices, the combat effectiveness of the WSoS is calculated. The evaluation results are compared in

Table 5. Effectiveness evaluation results for scenarios I and II.

Scenario	Kill-Chain Count	Task Matching Degree	Task Completion Time	Task Completion Probability	Anti-Destructiveness	Agility	Communication Efficiency
I	8	0.94	72.1	0.45	2.33	4	0.19
II	10	0.92	78.58	0.43	3.25	5	0.17

. The connectivity between $R_2$ and $R_8$ in the two scenarios affects the system’s effectiveness. The number of KCs in scenario I is two fewer than in scenario II, but due to the impact of the KC closure probability, its task matching degree is comparable to that of scenario II. In scenario II, the increased number of KCs compensates for the impact of $R_2$’s failure on the WSoS. Although there are more KCs, the additional ones are generated through relay nodes that transmit information indirectly, leading to more operational links. As a result, scenario II has lower task completion speed and task completion probability compared to scenario I. The number of KCs in scenario I is two less than in scenario II, but due to the reduced closure probability of the KCs, its task matching degree is comparable to that of scenario II. The increase in the number of KCs in scenario II improves its resilience and redundancy, making it superior to scenario I in these aspects. However, the loss of the communication link between $R_2$ and $R_8$ in scenario II results in lower communication efficiency compared to scenario I. In summary, although the use of information relays in scenario II compensates for the generation of KCs targeting $T_1$ and improves the TMD, resilience, and redundancy, the closure of relay-generated KCs may be less effective than that of standard KCs. Therefore, scenario II is inferior to scenario I in terms of task completion speed and task completion probability.

4.3. Comparison of Experimental Results

To assess the effectiveness of the proposed model and the performance of the algorithm, we select three WSoS KC construction methods for comparison [15,17,19], to which we refer hereinafter using the relevant citation numbers. Of these, [15] is the standard form of the KC, [17] defines four types of KCs based on this, using a higher-order adjacency matrix method to obtain the number of KCs [19]. Using the layered search approach, all simple paths between two vertices can be obtained. By replacing the RCGA algorithm (lines 7 and 12) in Algorithm 1 with [19], all the kill chains formed by simple paths in the scenario can be obtained. Given that [19] relies on integrating the framework of Algorithm 1 to generate kill chains composed of simple paths, we will continue to use [19] to represent all the linkages obtained by substituting the RCGA algorithm in Algorithm 1 with the simple path generation algorithm for the sake of comparative analysis. By applying the KC information obtained from the three methods to the KC closure and effectiveness evaluation models, the performance of the proposed algorithm is compared and analyzed. Because [17] can obtain only the number of KCs, it cannot provide information about the structure, closure time, and closure probability of individual KCs nor the related effectiveness indicators such as TMD, task completion time, and task completion probability. The KC information generated by each algorithm in both scenarios is given in

Table 6. Comparison of KC information from different algorithms.

Scenario		Kill Chain Count	${\mathit{T}}_1$			${\mathit{T}}_2$
			Kill Chain Structure	Time [s]	Probability	Kill Chain Structure	Time [s]	Probability
[15]	I	3	$T_1$→$S_2$→$D_8$→$I_4$→$T_1$	61	0.5	$T_2$→$S_5$→$D_7$→$I_5$→$T_2$	53	0.38
			$T_1$→$S_2$→$D_8$→$I_9$→$T_1$	79	0.5
	II	1	∅	∅	∅	$T_2$→$S_5$→$D_7$→$I_5$→$T_2$	53	0.38
[17]	I	4	/(2)	/	/	/(2)	/	/
	II	2	/(0)	/	/	/(2)	/	/
[19]	I	14				$T_2$→$S_5$→$D_7$→$I_5$→$T_2$	53	0.38
			$T_1$→$S_2$→$D_8$→$I_4$→$T_1$	61	0.5	$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{11}$ →$I_6$→$T_2$	91	0.37
			$T_1$→$S_2$→$C_9$→$C_{12}$→$D_8$ →$I_4$→$T_1$	77	0.42	$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{11}$ →$C_8$→$C_9$→$C_{12}$→$I_6$→$T_2$	108	0.2
			$T_1$→$S_2$→$C_{11}$→$D_8$→$I_4$ →$T_1$	71	0.5	$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{12}$ →$I_6$→$T_2$	86	0.24
			$T_1$→$S_2$→$D_8$→$I_9$→$T_1$	79	0.5	$T_2$→$\left(S_7\right)$→$D_7$→$I_5$→$T_2$	48	0.55
			$T_1$→$S_2$→$C_9$→$C_{12}$→$D_8$ →$I_9$→$T_1$	95	0.43	$T_2$→$S_7$→$D_{10}$→$C_{11}$→$I_6$ →$T_2$	86	0.53
			$T_1$→$S_2$→$C_{11}$→$D_8$→$I_9$ →$T_1$	89	0.51	$T_2$→$S_7$→$D_{10}$→$C_{11}$→$C_8$ →$C_9$→$C_{12}$→$I_6$→$T_2$	103	0.29
						$T_2$→$S_7$→$D_{10}$→$C_{12}$→$I_6$ →$T_2$	81	0.34
	II	12				$T_2$→$S_5$→$D_7$→$I_5$→$T_2$	53	0.38
						$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{11}$ →$I_6$→$T_2$	91	0.37
			$T_1$→$S_2$→$C_9$→$C_{12}$→$D_8$ →$I_4$→$T_1$	77	0.42	$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{11}$ →$C_8$→$C_9$→$C_{12}$→$I_6$→$T_2$	108	0.2
			$T_1$→$S_2$→$C_{11}$→$D_8$→$I_4$ →$T_1$	71	0.5	$T_2$→$S_5$→$C_7$→$D_{10}$→$C_{12}$ →$I_6$→$T_2$	86	0.24
			$T_1$→$S_2$→$C_9$→$C_{12}$→$D_8$ →$I_9$→$T_1$	95	0.43	$T_2$→$\left(S_7\right)$→$D_7$→$I_5$→$T_2$	48	0.55
			$T_1$→$S_2$→$C_{11}$→$D_8$→$I_9$ →$T_1$	89	0.51	$T_2$→$S_7$→$D_{10}$→$C_{11}$→$I_6$ →$T_2$	86	0.53
						$T_2$→$S_7$→$D_{10}$→$C_{11}$→$C_8$ →$C_9$→$C_{12}$→$I_6$→$T_2$	103	0.29
						$T_2$→$S_7$→$D_{10}$→$C_{12}$→$I_6$ →$T_2$	81	0.34

, with the information that could not be obtained in [17] indicated by “/”. The content in parentheses (kill chain structure) represents the link count information. Additionally, ∅ indicates the absence of relevant information.

For $T_2$, because the communication restriction between $R_2$ and $R_8$ affects only the link composition related to $T_1$, the KC information for $T_2$ is consistent across both scenarios for each algorithm. Ref. [17] defines three types of link forms in addition to the standard KC, resulting in one more KC compared to [15]. For $T_1$, in scenario I after filtering out the relay links, KCGA performs similarly to [15,17], but by not considering the constraints of the KC, ref. [19] searches for a large number of redundant relay links based on connectivity, leading to an inaccurate description of WSoS performance. In scenario II for $T_1$’s KCs, the direct link between $R_2$ and $R_8$ is lost in [15,17], resulting in two fewer KCs compared to scenario I. At this point, the failure of $R_2$ prevents the formation of a KC for $T_1$. KCGA—which considers information relays during $R_2$’s failure—adds four more KCs related to $R_2$ compared to the algorithms [15,17], compensating for the impact of $R_2$’s failure on the WSoS performance. Although [19] considers $R_2$’s information relay, it loses the standard chain for the transmission of $R_2$’s perception information while acquiring too many redundant KCs, resulting in two fewer links compared to scenario I. By considering relay link constraints, KCGA ensures that no redundant relay chains are generated during the KC creation process.

Based on the information about each KC from the different algorithms in Table 6, we calculate the combat effectiveness of the WSoS, and

Table 7. Comparison of effectiveness evaluation results of different algorithms.

Scenario		Kill Chain Count	Task Matching Degree	Task Completion Time	Task Completion Probability	Anti-Destructiveness	Agility	Communication Efficiency
KCGA	I	8	0.94	72.1	0.45	2.33	4	0.19
	II	10	0.92	78.58	0.43	3.25	5	0.17
[15]	I	3	0.63	61.5	0.44	0.67	1.5	0.19
	II	1	0.65	null	0.19	0.17	0.5	0.17
[17]	I	4	/	/	/	0.83	2	0.19
	II	2	/	/	/	0.33	1	0.17
[19]	I	14	0.85	80.3	0.42	5	7	0.19
	II	12	0.96	82.5	0.41	4.5	6	0.17

compares the effectiveness evaluation results. The analysis is conducted via both self-comparison (horizontal) and inter-comparison (vertical) of the algorithms in the two scenarios. In the horizontal comparison, because [15,17] do not consider information relays and only generate KCs with a determined structure, the failure of $R_2$ in scenario II severely affects the generation of KCs for $T_1$, resulting in poorer performance for these two algorithms in scenario II compared to scenario I. In particular, for scenario II, because [15] does not form any KCs for target $T_1$, its task completion speed metric is meaningless and, so, is represented as “null.” In the vertical comparison, the number of KCs generated by KCGA for each target in both scenarios is significantly better than [15], so KCGA’s task matching degree is superior to [15]. Although the number of KCs in [19] exceeds that of KCGA, the limitation of KC closure probability causes its task matching degree in scenario I to be worse than KCGA’s but slightly better in scenario II. Since KCGA considers necessary information relay, the task completion probability in scenario II is better than [15] and comparable to [15] in scenario I. Regarding task completion time, because KCGA’s KCs in scenario I include information relay, the efficiency of information transmission is worse than [15]. The number and structure of KCs affect the quantification of survivability and redundancy metrics; therefore, KCGA and [19] outperform [15,17] in these two metrics in both scenarios. In terms of communication efficiency, the relay adjacency matrix is the same in each scenario; therefore, so is the communication efficiency. In summary, KCGA demonstrates a significant superiority in KCs generation and effectiveness evaluation in both scenarios.

This paper constructs the performance evaluation indicators of the WSoS based on the concept of the kill chains. Therefore, in order to verify the effectiveness and discriminative power of the proposed indicators, an analysis of the sufficiency and redundancy of the generated kill chains is conducted. Ref. [19] utilized a hierarchical search approach to obtain all simple paths between two vertices. By replacing the RCGA algorithm in Algorithm 1 with the algorithm for obtaining simple paths, all the kill chains composed of these simple paths in the scenarios were derived. Table 6 presents all the kill chains composed of simple path combinations obtained in [19], with a total of 14 kill chains in scenario I and 12 in scenario II. In scenario I, regarding the kill chains involving $T_1$, since $S_2$ and $D_8$ can communicate directly, the links $T_1\to S_2\to C_9\to C_{12}\to D_8\to I_4\to T_1$, $T_1\to S_2\to C_{11}\to D_8\to I_4\to T_1$, $T_1\to S_2\to C_9\to C_{12}\to D_8\to I_9\to T_1$ and $T_1\to S_2\to C_{11}\to D_8\to I_9\to T_1$ are redundant. After removing these redundant links, the remaining links $T_1\to S_2\to D_8\to I_4\to T_1$ and $T_1\to S_2\to D_8\to I_9\to T_1$ match those related to $T_1$ in scenario I, as shown in Table 4. Algorithm 1 successfully obtained all simple paths that meet the constraints, i.e., the kill chains, ensuring the validity of the evaluation metrics based on kill chains as fundamental elements. Similarly, for the kill chains involving $T_2$ in scenario I, since $C_{11}$ and $I_6$ could communicate directly, the links $T_2\to S_5\to C_7\to D_{10}\to C_{11}\to C_8\to C_9\to C_{12}\to I_6\to T_2$ and $T_2\to S_7\to D_{10}\to C_{11}\to C_8\to C_9\to C_{12}\to I_6\to T_2$ are redundant. After removing these redundant links, the remaining links match those related to $T_2$ in scenario I, as shown in Table 4. In scenario II, the connectivity between $R_2$ and $R_8$ fails, which only affects the generation of kill chains involving $T_1$. Therefore, the kill chains composed of simple paths involving $T_2$ in both scenarios are identical, and after eliminating redundant links, they match the links related to $T_2$ in Table 4. For $T_1$ in scenario II, all four kill chains composed of simple paths meet the constraints and match the links related to $T_1$ in scenario II, as shown in Table 4. In summary, Algorithm 1 is capable of obtaining all simple paths that satisfy the constraints, ensuring the validity of evaluation metrics based on kill chains as fundamental elements.

5. Conclusions

This study delves deeply into the evaluation of the effectiveness of the WSoS based on kill chains under communication constraints. It not only innovatively constructs a generalized information relay supernetwork model and its corresponding directed hypernetwork model, but also establishes an accurate time and probability capability matrix to quantify the situational information of the WSoS. Furthermore, an efficient kill chain generation strategy is proposed. From the perspective of red–blue adversarial games, we have carefully developed a comprehensive WSoS effectiveness evaluation index system, which focuses on both the structural robustness of the combat system and the accuracy and timeliness of combat tasks. Numerical simulation results showed that this method outperforms existing methods. This paper primarily investigates the network construction and capability analysis methods of the WSoS under communication constraints, transforming the communication constraint issue into a problem of whether communication can occur. However, it does not analyze the impact of the degree of communication constraint on the closure of kill chains. Future work will model the effects of electronic warfare and other factors on equipment communication capabilities, integrating these models into the analysis of kill chain closure and the effectiveness evaluation model of kill web, thus providing a more comprehensive description of the WSoS under communication constraints.