An Exact Algorithm for Continuous Ship Unloading Based on Vehicle Routing
Abstract
1. Introduction
- Constraints related to continuous unloading operations due to liquid-based products, vehicle routing, multiple daily time windows, driver scheduling, and heterogeneous fleet composition are simultaneously and uniquely incorporated in the objective of minimizing the total transportation costs;
- This study uniquely investigates the optimal timing and duration of breaks or rest periods for truck drivers operating within a continuous ship-unloading-based FTL network;
- The continuity of ship unloading is uniquely discretized by generating corresponding supply nodes with specific time window structures, enabling the application of efficient exact VRP solution methods alongside appropriate acceleration techniques;
- The nested label setting algorithm is customized to align with the specific characteristics of the FTL structure and is uniquely adapted to incorporate port-related constraints, such as continuous unloading, as well as vehicle-related constraints, including a requirement that each vehicle be loaded a certain minimum number of times;
- Acceleration techniques are also specifically adapted to account for the dynamics of the port–truck integration, thereby enhancing the performance of the nested label setting algorithm;
- This study presents a unique and detailed performance evaluation regarding long continuous ship unloading with the FTL delivery problem using the proposed algorithm.
2. Literature Review
3. Problem Description
3.1. Problem Definition
- The port does not have time windows;
- The fleet comprises both rented and company-owned vehicles;
- Unloading starts as soon as the vessel is assigned to a berth at the port;
- There are not multiple vessels for unloading;
- A single type of liquid product is unloaded from the vessel;
- The vessel does not have multiple compartments;
- The vessel cannot pump the liquid into multiple vehicles at the same time;
- Trailers are attached to the vehicles for transporting the liquid product;
- Drivers are prohibited from operating vehicles in violation of the legally mandated rest and break regulations of the United States;
- A minimum number of vehicles is always present at the port during unloading operations;
- No vehicle is exclusively assigned to remain at the port solely as a backup;
- Drivers are not allowed to take rests or breaks when they are at the port;
- The transportation network is comprised of a departure and a terminal/garage node;
- The transportation network has multiple supply and customer nodes;
- There are not multiple distribution layers;
- With respect to trucks, loading operations are carried out at supply nodes, whereas unloading operations take place at customer nodes;
- Supply nodes have one time window, whereas customer nodes have multiple time windows.
- Environmental influences such as traffic jams are disregarded;
- No additional waiting time is required for the ship’s arrival at the port, as the arrival is already scheduled before;
- The time window bounds of a supply node are equal to each other to reflect the continuous ship unloading in the specified FTL problem’s network;
- The ship does not wait in the queue at the port;
- Drivers are identical;
- Drivers do not impose any constraint except driver scheduling rules;
- The port has unlimited vehicle capacity;
- The port does not have roadway capacity;
- There is no equipment constraint for pumps intended for liquid cargo, such as availability;
- The service rate of pumps is constant;
- The pumping of liquid is continuous;
- Multiple time windows are separate, daily, consecutive, and limited;
- A restricted number of owned and rented vehicles are available;
- Travel costs along arcs are fixed and known in advance;
- All trailers that are capable of transporting the relevant liquid cargo are considered identical in terms of capacity and specifications;
- The expense of transporting a loaded vehicle is twice as high as that of transporting an unloaded one;
- A fixed set of supply and customer nodes are involved;
- Travel times between all nodes are predefined;
- A predetermined minimum number of vehicles are available as backup during unloading operations;
- Each designated vehicle serves at least a specified minimum number of customer nodes;
- Minimum required durations for driver rest and break periods are enforced;
- A maximum allowable driving time without rest is imposed;
- A maximum allowable driving time without a break is specified;
- A maximum permissible elapsed time without rest is defined;
- A maximum permissible elapsed time without a break is also established;
- There is no probabilistic or stochastic condition for the operations involved in the problem.
3.2. Mathematical Formulation
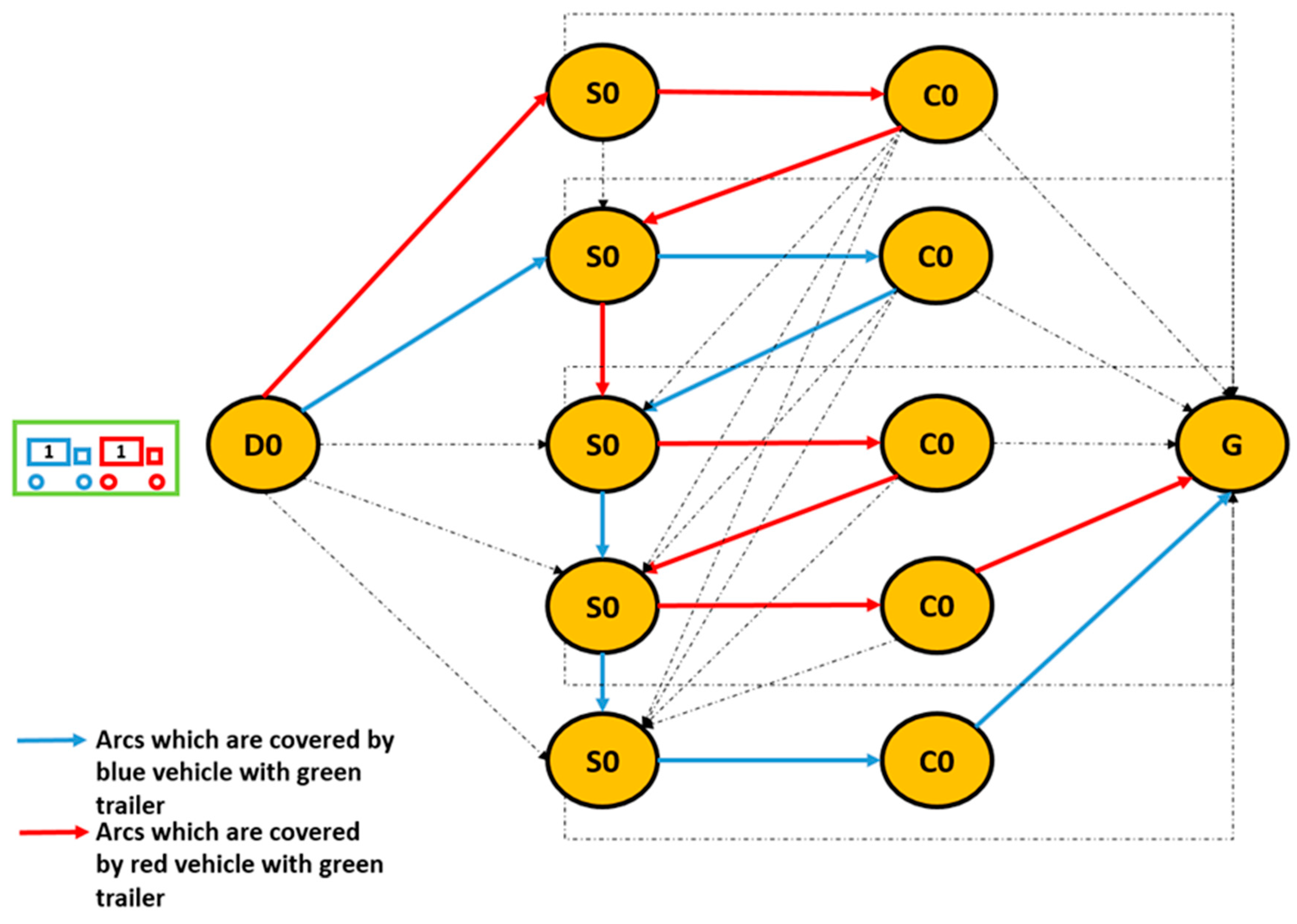
3.3. Network Representation
4. Methodology
| Algorithm 1. Steps of Overall Algorithm |
| 1: Employ the construction heuristic algorithm to derive initial routes 2: Obtain the initial routes that will serve as initial columns for the column generation algorithm 3: Let initial routes be located in the RMP 4: Solve the RMP 5: Obtain the dual variables 6: Execute the nested label setting algorithm with the help of dual variables 7: Obtain a feasible route/column, which can improve the RMP, as a result of the nested label setting algorithm, add this promising route/column to the RMP, and return to Line 4 8: If no feasible route/column is found, then the RMP has reached optimality, which serves as a lower bound 9: Solve the integer version of the RMP with the generated columns so far and find an upper bound 10: Calculate the optimality gap |
4.1. Construction Heuristic
4.2. Column Generation Algorithm
4.2.1. Nested Label Setting Algorithm
- i.
- During travel, if and , then a drive period should take place subsequently;
- ii.
- Minimum rest and break periods should be taken at first, which are and , respectively;
- iii.
- No two consecutive break or rest periods can exist;
- iv.
- Assuming and are two forward labels regarding the node, can dominate if , , , , , , , , and . Thus, can be discarded.
4.2.2. Acceleration Techniques
Heuristic Column Generation
Subproblem Selection
Bi-directional Search
5. Computational Study
5.1. Creation of Instances
5.2. Performance Results of the Proposed Algorithm
5.3. Discussion of Results
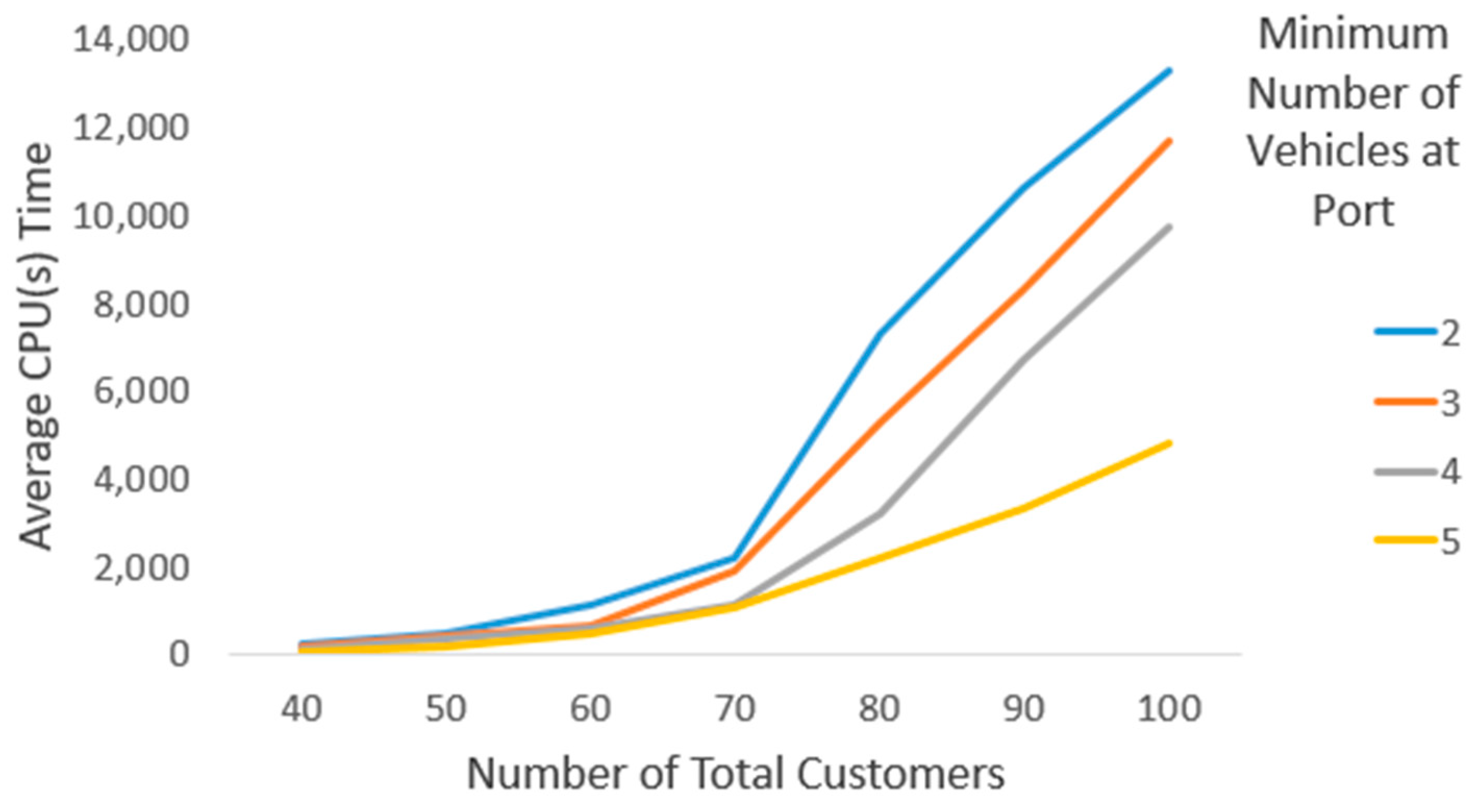
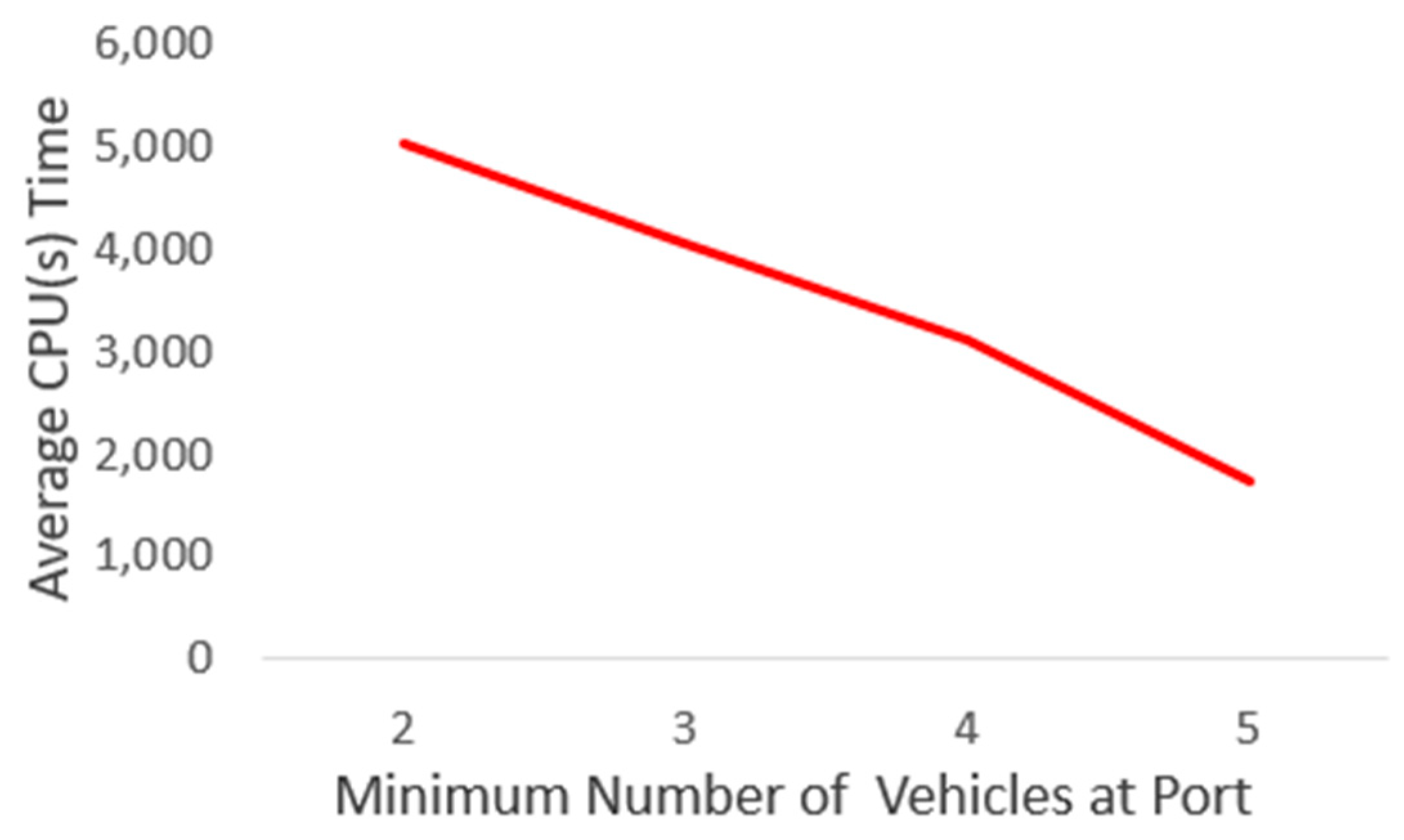
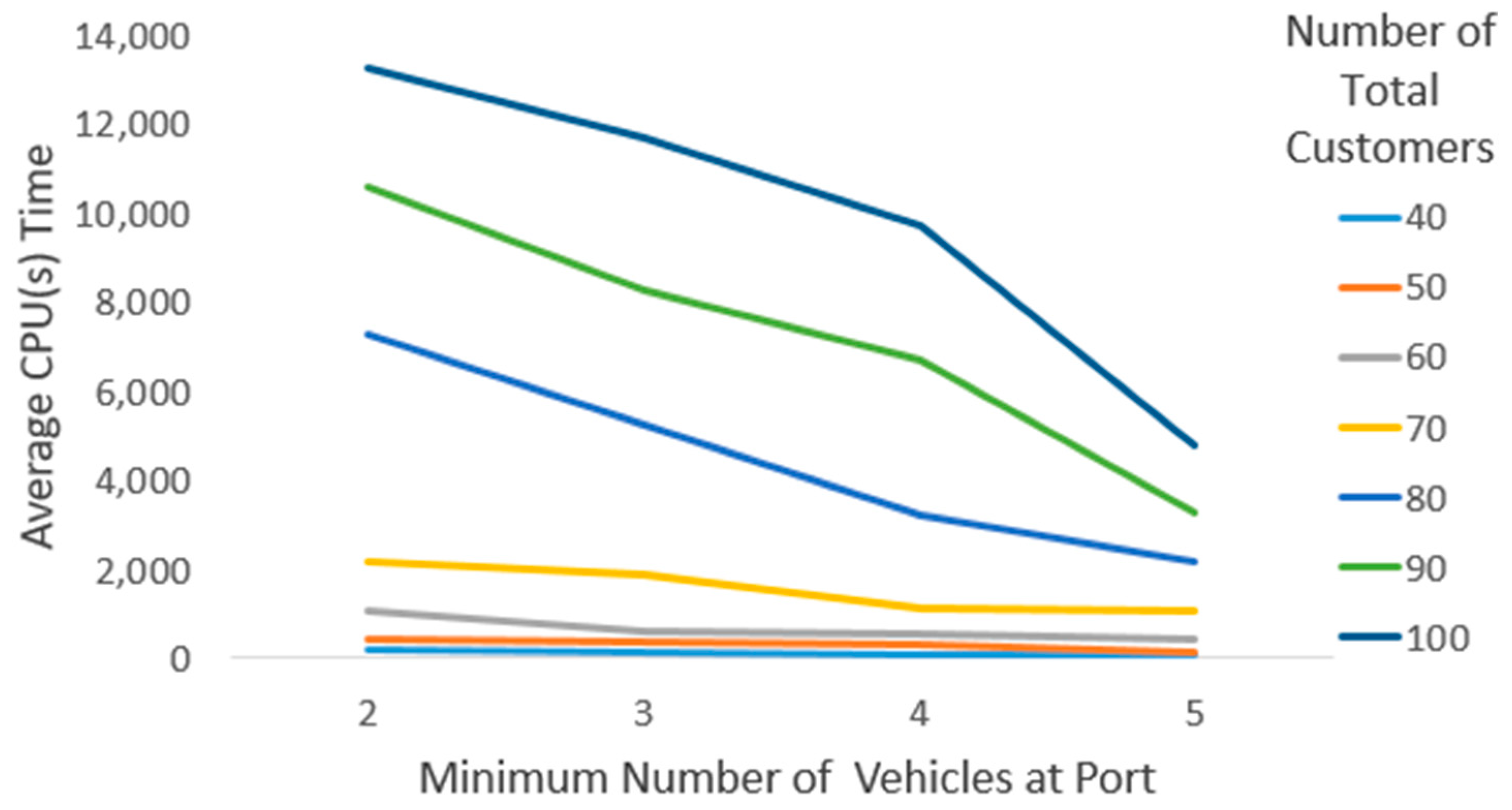
5.3.1. Solution Time Analysis Based on the Number of Customer Nodes and Minimum Number of Vehicles at the Port
- With a minimum of two vehicles at the port, the computational time escalates sharply, exhibiting an approximately 6700% increase;
- For a minimum of three vehicles, the increase reaches roughly 7900%;
- With four vehicles, the computational time surges by approximately 11,400%;
- For five vehicles, the rise amounts to around 8800%.
- With 40 customers, the increase is approximately 366%;
- With 50 customers, it is about 292%;
- With 60 customers, computational time grows by roughly 235%;
- With 70 customers, the increase is about 207%;
- With 80 customers, the rise reaches approximately 339%;
- With 90 customers, it is around 322%;
- With 100 customers, the computational time is roughly 3.22 times greater.
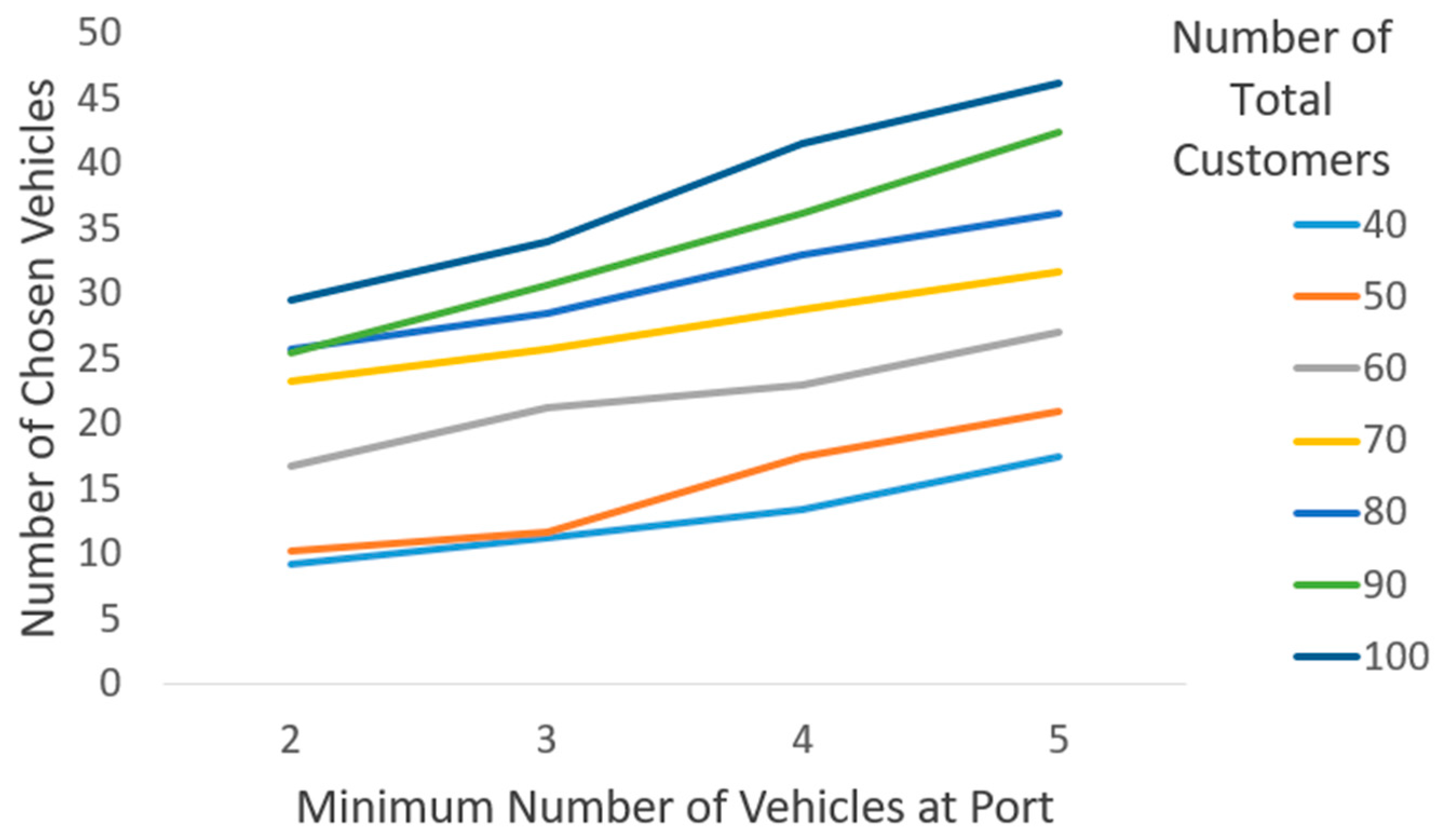
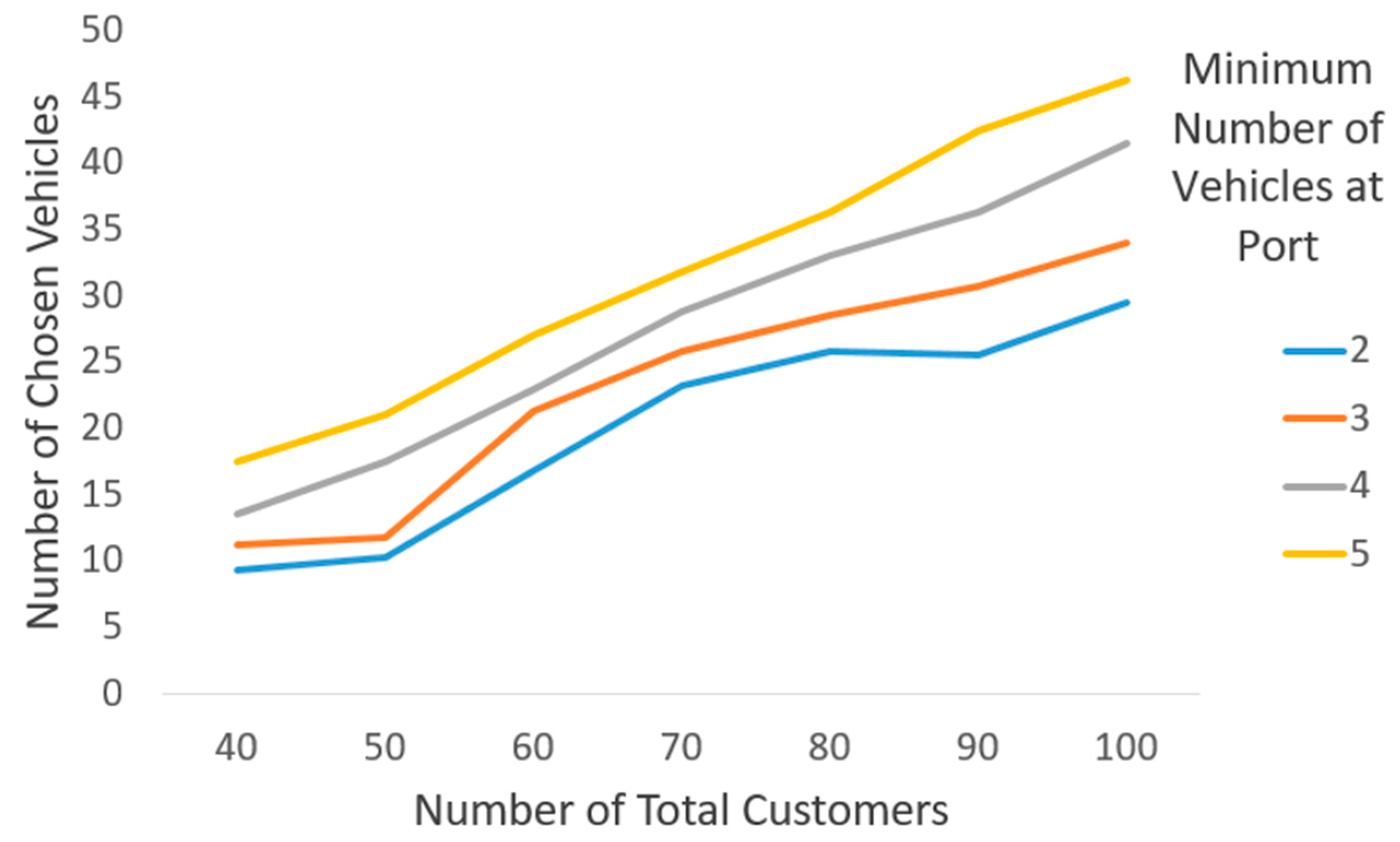
5.3.2. Number of Used Vehicles Analysis Based on the Number of Customer Nodes and Minimum Number of Vehicles at the Port
- When the minimum number of vehicles at the port is set to two, the number of selected vehicles rises by approximately 318%;
- With a minimum requirement of three vehicles, the increase amounts to 302%.
- For a minimum of four vehicles, the number of selected vehicles grows by 307%.
- When the minimum requirement is five vehicles, the observed increase is 264%.
- For 40 customers, the number of selected vehicles increases by approximately 189%;
- For 50 customers, the growth is around 204%;
- For 60 customers, the increase is 161%;
- For 70 customers, the growth is 136%;
- For 80 customers, the number of vehicles rises by 141%;
- For 90 customers, the growth is approximately 166%;
- For 100 customers, the increase reaches a factor of 1.56.
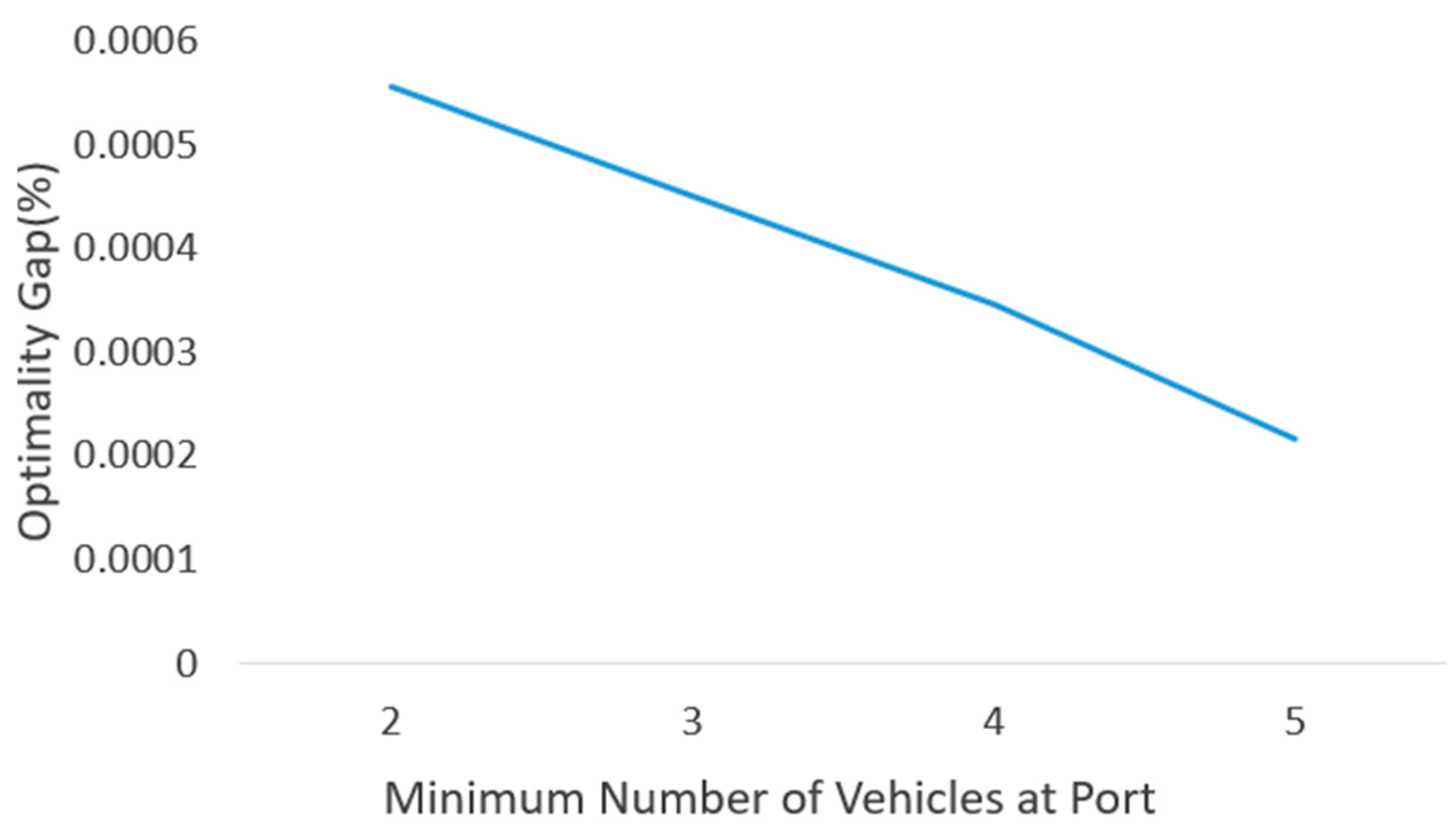
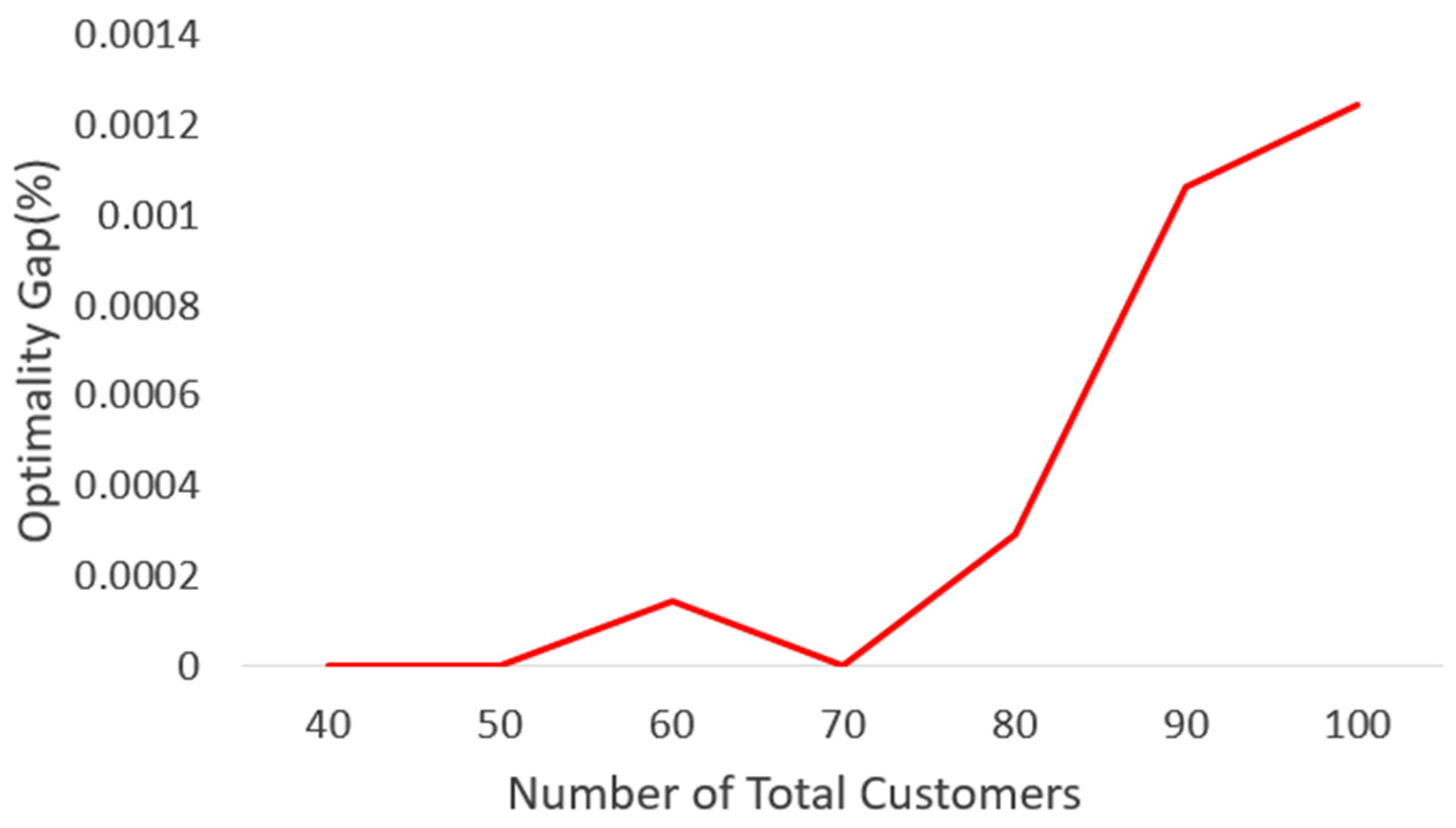
5.3.3. Optimality Gap Analysis Based on the Number of Customer Nodes and Minimum Number of Vehicles at the Port
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Konstantakopoulos, G.D.; Gayialis, S.P.; Kechagias, E.P. Vehicle routing problem and related algorithms for logistics distribution: A literature review and classification. Oper. Res. 2022, 22, 2033–2062. [Google Scholar] [CrossRef]
- Kennedy, J.; Russell, E. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA; Volume 4. [Google Scholar]
- Ropke, S.; Pisinger, D. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows. Transp. Sci. 2006, 40, 455–472. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Moscato, P. On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms. Caltech Concurr. Comput. Program C3P Rep. 1989, 826, 37. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems, 1st ed.; University of Michigan Press: Ann Arbor, MI, USA, 1975; pp. 29–41. [Google Scholar]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Lin, S. Computer solutions of the traveling salesman problem. Bell Syst. Tech. J. 1965, 44, 2245–2269. [Google Scholar] [CrossRef]
- Righini, G.; Salani, M. Symmetry helps: Bounded bi-directional dynamic programming for the elementary shortest path problem with resource constraints. Discret. Optim. 2006, 3, 255–273. [Google Scholar] [CrossRef]
- Desaulniers, G.; Lessard, F.; Hadjar, A. Tabu search, partial elementarity, and generalized k-path inequalities for the vehicle routing problem with time windows. Transp. Sci. 2008, 42, 387–404. [Google Scholar] [CrossRef]
- Ball, M.O.; Golden, B.L.; Assad, A.A.; Bodin, L.D. Planning for truck fleet size in the presence of a common-carrier option. Decis. Sci. 1983, 14, 103–120. [Google Scholar] [CrossRef]
- Desrosiers, J.; Laporte, G.; Sauve, M.; Soumis, F.; Taillefer, S. Vehicle routing with full loads. Comput. Oper. Res. 1988, 15, 219–226. [Google Scholar] [CrossRef]
- Tilk, C. Branch-and-Price-and-Cut for the Vehicle Routing and Truck Driver Scheduling Problem; No. 1616; Gutenberg School of Management and Economics, Johannes Gutenberg-University Mainz: Mainz, Germany, 2016. [Google Scholar]
- Goel, A.; Irnich, S. An exact method for vehicle routing and truck driver scheduling problems. Transp. Sci. 2017, 51, 737–754. [Google Scholar] [CrossRef]
- Tilk, C.; Goel, A. Bidirectional labeling for solving vehicle routing and truck driver scheduling problems. Eur. J. Oper. Res. 2020, 283, 108–124. [Google Scholar] [CrossRef]
- El Bahi, Y.F.; Ezzine, L.; Aman, Z.; El Moussami, H. Distribution management problem: Case of vehicle routing problem with capacity constraints “CVRP” in the Moroccan petroleum sector. In Proceedings of the 2022 8th International Conference on Control, Decision and Information Technologies (CoDIT), Istanbul, Turkey, 17–20 May 2022; IEEE: Piscataway, NJ, USA; Volume 1. [Google Scholar]
- Budiyanto, M.A.; Novrian, G.R.; Riadi, A.; Putra, G.L.; Theotokatos, G. Shipping cost feasibility of LNG distribution with multiple island gas power plant destinations. Front. Energy Res. 2025, 13, 1502518. [Google Scholar] [CrossRef]
- Heidari, N.; Hemmati, A. An ALNS-based matheuristic algorithm for a multi-product many-to-many maritime inventory routing problem. Comput. Manag. Sci. 2023, 20, 44. [Google Scholar] [CrossRef]
- Shafipour-Omrani, B.; Komijan, A.R.; Ghasemi, P.; Ghasemzadeh, E.; Babaeinesami, A. A simulation-optimization model for liquefied natural gas transportation considering product variety. Int. J. Manag. Sci. Eng. Manag. 2021, 16, 279–289. [Google Scholar] [CrossRef]
- Santos, A.; Soares, C.G. Cost optimization of shuttle tanker offloading operations. Ocean Eng. 2024, 301, 117378. [Google Scholar] [CrossRef]
- Budiyanto, M.A.; Singgih, I.K.; Riadi, A.; Putra, G.L. Study on the LNG distribution to Mobile Power Plants using a Small-Scale LNG Carrier for the case of the Sulawesi region of Indonesia. Energy Rep. 2022, 8, 374–380. [Google Scholar] [CrossRef]
- Gao, Z.; Sun, D.; Zhao, R.; Dong, Y. Ship-unloading scheduling optimization for a steel plant. Inf. Sci. 2021, 544, 214–226. [Google Scholar] [CrossRef]
- Fu, J.; Pan, S.; Liao, J.; Zhang, S. Application of Hybrid Optimization Algorithm Considering Yard Priority to Port Vehicle Scheduling. In Proceedings of the 2025 8th World Conference on Computing and Communication Technologies (WCCCT), Shenzhen, China, 11–13 April 2025; IEEE: Piscataway, NJ, USA. [Google Scholar]
- Larsen, R.B.; Atasoy, B.; Negenborn, R.R. Model predictive control for simultaneous planning of container and vehicle routes. Eur. J. Control 2021, 57, 273–283. [Google Scholar] [CrossRef]
- Baldouski, D.; Krész, M.; Dávid, B. Scheduling truck arrivals for efficient container flow management in port logistics. Central Eur. J. Oper. Res. 2025, 33, 791–818. [Google Scholar] [CrossRef]
- He, X.; Yang, Z.; Fan, T.; Gao, J.; Zhen, L.; Lyu, J. Branch and price algorithm for route optimization on customized bus service. Ann. Oper. Res. 2024, 335, 205–236. [Google Scholar] [CrossRef]
- Joo, J.; Lee, C. A branch-and-price algorithm for robust drone-vehicle routing problem with time windows. Inf. J. Comput. 2025; ahead of print. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Wolfe, P. Decomposition principle for linear programs. Oper. Res. 1960, 8, 101–111. [Google Scholar] [CrossRef]
- Desrosiers, J.; Soumis, F.; Desrochers, M. Routing with time windows by column generation. Networks 1984, 14, 545–565. [Google Scholar] [CrossRef]
- Barnhart, C.; Johnson, E.L.; Nemhauser, G.L.; Savelsbergh, M.W.P.; Vance, P.H. Branch-and-price: Column generation for solving huge integer programs. Oper. Res. 1998, 46, 316–329. [Google Scholar] [CrossRef]
- Ropke, S.; Cordeau, J.-F. Branch and cut and price for the pickup and delivery problem with time windows. Transp. Sci. 2009, 43, 267–286. [Google Scholar] [CrossRef]
- Costa, L.; Contardo, C.; Desaulniers, G. Exact branch-price-and-cut algorithms for vehicle routing. Transp. Sci. 2019, 53, 946–985. [Google Scholar] [CrossRef]
- Kohl, N.; Desrosiers, J.; Madsen, O.B.G.; Solomon, M.M.; Soumis, F. 2-path cuts for the vehicle routing problem with time windows. Transp. Sci. 1999, 33, 101–116. [Google Scholar] [CrossRef]
- Kallehauge, B.; Larsen, J.; Madsen, O.B.G.; Solomon, M.M. Vehicle Routing Problem with Time Windows; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Dial, R.; Glover, F.; Karney, D.; Klingman, D. A computational analysis of alternative algorithms and labeling techniques for finding shortest path trees. Networks 1979, 9, 215–248. [Google Scholar] [CrossRef]
- Feillet, D.; Dejax, P.; Gendreau, M.; Gueguen, C. An exact algorithm for the elementary shortest path problem with resource constraints: Application to some vehicle routing problems. Netw. Int. J. 2004, 44, 216–229. [Google Scholar] [CrossRef]
- Floyd, R.W. Algorithm 97: Shortest path. Commun. ACM 1962, 5, 345. [Google Scholar] [CrossRef]
- Wu, Y.; Qureshi, A.G.; Yamada, T.; Yu, S. Branch-and-price-and-cut algorithm for the capacitated single allocation hub location routeing problem. J. Oper. Res. Soc. 2024, 75, 410–422. [Google Scholar] [CrossRef]







| Studies | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| El Bahi et al. [16] | X | X | X | |||||
| Tilk and Goel [15] | X | X | X | X | X | |||
| Goel and Irnich [14] | X | X | X | X | X | |||
| Budiyanto et al. [17] | X | X | X | X | ||||
| Heidari et al. [18] | X | X | X | X | ||||
| Gao et al. [22] | X | X | X | X | X | |||
| Fu et al. [23] | X | X | X | |||||
| Shafipour et al. [19] | X | X | X | X | ||||
| Santos et al. [20] | X | X | X | |||||
| Our Work | X | X | X | X | X | X | X | X |
| Sets | |
|---|---|
| Set of customer nodes | |
| Set of supply nodes | |
| Set of departure nodes | |
| Terminal/garage node | |
| Set of vehicle types | |
| Number of idle vehicles at the relevant departure node for given | |
| Set of feasible routes | |
| for each arc , where and includes just if does not exist, otherwise it includes both and | |
| Set of subsets, each of which consists of two customers | |
| Subset of inward arcs for | |
| Variables | |
| Binary route variable | |
| Parameters | |
| How many times exists in | |
| How many times exists in | |
| How many times an arc takes place in | |
| Cost of |
| Parameters | Value | Explanation |
|---|---|---|
| 11 h | Maximum driving time between two consecutive rest periods | |
| 30 min | Minimum length of a break period | |
| 10 h | Minimum length of a rest period | |
| 8 h | Maximum time after the end of the rest or break period until a driver can drive | |
| 14 h | Maximum time period after the end of the rest period until a driver can drive |
| Labels | Explanation |
|---|---|
| Reduced cost of the forward path | |
| Elapsed time since the start of the forward path | |
| Remaining drive time to next customer on the forward path | |
| Accumulated drive time since the last rest on the forward path | |
| Elapsed time starting from the end of the previous rest on the forward path | |
| Elapsed time starting from the end of the previous break on the forward path | |
| Latest possible time point to which previous rest period can be extended without violating scheduling constraints | |
| Latest possible time point to which previous break period can be extended without violating scheduling constraints |
| Labels/Functions | ||||
|---|---|---|---|---|
| 0 | ||||
| 0 | ||||
| 0 | 0 | |||
| ∞ | ||||
| ∞ | ∞ |
| Labels/Function | |
|---|---|
| Labels/Function | |
|---|---|
| Number of Total Customers | Minimum Number of Vehicles at Port | Time (s) | Optimality Gap (%) | Number of Used Vehicles |
|---|---|---|---|---|
| 40 | 2 | 207 | 0 | 9 |
| 40 | 2 | 191 | 0 | 9 |
| 40 | 2 | 183 | 0 | 9 |
| 40 | 2 | 211 | 0 | 10 |
| 40 | 3 | 148 | 0 | 11 |
| 40 | 3 | 171 | 0 | 10 |
| 40 | 3 | 144 | 0 | 12 |
| 40 | 3 | 129 | 0 | 12 |
| 40 | 4 | 94 | 0 | 14 |
| 40 | 4 | 77 | 0 | 15 |
| 40 | 4 | 80 | 0 | 12 |
| 40 | 4 | 89 | 0 | 13 |
| 40 | 5 | 65 | 0 | 18 |
| 40 | 5 | 45 | 0 | 17 |
| 40 | 5 | 49 | 0 | 16 |
| 40 | 5 | 56 | 0 | 19 |
| 50 | 2 | 428 | 0 | 10 |
| 50 | 2 | 380 | 0 | 9 |
| 50 | 2 | 455 | 0 | 12 |
| 50 | 2 | 470 | 0 | 10 |
| 50 | 3 | 385 | 0 | 12 |
| 50 | 3 | 342 | 0 | 11 |
| 50 | 3 | 416 | 0 | 10 |
| 50 | 3 | 401 | 0 | 14 |
| 50 | 4 | 327 | 0 | 17 |
| 50 | 4 | 303 | 0 | 15 |
| 50 | 4 | 298 | 0 | 19 |
| 50 | 4 | 367 | 0 | 19 |
| 50 | 5 | 151 | 0 | 22 |
| 50 | 5 | 111 | 0 | 17 |
| 50 | 5 | 142 | 0 | 25 |
| 50 | 5 | 189 | 0 | 20 |
| 60 | 2 | 1090 | 0 | 17 |
| 60 | 2 | 987 | 0 | 17 |
| 60 | 2 | 950 | 0 | 16 |
| 60 | 2 | 1290 | 0 | 17 |
| 60 | 3 | 634 | 0 | 21 |
| 60 | 3 | 443 | 0 | 19 |
| 60 | 3 | 489 | 0 | 23 |
| 60 | 3 | 890 | 0 | 22 |
| 60 | 4 | 568 | 0.000070 | 24 |
| 60 | 4 | 505 | 0.000072 | 22 |
| 60 | 4 | 499 | 0.000128 | 24 |
| 60 | 4 | 629 | 0.001037 | 22 |
| 60 | 5 | 442 | 0.000087 | 27 |
| 60 | 5 | 401 | 0.000445 | 27 |
| 60 | 5 | 482 | 0.000057 | 28 |
| 60 | 5 | 507 | 0.000428 | 26 |
| 70 | 2 | 2115 | 0 | 23 |
| 70 | 2 | 1910 | 0 | 25 |
| 70 | 2 | 2386 | 0 | 24 |
| 70 | 2 | 2217 | 0 | 21 |
| 70 | 3 | 1841 | 0 | 25 |
| 70 | 3 | 1663 | 0 | 27 |
| 70 | 3 | 1998 | 0 | 26 |
| 70 | 3 | 2100 | 0 | 25 |
| 70 | 4 | 1194 | 0 | 28 |
| 70 | 4 | 1318 | 0 | 30 |
| 70 | 4 | 961 | 0 | 30 |
| 70 | 4 | 1001 | 0 | 27 |
| 70 | 5 | 1100 | 0 | 32 |
| 70 | 5 | 911 | 0 | 31 |
| 70 | 5 | 855 | 0 | 31 |
| 70 | 5 | 1295 | 0 | 33 |
| 80 | 2 | 7337 | 0 | 25 |
| 80 | 2 | 6802 | 0 | 26 |
| 80 | 2 | 7821 | 0 | 27 |
| 80 | 2 | 7265 | 0 | 25 |
| 80 | 3 | 5318 | 0 | 29 |
| 80 | 3 | 5148 | 0 | 29 |
| 80 | 3 | 5599 | 0 | 28 |
| 80 | 3 | 4923 | 0 | 28 |
| 80 | 4 | 3119 | 0.000048 | 33 |
| 80 | 4 | 3334 | 0.001277 | 33 |
| 80 | 4 | 2821 | 0.000223 | 33 |
| 80 | 4 | 3506 | 0.000941 | 33 |
| 80 | 5 | 2223 | 0.000064 | 38 |
| 80 | 5 | 2001 | 0.001769 | 37 |
| 80 | 5 | 2133 | 0.000120 | 35 |
| 80 | 5 | 2254 | 0.000242 | 35 |
| 90 | 2 | 10,975 | 0.000611 | 26 |
| 90 | 2 | 9712 | 0.002883 | 27 |
| 90 | 2 | 10,102 | 0.001769 | 24 |
| 90 | 2 | 11,634 | 0.002418 | 25 |
| 90 | 3 | 8402 | 0 | 30 |
| 90 | 3 | 7841 | 0.001801 | 31 |
| 90 | 3 | 8139 | 0.003242 | 31 |
| 90 | 3 | 8666 | 0.001450 | 31 |
| 90 | 4 | 6717 | 0.000099 | 36 |
| 90 | 4 | 6265 | 0 | 33 |
| 90 | 4 | 6611 | 0.000107 | 39 |
| 90 | 4 | 7115 | 0.002189 | 37 |
| 90 | 5 | 3321 | 0 | 43 |
| 90 | 5 | 2978 | 0 | 39 |
| 90 | 5 | 3504 | 0.000421 | 43 |
| 90 | 5 | 3334 | 0 | 45 |
| 100 | 2 | 14,222 | 0.000081 | 30 |
| 100 | 2 | 12,032 | 0.003194 | 29 |
| 100 | 2 | 13,991 | 0.001608 | 30 |
| 100 | 2 | 12,816 | 0.003026 | 29 |
| 100 | 3 | 12,061 | 0 | 34 |
| 100 | 3 | 11,312 | 0.002424 | 34 |
| 100 | 3 | 11,828 | 0.001620 | 33 |
| 100 | 3 | 11,554 | 0.002079 | 35 |
| 100 | 4 | 9791 | 0.000021 | 40 |
| 100 | 4 | 9544 | 0.001768 | 43 |
| 100 | 4 | 9419 | 0.001413 | 41 |
| 100 | 4 | 10,056 | 0.000301 | 42 |
| 100 | 5 | 5023 | 0.000370 | 47 |
| 100 | 5 | 4322 | 0.000888 | 47 |
| 100 | 5 | 4839 | 0.000773 | 45 |
| 100 | 5 | 4929 | 0.000389 | 46 |
| Minimum Number of Vehicles at the Port | ||||||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | |||
| Total Number of Customers | 40 | Avg CPU(s) | 198 | 148 | 85 | 53.75 |
| Min CPU(s) | 183 | 129 | 77 | 45 | ||
| Max CPU(s) | 211 | 171 | 94 | 65 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 50 | Avg CPU(s) | 433.25 | 386 | 323.75 | 148.25 | |
| Min CPU(s) | 380 | 342 | 298 | 111 | ||
| Max CPU(s) | 470 | 416 | 367 | 189 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 60 | Avg CPU(s) | 1079.25 | 614 | 550.25 | 458 | |
| Min CPU(s) | 950 | 443 | 499 | 401 | ||
| Max CPU(s) | 1290 | 890 | 629 | 507 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 70 | Avg CPU(s) | 2157 | 1900.5 | 1118.5 | 1040.25 | |
| Min CPU(s) | 1910 | 1663 | 961 | 855 | ||
| Max CPU(s) | 2386 | 2100 | 1318 | 1295 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 80 | Avg CPU(s) | 7306.25 | 5247 | 3195 | 2152.75 | |
| Min CPU(s) | 6802 | 4923 | 2821 | 2001 | ||
| Max CPU(s) | 7821 | 5599 | 3506 | 2254 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 90 | Avg CPU(s) | 10,605.75 | 8262 | 6677 | 3284.25 | |
| Min CPU(s) | 9712 | 7841 | 6265 | 2978 | ||
| Max CPU(s) | 11,634 | 8666 | 7115 | 3504 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 100 | Avg CPU(s) | 13,265.25 | 11,688.75 | 9702.5 | 4778.25 | |
| Min CPU(s) | 12,032 | 11,312 | 9419 | 4322 | ||
| Max CPU(s) | 14,222 | 12,061 | 10,056 | 5023 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| Minimum Number of Vehicles at the Port | ||||||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | |||
| Total Number of Customers | 40 | Avg Number of Used Vehicles | 9.25 | 11.25 | 13.5 | 17.5 |
| Min Number of Used Vehicles | 9 | 10 | 12 | 16 | ||
| Max Number of Used Vehicles | 10 | 12 | 15 | 19 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 50 | Avg Number of Used Vehicles | 10.25 | 11.75 | 17.5 | 21 | |
| Min Number of Used Vehicles | 9 | 10 | 15 | 17 | ||
| Max Number of Used Vehicles | 12 | 14 | 19 | 25 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 60 | Avg Number of Used Vehicles | 16.75 | 21.25 | 23 | 27 | |
| Min Number of Used Vehicles | 16 | 19 | 22 | 26 | ||
| Max Number of Used Vehicles | 17 | 23 | 24 | 28 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 70 | Avg Number of Used Vehicles | 23.25 | 25.75 | 28.75 | 31.75 | |
| Min Number of Used Vehicles | 21 | 25 | 27 | 31 | ||
| Max Number of Used Vehicles | 25 | 27 | 30 | 33 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 80 | Avg Number of Used Vehicles | 25.75 | 28.5 | 33 | 36.25 | |
| Min Number of Used Vehicles | 25 | 28 | 33 | 35 | ||
| Max Number of Used Vehicles | 27 | 29 | 33 | 38 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 90 | Avg Number of Used Vehicles | 25.5 | 30.75 | 36.25 | 42.5 | |
| Min Number of Used Vehicles | 24 | 30 | 33 | 39 | ||
| Max Number of Used Vehicles | 27 | 31 | 39 | 45 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 100 | Avg Number of Used Vehicles | 29.5 | 34 | 41.5 | 46.25 | |
| Min Number of Used Vehicles | 29 | 33 | 40 | 45 | ||
| Max Number of Used Vehicles | 30 | 35 | 43 | 47 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| Minimum Number of Vehicles at the Port | ||||||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | |||
| Total Number of Customers | 40 | Avg Optimality Gap (%) | 0 | 0 | 0 | 0 |
| Min Optimality Gap (%) | 0 | 0 | 0 | 0 | ||
| Max Optimality Gap (%) | 0 | 0 | 0 | 0 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 50 | Avg Optimality Gap (%) | 0 | 0 | 0 | 0 | |
| Min Optimality Gap (%) | 0 | 0 | 0 | 0 | ||
| Max Optimality Gap (%) | 0 | 0 | 0 | 0 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 60 | Avg Optimality Gap (%) | 0 | 0 | 0.00033 | 0.00025 | |
| Min Optimality Gap (%) | 0 | 0 | 0.00007 | 0.00006 | ||
| Max Optimality Gap (%) | 0 | 0 | 0.00104 | 0.00044 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 70 | Avg Optimality Gap (%) | 0 | 0 | 0 | 0 | |
| Min Optimality Gap (%) | 0 | 0 | 0 | 0 | ||
| Max Optimality Gap (%) | 0 | 0 | 0 | 0 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 80 | Avg Optimality Gap (%) | 0 | 0 | 0.00062 | 0.00055 | |
| Min Optimality Gap (%) | 0 | 0 | 0.00005 | 0.00006 | ||
| Max Optimality Gap (%) | 0 | 0 | 0.00128 | 0.00177 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 90 | Avg Optimality Gap (%) | 0.00192 | 0.00162 | 0.00060 | 0.00011 | |
| Min Optimality Gap (%) | 0.00061 | 0 | 0 | 0 | ||
| Max Optimality Gap (%) | 0.00288 | 0.00324 | 0.00219 | 0.00042 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
| 100 | Avg Optimality Gap (%) | 0.00198 | 0.00153 | 0.00088 | 0.00061 | |
| Min Optimality Gap (%) | 0.00008 | 0 | 0.00002 | 0.00037 | ||
| Max Optimality Gap (%) | 0.00319 | 0.00242 | 0.00177 | 0.00089 | ||
| Number of Instances | 4 | 4 | 4 | 4 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emre, T.; Erol, R. An Exact Algorithm for Continuous Ship Unloading Based on Vehicle Routing. Systems 2025, 13, 883. https://doi.org/10.3390/systems13100883
Emre T, Erol R. An Exact Algorithm for Continuous Ship Unloading Based on Vehicle Routing. Systems. 2025; 13(10):883. https://doi.org/10.3390/systems13100883
Chicago/Turabian StyleEmre, Toygar, and Rızvan Erol. 2025. "An Exact Algorithm for Continuous Ship Unloading Based on Vehicle Routing" Systems 13, no. 10: 883. https://doi.org/10.3390/systems13100883
APA StyleEmre, T., & Erol, R. (2025). An Exact Algorithm for Continuous Ship Unloading Based on Vehicle Routing. Systems, 13(10), 883. https://doi.org/10.3390/systems13100883






