Decision-Making and Contract Coordination of Closed-Loop Supply Chain with Dual-Competitive Retail and Recycling Markets

Abstract

Sales competition and recycling rivalry are critical factors affecting the operation of closed-loop supply (CLSC). The existing research on competitive CLSCs primarily analyzes the impact of competition between two sales entities and/or two recycling entities on management decisions. To make the study more realistic, this study constructs a Stackelberg game model with the manufacturer as a leader, and analyzes the impacts of competition among $n$ retailers ($\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} n\ge 2$) and rivalry among $m$ third-party recyclers $(\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} m\ge 2)$ on the decision-making and profits of both node enterprises and the supply chain system, and proposes a linear transfer-payment contract to coordinate the CLSC from an economic perspective. Numerical analyses are conducted to visualize the effects of competition on the decisions and profits. The key findings are as follows: (1) In the centralized system, inter-retailer competition reduces optimal order quantities but does not affect optimal retail prices. In the decentralized system, however, it decreases both optimal order quantities and retail prices. (2) Rivalry among recyclers reduces their optimal recycling volumes but does not affect their optimal recycling prices in the centralized system. In the decentralized system, however, such rivalry not only decreases recycling volumes but also increases optimal recycling prices. (3) The manufacturer’s product wholesale price and used product recycling price remain independent of competitive interactions among retailers and recyclers in the decentralized system. (4) Competition among retailers and recyclers positively affects the profits of the CLSC and the manufacturer, but negatively impacts those of retailers and recyclers. (5) When the reward–penalty factors for product order and used product recycling fall within a specific range, the linear transfer-payment contract can coordinate the CLSC in the presence of competition in both retail and recycling. (6) All enterprises’ profits are sensitive to the penalty–reward factor, but this sensitivities also gradually decrease as the number of retailers and (or) recyclers increases.

1. Introduction

The rapid development of industrialization and the accelerated pace of product replacement have led to the generation of numerous used products [1]. Directly discarding them will not only cause environmental pollution but also result in significant waste of recoverable resources. As a result, the recycling and remanufacturing of used products have become a prevalent option in today’s world [2]. As a cleaner production method, remanufacturing can not only generate revenue, promote economic growth, and create many new job opportunities, but also create environmental incentives for manufacturers [3]. Many countries have therefore enacted legislation requiring manufacturers to adopt integrated green management systems and remanufacturing practices throughout the product lifecycle, from material sourcing to end-of-life recycling [4].

Research in the management of the CLSC has analyzed the impacts of various factors on decisions and profits. These factors include information sharing [5,6], environmental awareness [7,8], government subsidies [9,10], return effort or return rate [11,12], and contract coordination [13,14], among others. However, the influence of dual competition in both forward and reverse channels on the CLSC has rarely been explored. In practice, manufacturers typically sell products through multiple retailers and outsource the collection of used products to numerous recyclers.

The profitability of a manufacturer implementing recycling and remanufacturing of used products exhibits dual dependencies. It depends on both the manufacturer’s endogenous decisions and the exogenous operational decisions of retailers and third-party recyclers. However, traditional investment return theory is limited in analyzing such strategic dependence issues. Game theory, particularly Stackelberg game models, offers an effective approach to analyzing these problems [15]. This method has been widely applied in research on the CLSC management for remanufacturing.

In order to provide a reference for management decisions and incentive mechanisms in closed-loop supply chains with multiple sellers and multiple recyclers, this paper employs Stackelberg game theory to investigate management decisions, contract design, and the impact of competition within a CLSC comprising one manufacturer, $n$ retailers $\left(n\ge 2\right)$, and $m$ recyclers $(m\ge 2)$.

This study tries to find the answers to the following questions:

(1)

What is the effect of changing the number of retailers and collectors on the decisions and profits of supply chain members and the system as a whole?

(2)

How can a contract be designed to achieve perfect coordination in a closed-loop supply chain with dual-competitive retail and recycling markets?

The contributions of this paper with respect to the existing literature are as follows:

(1)

To our knowledge, this study represents the first attempt to investigate management decisions in a closed-loop supply chain system comprising one manufacturer, $n$ retailers, and $m$ recyclers.

(2)

The study uncovers the dynamics of how competition influences supply chain management decision-making.

(3)

The research involves a linear transfer-payment contract designed to achieve perfect coordination within the supply chain.

The remainder of this paper is organized as follows. Section 2 reviews the relevant literature. The problem description, notations, and assumptions are provided in Section 3, followed by the model formulation in Section 4. The numerical analysis is shown in Section 5, and the last section concludes the paper with main findings, management insights, limitations, and directions for future research.

2. Literature Review

In this study, the literature relevant to this text is reviewed in three ways: competition in sales channels, competition in recycling channels, and dual competition in sales channels and recycling channels in closed-loop supply chains.

2.1. Competition in Sales Channels

The presence of multiple sales entities distributing products from the same manufacturer has intensified market competition. Consequently, scholars have extensively investigated decision-making in CLSC management involving sales competition within the forward supply chain. Zheng et al. [16] and Pal and Sana [17] examined the effects of forward-channel sales competition on dual-channel CLSCs, which comprise a manufacturer, a retailer, and a collector. The manufacturer may wholesale products to the retailer or sell directly to consumers, while the collector manages used product collection. Xie et al. [18] developed a revenue and cost-sharing contract to coordinate a CLSC with dual sales channels. Zheng et al. [19] examined manufacturers’ reverse channel choices and coordination mechanisms in CLSCs with competitive dual sales channels. Wei and Zhao [20] incorporated fuzziness into collection and remanufacturing costs, using game theory and fuzzy set theory to study optimal pricing decisions for wholesale/retail prices and remanufacturing rates in a fuzzy CLSC with retail competition. Similarly, Ke et al. [21] addressed pricing and remanufacturing decisions in a fuzzy CLSC with one manufacturer, two competitive retailers, and one third-party collector. Das et al. [22] applied fuzzy theory to analyze the impact of online sales by one manufacturer competing with offline sales by one retailer on the closed-loop supply chain and designed a two-part tariff contract to coordinate the supply chain.

2.2. Competition in Recycling Channels

In light of the competitive landscape in used product collection, scholars have explored decision-making challenges in CLSC management, building on Savaskan’s foundational models. These studies typically address recycling competition within reverse supply chains. Ranjbar et al. [2] evaluated optimal pricing and collection decisions in a three-level CLSC under channel leadership with competitive dual-recycling channels: retailer collection and third-party collection. Shu et al. [23] analyzed the impact of two collectors’ fairness concerns on pricing decisions and coordination. Suvadarshini et al. [24] analyzed three return-channel structures under simultaneous influences of competition, collection efficiencies, individual rationality, and information asymmetry. Gaula and Jha [25] studied pricing and quality improvement strategies in a CLSC with dual-collection channels. To explore consumer behavior effects on competitive dual-collection supply chains, Wang et al. [26] developed two CLSC models: (1) retailer and third-party collection, and (2) manufacturer and third-party collection. He et al. [27] proposed a hybrid game-theoretic CLSC model with a manufacturer, a retailer, and a third-party collector, devising collection functions accommodating varying competition levels—from monopoly to duopoly and hybrid scenarios.

2.3. Dual Competition in Sales Channels and Recycling Channels

To better align research with real-world complexities, a limited number of scholars have investigated optimization problems in CLSCs involving both retail competition and recycling competition. Giri et al. [28] analyzed a CLSC with two dual channels: a forward dual channel where a manufacturer sells products through traditional retail and e-tail channels, and a reverse dual channel where it collects used products for remanufacturing through third-party logistics and e-tail channels. Under the premise of considering the manufacturer’s direct online sales, Zhang et al. [29] examined the impact of sales competition and recycling competition between manufacturer and retailer on CLSC management, while considering product quality and returns. They also designed an effective revenue-sharing contract to motivate retailers’ recycling efforts. Hosseini-Motlagh et al. [30] studied a CLSC comprising a manufacturer investing in remanufacturing and energy-saving efforts, two retailers competing in sales, and two collectors competing in used product collection, proposing a cost–tariff contract for system coordination.

In summary, the studies presented in [5,6,7,8,9,10,11,12,13,14] have enriched the theoretical foundations of CLSC management, but most studies assume bilateral or trilateral monopolies within the supply chain, overlooking the influence of competitive factors. The literature in Section 2.1 focused solely on competition in the forward sales channel while ignoring competition in the reverse recycling channel. In contrast, the studies in Section 2.2 only considered competition in the reverse recycling channel while failing to account for it in the forward sales channel. The studies in Section 2.3 have considered competitions in the sales channel and recycling channel, but mainly from the perspective of competition between two entities. In reality, however, oligopolistic markets formed by multiple retailers are common within a regional context, such as the dominance of Walmart, Carrefour, CR Vanguard, and Hualian in the retail sectors. Additionally, a manufacturer typically outsources used product collection to multiple professional third-party collectors. Building on existing research and drawing on Cachon’s revenue function, this paper intends to explore decisions and contract coordination in a CLSC with competition in both retail and recycling, with one manufacturer, $n\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{s}(n\ge 2)$, and $m\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{s}(m\ge 2)$, to enhance the conclusion generalizability.

Table 1. A comparison of the present model with the existing CLSC models on competition in both forward and reverse channels.

Author(s)	Forward Channel		Reverse Channel		Coordination Contract
	Selling Entity	Relationship Between Sales Volume and Price	Collection Entity	Relationship Between Collection Amount and Price
Giri et al. [28]	A manufacturer and a retailer	Competitive selling prices govern sales volume	A manufacturer and a third party	The recycling price is independent of the collection amount	×
Zhang et al. [29]	A manufacturer and a retailer	Competitive selling prices govern sales volume	A manufacturer and a retailer	The recycling price is independent of the collection amount	Revenue-sharing contract
Hosseini-Motlagh et al. [30]	A manufacturer and two retailers	Competitive selling prices govern sales volume	Two collectors	The recycling price is independent of the collection amount	Cost–tariff contract
Our model	$n$ retailers	Sales volume governs selling prices	$m$ recyclers	Collection amount governs recycling price	Linear transfer-payment contract

where “×” denotes the absence of a designed coordination contract.

highlights the main differences between this study and the previous studies on competition in both forward and reverse channels.

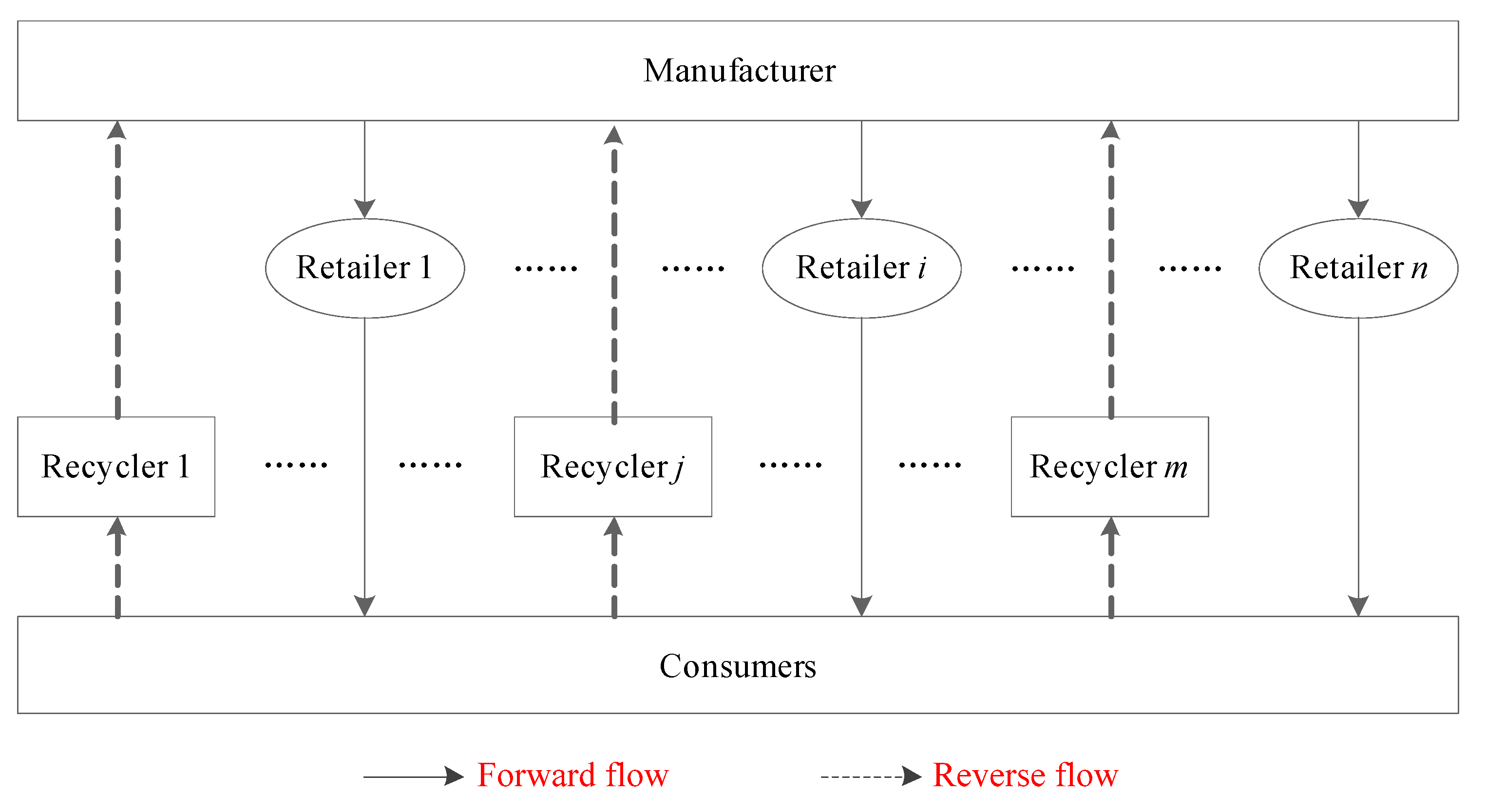
3. Problem Description and Notations

We consider the CLSC consisting of one manufacturer, $n$ retailers, and $m$ third-party collectors. The manufacturer engages in dual production modes: traditional manufacturing (using new materials) and remanufacturing (using used products). The $n$ retailers submit orders to the manufacturer and sell products to consumers. The $m$ third-party collectors collect used products from consumers and supply them to the manufacturer (see Figure 1).

The notations and their definitions used in this paper are listed in

Table 2. Notations and definitions.

Notations	Definitions
$c$	Unit cost of manufacturing new products using new materials (USD/unit)
$c_r$	Unit cost of remanufacturing used products (USD/unit)
$∆$	Unit remanufacturing cost savings, $∆=c-c_r>0$ (USD/unit)
$b$	Unit recycling price of used products paid by the manufacturer to the third-party recycler (USD/unit)
$w$	Wholesale price per unit set by the manufacturer (USD/unit)
$q_i$	Retailer i’s order quantity from the manufacturer $(i=\mathrm{1,2},\dots \dots ,n)$ (units)
$l_j$	Collection quantity of used products by the third-party collector $j$ from consumers $(j=\mathrm{1,2},\dots \dots ,m)$ (units)
$h$	The selling price of the product when all retailers’ order sizes are zero (USD/unit)
$\alpha$	The competitive intensity in the retail market
$k$	The recycling price of used products when the collection quantities of all recyclers are zero (USD/unit)
$\beta$	The competitive intensity in the recycling market
$\gamma$	Reward–penalty factor for product-ordering within a linear transfer-payment contract (USD/unit)
$\delta$	Reward–penalty factor for recycling of used products within a linear transfer-payment contract (USD/unit)
$q_0$	Minimum order quantity required by the manufacturer within a linear transfer-payment contract (units)
$l_0$	Minimum recycling quantity required by the manufacturer within a linear transfer-payment contract (units)
${\pi }_s$	Profit of the manufacturer (USD)
${\pi }_{ri}$	Profit of the retailer $i$ $(i=\mathrm{1,2},\dots \dots ,n)$ (USD)
${\pi }_{rcj}$	Profit of the recycler $j$ $(j=\mathrm{1,2},\dots \dots ,m)$ (USD)
${\pi }_{clsc}$	Profit of the CLSC (USD)
$*$	Index of the decentralized decision-making
$**$	Index of the centralized decision-making
$tr$	Index of the coordinated decision-making

.

The mathematical models in this analysis rest on the following assumptions:

Hypothesis 1.

Following the modeling precedent of the literature [31], it is assumed that remanufactured products are identical to new products in function and quality, and therefore the manufacturer sells both to the retailer at a uniform price.

Hypothesis 2.

The manufacturer acquires used products from third-party recyclers at a uniform price. All collected products meet remanufacturing quality standards.

Hypothesis 3.

Retailer competition adheres to a Cournot model, with the retail price facing retailer $i$ expressed as follows:

$$p_i=h-q_i-\alpha \sum _{e\ne i}{q}_e$$

(1)

Hypothesis 4.

Analogously, the acquisition price by recycler  $j$ takes the following form:

$$b_{rcj}=k+l_j+\beta \sum _{f\ne j}{l}_f$$

(2)

Hypothesis 5.

The manufacturer serves as the Stackelberg leader in the CLSC, with retailers and recyclers acting as followers.

Hypothesis 6.

All node enterprises in the CLSC are rational profit-maximizers with complete market information.

Hypothesis 7.

An increase in order quantity by retailer $e(e\ne i)$ may negatively impact retailer $i$’s profit (i.e., ${\displaystyle \frac{\partial {\pi }_{ri}}{\partial q_e}}<0$). An increase in recycling quantity by recycler $f$ $(f\ne j)$ may negatively impact recycler j’s profit (i.e., ${\displaystyle \frac{\partial {\pi }_{rcj}}{\partial l_f}}<0$).

Hypothesis 8.

The unsold product inventories of retailer  $e$ and retailer  $i$  are interchangeable (i.e.,  ${\displaystyle \frac{{{\partial }^2\pi }_{ri}}{\partial q_i\partial q_e}}\le 0$). The recycling volumes of recycler  $f$  and recycler  $j$  are interchangeable (i.e.,  ${\displaystyle \frac{{{\partial }^2\pi }_{rcj}}{\partial l_j\partial l_f}}\le 0$).

The profit functions of the manufacturer, retailer  $i$, recycler $j$, and the CLSC can be expressed as follows:

$${\pi }_s=\sum _{i=1}^n\left(w-c\right)q_i+\sum _{j=1}^m\left(∆-b\right)l_j$$

(3)

$${\pi }_{ri}=\left(h-q_i-\alpha \sum _{e\ne i}{q}_e\right)q_i-w{q}_i$$

(4)

$${\pi }_{rcj}=b{l}_j-\left(k+l_j+\beta \sum _{f\ne j}{l}_f\right)l_j$$

(5)

$${\pi }_{clsc}=\sum _{i=1}^n{q}_i\left(h-q_i-\alpha \sum _{e\ne i}{q}_e-c\right)+\sum _{j=1}^m{l}_j\left(∆-k-l_j-\beta \sum _{f\ne j}{l}_f\right)$$

(6)

4. The Model

Based on the above research assumptions, this section will examine the decision-making in CLSC under three distinct scenarios.

4.1. Centralized Decision-Making

Centralized decision-making is modeled for a single selling period under a Cournot competition involving both sales and recycling. In the centralized system, all supply chain members are vertically integrated, and an unbiased decision-maker decides order quantities of retailers and recycling quantities of recyclers to maximize the total profit (${\pi }_{clsc}$). The decision vectors are $\overrightarrow{q}=(q_1,q_2,\dots ,q_n)$ and $\overrightarrow{l}=(l_1,l_2,\dots ,l_m)$. The corresponding decision-making problem is as follows:

$$\underset{\overrightarrow{q},\overrightarrow{l}}{\max }{\pi }_{clsc}=\sum _{i=1}^n{q}_i\left(h-q_i-\alpha \sum _{e\ne i}{q}_e-c\right)+\sum _{j=1}^m{l}_j\left(∆-k-l_j-\beta \sum _{f\ne j}{l}_f\right)$$

(7)

By solving the equations ${\displaystyle \frac{\partial {\pi }_{clsc}}{\partial q_i}}=0$ and ${\displaystyle \frac{\partial {\pi }_{clsc}}{\partial l_j}}=0$, Proposition 1 is obtained.

Proposition 1.

Under the centralized decision-making, the optimal order quantities and recycling quantities are as follows:

$$q_i^{**}={\displaystyle \frac{h-c}{2\alpha \left(n-1\right)+2}}i=\mathrm{1,2},\dots n$$

(8)

$$l_j^{**}={\displaystyle \frac{∆-k}{2\beta \left(m-1\right)+2}}j=\mathrm{1,2},\dots m$$

(9)

Substituting $q_i^{**}$ and $l_j^{**}$ into Equation (6) yields the optimal system profit (${\pi }_{clsc}^{**}$).

Proposition 2.

Under centralized decision-making, the optimal order quantities decrease as the number of retailers increases, and the optimal recycling quantities decrease as the number of recyclers increases.

4.2. Decentralized Decision-Making

Under decentralized decision-making, the manufacturer, as the leader of the CLSC, first determines the wholesale price $w$ of the products and the recycling price $b$ of used products to maximize its profit. Subsequently, competitive retailers determine their order quantities based on $w$, and competitive recyclers determine their recycling quantities based on $b$, to maximize their respective profits. This decision-making problem is formulated as follows:

$$\left\{\begin{array}{l}\underset{w,b}{\max }{\pi }_s={\displaystyle \sum _{i=1}^n}{q}_i\left(w-c\right)+{\displaystyle \sum _{j=1}^m}{l}_j\left(∆-b\right)\\ s.t.\underset{q_i}{\max }{\pi }_{ri}=(h-q_i-\alpha {\displaystyle \sum _{e\ne i}}{q}_e)q_i-w{q}_{i}i=\mathrm{1,2},\dots \dots ,n\\ {\displaystyle \underset{l_j}{\max }}{\pi }_{rcj}=b{l}_j-(k+l_j+\beta {\displaystyle \sum _{f\ne j}}{l}_f)l_{j}j=\mathrm{1,2},\dots \dots ,m\end{array}\right.$$

(10)

Using backward induction, solve ${\displaystyle \frac{\partial {\pi }_{ri}}{\partial q_i}}=0$ and ${\displaystyle \frac{\partial {\pi }_{rcj}}{\partial l_j}}=0$ to obtain $q_i^{*}={\displaystyle \frac{h-w}{\alpha \left(n-1\right)+2}}$ and $l_j^{*}={\displaystyle \frac{b-k}{\beta \left(m-1\right)+2}}$. Substituting $q_i^{*}$ and $l_j^{*}$ into Equation (3) and solving ${\displaystyle \frac{\partial {\pi }_s}{\partial w}}=0$ and ${\displaystyle \frac{\partial {\pi }_s}{\partial b}}=0$, the manufacturer’s optimal decentralized wholesale price $w^{*}$ and recycling price $b^{*}$ are derived. Substituting $w^{*}$ into $q_i^{*}$ and $b^{*}$ into $l_j^{*}$ yields the optimal decentralized order quantities for retailers and recycling quantities for recyclers.

Proposition 3.

Under decentralized decision-making, the optimal wholesale price, recycling price, order quantities, and recycling quantities are as follows:

$$w^{*}={\displaystyle \frac{h+c}{2}}$$

(11)

$$b^{*}={\displaystyle \frac{k+∆}{2}}$$

(12)

$$q_i^{*}={\displaystyle \frac{h-c}{2\alpha \left(n-1\right)+4}}i=\mathrm{1,2},\dots ,n$$

(13)

$$l_j^{*}={\displaystyle \frac{∆-k}{2\beta \left(m-1\right)+4}}j=\mathrm{1,2},\dots ,m$$

(14)

Proposition 4.

Under decentralized decision-making, the manufacturer’s optimal wholesale price and recycling price are independent of the numbers of retailers and recyclers. The optimal order quantities decrease as the number of retailers increases. The optimal recycling quantities decrease as the number of recyclers increases.

Using $w^{*}$, $b^{*}$, $q_i^{*}$, and $l_j^{*}$, the optimal profits ${\pi }_s^{*}$ for the manufacturer, ${\pi }_{ri}^{*}$ for retailers, and ${\pi }_{rcj}^{*}$ for recyclers are derived under decentralized decision-making.

4.3. Coordinated Decision-Making

Proposition 5 can be obtained by comparing $q_i^{*}$ with $q_i^{**}$ and $l_j^{*}$ with $l_j^{**}$.

Proposition 5.

The optimal order quantities and recycling quantities in decentralized decision-making are less than those in centralized decision-making.

Proposition 5 indicates that decentralized decision-making can result in a loss of profit for the CLSC, implying that there is still room for improvement in the equilibrium profit of the decentralized supply chain compared to the optimal profit of the integrated supply chain. Therefore, as the leader of the CLSC, the manufacturer can provide a cooperation contract to induce retailers and recyclers to make centralized decisions. This will maximize the profit of the supply chain while ensuring that the profits of supply chain members are no less than their corresponding profits under decentralized decision-making.

Here, a linear transfer-payment contract is introduced to coordinate the CLSC. The manufacturer provides a linear transfer-payment contingent on the retailer’s order quantity, defined as ${\theta }_i\left(q_i\right)=\gamma \left(q_i-q_0\right)$ for $i=\mathrm{1,2},\dots ,n$, aiming to incentivize retailers to increase their order quantities. Similarly, the manufacturer provides a linear transfer payment based on the recyclers’ recycling quantities, formulated as ${\phi }_j\left(l_j\right)=\delta \left(l_j-l_0\right)$ for $j=\mathrm{1,2},\dots ,m$, aiming to incentivize recyclers to increase their recycling volumes. Furthermore, the manufacturer strategically sets the minimum order quantity $q_0$ and the minimum recycling amount $l_0$, with $q_0$ depending on the competing retailers’ sales capacity and $l_0$ determined by the recyclers’ recycling capacity. To achieve coordination under this contract, the manufacturer determines the reward–penalty factors for product-ordering and used product collection.

Under the linear transfer-payment contract, the profit functions of the manufacturer, competitive retailers, and recyclers are as follows:

$${\pi }_s^{tr}={\displaystyle \sum _{i=1}^n}{q}_i\left(w-c\right)+{\displaystyle \sum _{j=1}^m}{l}_j\left(∆-b\right)-{\displaystyle \sum _{i=1}^n}{\theta }_i\left(q_i\right)-{\displaystyle \sum _{j=1}^m}{\phi }_j\left(l_j\right)$$

(15)

$${\pi }_{ri}^{tr}=\left(h-q_i-\alpha \sum _{e\ne i}{q}_e\right)q_i-w{q}_i+{\theta }_i\left(q_i\right)$$

(16)

$${\pi }_{rcj}^{tr}=b{l}_j-\left(k+l_j+\beta \sum _{f\ne j}{l}_f\right)l_j+{\phi }_j\left(l_j\right)$$

(17)

Proposition 6.

Under the linear transfer-payment contract  $(w^{tr},b^{tr},\mathsf{\gamma },\mathsf{\delta })$, the CLSC can achieve perfect coordination when  $w^{tr}=\gamma +{\displaystyle \frac{\alpha \left(n-1\right)\left(h+c\right)+2c}{2\alpha \left(n-1\right)+2}}$,  $b^{tr}=-\delta +{\displaystyle \frac{\beta \left(m-1\right)\left(∆+k\right)+2∆}{2\beta \left(m-1\right)+2}}$, provided that the reward–penalty factors  $\gamma$  and  $\delta$  satisfy the participation constraints of the manufacturer, retailers, and recyclers.

Proof of Proposition 6.

To achieve perfect coordination in the CLSC, decentralized decisions by competing retailers, on order quantities, and by recyclers, on used product recovery volumes, under a linear transfer-payment contract must align with centralized decision-making outcomes. By taking the partial derivatives of ${\pi }_{ri}^{tr}$ with respect to $q_i$ and of ${\pi }_{rcj}^{tr}$ with respect to $l_j$, setting them equal to zero, and solving the resulting system of $n+m$ equations simultaneously, we obtain the following:

$$q_i^{tr}={\displaystyle \frac{h-w+\gamma }{\alpha \left(n-1\right)+2}}$$

(18)

$$l_j^{tr}={\displaystyle \frac{b-k+\delta }{\beta \left(m-1\right)+2}}$$

(19)

By comparing $q_i^{tr}$ with $q_i^{**}$ and $l_j^{tr}$ with $l_j^{**}$, we can conclude the following:

$$w^{tr}=\gamma +{\displaystyle \frac{\alpha \left(n-1\right)\left(h+c\right)+2c}{2\alpha \left(n-1\right)+2}}$$

(20)

$$b^{tr}=-\delta +{\displaystyle \frac{\beta \left(m-1\right)\left(∆+k\right)+2∆}{2\beta \left(m-1\right)+2}}$$

(21)

Furthermore, to coordinate the CLSC, the manufacturer’s linear transfer-payment contract must satisfy the participation constraints of all supply chain members. This can be achieved by selecting appropriate values for the reward–penalty factors $\gamma$ and $\delta$.

Therefore, when the reward–penalty factors $\gamma$ and $\delta$ satisfy the participation constraints of all supply chain members, the linear transfer-payment contract achieves perfect coordination of the CLSC with competition in both retailing and recycling. □

5. Numerical Analysis

To validate the findings in Section 4, we will perform some numerical simulations on a CLSC consisting of one manufacturer, $n$ retailers $(\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}n=4,5,6,7)$, and $m$ recyclers $(\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}m=2,3,4,5)$ by making use of MATLAB 7.5.0. The values of key parameters are set as $c=255$, $c_r=130$, $h=1245$, $k=5$, $\mathsf{\alpha }=0.4,$ and $\beta =0.1$.

5.1. Changing Trends

Using the above parameters, this subsection will analyze the changing trends in the optimal values of decision variables and in the maximum profits under decentralized and centralized decision-making scenarios as the numbers of retailers and recyclers vary.

Figure 2 illustrates the variation of order quantities as $n$ increases from 4 to 7. Three conclusions are drawn:

(1)

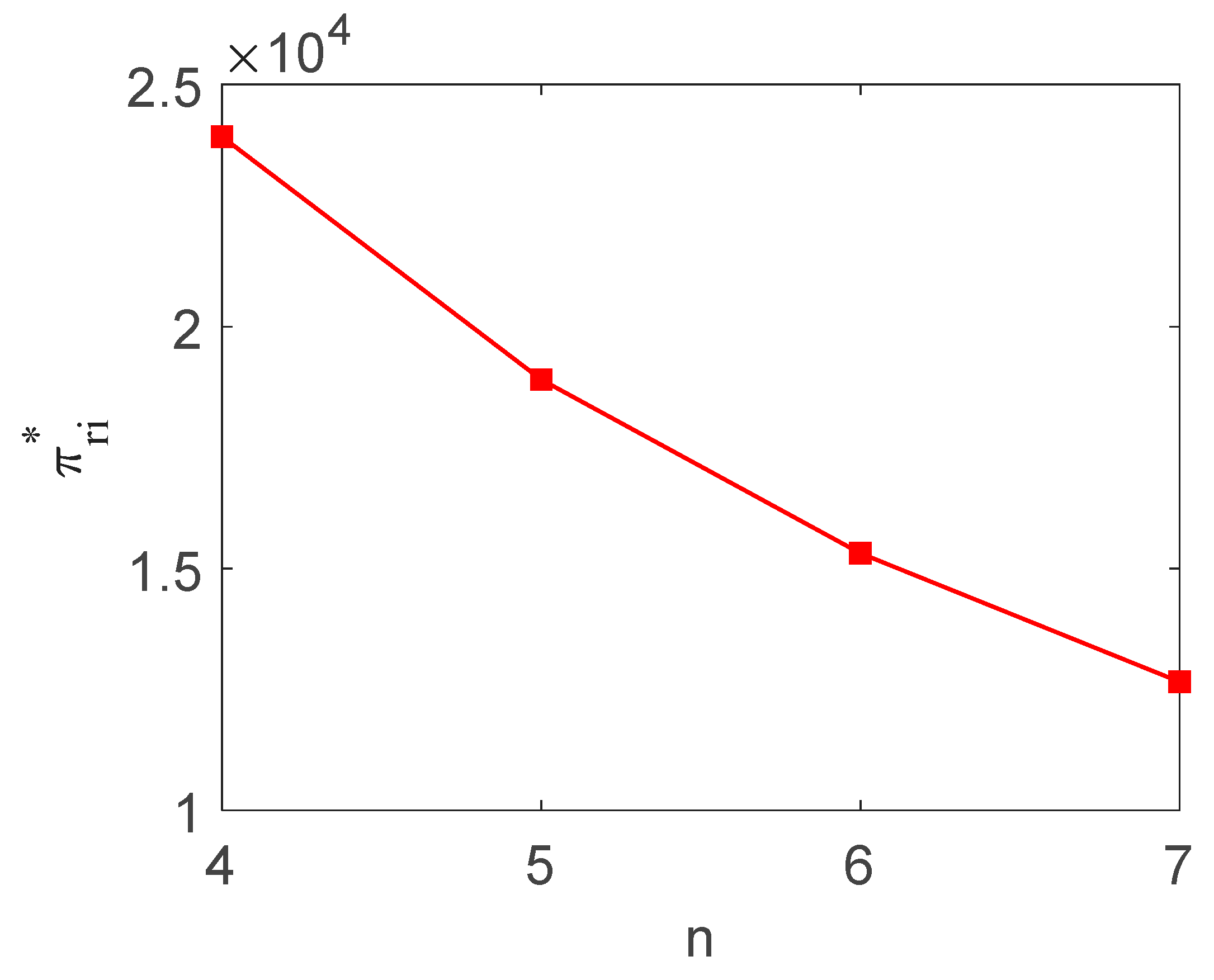
Regardless of whether decision-making is decentralized or centralized, the optimal order quantities decrease as the number of retailers increases.

(2)

Under decentralized decision-making, the optimal order quantities are consistently lower than those under the centralized scenario.

(3)

The gap between $q_i^{**}$ and $q_i^{*}$ gradually decreases as $n$ increases.

Figure 3 shows how the recycling quantities change as $m$ increases from 2 to 5. From this figure, three key observations emerge:

(1)

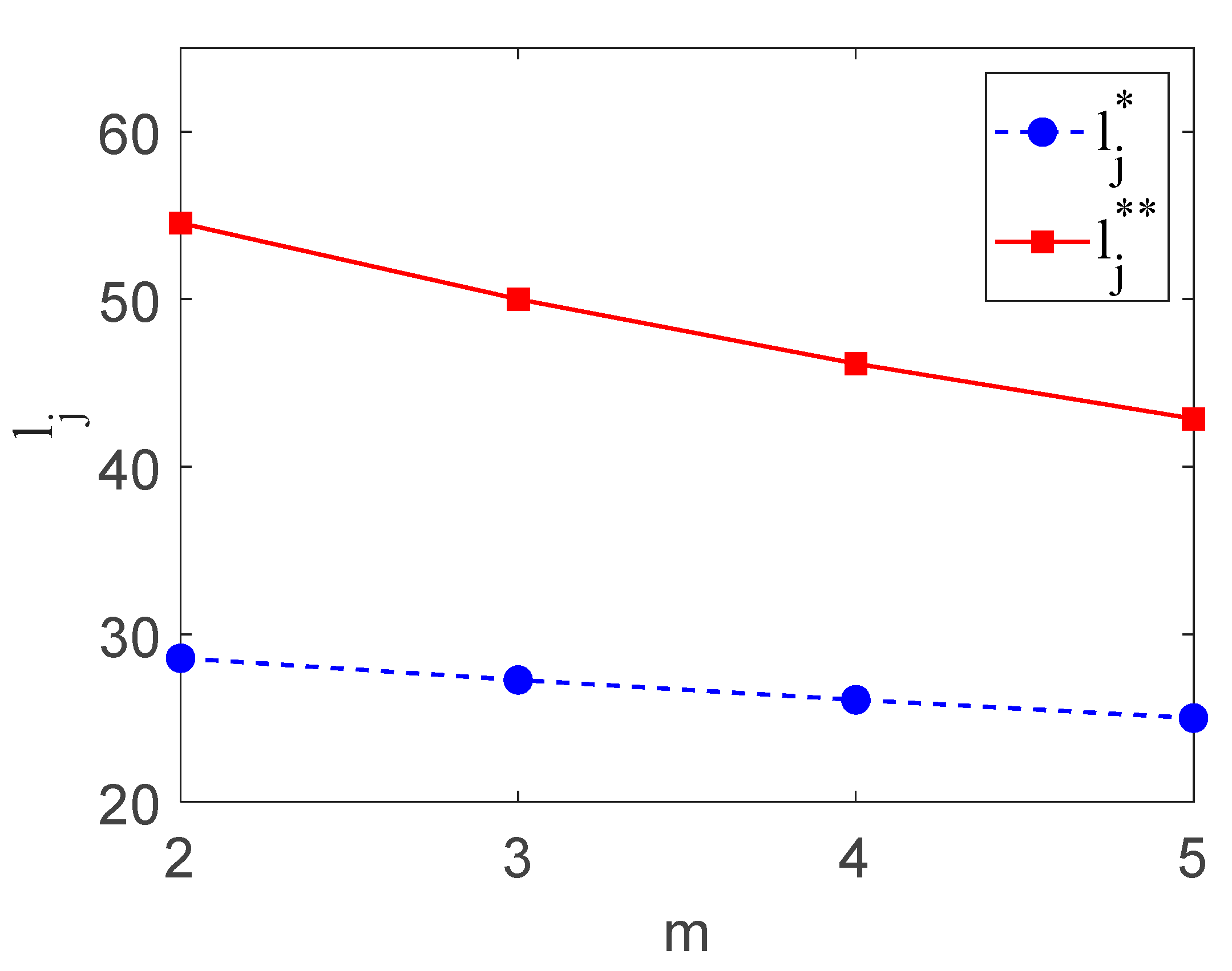
Under both decentralized and centralized decision-making, the optimal recycling quantities decline as $m$ increases.

(2)

The optimal recycling quantities under decentralized decision-making are consistently lower than those under the centralized scenario.

(3)

As $m$ increases, the difference between $l_j^{**}$ and $l_j^{*}$ gradually decreases.

Figure 4 illustrates the variation in retail price as $n$ increases from 4 to 7. Under centralized decision-making, the optimal retail price remains constant regardless of the number of retailers. In contrast, under the decentralized scenario, the optimal retail price decreases with an increasing number of retailers. As $n$ increases, the discrepancy between $p_i^{**}$ and $p_i^{*}$ gradually decreases.

Figure 5 shows how the recycling price changes as $m$ increases from 2 to 5. Under centralized decision-making, the optimal recycling price remains constant regardless of the number of recyclers. However, under decentralized decision-making, the optimal recycling price increases as the number of recyclers increases. As $m$ increases, the difference between $b_{rcj}^{**}$ and $b_{rcj}^{*}$ gradually decreases.

Figure 6 and Figure 7 show how the profits of the CLSC change as $n$ varies from 4 to 7 and $m$ from 2 to 5. From these figures, two conclusions are drawn:

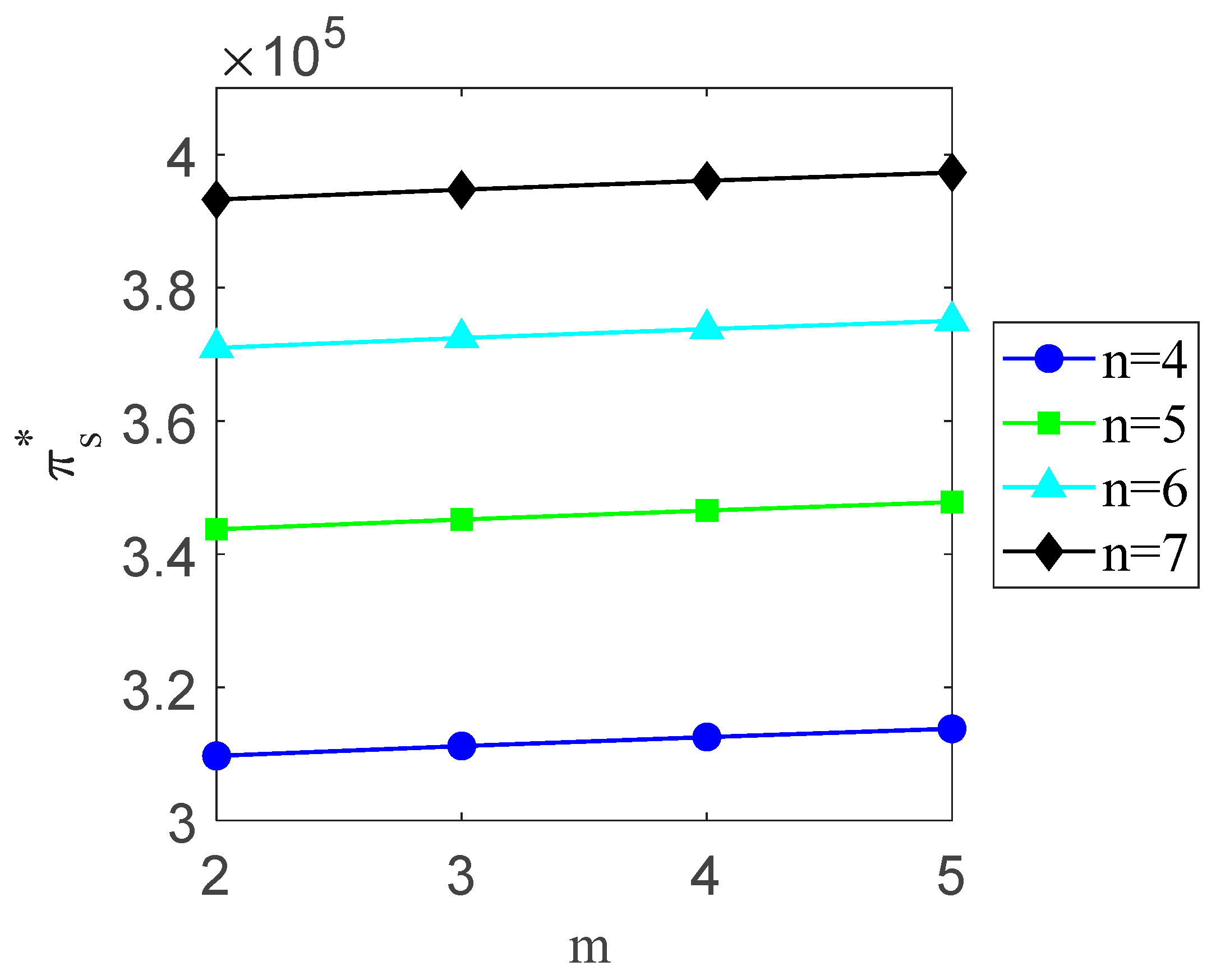
(1)

Under both decentralized and centralized decision-making, the optimal profits of the supply chain increase with the number of retailers or recyclers.

(2)

The optimal profits of the supply chain under decentralized decision-making are always lower than those under a centralized scenario. These lower profits indicate that the supply chains are in a state of discoordination.

Figure 8 shows the variation in the manufacturer’s optimal profits as $n$ ranges from 4 to 7 and $m$ ranges from 2 to 5. Profits exhibit a positive correlation with retailer count and recycler count.

Figure 9 demonstrates a negative correlation between the number of retailers and their optimal profits, while Figure 10 illustrates a similar inverse relationship between the number of recyclers and their optimal profits.

5.2. Contract Coordination Effect

The minimum order quantity and recycling quantity required by the manufacturer within a linear transfer-payment contract are set as $q_0=140$ and $l_0=37$. Based on the participation constraints of the node enterprises and the condition $b^{tr}>0$, the reward–penalty factors of the contract must satisfy the following derived conditions for each pair $(n,m)$ in $\{\left(\mathrm{5,2}\right)$, $\left(\mathrm{6,3}\right)$, $\left(\mathrm{7,4}\right)\}$.

$$\begin{gathered} \left\{\begin{array}{l}700\gamma +74\delta +290,565.4287\ge \mathrm{343,740}\\ \mathrm{36,246.3073}-140\gamma \ge \mathrm{18,906}\\ \begin{array}{c}2975.2061-37\delta \ge 816.3266\\ \begin{array}{l}\hspace{1em}0<\delta <119.5455\\ \hspace{1em}\gamma >0\end{array}\end{array}\end{array}\right.\left\{\begin{array}{l}1140\gamma +111\delta +\mathrm{328,200}\ge \mathrm{372,450}\\ \mathrm{27,225}-140\gamma \ge \mathrm{15,314}\\ \begin{array}{c}2500-37\delta \ge 743.8018\\ \begin{array}{l}\hspace{1em}0<\delta <115\\ \hspace{1em}\gamma >0\end{array}\end{array}\end{array}\right. \\ \left\{\begin{array}{l}980\gamma +148\delta +\mathrm{358,647.8641}\ge \mathrm{396,070}\\ \mathrm{21,195.9240}-140\gamma \ge \mathrm{12,656}\\ \begin{array}{c}2130.1760-37\delta \ge 680.5290\\ \begin{array}{l}\hspace{1em}0<\delta <111.1538\\ \hspace{1em}\gamma >0\end{array}\end{array}\end{array}\right. \end{gathered}$$

(22)

Using the above system of inequalities and related parameters, we can obtain appropriate values for the reward-penalty factors along with corresponding coordination variable values and node enterprise profits in

Table 3. Values of coordination variables.

$\left(\mathit{n},\mathit{m}\right)$	$\mathsf{\gamma }$	$\mathsf{\delta }$	${\mathit{w}}^{\mathit{t}\mathit{r}}$	${\mathit{b}}^{\mathit{t}\mathit{r}}$
$\left(\mathrm{5,2}\right)$	100	50	659.6154	69.5455
$\left(\mathrm{6,3}\right)$	50	40	635	75
$\left(\mathrm{7,4}\right)$	35	30	639.4118	81.1538

and

Table 4. Evaluation of coordination effects.

$\left(\mathit{n},\mathit{m}\right)$	${\mathit{\pi }}_{\mathit{c}\mathit{l}\mathit{s}\mathit{c}}^{\mathit{t}\mathit{r}}\left({\mathit{\pi }}_{\mathit{c}\mathit{l}\mathit{s}\mathit{c}}^{**}\right)$	${\mathit{\pi }}_{\mathit{s}}^{\mathit{t}\mathit{r}}$	${\mathit{\pi }}_{\mathit{r}\mathit{i}}^{\mathit{t}\mathit{r}}$	${\mathit{\pi }}_{\mathit{r}\mathit{c}\mathit{j}}^{\mathit{t}\mathit{r}}$
$\left(\mathrm{5,2}\right)$	477,750	364,265	22,246	1125
	${\pi }_{clsc}^{*}$	${\pi }_s^{*}$	${\pi }_{ri}^{*}$	${\pi }_{rcj}^{*}$
	439,900	343,740	18,906	816.3266
$\left(\mathrm{6,3}\right)$	${\pi }_{clsc}^{tr}\left({\pi }_{clsc}^{**}\right)$	${\pi }_s^{tr}$	${\pi }_{ri}^{tr}$	${\pi }_{rcj}^{tr}$
	499,050	374,640	20,225	1020
	${\pi }_{clsc}^{*}$	${\pi }_s^{*}$	${\pi }_{ri}^{*}$	${\pi }_{rcj}^{*}$
	466,570	372,450	15,314	743.8018
$\left(\mathrm{7,4}\right)$	${\pi }_{clsc}^{tr}\left({\pi }_{clsc}^{**}\right)$	${\pi }_s^{tr}$	${\pi }_{ri}^{tr}$	${\pi }_{rcj}^{tr}$
	515,542	397,390	16,296	1020
	${\pi }_{clsc}^{*}$	${\pi }_s^{*}$	${\pi }_{ri}^{*}$	${\pi }_{rcj}^{*}$
	487,380	396,070	12,656	680.5290

where ${\pi }_{clsc}^{tr}={\pi }_s^{tr}+n{\pi }_{ri}^{tr}+m{\pi }_{rcj}^{tr}$.

(a brief worked example can be found in Appendix A).

From Table 4, two key conclusions can be drawn: (1) Under the linear transfer-payment contract, the profits of all supply chain members consistently exceed those under the decentralized scenario. (2) The total profit under this contract matches the maximum profit achievable by an integrated supply chain. These results demonstrate that the linear transfer-payment contract can achieve perfect coordination of the CLSC.

5.3. Sensitivity Analyses

The value of the reward–penalty factors directly influences the optimal profits of node enterprises under the coordination contract. The sensitivity analyses of the latter to the former are presented below:

Table 5. Sensitivity analysis of ${\pi }_s^{tr}$ (${\pi }_{ri}^{tr}$) to $\mathsf{\gamma }$.

$\mathit{\delta }$	$(\mathbf{n},\mathbf{m})$	$\mathbf{The}\mathbf{Value}\mathbf{of}\mathsf{\gamma }$	Profit
			${\mathit{\pi }}_{\mathit{s}}^{\mathit{t}\mathit{r}}$	${\mathit{\pi }}_{\mathit{r}\mathit{i}}^{\mathit{t}\mathit{r}}$
50	$(5,2)$	75	370,563.5173	20,986.6885
		80	369,303.9023	21,238.6115
		85	368,044.2873	21,490.5345
		90	366,784.6723	21,742.4575
40	$(6,3)$	45	375,390	20,100
		50	374,640	20,225
		55	373,890	20,350
		60	373,140	20,475
30	$(7,4)$	35	397,387.8641	16,295.9415
		40	397,192.2771	16,323.8825
		45	396,996.6901	16,351.8235
		50	396,801.1031	16,379.7645

and

Table 6. Sensitivity analysis of ${\pi }_s^{tr}$ (${\pi }_{rcj}^{tr}$) to $\delta$.

$\mathit{\gamma }$	$(\mathbf{n},\mathbf{m})$	$\mathbf{The}\mathbf{Value}\mathbf{of}\mathit{\delta }$	Profit
			${\mathit{\pi }}_{\mathit{s}}^{\mathit{t}\mathit{r}}$	${\mathit{\pi }}_{\mathit{r}\mathit{c}\mathit{j}}^{\mathit{t}\mathit{r}}$
100	$(5,2)$	35	364,791.8037	862.0264
		40	364,616.3523	947.7539
		45	364,440.8973	1037.4814
		50	364,265.4423	1125.2089
50	$(6,3)$	30	375,030	890
		35	374,835	955
		40	374,640	1020
		45	374,445	1080
35	$(7,4)$	23	394,644.1705	956.0995
		28	397,461.0945	1001.8685
		33	397,278.0185	1047.6375
		38	397,094.9425	1093.4065

show the sensitivities of the node enterprises’ profits to reward–penalty factors. From these tables, the following conclusions are drawn:

(1)

The manufacturer’s profit is sensitive to the penalty–reward factors, but this sensitivity gradually decreases as the number of retailers and recyclers increases.

(2)

Every retailer’s (recycler’s) profit is sensitive to the penalty–reward factor for product-ordering (recycling of used products), but this sensitivity gradually decreases as the number of recyclers (recyclers) increases.

(3)

Within a defined supply chain system, the manufacturers are consistently more sensitive to the penalty–reward factor for product-ordering (recycling of used products) compared to retailers (recyclers).

6. Conclusions, Managerial Implications, and Limitations

6.1. Conclusions

To better align the research question with real-world contexts and enhance the generalizability of the findings, this study examines a CLSC consisting of a manufacturer, $n$ retailers, and $m$ recyclers, highlighting the impact of retailers’ and recyclers’ competition on order quantities, recycling volumes, and profits. A linear transfer-payment contract model is developed to maximize the total profit of the CLSC based on the Cachon profit function. The numerical results validate the theoretical analysis. The following conclusions can be derived:

(1)

Under decentralized decision-making, an increase in the number of retailers reduces their optimal order quantities and retail prices. In contrast, under centralized decision-making, more retailers lower optimal order quantities but leave the optimal retail price unaffected. For recyclers, decentralized decision-making results in decreased recycling volumes yet higher optimal recycling prices as their numbers grow. Under centralized decision-making, however, more recyclers reduce recycling volumes, while the optimal recycling price remains stable.

(2)

Competition among retailers or recyclers enhances profits for the supply chain and the manufacturer, whereas retailer competition erodes retailers’ profits, and recycler competition similarly diminishes recyclers’ profits.

(3)

When the order quantity reward–penalty factor $\gamma$ and the recycling volume reward–penalty factor $\delta$ fall within specified ranges, the linear transfer-payment contract achieves coordination in a competitive CLSC comprising one manufacturer, $n$ retailers, and $m$ recyclers.

(4)

Every enterprise’s profit is sensitive to the penalty–reward factor, but this sensitivity also gradually decreases as the number of retailers and (or) recyclers increases.

6.2. Managerial Implications

Based on the research conclusions, the following managerial implications can be derived:

(1)

Initially, the dominant manufacturer should collaborate with as many retailers and recyclers as possible, provided they are willing, as this benefits the manufacturer, the supply chain, and consumers.

(2)

After a period of collaboration with all retailers and recyclers, the dominant manufacturer should conduct a systematic evaluation of their commercial credibility and default risks, and subsequently establish long-term partnerships with as many retailers and recyclers as possible who demonstrate high commercial credibility and low default risks.

(3)

The dominant manufacturer introduces the linear transfer-payment contract to all long-term partners (retailers and recyclers), elaborating on its benefits for all supply chain members.

(4)

Based on historical commercial collaboration data and participation constraints, the manufacturer preliminarily determines the value of the reward–penalty factor in the cooperation contract, and finalizes its value through negotiations with retailers and recyclers.

(5)

All supply chain members engage in a new round of commercial cooperation based on a linear transfer-payment contract.

(6)

At the end of a collaboration cycle, the manufacturer evaluates the collaborative performance, identifies issues, analyzes their causes, and implements solutions to ensure the continuity of the cooperation.

6.3. Limitations

Further research should address the limitations of this study. First, this study assumes that new and remanufactured products are priced equally. Exploring scenarios where remanufactured products are sold at a discount relative to new ones could be a valuable extension. Second, the model in this paper does not account for the non-remanufacturing rate of used products. Future work could integrate the fuzzy set theory to quantify the non-remanufacturing rate. Third, manufacturer competition is excluded from the current framework. Given that product homogeneity intensifies market competition, extending the model to include multiple manufacturers would better reflect the real-world dynamics. Fourth, a key limitation of this study is its assumption of perfect information among all supply chain members. A valuable avenue for future research would therefore be to research decision-making in competitive closed-loop supply chains when information is incomplete. Fifth, this study employs simulated data in the numerical analysis. Future research could utilize real-world data from supply chain members.