Nash–Cournot Equilibrium and Its Impact on Network Transmission Congestion

Abstract

This paper evaluates the impact of congestion on transmission lines when the operation cost is minimized using economic dispatch (ED), comparing the results obtained with the Nash–Cournot Equilibrium (NCE). A methodology is developed for the optimal power flow solution through the NCE, considering the network topology (upper and lower generation limits, upper and lower limits of the transmission lines, and power balance) for a nine-node system without and considering two bilateral power transactions. The results show that the operation cost is higher when the NCE is implemented than ED. However, the problem of congestion in the transmission lines is reduced due to the equilibrium obtained in the power dispatch against minimizing the operation cost in the dispatch; the transmission lines with the most significant participation tend to become congested when additional bilateral transactions occur. Finally, the above is verified by obtaining the mean and median of the transmission line percentages used in the two simulations.

1. Introduction

A deregulated power system is one where a single entity no longer monopolizes the generation and commercialization of electrical energy. Instead, private generating companies play a significant role in selling electrical power through power dispatch. This shift in the energy market introduces new challenges, particularly in managing the behavior of the electricity market with its diverse participant objectives [1].

The objective of power generators is to sell the most significant amount of power to increase their profit, unlike the Independent System Operator (ISO), which seeks to minimize the operating cost of the electrical power system. However, in either case, whether maximizing or minimizing costs, operational factors must be considered since any result provided by economic dispatch must comply with the system’s constraints and limitations.

With so many agents interacting in the same economic and operational environment, game theory, which studies the strategic interaction between players, can be applied [1]. Game theory is an interdisciplinary approach to studying human behavior between two or more players, in which each player seeks the most significant profit, with the characteristic that the result of the game depends on the interactive strategies between players. Since game theory is a tool for participants to make decisions, it is also known as strategic decision theory [2]. Game theory is divided into two main approaches: cooperative games and non-cooperative games. Likewise, from this first division, non-cooperative games are divided into zero-sum and non-zero-sum games, static and dynamic games, and complete and incomplete information games [3,4,5].

Game theory, a versatile tool, finds practical application in various aspects of electrical power systems. In [6], cooperative games tackle a general optimal control problem where all players unite in a coalition. This approach is beneficial for simulating a system’s primary and secondary frequency controls. In reference [7], a new theoretical model is proposed that applies non-cooperative games and the Nash equilibrium for the demand management of a smart grid, considering the packet error rate in the formulation.

Reference [8] presents an efficient method to evaluate the components’ criticality for a test system’s overall reliability and its major maintenance focuses. The above uses the Shapely value, a concept from cooperative game theory that reasonably identifies the contribution of each component to the system’s reliability. This paper helps realize where investments and maintenance are needed in the grid to ensure a desirable system reliability performance. In reference [9], the Cournot model is employed to study storage systems in electricity markets. In this context, each owner of commercial storage aims to maximize their profit. At the same time, as the decision-maker in the centralized economic dispatch, the ISO plays a crucial role in maximizing social welfare.

References [10,11,12] focus on game theory as a tool for strategic bidding with significant practical implications. In [10], a stochastic approach to energy offers based on the Cournot model involving the uncertainty of renewable generation and loads is developed. Reference [11] examines bidding strategies in a bilateral market using the Nash equilibrium, which is derived from a generic matrix of generation costs and the vector of willingness to pay for the loads. The reference [12] examines the bidding strategies in a pool-based electricity market where generating companies submit bids for the available loads, with practical implications for market participants.

The application of game theory in economic power dispatch becomes valuable because it involves participants who seek the best of their profits in an environment that affects them and the entire system around them. In [13], the Cournot equilibrium in three market players in a constrained transmission system is investigated, and the non-constant marginal cost is considered. This research has practical implications, showing that a pure strategic equilibrium can fail even when a transmission constraint exceeds the value of the unconstrained Cournot equilibrium flow. Reference [14] presents a Cournot model of the day-ahead wholesale electricity market, in which strategic bidding competition and bilateral contract transactions are considered. The most intriguing part is the use of the equivalence of the optimality condition (Karush–Kuhn–Tucker condition) to convert the Cournot equilibrium model into an optimization model, and a distributed algorithm is applied to solve the optimization model.

Considering the deregulation in the generation and commercialization of electrical energy that characterizes deregulated systems, the behavior of the power dispatch takes an important role economically and technically. Its relevance extends beyond simply choosing the generator with the lowest operating cost to also considering how this decision will impact the components of the electrical power system. For example, when choosing the generator with the lowest operating cost, it is crucial to ensure that the power generated does not exceed the upper and lower generation limits, as well as the upper transmission limits of the lines. This is because traditional economic dispatch methods aim to minimize the operating cost of the system, and although the restrictions mentioned above are considered, favoring generators with lower generation costs may result in congestion of the associated transmission lines, potentially posing risks to the electrical system.

The NCE is a vector that maximizes the profit function for a general cost and demand inverse function [15]. The NCE aims to find the equilibrium point at which the generated power allows it to maximize its profits and comply with the system’s restrictions, such as the upper and lower generation limits of the participants and the maximum limits of transmission of the lines. By achieving this balance point, the equilibrium ensures that all participants operate at optimal levels, extending this balance to the other electrical power system components, such as the power flows in the transmission lines [1].

The contributions of this paper are outlined below.

• The analysis/evaluation of congestion on transmission lines comparing economic dispatch using the NCE against conventional power dispatch (ED) provides practical insights. The findings validate the profits of the NCE method, as it leads to a lower percentage of use in the test system compared to the conventional economic dispatch, thereby reducing congestion in the transmission line.
• Unlike references [1,12,13,14], which do not consider the constraints of maximum transmission line flows, reference angles, and power balance, this research develops an economic dispatch model using NCE while considering the limitations mentioned in the cited published literature.
• The model developed in this article incorporates bilateral power transactions to analyze congestion in transmission lines. Bilateral transactions are treated as constant power injections within the economic dispatch solution using NCE and conventional dispatch methods.

This article is organized as follows: Section 2 introduces the concept of the Cournot model, describes its components, and explains how it integrates with the Nash equilibrium. Section 3 presents the Cournot model as an optimization problem and emphasizes its practical application in power dispatch. The methodology for this application is developed. Section 4 shows the results obtained from the ED solution and by the NCE, as well as impacts on the congestion of transmission lines. Finally, Section 5 presents the conclusions of this work.

2. The Cournot Model

The Cournot model is an oligopolistic market model in which competition is formed between players based on the production quantity of the same product [1,16,17]. To describe the players’ behavior in the Cournot model, we start from the base concept of game theory, where it is mentioned that there is an interdependence between market participants in any type of game (cooperative or non-cooperative). Therefore, in this model, players seek to make strategic decisions that maximize their profit by anticipating how much quantity they or their opponents will produce. In addition to their opponents’ choices, players must consider the market price function and the generation cost function of each participant.

Let $K=\{\mathrm{1,2},\dots ,n\}$, where $n$ is the total number of players. The market price function $P\left(Q_T\right)$ which is defined as a positive inverse demand is given by:

$$P\left(Q_T\right)=\alpha -\beta Q_T$$

(1)

where

$Q_T=\sum _{i=1}^n{q}_i$ represents the sum of the power generated by all the players.

$\alpha$ and $\beta$ are the coefficients of the market price function.

For this work, the players are considered thermal generators; therefore, a quadratic function is chosen to be used as the cost function. It is widely recognized in the published literature that thermal unit input/output is best fitted with a quadratic function. This affirmation is backed up by accurate data from conventional thermal plants where fuel is oil, coal, and gas [18,19]. Moreover, the quadratic cost functions not only fit the data well but also allow for dealing with a convex optimization problem, ensuring that the solution is a global optimum [20,21]. The cost function $C_i\left(q_i\right)$ for each $i\in K$ is expressed as:

$$C_i\left(q_i\right){=a}_i+b_i{q}_i+c_i{q}_i^2$$

(2)

where

$C_i$ is the generation cost of player $i$.

$a_i$ $b_i$ and $c_i$ are the coefficients of the players’ quadratic cost curve.

$q_i$ is the power delivered by the player $i$.

As mentioned above, the main objective of the Cournot model is the maximization of the profits of the players in the market, and these profits are obtained through the payoff function expressed in Equation (3) as follows:

$${\pi }_i\left(q\right)=q_{i}P\left(Q_T\right)-C_i\left(q_i\right)$$

(3)

where

${\pi }_i$ is the individual profit obtained from each player $i$.

Substituting the market price function (1) and the generation cost function (2) in (3), the profit function ${\pi }_i\left(q\right)$ for each generator $i$ is obtained in the form developed in expression (4).

$${\pi }_i(q)=q_i\left(\alpha -\beta \sum _{j=1}^n{q}_j\right)-a_i-b_i{q}_i-c_i{q}_i^2$$

(4)

Applying the Cournot model in the optimal power flow solution, all players (generators in this case) decide how much power they are going to generate to satisfy one or more loads (users), with the characteristic of obtaining the most significant possible profit from the players [13]. Although the initial definition is given in two companies, it can easily be transformed into a model for n companies, thus converting it into an oligopoly model.

The Nash–Cournot Equilibrium

Understanding the competitive environment of the Cournot model and the elements necessary to carry it out, the next step is to obtain the quantities to be produced (in this case, power to be generated) by the players through the NCE. John F. Nash proposed the Nash equilibrium in the 1950s as a solution method for non-cooperative games, and, as its name indicates, its objective is to find an equilibrium point where all players can achieve the best results in the game without the ability to affect this outcome individually. Therefore, by applying the concept of the Nash equilibrium in the Cournot model, an equilibrium point known as the NCE is obtained in which the powers generated by the participants seek to maximize their profits without them being able to make individual decisions that affect the outcome of the game [1]. Continuing with the preliminaries on game theory introduced above, the Nash–Cournot equilibrium can be defined as follows [15]:

Definition 1.

The NCE is a vector of outputs $q^{*}\in {\mathbb{R}}^n$, such that for any player, $i\in K$:

$${\pi }_i\left(q^{*}\right)={\max }_{q_i\ge 0}{\pi }_i\left(q_i^{*},\dots ,q_{i-1}^{*},q_i,q_{i+1}^{*},\dots ,q_n^{*}\right)$$

(5)

Therefore, the NCE can be obtained as the solution of an optimization problem set for each player $i$ as shown in (5). The Karush–Kuhn–Tucker (KKT) conditions, which optimal solutions to optimization problems must satisfy, take the form of a set of partial derivative equations with respect to $q_i$. Thus, a NCE can be calculated as the solution to the set of equations, with as many equations as variables $q_i$ [20]. For this work, the NCE is found by solving the set of equations obtained by the KKT conditions of the payment functions of each generator that consider the decision variables (power to be generated) of the adversary generators.

3. The Cournot Model as an Optimization Problem

An optimization problem is one in which we seek to maximize or minimize a variable (e.g., minimize costs or maximize profits) through an objective function subject to different restrictions [20]. The general structure of an optimization problem is given by expressions (6)–(8).

$$\min f\left(x\right)$$

(6)

subject to

$$g_j\left(x\right)\le 0 \forall j=\mathrm{1,2},\cdots$$

(7)

$$h_k\left(x\right)=0 \forall k=\mathrm{1,2},\cdots$$

(8)

In this expression, $f\left(x\right)$ represents the objective function to be minimized (or maximized, depending on the case), and, therefore, $x$ is the vector composed of the variables to be optimized. The restrictions that the optimal point to be found (minimum or maximum) of this optimization problem must respect are presented in Equations (7) and (8), where $g_j$($x$) are the functions for the constraints of inequality and $h_k$($x$) are the functions for the equality constraints [20].

Taking as reference the general structure of the optimization problem shown in (6), the Cournot model is formulated in (9)–(13) to find the NCE point where the profit function for the generators is maximized, considering that the system reference angle, the power balance restriction, the maximum and minimum generation limits, and the maximum transmission limits of the lines must be respected.

$$\max {\pi }_i(q)=q_i\left(\alpha -\beta \sum _{j=1}^n{q}_j\right)-a_i-b_i{q}_i-c_i{q}_i^2$$

(9)

subject to

$${\delta }_i=0$$

(10)

$$\sum _{j\in \mathcal{N}}{B}_{ij}({\delta }_i-{\delta }_j)+q_i=d_i, \forall i$$

(11)

$$q_i^{min}\le q_i\le q_i^{max}$$

(12)

$${-F_{ij}^{max}\le B}_{ij}({\delta }_i-{\delta }_j) \le F_{ij}^{max}$$

(13)

where

${\delta }_i$ is the angle of node $i$.

$B_{ij}$ is the element of the susceptance matrix B corresponding to the transmission line between node $i$ and $j$.

$d_i$ is the load of node $i$.

$q_i^{min}$ and $q_i^{max}$ are the generation limits (maximum and minimum) of each participant $i$.

$F_{ij}^{max}$ is the maximum power flow that the transmission line can carry between node $i$ and $j$.

$\mathcal{N}$ is the transmission lines set.

According to [22,23,24,25], let $x=\left(x_1,x_2,\dots ,x_n\right)\in {\mathbb{R}}^n$, $\mathsf{\Omega }={\mathsf{\Omega }}_1\times {\mathsf{\Omega }}_2\times \dots \times {\mathsf{\Omega }}_n\subset {\mathbb{R}}^n$ be a compact convex set, where ${\mathsf{\Omega }}_i$ is the action set of each player $i=1,\dots ,n$ and ${\pi }_i$ are continuous in $x$ and concave in $x_i$. Then we have the following affirmations:

• The NCE exists.
• Moreover, if the game map associated with (9)–(13), defined as

$$L\left(x\right)=-({\nabla }_{x_1}{\pi }_1, {\nabla }_{x_2}{\pi }_2,..,{\nabla }_{x_n}{\pi }_n)$$

is strictly monotone, the NCE is unique.

Based on the abovementioned conditions, the game problem presented in (9)–(13) has a unique NCE. As discussed in Section 2, solving the Cournot model as an optimization problem and finding the NCE requires obtaining the KKT conditions. This approach presents the optimization problem as an equilibrium problem, i.e., as the solution to joint optimization problems. As mentioned in Section 2, Appendix A provides the thorough formulation of the KKT conditions necessary for solving the game problem in (9)–(13).

4. Results

The test system presented in this work is a nine-node system [26]. The simulation data, such as the constants of the inverse function [1], the coefficients of the quadratic function [1], the load data, and the reactances and susceptances [27], are shown in Appendix B. The study that was simulated considers a total load of 520 MW, increasing the power flow in the transmission lines by up to 80% of its previously defined capacity (315 MW) in the base case [27]. It is worth noting that all the data from the test system and how to solve the problem of optimal power flows are common knowledge for all players.

Under this power system operating condition, the dispatch problem is solved using ED (minimizing the sum of the cost function) [19,28], comparing the results obtained with the objective function presented in Section 3. ED and NCE methods are solved using codes programmed in AMPL (a modeling language for mathematical programming).

4.1. Simulation for the Nine-Node Test System—Base Case

The results for the nine-node system are presented below in

Table 1. Power Dispatch for the nine-node system—base case.

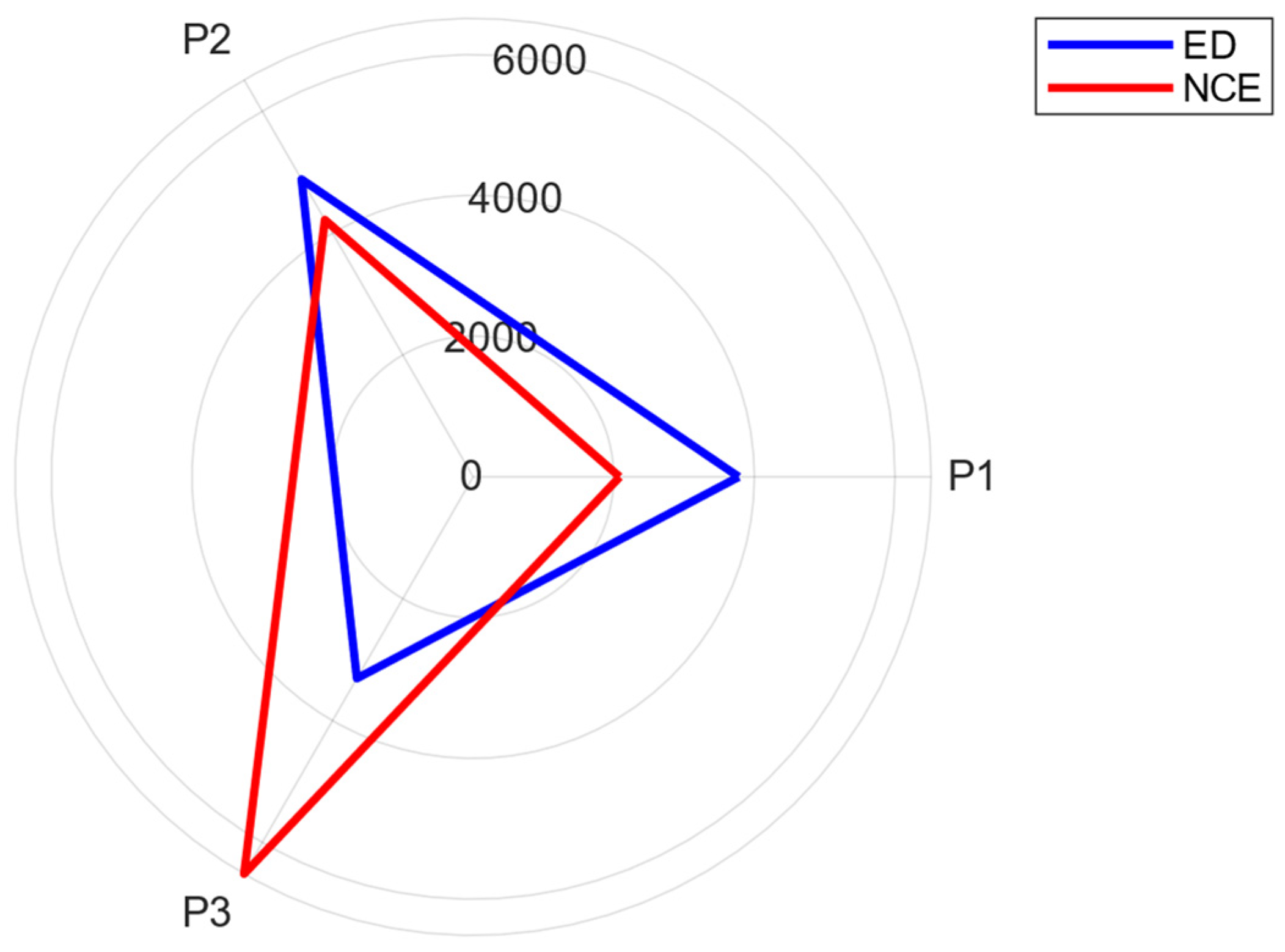
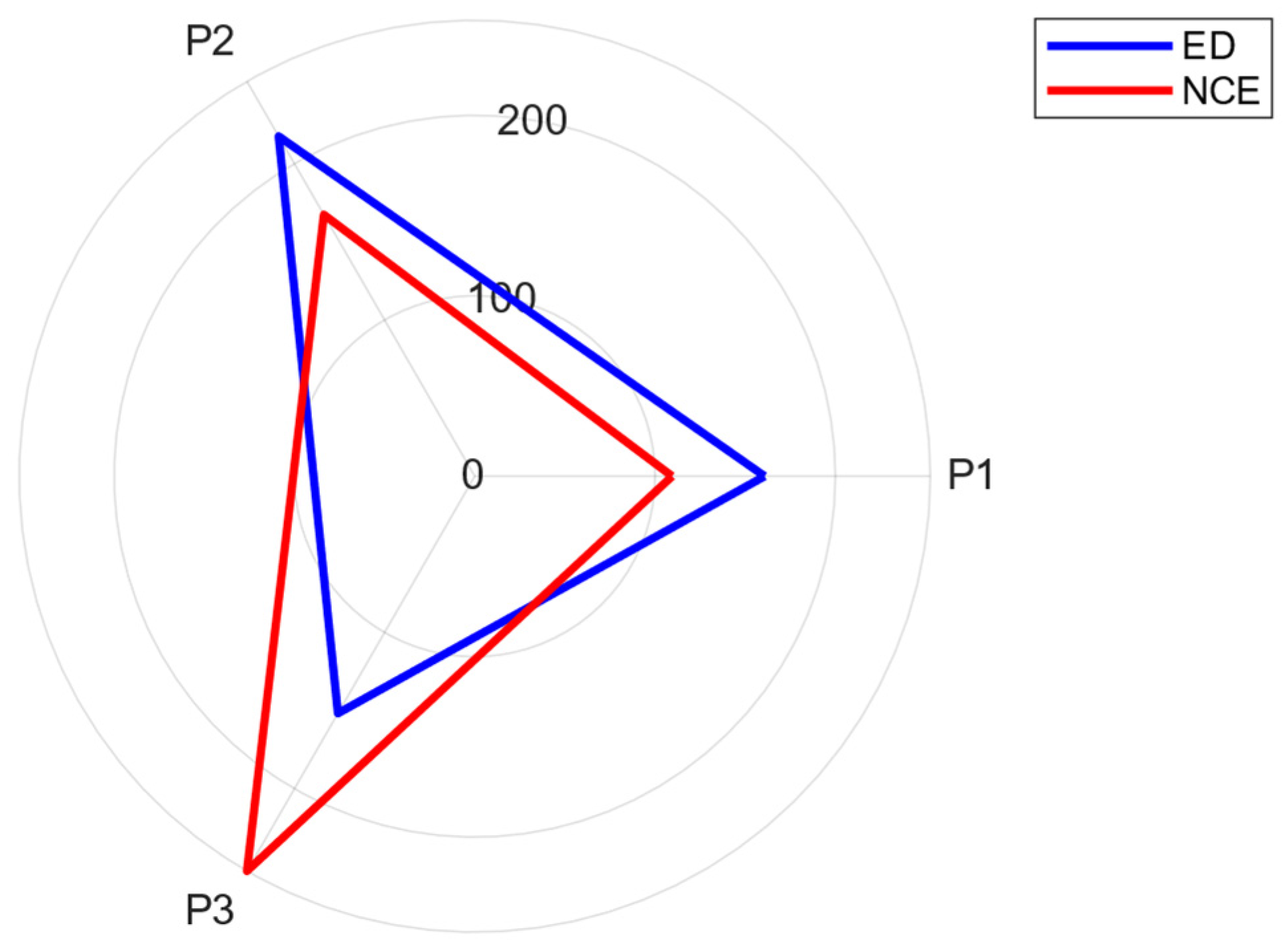
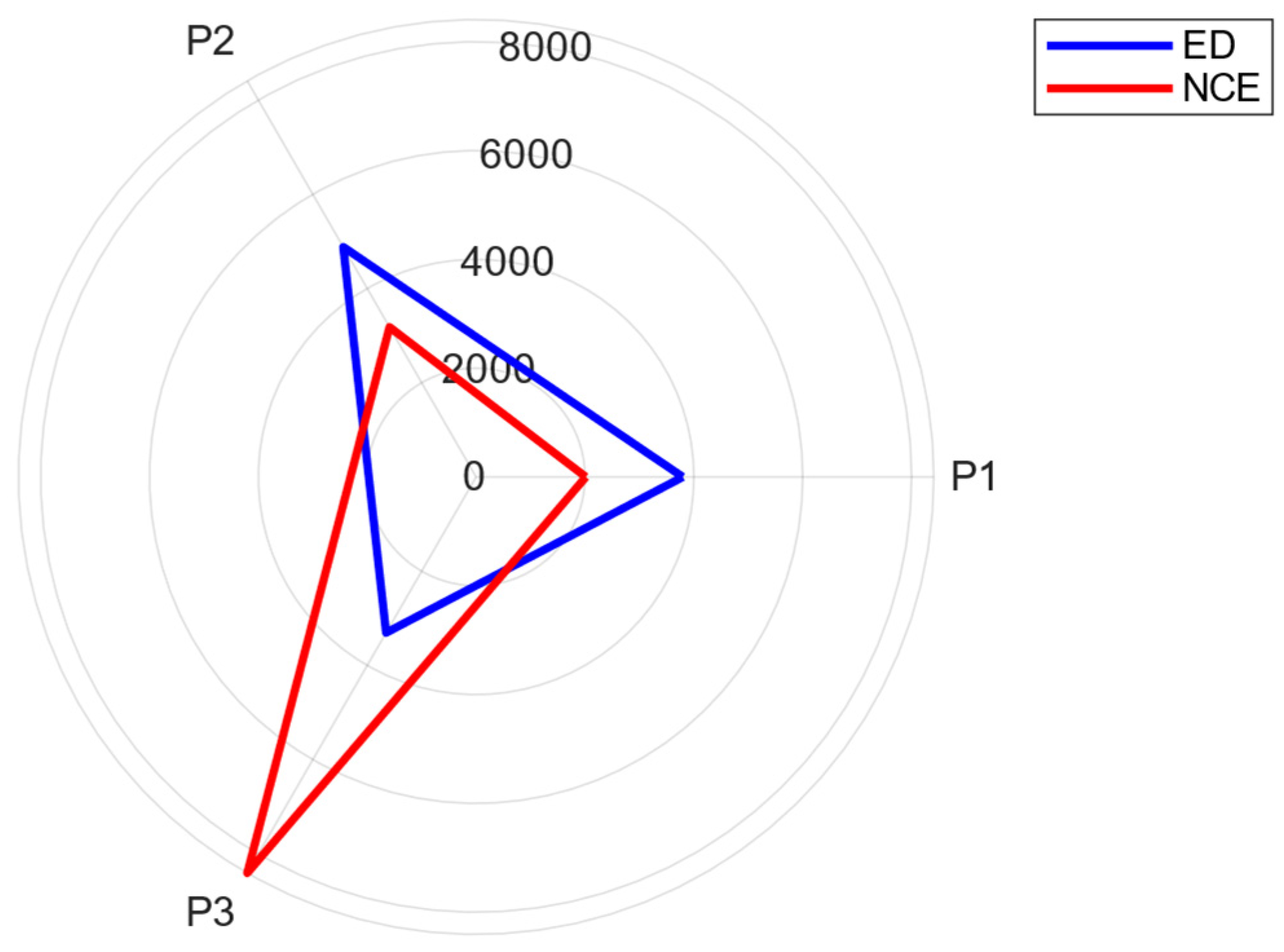
Players	Solution Approach
	ED		NCE
	Power (MW)	Angle	Power (MW)	Angle
1	160.32	0	111.84	0
2	217.49	9.1	199.35	12.29
3	151.73	1.57	220.56	11.2
Total:	529.54	-	531.75	-

and

Table 2. Operation costs and individual and total profits for the nine-node system—base case.

Players	Solution Approach
	ED		NCE
	Cost (USD/MWh)	Profit (USD/MWh)	Cost (USD/MWh)	Profit (USD/MWh)
1	3778.875	71,645.2719	2085.1004	50,283.9795
2	4881.649	97,438.6958	4217.1559	89,128.4815
3	3306.924	68,075.9716	6514.7824	96,762.4375
Total:	11,967.448	237,159.939	12,817.038	236,174.898

, in which the following is observed: Table 1 shows how the NCE preserves the equilibrium between players 2 and 3. The above can also be seen in Figure 1, where the three players form an almost equilateral triangle. Unlike ED, since this approach gives preference to player 2, sending him very close to his upper generation limit, as can be seen in Figure 1, where player 2 is at the maximum edge of the solution area, unlike the other players 1 and 3, who remain close to their lower generation limit.

Table 2 presents the operating costs and individual and total profits resulting from the system. This table shows that the NCE does not aim to minimize the operating cost, so the resulting cost through the NCE is higher compared to ED, as well as its profits. The above is because the NCE seeks the best solution that can be obtained, considering the players’ results. In the case of ED, it dispatches the generator with the lowest operating cost as much as possible, considering the system restrictions, causing a lower operating cost.

Figure 2 shows the behavior of the individual costs of the players, showing the difference in costs between both approaches. In the NCE, there is a considerable difference in player 3 compared to players 1 and 2 since it has a higher cost. The above is contrary to ED, which shows the decrease in cost in player 3 in his cost minimization objective and increases the cost of player 2, remembering that this is the player with the lowest cost.

Table 3. Power flows and losses in transmission lines for the nine-node system—base case.

Transmission Line		Solution Approach
Sending Node	Receiving Node
		ED		NCE
		Power Flow (MW)	Losses (MW)	Power Flow (MW)	Losses (MW)
1	4	160.32	0	111.84	0
2	7	217.49	0	199.35	0
3	9	151.73	0	220.56	0
4	5	46.04	0.41	32.91	0.24
4	6	114.28	1.39	78.93	0.7
5	7	84.37	3.08	97.33	4.15
6	9	−77.11	2.08	−111.77	4.51
7	8	130.04	2.09	97.87	1.19
8	9	72.05	0.48	103.31	0.97

shows the results of the power flows and losses in the resulting transmission lines using the NCE and ED. It observes that the number of losses for this base case is greater using the NCE compared to the amount obtained through ED.

Likewise,

Table 4. Percentage of use of the transmission lines of the nine-node system—base case.

Transmission Line		Solution Approach
Sending Node	Receiving Node
		ED	NCE
		Percentage of Use (%)	Percentage of Use (%)
1	4	64.12	44.73
2	7	80.55	73.83
3	9	50.57	73.52
4	5	18.41	13.16
4	6	45.71	31.57
5	7	56.24	64.88
6	9	30.84	44.70
7	8	52.01	39.14
8	9	28.82	41.32
Median:		50.57	44.70
Mean:		47.47	47.43

shows the percentages of use of the transmission lines obtained through the NCE and ED. This table shows that the percentage of use is lower in most of the lines when using the NCE compared to ED, verified by calculating the mean and median of the percentages of use of both methods for the base case. In both parameters, a lower percentage of use is obtained when using the NCE.

The above is because the NCE found in the power delivered is reflected in the power flows of the lines, providing a more homogeneous distribution. Contrary to the results using ED, it tends to mostly congest the transmission lines, as seen in lines 2–7, which is the player close to its upper generation limit and the maximum transmission limit.

4.2. Simulation for the Nine-Node Test System—with Two Bilateral Power Transactions

The study considers a total load of 520 MW and two bilateral power transactions of 50 MW each. These transactions are between nodes 1–8 and 2–6 to perform two injections of fixed power into the system.

The results for the nine-node system considering two bilateral power transactions are presented below, in which the following is observed.

In

Table 5. Power dispatch for the nine-node system—with two bilateral power transactions.

Players	Solution Approach
	ED		NCE
	Power (MW)	Angle	Power (MW)	Angle
1	160.8	0	109.49	0
2	217.49	9.27	167.34	10.03
3	151.73	−3.37	252.66	8.96
Total:	530.02	-	529.49	-

and Figure 3, the resulting power dispatch is presented, where it is observed that in the dispatch solution, the 100 MW corresponding to the bilateral transactions between the nodes are not being considered. However, this transaction does affect the result of the dispatch since players 1 and 2 must consider the additional power that they must deliver both in their generation limits and in the maximum limits of the transmission lines with which they have a connection, which causes there to be a different distribution of power compared to the base case presented in the previous section.

In the case of the NCE, player 3 is the one that dispatches the most significant amount of power to compensate for the additional power that players 1 and 2 must generate to comply with the bilateral power transaction. Contrary to ED, which maintains practically the same dispatch of the base case. However, with the resulting dispatch, a higher total generated power is observed when using ED compared to the NCE, which means that more significant losses occur when implementing ED.

Table 6. Operation Costs and individual and total profits for the nine-node system—With two bilateral power transactions.

Players	Solution Approach
	ED		NCE
	Cost (USD/MWh)	Profit (USD/MWh)	Cost (USD/MWh)	Profit (USD/MWh)
1	3798.230	71,774.553	2016.136	49,500.003
2	4881.649	97,334.300	3181.035	75,554.108
3	3306.924	68,003.141	8407.701	110,471.355
Total:	11,986.804	237,111.996	13,604.873	235,525.466

and Figure 4 present the operating costs and individual and total profits from the system considering two bilateral transactions. Table 6 shows that the operating cost obtained with the NCE is again higher than ED, remembering that the NCE does not have the minimization of the operating cost among its objectives. Likewise, it is observed that the profit obtained by the NCE is lower compared to that obtained by ED since, although it is true that one of the objectives of the NCE is the maximization of profits, this method is resolved using an equilibrium point, so not in all cases a maximum total profit will be obtained.

The previous results show the effect of bilateral power transactions, which, although the powers demanded by the transactions are not part of the dispatch solution, are reflected in the economic aspect of the system.

Table 7. Power flows and losses in transmission lines for the nine-node system—with two bilateral power transactions.

Transmission Line		Solution Approach
Sending Node	Receiving Node
		ED		NCE
		Power Flow (MW)	Losses (MW)	Power Flow (MW)	Losses (MW)
1	4	214.12	0	164.23	0
2	7	267.49	0	217.34	0
3	9	151.73	0	252.65	0
4	5	46.26	0.42	40.12	0.33
4	6	167.86	3.07	124.11	1.73
5	7	−84.16	3.14	−90.21	3.59
6	9	−75.21	2.05	−117.61	5.13
7	8	180.18	4.11	123.55	1.93
8	9	−73.92	0.54	−128.38	1.53

shows the results of the power flows and losses in the resulting transmission lines using the NCE and ED. In both approaches, the powers generated for bilateral power transactions are observed, corresponding to nodes 1–8 and 2–6, checking that they are being done.

Likewise,

Table 8. Percentage of use of the transmission lines of the nine-node system—with two bilateral power transactions.

Transmission Line		Solution Approach
Sending Node	Receiving Node
		ED	NCE
		Percentage of Use (%)	Percentage of Use (%)
1	4	85.64	65.69
2	7	99.07	80.49
3	9	50.57	84.21
4	5	18.50	16.04
4	6	67.14	49.64
5	7	56.10	60.14
6	9	30.08	47.04
7	8	72.07	49.42
8	9	29.56	51.35
Median:		56.10	51.35
Mean:		56.53	56.00

shows the percentages of use of the transmission lines obtained through the NCE and ED. This table shows that, although there are two bilateral transactions in the system, the percentage of use is lower when using the NCE compared to ED, verified by the mean and median values obtained. The above is reflected in lines 2–7, which have a usage percentage of 80.49% when using the NCE, considering that node 2 is one of the nodes that participate in bilateral transactions, in contrast to almost 100% of use resulting from ED, causing possible congestion on this transmission line.

5. Conclusions

This article evaluates the impact of the NCE on the congestion of transmission lines in power dispatch, comparing the results obtained with conventional methods (ED). It is crucial to note that, despite the operational cost associated with the NCE, it significantly reduces congestion in the transmission lines. This is verified by calculating the mean and median of the percentages of use of the transmission lines. In a scenario where the transmission lines are at 80% of their capacity, reducing congestion by finding a balance point in terms of power flow becomes essential. This is particularly true in bilateral power transactions, where power injections into the system and energy consumption are constantly considered, leading to potential congestion. Therefore, implementing the methodology developed using the NCE provides a practical and effective option to distribute balanced power flows, thus reducing congestion on transmission lines.