Operational Decisions of Construction and Demolition Waste Recycling Supply Chain Members under Altruistic Preferences
Abstract
1. Introduction
2. Literature Review
2.1. Studies on Green Demolition Technology
2.2. Studies on Altruistic Preferences
2.3. Studies on the Reciprocal Altruism Theory
2.4. Studies on Operational Decisions in a CDW Recycling Supply Chain
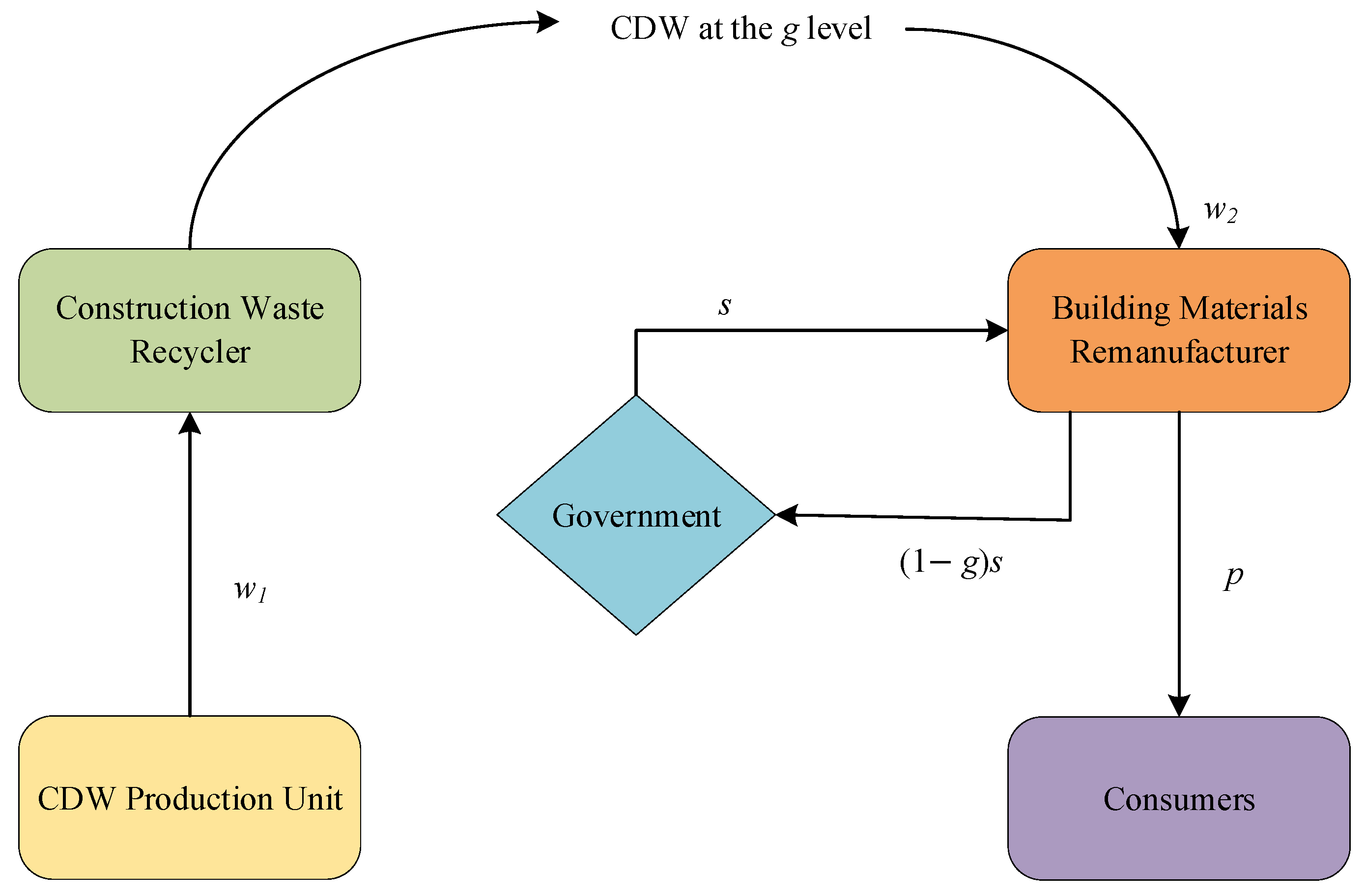
3. Problem Description and Relevant Assumptions
- (1)
- In the real market, the remanufacturer decides the price to be paid to the recycler for the recycled CDW, so it tends to have more initiative. Additionally, compared with the recycler, the remanufacturer is closer to the building materials sales market. The remanufacturer can deliver valuable market information to the recycler to support the recycler’s effective decision-making. Therefore, this paper recognizes that the remanufacturer is the leader in the supply chain [24].
- (2)
- Without loss of generality and to make the model easy to solve, this paper considers that all CDW recycled can be reused [25], neglecting the effect of green dismantling technological level on the proportion of CDW reused.
- (3)
- As previously emphasized, it has been shown that altruistic preferences have a significant effect on enterprises’ technological innovation [53]. Society is a vast network of complex interactions among countless people, altruistic preferences are prevalent in all fields and have received attention from scholars [53,54,55]. In order to align the model with reality and to explore whether the altruistic preferences of enterprises in the CDW recycling supply chain could increase recyclers’ level of green dismantling technology. This paper assumes that the recycler and remanufacturer’s altruistic preference coefficients are , , respectively. The recycler and remanufacturer’s utility functions are and , respectively [33].
- (4)
- Improved green dismantling technology by recyclers not only help to reduce noise and resource wastage, but also represent a significant opportunity to reduce the cost of carbon emissions for remanufacturers. This is because recyclers can reduce the disposal process for remanufacturers by adopting green dismantling technology that enable the separation of CDW during the demolition of buildings [12]. To realize a low-carbon and circular economic development model as early as possible, governments around the world have established incentives and penalties to limit carbon emissions from the construction industry. In this paper, it is assumed that a penalty s is required to be paid per unit of carbon emissions. For ease of calculation, every unit of recycled building material generates 1 unit of carbon emissions. According to a similar study [56], the cost of the remanufacturers due to carbon emissions is .
- (5)
- The basic market size of CDW is constant a, and the supply is q. Due to financial constraints, if recyclers increase their investment in R&D of green dismantling technology, the recycling price paid to CDW production unit will inevitably decrease. On the other hand, the green demolition behavior of CDW recyclers can improve their green image [51], thus promote the willingness of CDW production unit to supply CDW and offsetting part of the price effect. It is assumed that the influence coefficient of the green dismantling technological level on the recycling price paid by recyclers to CDW production unit is η. Drawing on Zheng and Jin [50], this paper constructs the inverse supply function for CDW as .
- (6)
- To incentivize recyclers to develop green dismantling technologies, the penalty per unit of carbon emissions should be sufficiently high. At the same time, to ensure the decision variables are positive, this paper assumes that .
- (7)
- Different altruistic models have optimal solutions within the full set of altruistic coefficients when . To ensure that the model fits a realistic scenario, the profits of the remanufacturers and recyclers are positive, deducing that , .
4. Model Developed and Solved
4.1. Optimal Solutions under Non-Altruistic Model
4.2. Optimal Solutions under Recycler Altruistic Model (R)
4.3. Optimal Solutions under Remanufacturer Altruistic Model (M)
4.4. Optimal Solutions under Mutual Altruistic Model (MR)
5. Analysis of Propositions
- (1)
- , , .
- (2)
- , , .
- (1)
- (2)
- When , if , , if , ; When , .
- (1)
- When , ; When , .
- (2)
- .
- (1)
- If , .
- (2)
- If , .
- (1)
- When, there is.
- (2)
- When, there is.
6. Numerical Simulation
6.1. Influence of Altruistic Preference Degree on Supply Chain Members’ Operational Decisions under Unilateral Altruistic Model
6.2. Influence of Altruistic Preference Degree on Supply Chain Members’ Operational Decisions under Mutual Altruistic Model
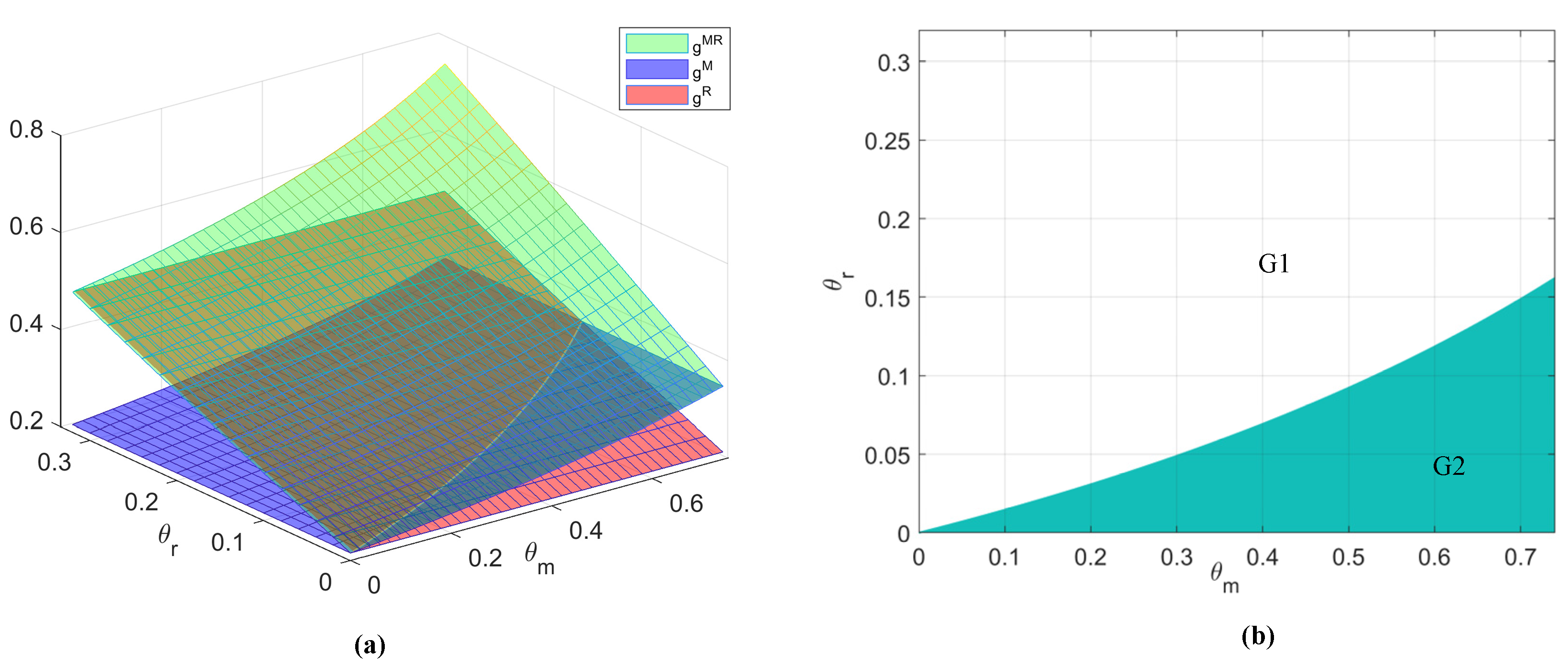
6.3. Comparison of Green Dismantling Technological Level under Different Altruistic Models
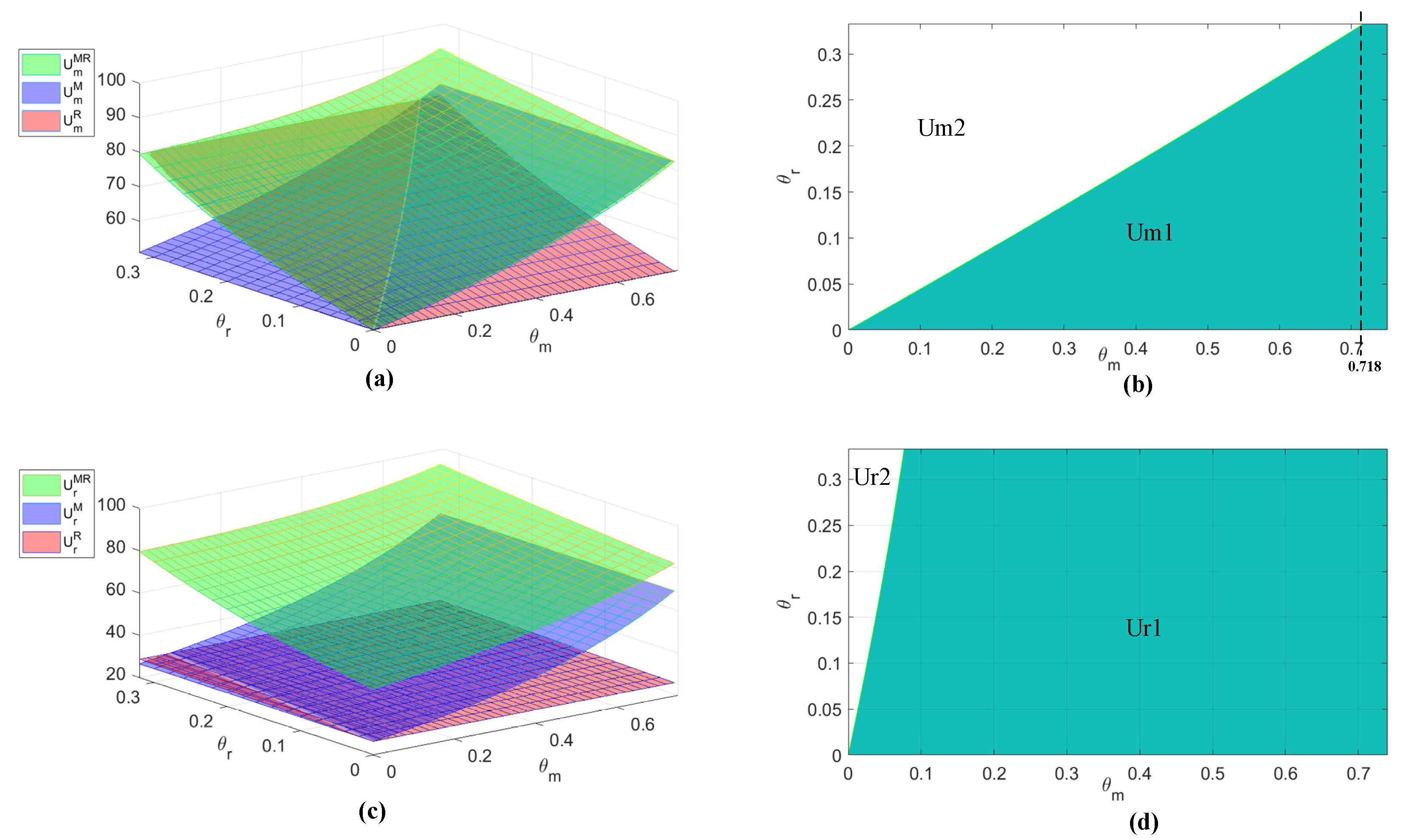
6.4. Comparison of Supply Chain Members’ Utility under Different Altruistic Models
6.5. Summary of Comparative Differences in Different Altruistic Models
7. Conclusions and Management Insights
7.1. Conclusions
- (1)
- Under the unilateral altruism model, supply chain members’ operational decisions are positively influenced by the remanufacturer’s altruistic preference degree. However, the recycling price to the recycler decreases with altruistic preference of the recycler. In the case that the remanufacturer’s altruistic preference degree is low, the recycler’s altruistic preference leads the amount of CDW recycled to increase; otherwise, inverted U-shaped change in the amount of CDW recycled in relation to the recycler’s altruistic preference degree.
- (2)
- Under the mutual altruistic model, the green dismantling technological level and the supply chain members’ utility are maximized. Under unilateral altruism model, the results of the comparison of the remanufacturer altruism model and the recycler altruism model are uncertain.
- (3)
- When the weaker party unilaterally shows altruistic preference characteristics to the stronger party, it will bring negative impacts to itself. Moreover, the stronger party’s altruistic preference behavior is crucial in improving supply chain members’ benefits.
7.2. Management Insights
- (1)
- For remanufacturers, they should actively assume supply chain responsibility and continuously enhance the concept of pursuing win–win co-operation. Specifically, remanufacturers can increase the recovery price per unit of CDW paid to recyclers, in effect supporting recyclers’ innovative green dismantling technology activities.
- (2)
- For recyclers, it is important not to pander to remanufacturers, which may be counterproductive. They should enhance their negotiating power based on their resource and supplier strengths and force the remanufacturers to compromise. At the same time, recyclers should determine their own level of altruism based on a full assessment of the wholesale prices offered by the remanufacturers in order to increase the recycling rate of CDW.
- (3)
- For the government, it should continuously optimize the carbon tax policy, coordinate the interests of recyclers and remanufacturers, and alleviate the conflicts in the supply chain. It should fully guide remanufacturers and recyclers to establish win–win cooperation to promote the development of CDW recycling and resource utilization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Proof of profitable altruistic cooperation intervals.
- (1)
- ,
- (2)
- . And, there is . The analysis shows that > 0, when , .
- 2.
- Proof of Proposition 1.
- 3.
- Proof of Proposition 2.
- 4.
- Proof of Proposition 3.
- 5.
- Proof of Proposition 4.
- 6.
- Proof of Proposition 5.
- 7.
- Proof of Proposition 6.
- 8.
- Proof of Proposition 7.
References
- Haque, S.E.; Nahar, N.; Haque, M.S. A study on the waste generation rates and recycling potential for the construction and demolition waste in Dhaka. Environ. Monit. Assess. 2024, 196, 183. [Google Scholar] [CrossRef]
- Mavlutova, I.; Atstaja, D.; Gusta, S.; Hermanis, J. Management of Household-Generated Construction and Demolition Waste: Circularity Principles and the Attitude of Latvian Residents. Energies 2023, 17, 205. [Google Scholar] [CrossRef]
- Ma, W.; Hao, J.L. Enhancing a circular economy for construction and demolition waste management in China: A stakeholder engagement and key strategy approach. J. Clean. Prod. 2024, 450, 141763. [Google Scholar] [CrossRef]
- Cristóbal, J.; Foster, G.; Caro, D.; Yunta, F.; Manfredi, S.; Tonini, D. Management of excavated soil and dredging spoil waste from construction and demolition within the EU: Practices, impacts and perspectives. Sci. Total Environ. 2024, 944, 173859. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Li, X.; Ding, Z. Optimal supply chain performance: Risk aversion to green innovation. Manag. Decis. 2024. early access. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, W.; Peng, J.; Wang, Y.; Zeng, L.; Gao, P.; Li, X. Pricing Decisions in Construction and Demolition Waste Recycling Supply Chains under Carbon Tax Scenarios. Systems 2024, 12, 35. [Google Scholar] [CrossRef]
- Marín-Cortés, S.; Fernández-Álvarez, M.; Enríquez, E.; Fernández, J.F. Experimental characterization data on aggregates from construction and demolition wastes for the assistance in sorting and recycling practices. Constr. Build. Mater. 2024, 435, 136798. [Google Scholar] [CrossRef]
- Yi, B.; Zou, Y.; Chen, W.; Li, Z.; He, Y.; Jin, Z.; Zhang, H.; Li, X. Coevolution Mechanism of Remanufacturer–Construction Enterprise–Public in Construction and Demolition Waste Resource Utilization Projects under Green Value Co-Creation. Buildings 2024, 14, 2214. [Google Scholar] [CrossRef]
- Gao, P.; Liu, S.; Zeng, L.; Peng, J.; Wang, Y.; Zhang, H.; Li, X. Leader and Employee Behavioral Decision-Making in Construction and Demolition Waste Recycling Projects under Psychological Contract Theory. Buildings 2024, 14, 2519. [Google Scholar] [CrossRef]
- Li, X.; He, J. Mechanism of the green supply chain profit of building materials considering the duopoly competition model and consumer green preference. Int. J. Syst. Sci.-Oper. Logist. 2024, 11, 2311283. [Google Scholar] [CrossRef]
- Pun, S.K.; Liu, C.; Langston, C. Case study of demolition costs of residential buildings. Constr. Manag. Econ. 2006, 24, 967–976. [Google Scholar] [CrossRef]
- Hoang, N.H.; Ishigaki, T.; Watari, T.; Yamada, M.; Kawamoto, K. Current state of building demolition and potential for selective dismantling in Vietnam. Waste Manag. 2022, 149, 218–227. [Google Scholar] [CrossRef]
- Hou, W.; Liang, S.; Zhang, T.; Ma, T.; Han, Y. Low-Carbon Emission Demolition of an Existing Urban Bridge Based on SPMT Technology and Full Procedure Monitoring. Buildings 2023, 13, 1379. [Google Scholar] [CrossRef]
- Sun, L.; Jiang, Z.; Xu, C.; Lu, D.; Li, R.; Tan, Y.; Lu, H. Contribution of soundless chemical demolition and induction heating demolition to carbon emissions reduction in urban demolition industry. Energy Build. 2023, 300, 113671. [Google Scholar] [CrossRef]
- Lotem, A.; Fishman, M.A.; Stone, L. From reciprocity to unconditional altruism through signalling benefits. Proc. R. Soc. London. Ser. B Biol. Sci. 2003, 270, 199–205. [Google Scholar] [CrossRef]
- Hauser, M.; McAuliffe, K.; Blake, P.R. Evolving the ingredients for reciprocity and spite. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 3255–3266. [Google Scholar] [CrossRef][Green Version]
- Kurzban, R.; Burton-Chellew, M.N.; West, S.A. The evolution of altruism in humans. Annu. Rev. Psychol. 2015, 66, 575–599. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Ke, H.; Zhang, R.; Duan, K. Who exhibits fairness concern is better for supply chain stability and the environment. J. Clean. Prod. 2023, 386, 135645. [Google Scholar] [CrossRef]
- Choi, T.M.; Zhang, T. Will being an angel bring more harm than good? Altruistic newsvendors with different risk attitudes. Eur. J. Oper. Res. 2023, 305, 1153–1165. [Google Scholar] [CrossRef]
- Johnstone, R.A.; Bshary, R. Evolution of spite through indirect reciprocity. Proc. R. Soc. London. Ser. B Biol. Sci. 2004, 271, 1917–1922. [Google Scholar] [CrossRef]
- Roberts, G. Competitive altruism: From reciprocity to the handicap principle. Proc. R. Soc. London. Ser. B Biol. Sci. 1998, 265, 427–431. [Google Scholar] [CrossRef]
- Wang, H.; He, Y.; Ding, Q. The impact of network externalities and altruistic preferences on carbon emission reduction of low carbon supply chain. Environ. Sci. Pollut. Res. 2022, 29, 66259–66276. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, J.; Ren, X.; Zhou, X. Greenness and pricing decisions of cooperative supply chains considering altruistic preferences. Int. J. Environ. Res. Public Health 2019, 16, 51. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Li, X.; Zhu, X.; Huang, Y.; Liu, Z.; Liu, Y.; Li, C. Impact of recycler information sharing on supply chain perfor-mance of construction and demolition waste resource utilization. Int. J. Environ. Res. Public Health 2022, 19, 3878. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; He, J.; Li, Y.; Chen, W.; Zhang, Y.; Zhang, H.; Li, X. Green independent innovation or green imitation innovation? Supply chain decision-making in the operation stage of construction and demolition waste recycling public-private partnership projects. Systems 2023, 11, 94. [Google Scholar] [CrossRef]
- Suk, C.; Jung, W.; Park, H.; Kim, N.; Katsuyama, K. Application study of explosive demolition for the wall-slab building. Sci. Technol. Energetic Mater. 2008, 69, 51. [Google Scholar]
- Jiang, Z.; Zheng, W.; Wang, Y.; Li, S.; Sun, L. Green demolition technology of reinforced concrete slab: Application of soundless chemical demolition agents and its evaluation system. Struct. Concr. 2023, 24, 4549–4564. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, C.; Jiang, Y.; Zhong, J.; Zhu, J. Efficient separation of coarse aggregates and cement mortar in the recycled concrete by water jet demolition. Mater. Lett. 2023, 333, 133623. [Google Scholar] [CrossRef]
- Xiao, J.; Zeng, L.; Ding, T.; Xu, H.; Tang, H. Deconstruction evaluation method of building structures based on digital technology. J. Build. Eng. 2023, 66, 105901. [Google Scholar] [CrossRef]
- Kunieda, Y.; Codinhoto, R.; Emmitt, S. Increasing the efficiency and efficacy of demolition through computerised 4D simulation. Eng. Constr. Archit. Manag. 2019, 26, 2186–2205. [Google Scholar] [CrossRef]
- Fan, R.; Lin, J.; Zhu, K. Study of game models and the complex dynamics of a low-carbon supply chain with an altruistic retailer under consumers’ low-carbon preference. Phys. A Stat. Mech. Its Appl. 2019, 528, 121460. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, S.; Zhang, Y. Impact of altruism preference difference on the optimal reward structure in online referral marketing. Manag. Decis. Econ. 2024, 45, 247–263. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, B. How should e-commerce platforms subsidize retailers with logistics constraints during an epidemic scenario? Considering power structure and altruistic preference. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 1680–1701. [Google Scholar] [CrossRef]
- Rong, L.; Xu, M. Impact of altruistic preference and government subsidy on the multinational green supply chain under dynamic tariff. Environ. Dev. Sustain. 2022, 24, 1928–1958. [Google Scholar] [CrossRef]
- Liu, W.; Yan, X.; Wei, W.; Xie, D.; Wang, D. Altruistic preference for investment decisions in the logistics service supply chain. Eur. J. Ind. Eng. 2018, 12, 598–635. [Google Scholar] [CrossRef]
- Wei, G.; Chen, X.; Qin, X. Product greenness and pricing strategy of supply chain incorporating asymmetric heterogeneous preferences. IEEE Access 2021, 9, 11563–11584. [Google Scholar] [CrossRef]
- Yu, T.; Guan, Z.; Zhang, J.; Dong, J. Blockchain adoption and contract coordination of poverty alleviation supply chain considering altruistic preference. Comput. Ind. Eng. 2024, 188, 109879. [Google Scholar] [CrossRef]
- Molm, L.D.; Collett, J.L.; Schaefer, D.R. Building solidarity through generalized exchange: A theory of reciprocity. Am. J. Sociol. 2007, 113, 205–242. [Google Scholar] [CrossRef]
- Sylwester, K.; Roberts, G. Reputation-based partner choice is an effective alternative to indirect reciprocity in solving social dilemmas. Evol. Hum. Behav. 2013, 34, 201–206. [Google Scholar] [CrossRef]
- Gintis, H. Strong reciprocity and human sociality. J. Theor. Biol. 2000, 206, 169–179. [Google Scholar] [CrossRef]
- Deng, K.; Gintis, H.; Chu, T. Strengthening strong reciprocity. J. Theor. Biol. 2011, 268, 141. [Google Scholar] [CrossRef] [PubMed]
- Brosnan, S.F.; Silk, J.B.; Henrich, J.; Mareno, M.C.; Lambeth, S.P.; Schapiro, S.J. Chimpanzees (Pan troglodytes) do not develop contingent reciprocity in an experimental task. Anim. Cogn. 2009, 12, 587–597. [Google Scholar] [CrossRef] [PubMed]
- Gouldner, A.W. The norm of reciprocity: A preliminary statement. Am. Sociol. Rev. 1960, 25, 161–178. [Google Scholar] [CrossRef]
- Du, L.; Feng, Y.; Lu, W.; Kong, L.; Yang, Z. Evolutionary game analysis of stakeholders’ decision-making behaviours in construction and demolition waste management. Environ. Impact Assess. Rev. 2020, 84, 106408. [Google Scholar] [CrossRef]
- Guo, F.; Wang, J.; Song, Y. How to promote sustainable development of construction and demolition waste recycling systems: Production subsidies or consumption subsidies? Sustain. Prod. Consum. 2022, 32, 407–423. [Google Scholar] [CrossRef]
- Han, Y.; Zheng, H.; Huang, Y.; Li, X. Considering consumers’ green preferences and government subsidies in the decision making of the construction and demolition waste recycling supply chain: A stackelberg game approach. Buildings 2022, 12, 832. [Google Scholar] [CrossRef]
- Su, Y.; Chen, J.; Si, H.; Wu, G.; Zhang, R.; Lei, W. Decision-making interaction among stakeholders regarding construction and demolition waste recycling under different power structures. Waste Manag. 2021, 131, 491–502. [Google Scholar] [CrossRef]
- China News Network. Available online: http://m.chinanews.com/wap/detail/zw/gn/2020/01-22/9067544.shtml (accessed on 25 August 2024).
- Luciano, A.; Cutaia, L.; Altamura, P.; Penalvo, E. Critical issues hindering a widespread construction and demolition waste (CDW) recycling practice in EU countries and actions to undertake: The stakeholder’s perspective. Sustain. Chem. Pharm. 2022, 29, 100745. [Google Scholar] [CrossRef]
- Zheng, B.; Jin, L. Relicensing scheme selection in closed-loop supply chains with differentiated new and remanufactured products. Comput. Ind. Eng. 2022, 171, 108443. [Google Scholar] [CrossRef]
- Doan, D.T.; Chinda, T. Modeling construction and demolition waste recycling program in Bangkok: Benefit and cost analysis. J. Constr. Eng. Manag. 2016, 142, 05016015. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chang, S.; Kang, Y. Product innovation and process innovation in a dynamic Stackelberg game. Comput. Ind. Eng. 2019, 130, 395–403. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Y.; Liu, Z.; Peng, H.; Yang, X. Optimal strategy for enterprises’ green technology innovation considering individual disappointment avoidance and altruistic reference based on differential game theory. Clean Technol. Environ. Policy 2024. early access. [Google Scholar] [CrossRef]
- Tambo, J.A.; Baraké, E.; Kouevi, A.; Munthali, G.T. Copyright or copyleft: An assessment of farmer-innovators’ attitudes towards intellectual property rights. J. Rural Stud. 2020, 74, 133–141. [Google Scholar] [CrossRef]
- Hsieh, C.S.; Lin, X. Gender and racial disparities in altruism in social networks. Reg. Sci. Urban Econ. 2024, 108, 104025. [Google Scholar] [CrossRef]
- Zou, Q.M.; Hu, L.Q.; Zhou, T.J. Pricing and Coordination of a Supply Chain with Fairness Concerns under Carbon Cap-and-Trade Mechanism. Chin. J. Manag. Sci. 2022, 30, 142–154. [Google Scholar]
- Xing, Q.; Ran, L.; Li, Y.; Zhou, B. Blockchain technology embedded in the power battery for echelon recycling selection under the mechanism of traceability. Sci. Rep. 2024, 14, 15069. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, J.; Li, C.; Li, Y.; Zhou, C.; Zheng, H.; Li, X. How can construction and demolition waste recycling public–private partnership projects performance compensate during the operation period? A two-stage perspective of recycling and remanufacturing. Systems 2023, 11, 170. [Google Scholar] [CrossRef]
- Dey, S.K.; Giri, B.C. Analyzing a closed-loop sustainable supply chain with duopolistic retailers under different game structures. CIRP J. Manuf. Sci. Technol. 2021, 33, 222–233. [Google Scholar] [CrossRef]
- Yang, L.; Hu, Y.; Huang, L. Collecting mode selection in a remanufacturing supply chain under cap-and-trade regulation. Eur. J. Oper. Res. 2020, 287, 480–496. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Tang, D.; Zhao, Z.; Boamah, V. Stackelberg game analysis of government subsidy policy in green product market. Environ. Dev. Sustain. 2024, 26, 13273–13302. [Google Scholar] [CrossRef]
- Stevens, J.R.; Hauser, M.D. Why be nice? Psychological constraints on the evolution of cooperation. Trends Cogn. Sci. 2004, 8, 60–65. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yu, Z.; Shen, L.; Dong, W. Impacts of altruistic preference and reward-penalty mechanism on decisions of E-commerce closed-loop supply chain. J. Clean. Prod. 2021, 315, 128132. [Google Scholar] [CrossRef]
- Zhu, J.; Lu, Y.; Feng, T. The influence of the altruistic preferences of e-commerce platforms on the carbon emission reduction of manufacturers. Electron. Commer. Res. 2023. early access. [Google Scholar] [CrossRef]


| Topic | Content of Relevant Studies | Bibliography |
|---|---|---|
| Studies on green dismantling techniques | Technologies directly applied to the dismantling process | [12,14,26,27,28] |
| Technologies used for assessment and control prior to dismantling | [29,30] | |
| Studies on altruistic preferences | Effect of altruistic preferences of enterprises | [18,32,33,34,35] |
| How to address negative effects of altruistic preferences | [35,37] | |
| Studies on the reciprocal altruism theory | Traditional reciprocal altruism theory | [20,21,38] |
| Extension of reciprocal altruism theory | [21,39,40,41,42,43] | |
| Studies on operational decisions in a CDW recycling supply chain | External factors | [5,6,44,45,46] |
| Internal factors | [24,25,47] |
| Variable | Meaning | Reference |
|---|---|---|
| a | Basic market size for CDW | [5] |
| q | Quantity of CDW recycling (decision variable) | [50] |
| g | Green dismantling technological level by the recycler (decision variable) | [5] |
| p | Sales price of recycled building materials | [25] |
| w1 | Unit recycling price for CDW paid by the recycler to CDW production unit | [24] |
| w2 | Unit recycling price for CDW paid by the remanufacturer to recycler (decision variable) | [24] |
| η | Influence coefficient of green dismantling technological level on the recycling price | [50,51] |
| h | Cost coefficient of green dismantling technological level | [52] |
| s | Tax per unit of carbon emissions | [6] |
| Altruistic preference coefficient for the remanufacturer, | [34] | |
| Altruistic preference coefficient for the recycler, | [34] |
| Variable | Distribution of Altruism | Recycler Altruism Model | Remanufacturer Altruism Model |
|---|---|---|---|
| g | G1 | H | - |
| G2 | - | H | |
| U | Um1, Ur1 | - | H |
| Um2, Ur2 | H | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Zhang, H.; Chen, W.; Li, X. Operational Decisions of Construction and Demolition Waste Recycling Supply Chain Members under Altruistic Preferences. Systems 2024, 12, 346. https://doi.org/10.3390/systems12090346
Zhu J, Zhang H, Chen W, Li X. Operational Decisions of Construction and Demolition Waste Recycling Supply Chain Members under Altruistic Preferences. Systems. 2024; 12(9):346. https://doi.org/10.3390/systems12090346
Chicago/Turabian StyleZhu, Junlin, Hao Zhang, Weihong Chen, and Xingwei Li. 2024. "Operational Decisions of Construction and Demolition Waste Recycling Supply Chain Members under Altruistic Preferences" Systems 12, no. 9: 346. https://doi.org/10.3390/systems12090346
APA StyleZhu, J., Zhang, H., Chen, W., & Li, X. (2024). Operational Decisions of Construction and Demolition Waste Recycling Supply Chain Members under Altruistic Preferences. Systems, 12(9), 346. https://doi.org/10.3390/systems12090346








