How to Promote Traditional Automobile Companies’ Intelligent-Connected Transformation under the New Dual-Credit Policy? A Tripartite Evolutionary Game Analysis Combined with Funding Time Delay
Abstract
1. Introduction
2. Literature Review
2.1. Policy Factors
2.2. Internet Technology
2.3. Evolutionary Game Theory
3. Questions and Assumptions
3.1. Problem Description
3.2. Assumptions
4. Models and Methods
4.1. Stability Analysis of Unilateral Game Players
4.1.1. Traditional Automobile Companies
4.1.2. Internet Companies
4.1.3. Financial Institutions
4.2. Stability Analysis of System Evolution
5. Simulation Analysis
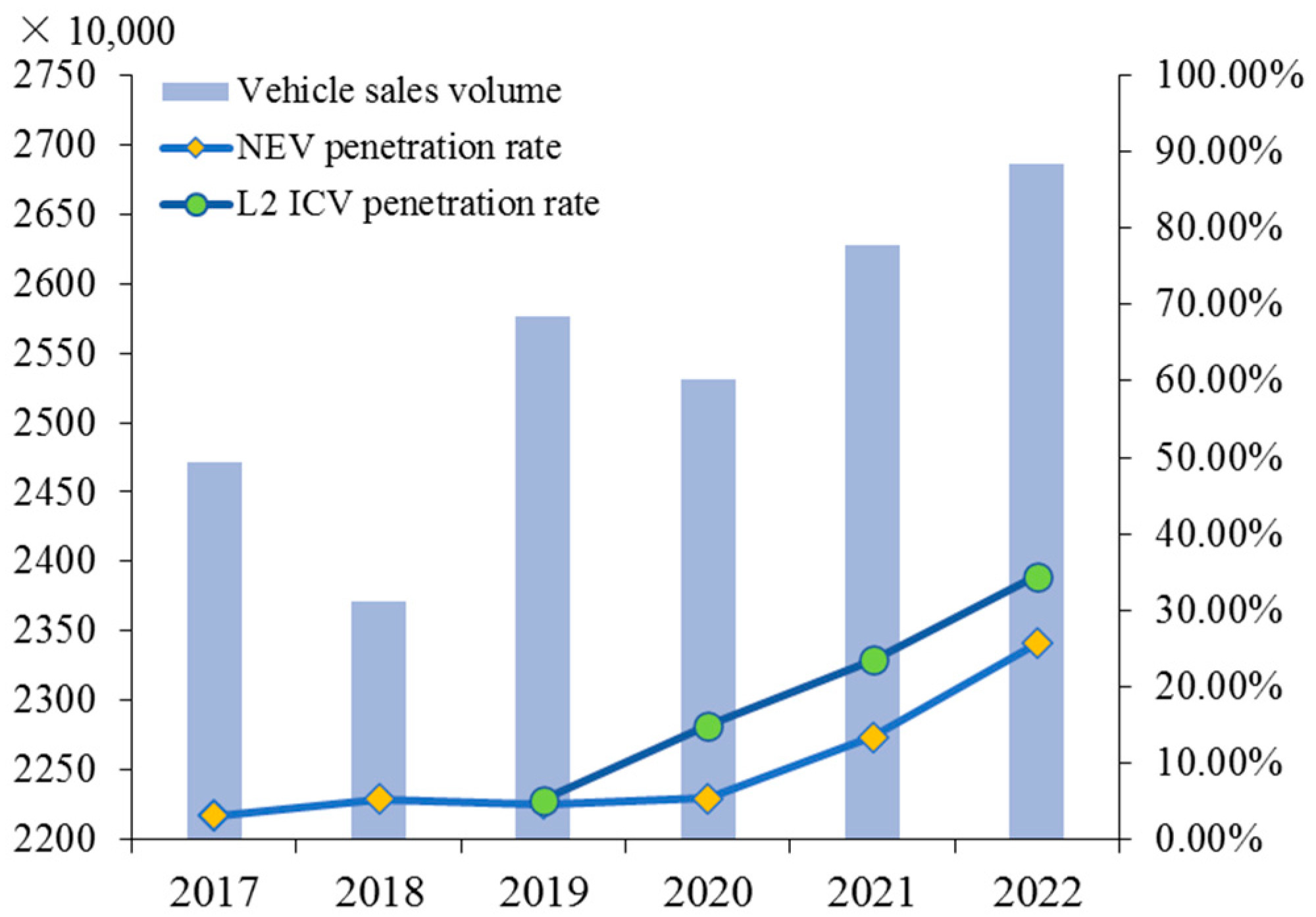
5.1. Data Processing and Analysis
5.2. Influence of Changes in Collaborative Parameters between Traditional Automobile Companies and Internet Companies on System Evolution
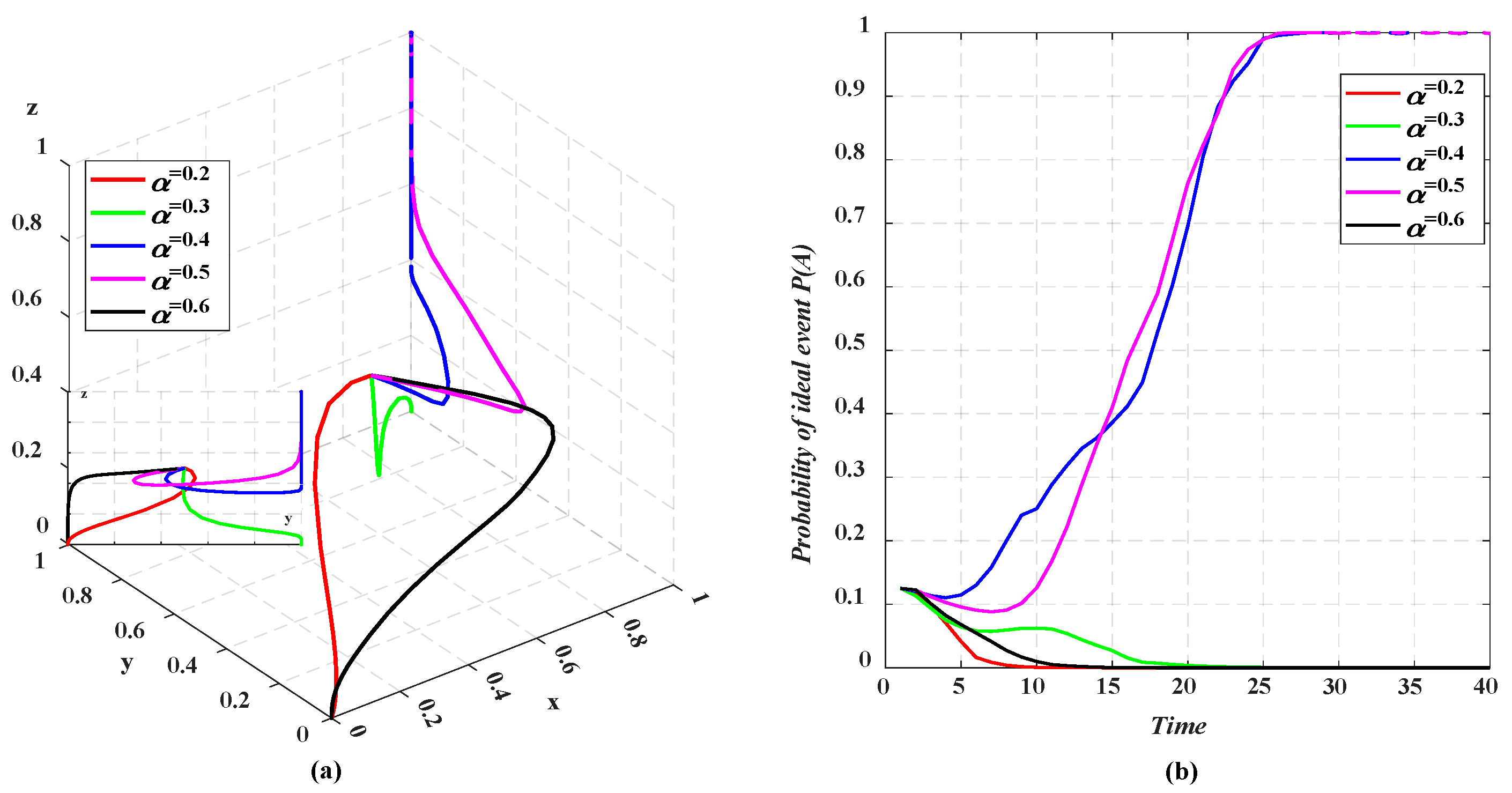
5.2.1. Profit Sharing Coefficient
5.2.2. Cost-Sharing Coefficient
5.3. Influence of Changes in Financing Parameters of Financial Institutions on System Evolution
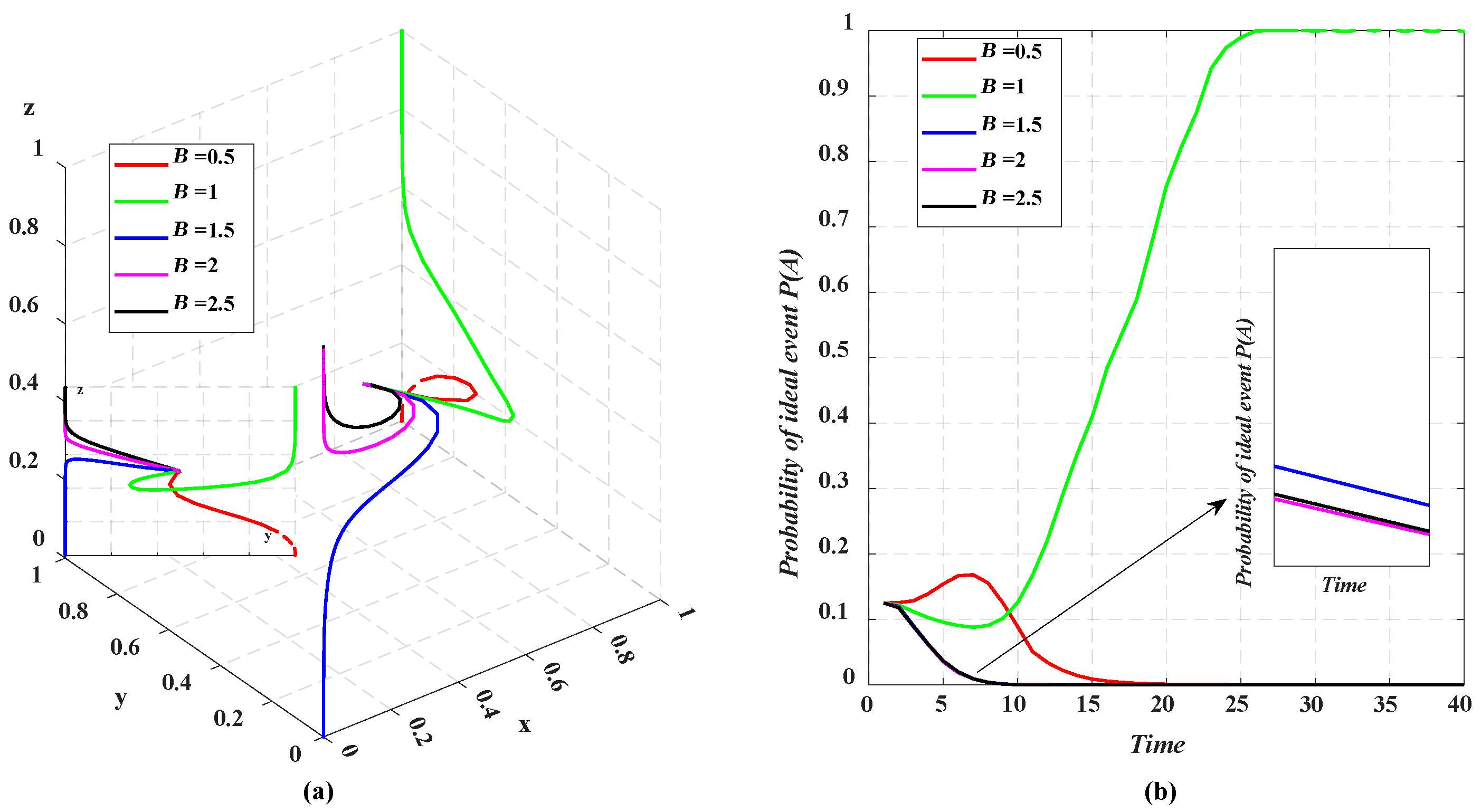
5.3.1. Financing Amount
5.3.2. Regulatory Cost of Financial Institutions
5.4. Influence of Changes in Policy Parameters of New Dual-Credit Policy on System Evolution
5.4.1. Credit Trading Price
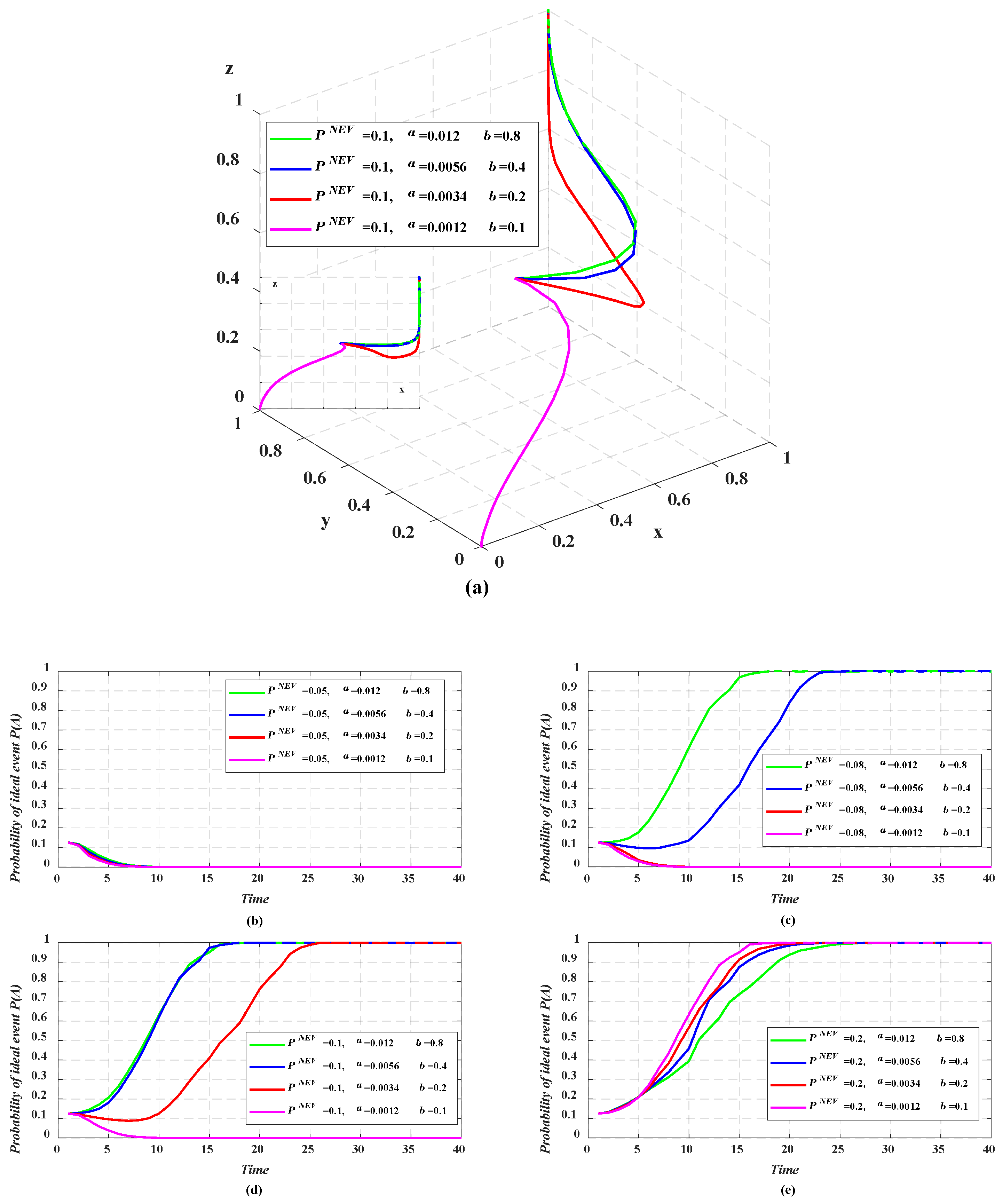
5.4.2. NEV Credit Accounting Coefficients and for Standard Vehicle Model
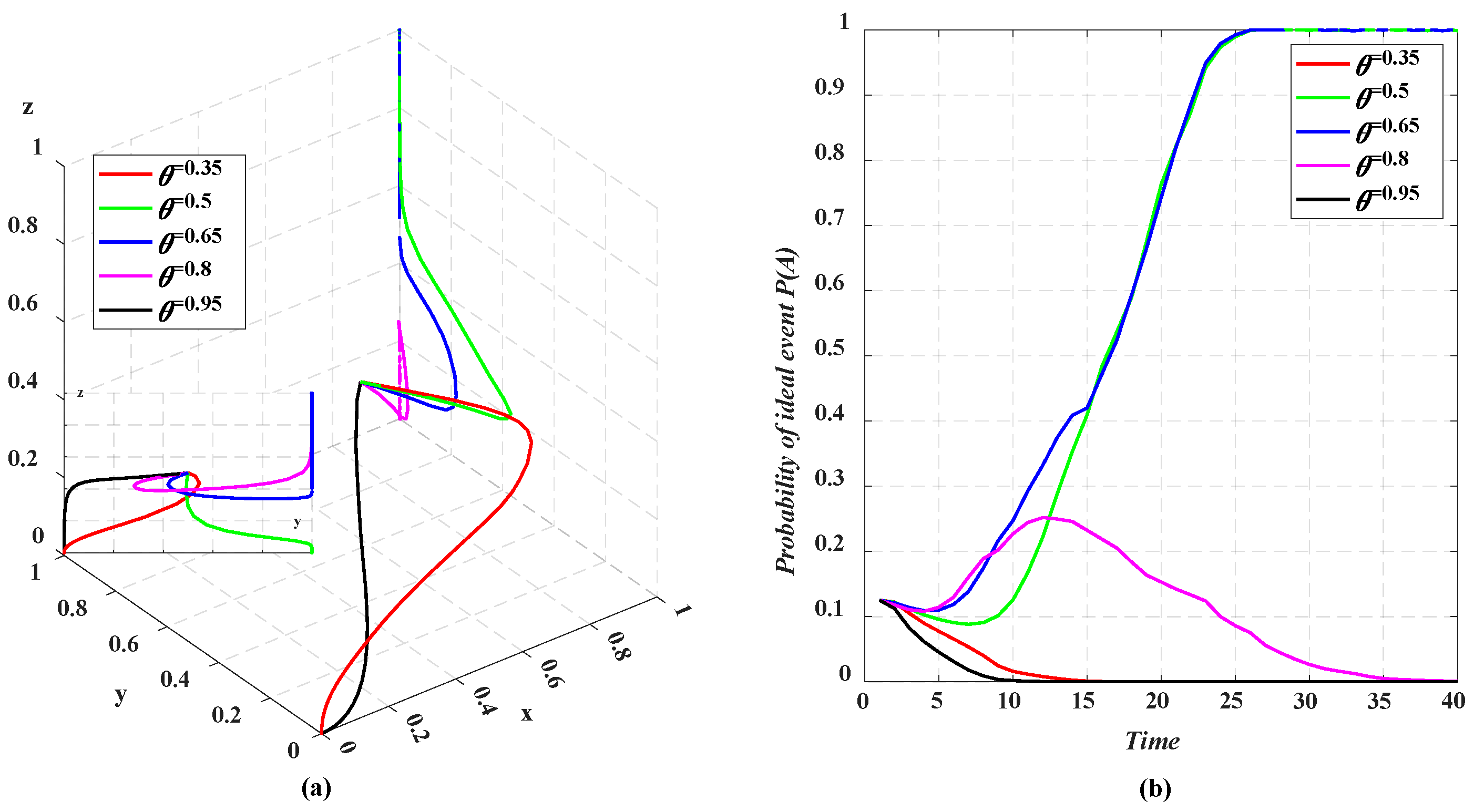
5.4.3. NEV Credit Ratio Requirement
6. Conclusions and Policy Recommendations
6.1. Conclusions
6.2. Policy Recommendations
6.3. Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | ICVs are classified as assisted driving stage (L1), partial driving stage (L2), conditional autonomous driving stage (L3), highly automated driving stage (L4) and fully automated driving stage (L5), and the mass production and popularization of L2 Level vehicles were achieved in 2019. |
| 2 | https://price.pcauto.com.cn/salescar/sg28312/ (accessed on 1 July 2023). |
| 3 | https://price.pcauto.com.cn/salescar/sg27941/ (accessed on 1 July 2023). |
| 4 | https://price.pcauto.com.cn/salescar/sg24393/ (accessed on 1 July 2023). |
| 5 | https://www.deepal.com.cn/sl03 (accessed on 1 July 2023). |
| 6 |
References
- China Academy of Information and Communications Technology (CAICT). Cloud Computing White Paper (2023). Available online: http://www.caict.ac.cn/kxyj/qwfb/bps/202307/t20230725_458185.htm (accessed on 20 July 2023).
- The State Council. Development Plan for the New Energy Vehicle Industry (2021–2035). Available online: https://www.gov.cn/gongbao/content/2020/content_5560291.htm (accessed on 20 October 2020).
- Yang, D.; Jiang, K.; Zhao, D.; Yu, C.; Cao, Z.; Xia, S.; Xiao, Z.; Jiao, X.; Wang, S.; Zhang, K. Intelligent and connected vehicles: Current status and future perspectives. Sci. China Technol. Sci. 2018, 61, 1446–1471. [Google Scholar] [CrossRef]
- Ministry of Industry and Information Technology (MIIT). Economic Operation of the Automotive Industry in December 2022. Available online: https://www.miit.gov.cn/gxsj/tjfx/zbgy/qc/art/2023/art_610c626d34b8424c9c1077ac5e5a40fe.html (accessed on 12 January 2023).
- MIIT. Decision on Amending the “Measures for Parallel Management of Average Fuel Consumption of Passenger Car Enterprises and New Energy Vehicle Credits”. Available online: https://www.miit.gov.cn/jgsj/zbys/gzdt/art/2023/art_02e935e2cce74be4a641d7b8ca5621b4.html (accessed on 6 July 2023).
- MIIT. Measures for Parallel Management of Average Fuel Consumption of Passenger Car Enterprises and New Energy Vehicle Credits. Available online: https://www.miit.gov.cn/jgsj/zbys/qcgy/art/2020/art_f09be90b302f4875928ac1c05a5c3bbc.html (accessed on 28 September 2017).
- Zhao, D.; Yan, X.C.; Wang, H.P.; Li, Y. Evolutionary game analysis of cooperative innovation of automakers under dual-credit policy. Chin. J. Manag. Sci. 2024, 32, 279–292. [Google Scholar] [CrossRef]
- Liao, H.; Peng, S.; Li, L.; Yi, Z. The role of governmental policy in game between traditional fuel and new energy vehicles. Comput. Ind. Eng. 2022, 169, 108292. [Google Scholar] [CrossRef]
- MIIT. Annual Report on the Implementation of Parallel Management of Average Fuel Consumption and New Energy Vehicle Credits in Passenger Vehicle Enterprises (2023). Available online: http://www.miit-eidc.org.cn/module/download/downfile.jsp?classid=0&filename=cdd994c1750b4c2f8ba7468c146bccff.pdf (accessed on 25 April 2023).
- Smith, J.M.; Price, G.R. The logic of animal conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Cai, G.; Kock, N. An evolutionary game theoretic perspective on e-collaboration: The collaboration effort and media relativeness. Eur. J. Oper. Res. 2009, 194, 821–833. [Google Scholar] [CrossRef]
- Axelrod, R.; Hamilton, W.D. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef]
- McClure, S.M.; Laibson, D.I.; Loewenstein, G.; Cohen, J.D. Separate neural systems value immediate and delayed monetary rewards. Science 2004, 306, 503–507. [Google Scholar] [CrossRef]
- Ma, H.; Lou, G.; Fan, T.; Chan, H.; Chung, S. Conventional automotive supply chains under China’s dual-credit policy: Fuel economy, production and coordination. Energy Policy 2021, 151, 112166. [Google Scholar] [CrossRef]
- Wang, N.; Fang, T.; Liu, X.; Shu, Y.J. Research on the influence of dual-credit policy on Chinese automobile market and policy trend. China Soft. Sci. 2019, S01, 203–215. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Z.; Liu, Y.; Zhang, Z. Vehicle product-line strategy under dual-credit and subsidy back-slope policies for conventional/new energy vehicles. Comput. Ind. Eng. 2023, 177, 109020. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Li, H.; Tang, Y.Y.; Liu, B.Y. The impact of dual-credit scheme on the development of the new energy vehicle industry. Energy Procedia 2019, 158, 4311–4317. [Google Scholar] [CrossRef]
- Wu, F.; Li, P.; Dong, X.; Lu, Y. Exploring the effectiveness of China’s dual credit policy in a differentiated automobile market when some consumers are environmentally aware. Energy Econ. 2022, 111, 106077. [Google Scholar] [CrossRef]
- Cheng, Y.; Fan, T.; Zhou, L. Optimal strategies of automakers with demand and credit price disruptions under the dual-credit policy. J. Manag. Sci. Eng. 2022, 7, 453–472. [Google Scholar] [CrossRef]
- Li, J.Z.; Ku, Y.Y.; Li, L.Y.; Liu, C.L.; Deng, X.D. Optimal channel strategy for obtaining new energy vehicle credits under dual credit policy: Purchase, self-produce, or both? J. Clean. Prod. 2022, 342, 130852. [Google Scholar] [CrossRef]
- Cheng, Y.; Fan, T. Production coopetition strategies for an FV automaker and a competitive NEV automaker under the dual-credit policy. Omega 2021, 103, 102391. [Google Scholar] [CrossRef]
- Ma, M.; Meng, W.; Li, Y.; Huang, B. Impact of dual credit policy on new energy vehicles technology innovation with information asymmetry. Appl. Energy 2023, 332, 120524. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Cao, S. Carrot and stick: Does dual-credit policy promote green innovation in auto firms? J. Clean. Prod. 2023, 403, 136863. [Google Scholar] [CrossRef]
- Prospective Economist. An Article Will Explain the Advantages and Disadvantages of the Dual Point Policy on the Development of China’s New Energy Vehicle Industry! Available online: https://baijiahao.baidu.com/s?id=1649503891247096241&wfr=spider&for=pc (accessed on 11 July 2019).
- Wang, Y. Comparison of California ZEV Mandate with China’s Dual-Credit Regulation and Its Simulation Result. Available online: https://www.d1ev.com/kol/49713 (accessed on 3 July 2017).
- Plantec, Q.; Deval, M.A.; Hooge, S.; Weil, B. Big data as an exploration trigger or problem-solving patch: Design and integration of AI-embedded systems in the automotive industry. Technovation 2023, 124, 102763. [Google Scholar] [CrossRef]
- Carlos, L.A.; Francisco, R.; Francisco, V. Impact of digital transformation on the automotive industry. Technol. Forecast. Soc. Change 2021, 162, 120343. [Google Scholar] [CrossRef]
- Ou, S.; Hsieh, I.; He, X.; Lin, Z.; Yu, R.; Zhou, Y.; Bouchard, J. China’s vehicle electrification impacts on sales, fuel use, and battery material demand through 2050: Optimizing consumer and industry decisions. iScience 2021, 24, 103375. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Li, S.; Wang, S.; Chen, Z.; Zhang, J.; Zhao, J.; Ma, F. Electrification decisions of traditional automakers under the dual-credit policy regime. Transp. Res. Part D Transp. Environ. 2021, 98, 102956. [Google Scholar] [CrossRef]
- Zhao, C.; Guo, Q.; Jia, R.; Dong, K.; Wang, K. How does clean energy transition promote original design manufacturers? A three-party evolutionary game analysis. Energy Econ. 2023, 126, 106965. [Google Scholar] [CrossRef]
- Tang, J.; Wu, W.; Zhao, D.; Chen, X. Evolutionary Game and Simulation Analysis of Intelligent Connected Vehicle Industry with Cross-Border Collaborative Innovation. IEEE Access 2023, 11, 17721–17730. [Google Scholar] [CrossRef]
- Huang, J.; Guo, G.X.; Min, L.; Qin, Y. Research on the Intelligent Transformation and Upgrade Path of China’s Automobile Manufacturing Enterprises from the Perspective of Dynamic Capabilities—Case Study based on 3 Domestic Manufacturing Companies. Sci. Technol. Prog. Policy 2018, 35, 121–129. [Google Scholar] [CrossRef]
- Yu, F.; Chen, J. The impact of industrial internet platform on green innovation: Evidence from a quasi-natural experiment. J. Clean. Prod. 2023, 414, 137645. [Google Scholar] [CrossRef]
- Wang, X.P.; Zhang, Z.M.; Guo, Z.H.; Su, C.; Sun, L.H. Energy structure transformation in the context of carbon neutralization: Evolutionary game analysis based on inclusive development of coal and clean energy. J. Clean. Prod. 2023, 398, 136626. [Google Scholar] [CrossRef]
- Zou, C.; Huang, Y.; Hu, S.; Huang, Z. Government participation in low-carbon technology transfer: An evolutionary game study. Technol. Forecast. Soc. Chang. 2023, 188, 122320. [Google Scholar] [CrossRef]
- Tian, T.; Sun, S. Low-carbon transition pathways in the context of carbon-neutral: A quadrilateral evolutionary game analysis. J. Environ. Manag. 2022, 322, 116105. [Google Scholar] [CrossRef]
- Wang, J.; Jia, L.; He, P.; Wang, P.; Huang, L. Engaging stakeholders in collaborative control of air pollution: A tripartite evolutionary game of enterprises, public and government. J. Clean. Prod. 2023, 418, 138074. [Google Scholar] [CrossRef]
- Wang, W.; Li, J. A tripartite evolutionary game model for the hydrogen fuel cell vehicle industry development under government regulation in China. Fuel 2023, 348, 128223. [Google Scholar] [CrossRef]
- Huang, T.F.; Hu, C.H.; He, Q.Y.; Yang, D.X.; He, T.; Fu, Y. A coordination analysis of stakeholder interests on the new subsidy policy of hydrogen fuel cell vehicles in China: From the perspective of the evolutionary game theory. Int. J. Hydrogen Energy 2022, 47, 24493–24510. [Google Scholar] [CrossRef]
- Zhao, D.; Ji, S.F.; Wang, H.P.; Jiang, L.W. How do government subsidies promote new energy vehicle diffusion in the complex network context? A three-stage evolutionary game model. Energy 2021, 230, 120899. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.Y.; Li, C.C.; Liu, Y.; Zhao, F.; Feng, G.Z.; Wang, S.Y. Tripartite cooperation evolutionary strategy of industrial Internet platform, developer and enterprise—The role of government subsidies and revenue sharing. Chin. J. Manag. Sci. 2024, 32, 1–14. [Google Scholar]
- Zeng, J.; Qian, Y.; Li, J.; Zhang, Y.; Xu, D. Congestion and energy consumption of heterogeneous traffic flow mixed with intelligent connected vehicles and platoons. Phys. A Stat. Mech. Its Appl. 2023, 609, 128331. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, T.; Ma, L.; Wu, Y.; Zhang, W. Vibration warning design for reaction time reduction under the environment of intelligent connected vehicles. Appl. Ergon. 2021, 96, 103490. [Google Scholar] [CrossRef]
- Liu, J.; Liao, X.; Dong, J.; Mansoori, A. A neurodynamic approach for nonsmooth optimal power consumption of intelligent and connected vehicles. Neural Netw. 2023, 161, 693–707. [Google Scholar] [CrossRef]
- Wang, H.P.; Yan, X.C.; Zhao, D.; Ge, L.J. Research on production-decision of automakers considering consumer’s low-carbon preference under the government reward-penalty mechanism. Syst. Eng.-Theory Pract. 2023, 49, 2669–2684. [Google Scholar] [CrossRef]
- Liao, D.; Tan, B. An evolutionary game analysis of new energy vehicles promotion considering carbon tax in post-subsidy era. Energy 2023, 264, 126156. [Google Scholar] [CrossRef]
- Hu, L.; Qiu, X. Stability analysis of game models with fixed and stochastic delays. Appl. Math. Comput. 2022, 435, 127473. [Google Scholar] [CrossRef]
- Cheng, H.; Meng, X. Multistability and Hopf bifurcation analysis for a three-strategy evolutionary game with environmental feedback and delay. Phys. A Stat. Mech. Its Appl. 2023, 620, 128766. [Google Scholar] [CrossRef]
- Krawiec, A.; Szydłowski, M. Economic growth cycles driven by investment delay. Economic Modelling 2017, 67, 175–183. [Google Scholar] [CrossRef]
- MIIT. Decision on Amending the “Measures for Parallel Management of Average Fuel Consumption of Passenger Car Enterprises and New Energy Vehicle Credits”. Available online: https://www.miit.gov.cn/xwdt/gxdt/sjdt/art/2020/art_e78f4efb0deb421c9970d7c35abb8afe.html (accessed on 22 June 2020).
- Chongqing Chana Automobile Co., Ltd. 2022 Annual Report. Available online: https://www.changan.com.cn/uploads/chan_reportreportfile/700b7118195d571b8e31e9ec03860bfc.pdf (accessed on 24 April 2023).
- China Automotive News. Credits Pool “in Place” Trading Market Stabilized Dual Credits Timely Change. Available online: http://www.cnautonews.com/shendu/2023/07/24/detail_20230724358349.html (accessed on 24 July 2023).
- Zhao, B.; Ziedonis, R. State governments as financiers of technology startups: Evidence from Michigan’s R&D loan program. Res. Policy 2020, 49, 103926. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, K.; Hill, R.V. Delayed premium payment, insurance adoption, and household investment in rural China. Am. J. Agric. Econ. 2020, 102, 1177–1197. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Yamamura, T. Stability analysis of the Kaldor model with time delays: Monetary policy and government budget constraint. Nonlinear Anal. Real World Appl. 2004, 5, 277–308. [Google Scholar] [CrossRef]
- Kalecki, M. A macrodynamic theory of business cycles. Econometrica 1935, 3, 327–344. [Google Scholar] [CrossRef]




| Symbols | Definitions | Symbols | Definitions |
|---|---|---|---|
| Initial tripartite profits | Regulatory cost of financial institutions | ||
| Credit trading price | NEV credit ratio requirement | ||
| NEV credit accounting multiplication coefficient | CAFC credit coefficient of unit NEV | ||
| NEV credit accounting additive coefficient | Credit reward coefficient of ICVs | ||
| Driving range (CLTC) | Innovation profit between traditional automobile companies and internet companies | ||
| Value-added profit of between traditional automobile companies and internet companies when financial institutions choose the financing strategy | Value-added profits of financial institutions financing when traditional automobile companies and internet companies choose innovation | ||
| Profit-sharing coefficient of collaborative innovation | Cost-sharing coefficient of collaborative innovation | ||
| Financing rate | Financing amount | ||
| Cost of collaborative innovation when financial institutions choose the financing strategy | Cost of collaborative innovation when financial institutions choose the non-financing strategy | ||
| Innovating cost of traditional automobile companies when financial institutions choose the financing strategy | Innovating cost of traditional automobile companies when financial institutions choose the non-financing strategy | ||
| Innovating cost of internet companies when financial institutions choose the financing strategy | Innovating cost of internet companies when financial institutions choose the non-financing strategy | ||
| Penalty for collaborative innovation | Success probability of collaborative innovation | ||
| Production of high-end ICVs | Production of mid-end ICVs | ||
| Production of TFVs | Probability of traditional automobile companies choosing collaborative innovation strategy | ||
| Probability of internet companies choosing collaborative innovation strategy | Probability of financial institutions choosing financing strategy |
| Traditional Automobile Companies | Internet Companies | Financial Institutions | |
|---|---|---|---|
| Financing (z) | Non-Financing (1 − z) | ||
| Collaborative innovation (x) | Collaborative innovation (y) | ||
| Non- Collaborative innovation (1 − y) | |||
| Non- collaborative innovation (1 − x) | Collaborative innovation (y) | ||
| Non- collaborative innovation (1 − y) | |||
| Equilibrium Points | Characteristic Values | Result |
|---|---|---|
| ESS | ||
| Instability point | ||
| Instability point | ||
| Saddle point | ||
| Saddle point | ||
| Saddle point | ||
| Saddle point | ||
| ESS |
| Parameters | |||||||||
| Initial value | 1 | 0.0034 | 0.25 | 1.2 | 0.1 × 10−4 | 1.9 | 2.2 | 1 | 0.047 |
| Unit | ten thousand vehicles | - | billions | - | billions | billions | billions | billions | - |
| Parameters | |||||||||
| Initial value | 3 | 0.2 | 530 | 0.18 | 0.89 | 9.63 | 2.45 | 1.5 | 0.5 |
| Unit | ten thousand vehicles | - | km | - | billions | billions | billions | billions | - |
| Parameters | |||||||||
| Initial value | 11 | 0.5 | 0.5 | 0.5 | 2.5 | 2.8 | 2.4 | 2.65 | |
| Unit | ten thousand vehicles | - | - | - | billions | billions | billions | billions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Li, Y.; Wang, J.; Tang, J. How to Promote Traditional Automobile Companies’ Intelligent-Connected Transformation under the New Dual-Credit Policy? A Tripartite Evolutionary Game Analysis Combined with Funding Time Delay. Systems 2024, 12, 319. https://doi.org/10.3390/systems12090319
Zhao D, Li Y, Wang J, Tang J. How to Promote Traditional Automobile Companies’ Intelligent-Connected Transformation under the New Dual-Credit Policy? A Tripartite Evolutionary Game Analysis Combined with Funding Time Delay. Systems. 2024; 12(9):319. https://doi.org/10.3390/systems12090319
Chicago/Turabian StyleZhao, Dan, Yekai Li, Jian Wang, and Jinhuan Tang. 2024. "How to Promote Traditional Automobile Companies’ Intelligent-Connected Transformation under the New Dual-Credit Policy? A Tripartite Evolutionary Game Analysis Combined with Funding Time Delay" Systems 12, no. 9: 319. https://doi.org/10.3390/systems12090319
APA StyleZhao, D., Li, Y., Wang, J., & Tang, J. (2024). How to Promote Traditional Automobile Companies’ Intelligent-Connected Transformation under the New Dual-Credit Policy? A Tripartite Evolutionary Game Analysis Combined with Funding Time Delay. Systems, 12(9), 319. https://doi.org/10.3390/systems12090319





