Taxi Travel Distance Clustering Method Based on Exponential Fitting and k-Means Using Data from the US and China
Abstract
1. Introduction
- We introduce a relative distance method to analyze and model the taxi travel distance distribution, providing a unified approach for handling multi-year and multi-city data.
- We propose a taxi travel distance clustering method based on the k-means approach, which offers a visual and accurate classification of travel distances, aiding in urban transportation planning and service optimization.
- We carried out extensive experiments on real taxi driving data in New York and China, in order to verify the effectiveness of our proposed method.
2. Background
| City | Year | Average Distance | Mode Distance | Interval | Order Type |
|---|---|---|---|---|---|
| Beijing [7] | 2015 | 6.53 km | 1.90 km | 2.00 km/10.00 km | Taxi |
| Beijing [21] | 2015 | 8.60 km | - | - | Taxi |
| Beijing [21] | 2016 | 17.70 km | 10.00 km | 2.00 km | OCH |
| Beijing [28] | 2015 | - | - | - | Taxi |
| Beijing [28] | 2016 | - | - | - | OCH |
| Shanghai [26] | 2014 | 7.00 km | 3.00–4.00 km | 1.00 km/3.00 km | Taxi |
| Shanghai [23] | 2015 | 8.69 km | 3.00–6.00 km | 3.00/4.00/5.00 km | Taxi |
| Shanghai [24] | 2015 | - | 1.85 km | 5.00 km | Taxi |
| Xian [27] | 2008 | 5.75 km | - | - | Taxi |
| Xian [29] | 2011 | - | 0–2.00 km | 2.00 km | Taxi |
| Xian [30] | 2011 | - | 0–2.00 km | 2.00 km | Taxi |
| Xian [27] | 2013 | 5.08 km | 3.00–4.00 km | 1.00 km | Taxi |
| Chengdu [24] | 2016 | - | 4.50 km | 3.00 km | Taxi |
| Chengdu [25] | 2016 | 5.00 km | 4.00 km | 10.00 km | OCH |
| Harbin [10] | 2012 | - | 3 km | - | Taxi |
| Qingdao [31] | 2015 | 7.20 km | - | - | Taxi |
| Nanchang [32] | 2019 | 6.80 km | 3.00–6.00 km | 3.00 km | Taxi |
| San Francisco [6] | 2008 | - | 1.30 km | 5.00 km | Taxi |
| San Francisco [33] | 2014 | 6.20 km 5.10 km | - - | - - | Taxi Taxi (ridesourcing) |
| New York [26] | 2014 | 4.83 km | 0–3.00 km | - | Taxi |
| Chicago [34] | 2019 2019 | 6.94 km 7.98 km | 1.00–2.00 km 1.00–2.00 km | 1.00 km 1.00 km | Taxi OCH |
3. Methodology
3.1. Mode-Aware Travel Distance Fitting
3.2. Modified Exponential Fitting Optimization
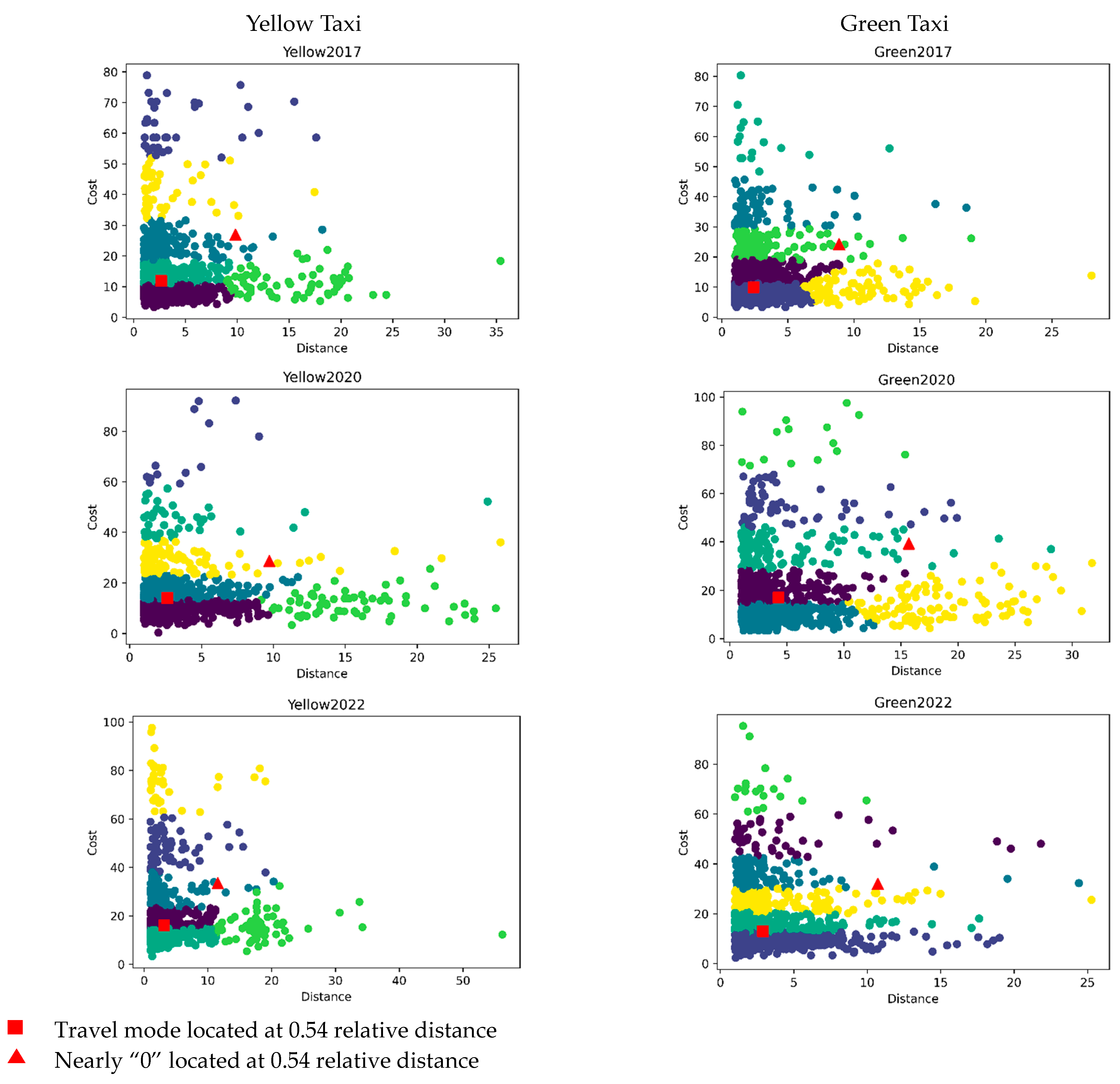
3.3. Travel Distance Clustering Method Based on k-Means
4. Experiments and Results
4.1. Data Collection
4.2. Data Processing
4.3. Analysis of Travel Distance Modes
4.4. Fitting Results
4.5. Travel Distance Clustering Results
4.6. Reflections
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing travel patterns and city structure with taxi trip data. J. Transp. Geogr. 2015, 43, 78–90. [Google Scholar] [CrossRef]
- Liang, X.; Zheng, X.; Lv, W.; Zhu, T.; Xu, K. The scaling of human mobility by taxis is exponential. Phys. A Stat. Mech. Its Appl. 2012, 391, 2135–2144. [Google Scholar] [CrossRef]
- Veloso, M.; Phithakkitnukoon, S.; Bento, C.; Fonseca, N.; Olivier, P. Exploratory study of urban flow using taxi traces. In Proceedings of the First Workshop on Pervasive Urban Applications (PURBA) in conjunction with Pervasive Computing, San Francisco, CA, USA, 12–15 June 2011. [Google Scholar]
- Vizuete-Luciano, E.; Guillén-Pujadas, M.; Alaminos, D.; Merigó-Lindahl, J.M. Taxi and urban mobility studies: A bibliometric analysis. Transp. Policy 2023, 133, 144–155. [Google Scholar] [CrossRef]
- Calabrese, F.; Diao, M.; Di Lorenzo, G.; Ferreira, J., Jr.; Ratti, C. Understanding individual mobility patterns from urban sensing data: A mobile phone trace example. Transp. Res. Part C Emerg. Technol. 2013, 26, 301–313. [Google Scholar] [CrossRef]
- Wang, W.; Pan, L.; Yuan, N.; Zhang, S.; Liu, D. A comparative analysis of intra-city human mobility by taxi. Phys. A Stat. Mech. Its Appl. 2015, 420, 134–147. [Google Scholar] [CrossRef]
- Jiang, S.; Guan, W.; Zhang, W.; Chen, X.; Yang, L. Human mobility in space from three modes of public transportation. Phys. A Stat. Mech. Its Appl. 2017, 483, 227–238. [Google Scholar] [CrossRef]
- Zhou, Z.; Dou, W.; Jia, G.; Hu, C.; Xu, X.; Wu, X.; Pan, J. A method for real-time trajectory monitoring to improve taxi service using GPS big data. Inf. Manag. 2016, 53, 964–977. [Google Scholar] [CrossRef]
- Scholz, R.W.; Lu, Y. Detection of dynamic activity patterns at a collective level from large-volume trajectory data. Int. J. Geogr. Inf. Sci. 2014, 28, 946–963. [Google Scholar] [CrossRef]
- Tang, J.; Liu, F.; Wang, Y.; Wang, H. Uncovering urban human mobility from large scale taxi GPS data. Phys. A Stat. Mech. Its Appl. 2015, 438, 140–153. [Google Scholar] [CrossRef]
- Zheng, Z.; Rasouli, S.; Timmermans, H. Two-regime Pattern in Human Mobility: Evidence from GPS Taxi Trajectory Data. Geogr. Anal. 2015, 48, 157–175. [Google Scholar] [CrossRef]
- Alemi, F.; Circella, G.; Handy, S.; Mokhtarian, P. What influences travelers to use Uber? Exploring the factors affecting the adoption of on-demand ride services in California. Travel Behav. Soc. 2018, 13, 88–104. [Google Scholar] [CrossRef]
- Kamga, C.; Yazici, M.A.; Singhal, A. Analysis of taxi demand and supply in New York City: Implications of recent taxi regulations. Transp. Plan. Technol. 2015, 38, 601–625. [Google Scholar] [CrossRef]
- Qian, X.; Ukkusuri, S.V. Spatial variation of the urban taxi ridership using GPS data. Appl. Geogr. 2015, 59, 31–42. [Google Scholar] [CrossRef]
- Zhan, X.; Hasan, S.; Ukkusuri, S.V.; Kamga, C. Urban link travel time estimation using large-scale taxi data with partial information. Transp. Res. Part C Emerg. Technol. 2013, 33, 37–49. [Google Scholar] [CrossRef]
- He, M.; Pu, L.; Liu, Y.; Shi, Z.; He, C.; Lei, J. Research on Nonlinear Associations and Interactions for Short-Distance Travel Mode Choice of Car Users. J. Adv. Transp. 2022, 2022. [Google Scholar] [CrossRef]
- Liu, S.; Zhu, J.; Easa, S.M.; Guo, L.; Wang, S.; Wang, H.; Xu, Y. Travel Choice Behavior Model Based on Mental Accounting of Travel Time and Cost. J. Adv. Transp. 2021, 2021. [Google Scholar] [CrossRef]
- Tang, J.; Bi, W.; Liu, F.; Zhang, W. Exploring urban travel patterns using density-based clustering with multi-attributes from large-scaled vehicle trajectories. Phys. A Stat. Mech. Its Appl. 2020, 561, 125301. [Google Scholar] [CrossRef]
- Liu, F.; Bi, W.; Hao, W.; Gao, F.; Tang, J. An Improved Fuzzy Trajectory Clustering Method for Exploring Urban Travel Patterns. J. Adv. Transp. 2021, 2021. [Google Scholar] [CrossRef]
- Chen, H.; Yang, C.; Xu, X. Clustering Vehicle Temporal and Spatial Travel Behavior Using License Plate Recognition Data. J. Adv. Transp. 2017, 2017. [Google Scholar] [CrossRef]
- Yu, B.; Ma, Y.; Xue, M.; Tang, B.; Wang, B.; Yan, J.; Wei, Y.-M. Environmental benefits from ridesharing: A case of Beijing. Appl. Energy 2017, 191, 141–152. [Google Scholar] [CrossRef]
- Lv, Z.; Wu, J.; Yao, S.; Zhu, L. FCD-based analysis of taxi operation characteristic: A case of Shanghai. J. East China Norm. Univ. (Nat. Sci.) 2017, 5, 133–144. [Google Scholar]
- Wang, W. Study on the Calculation of Urban Accessibility Based on Taxi Trajectory; Chang’an University: Xi’an, China, 2018. [Google Scholar]
- Liu, H.; Liu, P.; Zhang, T. Research on travel patterns of urban population based on taxi GPS data. Jiangsu Sci. Technol. Inf. 2019, 6, 48–51. [Google Scholar]
- Zhang, B. Analysis of Temporal and Spatial Characteristics of Residents’ Travel Based on Online Car-Hailing Data; Southeast University: Nanjing, China, 2019. [Google Scholar]
- Ge, W.; Shao, D.; Xue, M.; Zhu, H.; Cheng, J. Urban taxi ridership analysis in the emerging metropolis: Case study in Shanghai. Case Stud. Transp. Policy 2020, 8, 173–179. [Google Scholar] [CrossRef]
- Xin, F.U.; Yu, Y.A.; Hao, S.U. Structural complexity and spatial differentiation characteristics of taxi trip trajectory network. J. Traffic Transp. Eng. 2017, 4, 106–116. [Google Scholar]
- Cui, Y.-C.; Guan, H.-Z.; Si, Y.; Qin, Z.T. Residents’ Travel Characteristics Based on Order Data of On-Line Car-Hailing: A Case Study of Beijing. Transp. Res. 2018, 5, 20–28. [Google Scholar]
- Dua, Z.; Chen, Z.; Chen, Z.; Kang, J. Analysis of Taxi Passenger Travel Characteristics Based on Spark Platform. Comput. Syst. Appl. 2017, 3, 37–43. [Google Scholar]
- Chen, Z. Research on Extraction and Analysis of Taxi Passenger Travel Characteristics Based on Big Data; Chang’an University: Xi’an, China, 2017. [Google Scholar]
- Wang, Z.; Zhang, Z.; Zhuo, B. Research on urban travel characteristics based on multi-source big data—Taking Qingdao as an example. In Proceedings of the China Urban Transport Planning Annual Conference, Chengdu, China, 14 June–16 July 2019. [Google Scholar]
- Luo, J.; Pan, J. A Method of Taxi Characteristics Analysis Based on GPS Data Mining. Traffic Transp. 2020, 33, 49–54. [Google Scholar]
- Rayle, L.; Dai, D.; Chan, N.; Cervero, R.; Shaheen, S. Just a better taxi? A survey-based comparison of taxis, transit, and ridesourcing services in San Francisco. Transp. Policy 2015, 45, 168–178. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Y.; Jia, B.; Gao, Z. Comparative Analysis of Usage Patterns and Underlying Determinants for Ride-hailing and Traditional Taxi Services: A Chicago Case Study. Transp. Res. Part A Policy Pract. 2024, 179, 103912. [Google Scholar] [CrossRef]
- Jiang, B.; Yin, J.; Zhao, S. Characterizing the human mobility pattern in a large street network. Phys. Rev. E 2009, 80, 021136. [Google Scholar] [CrossRef]
- Kang, C.; Ma, X.; Tong, D.; Liu, Y. Intra-urban human mobility patterns: An urban morphology perspective. Phys. A Stat. Mech. Its Appl. 2012, 391, 1702–1717. [Google Scholar] [CrossRef]
- Chen, M.; Wang, N.; Lin, G.; Shang, J.S. Network-Based Trajectory Search over Time Intervals. Big Data Res. 2021, 25, 100221. [Google Scholar] [CrossRef]
- Neilson, A.; Indratmo; Daniel, B.; Tjandra, S. Systematic Review of the Literature on Big Data in the Transportation Domain: Concepts and Applications. Big Data Res. 2019, 17, 35–44. [Google Scholar] [CrossRef]
- Yang, G.; Yuan, E.; Zhang, X.; Zhou, H. A route planning mechanism for supermarket shuttle service based on taxi traces. Res. Transp. Bus. Manag. 2020, 38, 100502. [Google Scholar] [CrossRef]
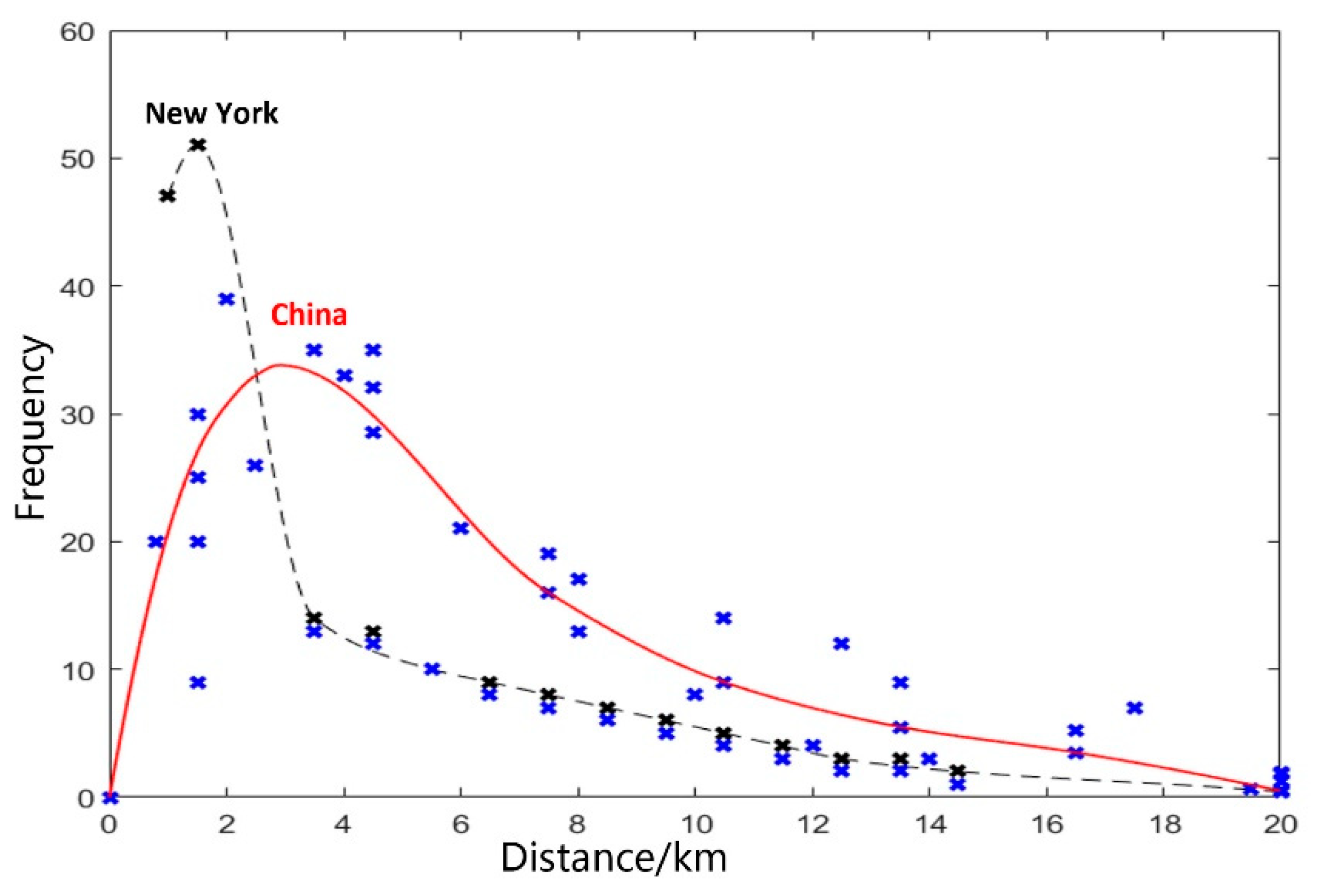
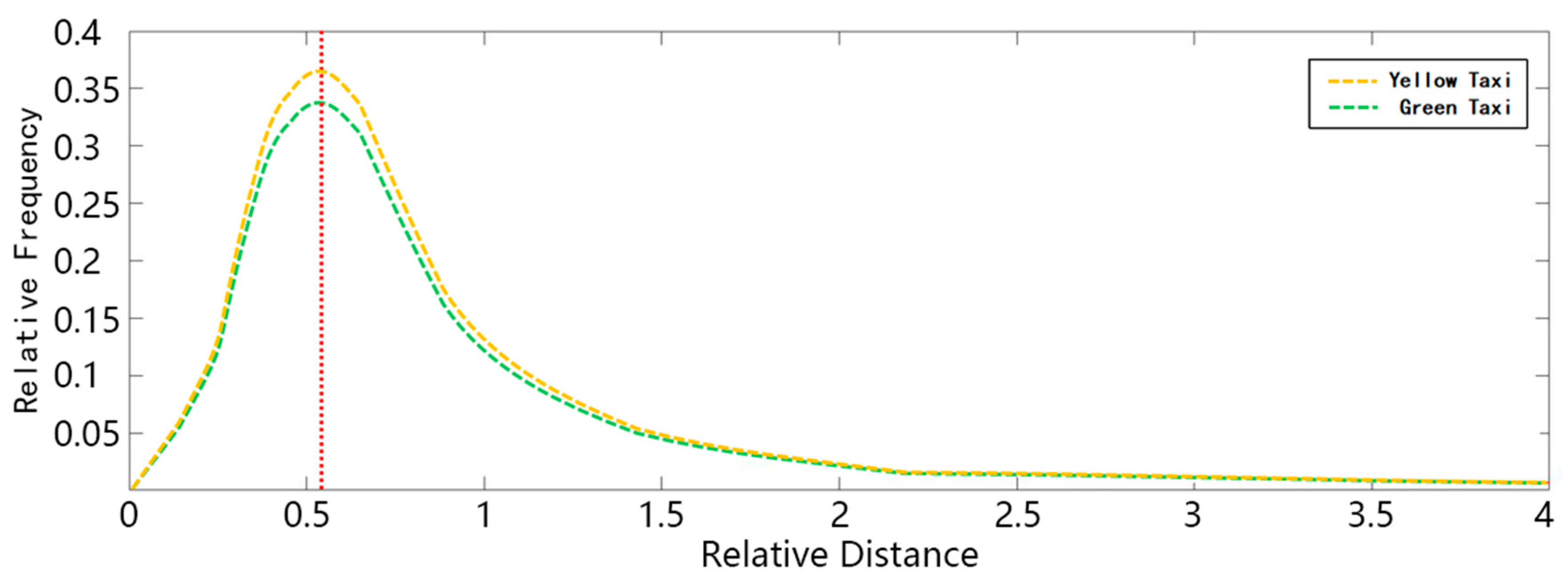
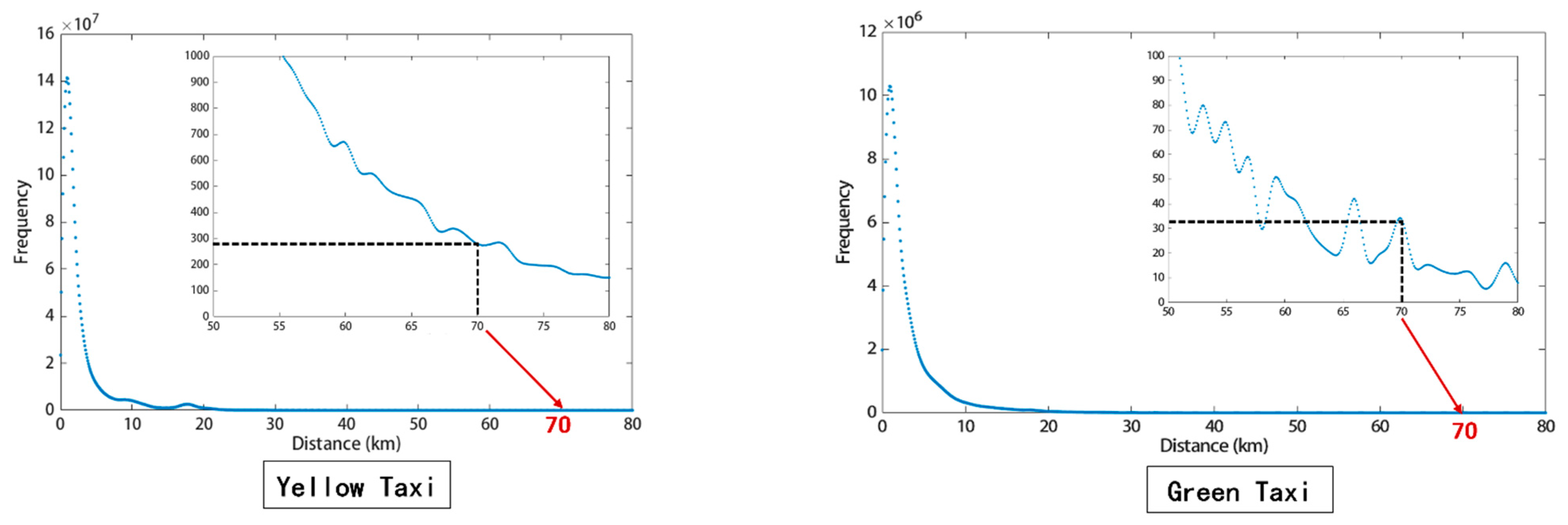
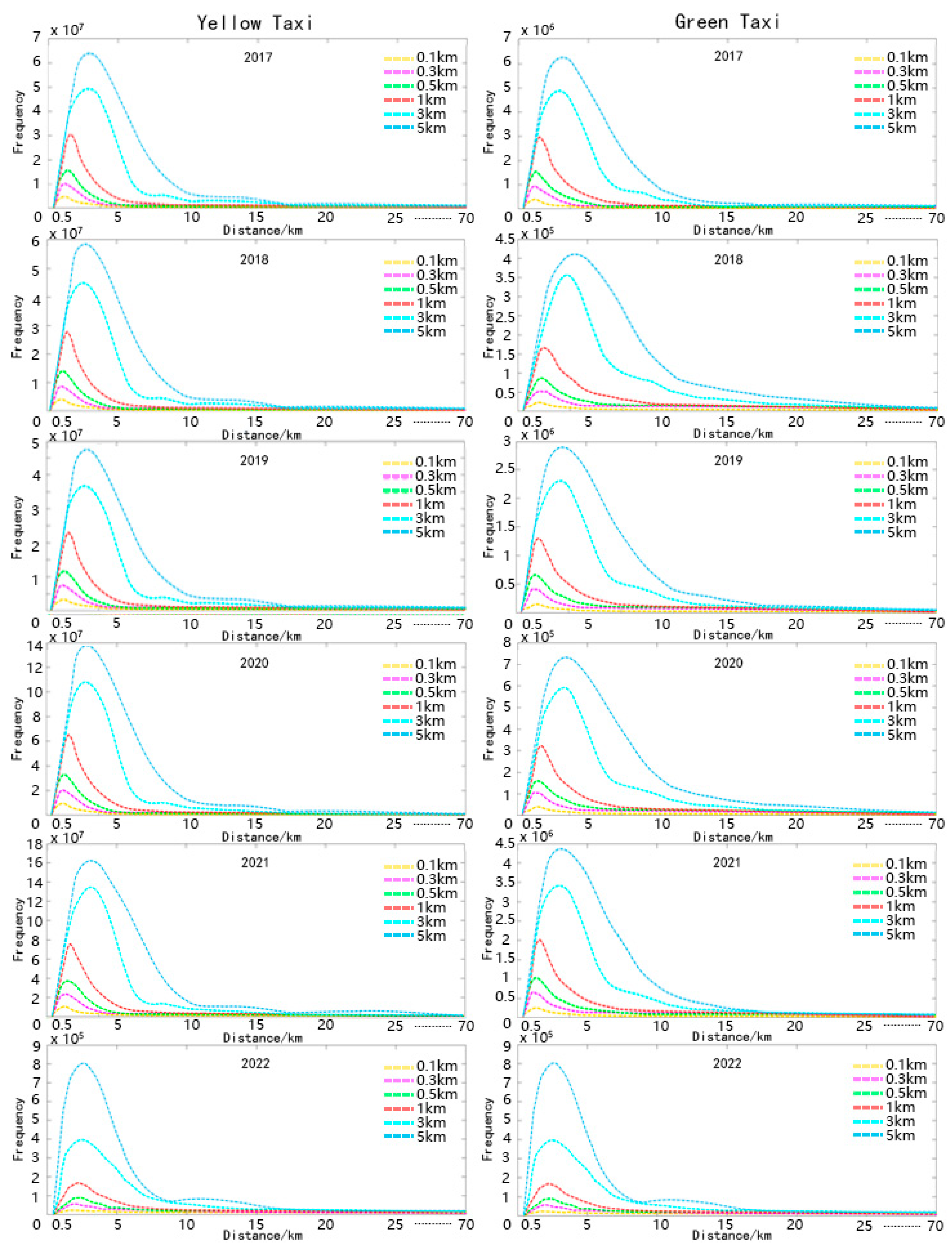
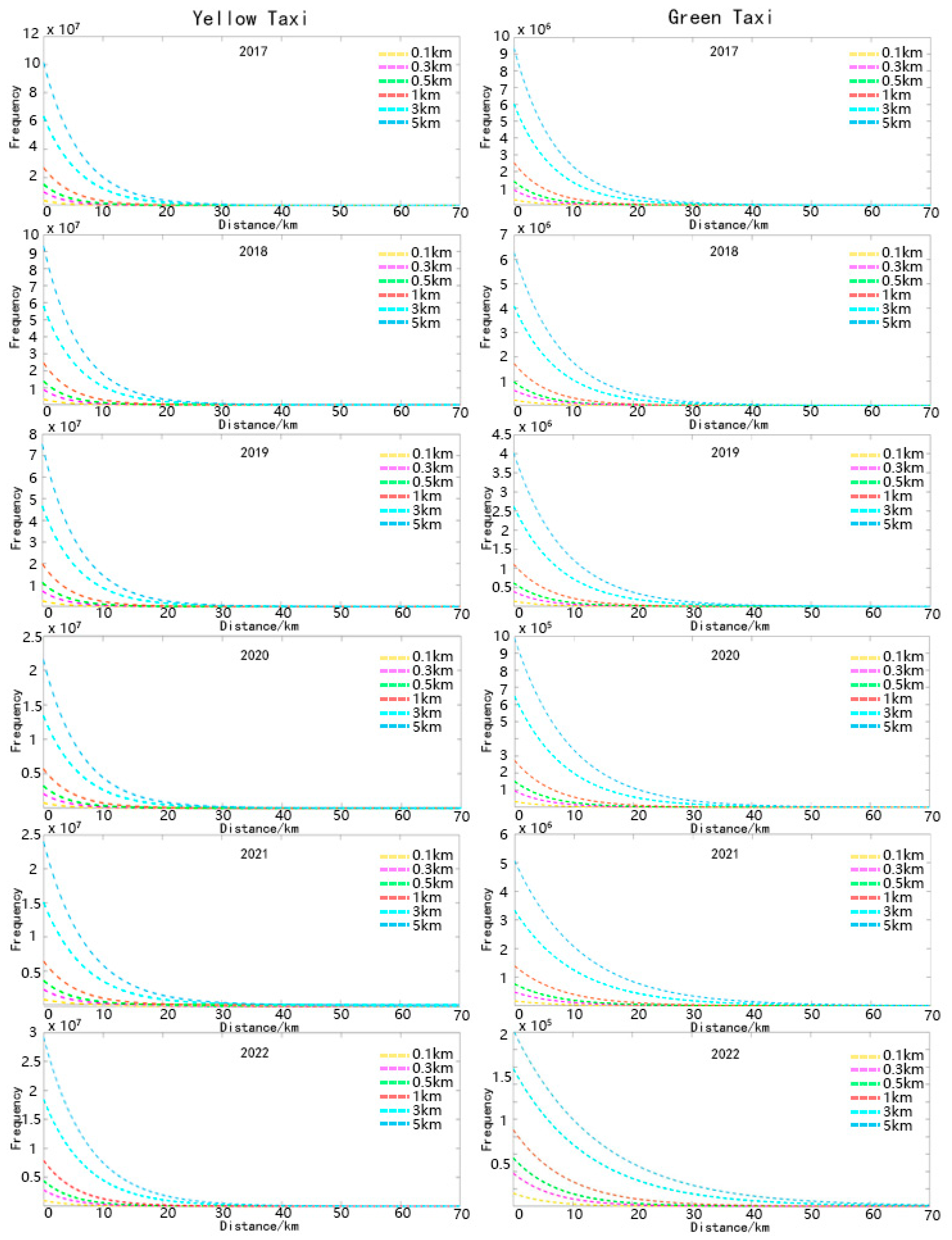
| Year | Yellow Taxi | Green Taxi | ||||
|---|---|---|---|---|---|---|
| Data Amount | Filtered Data | Effective Data Proportion | Data Amount | Filtered Data | Effective Data Proportion | |
| 2017 | 113,500,327 | 107,786,054 | 94.97% | 11,737,059 | 11,079,601 | 94.40% |
| 2018 | 102,871,387 | 97,445,704 | 94.73% | 8,899,718 | 8,431,778 | 94.74% |
| 2019 | 84,598,444 | 82,005,483 | 96.93% | 6,300,985 | 5,895,573 | 93.57% |
| 2020 | 24,649,092 | 23,257,355 | 94.35% | 1,068,755 | 994,806 | 93.08% |
| 2021 | 30,904,308 | 29,483,301 | 95.40% | 705,650 | 639,146 | 90.58% |
| 2022 | 39,656,098 | 38,595,659 | 97.33% | 840,402 | 773,846 | 92.08% |
| Total | 396,179,656 | 378,573,556 | 95.62% | 29,552,569 | 27,814,750 | 93.08% |
| Yellow Taxi | ||||||||
| Mode (km) | Year | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
| Intervals | ||||||||
| 0.10 | 1.45 | 1.45 | 1.45 | 1.45 | 1.45 | 1.45 | ||
| 0.30 | 1.55 | 1.55 | 1.55 | 1.55 | 1.55 | 1.55 | ||
| 0.50 | 1.75 | 1.75 | 1.75 | 1.75 | 1.75 | 1.75 | ||
| 1.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | ||
| 3.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | ||
| 5.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | ||
| Green Taxi | ||||||||
| Mode (km) | Year | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | |
| Intervals | ||||||||
| 0.10 | 1.45 | 2.35 | 1.45 | 1.45 | 2.35 | 2.35 | ||
| 0.30 | 1.55 | 2.45 | 1.55 | 1.55 | 2.45 | 2.45 | ||
| 0.50 | 1.75 | 2.25 | 1.75 | 1.75 | 2.25 | 2.25 | ||
| 1.00 | 2.00 | 3.00 | 2.00 | 2.00 | 3.00 | 3.00 | ||
| 3.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | ||
| 5.00 | 3.00 | 8.00 | 3.00 | 3.00 | 8.00 | 3.00 | ||
| Yellow Taxi | ||||||
| Year | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
| Mean (km) | 4.91 | 4.93 | 5.08 | 4.86 | 5.33 | 5.77 |
| Green Taxi | ||||||
| Year | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
| Mean (km) | 4.44 | 5.37 | 6.05 | 7.84 | 5.46 | 5.36 |
| Year | Interval (km) | Yellow Taxi | Green Taxi | ||||
|---|---|---|---|---|---|---|---|
| a1 | b1 | R12 | a2 | b2 | R22 | ||
| 2017 | 0.1 | 3.506 × 106 | −0.2768 | 0.7546 | 3.228 × 105 | −0.2442 | 0.8529 |
| 0.3 | 9.722 × 106 | −0.2549 | 0.8125 | 9.039 × 105 | −0.2267 | 0.8388 | |
| 0.5 | 1.507 × 107 | −0.2361 | 0.7749 | 1.415 × 106 | −0.2120 | 0.8055 | |
| 1 | 2.692 × 107 | −0.2104 | 0.7532 | 2.532 × 106 | −0.1885 | 0.7691 | |
| 3 | 6.338 × 107 | −0.1661 | 0.8760 | 6.030 × 106 | −0.1500 | 0.8837 | |
| 5 | 1.017 × 108 | −0.1621 | 0.9826 | 9.364 × 106 | −0.1412 | 0.9677 | |
| 2018 | 0.1 | 3.227 × 106 | −0.2818 | 0.7678 | 2.172 × 105 | −0.2256 | 0.8632 |
| 0.3 | 8.938 × 106 | −0.2592 | 0.8145 | 6.104 × 105 | −0.2099 | 0.8460 | |
| 0.5 | 1.384 × 107 | −0.2398 | 0.7762 | 9.587 × 105 | −0.1965 | 0.8141 | |
| 1 | 2.468 × 107 | −0.2135 | 0.7534 | 1.720 × 106 | −0.1748 | 0.7782 | |
| 3 | 5.809 × 107 | −0.1686 | 0.8801 | 4.081 × 106 | −0.1373 | 0.8824 | |
| 5 | 9.341 × 107 | −0.1649 | 0.9841 | 6.277 × 106 | −0.1277 | 0.9667 | |
| 2019 | 0.1 | 2.596 × 106 | −0.2774 | 0.7866 | 1.387 × 105 | −0.2108 | 0.8705 |
| 0.3 | 7.202 × 106 | −0.2555 | 0.8134 | 3.914 × 105 | −0.1967 | 0.8513 | |
| 0.5 | 1.117 × 107 | −0.2369 | 0.7754 | 6.167 × 105 | −0.1847 | 0.8202 | |
| 1 | 1.991 × 107 | −0.2106 | 0.7480 | 1.110 × 106 | −0.1645 | 0.7833 | |
| 3 | 4.680 × 107 | −0.1659 | 0.8729 | 2.630 × 106 | −0.1284 | 0.8709 | |
| 5 | 7.539 × 107 | −0.1626 | 0.9834 | 4.027 × 106 | −0.1186 | 0.9611 | |
| 2020 | 0.1 | 7.415 × 105 | −0.2696 | 0.7997 | 3.379 × 104 | −0.1938 | 0.8753 |
| 0.3 | 2.064 × 106 | −0.2491 | 0.8168 | 9.570 × 104 | −0.1814 | 0.8544 | |
| 0.5 | 3.211 × 106 | −0.2318 | 0.7792 | 1.514 × 105 | −0.1708 | 0.8254 | |
| 1 | 5.727 × 106 | −0.2062 | 0.7488 | 2.736 × 105 | −0.1524 | 0.7874 | |
| 3 | 1.347 × 107 | −0.1627 | 0.8607 | 6.484 × 105 | −0.1183 | 0.8576 | |
| 5 | 2.162 × 107 | −0.1588 | 0.9786 | 9.870 × 105 | −0.1083 | 0.9550 | |
| 2021 | 0.1 | 8.138 × 107 | −0.2381 | 0.7927 | 1.654 × 104 | −0.1549 | 0.8660 |
| 0.3 | 2.288 × 106 | −0.2223 | 0.8048 | 4.741 × 104 | −0.1468 | 0.8488 | |
| 0.5 | 3.591 × 106 | −0.2085 | 0.7693 | 7.576 × 104 | −0.1398 | 0.8228 | |
| 1 | 6.425 × 106 | −0.1866 | 0.7339 | 1.390 × 105 | −0.1266 | 0.7840 | |
| 3 | 1.512 × 107 | −0.1459 | 0.8047 | 3.332 × 105 | −0.0987 | 0.7917 | |
| 5 | 2.401 × 107 | −0.1411 | 0.9562 | 5.068 × 105 | −0.0902 | 0.9143 | |
| 2022 | 0.1 | 9.929 × 105 | −0.2320 | 0.7927 | 1.503 × 104 | −0.1726 | 0.7854 |
| 0.3 | 2.795 × 106 | −0.2166 | 0.8000 | 3.795 × 104 | −0.1498 | 0.7129 | |
| 0.5 | 4.389 × 106 | −0.2033 | 0.7653 | 5.556 × 104 | −0.1352 | 0.6499 | |
| 1 | 7.893 × 106 | −0.1819 | 0.7286 | 8.786 × 104 | −0.1132 | 0.5542 | |
| 3 | 1.846 × 107 | −0.1413 | 0.7969 | 1.581 × 105 | −0.0798 | 0.4445 | |
| 5 | 2.918 × 107 | −0.1360 | 0.9539 | 2.025 × 105 | −0.0704 | 0.4683 | |
| b | Yellow Taxi Trail R2 | Green Taxi Trail R2 |
|---|---|---|
| −1.00 | 0.4484 | 0.5209 |
| −1.10 | 0.5144 | 0.5902 |
| −1.30 | 0.6303 | 0.7066 |
| −1.50 | 0.7220 | 0.7933 |
| −1.80 | 0.8144 | 0.8729 |
| −1.90 | 0.8339 | 0.8877 |
| −2.00 | 0.8484 | 0.8973 |
| −2.10 | 0.8582 | 0.9024 |
| −2.20 | 0.8636 | 0.9033 |
| −2.30 | 0.8652 | 0.9005 |
| −2.40 | 0.8633 | 0.8945 |
| −2.80 | 0.8277 | 0.8451 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Z.; Cai, J.; Yang, Q. Taxi Travel Distance Clustering Method Based on Exponential Fitting and k-Means Using Data from the US and China. Systems 2024, 12, 282. https://doi.org/10.3390/systems12080282
Song Z, Cai J, Yang Q. Taxi Travel Distance Clustering Method Based on Exponential Fitting and k-Means Using Data from the US and China. Systems. 2024; 12(8):282. https://doi.org/10.3390/systems12080282
Chicago/Turabian StyleSong, Zhenang, Jun Cai, and Qiyao Yang. 2024. "Taxi Travel Distance Clustering Method Based on Exponential Fitting and k-Means Using Data from the US and China" Systems 12, no. 8: 282. https://doi.org/10.3390/systems12080282
APA StyleSong, Z., Cai, J., & Yang, Q. (2024). Taxi Travel Distance Clustering Method Based on Exponential Fitting and k-Means Using Data from the US and China. Systems, 12(8), 282. https://doi.org/10.3390/systems12080282





