Performance Evaluation of Carbon-Neutral Cities Based on Fuzzy AHP and HFS-VIKOR

Abstract

Climate change threatens human survival and development. Cities, as the main gathering places for human production and life, serve as the focal points for the implementation of the policies related to energy efficiency, energy transition, and environmental protection. This study constructs an index system for the evaluation of carbon-neutral cities from the perspectives of carbon sources and carbon sinks. The system includes thirteen indicators under six dimensions. It combines objective and subjective data (i.e., statistical data and expert evaluations) by integrating two approaches: the fuzzy analytic hierarchy process (fuzzy AHP) and vise kriterijumska optimizacija i kompromisno resenje with hesitant fuzzy sets (HFS-VIKOR). We verify the efficacy of the proposed approach through a case study of thirteen low-carbon pilot cities in China. The results indicate that among these cities, Shenzhen performs the best, followed by Guangzhou and Hangzhou, while Kunming, Baoding, and Tianjin show poor performance in terms of carbon neutrality. Kunming and Baoding exhibit shortcomings mainly in carbon sources, while Tianjin faces deficiencies in both carbon sources and carbon sinks. Sensitivity analysis and comparative analysis show the availability and effectiveness of the proposed method. The proposed radar chart further highlights the improvement directions for each city to achieve carbon neutrality.

1. Introduction

Global climate change and global warming pose formidable challenges to the sustainable development of economies and societies [1]. To address this issue, the “Paris Agreement”, reached in 2015 by 178 countries and regions worldwide, set the goal of achieving net-zero greenhouse gas emissions globally in the second half of the 21st century, ensuring that the increase in global surface temperature relative to the pre-industrial era is controlled within 2 °C by the end of the 21st century [2]. In the following years, driven and guided by the European Union, the concept of carbon neutrality has surged across the world [3,4]. As the largest developing country and the world’s second-largest economy, China has undertaken various initiatives related to eco-cities, green cities, and low-carbon cities to effectively address climate change. In 2021, China included the “dual-carbon goal” (peak carbon emissions and carbon neutrality before 2060) in its medium- and long-term national economic and social development plan. The successful implementation of these policies has reversed the trend of rapid carbon emission growth in China over the past decade [5].

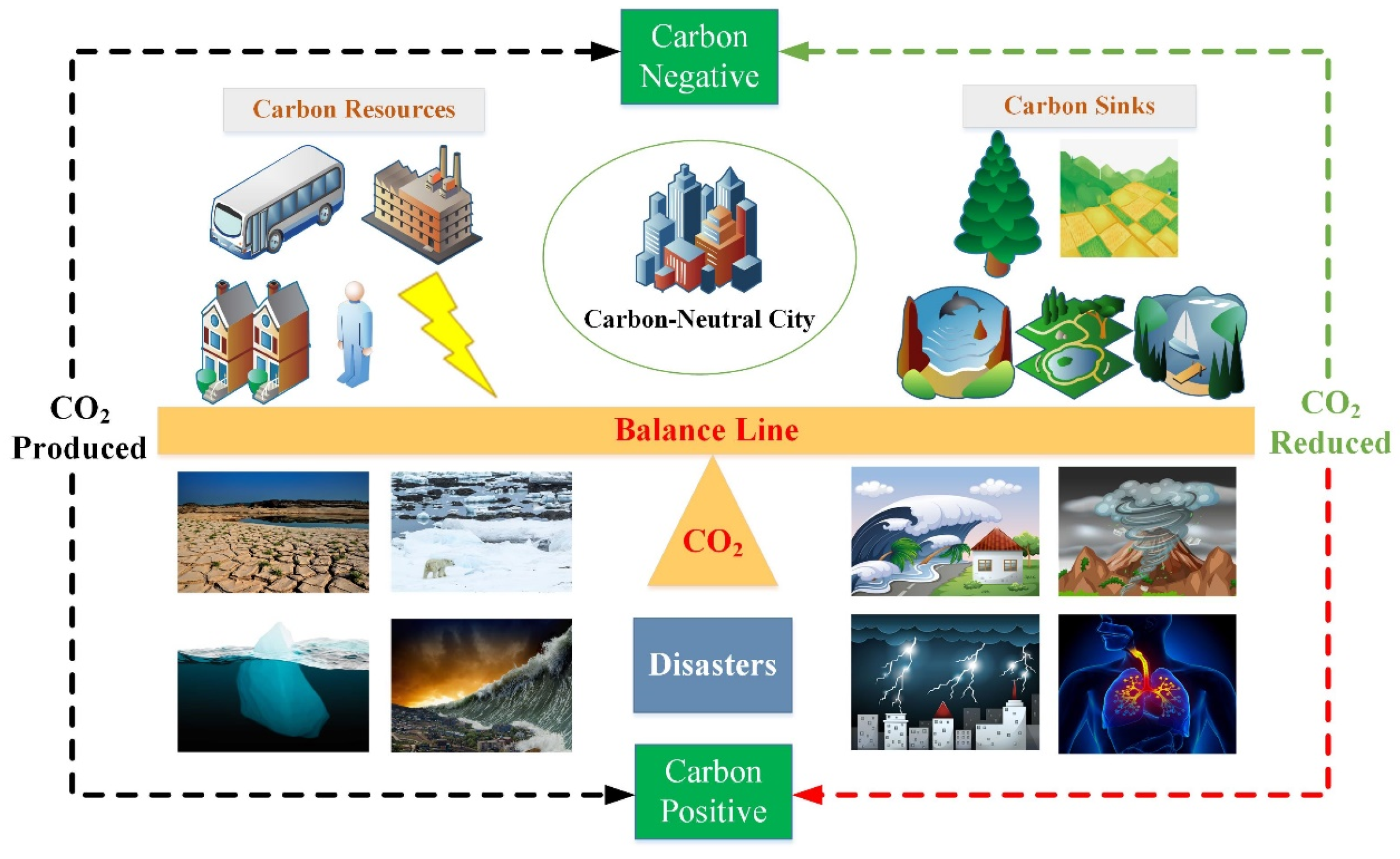
Carbon neutrality refers to the calculation of the total greenhouse gas emissions, both direct and indirect, generated by enterprises, organizations, or individuals over a certain period of time. Through activities such as afforestation, energy conservation, and emission reduction, carbon neutrality aims to offset the carbon dioxide (CO₂) emissions produced, achieving net-zero CO₂ emissions [6]. The concept of carbon neutrality can be simply divided into two aspects: carbon sources and carbon sinks. Carbon sources include the production and consumption of energy, transportation, building and community structures, waste management, food production, and consumption. Carbon sinks include plants, sequestration technologies, natural water resources, and biodiversity. In addition to carbon neutrality, concepts such as zero carbon have been proposed. Zero carbon imposes higher requirements than carbon neutrality, as the former requires the elimination of all carbon emissions. It is not as flexible as carbon neutrality, which allows for the offsetting of carbon emissions through third-party purchases of compensation beyond city boundaries [7,8].

Carbon neutrality can only be accomplished when a balance is struck between carbon sources and carbon sinks [9]. The realization of carbon neutrality involves multiple aspects, including economic development, social activities, ecological capacity, and the development of alternative energy sources [10]. Existing studies on carbon neutrality have focused on calculating the carbon emissions and absorption in cities to assess the feasibility of achieving carbon neutrality [11]. Production-based carbon emissions are currently used to monitor progress toward the goals of the Paris Agreement [12,13]. Life cycle assessment involves evaluating the lifecycle emissions of the energy, goods, and services consumed by a city. Compared to consumption-based emissions accounting, this method may increase the total emissions and carries the risk of double counting [14]. Consumption-based accounting utilizes various advanced technological means and tools for real-time monitoring. Zhao et al. [15] used the logarithmic mean Dickson index method to clarify the driving forces and investigate the carbon emissions of the construction industry in Hangzhou, China. However, due to the lack of consistency in the calculation methods, data sources, and emission ranges, it is difficult to compare and benchmark progress towards carbon-neutrality goals between cities [16]. In addition, constrained by the current emission coefficient calculations, the emission reports of most cities tend to focus on energy monitoring and overlook carbon sinks.

As the primary hubs for human production and life, cities are not only the centers of economic activities but also the focal points for implementing policies such as energy conservation, emission reduction, and environmental protection [17]. Cities accommodate nearly 40% of the population and contribute to about 75% of the national economy [18]; however, they require a significant amount of energy to maintain [10]. It is estimated that the energy consumption in Chinese cities accounts for 75% of the country’s total energy consumption, and its CO₂ emissions account for 84% of the total [18,19]. China’s extensive use of energy and its coal-based energy structure have brought enormous pressure to the climate and the environment [5]. As economic and policy action hubs, cities play a crucial role in mitigating global climate change and have significant implications for achieving carbon neutrality [20]. The survey results from the Energy and Climate Intelligence Unit show that 13% of cities with a population of over 500,000 worldwide have committed to achieving net-zero emissions, covering 638 million people [21]. Copenhagen, the capital of Denmark, set a goal in 2009 to become the world’s first carbon-neutral city by 2025 [22]. The United Arab Emirates is planning for the city of Masdar in Abu Dhabi to be a “carbon-neutral and zero-waste” urban cluster [23]. Adelaide in Australia began implementing the “Adelaide 2020–2024 Strategic Plan” in July 2020, with the goal of becoming a carbon-neutral city by 2025. Its plan specifies two pathways to achieve carbon neutrality: carbon emission reductions and carbon credits [24]. Helsinki, the capital of Finland, set a goal in 2018 to achieve carbon neutrality by 2035 through 80% carbon emission reductions and the remaining 20% through compensation and carbon sinks [25]. New York City in the United States aims to achieve carbon neutrality by 2050 through “carbon emission reductions + carbon credits/offsets” [26]. In China, since 2010, three batches of 81 low-carbon city pilot projects have been initiated [27]. Carbon neutrality is thus a shared goal for countries and territories worldwide, with major cities formulating construction plans and development strategies based on the management of carbon sources and carbon sinks.

The performance of carbon-neutral city construction has the most direct impact on achieving carbon neutrality goals. Before embarking on full-scale city construction, governments often initiate the construction of low-carbon pilot cities. Tan et al. [28] proposed that the evaluation of low-carbon cities can provide precise suggestions for the sustainable development of subsequent cities. Yu and Zhang [27] pointed out that the low-carbon city pilot project has a significant effect on reducing CO₂ emissions for both implemented and neighboring cities. However, there are some challenges to be overcome:

• Difficulty obtaining carbon sink data: Data related to carbon sinks are challenging to acquire. Carbon-neutral cities, as opposed to low-carbon cities, emphasize energy-saving and emission-reduction effects. The majority of existing studies have also focused on carbon sources. Current carbon sink technologies are immature, and there is a lack of consensus on the methodologies. Furthermore, carbon sequestration data are difficult to obtain; statistical yearbooks and reports of each province/city are the most commonly used, but qualitative indicators are lacking [29,30];
• Inconsistent performance evaluation: Different cities adopt different indicators based on their unique ecological conditions, economic foundations, and development levels, which makes it difficult to compare the evaluation results [31];
• Ambiguity and complexity of indicators: Most existing methods for evaluating carbon neutrality are based on calculating the difference between carbon emissions and carbon absorption. However, it is difficult to calculate the overall carbon emissions in cities, and indicators are often singular, fuzzy, and uncertain. Therefore, a consistent universal evaluation method is needed [32].

Thus, the current study sought to (1) propose a comprehensive performance evaluation system for carbon-neutral cities, (2) study paths towards carbon neutrality and the problems encountered, and (3) provide practical suggestions for policymakers and city planners. To reach these objectives, we considered two key processes for achieving carbon neutrality: reducing carbon emissions (including energy conservation, enhanced energy efficiency, and the development of alternative energy sources) and increasing carbon absorption capacity (including improving ecosystems and developing carbon sequestration technologies). These two processes form the basis of our comprehensive and integrated evaluation system for carbon-neutral cities. We used a combination of subjective and objective data to address the shortcomings of previous studies. The fuzzy analytic hierarchy process (fuzzy AHP) was used to assign weights to the indicators, and vise kriterijumska optimizacija i kompromisno resenje with hesitant fuzzy sets (HFS-VIKOR) was applied to solve the problem of ranking indicators in fuzzy environments. Together, these methods convey group decision-making information, retain the original evaluation information as comprehensively as possible, and address the problem of fuzzy, imprecise, and difficult-to-quantify indicators. We applied the proposed approach to analyze thirteen cities from the first batch of low-carbon pilot cities in China and provide targeted suggestions for improvement. This study contributes to the existing literature by proposing a novel hybrid application of fuzzy AHP and HFS-VIKOR to evaluate the performance of carbon-neutral cities in terms of carbon sources and carbon sinks. Our practical contributions include accurate performance evaluation that integrates different data types. The proposed evaluation system reveals how the mixed indicators of carbon sources and carbon sinks affect the efficiency ranking of each city. We further provide a user-friendly visual analysis for policymakers and city planners working toward carbon neutrality.

The remainder of this paper is organized as follows. Section 2 presents the indicators relevant to the evaluation of carbon-neutral cities, and briefly reviews the fuzzy AHP and HFS-VIKOR. Section 3 presents the details of the proposed framework. A case study is given in Section 4 to illustrate the proposed method and algorithm. Sensitivity analysis and comparative analysis were used to demonstrate the advantages of the proposed method. Conclusions are drawn in Section 5.

2. Materials and Methods

2.1. Index System for the Performance Evaluation of Carbon-Neutral Cities

Most ecological and environmental issues, such as environmental pollution, climate change, and loss of biodiversity, are closely related to urban development [1,33]. To address climate change as well as provide people with a comfortable living environment and reduce the negative impact of urban development on ecosystems, various city concepts have been proposed. These include ecological cities, green cities, low-carbon cities, and carbon-neutral cities [34,35,36]. To evaluate the effectiveness of these policies, De Flander [37] proposed the construction of a comprehensive evaluation system based on multiple perspectives to avoid overemphasizing a single resource and the negative feedback of other resource flows. Constructing a reasonable performance evaluation index system is helpful for effectively evaluating the performance of city construction. Past studies on urban sustainability focused on the low-carbon aspects, with the indicators concentrated on effective energy utilization and green living. In 1990, Kaya proposed the following four indicators for total carbon emissions [12,38]: population, per capita GDP, energy intensity, and energy intensity. Copenhagen, the first city to propose carbon-neutral goals, monitors its energy consumption, energy production, low-carbon transportation, and low-carbon municipal planning [39]. Michael et al. [40] selected 21 indicators from economic, social, energy, and environmental dimensions to assess the effectiveness of low-carbon city construction in Malaysia. Wang et al. [31] constructed an evaluation index system for low-carbon city development consisting of 25 indicators from the dimensions of low-carbon economy, low-carbon society, urban planning, energy utilization, and low-carbon environment. Liu et al. [41] considered nine indicators including population size, economic scale, per capita GDP, wage level, and fiscal level to analyze whether 285 prefecture-level cities in China had achieved their carbon reduction goals.

Low-carbon cities are of great significance for a sustainable future. However, compared to carbon-neutral cities, low-carbon cities primarily focus on energy conservation and carbon emission reductions. Carbon neutrality means that the emission of CO₂ into the atmosphere and the removal of CO₂ from the atmosphere remain in balance over a certain period [15]. Thus, evaluating carbon neutrality requires the consideration not only of carbon sources but also of carbon sinks. Figure 1 illustrates the conceptual framework of carbon-neutral cities.

The population, economy, land changes, and energy structure are closely related to carbon emissions in the process of urbanization [23,42,43]. Zhou et al. [44] stated that the combustion of fossil fuels is the main factor of CO₂ generation, while city construction and development are the major contributors to the use of fossil fuels and related carbon sources. Colmenar-Santos et al. [45] and Doust and Otkur [46] pointed out that city transportation is the primary source of carbon emissions, with vehicular exhaust being the main contributor to transportation-related carbon emissions. Phdungsilp [47] proposed that the shift in Bangkok, Thailand, from private passenger vehicles to public transportation systems can significantly reduce energy demand, carbon emissions, and air pollutants. Aslam et al. [48] indicated that population density, industrialization, and trade have increased China’s CO₂ emissions, and in the long term, per capita GDP will worsen CO₂ emissions.

There are three main sources of carbon sinks:

• Plants: Forest ecosystems are the main carbon sequestration agents. The carbon sequestration effect of forests does not require excessive human intervention. It is a natural carbon sequestration process with low economic costs. Additionally, forests provide significant ecological benefits such as biodiversity conservation and water source conservation [49]. Forests not only reduce CO₂ through carbon sequestration but also absorb carbon from the atmosphere for conversion [50]. Beecham [51] stated that in Australia, four trees can offset the carbon emissions from 100 square meters of road surface over 50 years.
• Carbon capture, utilization, and storage (CCUS) technologies: The evaluation of CCUS technologies has been constrained by difficulties in obtaining statistical data, and comprehensive evaluations are often lacking. However, with the development of technology, carbon capture techniques have improved and are expected to play a greater role in the future [52,53,54].
• Farmland and aquatic ecosystems: Farmland and aquatic ecosystems are a means of carbon sequestration which rely on natural means to store and convert the carbon in CO₂ [55,56].

Figure 2 presents the index system proposed by the current study for the performance evaluation of carbon-neutral cities.

Table 1. Proposed performance evaluation system for carbon-neutral cities.

Dimension	Criteria	Indicator	Unit	Polarity	Description [Reference]
Carbon sources (M1)	Energy consumption (Y1)	The energy consumption per 10,000 CNY of GDP (C1)	Tons of standard coal/10,000 CNY	Negative	Energy consumption per GDP [57]
		The use of clean energy (C2)	—	Positive	Clean energy is either renewable or non-polluting. Renewable energy sources include hydro, wind, geothermal, tidal, and other non-fossil energy sources. Non-polluting energy sources generate low to zero environmental pollution in their production and consumption processes, such as natural gas, clean coal, and nuclear energy [58]
	Industrial production (Y2)	Carbon emission intensity (C3)	Tons/10,000 CNY	Negative	Total carbon emissions per GDP [30,41,57]
		The proportion of tertiary industry (C4)	%	Positive	Output value of tertiary industry per GDP [28,57]
	Residents (Y3)	Per capita CO2 emissions (C5)	Tons/person	Negative	CO2 emissions attributable to urban population [28,41,57]
		Per capita residential electricity consumption (C6)	KWh/person	Negative	The total electricity consumption of urban residents [59]
	Transportation (Y4)	Number of private vehicles (C7)	Vehicles/100 people	Negative	Car ownership by the urban population [28,31]
		The number of public electric (bus) vehicles per 10,000 people (C8)	Vehicles/10,000 people	Positive	The number of public electric (bus) vehicles per urban resident [28,31]
Carbon sinks (M2)	Plant-based (Y5)	Forest coverage rate (C9)	%	Positive	The ratio of forested area to urban land [49,50,51]
		The green coverage rate in built-up areas (C10)	%	Positive	The ratio of green areas in built-up areas to the total built-up land [31,57]
		Per capita park area (C11)	m2/person	Positive	The ratio of the total park space to urban residents [28,31]
	Others (Y6)	The level of CCUS and similar technologies (C12)	—	Positive	The development and usage of CCUS and similar technologies in cities to offset carbon emissions [52,53,54,58]
		The development and utilization of ecosystems (C13)	—	Positive	The development and utilization of the carbon sequestration capacity of natural ecosystems such as farmland and water sources [55,56]

provides detailed descriptions of the thirteen indicators of the proposed system.

2.2. Fuzzy AHP

For a decision-making problem, creating a decision hierarchy structure is crucial. In addition, after appropriate indicators have been determined, these indicators must be weighted. Satty [60] proposed the AHP, which is a powerful and flexible quantitative technique of multi-criteria decision-making (MCDM). The AHP divides complex decision-making problems into a hierarchical structure of elements, including a goal, evaluation criteria or objectives, and alternatives, and conducts pairwise comparisons to establish the relationships within the structure [61]. Figure 3 shows an example of this type of multi-level hierarchical structure.

Compared to other MCDM techniques (including the analytic network process (ANP), Delphi method, data envelopment analysis (DEA), and decision-making and trial evaluation laboratory (DEMATEL)), the AHP is easy to use and effectively provides weights and rankings [62]. However, because the AHP uses explicit values to express expert judgments and does not consider uncertainty and subjectivity, it is only applicable to crisp environments [63]. In addition, in the AHP method, experts need to conduct multiple pairwise comparisons with a highly unbalanced scale of judgment to arrive at the final result [64]. This leads to difficulties in comparing indicators with each other, especially when involving a large number of indicators. Clearly, there are limitations to the application of Saaty’s AHP. To address this, the fuzzy AHP was developed using the fuzzy sets theory [65]. The fuzzy AHP is widely used for determining indicator weights from both subjective and objective perspectives [66,67]. The fuzzy AHP treats the evaluation objects as systems and then makes decisions based on the decomposition, comparison, comparative judgments, and synthesis of priorities [68]. The fuzzy AHP has been applied to a diverse range of fields, including, for example, the airline industry [69], large data matrices [70], environmental decision support systems [71], human-machine interface design evaluation [72], solar panel selection [73], stationary hydrogen storage [74], and stock portfolio selection [75].

2.3. HFS

The performance evaluation of carbon-neutral cities involves various aspects, such as energy conservation, economic structure, and residents’ lifestyles, making it a multi-criteria decision-making problem. Due to the differences in geographical location, natural resources, and economic conditions among cities, it is difficult for a city to perform optimally in all aspects. In addition to utilizing objective data from government statistical reports, subjective data were gathered through expert group evaluations. Considering that differences in experts’ backgrounds, decision preferences, and experiences may lead to differences and conflicts in the evaluation scores, we adopted the hesitant fuzzy sets (HFSs) [76].

Zadeh [77] proposed the theory of fuzzy sets, which can be defined as follows [78]:

Definition 1.

Let U be the universe of discourse. The fuzzy set A of U is defined by membership function ${\mu }_{\tilde{A}}(u)$, which maps each element u in U in the range [0, 1], as follows:

$${\mu }_{\tilde{A}}: u\to {\mu }_{\tilde{A}}(u)$$

(1)

In the evaluation process, to overcome the limitations of individual decision-making, it is common to invite multiple experts to make decisions on a particular issue. However, due to the diverse backgrounds of experts, reaching a consensus can be difficult. Methods such as majority rule or other consensus-reaching approaches may lead to the neglect of some opinions and viewpoints [79]. To address this, Torra [77] expanded on fuzzy sets through the introduction of HFSs. Compared to traditional fuzzy sets, an HFS allows an element to have multiple degrees of membership. The fundamental component of an HFS is the hesitant fuzzy element (HFE), which is a set composed of several possible values. The definition of an HFS is as follows:

Definition 2.

Hesitant fuzzy set E on fixed set X is function h_E that when used on X returns a subset of [0, 1], which can be represented as follows:

$$E=\left\{\langle x,h_E(x)\rangle |x\in X\right\}$$

(2)

where function $h_E(x)$ is a set of some values in [0, 1], denoting the possible membership degrees of element $x\in X$ to set E.

It is noted that due to the presence of several possible membership values and the non-uniqueness of the number of elements in the HFE, comparing their sizes may be difficult. This issue is solved through the use of score functions.

Definition 3.

The score function can be defined as follows [80]:

$$S\left(h_E(x)\right)=\frac{1}{\#h_E(x)}{\displaystyle \sum _{{\gamma }_x\in h_E(x)}{\gamma }_x}$$

(3)

where $\#h_E(x)$ represents the number of membership values ${\gamma }_x$ in the HFE. The larger the value of the score function, the greater the HFE.

Distance measurement is an effective tool for evaluating the dissimilarity between different objects. Through distance measurement, it is possible to effectively identify the gap between the various aspects of a city and the ideal solution for achieving carbon neutrality [81]. In most cases, when two HFEs have inconsistent lengths, it is necessary to extend the shorter HFE to make them comparable. Numerical values can be added based on decision makers’ subjective preferences. In general, optimistic decision makers add the maximum membership value, while pessimistic decision makers add the minimum membership value. Note that a value of 0 can also be added to ensure that the lengths of the two HFEs are consistent. The membership values in the HFE also need to be arranged in ascending or descending order [82].

Definition 4.

For two HFEs, $h_1(x)=\left\{{\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_{\#h_1}\right\}$ and $h_2(x)=\left\{{\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_{\#h_2}\right\}$, the generalized hesitant normalized distance is given by the following:

$$d_{ghn}\left(h_1(x_i),h_2(x_i)\right)={\left(\frac{1}{l_{x_i}}{\displaystyle \sum _{j=1}^{l_{x_i}}{\left|h_1^{\sigma (j)}(x_i)-h_2^{\sigma (j)}(x_i)\right|}^{\lambda }}\right)}^{1/\lambda }$$

(4)

where $l_{x_i}=\max \left\{\#h_1(x),\#h_2(x)\right\}$, in which $\#h_1(x)$ and $\#h_2(x)$ are the number of membership values for $h_1(x)$ and $h_2(x)$, respectively, and $h_1^{\sigma (j)}(x_i)$ and $h_2^{\sigma (j)}(x_i)$ are the jth largest values ($0<j\le l_{x_i}$) in $h_1(x_i)$ and $h_2(x_i)$, respectively. When λ = 1, the formula is reduced to the hesitant normalized Hamming distance; when λ = 2, the formula is reduced to the hesitant normalized Euclidean distance.

2.4. HFS-VIKOR

The purpose of evaluating carbon-neutral cities is to understand a city’s progress in regard to carbon neutrality, rather than selecting the best-performing city. VIKOR is a compromise ranking method for complex MCDM problems with disproportionate and conflicting indicators based on the method of ideal solutions. It not only addresses the conflicts among indicators but also performs compromise ranking based on limited decision alternatives by maximizing the group utility and minimizing the individual regret. This method seeks a balance between the overall and individual performance and can be effectively applied in situations where the collective interests are conflicting [83]. VIKOR is a well-known method in MCDM, and readers can refer to [84,85] for more information.

In real-world decision-making processes, decision makers often tend to express their preferences in the form of discrete sets [86]. In such cases, in consideration of the effectiveness of VIKOR and HFS, an increasing number of researchers are opting to use HFS-VIKOR to handle decision problems [87]. Narayanamoorthy et al. [88] proposed an approach for the selection of industrial robots; that approach integrates the interval valued intuitionistic hesitant fuzzy entropy and interval valued intuitionistic hesitant fuzzy VIKOR methods. Çolak and Kaya [89] utilized an integrated MCDM model consisting of the hesitant fuzzy AHP and hesitant fuzzy VIKOR for the evaluation of energy storage technologies in Turkey. Tu et al. [90] used a hybrid MCDM method with different hesitant fuzzy linguistic term sets for regional water resource coordination. Mishra et al. [91] developed a novel approach based on Fermatean hesitant fuzzy sets (FHFSs) and the modified VIKOR method for multi-attribute decision-making (MADM). de Oliveira et al. [92] used the supplier selection process of an electrical services company as a case study to compare the extended hesitant fuzzy linguistic VIKOR (EHFLVIKOR) and hesitant fuzzy linguistic VIKOR with possibility distribution (PDHFLVIKOR) methods. Zhang et al. [93] presented a Pythagorean hesitant fuzzy VIKOR (PHF-VIKOR) method for component supplier selection. Finally, Gao et al. [94] applied a novel hesitant 2-tuple linguistic Pythagorean fuzzy decision-making method for the evaluation of a single-pilot operation mechanism.

3. Framework for the Performance Evaluation of Carbon-Neutral Cities

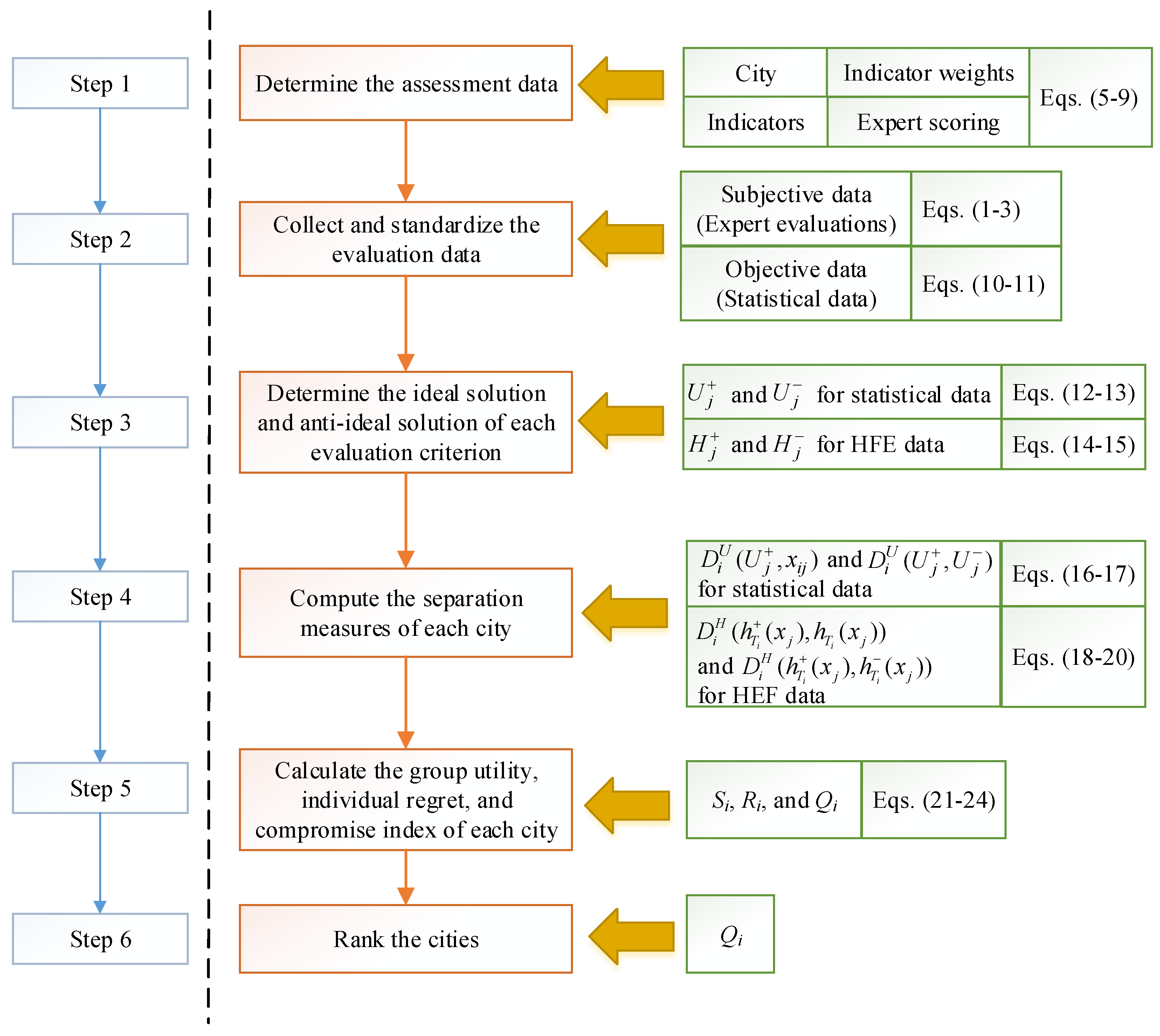
The aim of this study was to evaluate the performance of carbon-neutral cities based on qualitative and quantitative data. The fuzzy AHP was first applied to assign weights to different indicators, and then HFS-VIKOR was used to obtain the final rankings of each city. Figure 4 illustrates our research framework. The proposed methodology proceeded as follows:

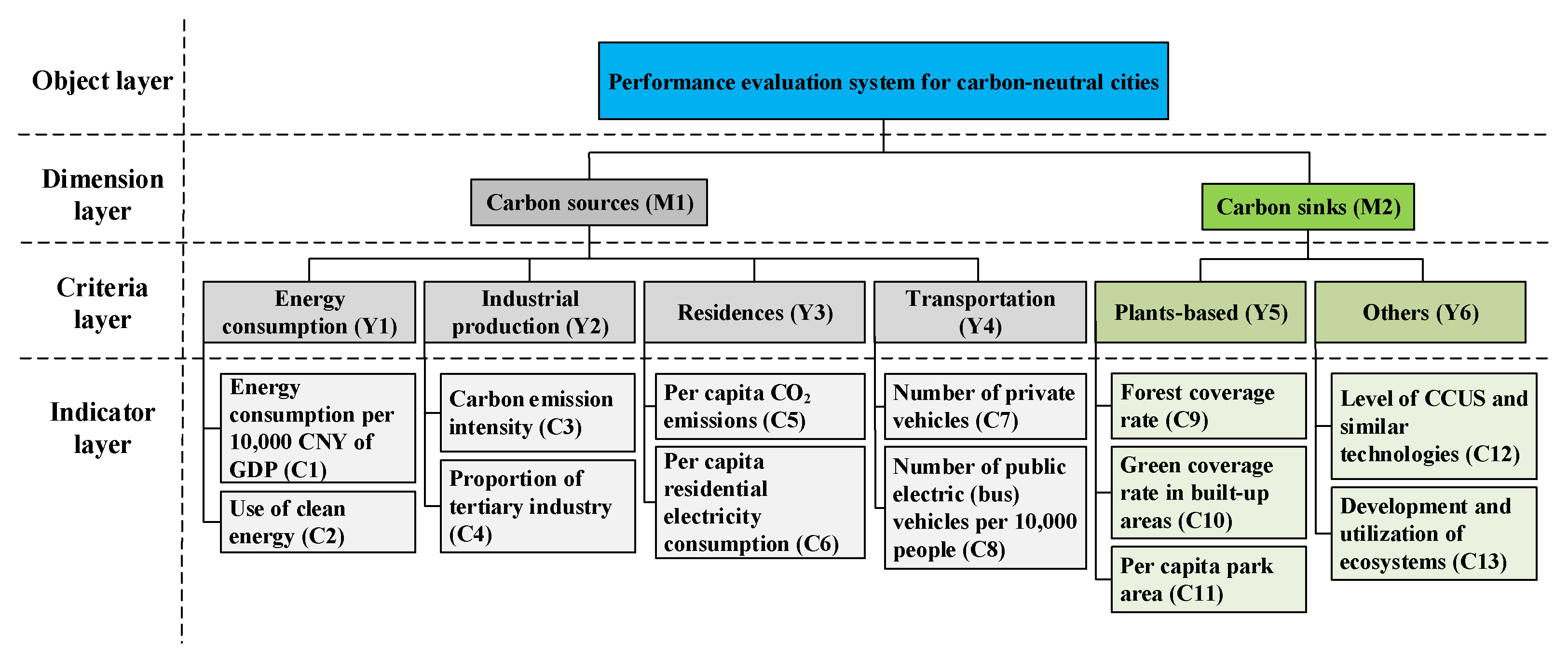
Step 1: Use the fuzzy AHP to determine the indicators and their weights: For our research aims, we selected the thirteen indicators presented in Table 1. The indicator weights reflect the importance of each indicator to the overall evaluation objective. The larger the weights of the indicator, the more important it is in the evaluation process and the greater its impact on the overall performance value. The fuzzy AHP proceeds as follows [95]:

Definition 5.

Define fuzzy judgment matrix $\tilde{A}={(a_{ij})}_{n\times n}$, where $a_{ij}$ reflects how many more times that indicator i is preferred to indicator j in situations with a certain degree of uncertainty and/or ambiguity. If $0\le a_{ij}\le 1$, $(i,j=1,2,\dots n)$, then $\tilde{A}$ is a fuzzy judgment matrix.

Definition 6.

For fuzzy judgment matrix $\tilde{A}={(a_{ij})}_{n\times n}$, if $a_{ij}+a_{ji}=1$, $(i,j=1,2,\dots n)$, then $\tilde{A}$ is a fuzzy complementary matrix.

Definition 7.

For fuzzy complementary matrix $\tilde{A}={(a_{ij})}_{n\times n}$, if $a_{ij}=a_{ik}-a_{jk}+0.5$, $(i,j,k=1,2,\dots n)$, then $\tilde{A}$ is a fuzzy consistent matrix.

1.1: Construct a multi-level hierarchical structure. Decompose the research problem hierarchically, with levels organized from high to low according to dimension layer M, criteria layer $Y_1,Y_2,\dots ,Y_n$, and indicator layer $C_1,C_2,\dots ,C_n$. The upper levels are determined by the lower levels.

1.2: Establish fuzzy complementary matrix $\tilde{A}$ with all the dimensions of the multi-level hierarchical structure. Let $C_1,C_2,\dots ,C_n$ denote the set of indicators and $a_{ij}$ represent a quantified judgment on a pair of indicators C_i and C_j.

Table 2. Scores of the fuzzy AHP.

Score	Definition	Description
0.5	Equally important	ai and aj are equally important.
0.6	Slightly important	ai is slightly more important than aj.
0.7	Important	ai is more important than aj.
0.8	Very important	ai is much more important than aj.
0.9	Extremely important	ai is very much more important than aj.
0.1, 0.2, 0.3, 0.4	Anti-comparison	aji = 1 − aij

represents the relative importance of lower levels to the upper levels, obtained through pairwise comparison based on expert opinions. Obviously, $0<{\tilde{a}}_{ij}<1$; ${\tilde{a}}_{ij}+{\tilde{a}}_{ji}=1$; and ${\tilde{a}}_{ij}=0.5 (i=j)$. This yields the following n-by-n fuzzy judgment matrix $\tilde{A}={({\tilde{a}}_{ij})}_{n\times n}$:

$$\tilde{A}=\left[\begin{array}{cccc}{\tilde{a}}_{11}& {\tilde{a}}_{12}& \cdots & {\tilde{a}}_{1n}\\ {\tilde{a}}_{21}& a_{22}& \cdots & {\tilde{a}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{a}}_{n1}& {\tilde{a}}_{n2}& \cdots & a_{nn}\end{array}\right]=\left[\begin{array}{cccc}{\tilde{a}}_{11}& {\tilde{a}}_{12}& \cdots & {\tilde{a}}_{1n}\\ 1/{\tilde{a}}_{21}& {\tilde{a}}_{22}& \cdots & {\tilde{a}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ 1/{\tilde{a}}_{n1}& 1/{\tilde{a}}_{n2}& \cdots & {\tilde{a}}_{nn}\end{array}\right]$$

(5)

1.3: Construct a fuzzy consistent matrix. Use the following to obtain fuzzy consistent matrix $\tilde{R}$ where ${\tilde{r}}_{ij}={\tilde{r}}_{ik}-{\tilde{r}}_{jk}+0.5$ $(i,j,k=1,2,\dots n)$:

$${\tilde{r}}_i={\displaystyle \sum _{k=1}^n{\tilde{a}}_{ik}}(i=1,2,\dots ,n)$$

(6)

$${\tilde{r}}_{ij}=\frac{{\tilde{r}}_i-{\tilde{r}}_j}{2(n-1)}$$

(7)

$$\tilde{R}=\left[\begin{array}{cccc}{\tilde{r}}_{11}& {\tilde{r}}_{12}& \cdots & {\tilde{r}}_{1j}\\ {\tilde{r}}_{21}& {\tilde{r}}_{22}& \cdots & {\tilde{r}}_{2j}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{r}}_{i1}& {\tilde{r}}_{i2}& \cdots & {\tilde{r}}_{ij}\end{array}\right]$$

(8)

1.4: Calculate the fuzzy weight vector of each indicator $\tilde{W}={\left[{\tilde{w}}_1,{\tilde{w}}_2,\dots {\tilde{w}}_n\right]}^T$. Use the following to calculate the fuzzy weights of each indicator:

$${\tilde{w}}_i=\frac{1}{n}-\frac{1}{n-1}+\frac{2}{n(n-1)}\times {\displaystyle \sum _{k=1}^n{\tilde{r}}_{ik}}(i=1,2,\dots ,n)$$

(9)

Step 2: Collect and standardize the evaluation data: In this step, a method is selected to standardize the indicator data, thereby eliminating the influence of different dimensions on the evaluation results. If we assume that there are m cities serving as evaluation objects, $T(T_1,T_2,\dots ,T_m)$, and n evaluation indicators, $X(x_1,x_2,\dots ,x_n)$, then for the expert evaluation information represented by the HFS, we let the ith city with respect to the jth evaluation indicator be $h_{T_i}(x_j)=\left\{\gamma |\gamma \in h_{T_i}(x_j),0\le \gamma \le 1\right\}$. Because the indicator values obtained from statistical data will not be within the range of [0, 1], standardization is required.

For positive indicators in the statistical data,

$$x_{ij}=\frac{x_{ij}-\min x_{ij}}{\max x_{ij}-\min x_{ij}}.$$

(10)

For negative indicators in the statistical data,

$$x_{ij}=\frac{\max x_{ij}-x_{ij}}{\max x_{ij}-\min x_{ij}}$$

(11)

where x_ij is the values of the ith city with respect to the jth evaluation indicator and max x_ij and min x_ij are the maximum value and minimum values in x_ij, respectively.

Step 3: Determine the ideal solution and anti-ideal solution of each evaluation criterion:

3.1. Ideal solution $U_j^{+}$ and anti-ideal solution $U_j^{-}$ for the statistical data are computed as follows:

$$U_j^{+}=\underset{i}{\max }\left\{x_{ij}\right\}; U_j^{-}=\underset{i}{\min }\left\{x_{ij}\right\} (\mathrm{positive\; indicator})$$

(12)

$$U_j^{+}=\underset{i}{\min }\left\{x_{ij}\right\}; U_j^{-}=\underset{i}{\max }\left\{x_{ij}\right\} (\mathrm{negative\; indicator})$$

(13)

3.2. Ideal solution $H_j^{+}$ and anti-ideal solution $H_j^{-}$ for the HFE data (expert evaluations) are computed as follows:

$$H_j^{+}=\left\{\underset{j}{\max } h_{T_i}(x_j)\right\}; H_j^{-}=\left\{\underset{i}{\min } h_{T_i}(x_j)\right\} (\mathrm{positive\; indicator})$$

(14)

$$H_j^{+}=\left\{\underset{j}{\min } h_{T_i}(x_j)\right\}; H_j^{-}=\left\{\underset{i}{\max } h_{T_i}(x_j)\right\} (\mathrm{negative\; indicator})$$

(15)

where $h_{T_i}(x_j)=\frac{1}{\#h_{T_i}(x_j)}{\displaystyle \sum _{\gamma \in h_{T_i}(x_j)}{\gamma }_x}$.

Step 4: Compute the separation measures of each city with respect to each evaluation criterion from the ideal solution and anti-ideal solution:

4.1. The separation measures of each city with respect to each evaluation criterion for the statistical data are computed as follows:

$$D_i^U(U_j^{+},x_{ij})=\left|U_j^{+}-x_{ij}\right|$$

(16)

$$D_i^U(U_j^{+},U_j^{-})=\left|U_j^{+}-U_j^{-}\right|$$

(17)

4.2. The separation measures of each city with respect to each evaluation criterion for the HFE data are computed as follows:

The following equation extends the shorter HFE to enable comparison:

$$D\left(h_{T_1}(x_j),h_{T_2}(x_j)\right)=\left(\frac{1}{l_{h(x)}}{\displaystyle \sum _{j=1}^{l_{h(x)}}\left|h_{T_1}^{\sigma (t)}(x_j)-h_{T_2}^{\sigma (t)}(x_j)\right|}\right)$$

(18)

where $l_{h(x)}=\max \left\{\#h_{T_1}(x_j),\#h_{T_2}(x_j)\right\}$, $\#h_{T_1}(x_j)$ and $\#h_{T_2}(x_j)$ are the number of membership values for $h_{T_1}(x_j)$ and $h_{T_2}(x_j)$, respectively, and $h_{T_1}^{\sigma (t)}(x_j)$ and $h_{T_2}^{\sigma (t)}(x_j)$ are the jth largest values $(0<t\le l_{h(x)})$ in $h_1(x_j)$ and $h_2(x_j)$, respectively.

Then, the separation measures can be obtained as follows:

$$D_i^H\left(h_{T_i}^{+}(x_j),h_{T_i}(x_j)\right)=\frac{1}{l_{h(x)}}{\displaystyle \sum _{j=1}^{l_{h(x)}}\left|h_{T_i}^{+\sigma (t)}(x_j)-h_{T_i}^{\sigma (t)}(x_j)\right| (\mathrm{positive\; indicator})}$$

(19)

$$D_i^H\left(h_{T_i}^{+}(x_j),h_{T_i}^{-}(x_j)\right)=\frac{1}{l_{h(x)}}{\displaystyle \sum _{j=1}^{l_{h(x)}}\left|h_{T_i}^{+\sigma (t)}(x_j)-h_{T_i}^{-\sigma (t)}(x_j)\right| (\mathrm{negative\; indicator})}$$

(20)

Step 5: Calculate the values of the group utility $S_i$, individual regret $R_i$, and compromise index $Q_i$ of each city as follows:

$$Q_i=v{S}_i+(1-v)R_{iq}$$

(21)

where

$$S_i={\displaystyle \sum _{j=1}^n{w}_j\left[D_i^U(U_j^{+},x_{ij})/D_i^U(U_j^{+},U_j^{-})\right]}+{\displaystyle \sum _{j=1}^n{w}_j\left[D_i^H\left(h_{T_i}^{+}(x_j),h_{T_i}(x_j)\right)/D_i^H\left(h_{T_i}^{+}(x_j),h_{T_i}^{-}(x_j)\right)\right]}$$

(22)

$$R_{i1}=\underset{j}{\max } w_j\left[D_i^U(U_j^{+},x_{ij})/D_i^U(U_j^{+},U_j^{-})\right], q=1 \mathrm{for\; the\; statistical\; data}$$

(23)

$$R_{i2}=\underset{j}{\max } w_j\left[D_i^H\left(h_{T_i}^{+}(x_j),h_{T_i}(x_j)\right)/D_i^H\left(h_{T_i}^{+}(x_j),h_{T_i}^{-}(x_j)\right)\right], q=2 \mathrm{for\; the\; HFE\; data}$$

(24)

and $v\in \left[0,1\right]$ is the weight for the strategy of maximum group utility and 1 − v is the weight of the individual regret. Usually, the value of v is set at 0.5 [83].

Step 6. Rank the cities according to the values of Q_i in ascending order: a smaller Q_i value indicates better performance for the city, while a larger Q_i value indicates poor carbon neutrality.

4. Results

4.1. Implementation and Computation

China began the construction on its first batch of low-carbon pilot cities in 2010, which included five provinces and eight cities. Based on the principles of comparability and data integrity, this study selected thirteen cities as representatives to verify the efficacy of the proposed methodology: Guangzhou, Shenyang, Wuhan, Xi’an, Kunming, Tianjin, Chongqing, Shenzhen, Xiamen, Hangzhou, Nanchang, Guiyang, and Baoding.

The data for this study included both objective and subjective data. The objective quantitative data were primarily taken from various city statistical yearbooks, national economic and social development statistical bulletins, city landscaping and forestry bureau reports, the China Urban Rail Transit Yearbook, and the China Urban Statistical Yearbook. As statistical yearbooks do not include CO₂ emission data, the CO₂ emissions for each city were obtained from the China Emission Accounts and Datasets (CEADs) “https://www.ceads.net/ (accessed on 6 March 2024)”. To collect subjective data, we employed expert scoring. Experts in the fields of city development and carbon neutrality were invited to evaluate the performance of the cities. The expert group consisted of five experts (P1, P2, P3, P4, and P5), including university scholars, researchers from government units, and a researcher from a social research institution. Each expert had at least 10 years of work experience. The proposed methodology presented in Section 3 was used to evaluate the performance of the selected carbon-neutral cities under the following operating procedure:

Step 1: The weights of the dimensions, criteria, and indicators were calculated:

$$M_{1-2}=\left[\begin{array}{cc}0.50& 0.80\\ 0.20& 0.50\end{array}\right] (\mathrm{Dimension\; layer})$$

$$M_{Y_1-Y_4}^1=\left[\begin{array}{cccc}0.50& 0.64& 0.88& 0.73\\ 0.36& 0.50& 0.67& 0.45\\ 0.12& 0.33& 0.50& 0.37\\ 0.27& 0.63& 0.63& 0.50\end{array}\right] \mathrm{and} M_{Y_5-Y_6}^2=\left[\begin{array}{cc}0.50& 0.84\\ 0.16& 0.50\end{array}\right] (\mathrm{Criteria\; layer})$$

$$M_{C_1-C_2}^{Y_1}=\left[\begin{array}{cc}0.50& 0.57\\ 0.43& 0.50\end{array}\right], M_{C_3-C_4}^{Y_2}=\left[\begin{array}{cc}0.50& 0.64\\ 0.36& 0.50\end{array}\right], M_{C_5-C_6}^{Y_3}=\left[\begin{array}{cc}0.50& 0.91\\ 0.09& 0.50\end{array}\right], M_{C_7-C_8}^{Y_4}=\left[\begin{array}{cc}0.50& 0.36\\ 0.64& 0.50\end{array}\right]$$

$$M_{C_9-C_{11}}^{Y_5}=\left[\begin{array}{ccc}0.50& 0.72& 0.65\\ 0.28& 0.50& 0.56\\ 0.35& 0.44& 0.50\end{array}\right], \mathrm{and} M_{C_{12}-C_{13}}^{Y_6}=\left[\begin{array}{cc}0.50& 0.44\\ 0.56& 0.50\end{array}\right] (\mathrm{Indicator\; layer})$$

Then, the fuzzy complementary matrix was derived by using Equations (6)–(8). For example, the fuzzy complementary matrix for carbon-source criteria is as follows:

$${\tilde{A}}_{Y_1-Y_4}^{M_1}=\left[\begin{array}{cccc}0.50& 0.60& 0.68& 0.59\\ 0.40& 0.50& 0.58& 0.49\\ 0.32& 0.42& 0.50& 0.41\\ 0.41& 0.51& 0.59& 0.50\end{array}\right]$$

The fuzzy weight vector for each element was obtained by using Equation (9). For example, the fuzzy weight vector for carbon-source criteria is as follows:

$${\tilde{W}}_{Y_1-Y_4}^{M_1}=\left\{0.31, 0.25, 0.19, 0.25\right\}$$

The calculated fuzzy weights are shown in

Table 3. The fuzzy weights of each criterion for carbon-neutral cities.

Dimension	Weights	Criteria	Weights	Indicator	Weights
M1	0.65	Y1	0.202	C1	0.108
				C2	0.094
		Y2	0.160	C3	0.091
				C4	0.069
		Y3	0.125	C5	0.088
				C6	0.037
		Y4	0.163	C7	0.070
				C8	0.093
M2	0.35	Y5	0.235	C9	0.093
				C10	0.072
				C11	0.070
		Y6	0.115	C12	0.054
				C13	0.061

.

Step 2:

Table 4. Initial subjective evaluations by experts for each city.

City	C2	C12	C13
Guangzhou	{0.70, 0.80}	{0.40, 0.60}	{0.60, 0.80}
Shenyang	{0.40, 0.60}	{0.30, 0.40}	{0.50, 0.60}
Wuhan	{0.50, 0.60, 0.70}	{0.70, 0.80, 0.90}	{0.70, 0.80}
Xi’an	{0.60}	{0.80, 0.90}	{0.40, 0.50, 0.60}
Kunming	{0.70, 0.80, 0.90}	{0.30}	{0.50}
Tianjin	{0.30, 0.40}	{0.80, 0.90}	{0.50, 0.80}
Chongqing	{0.50, 0.60}	{0.70, 0.90}	{0.50, 0.60}
Shenzhen	{0.60, 0.80, 0.90}	{0.50, 0.60}	{0.70, 0.80}
Xiamen	{0.40, 0.50}	{0.30}	{0.60, 0.70, 0.80}
Hangzhou	{0.50, 0.70}	{0.50, 0.70}	{0.60, 0.70}
Nanchang	{0.40, 0.50}	{0.30, 0.40}	{0.50}
Guiyang	{0.40, 0.50}	{0.30, 0.40}	{0.50}
Baoding	{0.20, 0.30}	{0.30}	{0.40, 0.50}

shows the initial subjective evaluation data (HFE data) of each city with respect to each criterion, and

Table 5. Initial statistical data for each city.

City	C1	C3	C4	C5	C6	C7	C8	C9	C10	C11
Guangzhou	0.25	0.40	71.56	0.60	671.27	15.92	8.29	41.60	45.52	18.00
Shenyang	0.16	0.90	60.00	0.71	591.18	28.92	6.59	14.10	40.68	13.65
Wuhan	0.37	0.72	62.50	0.94	809.80	26.82	7.02	22.88	43.07	14.49
Xi’an	0.34	0.30	63.57	0.24	612.69	28.38	7.11	48.00	41.54	11.79
Kunming	0.47	1.19	63.70	1.01	488.43	31.05	7.75	52.62	41.60	7.90
Tianjin	0.58	1.01	61.30	1.15	591.58	23.97	9.03	12.07	38.30	9.70
Chongqing	0.35	0.56	53.00	0.49	414.56	15.70	2.97	52.50	42.53	16.33
Shenzhen	0.17	0.14	63.00	0.25	829.33	20.00	21.70	38.79	43.00	12.44
Xiamen	0.24	0.22	59.00	0.29	837.86	29.17	8.17	42.07	45.65	14.84
Hangzhou	0.29	0.25	67.90	0.37	728.58	23.08	8.32	66.85	39.74	13.55
Nanchang	0.56	0.37	48.00	0.38	588.31	21.83	6.81	21.96	43.00	13.05
Guiyang	0.24	0.63	60.20	0.50	1001.83	26.87	4.90	55.00	41.80	13.62
Baoding	0.51	0.91	52.60	0.37	366.60	29.31	1.78	33.66	43.57	11.16

shows the objective evaluation data (statistical data) for each city with respect to each criterion. Using Equations (10) and (11), the normalized data for each city with respect to each criterion was calculated (see

Table 6. Standardized data for each city.

City	C1	C3	C4	C5	C6	C7	C8	C9	C10	C11
Guangzhou	0.79	0.75	1.00	0.60	0.52	0.99	0.33	0.54	0.98	1.00
Shenyang	1.00	0.28	0.51	0.48	0.65	0.14	0.24	0.04	0.32	0.57
Wuhan	0.50	0.45	0.62	0.23	0.30	0.28	0.26	0.20	0.65	0.65
Xi’an	0.57	0.85	0.66	1.00	0.61	0.17	0.27	0.66	0.44	0.39
Kunming	0.26	0.00	0.67	0.15	0.81	0.00	0.30	0.74	0.45	0.00
Tianjin	0.00	0.17	0.56	0.00	0.65	0.46	0.36	0.00	0.00	0.18
Chongqing	0.55	0.60	0.21	0.73	0.92	1.00	0.06	0.74	0.58	0.83
Shenzhen	0.98	1.00	0.64	0.99	0.27	0.72	1.00	0.49	0.64	0.45
Xiamen	0.81	0.92	0.47	0.95	0.26	0.12	0.32	0.55	1.00	0.69
Hangzhou	0.69	0.90	0.84	0.86	0.43	0.52	0.33	1.00	0.20	0.56
Nanchang	0.05	0.78	0.00	0.85	0.65	0.60	0.25	0.18	0.64	0.51
Guiyang	0.81	0.53	0.52	0.71	0.00	0.27	0.16	0.78	0.48	0.57
Baoding	0.17	0.27	0.20	0.86	1.00	0.11	0.00	0.39	0.72	0.32

).

Step 3: Due to standardization, the indicator values of the statistical data fall within the range of [0, 1]. For subjective evaluation data, it is necessary to calculate the score function.

Table 7. Score function for each city with respect to each criterion.

City	C2	C12	C13
Guangzhou	0.75	0.50	0.70
Shenyang	0.50	0.35	0.55
Wuhan	0.60	0.80	0.75
Xi’an	0.60	0.85	0.50
Kunming	0.80	0.30	0.50
Tianjin	0.35	0.85	0.65
Chongqing	0.55	0.80	0.55
Shenzhen	0.77	0.55	0.75
Xiamen	0.45	0.40	0.70
Hangzhou	0.60	0.60	0.65
Nanchang	0.45	0.35	0.50
Guiyang	0.45	0.35	0.50
Baoding	0.25	0.30	0.45

shows the results of the score function for each city with respect to each criterion using Equations (14) and (15). The ideal solution and anti-ideal solution for the statistical data and HFE data are, respectively, as follows:

$$U^{+}=\left\{1, 1, 1, 1, 1, 1, 1, 1, 1, 1\right\} \mathrm{and} U^{-}=\left\{0, 0, 0, 0, 0, 0, 0, 0, 0, 0\right\}$$

$$H^{+}=\langle \left\{0.7,0.8,0.9\right\},\left\{0.8,0.9\right\},\left\{0.7,0.8\right\}\rangle \mathrm{and} H^{-}=\langle \left\{0.2,0.3\right\},\left\{0.3\right\},\left\{0.4,0.5\right\}\rangle$$

Step 4:

Table 8. Separation measures for each city with respect to each criterion.

City	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13
Ideal solution	1.00	{0.70, 0.80, 0.90}	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	{0.80, 0.90}	{0.70, 0.80}
Anti-ideal solution	0.00	{0.20, 0.30}	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	{0.30}	{0.40, 0.50}
D(+,−)	1.00	0.53	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.55	0.30
Guangzhou	0.21	0.03	0.25	0.00	0.40	0.48	0.01	0.67	0.46	0.02	0.00	0.35	0.05
Shenyang	0.00	0.27	0.72	0.49	0.52	0.35	0.86	0.76	0.96	0.68	0.43	0.50	0.20
Wuhan	0.50	0.20	0.55	0.38	0.77	0.70	0.72	0.74	0.80	0.35	0.35	0.07	0.00
Xi’an	0.43	0.20	0.15	0.34	0.00	0.39	0.83	0.73	0.34	0.56	0.61	0.00	0.27
Kunming	0.74	0.00	1.00	0.33	0.85	0.19	1.00	0.70	0.26	0.55	1.00	0.55	0.25
Tianjin	1.00	0.43	0.83	0.44	1.00	0.35	0.54	0.64	1.00	1.00	0.82	0.00	0.10
Chongqing	0.45	0.23	0.40	0.79	0.27	0.08	0.00	0.94	0.26	0.42	0.17	0.05	0.20
Shenzhen	0.02	0.03	0.00	0.36	0.01	0.73	0.28	0.00	0.51	0.36	0.55	0.30	0.00
Xiamen	0.19	0.33	0.08	0.53	0.05	0.74	0.88	0.68	0.45	0.00	0.31	0.55	0.07
Hangzhou	0.31	0.17	0.10	0.16	0.14	0.57	0.48	0.67	0.00	0.80	0.44	0.25	0.10
Nanchang	0.95	0.33	0.22	1.00	0.15	0.35	0.4	0.75	0.82	0.36	0.49	0.50	0.25
Guiyang	0.19	0.33	0.47	0.48	0.29	1.00	0.73	0.84	0.22	0.52	0.43	0.50	0.25
Baoding	0.83	0.53	0.73	0.80	0.14	0.00	0.89	1.00	0.61	0.28	0.68	0.55	0.30

shows the results of the separation measures for each city with respect to each criterion.

Steps 5 to 6:

Table 9. Final ranking of all cities (v = 0.5).

City	Si	Ri	Qi	Rank
Guangzhou	0.26	0.06	0.16	2
Shenyang	0.59	0.09	0.34	9
Wuhan	0.51	0.07	0.29	7
Xi’an	0.43	0.07	0.25	5
Kunming	0.65	0.09	0.37	11
Tianjin	0.73	0.11	0.42	13
Chongqing	0.41	0.09	0.25	5
Shenzhen	0.22	0.05	0.13	1
Xiamen	0.41	0.06	0.24	4
Hangzhou	0.35	0.06	0.20	3
Nanchang	0.61	0.10	0.36	10
Guiyang	0.53	0.08	0.31	8
Baoding	0.71	0.09	0.40	12

shows the values of $S_i$, $R_i$, and $Q_i$ of each city with respect to each criterion.

4.2. Sensitivity Analysis

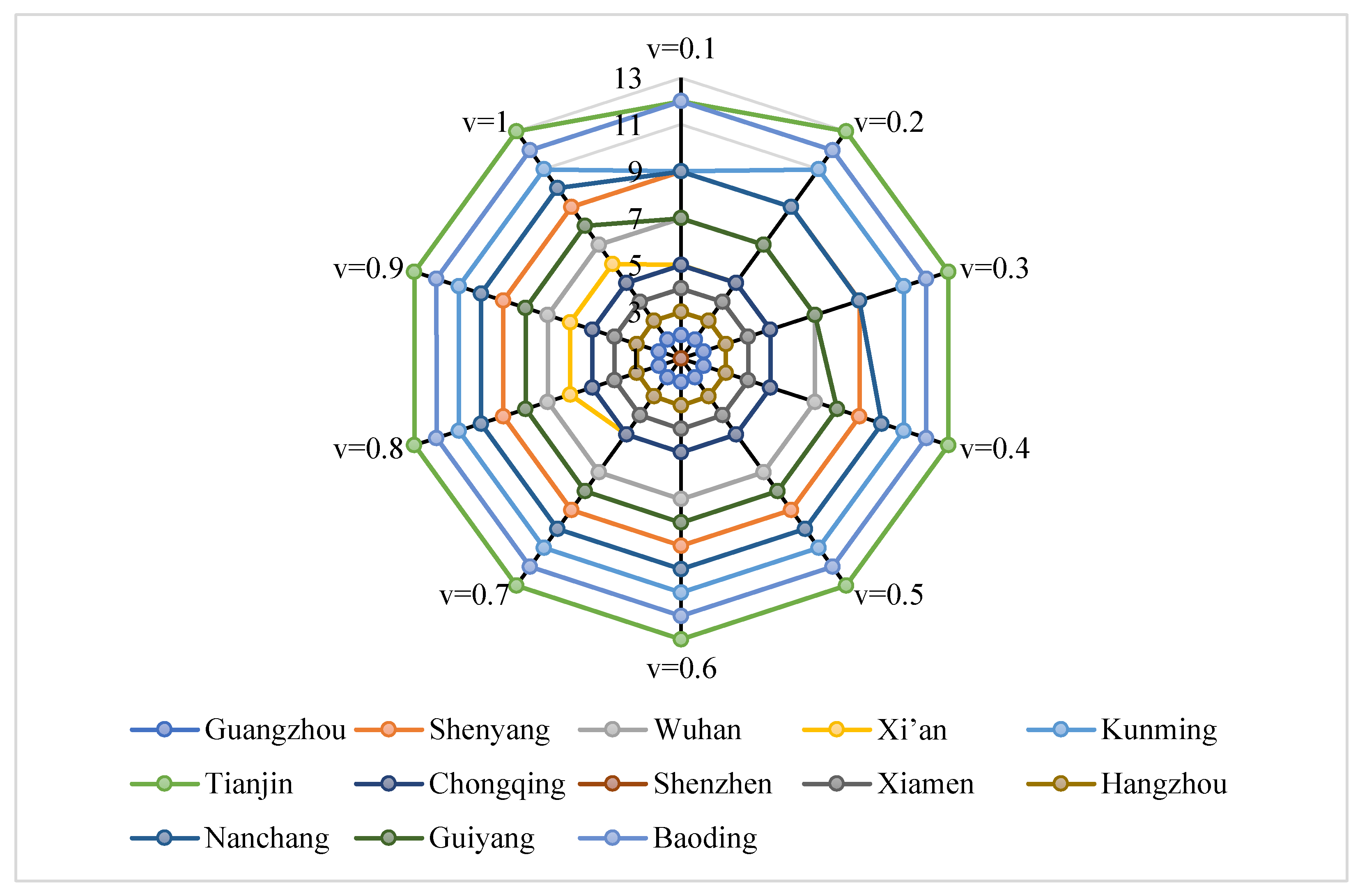
The proposed methods offer advantages when dealing with uncertainty; however, they also introduce complexities that may influence the interpretation of results. In order to evaluate the stability of the proposed method, we conducted sensitivity analysis for the compromise solution based on different values of v, the results of which are shown in Figure 5. Shenzhen, Guangzhou, Hangzhou, Xiamen, and Chongqing consistently ranked in the top five. Slight changes in the ranking of all cities occurred when v = 0.1, 0.4, and 0.8. These results indicate the robustness of the proposed method in terms of selecting an optimal solution among multiple alternatives. Thus, in practice, this method integrates the preferences of multiple decision makers.

4.3. Comparative Analysis

To demonstrate the rationality and effectiveness of the proposed approaches, we compared our results with those of the TOPSIS method. The basic concept of TOPSIS uses the best and worst solutions as reference points. It calculates the closeness based on the distance from the ideal solution to the anti-ideal solution, thus ranking the performance of different cities in terms of carbon neutrality [83]. As shown in

Table 10. Comparison of the proposed method with TOPSIS.

City	TOPSIS		Proposed Method
	Closeness Coefficient (Ci)	Rank	Compromise Index (Qi)	Rank
Guangzhou	0.74	2	0.16	2
Shenyang	0.41	9	0.34	9
Wuhan	0.45	8	0.29	7
Xi’an	0.58	6	0.25	5
Kunming	0.34	11	0.37	11
Tianjin	0.23	13	0.42	13
Chongqing	0.60	5	0.25	5
Shenzhen	0.77	1	0.13	1
Xiamen	0.61	4	0.24	4
Hangzhou	0.65	3	0.20	3
Nanchang	0.41	9	0.36	10
Guiyang	0.49	7	0.31	8
Baoding	0.32	12	0.40	12

, there are slight differences in the ranking results obtained via the proposed method and TOPSIS method. The main difference lies in the middle-ranked cities, i.e., those ranked from sixth to tenth. The cities ranked at the top and bottom remain almost unchanged. This is because the TOPSIS method considers the distance between city performance and the anti-ideal solution when calculating the closeness. It seeks the optimal solution that is as close as possible to the positive ideal and as far as possible from the anti-ideal solution. Hence, the rankings of well-performing and poorly performing cities are stable. In the proposed method, although the negative ideal solution is mentioned, it does not require a specific relationship between the optimal solution and the negative ideal point. The proposed method also considers the anti-ideal solution but does not require a relationship between the optimal solution and the anti-ideal solution. In the evaluation of carbon neutrality, the selection of reference points is crucial. City leaders often choose cities with optimal performance as targets rather than accentuating the differences with the poorest-performing cities.

Decision-making is a complex process that requires close monitoring to find suitable solutions. Compared to traditional MCDM methods, the method proposed in this study is a user-friendly tool for integrating multiple expert opinions (qualitative data) with numerous quantitative indicators. Furthermore, this method quantifies imprecise human perceptions and thoughts through fuzzy theory. The proposed method does not necessarily require the expertise of decision system experts, thus providing an accurate, efficient, and effective decision support tool for cities working towards carbon neutrality. The comparative analysis results confirm the stability and reliability of the proposed approach.

4.4. Discussion

To further illustrate the performance of each city with respect to each indicator, this study applied radar charts to show the weighted separation measure values for each city with respect to each indicator of carbon sources and carbon sinks (see Figure 6 and Figure 7).

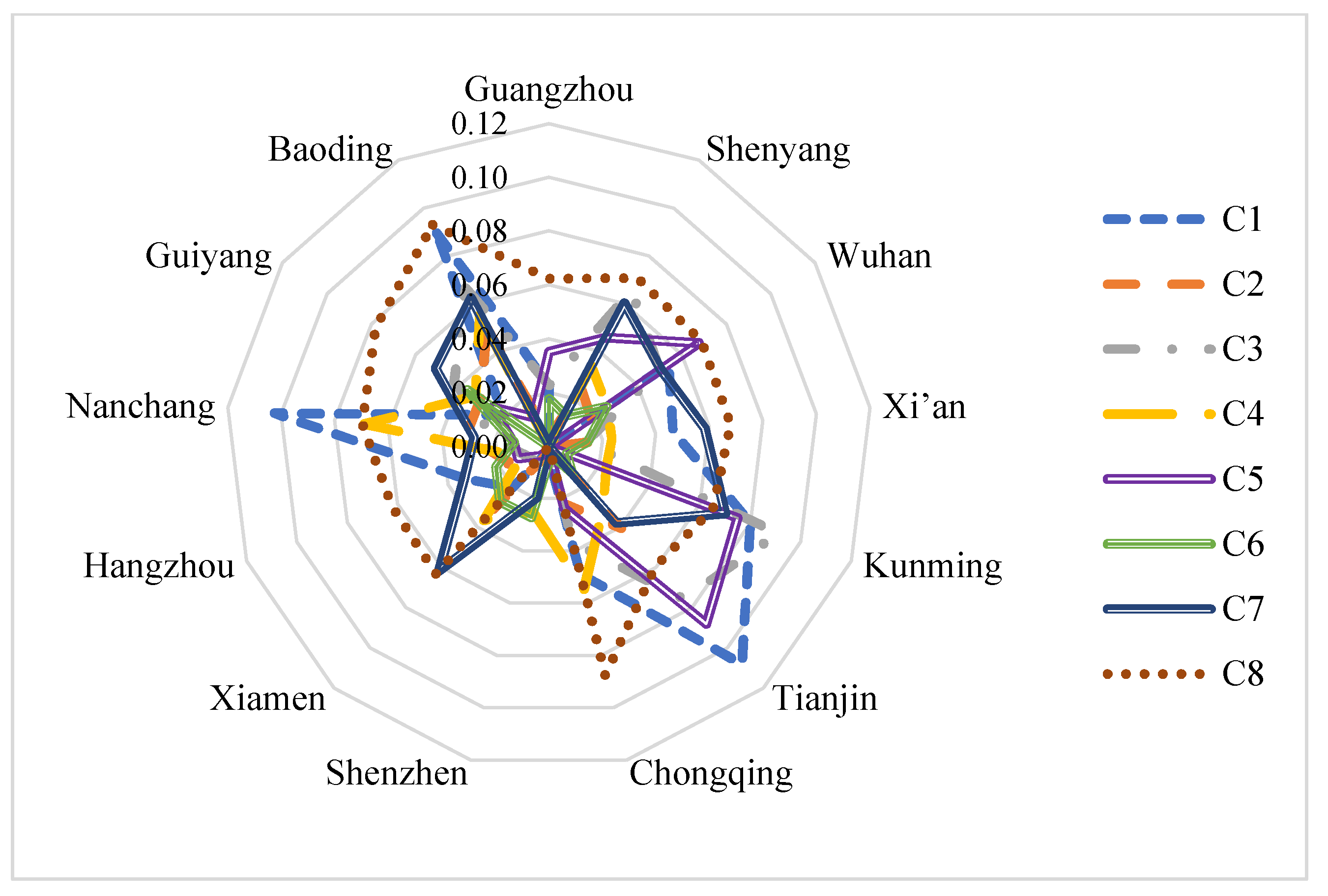
First, in terms of carbon sources, each city exhibits small differences in the weighted separation measure values of these indicators, such as per capita residential electricity consumption (C6), use of clean energy (C2), and the proportion of tertiary industry (C4); however, significant differences existed in the indicators such as the number of public electric (bus) vehicles per 10,000 people (C8), energy consumption per CNY 10,000 of GDP (C1), and the number of private vehicles (C7). Shenzhen excels in many aspects and serves as an ideal solution for other cities in regard to numerous indicators. However, it falls short of the optimum for three indicators: the proportion of tertiary industry (C4), per capita residential electricity consumption (C6), and number of private vehicles (C7). Among these, the per capita residential electricity consumption (C6) is a key indicator that Shenzhen needs to improve. Guangzhou and Hangzhou should focus on low-carbon construction in transportation. Guangzhou can emphasize public transportation construction, while Hangzhou, in addition to developing public transportation, should also promote green commuting and encourage citizens to reduce their private car usage. Tianjin, Baoding, and Kunming have several shortcomings in terms of carbon sources. Tianjin performs poorly, particularly in terms of energy consumption per CNY 10,000 of GDP (C1) as well as in terms of per capita CO₂ emissions (C5) and carbon emission intensity (C3). Baoding exhibits poor performance in transportation, with significant deficiencies in the construction of public transportation. Chongqing also faces challenges in the construction of public transportation, partly due to the geographical constraints and partly due to a large population, resulting in the lowest score for the number of public electric (bus) vehicles per 10,000 people (C8). Kunming performs worst in regard to the carbon source indicators, specifically the carbon emission intensity (C3), followed by the energy consumption per CNY 10,000 of GDP (C1). In Figure 6, we can see that cities such as Wuhan, Shenyang, Xi’an, and Xiamen are in the middle range in terms of carbon source indicators, indicating potential areas for improvement.

In terms of carbon sinks, there are significant differences in the indicators of forest coverage rate (C9) and green coverage rate in built-up areas (C10) and some small differences in the development and utilization of ecosystems (C13). Cities that rank high in carbon sink construction include Guangzhou, Chongqing, and Xiamen. Several cities, including Shenyang, Tianjin, Nanchang, and Wuhan, have significant differences in the overall carbon sink indicators, particularly the forest coverage rate (C9). Hangzhou shows a substantial gap in green coverage rate in built-up areas (C10) compared to the top-performing Xiamen. In terms of the level of CCUS and similar technologies (C12), Wuhan, Xi’an, Tianjin, and Chongqing have developed well, while cities such as Kunming, Nanchang, and Baoding need to improve their construction in this regard. Regarding the indicator for the development and utilization of ecosystems (C13), Guangzhou, Wuhan, Shenzhen, and Xiamen perform the best; however, the difference between them and other cities is not significant, indicating good performance in this aspect for all cities.

The proposed method is a comprehensive evaluation system that considers not only carbon sources and carbon sinks but also different data types. Policymakers and city planners can adjust the system to suit their geographical and socio-economic contexts. This allows for the effective and efficient allocation of resources as well as the identification of the directions for achieving carbon neutrality. For example, coastal cities rely more on the development of international trade compared to inland cities. Thus, compared to inland cities such as Kunming, Chongqing, and Nanchang, economically developed coastal cities like Shenzhen, Guangzhou, and Xiamen exhibit poorer performance in regard to indicators such as per capita residential electricity consumption (C6) and the number of private vehicles (C7). However, they achieved higher scores for energy efficiency, the proportion of tertiary industry, public transportation infrastructure, and urban green space planning. In terms of transportation, cities with inadequate public transportation usually have a higher number of private vehicles, such as Chongqing and Kunming. Due to the geographical and climatic factors, there are significant differences in carbon sink performance among the cities. It is recommended that the cities enhance their green coverage rate in built-up areas, increase the forest coverage, and improve the per capita park green space area to progress towards carbon neutrality. The cities that primarily focus on industrial development (such as Shenyang and Tianjin) need to further optimize their industrial structure, reduce the proportion of high-energy consumption and high-pollution industries, and encourage the development of high-tech industries and service industries related to local resources. Meanwhile, the cities with strong technological innovation capabilities (such as Xi’an, Wuhan, and Hangzhou) can implement innovation-driven development strategies. By introducing advanced technologies and innovative tools, they can promote the improvement of local energy technology and equipment levels, thereby enhancing their energy efficiency. The cities such as Wuhan, Xiamen, and Shenzhen can also enhance their carbon sink capacity by leveraging their geographical characteristics and advantages. For example, Xiamen and Shenzhen can focus on developing marine carbon sinks, while Wuhan can explore ways to construct and shape a well-functioning wetland ecosystem.

5. Conclusions

Cities are one of the main contributors to energy consumption and greenhouse gas emissions. To address this, many countries have implemented a series of city-based energy-saving and environmental protection policies. The advantage of using cities as boundaries is that it allows for the measurement and evaluation of the carbon neutrality within a specific area. In this study, thirteen indicators of carbon sources and carbon sinks were selected, and an evaluation system for carbon-neutral cities was constructed. The fuzzy AHP and HFS-VIKOR were employed to evaluate the first batch of low-carbon pilot cities in China. The results show that Shenzhen performs the best in regard to all the indicators, followed by Guangzhou and Hangzhou. Kunming and Baoding, on the other hand, exhibit poor performance. It is noteworthy that Tianjin faces a formidable challenge in achieving carbon neutrality. We further employed radar charts to separately analyze the shortcomings of each city in terms of carbon neutrality. As shown in Figure 6 and Figure 7, Shenzhen and Guangzhou perform the best in terms of carbon sources, indicating that their efforts in terms of carbon emissions reduction are effective. The cities with better performance in carbon sinks are Guangzhou, Chongqing, and Hangzhou, indicating their success in carbon absorption.

While this study holds theoretical and practical significance for cities working towards carbon neutrality, it is important to acknowledge the limitations of our analysis. First, we used expert evaluation to address the issue of carbon sink data sources, but further consideration is needed regarding how to obtain subjective evaluation data that are closer to the real situation. Therefore, future research could focus on ensuring the correctness and reliability of data related to carbon sinks in order to yield more precise statistical findings. Furthermore, optimizing the calculation methods would make the results of carbon neutrality more intuitive and understandable.

The second limitation is the scope of the proposed performance evaluation system. This study not only considers carbon sources and carbon sinks but also integrates quantitative and qualitative data. However, achieving carbon neutrality is a long-term, complex, and challenging task, and the proposed thirteen indicators may not comprehensively cover the dynamics of carbon neutrality. Therefore, future research could include additional indicators.

The final limitation is related to the nature of cities. We focused on Chinese cities, and due to the different geographical regions and socio-economic contexts, our results may not be generalizable. In other words, different alternatives may arise under different conditions. Therefore, the proposed method could be usefully extended to more countries/cities. In subsequent studies, it would be valuable to classify cities based on their characteristics and geographical locations before conducting further analysis.