Data-Driven Strategies for Complex System Forecasts: The Role of Textual Big Data and State-Space Transformers in Decision Support

Abstract

In this research, an innovative state space-based Transformer model is proposed to address the challenges of complex system prediction tasks. By integrating state space theory, the model aims to enhance the capability to capture dynamic changes in complex data, thereby improving the accuracy and robustness of prediction tasks. Extensive experimental validations were conducted on three representative tasks, including legal case judgment, legal case translation, and financial data analysis to assess the performance and application potential of the model. The experimental results demonstrate significant performance improvements of the proposed model over traditional Transformer models and other advanced variants such as Bidirectional Encoder Representation from Transformers (BERT) and Finsformer across all evaluated tasks. Specifically, in the task of legal case judgment, the proposed model exhibited a precision of 0.93, a recall of 0.90, and an accuracy of 0.91, significantly surpassing the traditional Transformer model (with precision of 0.78, recall of 0.73, accuracy of 0.76) and performances of other comparative models. In the task of legal case translation, the precision of the proposed model reached 0.95, with a recall of 0.91 and an accuracy of 0.93, also outperforming other models. Likewise, in the task of financial data analysis, the proposed model also demonstrated excellent performance, with a precision of 0.94, recall of 0.90, and accuracy of 0.92. The state space-based Transformer model proposed not only theoretically expands the research boundaries of deep learning models in complex system prediction but also validates its efficiency and broad application prospects through experiments. These achievements provide new insights and directions for future research and development of deep learning models, especially in tasks requiring the understanding and prediction of complex system dynamics.

1. Introduction

In today’s data-driven world, the prediction and analysis of complex systems have emerged as hotspots in interdisciplinary research, spanning significant domains such as law [1], finance [2], and healthcare [3]. The complexity of these systems often stems from their highly nonlinear internal structures, dynamic changes, and intricate interactions with external environments. With the advent of the big data era [4], text-based big data analysis has provided new perspectives and methods for the prediction and decision-making of these complex systems. This paper focuses on the exploration of complex system prediction models based on text big data, utilizing a combination of state space models and the Transformer, aiming to offer more accurate and dynamic support for decision-making in complex systems.

As the internet and digital technology rapidly evolve, the volume of text data grows exponentially [5]. These text data contain rich information and knowledge, vital for understanding and predicting the behaviors of complex systems. However, the unstructured nature of text data and the inherent complexity of these systems pose challenges in effectively extracting useful information from text big data [6] and constructing accurate prediction models. Experiments by Wahba Yasmen [7] and others applying Support Vector Machine (SVM) to text data classification have shown that traditional SVM indeed offers cheaper and superior performance compared to pre-trained language models (PLM), yet SVM underperforms in handling the unstructured features of text.

Recent advancements in deep learning technologies have provided new tools and methods for addressing this issue. Notably, the success of RNN (Recurrent Neural Networks) [8] and LSTM (Long Short-Term Memory networks) [9] in sequence data processing, along with the breakthroughs of the Transformer model [10] in handling long-distance dependencies and parallel computing, have significantly advanced text-based data analysis technologies. However, these models still face limitations in predicting complex systems, such as capturing the dynamic changes in system states and computational efficiency issues with large-scale text data.

Sharaff Aakanksha et al. [11] introduced a novel method for text data quality assessment using a Deep Learning Convolutional Recurrent Neural Network (C-RNN) model, combining CNN and RNN for SMS data quality assessment; Kumar Anuj [12] employed RNN, CNN, LSTM, and Bidirectional Encoder Representation from Transformers (BERT) models to detect hate speech and aggressive language in text data. Moreover, they explored the impact of weighted and unweighted methods on the learning model system, with experiments showing that the pre-trained BERT model outperforms other models in both unweighted and weighted classifications, yet its performance is significantly hindered in scalar instances; Lee Hyejin et al. [13] used an LSTM model for text classification of Flickr data to address the issues in covering features of tourist activities, demonstrating how to identify tourism categories and analyzing the Return on Attention (ROA) preferences of tourists in detail. However, richer analyses are anticipated if image and text analyses are combined. Hasib Khan Md et al. [14] proposed a Multiclass Convolutional Neural Network (MCNN)-LSTM approach, combining CNN and LSTM deep learning techniques for text classification in news data, with results showing their method significantly outperforms machine learning approaches, achieving a 99.7% accuracy rate, yet challenges remain in handling highly imbalanced and noisy data sets.

Regarding the application of the Transformer model in text data, many researchers have also conducted explorations. For instance, Kumar Varun et al. [15] studied various models to provide a simple yet effective method for tuning pre-trained models for data augmentation—using autoregressive models (GPT-2), autoencoder models (BERT), and seq2seq models (BART) for conditional data augmentation. They also explored ways to preserve class label information; Phan Long N et al. [16] proposed the SciFive model for biomedical literature, comparing it with current State Of The Art (SOTA) methods (i.e., BERT, BioBERT, Base T5), showing that their method performs better in longer text output tasks, albeit with lower efficiency; Acheampong Francisca Adoma et al. [17] designed an Emotion Detection (ED) model based on the Transformer, assessing the effectiveness of pre-trained (GPT) models, Transformer-XL, cross-language models (XLM), and BERT in the task of text emotion detection, yet their contribution to resolving the polarity ambiguity in emotional expression words remains limited.

Addressing the challenges mentioned above, this paper proposes a novel complex system prediction method based on the state space Transformer model. State space models, effective tools for time series analysis, can describe the dynamic changes in system states and associate system states with observational data through an observation model. Combined with the powerful processing capabilities of the Transformer model, our method not only efficiently handles large-scale text data but also accurately captures and predicts the dynamic changes in complex systems, offering robust support for data-driven decision-making. The main innovations and contributions of this paper include:

• Introducing a new state space-based Transformer model, as discussed in Section 3.3: by integrating the state space model with the Transformer, a novel prediction model has been designed, capable of effectively processing text big data and accurately describing the dynamic changes in complex systems.
• Developing a set of text preprocessing and feature extraction methods for complex systems: considering the special requirements for predicting complex systems, a new set of text preprocessing and feature extraction processes has been developed, ensuring the model can extract the most useful information from text data for prediction, as discussed in Section 3.1 and Section 3.2.
• Conducting empirical studies on multiple complex systems: empirical studies have been conducted in various fields, including legal case judgment, legal case translation, and financial data analysis, verifying the effectiveness and versatility of our model.
• Performing extensive model comparisons and analyses, as shown in Section 4: by comparing our model with existing Transformer models, BERT, and other baseline models, the performance of our model has been comprehensively evaluated, and its advantages and potential application values have been thoroughly analyzed.

In summary, this work offers a new perspective and method for processing and predicting complex systems, bearing significant theoretical implications and wide application prospects. It is anticipated that the findings of this paper will provide new insights and contributions to the research and application of complex systems.

2. Related Work

2.1. RNN and LSTM

An in-depth understanding of the applications of RNN [18] and their improved variant, LSTM [19], in processing sequential data is deemed crucial, as shown in Figure 1. Through sophisticated network structure design and mathematical formulations, these models effectively address the challenges faced by traditional algorithms in handling time-series data [20,21], providing robust tools for prediction and analysis in complex systems.

RNNs [22], designed to remember the impact of preceding information for application in current computations, thereby outputting predictions at each point in a sequence, have demonstrated commendable performance in areas such as text processing [23] and speech recognition [24]. Unlike traditional neural networks, RNNs incorporate a temporal dimension, allowing the network to store historical information for future state predictions. This is particularly suited for tasks with variable sequence lengths, such as natural language processing and time series analysis. The fundamental structure of RNNs can be represented by the following equations [25,26]:

$$h_t=\sigma (W_{xh}{x}_t+W_{hh}{h}_{t-1}+b_h)$$

(1)

$$y_t=W_{hy}{h}_t+b_y$$

(2)

where $x_t$ denotes the input at time t, $h_t$ the hidden state at time t, and $y_t$ the output at time t. $W_{xh}$, $W_{hh}$, and $W_{hy}$ represent the weight matrices from input to hidden layer, hidden layer to hidden layer, and hidden layer to output layer, respectively. $b_h$ and $b_y$ are bias terms, and $\sigma$ denotes the activation function, typically a sigmoid or tanh function.

Despite RNNs’ potential for sequential data processing, they face challenges with gradient vanishing or exploding when dealing with long sequences in practical applications [27], limiting their capability to learn long-term dependencies. To overcome this limitation, LSTMs were introduced [28]. By incorporating a series of gate mechanisms, LSTMs effectively control the storage, updating, and forgetting of information, significantly enhancing the network’s capability to process long-sequence data. The core components of an LSTM unit include the forget gate, input gate, output gate, and cell state, enabling LSTMs to capture important information while disregarding the irrelevant in long sequences. The core equations of LSTM are as follows [29,30,31,32,33,34]:

$$f_t=\sigma (W_f·[h_{t-1},x_t]+b_f)$$

(3)

$$i_t=\sigma (W_i·[h_{t-1},x_t]+b_i)$$

(4)

$${\tilde{C}}_t=\tanh (W_C·[h_{t-1},x_t]+b_C)$$

(5)

$$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$$

(6)

$$o_t=\sigma (W_o·[h_{t-1},x_t]+b_o)$$

(7)

$$h_t=o_t\ast \tanh \left(C_t\right)$$

(8)

here, $f_t$, $i_t$, and $o_t$ represent the activation values of the forget gate, input gate, and output gate, respectively; ${\tilde{C}}_t$ is the candidate cell state; $C_t$ is the cell state; $h_t$ is the hidden state; ∗ denotes element-wise multiplication; $\sigma$ and tanh are the sigmoid function and hyperbolic tangent function, respectively; W and b are weight matrices and bias terms. Through these gate mechanisms, LSTMs efficiently manage the flow of information, solving the gradient vanishing problem faced by traditional RNNs in long sequence processing, thereby significantly enhancing model performance and reliability in complex system prediction [35].

In data-driven decision-making for complex systems, RNNs and LSTMs offer powerful tools [36,37], enabling researchers and decision-makers to learn patterns from historical data and predict the future behaviors of systems. For instance, LSTMs have been used to accurately predict stock price dynamics in financial data analysis [38]; in the realm of natural language processing, RNNs and LSTMs facilitate machine translation, text summarization, and sentiment analysis tasks [39,40], enhancing the capability to process complex language structures. Moreover, in meteorology, energy management, and public health, these models demonstrate substantial potential in addressing time series prediction problems [41,42]. Thus, the application of RNNs and LSTMs in solving sequence data processing and prediction issues within complex systems not only showcases the advanced and flexible technology but also provides reliable support for data-driven decision-making. The continuous optimization and improvement of these models are expected to yield deeper and more extensive outcomes in understanding and predicting complex systems.

2.2. Transformer

Since its introduction by Vaswani et al. in 2017 [43], the Transformer model has revolutionized the field of Natural Language Processing (NLP). Its core mechanisms—Self-Attention and Positional Encoding—endow the Transformer model with unique advantages in handling sequential data, particularly in capturing long-distance dependencies and in parallel data processing, as shown in Figure 2. These features have led to exceptional performance in language modeling, machine translation, text summarization, and other tasks [44,45], while also fostering the development of Transformer-based models (such as BERT, GPT, etc.), further advancing breakthroughs in NLP technology.

The Transformer is built entirely on self-attention mechanisms, eliminating the recurrent mechanism present in traditional RNNs and LSTMs, thus enabling efficient parallel processing of data. It comprises encoders and decoders, each made up of several identical layers, including self-attention mechanisms and position-wise fully connected feed-forward networks. The self-attention mechanism, the heart of the Transformer model, allows the model to consider all elements within a sequence when processing each sequence element, thereby capturing long-distance dependency information. The self-attention calculation is described by the following formula [46]:

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

(9)

here, Q, K, and V represent Query, Key, and Value, respectively, with $d_k$ being the dimension of the key. This formula enables the model to compute a weight for each key, which is then used to perform a weighted sum of values to calculate the output at each position. Given the Transformer model’s parallel structure, it inherently lacks the ability to capture the positional information of sequence elements. To address this issue, Positional Encoding is introduced to imbue each sequence element with positional information. Positional encoding is computed through the following formula [47,48]:

$${\mathrm{PE}}_{(pos,2i)}=\sin (pos/{10000}^{2i/d_{\mathrm{model}}})$$

(10)

$${\mathrm{PE}}_{(pos,2i+1)}=\cos (pos/{10000}^{2i/d_{\mathrm{model}}})$$

(11)

where $pos$ is the position and i is the dimension. Through this method, each position’s encoding is unique and distinguishable from others. The advantage of the Transformer model in processing sequential data plays a significant role in the research of complex systems within data-driven decision-making. Learning patterns from historical data and making future predictions in complex systems, especially those involving long-distance dependencies, presents a challenging task. The Transformer model’s ability to effectively capture these dependencies provides accurate data support for decision-making. For example, in financial data analysis, the Transformer can predict stock price movements by analyzing long-term dependencies in historical price sequences to forecast future trends [49]. In supply chain management, the Transformer model aids in predicting product demand by analyzing past order data to optimize inventory management [50]. In public health, it can be used to forecast pandemic trends by examining the history of the epidemic to predict future spread patterns [51]. With continuous development and optimization of the Transformer model and its derivatives, it is reasonable to believe that they will play an even more significant role in solving complex system problems in the future.

2.3. State Space Models and Mamba

State space models offer a powerful mathematical framework for time series analysis [52], introducing hidden states to describe the dynamic changes in systems across time. Particularly suited for analyzing and predicting complex systems whose internal states are not directly observable but can be inferred from indirect measurements, Mamba, as a modern computational framework designed for state space models, provides flexible and efficient solutions, supporting rapid development and accurate estimation of complex models [53], significantly advancing research on complex system prediction based on text big data. State space models typically consist of two main equations: the state equation and the observation equation, describing the time evolution of system states and how observational data are generated from these internal states, respectively [54,55].

$$x_t=F_t{x}_{t-1}+G_t{w}_t$$

(12)

$$y_t=H_t{x}_t+v_t$$

(13)

here, $x_t$ represents the system state at time t, and $y_t$ denotes the observational data at time t. $F_t$, $G_t$, and $H_t$ are the state transition matrix, system noise influence matrix, and observation matrix, respectively, controlling the evolution of system states, the impact of system noise on the states, and how observational data are generated from the states. $w_t$ and $v_t$ represent system noise and observation noise, respectively, typically assumed to follow a Gaussian distribution. The design of the Mamba framework thoroughly considers the flexibility and computational efficiency of state space models. It not only supports the construction of linear and nonlinear models but also offers efficient algorithms for parameter estimation and state inference. Through Mamba, researchers can easily model, analyze, and predict complex time series data, especially in handling large datasets, where Mamba’s high-performance computing capabilities become particularly significant [56].

Combining state space models with deep learning technologies (such as LSTM and Transformer) provides new perspectives for the analysis and prediction of complex systems [57]. This combination not only leverages deep learning models’ strengths in processing unstructured text data but also captures the dynamic evolution of system states through state space models, thereby enhancing the predictive and interpretative capabilities of the models on multiple levels. For instance, the outputs of LSTM or Transformer models can be incorporated as part of the state equation in state space models to simulate the dynamic characteristics of complex systems. Such composite models can capture long-term dependencies in sequence data while dynamically modeling and inferring system states through the state space model framework. In fields such as financial data analysis, environmental monitoring, and public health, state space models based on Mamba have demonstrated strong application potential [58]. By accurately modeling the dynamic changes in time series data, these models provide decision-makers with important information about the future states of systems, supporting the data-driven decision-making process. In the financial sector, models built with Mamba can analyze and predict the dynamics of financial time series, such as stock prices and exchange rates, aiding investors in making more scientifically informed investment decisions. In environmental monitoring, modeling meteorological data can predict weather changes, supporting disaster early warning systems [59]. In public health, state space models can be used for predicting trends in infectious diseases, providing a basis for the formulation of disease control and prevention strategies [60].

In summary, the Mamba framework offers robust computational support for the application of state space models in the analysis and prediction of complex systems. By integrating these models with deep learning technologies, the capability to handle unstructured text big data is further enhanced, providing more accurate and in-depth support for data-driven decision-making. With ongoing advancements in computational technology, state space models based on Mamba are expected to exhibit an even broader range of applications in future research on complex systems.

3. Materials and Methods

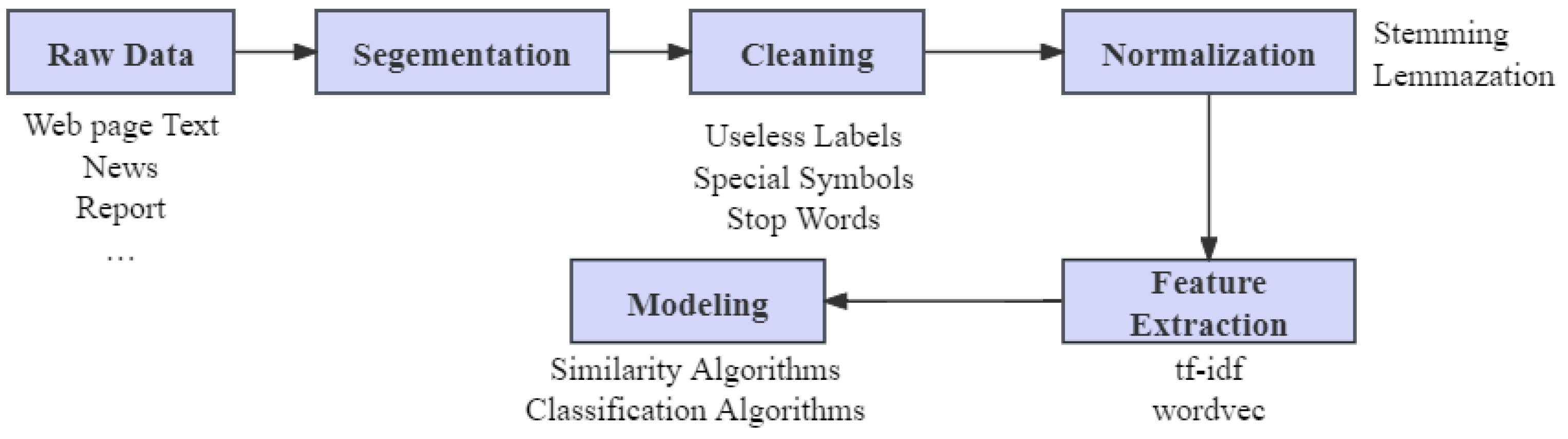
3.1. Dataset Collection

In conducting research on complex system prediction models driven by large-scale text data, the collection and annotation of datasets are foundational and critical. To construct a high-quality dataset, we utilized web crawler technology for automatic data collection and manual annotation to ensure data accuracy and consistency. Our study focused on three areas: legal case judgment texts, legal case translation datasets, and financial data analysis. Legal case judgment texts have a certain structure, such as case ID, case type, text content, case facts, and judgment outcomes, as shown in Figure 3a. They are relatively structured, facilitating data extraction. These texts involve legal terminology and complex legal logic, requiring models that can understand and process professional terms and logical relationships. Legal texts are often lengthy and information-dense, necessitating strong information extraction and induction capabilities. The diversity of case types, each with its specific characteristics and terminology, increases the complexity of model training. These features contribute to the high difficulty of the task, necessitating an understanding of deep legal terms and complex logical relations, while also dealing with the challenge of lengthy texts. The legal case translation dataset contains pairs of original texts and translations, involves multiple languages, and requires the model to handle multilingualism, as shown in Figure 3b. The quality of translation depends on the accuracy of the text and the correct expression of the context, demanding high standards for the translation model. Cultural and expressive differences between languages must be considered during translation to ensure the naturalness and accuracy of the translations. Beyond accuracy, the fluency of the translation is also a crucial criterion for assessing translation quality. The characteristics of these tasks make them moderately to highly challenging. The diversity of the texts and the complexity of the languages make the translation task challenging, especially in maintaining the original meaning and fluency. Financial data analysis not only contains numerical market data such as prices and trading volumes but may also include textual information like news headlines, as shown in Figure 3c. Financial data analysis is highly dynamic, updated in real-time, and requires high processing speed and timeliness. The factors influencing the market are complex and variable, making market trend predictions highly uncertain and challenging. Market data are often affected by unpredictable factors, featuring noise and outliers. The task is highly challenging, requiring the processing of large volumes of dynamically updated data, with a need for high prediction accuracy. Complex data preprocessing methods such as noise filtering and anomaly detection, as well as efficient real-time data processing technologies are necessary.

In practical tasks, processing legal texts not only requires language processing technology but also the introduction of legal expertise. The difficulty lies in understanding and applying complex legal terms and structures. Legal texts require advanced text analysis techniques, such as case fact correlation analysis and result reasoning, which may involve complex natural language processing technologies and the construction of knowledge graphs. Legal case translation needs to focus on the accuracy of language conversion and cultural adaptability. The challenge lies in how to accurately express the intent and emotion of the source language. Legal case translation emphasizes the application of statistical machine translation or neural machine translation technologies, requiring a large amount of bilingual corpora to train models, as well as excellent model architecture to ensure the naturalness and fluency of the translations. The difficulty in processing financial data lies in the fast dynamics of the data and the high demands for real-time processing and prediction accuracy, requiring fast-response data processing and high-accuracy prediction models. To acquire textual data from these fields, we designed and implemented a multi-stage web crawler program. Initially, by analyzing the structure and content of the target websites, we determined specific paths and strategies for data extraction, as shown in

Table 1. Dataset information.

Dataset	Quantity	Collection Method	Source	Time Period
Legal Case Judgment —English	3987	Web Crawling, Open Source Download	US Courts Website, UK Courts and Tribunals Website	2018.5–2023.5
Legal Case Judgment —Chinese	3712	Web Crawling, Open Source Download	China Judgments Online	2010.7–2023.7
Legal Case Translation —English	15,980	Open Source Download	European Parliament Proceedings, OpenSubtitles, Tatoeba	2020.8–2023.8
Legal Case Translation —Chinese	21,746	Web Crawling	Tatoeba	2020.9–2023.9
Financial Analysis —English	142,764	Web Crawling	Yahoo Finance	2003.11–2023.1
Financial Analysis —Chinese	187,156	Web Crawling	Flush Finance	2003.12–2023.1

.

For example, for legal case judgment texts, we primarily targeted public legal databases, which usually provide a wealth of case judgment documentation. We wrote specific crawler scripts to automatically extract case texts and related information from these databases. During the implementation of the crawler program, we adopted appropriate strategies to avoid unnecessary burdens on the target websites, such as setting reasonable request intervals and using proxy servers. Simultaneously, to enhance the efficiency and coverage of the crawler, we employed dynamic crawling techniques to handle content generated by JavaScript and distributed crawler technologies to accelerate the data collection process. After the dataset collection was completed, the next step was accurate data annotation. Given the diversity of our research fields and the complexity of the tasks, the data annotation process involved meticulous manual review and classification. To ensure the quality of the annotations, we first established a detailed annotation guide, which specified the annotation standards and procedures for various data types. For example, during the annotation process of legal case judgment texts, annotators needed to classify texts based on the nature of the cases and judgment outcomes; in the annotation of the legal case translation dataset, the quality and accuracy of the original and translated texts had to be assessed. To ensure consistency and accuracy in annotation, we adopted a dual-annotation strategy, where each document was independently annotated by at least two annotators, followed by verification and arbitration by a third senior annotator. During the annotation process, annotators regularly conducted cross-checks and discussions to resolve complex issues that arose during annotation and to standardize the annotation standards. Additionally, we utilized some automation tools to assist in the annotation process. For example, natural language processing technologies were used to pre-analyze text content, and automatically identify and mark key information to alleviate the burden of manual annotation. However, considering the potential errors of automation tools, all automatically annotated results were manually reviewed and corrected to ensure the accuracy of data annotation. To further ensure the quality of data annotation, we established a comprehensive quality control mechanism. This included regular training for annotators to familiarize them with the annotation guidelines and standards, enhancing the accuracy and consistency of annotations; regular inspections of annotated data to assess the quality of annotations and adjust the annotation guidelines and procedures based on inspection results; establishing a feedback mechanism to encourage annotators to raise questions and suggestions during the annotation process, continuously optimizing the annotation workflow.

3.2. Dataset Preprocessing

3.2.1. Standard Preprocessing Methods

In the processing of text big data and the construction of knowledge graphs, text preprocessing is a critical step, as shown in Figure 4. The quality of preprocessing directly impacts the effectiveness of subsequent tasks, such as information extraction, knowledge integration, entity disambiguation, and co-reference resolution. Text preprocessing refers to a series of steps that transform raw text data into a format usable for machine learning models.

In NLP, raw text often contains noise and redundant information, potentially affecting the learning efficiency and performance of models. The task of preprocessing is to clean and format data to enhance the accuracy and efficiency of subsequent tasks. Text preprocessing typically involves several core steps: Segmentation, Cleaning, and Normalization, as well as Stemming and Lemmatization. Segmentation is the process of dividing text into words or symbols. For English texts, segmentation is relatively straightforward, usually delimited by spaces and punctuation. For languages without clear word boundaries, such as Chinese, segmentation is more complex and relies on specific segmentation algorithms to identify word boundaries. Segmentation can be represented by the following formula [61]:

$$W=\mathrm{Segment}\left(T\right)$$

(14)

where T represents the original text, W represents the segmentation result, and $\mathrm{Segment}(·)$ is the segmentation function. Cleaning involves removing noise and unnecessary information from the text, such as HTML tags, special characters, and incorrect formatting. The cleaned text is more standardized and conducive to model processing [62].

$$T^{\prime }=\mathrm{Clean}\left(T\right)$$

(15)

Here, $T^{\prime }$ is the cleaned text, and $\mathrm{Clean}(·)$ is the cleaning function. Normalization is the process of converting words in the text to a standard form, for example, converting all characters to lowercase or converting numbers to words [63].

$$T^{″}=\mathrm{Normalize}\left(T^{\prime }\right)$$

(16)

$T^{″}$ is the normalized text, and $\mathrm{Normalize}(·)$ is the normalization function. Stemming and Lemmatization aim to reduce a word to its stem or root form to decrease redundancy caused by morphological variation. Stemming usually relies on simple heuristic rules, while lemmatization requires a complete set of morphological variation rules [64].

$$W^{\prime }=\mathrm{Stem}/\mathrm{Lemmatize}\left(W\right)$$

(17)

$W^{\prime }$ represents the set of words after stemming or lemmatization, and $\mathrm{Stem}/\mathrm{Lemmatize}(·)$ is the corresponding processing function.

TF-IDF (Term Frequency-Inverse Document Frequency) [65] and WordVec [66] are two widely used feature extraction methods in the field of text processing, each with its unique advantages and applications. TF-IDF assesses the importance of a word by multiplying its term frequency (TF) with its inverse document frequency (IDF) [67], thereby reducing the influence of common words in documents and emphasizing the significance of rare words. Term frequency TF is the number of times a word appears in a document divided by the total number of words in that document, while inverse document frequency IDF is the logarithm of the total number of documents divided by the number of documents containing the word. This method helps identify keywords suitable for filtering information from large volumes of text. WordVec transforms words into vector forms through training, capturing contextual relationships between words [68]. It is primarily implemented through two models: the Skip-gram model predicts the context, and the CBOW model predicts the current word from the context. These vectors can express the semantic content of words, particularly effective for understanding deeper textual semantics.

Applying TF-IDF and WordVec to the construction of knowledge graphs can significantly enhance the information retrieval capabilities and semantic parsing efficiency of knowledge graphs [69,70]. Using TF-IDF effectively identifies keywords or phrases that often carry crucial information linking different entities and attributes [71]. For example, when building a knowledge graph of legal documents, TF-IDF can help extract key legal terms and related definitions, which are fundamental to constructing entities and relationships. The application of WordVec further deepens this process; by analyzing the similarities between word vectors, we can explore and identify words with similar semantics, which is particularly important for building semantic links in knowledge graphs. For instance, through WordVec, we can recognize the semantic similarities between “contract” and “agreement” in the legal field and then connect these two entities in the knowledge graph through the corresponding semantic relationships. Additionally, the combined use of these two techniques can achieve more accurate and dynamic information updates and expansions in knowledge graphs, making the knowledge graphs not just static repositories of information, but dynamic systems capable of evolving and adapting to new knowledge. Through such methods, we can not only improve the quality of information retrieval but also enhance the predictive and decision-making capabilities of the model on multiple levels, providing robust support for handling large-scale text data in complex systems such as legal, financial, and medical fields.

3.2.2. Building Knowledge Graphs

Building knowledge graphs is a process that transforms scattered data information into interconnected, structured knowledge, as shown in Figure 5. It involves multiple steps, including data acquisition, information extraction, knowledge integration and reasoning, as well as the final graph generation and quality assessment. The construction of knowledge graphs begins with the acquisition of information from structured, semi-structured, and unstructured data. Structured data typically refer to tabular data in databases, semi-structured data can be XML or JSON format data, and unstructured data are free text, such as news articles and social media posts.

These data, after preprocessing steps like Segmentation, Cleaning, and Normalization, are transformed into a form that can be efficiently processed by computer programs. Subsequently, the information extraction step involves identifying and extracting entities, attributes, and relations from the preprocessed data, which is central to building knowledge graphs. Entity extraction identifies named entities in the text, such as names of people, places, and organizations; relation extraction determines semantic connections between entities; attribute extraction focuses on descriptive information about entities. Mathematically, the extraction of entities and relations can be represented as follows [72]:

$$\mathrm{Entities},\mathrm{Relations}=\mathrm{Extraction}\left(\mathrm{Standardized}\mathrm{Tokens}\right)$$

(18)

Knowledge fusion merges information extracted from various sources, resolves conflicts between them, and unifies different representations of the same entity. Fusion can be represented by the following formula [73]:

$$\mathrm{Unified}\mathrm{Knowledge}=\mathrm{Knowledge}\mathrm{Fusion}\left(\mathrm{Extracted}\mathrm{Information}\right)$$

(19)

During fusion, co-reference resolution and entity disambiguation are also involved, addressing referential issues and entity ambiguities in the text. Knowledge reasoning is the process of deriving new knowledge based on existing knowledge. This step often includes inferring new relations or attributes from existing facts to enrich the content of the knowledge graph. Quality assessment involves checking and evaluating the accuracy, completeness, and consistency of the knowledge graph to ensure the constructed knowledge graph reliably supports various applications. Ultimately, the output of these steps is a structured knowledge graph, containing rich entities, attributes, relations, and inferred knowledge, usable for numerous intelligent applications, such as search engines, recommendation systems, and automated question-answering.

3.3. Proposed Method

In this study, a novel state space-based Transformer model is introduced, aimed at enhancing performance in complex system prediction tasks, particularly for predictions based on text big data, as shown in Figure 6.

This method, by integrating the advantages of state space models and the Transformer model, captures the dynamic changes in time series data and processes and understands large-scale text data. The proposed method framework consists of three core components: the state space transition equation, the state space-based Transformer model, and the state space loss function, as shown in Figure 7.

This framework initially describes and captures the dynamic changes in complex systems in time series data through the state space model; then utilizes the powerful text processing capability of the Transformer model to understand and analyze text big data; finally, the designed state space loss function is employed to optimize the model, achieving higher accuracy and stability in predicting complex systems.

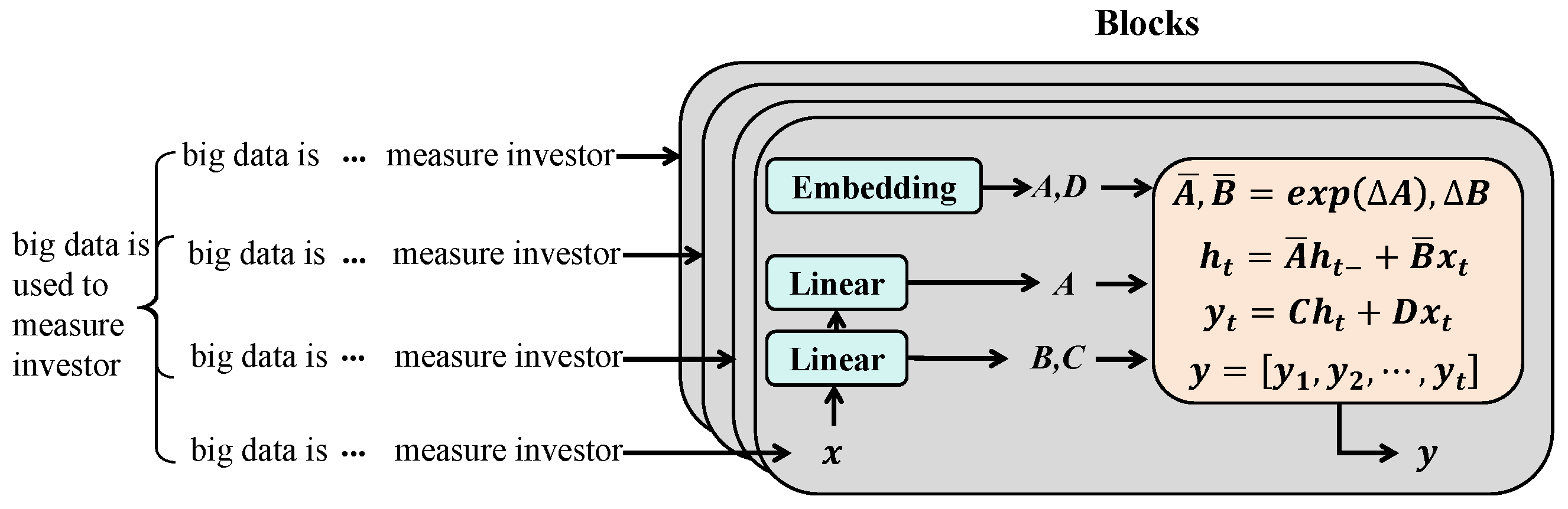
3.3.1. State Space-Based Transformer Model

A novel approach that combines state space models with the Transformer is proposed, aiming to enhance the accuracy of complex system prediction tasks. The detailed design of our model is illustrated in Figure 8.

The model takes text data as input, first transforming the text into dense vector representations through an embedding layer, known as Input Token Embeddings. These embeddings aim to capture the semantic information of each word or character in the text. The core of the model is a Transformer structure that integrates a State Space Model, not only processing sequential data to capture long-distance dependencies but also understanding and predicting the dynamic changes in complex systems through the state space model. Within each Block, “Learned Context IDs” are introduced to identify and learn different context states, allowing the model to distinguish and process information from various contexts. Each Block contains linear layers (for generating Key, Value, and Query, referred to as KVQ) and a cross-attention mechanism, enabling effective integration of information based on current input and previously learned context states. After processing through a series of Blocks, the model outputs Token Embeddings, which are subsequently used for predicting future states of complex systems. The entire process not only involves the deep processing of text data but also integrates state space theory to enhance the understanding of system dynamics. Key mathematical representations in the model include:

• Token Embedding Transformation [74]:

  $$E=\mathrm{Embed}\left(X\right)$$

  (20)

  where X is the input text data, and E is the token embeddings.
• Cross-attention Mechanism [75]:

  $$A=\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

  (21)

  where Q, K, V represent the query, key, and value vectors, respectively, $d_k$ is the dimension of the key vectors, and A is the output of the attention mechanism.
• State Space Model Integration [76]:

  $$S_{t+1}=F·S_t+G·A+H$$

  (22)

  where $S_t$ and $S_{t+1}$ represent the current and next time step system states, respectively, and F, G, and H are state-space model parameters, with A being the output of the cross-attention.

We propose a model based on an extension of the standard Transformer architecture, incorporating the Mamba state-space model to enhance its ability to model dynamic changes in sequence data. Specifically, our model includes the following main components:

Blocks: Our model consists of multiple blocks, each a variant of a Transformer layer that integrates features of the state-space model. Each block contains a self-attention mechanism and a feed-forward neural network and also embeds a state-space representation layer to simulate the temporal evolution characteristics of the input data. Inter-block Connections: Blocks are connected through residual connections and layer normalization. Residual connections allow information to flow directly from one block to another, while layer normalization helps maintain stability during training. Specific Parameters: Number of Blocks: The standard version of our model includes 12 blocks, each corresponding to a layer in a Transformer. Size of Each Block: Each block has 12 heads in the self-attention mechanism, with each head having a dimension of 64, giving a total dimension of 768 for each self-attention layer. The intermediate dimension of the feed-forward networks is 3072. State Space Representation Layer: Each block’s state space representation layer is designed to track and update state variables that change over time, typically set to match the input dimension, i.e., 768. Total Number of Parameters: Our model has a total of approximately 110 million parameters, including those for the self-attention layers, feed-forward networks, state space representation layers, and other components within the model.

3.3.2. State Space Transition Equation

In this study, the state space transition equation is introduced to enhance the prediction capability for complex systems. The state space transition equation, a core concept in dynamic system theory, describes the evolution of system states over time, as shown in Figure 9.

The design of the state transition equation in this research is based on the following mathematical representation [77,78,79]:

$$\widehat{A}=exp(\Delta A),\Delta B$$

(23)

$$h_t=\widehat{A}{h}_{t-1}+\Delta B{x}_t$$

(24)

$$y_t=C{h}_t+D{x}_t$$

(25)

where $h_t$ represents the hidden state at time t, $x_t$ represents the input at time t, and $y_t$ is the output of the model. Matrices $\widehat{A}$ and $\Delta B$ are updates for the state transition matrix and the input control matrix, respectively, while C and D represent the output matrix and the direct transfer matrix. The learning and updating of these matrices correspond to linear layers in the model. The linear assumption of the state space model allows for the use of an exponential map to update the state transition matrix, capturing the continuous changes in system dynamics [80]:

$$\widehat{A}=exp(\Delta A)$$

(26)

This exponential map ensures the stability of $\widehat{A}$, maintaining stable system dynamics even when $\Delta A$ changes. The update of the input control matrix $\Delta B$ allows the model to adjust state changes based on the input $x_t$, while C and D transform the hidden state into the final output. The rationale for adopting the state space transition equation design lies in its capability to simulate and predict the dynamic changes in actual complex systems. Through the state space model, a more accurate capture of the system state evolution over time is possible, crucial for complex system prediction based on time series data. The Transformer integrated with the state space model can be enhanced and optimized through:

• Enhanced temporal dynamic modeling: The state space transition equation enables the model to capture the dynamic changes in time series data more finely, improving prediction accuracy.
• Flexible parameter updates: The parameter update mechanism in the state space model allows the model to flexibly adapt to the characteristics of different complex systems, enabling targeted optimization.
• Enhanced data processing capability: The introduction of the state space model enables the model to handle data containing complex dynamics, such as financial data analysis or natural language text, often embodying implicit time series characteristics. The model can process not only static semantic information but also capture the evolution of data over time, critical for dynamic prediction.
• Optimized state change modeling: The state space transition equation provides a mathematically rigorous way to describe continuous state changes, enabling the model to predict future states more precisely in time series prediction tasks compared to conventional Transformer structures.
• Customized output equation: By combining the state space model’s output equation $y_t=C{h}_t+D{x}_t$ with the Transformer’s output layer, the model’s output incorporates information determined by the current state and also considers the impact of direct inputs, offering a more comprehensive prediction.

These enhancements not only improve model accuracy but also strengthen the model’s capability to predict complex system behavior and understand the deep semantics of text data. Furthermore, by integrating the concept of state space, the model is endowed with the ability to process and predict dynamic changes in systems, an ability not possessed by traditional Transformer models. The state space model provides a mathematical framework for describing and predicting the evolution of system states over time, essential for understanding the dynamic characteristics of complex systems such as financial markets and climate changes. Combined with the state space model, our Transformer becomes not just a powerful tool for processing text sequences but also a model capable of deeply analyzing and predicting the behavior of complex systems.

3.3.3. State Space Loss Function

In the research of complex system prediction, the design of the loss function is crucial for the learning and predictive capabilities of the model. The state space loss function proposed in this article is designed for a novel prediction model that integrates state space models with the Transformer architecture. It significantly differs from traditional Transformer model loss functions, mainly by considering both the dynamic characteristics of time series and the accuracy of predictions. The state space loss function not only measures the discrepancy between predicted outputs and true values but also considers the smoothness and coherence of model state transitions. Its mathematical expression is as follows [81]:

$$L\left(\theta \right)={\lambda }_1{L}_{predict}\left(\theta \right)+{\lambda }_2{L}_{smooth}\left(\theta \right)$$

(27)

where $L_{predict}\left(\theta \right)$ is the traditional prediction loss component, typically measured using Mean Squared Error (MSE) to quantify the difference between model outputs and true values [82]:

$$L_{predict}\left(\theta \right)=\frac{1}{N}\sum _{t=1}^N{\left(y_t-{\widehat{y}}_t\right)}^2$$

(28)

N is the total number of data points, $y_t$ is the true value at time t, and ${\widehat{y}}_t$ is the model’s predicted output.

$L_{smooth}\left(\theta \right)$ is the smoothness loss component unique to state space models, used to ensure the continuity and reasonableness of state transitions. A typical choice is the Frobenius norm of the changes in the state transition matrix as the smoothness term [83]:

$$L_{smooth}\left(\theta \right)={\left|\right|\Delta A\left|\right|}_F^2+{\left|\right|\Delta B\left|\right|}_F^2$$

(29)

where $\Delta A$ and $\Delta B$ are the changes in the state transition matrix and the control input matrix, respectively, and $\left|\right|·{\left|\right|}_F$ represents the Frobenius norm.

${\lambda }_1$ and ${\lambda }_2$ are weighting parameters used to balance the contributions of prediction loss and smoothness loss to the total loss. The choice of these parameters depends on the specific task and data characteristics, needing determination through cross-validation or other model selection techniques. The design of the state space loss function is motivated by the importance of not only prediction accuracy but also the smooth evolution of system states over time in complex system prediction tasks. The state space loss function encourages the model to learn smooth state transitions through the $L_{smooth}\left(\theta \right)$ term, capturing the system’s dynamic characteristics. Additionally, relying solely on prediction loss during model training often leads to overfitting. Introducing smoothness loss, the state space loss function enhances the model’s generalization ability, making it more robust on unseen data. Lastly, in practical applications, a conflict may exist between prediction accuracy and the smoothness of state transitions. By adjusting the values of ${\lambda }_1$ and ${\lambda }_2$, the state space loss function allows for finding an optimal balance between the two according to practical needs. Therefore, the state space loss function provides the following advantages in the complex system prediction tasks of this study:

• Consistency with dynamic prediction and loss function: The state space loss function aligns closely with the goal of dynamic system prediction, focusing simultaneously on the accuracy of predictions and the smoothness of state changes during the prediction process. This is crucial for dynamic systems where state changes are often smooth over time, and any abrupt changes may indicate system anomalies or data issues. The $L_{smooth}\left(\theta \right)$ part effectively reduces the likelihood of such abrupt changes, making the model’s predictions more credible.
• Prevention of overfitting: Traditional Transformer models might perform poorly on future data due to overfitting historical data. The smoothness loss component in the state space loss function helps improve model performance on unseen data by forcing the model to learn more generalized state change rules rather than merely memorizing patterns in the training dataset.
• Flexibility in parameter adjustment: By adjusting the values of ${\lambda }_1$ and ${\lambda }_2$, researchers can flexibly control the weight of prediction loss versus smoothness loss in the total loss function. For different complex system prediction tasks, these parameters can be optimized based on the specific characteristics of the system and task requirements to achieve the best prediction performance.
• Enhanced interpretability: The state space loss function not only optimizes the model’s predictive performance but also enhances its interpretability. Since the model needs to consider the coherence of state transitions, the trends learned by the model are more aligned with the physical or logical laws of the real world, allowing researchers to explain the model’s predictive behavior by analyzing the parameters of the state space model.
• Adaptability to complex tasks: Complex systems, like financial markets or weather systems, have multifactorial and nonlinear state changes. Traditional loss functions struggle to capture this complexity. The state space loss function, by simulating changes in the state transition matrix and control matrix, better adapts to this complexity, thereby enhancing model performance in such complex tasks.

3.4. Experimental Configuration

3.4.1. Hardware and Software Configuration

In the research of complex system prediction models driven by text big data, the configuration of hardware and software is a vital foundation to ensure the smooth progress of experiments and the reliability of results. The hardware platform utilized in the experiment comprises high-performance computer systems equipped with advanced NVIDIA GPUs and high-speed CPUs to ensure the efficiency of model training and testing. Specifically, the NVIDIA Tesla V100 GPU was employed, featuring 5120 CUDA cores and 16 GB of HBM2 memory, providing exceptional parallel processing capabilities and fast data transfer rates, crucial for handling large-scale text datasets and complex deep learning models. Additionally, servers equipped with Intel Xeon Gold 6154 CPUs, boasting up to 3.00 GHz processing speed and 22 cores, were deployed to effectively support parallel execution of model training and data processing tasks.

Regarding the software environment, experiments were conducted using the Python programming language. Python is widely utilized in the fields of scientific computing and machine learning due to its rich libraries and frameworks, excellent readability, and extensive community support. PyTorch was selected as the primary deep learning framework to support complex model training and data processing requirements. PyTorch offers powerful automatic differentiation capabilities, efficient tensor operations, and convenient tools for model definition and optimization, greatly facilitating the experimental process. During this study, multiple library functions and tools were utilized to support data processing, model construction, and experimental analysis. Here, are some key libraries and tools:

• NumPy: A fundamental scientific computing library in Python, NumPy provides powerful multi-dimensional array objects and a wide range of mathematical functions for efficiently handling large volumes of data. In this study, NumPy was extensively used for data preprocessing, feature extraction, and numerical computation tasks.
• Pandas: A data analysis and manipulation library, Pandas offers user-friendly data structures and data analysis tools. By using Pandas, various formats of datasets, including CSV and Excel, could be conveniently processed and analyzed.
• Matplotlib and Seaborn: Both libraries were utilized for data visualization. Matplotlib, a plotting library, provides extensive drawing functions supporting various formats and high-quality graphic output. Seaborn, built on Matplotlib, offers a higher-level interface focused on drawing statistical graphics, making data visualization more intuitive and attractive.
• Scikit-learn: A Python library for machine learning, Scikit-learn offers simple and efficient tools for data mining and data analysis. In this study, Scikit-learn was used for model evaluation, cross-validation, and various machine-learning tasks.
• Mamba: A computational framework tailored for state space models, Mamba supports the rapid development and accurate estimation of complex models. Through Mamba, effective parameter estimation and state inference for state space models were achieved, crucial for capturing dynamic changes in complex systems.

With such hardware and software configurations, combined with cutting-edge libraries and tools, this study was conducted in an efficient and reliable experimental environment. These configurations not only provided strong support for processing and analyzing large-scale text datasets but also laid a solid foundation for the development and evaluation of complex system prediction models driven by text big data.

3.4.2. Training Strategy

When conducting research on complex system prediction models based on text big data, formulating a reasonable training strategy and parameter setting is crucial for the model’s training effectiveness and generalization capability. This study adopted a comprehensive training strategy, including the choice and parameter setting of optimizers, the method of cross-validation, and the determination of batch size. These strategies and settings were essential to ensure the effectiveness of model training and the reliability of the results.

The choice of optimizer plays a significant role in the convergence speed and final performance of deep learning models during training. The Adam optimizer [84] was selected for its combination of advantages from momentum and RMSprop, offering good convergence under various conditions, especially suitable for handling large-scale datasets and complex model structures. The core of the Adam optimizer is its adaptive adjustment of learning rates for each parameter, dynamically tuning the learning step size during training, thus enhancing efficiency and stability. The learning rate was set to $1\times {10}^{-4}$, a relatively small value aimed at avoiding crossing the optimum solution too quickly, ensuring stable convergence to good performance. The learning rate choice was based on preliminary experiments and literature recommendations to adapt to the model’s learning needs with complex data. Furthermore, the ${\beta }_1$ and ${\beta }_2$ parameters in the Adam optimizer were set to 0.9 and 0.999, respectively. These parameters control the exponential decay rates for the gradients and squared gradients, reflecting the extent of past gradient information utilized, aiming to balance the retention of historical information and the impact of current gradients. To comprehensively evaluate the model’s generalization ability and reduce dependence on specific data splits, five-fold cross-validation was adopted. In k-fold cross-validation, the dataset is evenly divided into k subsets, each subset is used as the test set in turn, while the rest serve as the training set, this process repeats k times, each time with a different subset as the test set. This method ensures each data point has the chance to be part of the test set, providing a more comprehensive and reliable estimation of model performance. In practice, five-fold cross-validation means the entire dataset is divided into five parts, not only increasing the total number of training rounds but also requiring the model to adapt to different data distributions. This method is particularly important for assessing the model’s performance on unseen data, helping to reveal potential overfitting issues. Batch size, an important parameter in deep learning training, affects the learning efficiency, memory usage, and final performance of the model. In this study, the batch size was uniformly set to 32. This size was chosen considering the balance between training efficiency and hardware resource limitations, especially the GPU memory capacity. A moderate batch size ensures sufficient data volume in each iteration to estimate gradients while avoiding memory overflow problems caused by too large batch sizes. Additionally, an appropriate batch size helps improve the stability and generalization ability of model training, as it somewhat simulates a balance between full-batch training and stochastic gradient descent.

3.4.3. Model Evaluation Metrics

In this study, to comprehensively evaluate the performance of the proposed model in complex system prediction tasks, we selected three core metrics: precision, recall, and accuracy. Precision measures the proportion of correctly predicted positive samples among those predicted as positive, reflecting the model’s accuracy in predicting positive classes; recall indicates the proportion of correctly predicted positive samples out of all actual positive samples, measuring the model’s ability to capture positive samples; accuracy is the proportion of correctly predicted samples out of the total number of samples, providing an intuitive display of the model’s overall performance. These three indicators reflect the performance of the model from different perspectives, helping to fully understand the model’s effectiveness in practical applications and providing a basis for future model optimization.

3.5. Baseline

For a comprehensive evaluation of the performance of the proposed state space-based Transformer model in complex system prediction tasks, this paper has chosen Transformer [85], BERT [86], Whole Word Masking BERT (wwm-BERT) [87], and Finsformer [88] as baseline models for comparative analysis. These models have demonstrated their strong performance in the field of NLP, especially in text understanding and generation tasks.

BERT, introduced by Google in 2018 [89], is based on the encoder architecture of Transformer and utilizes a bidirectional training method to comprehend the context of language. A key innovation of BERT is the use of a Masked Language Model (MLM) for pre-training deep bidirectional representations, which can then be applied to downstream tasks without specific architectural modifications for the task at hand.

The MLM task of BERT can be represented as [90]:

$$L_{\mathrm{MLM}}=-\sum _{i\in M}\log p\left(w_i\right|w_{-i})$$

(30)

where M is the set of masked words, and $w_{-i}$ denotes all words except for the ith word. By predicting masked words, BERT learns rich linguistic features. Whole Word Masking BERT is a variant of BERT that masks entire words during the pre-training phase, instead of individual letters or characters [91]. This method better handles semantic information in language, especially for languages with complex structures like Chinese. The main improvement lies in the masking strategy. In wwm-BERT, instead of randomly masking individual characters or tokens, entire words are masked to better simulate real-world language usage and promote the model to learn more accurate word-level representations. This improvement is particularly effective for languages with a large number of compound words, enhancing the model’s performance in understanding and generating these languages. Finsformer is a Transformer-based model variant specifically designed for the financial domain. It introduces domain-specific knowledge and data processing mechanisms to the foundation of Transformer to better understand and predict financial text data. The core idea of Finsformer is to incorporate the relationships between financial entities into the self-attention mechanism as additional information, enabling the model to capture specific contexts and interactions between entities in financial texts more effectively [92]. This design results in improved performance for Finsformer on financial prediction tasks compared to traditional Transformer models.

These baseline models, with their respective core mechanisms and optimization objectives, demonstrate powerful capabilities in processing text data, particularly in capturing semantic and contextual information. The selection of these models as baselines is due to their representative status in the NLP field, their excellent performance in their respective domains, and their methodological complementarity and comparability to our proposed model. This choice aims to ensure our research is competitive with the current state of the art and provides a comprehensive and in-depth evaluation basis for the performance of our model in complex system prediction tasks.

4. Results and Discussion

4.1. Legal Case Judgment Prediction Results

The objective of this experiment was to verify the effectiveness of the proposed model in predicting legal case judgment. The legal case judgment prediction task requires the model to understand and analyze the complex linguistic structure of legal documents, making accurate predictions based on case facts and legal logic. This task challenges not only the model’s language understanding capabilities but also its logical reasoning ability. Experimental results, as shown in

Table 2. Legal case judgment results.

Model	Precision	Recall	Accuracy
Transformer [85]	0.80	0.77	0.79
BERT [86]	0.83	0.80	0.82
wwm-BERT [87]	0.86	0.83	0.85
Finsformer [88]	0.89	0.86	0.88
Proposed Method	0.93	0.90	0.91

, are presented below.

From the experimental results, it is observed that all models demonstrated capabilities in processing legal texts, yet significant gaps exist in precision, recall, and accuracy. Although the traditional Transformer model has advantages in processing sequential data, its performance is less optimal than BERT-based models due to the complexity and specificity of legal texts. The BERT model, with its deep bidirectional context understanding, has improved significantly in both precision and recall due to a better grasp of semantics within the text. As an improved version of BERT, wwm-BERT further enhances performance by adopting a more granular pre-training approach, better understanding the subtle differences between lexicons, especially in scenarios like the legal domain where differentiation is crucial. Although Finsformer is optimized for the financial domain and not an exact match for legal case judgment applications, its capability to capture complex, specialized texts also showed promising performance. The proposed model achieved the best results across all metrics, attributing its success to not only combining BERT’s deep contextual understanding but also enhancing the ability to capture dynamic changes in the text through the integration of state space models. In scenarios like legal case judgment, where case narratives, relevant legal provisions, and the judge’s logical reasoning all exhibit temporal variations as the case progresses, state space models excel. Therefore, compared to traditional Transformer structures, the proposed model can more finely capture temporal series changes in text data, such as judges’ remarks on case facts and the application of legal logic, which are key factors affecting legal judgment outcomes. Additionally, the introduction of the state space loss function also promotes the model’s ability to capture the logic of case development, enhancing prediction accuracy. By modeling these complex relationships more rigorously, the proposed model not only achieves mathematical precision but also captures and understands the complexity of legal texts more comprehensively in practical applications. The characteristics of legal cases demand high attention to detail and strict logical coherence, areas where traditional models fall short. By integrating state space models, the proposed model can fully consider the development and legal reasoning process of each case, rather than merely extracting static features from the text. This approach is crucial for improving the accuracy of legal text analysis.

4.2. Legal Case Translation Results

This section aims to verify the performance of different models in the machine translation task. Machine translation, a complex natural language processing task, requires models to not only accurately capture the semantic information of the source language but also correctly translate this information into the target language expressions. The challenge lies in effectively handling the structural differences, semantic equivalence, and contextual adaptability between the source and target languages. The experimental results are presented in

Table 3. Translation results.

Model	Precision	Recall	Accuracy
Transformer [85]	0.84	0.82	0.83
BERT [86]	0.86	0.84	0.85
wwm-BERT [87]	0.89	0.86	0.88
Finsformer [88]	0.92	0.88	0.90
Proposed Method	0.95	0.91	0.93

.

It is observed that as the model structure evolves from the basic Transformer to more advanced BERT, wwm-BERT, and Finsformer, model performance gradually improves. This trend indicates the increasing requirement for semantic understanding and context-capturing abilities in machine translation tasks. The original Transformer model relies on self-attention mechanisms to process sequence data, showcasing a clear advantage in capturing long-distance dependencies. However, its performance might be limited when dealing with complex semantic and structural transformations, especially in translations between multiple languages. In contrast, the BERT model, with its deep bidirectional context understanding through pre-training, offers enhanced semantic comprehension, thus performing better in machine translation tasks. wwm-BERT, an improvement on BERT, refines the handling of vocabulary by employing whole word masking during pre-training, enhancing the model’s ability to understand nuanced differences between words, which is particularly important in translation scenarios with significant grammatical and lexical disparities. Although Finsformer, optimized for the financial domain, was not initially designed for legal case judgment, its capability to capture complex, domain-specific texts also demonstrates commendable performance in the translation field. The proposed model outperforms other models on all metrics, benefiting from its combination of the dynamic nature of the state space model and the powerful semantic processing ability of the Transformer. In the machine translation task, understanding and predicting the rules of conversion between languages require models to grasp not just the static properties of language, such as semantics and syntax, but also the dynamic aspects, such as context flow and stylistic changes. By incorporating the state space model, the proposed model enhances understanding of the dynamics of language changes, crucial for improving translation accuracy. The state space loss function further optimizes the smoothness of state transitions and the coherence of predictions during the learning process, making the translation not merely a simple lexical substitution but closer to the logic and fluency of real language use.

A significant challenge in translation tasks is handling the differences in structure and expression between languages. For example, Chinese and English have substantial differences in syntactical structure and expression habits, demanding that translation models not only perform direct translations but also make appropriate semantic transformations and adjustments. Mathematically, by incorporating the state space model, the proposed model can more flexibly model and capture these transformation rules between languages. By learning the dynamic correspondences between languages, the proposed model is theoretically better equipped to adapt to these differences, achieving more natural and accurate translation outputs. Furthermore, the mathematical innovation of the proposed model, such as the integration of state space theory with deep learning, allows it to capture the temporal dependencies in sequence data, particularly important when translating long sentences and complex sentence types. In these cases, the correspondence between the source and target languages might not be one-to-one but requires capturing multiple dependencies. Here, the state space model demonstrates its superiority, offering more information and context to guide the translation.

4.3. Financial Data Analysis Results

This section is dedicated to testing and verifying the performance of different models in financial data analysis tasks, particularly in assessing investment risks. Financial data analysis is a highly complex and dynamic field, involving not just the processing of quantitative data but also the understanding and analysis of market news, reports, and other textual information. Thus, the aim of the experiment design is to evaluate the capability of various models to handle these complex data, with performance measured by three core metrics: precision, recall, and accuracy.

As can be observed from

Table 4. Financial data analysis results.

Model	Precision	Recall	Accuracy
Transformer [85]	0.82	0.80	0.81
BERT [86]	0.85	0.82	0.83
wwm-BERT [87]	0.88	0.85	0.86
Finsformer [88]	0.91	0.87	0.89
Proposed Method	0.94	0.90	0.92

, performance progressively improves from the traditional Transformer model to the proposed model. Although the original Transformer model effectively processes sequence data and captures long-distance dependencies, it may be limited when facing complex, noisy financial data. The BERT model and its variants, by handling deep contextual information, improve the understanding capability of the model, crucial for dealing with financial texts that often contain complex economic terms and implicit market logic. The wwm-BERT model refines the handling of vocabulary by fine-tuning BERT, enhancing the model’s comprehension of professional terms and specific concepts within financial texts. Such fine-grained understanding is necessary for accurately predicting market dynamics and investment risks. The Finsformer model, initially optimized for the financial domain, demonstrates that domain-specific optimization is highly effective in enhancing model performance. In financial data analysis, this optimization allows Finsformer to more precisely capture subtle market movements, leading to improvements across all metrics. Finally, the method proposed in this article performs the best among all models. This success is mainly due to the model’s deep integration and understanding of the unique dynamics of the financial domain. By incorporating the state space model, the proposed method captures not just the static features within texts but also understands the dynamic changes in these features over time, which is particularly crucial in financial data analysis. Moreover, the proposed state-space loss function further optimizes the accuracy of financial time series prediction. It focuses not only on the prediction accuracy at individual time points but also emphasizes the coherence of the entire time series and the prediction of dynamic trends, essential for comprehending the complexity of financial markets. Predicting financial markets requires not just accurate judgments of the current state but also continuous predictions of future trends, demanding that models capture not only precise information at single points but also understand the changing patterns of market dynamics overall.

4.4. Discussion on Results

Regarding the experimental results above, as a state-space model library Mamba’s main advantage lies in handling time-series data with high computational efficiency. In traditional applications, it is not designed to enhance the performance of models like Transformers. However, we observed that state-space models have unique advantages in capturing hidden state changes in dynamic systems, which is particularly crucial in complex system prediction tasks, especially when the predictions involve nonlinear relationships over time. One of our core contributions in this paper is demonstrating how state-space models can be combined with Transformers to enhance the latter’s capability in handling dynamic data. Our experiments confirm that this combination not only improves computational efficiency but, more importantly, significantly enhances model prediction performance. Specifically, the introduction of the state-space model allows the Transformer to capture temporal dependencies in the data more accurately, often manifesting as context dependencies or long-term dependencies, which traditional Transformer models struggle with. For example, in legal case judgment prediction, the development of the case and the legal argumentation process often involve complex temporal logic; in financial data analysis, predicting market behavior requires understanding and calculating the relationship between past actions and future trends. Our model has shown significant improvements in Precision, Recall, and Accuracy in these tasks, proving the effectiveness of combining state-space models with Transformers.

4.5. Different Loss Function Ablation Results

The experimental design in this section aims to explore the impact of different loss functions on model performance, especially across three distinct tasks: legal case judgment, legal case translation, and financial data analysis. By comparing the performances of Cross-Entropy Loss, Focal Loss, and the State Space Loss Function, the experiment seeks to validate the effectiveness of the proposed State Space Loss Function in enhancing model performance. The experimental results are shown in

Table 5. Different loss function ablation experiment results.

Model	Precision	Recall	Accuracy
Legal Case Judgment—Cross-Entropy Loss	0.82	0.80	0.81
Legal Case Judgment—Focal Loss	0.87	0.83	0.85
Legal Case Judgment—State Space Loss	0.93	0.90	0.91
Legal Case Translation—Cross-Entropy Loss	0.84	0.81	0.83
Legal Case Translation—Focal Loss	0.88	0.84	0.86
Legal Case Translation—State Space Loss	0.95	0.91	0.93
Financial Data Analysis—Cross-Entropy Loss	0.83	0.81	0.82
Financial Data Analysis—Focal Loss	0.87	0.85	0.86
Financial Data Analysis—State Space Loss	0.94	0.90	0.92

.

In the legal case judgment task, models utilizing Cross-Entropy Loss achieved a precision of 0.82, a recall of 0.80, and an accuracy of 0.81; models with Focal Loss showed improved precision to 0.87, a recall of 0.83, and an accuracy of 0.85; while models applying the State Space Loss Function reached the highest metrics across all indicators: precision of 0.93, recall of 0.90, and accuracy of 0.91. In the legal case translation task, the Cross-Entropy Loss models had a precision of 0.84, a recall of 0.81, and an accuracy of 0.83; Focal Loss models had a precision of 0.88, a recall of 0.84, and an accuracy of 0.86; State Space Loss models outperformed others with a precision of 0.95, a recall of 0.91, and an accuracy of 0.93. For the financial data analysis task, Cross-Entropy Loss models exhibited a precision of 0.83, a recall of 0.81, and an accuracy of 0.82; Focal Loss models showed a precision of 0.87, a recall of 0.85, and an accuracy of 0.86; models using the State Space Loss achieved the best performance with precision, recall, and accuracy metrics at 0.94, 0.90, and 0.92, respectively.

The experimental findings reveal that, across legal case judgment, legal case translation, and financial data analysis tasks, models employing the State Space Loss Function significantly outperform those using Cross-Entropy Loss and Focal Loss in terms of precision, recall, and accuracy. This trend indicates that, compared to traditional loss functions, the State Space Loss Function better drives models to capture and understand key information in complex tasks, thereby enhancing predictive performance. Cross-Entropy Loss, while widely used, focuses mainly on increasing the match between model outputs and actual labels but may not adequately address imbalanced samples or complex dependencies within tasks. Focal Loss, by giving more attention to samples that are hard to predict correctly, somewhat mitigates this issue, especially in tasks with severe sample imbalance. The design of the State Space Loss Function, considering the dynamic nature of tasks and prediction accuracy, not only emphasizes the consistency between model outputs and true labels but also introduces constraints on internal state changes through the mathematical properties of state space models. This approach encourages models to pay more attention to long-term, inherent dependencies during data learning rather than merely optimizing momentary output matching. In tasks such as legal case judgment, legal case translation, and financial data analysis, which often involve rich contextual information, long-term dependencies, and complex logical relationships, this design is particularly important. The State Space Loss Function prompts models to focus more on capturing these complex relationships, thereby improving prediction accuracy and robustness. In the task of legal case judgment, decisions often depend on a deep understanding of legal texts and an accurate grasp of case facts, requiring models to comprehend not just the literal meaning of texts but also the underlying logic and legal principles. By considering the coherence of model states, the State Space Loss Function aids models in better understanding and simulating the legal reasoning process, thus achieving better performance in complex legal text analysis tasks. For the legal case translation task, differences in structure and expression habits between languages pose a challenge in directly translating texts. The State Space Loss Function, by introducing constraints on the smoothness of state changes, encourages models to consider differences between languages and semantic continuity more finely during language translation, ensuring the naturalness and accuracy of translations. In the financial data analysis task, the volatility and uncertainty of market data require models to accurately predict future market trends. Traditional loss functions might struggle to capture subtle changes and long-term trends in market data. The State Space Loss Function, by constraining the model’s internal state changes, helps models better understand market dynamics, improving model performance in financial data analysis tasks.

Through ablation experiments with different loss functions, this study demonstrates the significant advantage of the State Space Loss Function in enhancing model performance. This provides new insights and methods for the future application of deep learning models in complex tasks. While continuing to explore and optimize loss functions, this also opens possibilities for deep learning models to address more complex and dynamic real-world problems.

4.6. Different Transformer Attention Ablation Results

The experimental design in this section aims to assess the performance differences among various Transformer architecture variants on specific tasks. The experiments span legal case judgment, legal case translation, and financial data analysis, involving variants such as the standard Transformer, sparse attention Transformer, and state space-based Transformer. By comparing the performance of these models in terms of precision, recall, and accuracy, the experiment seeks to reveal the specific impact of different attention mechanisms on model performance, and how the state space theory can optimize the Transformer model to adapt to complex data analysis tasks.

Results in

Table 6. Different transformer backbone ablation experiment results.

Model	Precision	Recall	Accuracy
Legal Case Judgment—Multi-head Attention	0.78	0.73	0.76
Legal Case Judgment—Sparse Attention	0.85	0.81	0.83
Legal Case Judgment—State Space-based Transformer	0.93	0.90	0.91
Legal Case Translation—Multi-head Attention	0.77	0.75	0.76
Legal Case Translation—Sparse Attention	0.86	0.83	0.85
Legal Case Translation—State Space-based Transformer	0.95	0.91	0.93
Financial Data Analysis—Multi-head Attention	0.78	0.72	0.74
Financial Data Analysis—Sparse Attention	0.85	0.80	0.82
Financial Data Analysis—State Space-based Transformer	0.94	0.90	0.92

demonstrate that in tasks such as legal case judgment, legal case translation, and financial data analysis, the state space-based Transformer model significantly outperforms both the standard Transformer and sparse attention Transformer models. This trend reveals the effectiveness of state space theory in enhancing the Transformer model’s capability to process complex data analysis tasks. Despite the significant advantage of the standard Transformer model in handling sequential data, its performance is limited in complex tasks requiring deep understanding and long-term dependency modeling. This limitation stems from the model’s focus on capturing local dependencies within sequences, with insufficient capability to grasp long-distance dependencies and complex logical structures. The sparse attention Transformer model, by introducing a sparsity mechanism to optimize attention computation, aims to improve efficiency and accuracy in processing long sequences. The sparse attention mechanism, by limiting the focus of attention, reduces interference from irrelevant information, thereby improving the model’s ability to capture long-distance dependencies to some extent. However, this method has limited effects on enhancing model understanding of complex logical structures, especially in scenarios requiring nuanced comprehension of task backgrounds and dynamic data changes. The state space-based Transformer model further extends the capabilities of the Transformer by incorporating state space theory to capture dynamic changes and intrinsic structures in sequence data. This model is particularly suited to tasks where data inherently possess time-series characteristics or require capturing time dynamics, such as financial data analysis. In financial markets, asset price movements are influenced by numerous factors, including macroeconomic indicators, market sentiment, and significant news events, among others, with complex interactions between these factors. The state space-based Transformer model, by simulating these dynamic changes, can more accurately predict future market trends, achieving higher precision, recall, and accuracy in financial data analysis tasks.

From a mathematical perspective, the advantage of the state space-based Transformer model lies in its ability to integrate the dynamic characteristics of time series with deep semantic information. The introduction of dynamic system theory in the state space model part provides a mathematical tool for describing and predicting the evolution of system states over time. When this theory is applied to the Transformer architecture, it not only enhances the model’s ability to capture the dynamic changes in time-series data but also retains the Transformer’s advantage in processing complex semantic relationships. This combination enables the model to understand not only the literal meaning of texts but also to capture the patterns and trends hidden behind time series, such as fluctuation trends in financial markets or reasoning processes in legal cases.

4.7. Limitations and Future Work

In this study, a State Space-based Transformer model is introduced, aimed at enhancing the accuracy of complex system prediction tasks, including legal case judgment, legal case translation, and financial data analysis, among others. Despite the model demonstrating exemplary performance across various tasks, it is acknowledged that limitations exist within the research process. Based on these limitations, future research directions are proposed. Firstly, although the State Space-based Transformer model excels in handling complex tasks, the training and inference computational costs are relatively high. Especially when processing large-scale datasets, the model’s efficiency may become a bottleneck. Furthermore, parameter tuning and optimization in the state space model component require extensive experimentation and computational resources, which could limit the model’s application scope under resource-constrained conditions. Secondly, while the model achieves good performance across multiple tasks, its generalization ability still needs further validation. Current experiments are primarily focused on specific datasets that, although representative, cannot cover all potential application scenarios. Therefore, whether the model maintains stable performance when faced with new tasks in different domains or with different characteristics requires additional research and experimentation. Moreover, although incorporating the state space model helps the Transformer better understand and predict the dynamic changes in complex systems, designing more effective state space representations and more accurately capturing the transition rules between states remain challenging. The current model relies on simplifications and assumptions of the state space model, which may limit its application in highly complex and nonlinear systems.

Addressing these limitations, future research work could explore several areas: Further research and development of more efficient model training and inference methods are needed. For example, reducing computational resource consumption and enhancing model efficiency could be achieved through model architecture improvements or the introduction of more advanced optimization algorithms. Additionally, exploring model compression and knowledge distillation techniques might be effective ways to alleviate model burden and improve applicability. Expanding the model’s application scope and generalization ability is also a crucial direction for future work. This includes testing the model’s performance in more domains and a wider range of tasks and validating the model’s adaptability in multilingual and cross-cultural environments. Through these efforts, the model’s generalization capability can be further assessed, and optimization strategies for different application scenarios can be explored. Regarding the state space model component, future research could explore more complex state representations and transition mechanisms. Introducing nonlinear dynamical systems theory, attention mechanisms from deep learning, or novel mathematical tools and model structures like graph networks may provide new perspectives and methods for capturing more complex system dynamics. Lastly, this study suggests the vast potential of deep learning models in understanding and processing complex systems. Therefore, future work could further explore combining machine learning with theories and methods from multiple disciplines such as systems science, economics, and social sciences.

5. Conclusions

In this study, a state space-based Transformer model is proposed to address the challenges of complex system prediction. The motivation and significance of this work stem from the fact that, although traditional deep learning models have achieved notable successes in processing sequential data, limitations still exist in understanding and predicting the dynamics and nonlinear characteristics inherent to complex systems. To tackle this issue, the model introduced innovatively integrates state space theory into the Transformer architecture, aiming to enhance the model’s capability to capture the dynamic changes in complex systems, thereby improving prediction accuracy and robustness.

In the experimental section, the model was validated and evaluated in three domains: legal case judgment, legal case translation, and financial data analysis. Experimental results demonstrate that the state space-based Transformer model proposed exhibits superior performance across all tasks when compared to standard Transformer models, sparse attention Transformers, and other advanced variants like BERT and Finsformer. Specifically, in the task of legal case judgment, the accuracy of the proposed model reached 91%, while in legal case translation and financial data analysis tasks, accuracies were 93% and 92%, respectively. These achievements can be attributed to comprehensive improvements in key metrics such as precision, recall, and accuracy. The exceptional performance of the state space-based Transformer model in various complex system prediction tasks is not coincidental but rather derives from several factors: Firstly, the integration of the state space model enables a better understanding and simulation of the dynamic changes in complex systems, providing the capability to capture the intrinsic dynamics of time series data. Secondly, through the carefully designed state space loss function, the model emphasizes not only the match between predicted outputs and actual values but more importantly, the smoothness and coherence of state changes during the prediction process, which is crucial for enhancing the model’s generalization ability and predictive accuracy. Furthermore, the introduction of the sparse attention mechanism further increases the efficiency of processing long sequence data, allowing the model to reduce computational resource consumption while maintaining high precision.

This work not only proposes a novel model architecture theoretically but also verifies its effectiveness through a series of rigorous experiments. These achievements not only enrich the research of deep learning in the field of complex system prediction but also offer new insights and directions for future research. Facing complex system prediction tasks, future studies can further explore new mechanisms combining state space models with deep learning based on the foundation of this work, developing more efficient and accurate predictive models. Additionally, attempts could be made to apply the proposed model to more domains and tasks, verifying and expanding its application range and practicality.