Comparing the Complexity and Efficiency of Composable Modeling Techniques for Multi-Scale and Multi-Domain Complex System Modeling and Simulation Applications: A Probabilistic Analysis
Abstract
1. Introduction
- A discussion of two prevalent composable modeling approaches, their motivations, and a detailed description of how they are applied.
- A new probabilistic analysis comparing the complexity and computational efficiency of these two approaches.
- A discussion on the trade-offs between the two approaches and the modeling circumstances which favor one approach or the other.
2. Related Work
- Both modeling techniques are designed to decompose a full system model into sub-models and coordinate interaction between sub-models as a way of modeling dynamics of the full system rather than using a non-composed model (i.e., a single, all-encompassing model).
- Both techniques are commonly used to capture systems with sub-systems of differing scales and/or from differing domains in which dynamics from one scale or domain propagate affect one or more other scales or domains.
3. Composable Modeling Methods: Motivations and Benefits
- High Resource Cost—Modeling all dynamics in a single model requires implementing sub-system dynamics from scratch for all sub-systems, unless there exists an already implemented model capable of capturing all dynamics relevant to the interaction system in question. In-house implementation may require significant engineering, modeling, and domain expertise, as well as a significant amount of time. If such a model already exists commercially, the access cost is also likely to be expensive. In either case, the cost may be prohibitive.
- Lack of Reusability/Extensibility—Multi-scale/multi-domain dynamics interwoven into a single model are often highly customized to the original problem and the addition of new dynamics or alterations to existing dynamics may require significant effort to integrate and test. For example, for the CPSS depicted in Figure 1, if the organization wishes to change the production process model, then this may entail changes to the cyber–physical network and software models. If all models are implemented in a single model, significant re-implementation may be necessary to integrate all changes. Ideally, a modeling approach should readily support model extensibility and reuse to minimize re-implementation costs when changes or additions are desired.
- Lack of Maintainability/Testability—Complex interwoven dynamics across multiple scales and/or domains makes testing and maintenance problematic. Unit tests focusing on individual scales require the inclusion of aspects from other scales. It may be hard to isolate sub-system dynamics and test their individual behaviors. For non-trivial systems, it can be difficult to verify that model implementation matches the intended design.
- Reduced Resource Cost—Full system models may be constructed by combining multiple sub-system models potentially originating from disparate sources. For example, a full model of the CPSS in Figure 1 could be constructed by combining pre-existing models of organizational behavior and production processing with custom-made models for the cyber–physical network and its underlying software layer. The ability to leverage existing sub-system models to compose a new full system model significantly reduces the time and domain expertise required to model a complex interaction system. Additionally, loosely interacting component models provide the opportunity for parallel model development, which can further reduce the time required to build a full system model.
- Increased Reusability/Extensibility—Models can be be more easily reused and/or altered due to their loose coupling. For example, for the CPSS in Figure 1, if a new cyber attack exploiting a particular software vulnerability is to be incorporated into to the full system model, it may only be necessary to alter the cyber–physical network software component model without changing other component models. If a software component model capturing the new cyber attack already exists, it potentially may be used in place of the previous software component model. The ability to combine and re-combine existing component models into new full-system models makes for increased model flexibility and adaptability.
- Increased Maintainability/Testability—Loose interdependence supports greater isolation of sub-system dynamics and makes unit testing and model code maintenance relatively easier than tight interdependence.
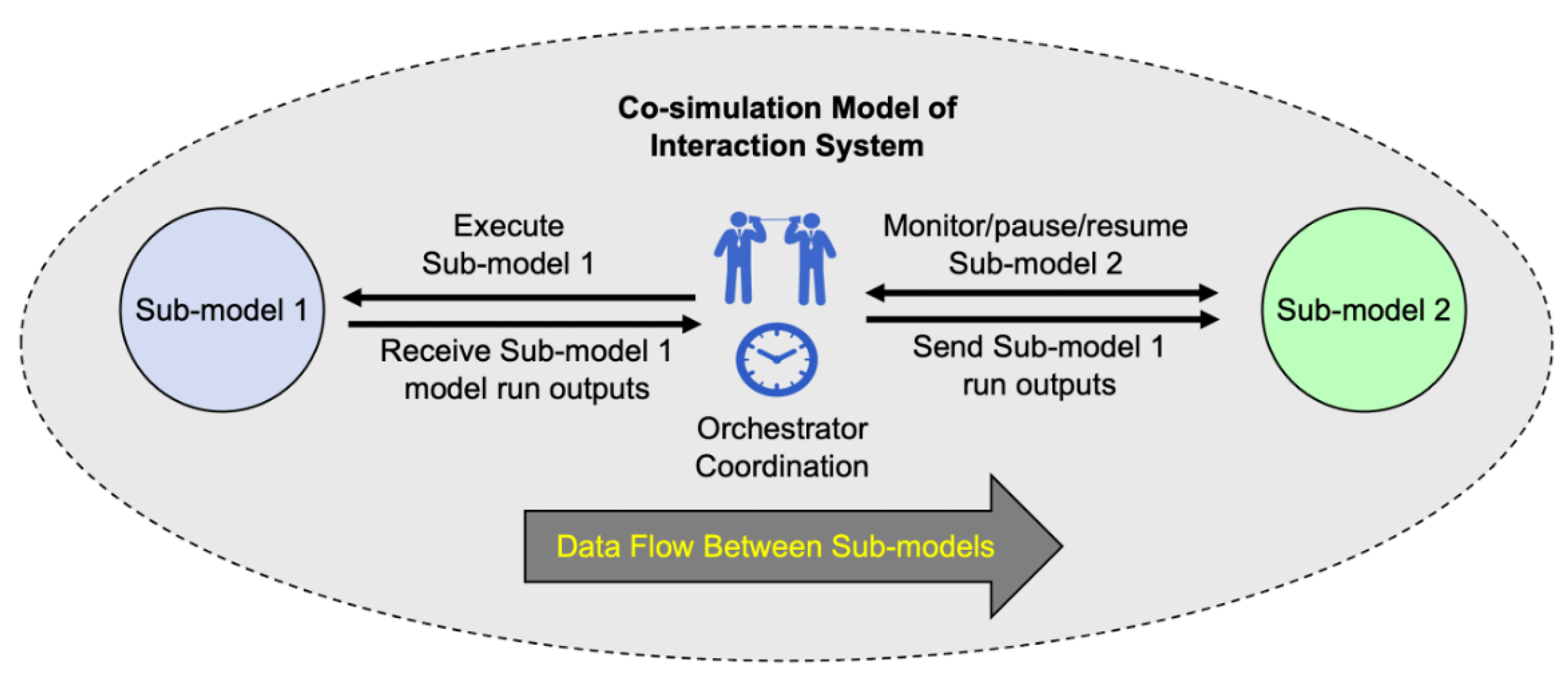
4. Composable Modeling Techniques
5. Foundations
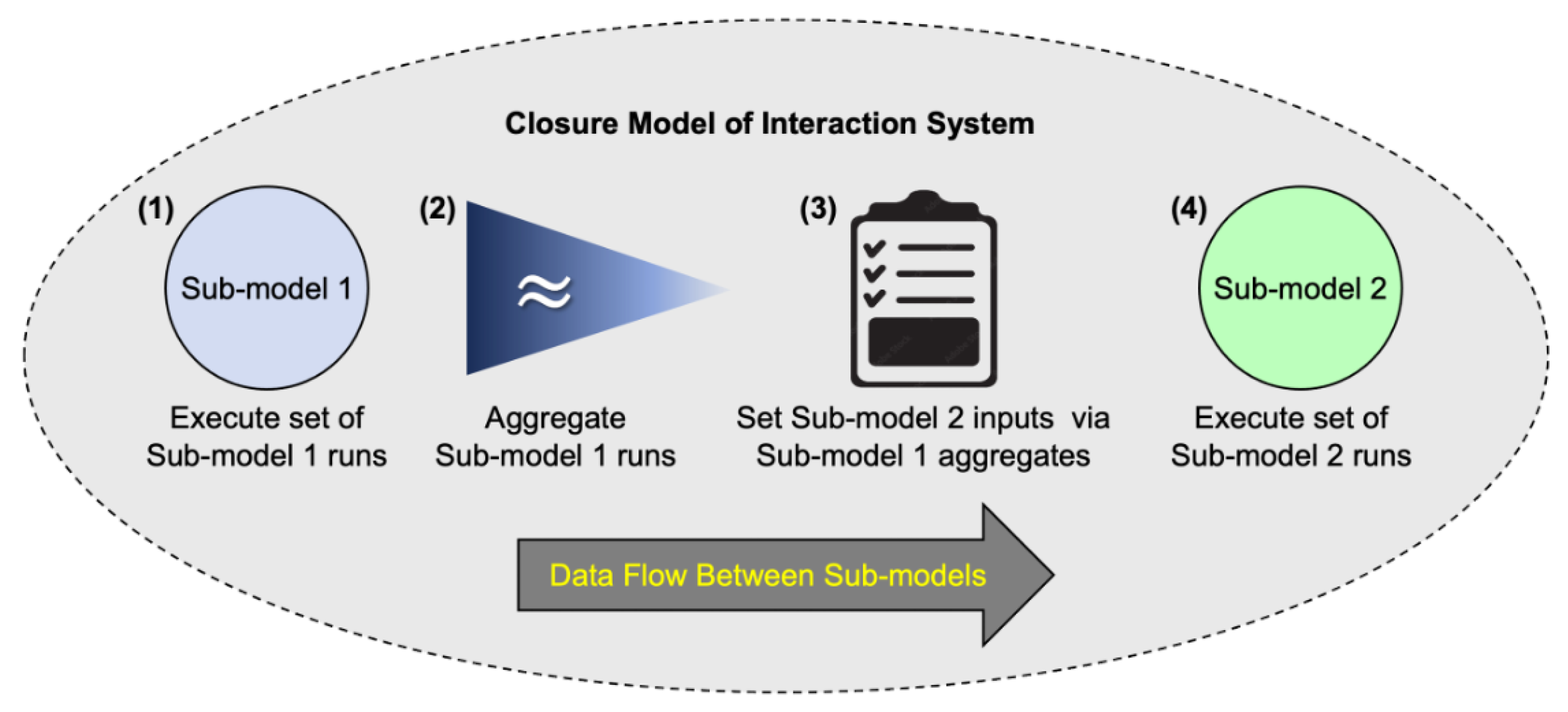
6. Analysis of a Simple System Model
- Model inputs and are specified.
- A set of experiments with set size is executed on with input parameters given by .
- The set of experiments executed on generates an output distribution which is aggregated to compute .
- A set of experiments with set size is executed on with input parameters given by and the computed .
- The set of experiments executed on generates an output distribution which is aggregated to compute .
7. Extension to Complex System Models
7.1. Additional Foundations
7.2. Sub-Model Interaction Patterns
7.2.1. Pattern 1: Interactions in Series
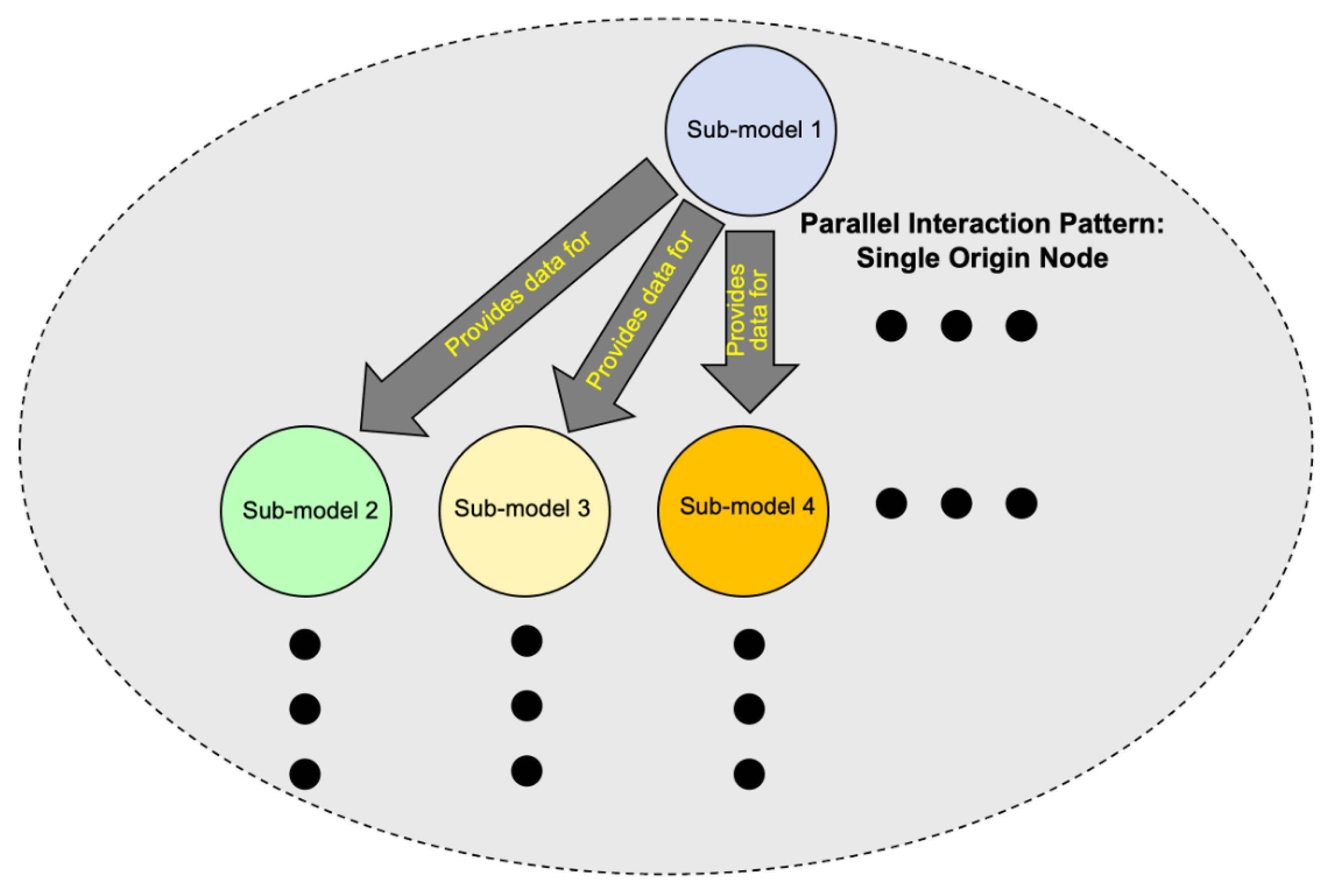
7.2.2. Pattern 2: Parallel Interactions Emanating from a Single Origin Node
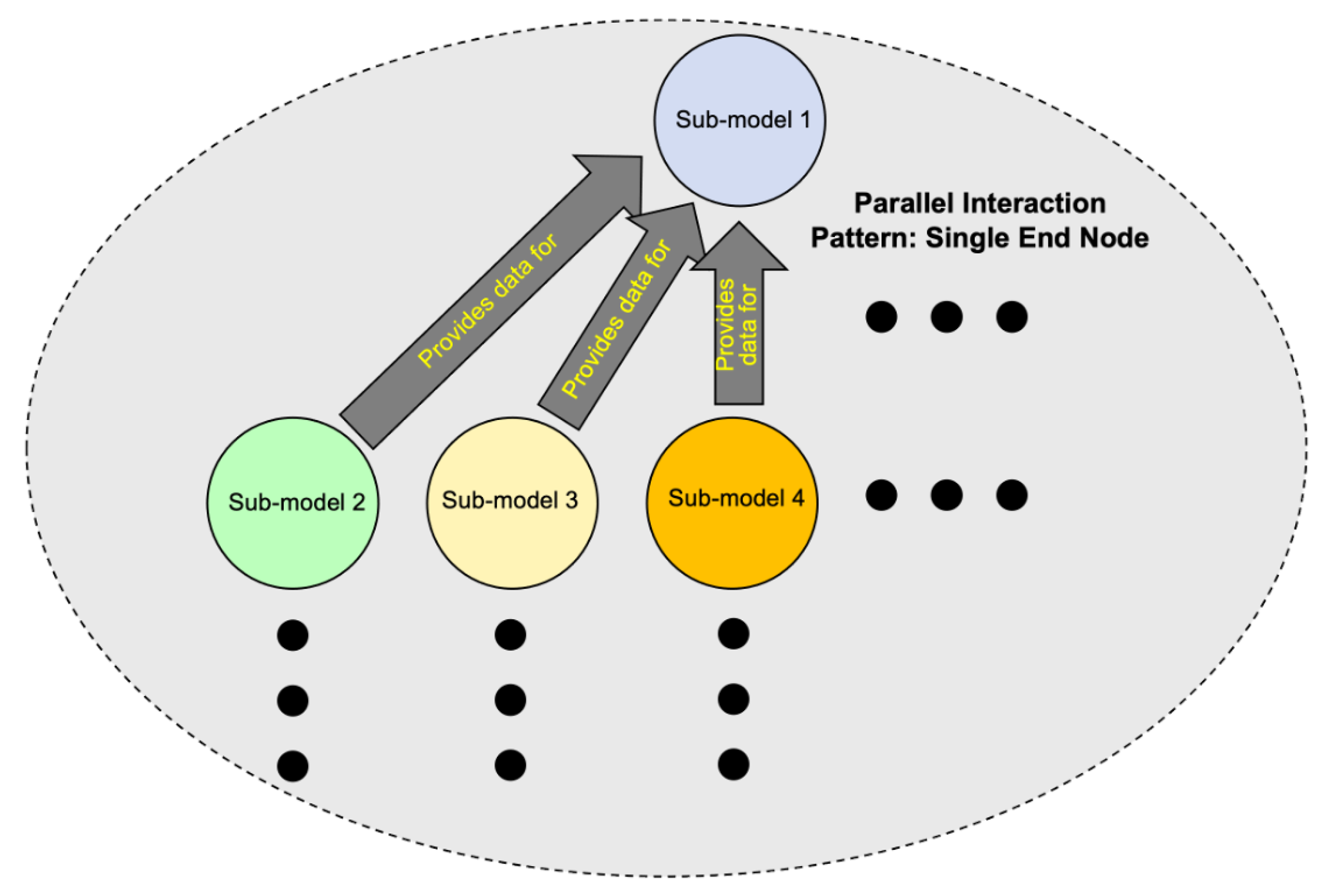
7.2.3. Pattern 3: Parallel Interactions Finishing at a Single End Node
7.2.4. Pattern 4: Parallel Interactions Emanating from a Single Origin-Node and Finishing at a Single End-Node
- Select either the parallel single origin node pattern (Section 7.2.2) or the parallel single end node pattern (Section 7.2.3) as a starting point for the computation.
- Temporarily ignore either the origin node or end node and its edges depending on which starting pattern is selected. That is, if the parallel single origin node pattern is selected as the starting pattern, then the end node and its edges are ignored. And vice versa if the parallel single end node pattern is selected as the starting pattern.
- Compute the pattern upper bound for the selected starting pattern using the appropriate co-simulation equations for that pattern (equations from either Section 7.2.2 or Section 7.2.3).
- Collapse all nodes and edges of the starting pattern into a single “composite” node representing the all nodes and edges of that pattern with associated computation time . Note that represents the upper bound computation time for all nodes and edges of the starting pattern.
- Construct a simpler interaction graph which connects the composite node with the temporarily ignored node by a single edge in the same direction as the previously ignored edges. Note that contains only two nodes and a single edge and is an instance of the serial pattern described in Section 7.2.1.
- Compute the upper bound of using Equation (20) (Section 7.2.1). This upper bound represents the final computation of for the original interaction graph and is given bywhere is the computation time for the starting pattern computed in Step 4 above and is the computation time of the remaining temporarily ignored node of .
7.3. A Generalized Algorithm
| Algorithm 1 General algorithm for computing upper bound computation time of a co-simulation model. |
|
8. Discussion
9. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siegenfeld, A.F.; Bar-Yam, Y. An introduction to complex systems science and its applications. Complexity 2020, 2020, 6105872. [Google Scholar] [CrossRef]
- Thurner, S.; Hanel, R.; Klimek, P. Introduction to the Theory of Complex Systems; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Camus, B.; Bourjot, C.; Chevrier, V. Considering a multi-level model as a society of interacting models: Application to a collective motion example. J. Artif. Soc. Soc. Simul. 2015, 18, 7. [Google Scholar] [CrossRef]
- Reine, R.; Juwono, F.H.; Sim, Z.A.; Wong, W.K. Cyber-Physical-Social Systems: An Overview. In Smart Connected World: Technologies and Applications Shaping the Future; Springer: Cham, Switzerland, 2021; pp. 25–45. [Google Scholar]
- Yin, D.; Ming, X.; Zhang, X. Understanding data-driven cyber-physical-social system (D-CPSS) using a 7C framework in social manufacturing context. Sensors 2020, 20, 5319. [Google Scholar] [CrossRef] [PubMed]
- Doostmohammadian, M.; Rabiee, H.R.; Khan, U.A. Cyber-social systems: Modeling, inference, and optimal design. IEEE Syst. J. 2019, 14, 73–83. [Google Scholar] [CrossRef]
- Dressler, F. Cyber physical social systems: Towards deeply integrated hybridized systems. In Proceedings of the International Conference on Computing, Networking and Communications (ICNC), Maui, HI, USA, 5–8 March 2018; pp. 420–424. [Google Scholar]
- Sheth, A.; Anantharam, P.; Henson, C. Physical-cyber-social computing: An early 21st century approach. IEEE Intell. Syst. 2013, 28, 78–82. [Google Scholar] [CrossRef]
- Baxter, G.; Sommerville, I. Socio-technical systems: From design methods to systems engineering. Interact. Comput. 2011, 23, 4–17. [Google Scholar] [CrossRef]
- Gomes, C.; Thule, C.; Broman, D.; Larsen, P.G.; Vangheluwe, H. Co-simulation: A survey. ACM Comput. Surv. 2018, 51, 49. [Google Scholar] [CrossRef]
- Wang, F.; Magoua, J.J.; Li, N. Modeling cascading failure of interdependent critical infrastructure systems using HLA-based co-simulation. Autom. Constr. 2022, 133, 104008. [Google Scholar] [CrossRef]
- Pedersen, N.; Lausdahl, K.; Sanchez, E.V.; Larsen, P.G.; Madsen, J. Distributed Co-Simulation of Embedded Control Software with Exhaust Gas Recirculation Water Handling System using INTO-CPS. In Proceedings of the 7th International Conference on Simulation and Modeling Methodologies, Technologies and Applications, Madrid, Spain, 26–28 July 2017. [Google Scholar]
- Oh, S.; Chae, S. A Co-Simulation Framework for Power System Analysis. Energies 2016, 9, 131. [Google Scholar] [CrossRef]
- Abad, A.-j.G.C.; Guerrero, L.M.F.G.; Ignacio, J.K.M.; Magtibay, D.C.; Purio, M.A.C.; Raguindin, E.Q. A simulation of a power surge monitoring and suppression system using LabVIEW and multisim co-simulation tool. In Proceedings of the International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management (HNICEM), Cebu, Philippines, 9–12 December 2015; pp. 1–3. [Google Scholar]
- Bian, D.; Kuzlu, M.; Pipattanasomporn, M.; Rahman, S.; Wu, Y. Real-time co-simulation platform using OPAL-RT and OPNET for analyzing smart grid performance. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Elsheikh, A.; Awais, M.U.; Widl, E.; Palensky, P. Modelica enabled rapid prototyping of cyber-physical energy systems via the functional mockup interface. In Proceedings of the Workshop on Modeling and Simulation of Cyber-Physical Energy Systems (MSCPES), Berkeley, CA, USA, 20 May 2013; pp. 1–6. [Google Scholar]
- Al-Hammouri, A.T. A comprehensive co-simulation platform for cyber-physical systems. Comput. Commun. 2012, 36, 8–19. [Google Scholar] [CrossRef]
- Cao, Q. Research on co-simulation of multi-resolution models based on HLA. Simulation 2023, 99, 515–535. [Google Scholar] [CrossRef]
- Roy, D.; Kovalenko, A. Biomolecular Simulations with the Three-Dimensional Reference Interaction Site Model with the Kovalenko-Hirata Closure Molecular Solvation Theory. Int. J. Mol. Sci. 2021, 10, 5061. [Google Scholar] [CrossRef]
- Baltussen, M.W.; Buist, K.A.; Peters, E.A.J.F.; Kuipers, J.A.M. Multiscale modelling of dense gas—Particle flows. Adv. Chem. Eng. 2018, 53, 1–52. [Google Scholar]
- Wagner, N.; Sahin, C.S.; Winterrose, M.; Riordan, J.; Hanson, D.; Peña, J.; Streilein, W.W. Quantifying the mission impact of network-level cyber defensive mitigations. J. Def. Model. Simul. 2017, 14, 201–216. [Google Scholar] [CrossRef]
- Samaey, G.; Lelièvre, T.; Legat, V. A numerical closure approach for kinetic models of polymeric fluids: Exploring closure relations for FENE dumbbells. Comput. Fluids 2011, 43, 119–133. [Google Scholar] [CrossRef]
- van der Hoef, M.A.; van Sint Annaland, M.; Deen, N.G.; Kuipers, J.A.M. Numerical simulation of dense gas-solid fluidized beds: A multiscale modeling strategy. Annu. Rev. Fluid Mech. 2008, 40, 47–70. [Google Scholar] [CrossRef]
- van der Hoef, M.A.; van Sint Annaland, M.; Andrews, A.T., IV; Sundaresan, S.; Kuipers, J.A.M. Multiscale modeling of gas-fluidized beds. Adv. Chem. Eng. 2006, 31, 65–149. [Google Scholar]
- Ahmed, R.; Shah, M.; Umar, M. Concepts of simulation model size and complexity. Int. J. Simul. Model. 2016, 15, 213–222. [Google Scholar] [CrossRef]
- Stockmeyer, L. Classifying the computational complexity of problems. J. Symb. Log. 1987, 52, 1–43. [Google Scholar] [CrossRef]
- Henriksen, J.O. Taming the complexity dragon. J. Simul. 2008, 2, 3–17. [Google Scholar] [CrossRef]
- Arthur, J.D.; Sargent, R.; Dabney, J.; Law, A.M.; Morrison, J.D. Verification and validation: What impact should project size and complexity have on attendant V&V activities and supporting infrastructure. In Proceedings of the WSC’99. 1999 Winter Simulation Conference, Phoenix, AZ, USA, 5–8 December 1999; pp. 148–155. [Google Scholar]
- Chwif, L.; Barretto, M.R.P.; Paul, R.J. On simulation model complexity. In Proceedings of the 2000 Winter Simulation Conference Proceedings, Orlando, FL, USA, 10–13 December 2000. [Google Scholar]
- Robinson, S. Modes of simulation practice: Approaches to business and military simulation. Simul. Model. Pract. Theory 2002, 10, 513–523. [Google Scholar] [CrossRef]
- Ward, S.C. Arguments for constructively simple models. J. Oper. Res. Soc. 1989, 40, 141–153. [Google Scholar] [CrossRef]
- Thompson, J.S.; Hodson, D.D.; Grimaila, M.R.; Hanlon, N.; Dill, R. Toward a Simulation Model Complexity Measure. Information 2023, 14, 202. [Google Scholar] [CrossRef]
- Sarjoughian, H.S. Restraining complexity and scale traits for component-based simulation models. In Proceedings of the Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 675–689. [Google Scholar]
- Yucesan, E.; Schruben, L. Complexity of simulation models: A graph theoretic approach. INFORMS J. Comput. 1998, 10, 94–106. [Google Scholar] [CrossRef][Green Version]
- Schruben, L.; Yucesan, E. Complexity of simulation models: A graph theoretic approach. In Proceedings of the 25th Conference on Winter Simulation, Los Angeles, CA, USA, 12–15 December 1993; pp. 641–649. [Google Scholar]
- Popovics, G.; Monostori, L. An approach to determine simulation model complexity. Procedia CIRP 2016, 52, 257–261. [Google Scholar] [CrossRef]
- Tolk, A. Interoperability and Composability: A Journey through Mathematics, Computer Science, and Epistemology. In Proceedings of the NATO MSG Symposium, NATO Report STO-MP-MSG-149, Lisbon, Portugal, 19–20 October 2017. [Google Scholar]
- Davis, P.K.; Anderson, R.H. Improving the composability of DoD models and simulations. J. Def. Model. Simul. 2004, 1, 5–17. [Google Scholar] [CrossRef]
- Zacharewicz, G.; Diallo, S.; Ducq, Y.; Agostinho, C.; Jardim-Goncalves, R.; Bazoun, H.; Wang, Z.; Doumeingts, G. Model-based approaches for interoperability of next-generation enterprise information systems: State of the art and future challenges. Inf. Syst.-Bus. Manag. 2016, 14, 495–519. [Google Scholar] [CrossRef]
- Geraci, A. IEEE Standard Computer Dictionary: Compilation of IEEE Standard Computer Glossaries; IEEE Press: New York, NY, USA, 1991. [Google Scholar]
- Page, E.H.; Opper, J.M. Observations on the complexity of composable simulation. In Proceedings of the 31st Conference on Winter Simulation: Simulation—A Bridge to the Future, Phoenix, AZ, USA, 5–8 December 1999; pp. 553–560. [Google Scholar]
- Yilmaz, L.; Oren, T.I. Exploring agent-supported simulation brokering on the semantic web: Foundations for a dynamic composability approach. In Proceedings of the 2004 Winter Simulation Conference, Washington, DC, USA, 5–8 December 2004. [Google Scholar]
- Tolk, A.; Bair, L.J.; Diallo, S.Y. Supporting Network Enabled Capability by extending the Levels of Conceptual Interoperability Model to an interoperability maturity model. J. Def. Model. Simul. 2013, 10, 145–160. [Google Scholar] [CrossRef]
- Diallo, S.Y.; Padilla, J.J.; Gore, R.; Herencia-Zapana, H.; Tolk, A. Toward a formalism of modeling and simulation using model theory. Complexity 2014, 19, 56–63. [Google Scholar] [CrossRef]
- Gander, M.J.; Al-Khaleel, M.; Ruchli, A.E. Optimized waveform relaxation methods for longitudinal partitioning of transmission lines. IEEE Trans. Circuits Syst. 2008, 56, 1732–1743. [Google Scholar]
- Jackiewicz, Z.; Kwapisz, M. Convergence of waveform relaxation methods for differential-algebraic systems. SIAM J. Numer. Anal. 1996, 33, 2303–2317. [Google Scholar] [CrossRef]
- White, J.A.; Odeh, F.; Vincentelli, A.S.; Ruehli, A.E. Waveform Relaxation: Theory and Practice; Electronics Research Laboratory, College of Engineering, UCB: Berkeley, CA, USA, 1985. [Google Scholar]
- Bouanan, Y.; Zacharewicz, G.; Vallespir, B. Discrete Event System Specification-Based Framework for Modelling and Simulation of Propagation Phenomena in Social Networks: Application to the Information Spreading in a Multi-Layer Social Network. Simulation 2019, 95, 411–427. [Google Scholar] [CrossRef]
- Sanz, V.; Urquia, A. Combining PDEVS and Modelica for describing agent-based models. Simulation 2023, 99, 455–474. [Google Scholar] [CrossRef]
- Tiller, M. Introduction to Physical Modeling with Modelica; Springer Science and Business Media: New York, NY, USA, 2012; Volume 615. [Google Scholar]
- Xu, X.; Dou, Y.; Ouyang, W.; Jiang, J.; Yang, K.; Tan, Y. A product requirement development method based on multi-layer heterogeneous networks. Adv. Eng. Inform. 2023, 58, 102184. [Google Scholar] [CrossRef]
- Myers, G.J. Reliable Software through Composite Design; Petrocelli-Charter: New York, NY, USA, 1975. [Google Scholar]
- Balci, O.; Ball, G.L.; Morse, K.L.; Page, E.; Petty, M.D.; Tolk, A.; Veautour, S.N. Model reuse, composition, and adaptation. In Research Challenges in Modeling and Simulation for Engineering Complex Systems; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Cellier, F.E.; Kofman, E. Continuous System Simulation; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Czekster, R.M.; Morisset, C.; Clark, J.A.; Soudjani, S.; Patsios, C.; Davison, P. Systematic review of features for co-simulating security incidents in cyber-physical systems. Secur. Priv. 2021, 4, e150. [Google Scholar] [CrossRef]
- Camus, B.; Bourjot, C.; Chevrier, V. Combining DEVS with multiagent concepts to design and simulate multi-models of complex systems. In Proceedings of the Symposium on Theory of Modeling and Simulation: DEVS Integrative M&S Symposium. Society for Computer Simulation International, Alexandria, VA, USA, 12–15 April 2015. [Google Scholar]
- Camus, B.; Galtier, V.; Caujolle, M.; Chevrier, V. Hybrid Co-simulation of FMUs using DEV and DESS in MECSYCO. In Proceedings of the Symposium on Theory of Modeling and Simulation—DEVS Integrative M&S Symposium (TMS/DEVS 16), Pasadena, CA, USA, 3–6 April 2016. [Google Scholar]
- Denil, J.; De Meulenaere, P.; Demeyer, S.; Vangheluwe, H. DEVS for AUTOSAR-based system deployment modeling and simulation. Simulation 2017, 93, 489–513. [Google Scholar] [CrossRef]
- Nutaro, J. Designing power system simulators for the smart grid: Combining controls, communications, and electro-mechanical dynamics. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–5. [Google Scholar]
- Quesnel, G.; Duboz, R.; Versmisse, D.; Ramat, É. DEVS coupling of spatial and ordinary differential equations: VLE framework. In Proceedings of the Open International Conference on Modeling and Simulation, Las Vegas, NV, USA, 27–30 June 2005; Volume 5, pp. 281–294. [Google Scholar]
- Wagner, N.; Sahin, C.S.; Hanson, D.; Peña, J.; Vuksani, E.; Tello, B. Quantitative analysis of the mission impact for host-level cyber defensive mitigations. In Proceedings of the 49th Annual Simulation Symposium, Pasadena, CA, USA, 3–6 April 2016; pp. 1–8. [Google Scholar]
- Dekking, F.M.; Kraaikamp, C.; Lopuhaä, H.P.; Meester, L.E. A Modern Introduction to Probability and Statistics: Understanding Why and How; Springer: London, UK, 2005. [Google Scholar]
- Sawilowsky, S.S. You think you’ve got trivials? J. Mod. Appl. Stat. Methods 2003, 1, 218–225. [Google Scholar] [CrossRef]
- Davis, P.K.; Hillestad, R. Aggregation, disaggregation, and the challenge of crossing levels of resolution when designing and connecting models. In Proceedings of the 4th Annual Conference on AI, Simulation and Planning in High Autonomy Systems, Tucson, AZ, USA, 20–22 September 1993; pp. 180–188. [Google Scholar]
- Zeigler, B.P.; Muzy, A.; Kofman, E. Abstraction: Constructing Model Families. In Theory of Modeling and Simulation: Discrete Event & Iterative System Computational Foundations; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]




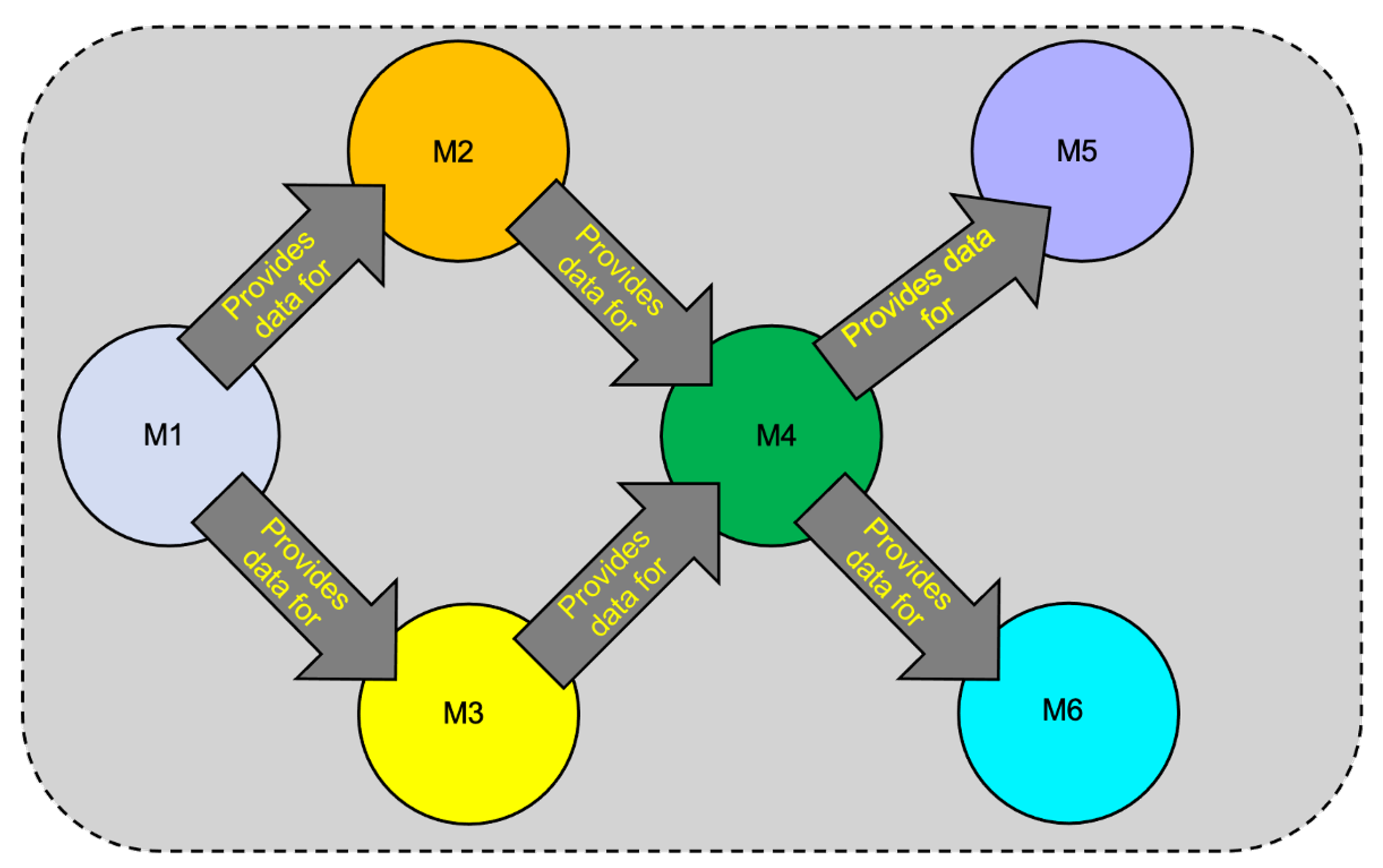


| Interaction Pattern | Description |
|---|---|
| Serial Pattern | Sub-model interactions that occur in serial. |
| Parallel Single Origin Pattern | Sub-model interactions that occur in parallel and start from a single origin sub-model. |
| Parallel Single End Pattern | Sub-model interactions that occur in parallel and end at a single ending sub-model. |
| Parallel Single-Origin-And-End Pattern | Sub-model interactions that occur in parallel, start from a single origin sub-model, and end at a single ending sub-model. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wagner, N. Comparing the Complexity and Efficiency of Composable Modeling Techniques for Multi-Scale and Multi-Domain Complex System Modeling and Simulation Applications: A Probabilistic Analysis. Systems 2024, 12, 96. https://doi.org/10.3390/systems12030096
Wagner N. Comparing the Complexity and Efficiency of Composable Modeling Techniques for Multi-Scale and Multi-Domain Complex System Modeling and Simulation Applications: A Probabilistic Analysis. Systems. 2024; 12(3):96. https://doi.org/10.3390/systems12030096
Chicago/Turabian StyleWagner, Neal. 2024. "Comparing the Complexity and Efficiency of Composable Modeling Techniques for Multi-Scale and Multi-Domain Complex System Modeling and Simulation Applications: A Probabilistic Analysis" Systems 12, no. 3: 96. https://doi.org/10.3390/systems12030096
APA StyleWagner, N. (2024). Comparing the Complexity and Efficiency of Composable Modeling Techniques for Multi-Scale and Multi-Domain Complex System Modeling and Simulation Applications: A Probabilistic Analysis. Systems, 12(3), 96. https://doi.org/10.3390/systems12030096





