Abstract
The dynamics of medical resource demand during public health crises pose significant challenges to emergency supply chain management, particularly within an evolving and complex social environment. To explore this, the interactive effects of information diffusion and virus spreading on medical resource demand are investigated using a novel three-layer coevolution “information–epidemic–resource” model through Markov process simulations. The study firstly identifies eight factors influencing demand fluctuations in terms of some city characteristics, such as media exposure, consistency of public opinion, self-protection level, and restrictive protection level, while categorizing resources into individual holdings and centralized storage. Then, extensive simulations are examined to elucidate the impact of these factors. The results reveal that various city characteristics can affect fluctuation in demand for both individual holdings and centralized storage. Inaccurate media information tends to inflate fluctuations, while higher public opinion consistency can reduce it. Reinforcing self-protection decreases the demand fluctuations of individuals, and effective restrictive protections can reduce fluctuations in centralized resource storage. Moreover, an analytical simulation of various city scenarios, underpinned by statistical data from selected Chinese and German cities, demonstrates that distinct city characteristics significantly influence medical resource demand changes during epidemics. This underscores the importance of tailoring emergency medical supply strategies to the specific developmental traits of different countries and cities. This study provides valuable insights to researchers, governments, and enterprises, enhancing their preparedness and response for emergency supply chain disruptions.
1. Introduction
The complexity and uncertainty of modern society paved the way for unforeseen events, such as the H1N1 influenza pandemic, the Ebola epidemic, COVID-19 and some other major public health emergencies (MPHEs). These emergencies profoundly impacted both global and local supply chains and, more importantly, public health. Epidemics induce volatilities in the supply of and demand for commodities, which are reflected in prices [1,2]. Banlangen granules, a common Traditional Chinese Medicine (TCM) used to treat colds, once saw a one-day sales increase of 3130 percent in China after a top respiratory disease expert suggested its potential to inhibit coronavirus [3]. Due to the overwhelming demand, its price also increased accordingly. Effective response and mitigation strategies for these emergencies need a sufficient supply of essential medical protective articles, medications, and other essential items. However, many countries affected by these outbreaks have struggled with shortages and surpluses of these vital resources [4,5], exposing inherent deficiencies and vulnerabilities in emergency preparedness. Additionally, the determinants affecting material supply and demand during epidemics have become increasingly complex. Temperature and population density [6], government policies [7], public perceptions and personal protective equipment training [8,9], availability of testing and treatment facilities [10] and other factors indirectly affect the number of infected cases, and subsequently amplify the requirement or reduce provision for resources [11].
This study investigates the dynamics of demand fluctuation during epidemics, with a particular focus on how information dissemination and human movements amplify these fluctuations. As its name suggests, demand fluctuation can be defined as variations in the demand for anti-epidemic products, including rapidly changing and often surging demands due to uncertainties in viral transmission, public behavior, government interventions and so on. The influencing mechanism of demand fluctuation is explored utilizing complex network theory. By integrating concepts from network science, epidemic modeling, and information diffusion, we seek to unravel the underlying mechanisms driving resource demand fluctuation and identify critical factors influencing resource demands during epidemics. Considering varying parameters related to information diffusion, epidemic spreading and resource allocation, extensive numerical simulations are processed to assess their impact on demand dynamics. Understanding the interplay between information diffusion and virus spreading is key to developing more effective strategies to mitigate the impact of demand fluctuation in epidemics and enhance preparedness for future outbreaks. Consequently, the findings of this research are expected to provide significant insights for epidemic control, emergency supply chain management and public health policymaking. This work not only addresses the immediate challenge of fluctuating resource demands during health crises but also contributes to a broader understanding of the systemic responses required in complex network environments.
The rest of the paper is organized as follows: a comprehensive literature review is conducted in Section 2; Section 3 defines the factors and notations, outlines the methodology of the two-layer and three-layer models; Section 4 processes extensive simulations to verify the hypotheses and analyze the city scenarios, and the theoretical and practical significant for this study are discussed; finally, the conclusion is given in Section 5.
2. Literature Review
This paper adopted a narrative and integrative approach to thoroughly explore topics related to our research, including “Fluctuation of Resources in Supply Chain Management”, “Information Diffusion in Epidemics”, “Virus Control Behaviors in Epidemics” and “Propagation Models for Information and Virus Spreading”. We utilized databases like Web of Science and Google Scholar, searching keywords such as “demand fluctuations”, “epidemic impact on supply chains”, “information diffusion during pandemics”, “multi-layer networks” and “epidemics” among others. By reviewing the existing literature, this section clarifies the concept of “demand fluctuation” during epidemics and introduces four characteristics that can influence information diffusion and virus spreading, including “media exposure”, “consistency of public opinion”, “self-protection level” and “restrictive protection level”. These characteristics will be further discussed in Section 4.2.
2.1. The Fluctuation of Resources in Supply Chain Management
Scholars have discussed the significance of material security in supply chain management from various perspectives, such as “Demand forecast for disaster relief materials [12,13]”, “matching supply with demand in health care management [14,15]” and “demand fluctuation [16]”. Both the change in supply and volatile demand have significant impacts on the stable operation [17]. Demand fluctuation also generates erratic bullwhip effects [18] on supply chains, and disruption of supply chain operations [19] in pandemics. Therefore, understanding the mechanisms behind medical resource demand fluctuations is of significant value for both supply chain management and healthcare. However, current research on demand fluctuation mainly analyzes the bullwhip effect in the retail industry, using parameters such as random demand, marketing prices, and random delivery times to measure material fluctuation, and the research results are mainly based on mathematical formula derivation [20,21]. This tells us about the academic need for exploring additional theories and methods to support the study of demand fluctuation and to visualize the material fluctuation process. Moreover, protective and cure-focused resources are two primary types of epidemic prevention materials. Protective resources aim to block the transmission route of the virus, safeguarding the public and medical staff, while cure-focused resources are employed to treat infected patients, alleviate symptoms and improve recovery rates [22]. Protective resources include masks, medical goggles, protective gloves and clothing, etc.; cure-focused resources mainly include vaccines, drugs, ventilators and other medical equipment [23].
2.2. The Information Diffusion in Epidemics
The topic of information propagation related to epidemics has also received widespread academic attention in the past few years. A key focus is the impact of media coverage on the public’s perception of disease information. Edition et al. proposed that extensive and accurate media reporting on infectious diseases can significantly enhance awareness and aid in preventing disease transmission [24]. However, information overload can easily lead to the sharing of unverified information [25]. Meanwhile, researchers confirm that people were susceptible to the influence of social media during the COVID-19 crisis, engaging in panic-buying behavior driven by uncertainty and insecurity, which further triggers changes in demand [26]. Hoarding personal protective equipment and daily consumer goods is a common response to the uncertainty in the supply of essential commodities [27], which can alleviate people’s anxiety [28]. Additionally, studies have shown that the social context influences the impact of information dissemination on epidemic spread, and there is a significant asymmetry in information dissemination between traditional and emerging media [29]. Furthermore, Winkielman and Nowak [30] highlighted the influence of information consistency on trust by reviewing that in the field of science [31] and law [32]. Given this, the paper highlights the level of media exposure as a crucial factor in spreading both accurate and inaccurate information. This paper also emphasizes that public trust in outbreak-related information is influenced not just by the content itself but also by the consistency of the different opinion fields. The concept of “consistency of opinion” is introduced in this study to describe the alignment between information disseminated by authoritative sources (such as the CDC and WHO) and views expressed by alternative media or individuals (such as blogs and social media accounts). Higher consistency can contribute to reducing the spread and facilitating the cessation of rumors, but only if the consistency is based on accurate and reliable information.
2.3. The Virus Control Behaviors in Epidemics
Various studies have examined the influence of human behavior on virus transmission and the effectiveness of prevention strategies. For example, unconstrained social interactions can dramatically increase epidemic spreading [33], while non-pharmaceutical interventions based on sustained physical distancing can reduce the magnitude of the epidemic peak [34]. What is more, factors such as “socially and economically vibrant”, “relatively young population” and “densely populated and traditional” have significant explanatory powers for the spread of the COVID-19 pandemic. This finding further suggests that countries characterized by vibrant economies, social and cultural activities, dense populations and traditional practices should implement strict action restrictions early on to mitigate the potential occurrence of a major infectious disease outbreak [35]. Governmental anti-pandemic policies, such as population mobility restrictions, effectively reduced the number of COVID-19 infection cases and deaths from it [36]. Therefore, this study categorizes the measures that can potentially reduce virus spread and associated demand fluctuation into two groups: “Self-protection measures” and “Restrictive protection”. Self-protection refers to individual actions taken voluntarily to safeguard oneself and others from the transmission and impact of an epidemic. Restrictive protection measures are policies or directives implemented at a regional or national level to control and mitigate the spread of an epidemic. These measures are typically mandated by public health authorities or government entities.
2.4. Classical Propagation Models and Network Propagation Models
Propagation dynamics models are foundational in our study for explaining the spread of information and diseases. In addition to classical propagation models, the network propagation models have also garnered significant attention from scholars in recent years. Ding, et al. (2021) established an SIQR model to restrain rumor spreading, considering the effects of truth propagation and measures like warnings and awareness [37]. Xian et al. (2020) developed a DISR model for the dynamic spread of rumors in multiplex networks, with the “D” representing users blocked from accessing the rumor [38]. An SEI information diffusion model was constructed to explore the transmission of rumor in social networks, defining the stages of information diffusion as known, known but not spread and spreading. They also verified the feasibility of transformation from non-adopter to thinker, and to adopter [39,40]. The exploration of networks serves an important role in enhancing propagation models. Integrating Interpretative Structural Modeling (ISM) with complex network theory has been proposed to create models that align more accurately with real-world logic [41].
Multilayer network modeling, extending beyond single networks, effectively captures complex propagation dynamics. In epidemiology, multiplex networks have been used to simulate COVID-19 spread. This approach finds application across physics, social sciences and engineering, based on its solid grounding in statistical physics [42]. Table 1 summarizes epidemic-related multilayer network studies, categorized by network layers and patterns. Research primarily focuses on two-layer networks, including “two virus networks”, “one information network plus one virus network” and “one virus network plus one resource network”. Jiang and Zhou (2018) studied the impact of resource control on virus transmission but did not treat resources as a separate network layer [43]. Sun et al. (2022) treated resources as a separate layer but only considered the transition of resources between two types of nodes, those with resources (R-Type) and those without resources (N-Type) [44]. A few studies established three-layer networks, mainly in the “information + virus + resource” and “anti-virus + virus1 + virus2” patterns. For instance, Wang et al. (2021) constructed a three-layer network with resource allocations as the third layer [45]. They investigated not only the suppress and worse effects of information diffusion on the epidemic spreading, but also the influence of different kinds of resources on the interplay between information and epidemic. Moreover, some studies have developed models with more than three layers. For example, Scabini et al. (2021) designed a six-layer model encompassing home, work, transport, school, religion and random layers to study virus transmission during an epidemic [46]. Li et al. (2021) established a 1+D-layer model, consisting of one layer of information network and D layers of virus networks, where D represents that the connection preference between nodes in the virus network is changing [47].

Table 1.
Literature about multilayer networks applied to epidemics.
2.5. Summary
Compared to the research articles mentioned above, our paper emphasizes that the dissemination of inaccurate information could trigger panic (in the information layer), and then lead people to hoard supplies from both neighbors and the central storage (in the resource layer). In addition to differentiating materials in terms of their effectiveness and efficiency as Wang et al. (2021) did in their paper, we also consider the resource exchange between individual holdings and the resource distribution from centralized storage [45]. More importantly, to the best of our knowledge, previous multilayer network studies have paid little attention to resource fluctuations, even though they have considered the effect of anti-epidemic supplies on the interactive spread of information and viruses. In summary, this study identifies important factors on information and human behavior that influence information dissemination and virus transmission, which in turn may affect the demand fluctuations. Then, we construct an information–epidemic–resource coevolution model grounded in complex network theory (as shown in Figure 1), aiming to investigate the demand fluctuation of different material types, and contribute to a deeper understanding of demand dynamics during epidemics.
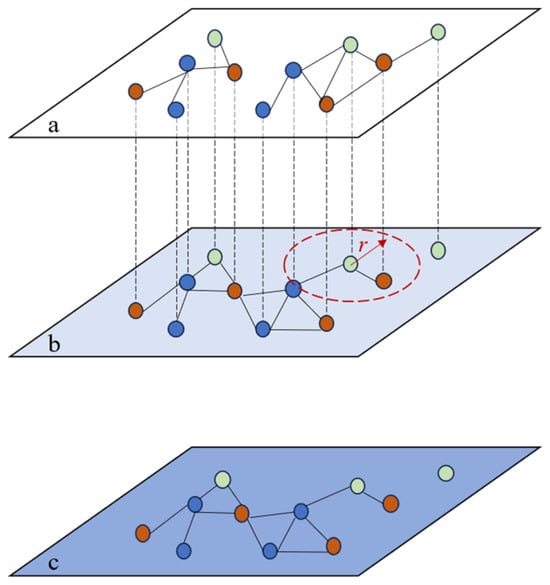
Figure 1.
The three-layer coevolution proposed in this study. The nodes symbolize individuals in the system and correspond one-to-one across the three layers. Layer (a) represents the information diffusion dynamic, and the edges indicate that news can be transmitted between two nodes, which is not influenced by the physical contact distance in the real world. Layer (b) illustrates the epidemic spread dynamic, and the radius r represents people’s short move distance. If the distance between two points is less than r, there will be a physical contact between these two nodes in the real world and the virus may spread. A node is connected to its neighboring nodes by edges. Layer (c) represents the resource allocation dynamic, and the edges indicate that anti-epidemic resources are shared amongst neighboring nodes.
3. Mathematical Models
3.1. Parameters and Notations Definition
This paper considers two forms of resource reserves: individual holdings and centralized storage. The number of individual holdings at time k + 1 is defined as the amount of medical resource held by each individual after the resource allocation process during the k time-step. The number of centralized storage refer to the number of medical resources that are centrally managed and controlled by a country or a region, which also changes over time.
To quantify the performance of these resources, we introduce two parameters: Resource Efficacy and Resource Efficiency. Resource Efficacy is measured on a scale from 0 to 1 that represents the performance of the material in terms of its ability to protect against the spread of the epidemic (protection performance) and its ability to effectively treat or address the impact of the epidemic (treatment performance). This concept aligns with the definitions provided by Wang et al. (2021) [45]. Resource Efficiency measures the influence of supply quantity on treatment success rates; higher values indicate a stronger reliance on ample supplies for improved treatment outcomes.
Additionally, this study identifies eight parameters that influence the information diffusion and epidemic spreading in the information–epidemic–resource coevolution model, detailed as follows:
- Information Diffusion Rate: the diffusion rate of normal information about the epidemic, such as the existence of the virus and the international public health alert of the virus. Media exposure plays a significant role in determining the speed and extent of information diffusion.
- Information Forgetting Rate: the forgetting rate of normal information about the epidemic. Individuals may forget or lose interest in certain information over time.
- Inaccurate Information Diffusion Rate: the diffusion rate of false or misleading representations and information about the epidemic. Media exposure and consistency of public opinion can drive the diffusion of inaccurate or false information.
- Inaccurate Information Forgetting Rate: the forgetting rate of inaccurate information. Similar to normal information, inaccurate information can be forgotten over time, and it can be influenced by the consistency of public opinion.
- Short Move Probability: the likelihood that individuals will engage in short-range movements within their local environment, such as hanging out in their neighborhood or going to a nearby grocery, which can be influenced by the self-protection level of individuals.
- Long Travel Probability: the likelihood of individuals engaging in long-distance movements, such as traveling to different regions or countries, which can also be influenced by the self-protection level of individuals.
- Short Move Distance: the average distance individuals move during short-range movements, which can be influenced by the level of restrictive protection measures implemented by regional or national authorities.
- Long Travel Distance: the average distance individuals travel during long-distance movements, which can also be influenced by the level of restrictive protection.
For more notations and their definitions in this paper, please see Table 2 below.

Table 2.
Notation definitions.
3.2. Information–Epidemic Two-Layer Model
This two-layer model is developed on a scenario that the virus spreading in the region is causing panic among the residents. An information diffusion model is established to track the dynamic of virus-related information, and an infectious disease model is developed to understand the dynamic of the virus’s spread. The dynamics and interactions of this two-layer complex network are analyzed using the Markov chain (MMC) theory. Some studies have verified the performance of this method in the multi-layer network study [45,57,58].
As shown in Figure 2, a U-A-I-U information diffusion model is established in the information diffusion layer. U is represented as unaware status, and individuals with U do not know any information about the spreading virus; A is for aware status and individuals with A know the existence of the spreading virus; Ia is for the inaccurate information affected status and individuals with Ia are affected by this inaccurate information and could spread inaccurate information of the virus with some probability to their neighbor nodes in the information layer. For virus spreading, we use an S-I-R model, which is a very typical and well-proven infectious disease model. S represents suspected, Ib represents infected and R represents recovered. This paper has described the advantages of applying complex networks to propagation dynamics problems, which can be reflected in Figure 2. The actual information diffusion rate , actual inaccurate information diffusion rate and actual virus spread rate are functions related to both time and the adjacency matrix or based on Equation (7).
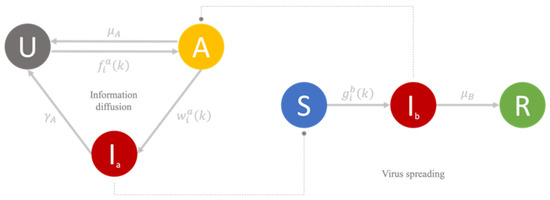
Figure 2.
Information–epidemic coevolution model.
The MMC equations for the information layer can be shown as follows. Regarding the superscripts in the equations, uppercase letters denote the state (U/A/Ia, S/Ib/R), whereas lowercase letters indicate the layer (layer a/layer b). For instance, represents the probability that node i is in the Unaware (U) state in layer a (the information layer) at time .
The MMC equations for the epidemic layer are as follows:
where
According to Equations (1)–(9), the system consists of six states: US (U in the information layer and S in the epidemic layer, below are the same), UR, AS, AI, AR and IS. Switching to A or Ia in the information layer, and to Ib in the epidemic layer, requires that the individual has at least one neighbor node with the corresponding status (Equations (1), (2), (4) and (5)). The recovery rate is influenced by the amount of material held by individuals in each time step (Equation (8)). The dotted lines in Figure 2 means that the nodes will be in aware status (A) in the information layer as soon as they become infected in the epidemic layer in a time step, and the nodes must be in suspected in the epidemic layer if they are inaccurate-information-affected nodes (Ia) in the information layer. Moreover, in the epidemic layer, individuals are likely to take a short or long move within a single time step, but infected individuals are restricted from the long-travel behavior. The settings for this random movement are reflected in the code, and the specific MATLAB program for this part can be found in Algorithm A1 of Appendix A. Above shows how the information layer interacts with the epidemic layer.
3.3. The Resource Layer
The three-layer model proposed in this paper can be simply described as adding a resource allocation model to the previously mentioned two-layer model. As for the resource allocation model, individuals request and/or share materials from and/or to their neighbors in one time step based on their status in time k; then, the material amount for each individual in time k + 1 can be updated using the following coupled MMC equations:
These coupled MMC equations were inspired by Wang et al. (2021) in their UAU-SIS model [45], which is for the resource allocation between individuals. We additionally set an equation for the resource distribution from the centralized storage:
In the resource allocation layer, there is an initial value of individual holdings for each node, and it is set so that one unit each node begins with an initial value of the number of individual holdings set at one unit ; and the initial value of centralized material storage has a multiplicative relationship with the sum of the individual material holdings. At each time step , the individuals with status of US, UR, AS and AR can share the resource with their neighbors and will equally divide the supplies they currently hold among their neighbors who ask for them and themselves (Equations (10)–(13)). Similarly, at each time step , individuals with a status of AS, AI and IS will request resources from their neighbors (Equations (13)–(15)). Beyond neighborly sharing, individuals with a status of AI and IS will obtain one unit of supplies from the centralized storage (Equations (14) and (15)). For example, local government organizes the distribution of epidemic prevention supplies to the people who need the resources most. According to Kar et al. (2023), this study postulates that individuals influenced by inaccurate information, represented by the status IS, are predisposed to hoard supplies [62]. Thus, the number of medical resources acquired by individuals in IS is set to be times that of other individuals (Equation (15)). Finally, the centralized storage will increase by in each time step until the virus is cleared in the system, which is called the automatic replenishment rate (Equation (16)), but after the virus is cleared, the centralized material storage will not be replenished automatically. Combined with the description of ‘amount of resource held by each individual affects their recovery rate’ as mentioned in Equation (8), this is how the resource layer interacts with the information layer and the epidemic layer; that is, how the three-layer network model evolves collectively.
4. Simulation and Results
4.1. Explanations
The simulation of the information–epidemic–resource three-layer coevolution process is performed on an Intel Core i9-12900K CPU. This section shows the implement of the three-layer model and visualizes the dynamic. There are 1000 individuals in this simulation (nodes = 1000). In the information layer, a Barabási–Albert (BA) scale-free network is established using a preferential attachment mechanism (Figure A1 in Appendix A). This network obeys power–law distribution as many complex networks in the real world do, and it is widely used in information dissemination research [63]. This BA scale-free network begins with three nodes. Each new node is connected to two existing nodes with a probability, and the initial connection is random. The links between every two points represent the possibility of information sharing between them.
In the epidemic layer (please refer to Figure A2 in Appendix A), each node could move 0.1 shortly ( = 0.1) with a probability of 0.8 ( = 0.8) or travel a long distance of 0.5 ( = 0.5) with a probability of 0.1 ( = 0.1) in each time step. The two nodes whose distance is no more than 0.07 can be connected (r = 0.07). The time delay from infection to recovery is seven time steps ( = 7).
In the resource layer, we set the resource as protective () not cure-focused, and the Resource Efficiency is very high (). The automatic replenishment rate of centralized material storage is 0.01 in this case. The initial number of resources is 1 for each individual, and the initial number of centralized storage is 20 times the total amount of material held by the individuals. The detailed parameter settings are summarized in Appendix A Table A1.
The explanations below can fully and clearly explain the simulation results shown in Figure 3: the number of infected people is low at the beginning and the centralized resources storage increases due to the automatic replenishment mechanism (area a). As the number of infected individuals and inaccurate information spreaders increase, the centralized resources storage gradually decreases (area b). In the later stages of the epidemic, the number of infected nodes decreases, and there are more and more recovered persons, so the centralized resources storage increases (area c). After the virus is cleared, the centralized resources storage no longer undergoes automatic replenishment. However, individuals who believe and spread inaccurate information continue hoarding supplies from the centralized resources storage, causing it to decrease (area d). The model assumes that individuals who are infected and have recovered do not disseminate inaccurate information. For instance, if infected persons believe the rumor that “drinking alcohol kills COVID-19”, they will try it out and find it ineffective, then they are unlikely to propagate this inaccurate information further. Consequently, the spread of inaccurate information is initially high but begins to diminish as the number of recovered individuals increases. The recovery period is set as 7 days, after which the density of inaccurate information spread begins to decline (area e). The reason that there are always a small number of inaccurate information propagators is that there are still some uninfected individuals until the end of the virus spreading in this simulation (area f). Most people have individual material holdings fluctuations at the beginning of the virus spreading. This fluctuation is going down as the density of those recovered increases and the density of inaccurate information spreaders decreases (area g). Although there are no infected individuals in the second half of the simulation, few individuals still exchange their resources disturbed by the inaccurate information, which leads to fluctuations in individual material holdings (area h). The detailed differences in the fluctuation of individual material holdings at different stages are shown in Figure 4.
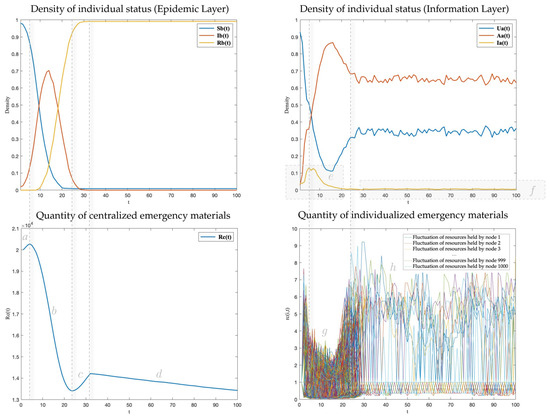
Figure 3.
Simulation results.
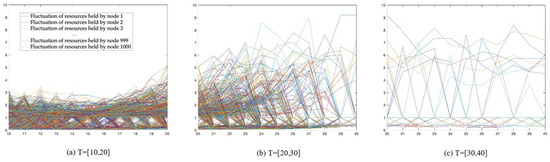
Figure 4.
Fluctuation of resources held by each individual in time step from 10 to 40. The fluctuation situation of individual material holdings varies at different stages: (1) when T = [10,20], the number of individuals having material fluctuations is large, but all fluctuations are low; (2) when T = [20,30], the number of individuals having material fluctuations is large, and most fluctuations are low but a few are high; (3) when T = [30,40], the number of individuals having material fluctuations is very small, but a few individuals have high fluctuations.
We further explored the implications of network topology by analyzing results under Watts–Strogatz (WS) and Erdős–Rényi (ER) network structures. Our findings indicate that variations in network topology do not alter the fundamental conclusions of this study. For detailed analysis, refer to Appendix B.
4.2. Hypotheses and Simulations
The above explanation reveals several noteworthy phenomena of the fluctuation. To quantify the fluctuation, the Standard Deviation (or ) is employed, which is a commonly used and understood quantitative metric to measure the variation or fluctuation of the price and energy resource [64,65]. In the context of centralized storage, fluctuation refers to the standard deviation of the number of materials stored during each time step. For individual holdings, fluctuation is computed as the mean standard deviation across all individuals during each time step. According to the literature review in Section 2, some hypotheses are proposed concerning “media exposure”, “the consistency of public opinion”, “self-protection level” and “restrictive protection level” as follows:
Hypothesis 1.
The larger the media exposure, the higher the fluctuation in individual material holdings and centralized material storage.
Hypothesis 2.
The higher the consistency of public opinion, the lower the fluctuation in individual material holdings and centralized material storage.
Hypothesis 3.
The lower the self-protection level, the higher the fluctuation in individual material holdings, and the centralized material storage does not fluctuate significantly.
Hypothesis 4.
The lower the restrictive protection level, the higher the fluctuation in centralized material storage, and the individual material holding does not fluctuate significantly.
Then, extensive simulations are performed to verify these hypotheses by varying the factors introduced in Section 3.1. Generally, according to Figure 5 and Figure 6, we find that for the individual holdings, protective resources held by individuals affected by the inaccurate information have higher fluctuations (please note that in the legend of Figure 5, “affected people” refers to “individuals affected by the inaccurate information”). For the centralized material storage, the fluctuations “during pandemic” are higher than that “after pandemic”. Either for individual holdings or centralized resources, the fluctuations of protective resources are higher than that of cure-focused resources. These findings appear to be in line with our common knowledge. However, we still need further exploration about which factors influence these fluctuations and to what extent. Thus, this study uses the least squares method for linear regression analysis on the fluctuating curves to fit trendlines. Subsequently, the significance of the trendline slope is assessed using the P-value to determine the overall trend in demand fluctuations. The numerical results are shown in Table 3. The detailed outcomes of Figure 5 and Figure 6 and Table 3 are plotted in Appendix C.
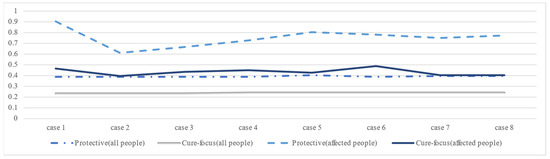
Figure 5.
The level of individual holdings fluctuations between different types of resources.
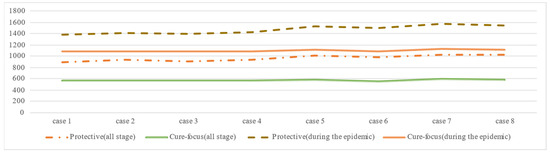
Figure 6.
The level of centralized storage fluctuations between different types of resources.

Table 3.
Numerical results of the parameters’ influence on the resource amount fluctuations.
Table 3 shows the impact of various parameters on resource fluctuations, presenting positive or negative influences with statistically significant p-values. Regarding information parameters, information diffusion rate has negative effects on fluctuations of both protective and cure-focused resources held by individuals. Conversely, it has positive effects on the fluctuation of centralized storage for both types of resources during the epidemic. Inaccurate information diffusion rate has significant positive effects on the fluctuations of protective resources held by individuals and protective centralized material storage, which has an opposite effect to the inaccurate information forgetting rate. In terms of traveling parameters, short move probability has a positive effect on the fluctuations of cure-focused resources held by individuals. Long travel probability has a slightly positive effect on the fluctuations of resources held by individuals who are affected by inaccurate information. Short move distance has a negative effect on the fluctuations of protective resources held by individuals but has significant positive influences on the centralized cure-focus (all the simulation stage) and protective (only during the epidemic) storage.
Finally, we found that the hypothesis we proposed was not entirely valid. The amendment of the hypothesis proposed is presented in Table 4.

Table 4.
Verification and amendment of the hypothesis proposed.
4.3. Scenarios Analysis
The previous section investigates the concurrence and divergence between the actual outcomes and the envisioned results by proposing and testing the hypotheses. Most importantly, the impact of different factors on the demand fluctuation for different types of resource are explored. In this section, we implement the model into four city scenarios to see whether the demand fluctuations for different types of resource vary across cities or not. We choose four cities from two countries as references to design these four city scenarios, which are Shanghai (China), Wuhan (China), Berlin (Germany) and Bremen (Germany). Cities are named as “SH”, “WH”, “BE” and “BR”. Combined with our previous results, we distinguish these four city scenarios using six characteristics, including population density, media exposure level, consistency of public opinion, self-protection level, restrictive protection level and production capacity. The simulation parameters of these four city scenarios are generated based on some statistical data of the corresponding cities. The statistical data we considered include population size, area, population density, internet user size, number of supermarkets, total track length of metro, the duration of COVID-19 travel restrictions, crime rate, opinion on fake news and number of medical devices companies. Following that, the characteristics of the four city scenarios are encapsulated in Table 5. For detailed parameter settings and the data source, please refer to Appendix A Table A2 and Table A3. The results presented are averaged from 1000 realizations of a Monte Carlo simulation.

Table 5.
Characteristics for the four city scenarios.
The quantity fluctuations of resources in the four city scenarios are illustrated in Figure 7. For individual holdings (left), Scenario WH exhibits the highest fluctuations, followed by Scenario SH. Scenario BE and Scenario BR show similar and relatively lower fluctuations. Notably, the use of protective resources with low dependence (0.1, 0.1) results in the most significant variation across different city scenarios. Therefore, cities with high population density, advanced media development, strong public opinion control, strict epidemic prevention measures, and efficient material supply should be vigilant about potential fluctuations in individual holdings, particularly concerning panic buying and hoarding during epidemics.
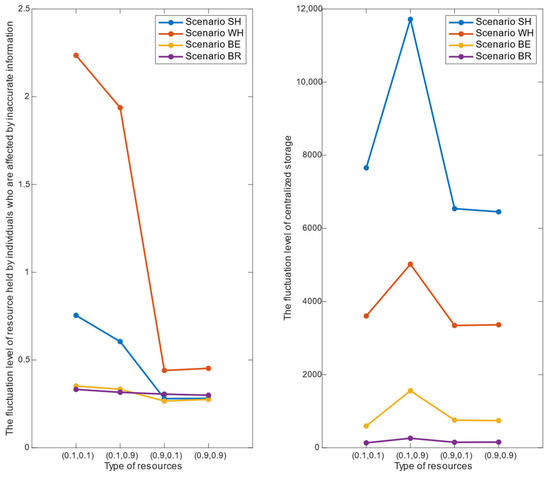
Figure 7.
Quantity fluctuations of different resources in different city scenarios.
For centralized storage (right), Scenario SH experiences the greatest fluctuations, followed by Scenario WH, Scenario BE and Scenario BR. Moreover, the protective and high-dependence resource (0.1, 0.9) significantly impacts the degree of fluctuation in centralized material storage. Hence, cities with high population density, advanced media development, strong control of public opinion, strict epidemic prevention measures and efficient material supply also need to closely monitor changes in the quantity of centralized material storage, especially for the protective and high dependence resource (0.1, 0.9).
Our configuration of parameters may not perfectly align with the real development status of each city. However, the results of city scenario simulations indicate that cities with different developmental characteristics indeed exhibit significantly varied demand dynamics in medical resources during epidemics. When an outbreak occurs, different cities will experience diverse changes in demand. Therefore, material supply policies need to be customized and strategically adapted to meet the unique needs of different nations and cities.
4.4. Discussion
By studying the coevolution effects of information diffusion and virus spreading on demand fluctuation, this paper expands our understanding of the complex dynamics of demand fluctuations during public health emergencies, which not only adds value to the literature, but also provides new insights for solving those material security problems in emergency supply chain management. For instance, monitoring individual holdings can serve as an indicator of hoarding behavior, while examining fluctuations in centralized storage can inform early warning systems for safety stock levels. Furthermore, our analysis of city scenarios reveals that different city settings exhibit varied demand fluctuations, reflected by their unique characteristics. As the COVID-19 daily updated data released by “Our World In Data” show, different countries have different trends (the timings reach peaks and troughs) on cases, hospitalizations, vaccinations, mortality risk, etc. [66]. Moreover, our findings emphasize that careful monitoring of changes in the quantity of centralized material storage, particularly for protective resources, is crucial. This necessity is indirectly corroborated by Fastenal’s experience during the early months of COVID-19. They encountered a surge in demand of masks and janitorial suppliers in the early month of COVID-19, but then in the third quarter of 2020, they met the oversupply of masks, and prices declined, which led to inventory imbalances, and this imbalance might take one year to correct itself [67]. To address this situation, the State Administration for Market Regulation, the National Medical Products Administration and the National Intellectual Property Administration of China jointly issued “Ten Measures to Support the Resumption of Work and Production in Enterprises”, encouraging the textile and apparel industry to shift towards the production of masks and protective suits. This adaptation allowed a smoother transition back to their normal production lines when the demand for masks decreased [68]. Finally, this study could provide suggestions for fluctuation assessment, demand prediction and safety stock warning in emergency supply chain management, while also reminding providers of emergency supplies during epidemics that general forecasts may not be applicable to emergency scenarios when developing production plans.
5. Conclusions
The rapid development of information technology and the complex social environment has made the demand responses in public health emergencies even more challenging. This paper investigated the interactive effects of information diffusion and virus spreading on medical resource demand during epidemics by developing a three-layer coevolution “information–epidemic–resource” model. Some city characteristics affecting information and virus spreading behavior were identified and defined from the literature, including media exposure, consistency of opinion, self-protection, and restrictive protection. Moreover, the concept of demand fluctuations in epidemics was clarified and some factors that could influence these fluctuations were proposed, including Information Diffusion Rate, Information Forgetting Rate, Inaccurate Information Diffusion Rate, Inaccurate Information Forgetting Rate, Short Move Probability, Long Travel Probability, Short Move Distance and Long Travel Distance. The reserves form of medical resource in this paper include both Individual Holdings and Centralized Material Storage, and resources are categorized into protective and cure-focused based on their respective efficacy. Finally, this study designed four city scenarios with different characteristics based on some statistical data of four cities in China and Germany, and analyzed and compared the demand fluctuation between these cities.
This study conducts extensive numerical simulations and concludes that the demand fluctuation of individual holdings and centralized storage can be influenced by different city characteristics. For the demand fluctuation of individual material holdings, the media exposure, consistency of public opinion and self-protection level in a region have positive or negative effects, which are evidenced by metrics such as information diffusion rate, inaccurate information diffusion rate, inaccurate information forgetting rate and short move probability. For the centralized storage, the demand fluctuation of that can be influenced by a region’s media exposure, consistency of public opinion and restrictive protection level, which can be demonstrated by the information diffusion rate, inaccurate information diffusion rate, inaccurate information forgetting rate and short move distance. In other words, media exposure in inaccurate information inflates fluctuations, while higher public opinion consistency can reduce it for both individual holdings and centralized resource storage. Reinforcing self-protection can reduce the demand fluctuations of individuals, which is similar to Yuen et al. (2020) who concluded that “Panic buying can be viewed as a self-protection mechanism to satisfy the safety needs of individuals”, and effective restrictive protections can reduce the fluctuations of centralized resource storage, then relieve pressure on material security for government decision-making centers [28]. Furthermore, protective resources are more susceptible to the changing environment than cure-focused resources.
This study contributes significantly to the field of emergency supply chain management and public health safety, offering valuable insights for researchers, policymakers and industry practitioners. Future work includes studying the demand fluctuation in a double three-layer network, which means we would explore the resource allocation between two cities with different city characteristics to minimize the overall demand fluctuations. Considering the heterogeneity of the public to distinguish their susceptibility to viruses or inaccurate information is also one of the future research directions.
Author Contributions
Conceptualization, Y.Z. and J.Z.; methodology, Y.Z.; software, Y.Z.; validation, J.Z.; formal analysis, Y.Z.; investigation, Y.Y.; resources, Y.Z. and Y.Y.; writing—original draft preparation, Y.Z. and Y.Y.; writing—review and editing, Y.Z. and J.Z.; visualization, Y.Z.; supervision, J.Z.; project administration, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Sino-German Mobility Programme of the National Natural Science Foundation of China, grant number M-0310”, the “Key Soft Science Project of Shanghai Municipal Science and Technology Commission, grant number 23692109300”, and “Shanghai Philosophy and Social Sciences Project, grant number 2022ZGL011”.
Data Availability Statement
Some or all data, models or code that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Figure A1.
The BA scale-free network in the information layer. Gray lines between two nodes indicate that they have connections in the information layer.
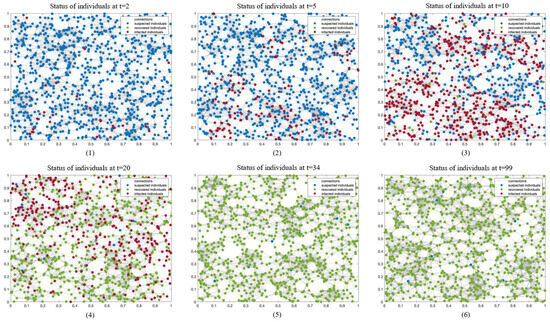
Figure A2.
Status evolution of individuals. The density of nodes in different states varies over time. The density of blue nodes, representing susceptible individuals, gradually diminishes over time. The density of red nodes representing infected individuals initially rises and then declines. Finally, there are almost all green nodes (recovered) and very few blue uninfected nodes remain in the system. Gray lines between two nodes indicate that they are connected in the epidemic layer and the resource layer.
| Algorithm A1. The movement of nodes in the epidemic layer at each time step |
| Input: the position matrix P, the state matrixes Sa, the parameters r1, r2, p1, p2, t |
| Output: the new position matrix P_new |
| T = t; |
| n = length (P); |
| % Randomly select nodes to move |
| move1 = rand(n,1) < p1;%0–1 |
| move2 = rand(n,1) < p2 & ~move1; |
| % Move nodes that are selected to move |
| move1_inds = find(move1); |
| move2_inds = find(move2); |
| for i = 1:length(move1_inds) |
| idx = move1_inds(i); |
| P_new = P(idx,:) + rand(1,2) * r1—r1/2; |
| if all(P_new >= 0) && all(P_new < = 1) |
| P(idx,:) = P_new; |
| end |
| end |
| for i = 1:length(move2_inds) |
| idx = move2_inds(i); |
| if Sa(idx) = 1 |
| P_new = P(idx,:) + rand(1,2) * r1 − r1/2; |
| else |
| P_new = P(idx,:) + rand(1,2) * r2 − r2/2; |
| end |
| if all(P_new >= 0) && all(P_new < = 1) |
| P(idx,:) = P_new; |
| end |
| end |

Table A1.
Parameters setting of the three-layer simulation.
Table A1.
Parameters setting of the three-layer simulation.
| Nodes = 1000, T = 100 | ||
|---|---|---|
| Information Layer | Epidemic Layer | Resource Layer |
| = 0.6 | =0.1 | = 0.2 |
| = 0.4 | r = 0.07 | = 0.9 |
| = 0.75 | = 7 | = 0.01 |
| = 0.09 | r1 = 0.1 | rc = 1 |
| r2 = 0.5 | ||
| p2 = 0.1 |

Table A2.
Parameters setting of the city scenarios simulation.
Table A2.
Parameters setting of the city scenarios simulation.
| Parameters | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|
| nodes | 2488 | 1245 | 365 | 57 |
| T | 200 | 200 | 200 | 200 |
| 0.60 | 0.60 | 0.40 | 0.40 | |
| 0.4 | 0.4 | 0.4 | 0.4 | |
| 0.9 | 0.9 | 0.7 | 0.7 | |
| 0.06 | 0.06 | 0.03 | 0.03 | |
| 0.2 | 0.2 | 0.8 | 0.8 | |
| 0.03 | 0.08 | 0.03 | 0.07 | |
| 7 | 7 | 7 | 7 | |
| 0.1 | 0.18 | 0.1 | 0.18 | |
| 0.6 | 0.6 | 0.9 | 0.9 | |
| 0.8 | 0.8 | 0.5 | 0.5 | |
| 0.05 | 0.05 | 0.2 | 0.2 | |
| 0.1/0.9 | 0.1/0.9 | 0.1/0.9 | 0.1/0.9 | |
| 0.1/0.9 | 0.1/0.9 | 0.1/0.9 | 0.1/0.9 | |
| 0.01 | 0.01 | 0.01 | 0.005 | |
| 1 | 1 | 1 | 1 | |
| 124,410 | 62,240 | 7290 | 569.352 |

Table A3.
Statistical data city scenarios simulation.
Table A3.
Statistical data city scenarios simulation.
| Scales | Shanghai | Wuhan | Berlin | Bremen | Data Source |
|---|---|---|---|---|---|
| Population size | 29,210,808 | 8,718,250 | 3,573,938 | 567,802 | World Population Review |
| Area city (square km) | 6341 | 8494 | 891 | 318 | Wikipedia |
| Population density | 4200 | 1026 | 4126 | 1700 | Wikipedia |
| Internet user size (million) | 1050 (in China) | 77.53 (in Germany) | DataReportal | ||
| Number of supermarkets | 2714 | 179 | 973 | 78 | Smartscrapers; CEIC; Google Map |
| Track length of metro (km) | 826 | 463 | 155.64 | no metro | Wikipedia |
| Lifting of COVID-19 travel restrictions | 29.04.2023 (for entry into China) | 11.06.2022 (for entry into Germany) | TRAVEL BANS | ||
| Crime rate and statistics | 0.5 (in China) | 0.94 (in Germany) | macrotrends | ||
| Opinion on fake news | 0.604 (in China) 1 | 47% (in Germany) 2 | [69]; statista | ||
| Number of medical devices companies | 32,632 (in China) | 10,679 (in Germany) | statista; BoldData | ||
1 [69]: the factor loading of “do not have enough time to check the accuracy of news” is 0.604. 2 statista: 47% of respondents (in Germany) were confident they could tell real news from fake.
Appendix B
Besides the Barabási–Albert (BA) network applied in this study, we introduced the Watts–Strogatz (WS) and Erdős–Rényi (ER) networks to assess whether network structure influences demand fluctuations. According to Figure A3 and Table A4, our results suggest that topology does not significantly influence our study’s conclusions regarding resource fluctuation during pandemics.
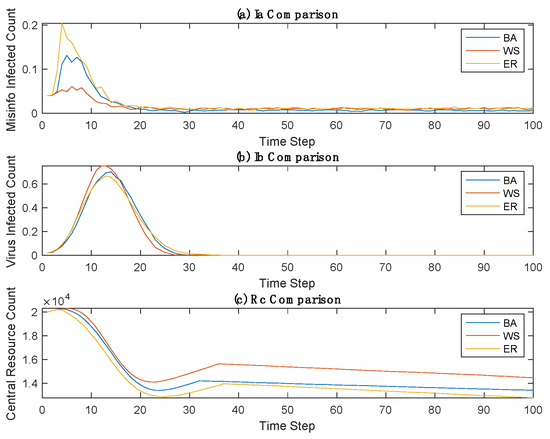
Figure A3.
The impact of topology on research outcome. This is a comparison between Barabási–Albert (BA), Watts–Strogatz (WS) and Erdős–Rényi (ER) network models. Different network structures show different inaccurate information spreading dynamics, notably in peak differences (see (a)), but do not show significant impact on virus transmission dynamics (see (b)). While network structure affects the quantity of central storage, it does not alter the trend/fluctuation (see (c)).

Table A4.
Statistical data city scenarios simulation.
Table A4.
Statistical data city scenarios simulation.
| Topology | Average Variance of Individual Holdings |
|---|---|
| Barabási–Albert (BA)-random-random | 0.240892879185805 |
| Watts–Strogatz (WS)-random-random | 0.252602085078648 |
| Erdős–Rényi (ER)-random-random | 0.286417945011199 |
Appendix C
For Figure A4, Figure A5, Figure A6 and Figure A7, higher positions of the curves represent higher standard deviation, which means higher fluctuations in the corresponding materials. This study uses the least squares method for linear regression analysis on the fluctuating curves to fit trendlines.
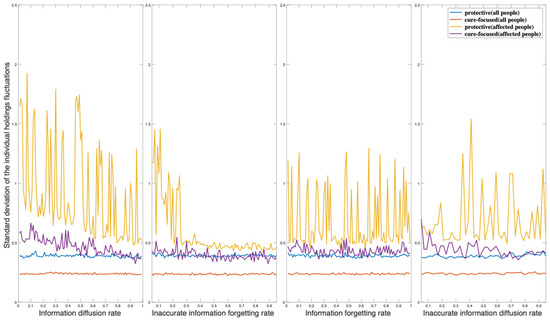
Figure A4.
Fluctuation of individual holding resource affected by information parameters.
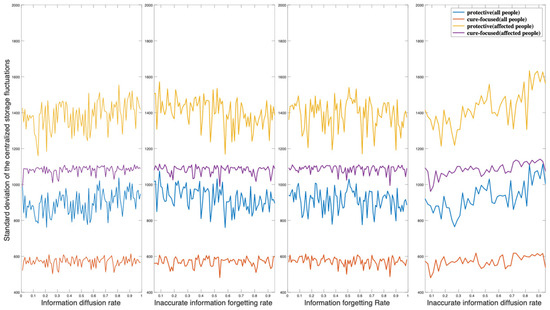
Figure A5.
Fluctuation of centralized storage affected by information parameters.
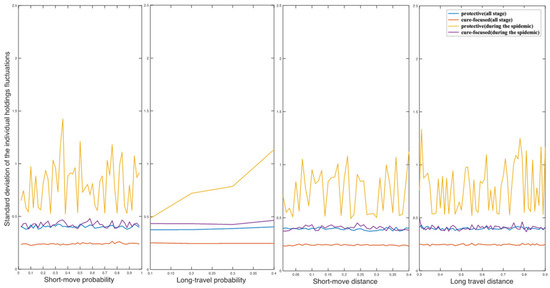
Figure A6.
Fluctuation of individual holding resource affected by travel parameters.
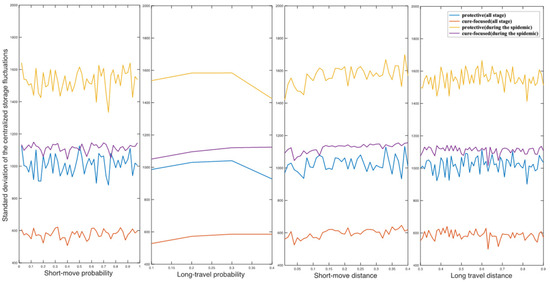
Figure A7.
Fluctuation of centralized storage affected by travel parameters.
References
- Ezeaku, H.C.; Asongu, S.A.; Nnanna, J. Volatility of international commodity prices in times of COVID-19: Effects of oil supply and global demand shocks. Extr. Ind. Soc. 2021, 8, 257–270. [Google Scholar] [CrossRef]
- Ahmed, M.Y.; Sarkodie, S.A. COVID-19 pandemic and economic policy uncertainty regimes affect commodity market volatility. Resour. Policy 2021, 74, 102303. [Google Scholar] [CrossRef]
- Global Times. Banlangen Popularity Soars after Expert ‘Backs’ Use against COVID-19. Global Times. 2020. Available online: https://www.globaltimes.cn/content/1203974.shtml (accessed on 19 October 2020).
- Van Oorschot, K.E.; Jahre, M.; Van Wassenhove, L.N. Collaboration–competition dilemma in flattening the COVID-19 curve. Prod. Oper. Manag. 2023, 32, 1345–1361. [Google Scholar] [CrossRef]
- Ahlqvist, V.; Dube, N.; Jahre, M.; Lee, J.S.; Moe, A.F.; Olivier, M.; Aardal, C.; Melaku, T.; Selviaridis, K.; Viana, J. Supply chain risk management strategies in normal and abnormal times: Policymakers’ role in reducing generic medicine shortages. Int. J. Phys. Distrib. Logist. Manag. 2023, 53, 206–230. [Google Scholar] [CrossRef]
- Smith, T.P.; Flaxman, S.; Gallinat, A.S.; Kinosian, S.P.; Stemkovski, M.; Unwin, H.J.T.; Watson, O.J.; Whittaker, C.; Cattarino, L.; Dorigatti, I.; et al. Temperature and population density influence SARS-CoV-2 transmission in the absence of non-pharmaceutical interventions. Proc. Natl. Acad. Sci. USA 2021, 118, e2019284118. [Google Scholar] [CrossRef] [PubMed]
- Sagan, A.; Bryndova, L.; Kowalska-Bobko, I.; Smatana, M.; Spranger, A.; Szerencses, V.; Webb, E.; Gaal, P. A reversal of fortune: Comparison of health system responses to COVID-19 in the Visegrad group during the early phases of the pandemic. Health Policy 2022, 126, 446–455. [Google Scholar] [CrossRef] [PubMed]
- Elhadi, M.; Msherghi, A.; Alkeelani, M.; Zorgani, A.; Zaid, A.; Alsuyihili, A.; Buzreg, A.; Ahmed, H.; Elhadi, A.; Khaled, A.; et al. Assessment of Healthcare Workers’ Levels of Preparedness and Awareness Regarding COVID-19 Infection in Low-Resource Settings. Am. J. Trop. Med. Hyg. 2020, 103, 828–833. [Google Scholar] [CrossRef] [PubMed]
- Haegdorens, F.; Franck, E.; Smith, P.; Bruyneel, A.; Monsieurs, K.G.; Van Bogaert, P. Sufficient personal protective equipment training can reduce COVID-19 related symptoms in healthcare workers: A prospective cohort study. Int. J. Nurs. Stud. 2021, 126, 104132. [Google Scholar] [CrossRef]
- WHO. Responding to Community Spread of COVID-19: Interim Guidance, 7 March 2020 (No. WHO/COVID-19/Community_Transmission/2020.1). World Health Organization. 2020. Available online: https://www.who.int/publications/i/item/responding-to-community-spread-of-covid-19 (accessed on 7 March 2020).
- Wincewicz-Bosy, M.; Sadowski, A.; Wąsowska, K.; Galar, Z.; Dymyt, M. Military Food Supply Chain during the COVID-19 Pandemic. Sustainability 2022, 14, 2464. [Google Scholar] [CrossRef]
- Chowdhury, P.; Paul, S.K.; Kaisar, S.; Moktadir, M.A. COVID-19 pandemic related supply chain studies: A systematic review. Transp. Res. Part E Logist. Transp. Rev. 2021, 148, 102271. [Google Scholar] [CrossRef]
- Shao, J.; Liang, C.; Liu, Y.; Xu, J.; Zhao, S. Relief demand forecasting based on intuitionistic fuzzy case-based reasoning. Socio-Econ. Plan. Sci. 2021, 74, 100932. [Google Scholar] [CrossRef]
- Li, T. Trans-Regional Medical Support in Public Health Emergencies: A Case Study of Wuhan in the Early COVID-19 Pandemic in China. Risk Manag. Healthc. Policy 2022, 15, 677–683. [Google Scholar] [CrossRef]
- Shao, H.; Jin, C.; Xu, J.; Zhong, Y.; Xu, B. Supply-demand matching of medical services at a city level under the background of hierarchical diagnosis and treatment—Based on Didi Chuxing Data in Haikou, China. BMC Health Serv. Res. 2022, 22, 1–12. [Google Scholar] [CrossRef]
- Cai, M.; Luo, J. Influence of COVID-19 on Manufacturing Industry and Corresponding Countermeasures from Supply Chain Perspective. J. Shanghai Jiaotong Univ. 2020, 25, 409–416. [Google Scholar] [CrossRef]
- Xie, K.; Zhu, S.; Gui, P.; Chen, Y. Coordinating an emergency medical material supply chain with CVaR under the pandemic considering corporate social responsibility. Comput. Ind. Eng. 2023, 176, 108989. [Google Scholar] [CrossRef]
- Brijball Parumasur, S.; Oodith, P.D.; Oodith, D. A Cursory Review of The Impact of COVID-19 On Panic-Buying. J. Posit. Sch. Psychol. 2023, 7, 1199–1218. Available online: https://journalppw.com/index.php/jpsp/article/view/15891 (accessed on 2 March 2023).
- Alla, L.; Bentalha, B.; Bouhtati, N. Assessing Supply Chain Performance in the COVID-19 Context: A Prospective Model. In Proceedings of the 2022 14th International Colloquium of Logistics and Supply Chain Management (LOGISTIQUA), El Jadida, Morocco, 25–27 May 2022; pp. 1–6. [Google Scholar]
- Michna, Z.; Disney, S.M.; Nielsen, P. The impact of stochastic lead times on the bullwhip effect under correlated demand and moving average forecasts. Omega 2020, 93, 102033. [Google Scholar] [CrossRef]
- Trapero, J.R.; Pedregal, D.J. A novel time-varying bullwhip effect metric: An application to promotional sales. Int. J. Prod. Econ. 2016, 182, 465–471. [Google Scholar] [CrossRef]
- Heymann, D.L.; Shindo, N. COVID-19: What is next for public health? Lancet 2020, 395, 542–545. [Google Scholar] [CrossRef]
- Wilson, N.M.; Norton, A.; Young, F.P.; Collins, D.W. Airborne transmission of severe acute respiratory syndrome coronavirus-2 to healthcare workers: A narrative review. Anaesthesia 2020, 75, 1086–1095. [Google Scholar] [CrossRef]
- Yuqian, Z.; Tailei, Z.; Wenshan, H.; Xueli, S. A delayed SIQR epidemic model with media effect and tracking quarantine. J. Zhejiang Univ. 2022, 49, 159–169. (In Chinese) [Google Scholar] [CrossRef]
- Laato, S.; Islam, A.K.M.N.; Islam, M.N.; Whelan, E. What drives unverified information sharing and cyberchondria during the COVID-19 pandemic? Eur. J. Inf. Syst. 2020, 29, 288–305. [Google Scholar] [CrossRef]
- Naeem, M. Do social media platforms develop consumer panic buying during the fear of COVID-19 pandemic. J. Retail. Consum. Serv. 2020, 58, 102226. [Google Scholar] [CrossRef]
- Sheth, J. Impact of COVID-19 on consumer behavior: Will the old habits return or die? J. Bus. Res. 2020, 117, 280–283. [Google Scholar] [CrossRef]
- Yuen, K.F.; Wang, X.; Ma, F.; Li, K.X. The Psychological Causes of Panic Buying Following a Health Crisis. Int. J. Environ. Res. Public Health 2020, 17, 3513. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Z.-K.; Wang, W.; Hou, D.; Xu, J.; Ye, X.; Li, S. Multiplex network reconstruction for the coupled spatial diffusion of infodemic and pandemic of COVID-19. Int. J. Digit. Earth 2021, 14, 401–423. [Google Scholar] [CrossRef]
- Winkielman, P.; Nowak, A. Beyond the features: The role of consistency in impressions of trust. Soc. Psychol. Bull. 2022, 17, 1–20. [Google Scholar] [CrossRef]
- Thagard, P.; Verbeurgt, K. Coherence as Constraint Satisfaction. Cogn. Sci. 1998, 22, 1–24. [Google Scholar] [CrossRef]
- Pennington, N.; Hastie, R. Explaining the evidence: Tests of the Story Model for juror decision making. J. Pers. Soc. Psychol. 1992, 62, 189–206. [Google Scholar] [CrossRef]
- Plazas, A.; Malvestio, I.; Starnini, M.; Díaz-Guilera, A. Modeling partial lockdowns in multiplex networks using partition strategies. Appl. Netw. Sci. 2021, 6, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Prem, K.; Liu, Y.; Russell, T.W.; Kucharski, A.J.; Eggo, R.M.; Davies, N.; Jit, M.; Klepac, P.; Flasche, S.; Clifford, S.; et al. The Effect of Control Strategies to Reduce Social Mixing on Outcomes of the COVID-19 Epidemic in Wuhan, China: A Modelling Study. Lancet Public Health 2020, 5, e261–e270. [Google Scholar] [CrossRef]
- Mogi, R.; Spijker, J. The influence of social and economic ties to the spread of COVID-19 in Europe. J. Popul. Res. 2022, 39, 495–511. [Google Scholar] [CrossRef]
- Fedorova, E.; Ledyaeva, S.; Kulikova, O.; Nevredinov, A. Governmental anti-pandemic policies, vaccination, population mobility, Twitter narratives, and the spread of COVID-19: Evidence from the European Union countries. Risk Anal. 2023, 43, 1975–2003. [Google Scholar] [CrossRef]
- Ding, L.; Hu, P.; Guan, Z.-H.; Li, T. An Efficient Hybrid Control Strategy for Restraining Rumor Spreading. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6779–6791. [Google Scholar] [CrossRef]
- Xian, J.; Yang, D.; Pan, L.; Liu, M.; Wang, W. Containing rumors spreading on correlated multiplex networks. J. Stat. Mech. Theory Exp. 2020, 2020, 023402. [Google Scholar] [CrossRef]
- Dhar, J.; Jain, A.; Gupta, V.K. A mathematical model of news propagation on online social network and a control strategy for rumor spreading. Soc. Netw. Anal. Min. 2016, 6, 57. [Google Scholar] [CrossRef]
- Jain, A.; Dhar, J.; Gupta, V. Rumor model on homogeneous social network incorporating delay in expert intervention and government action. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105189. [Google Scholar] [CrossRef]
- Peng, B.; Ge, J.; Wei, G.; Wan, A. Research on identification of key brittleness factors in emergency medical resources support system based on complex network. Artif. Intell. Med. 2022, 131, 102350. [Google Scholar] [CrossRef]
- Zhang, M.; Qin, S.; Zhu, X. Information diffusion under public crisis in BA scale-free network based on SEIR model—Taking COVID-19 as an example. Phys. A Stat. Mech. Appl. 2021, 571, 125848. [Google Scholar] [CrossRef]
- Jiang, J.; Zhou, T. Resource control of epidemic spreading through a multilayer network. Sci. Rep. 2018, 8, 1629. [Google Scholar] [CrossRef]
- Sun, Q.; Wang, Z.; Zhao, D.; Xia, C.; Perc, M. Diffusion of resources and their impact on epidemic spreading in multilayer networks with simplicial complexes. Chaos Solitons Fractals 2022, 164, 112734. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, X.; Tao, X.; Xiao, J.; Wang, W.; Lai, Y.-C. Anomalous role of information diffusion in epidemic spreading. Phys. Rev. Res. 2021, 3, 013157. [Google Scholar] [CrossRef]
- Scabini, L.F.; Ribas, L.C.; Neiva, M.B.; Junior, A.G.; Farfán, A.J.; Bruno, O.M. Social interaction layers in complex networks for the dynamical epidemic modeling of COVID-19 in Brazil. Phys. A Stat. Mech. Appl. 2020, 564, 125498. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Li, X. Epidemic Threshold in Temporal Multiplex Networks with Individual Layer Preference. IEEE Trans. Netw. Sci. Eng. 2021, 8, 814–824. [Google Scholar] [CrossRef]
- Sahneh, F.D.; Scoglio, C. Competitive epidemic spreading over arbitrary multilayer networks. Phys. Rev. E 2014, 89, 062817. [Google Scholar] [CrossRef]
- Wu, D.; Tang, M.; Liu, Z.; Lai, Y.-C. Impact of inter-layer hopping on epidemic spreading in a multilayer network. Commun. Nonlinear Sci. Numer. Simul. 2020, 90, 105403. [Google Scholar] [CrossRef]
- Huang, H.; Chen, Y.; Ma, Y. Modeling the competitive diffusions of rumor and knowledge and the impacts on epidemic spreading. Appl. Math. Comput. 2021, 388, 125536. [Google Scholar] [CrossRef]
- Li, M.; Liu, R.-R.; Peng, D.; Jia, C.-X.; Wang, B.-H. Roles of the spreading scope and effectiveness in spreading dynamics on multiplex networks. Phys. A Stat. Mech. Appl. 2018, 492, 1239–1246. [Google Scholar] [CrossRef]
- da Silva, P.C.V.; Velásquez-Rojas, F.; Connaughton, C.; Vazquez, F.; Moreno, Y.; Rodrigues, F.A. Epidemic spreading with awareness and different timescales in multiplex networks. Phys. Rev. E 2019, 100, 032313. [Google Scholar] [CrossRef]
- Fan, C.-J.; Jin, Y.; Huo, L.-A.; Liu, C.; Yang, Y.-P.; Wang, Y.-Q. Effect of individual behavior on the interplay between awareness and disease spreading in multiplex networks. Phys. A Stat. Mech. Appl. 2016, 461, 523–530. [Google Scholar] [CrossRef]
- Peng, K.; Lu, Z.; Lin, V.; Lindstrom, M.R.; Parkinson, C.; Wang, C.; Bertozzi, A.L.; Porter, M.A. A multilayer network model of the coevolution of the spread of a disease and competing opinions. Math. Model. Methods Appl. Sci. 2021, 31, 2455–2494. [Google Scholar] [CrossRef]
- Fan, J.; Yin, Q.; Xia, C.; Perc, M. Epidemics on multilayer simplicial complexes. Proc. R. Soc. A 2022, 478, 20220059. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Chen, X. Research on the information dissemination mechanisms of weibo in scale-free networks. Phys. A Stat. Mech. Appl. 2019, 532, 121877. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, W.; Zhang, Z. Interplay between epidemic and information spreading on multiplex networks. Math. Comput. Simul. 2021, 188, 268–279. [Google Scholar] [CrossRef]
- Yin, Q.; Wang, Z.; Xia, C. Information-epidemic co-evolution propagation under policy intervention in multiplex networks. Nonlinear Dyn. 2023, 111, 14583–14595. [Google Scholar] [CrossRef]
- You, X.; Zhang, M.; Ma, Y.; Tan, J.; Liu, Z. Impact of higher-order interactions and individual emotional heterogeneity on information-disease coupled dynamics in multiplex networks. Chaos Solitons Fractals 2023, 177, 114186. [Google Scholar] [CrossRef]
- Yin, Q.; Wang, Z.; Xia, C.; Bauch, C.T. Impact of co-evolution of negative vaccine-related information, vaccination behavior and epidemic spreading in multilayer networks. Commun. Nonlinear Sci. Numer. Simul. 2022, 109, 106312. [Google Scholar] [CrossRef]
- Cui, S.; Liu, F.; Jardón-Kojakhmetov, H.; Cao, M. Discrete-time layered-network epidemics model with time-varying transition rates and multiple resources. Automatica 2024, 159, 111303. [Google Scholar] [CrossRef]
- Kar, A.K.; Tripathi, S.N.; Malik, N.; Gupta, S.; Sivarajah, U. How Does Misinformation and Capricious Opinions Impact the Supply Chain—A Study on the Impacts During the Pandemic. Ann. Oper. Res. 2022, 327, 713–734. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Qing, F.; Wang, L. Rumor Dynamic Model considering Intentional Spreaders in Social Network. Discret. Dyn. Nat. Soc. 2022, 2022, 125848. [Google Scholar] [CrossRef]
- Xiuzhen, X.; Zheng, W.; Umair, M. Testing the fluctuations of oil resource price volatility: A hurdle for economic recovery. Resour. Policy 2022, 79, 102982. [Google Scholar] [CrossRef]
- Kumar, D. Renewable Energy Scenarios in Future Indian Smart Cities: A Geospatial Technology Perspective; Springer: Dordrecht, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Mathieu, E.; Ritchie, H.; Rodés-Guirao, L.; Appel, C.; Giattino, C.; Hasell, J.; Macdonald, B.; Dattani, S.; Beltekian, D.; Ortiz-Ospina, E.; et al. Coronavirus Pandemic (COVID-19), OurWorldInData.org. 2020. Available online: https://ourworldindata.org/coronavirus (accessed on 2 January 2024).
- Cosgrove, E. Fastenal Raced to Increase Mask Inventory. Now It Has an “Oversupply”. Supply Chain Dive. 2020. Available online: https://www.supplychaindive.com/news/mask-supply-fastenal-margins/586985/ (accessed on 14 October 2020).
- Guo, S.; Jian, Z. The National Medical Products Administration and the National Intellectual Property Administration of China Jointly Issued ‘Ten Measures to Support the Resumption of Work and Production in Enterprises’. No 30. 2020. Available online: https://www.gov.cn/zhengce/zhengceku/2020-02/15/content_5479457.htm (accessed on 15 February 2020).
- Tang, S.; Willnat, L.; Zhang, H. Fake news, information overload, and the third-person effect in China. Glob. Media China 2021, 6, 492–507. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).