Multi-Objective Optimization of Manufacturing Process Using Artificial Neural Networks
Abstract
1. Introduction
2. Theoretical Background
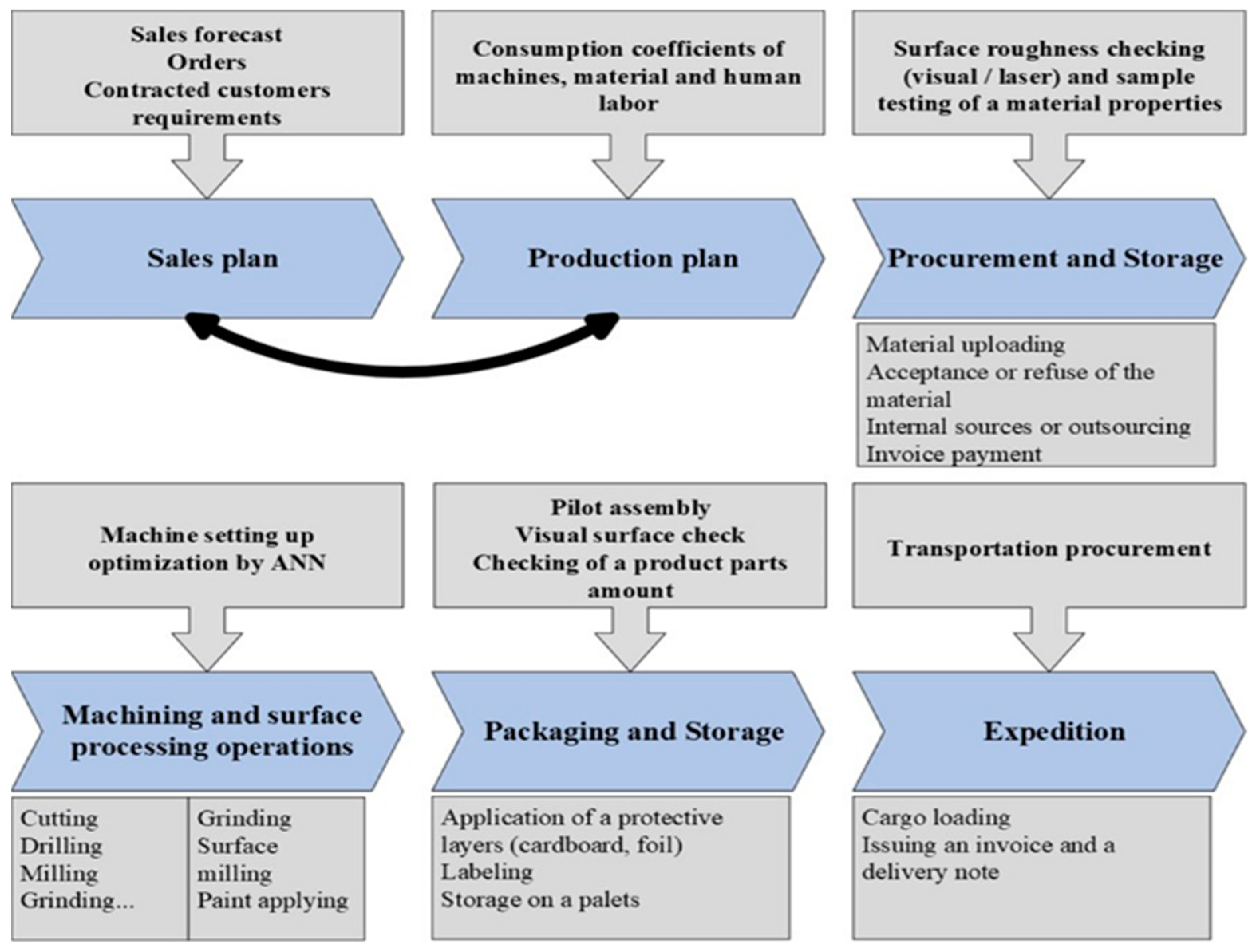
2.1. Furniture Manufacturing Processes
2.2. Systematic Manufacturing Process Optimization
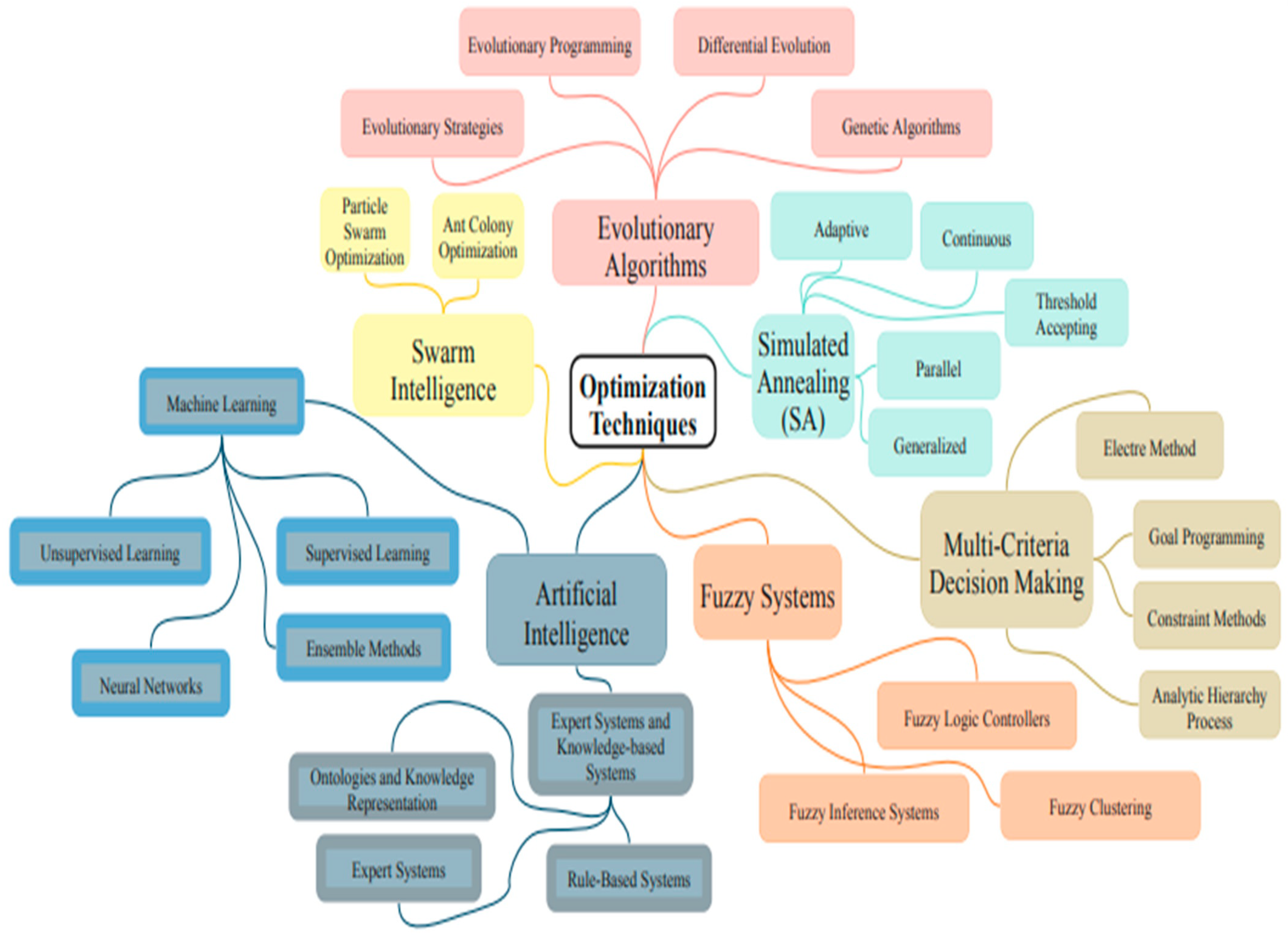
2.3. Optimization Methods and Techniques
3. Materials and Methods
- (1)
- Initially, it was measured using the laser profilometer LPM 4, assembled at the Department of Woodworking of the Technical University in Zvolen in collaboration with the development company [73].
- (2)
- Subsequently, a contact roughness tester MITUTOYO SJ-210 (Japan Mitutoyo, Kawasaki City, Japan) with a sliding heel for production measurements was used [74]. Five measurements were conducted within the test sample, with the evaluated length set at 12.5 mm.
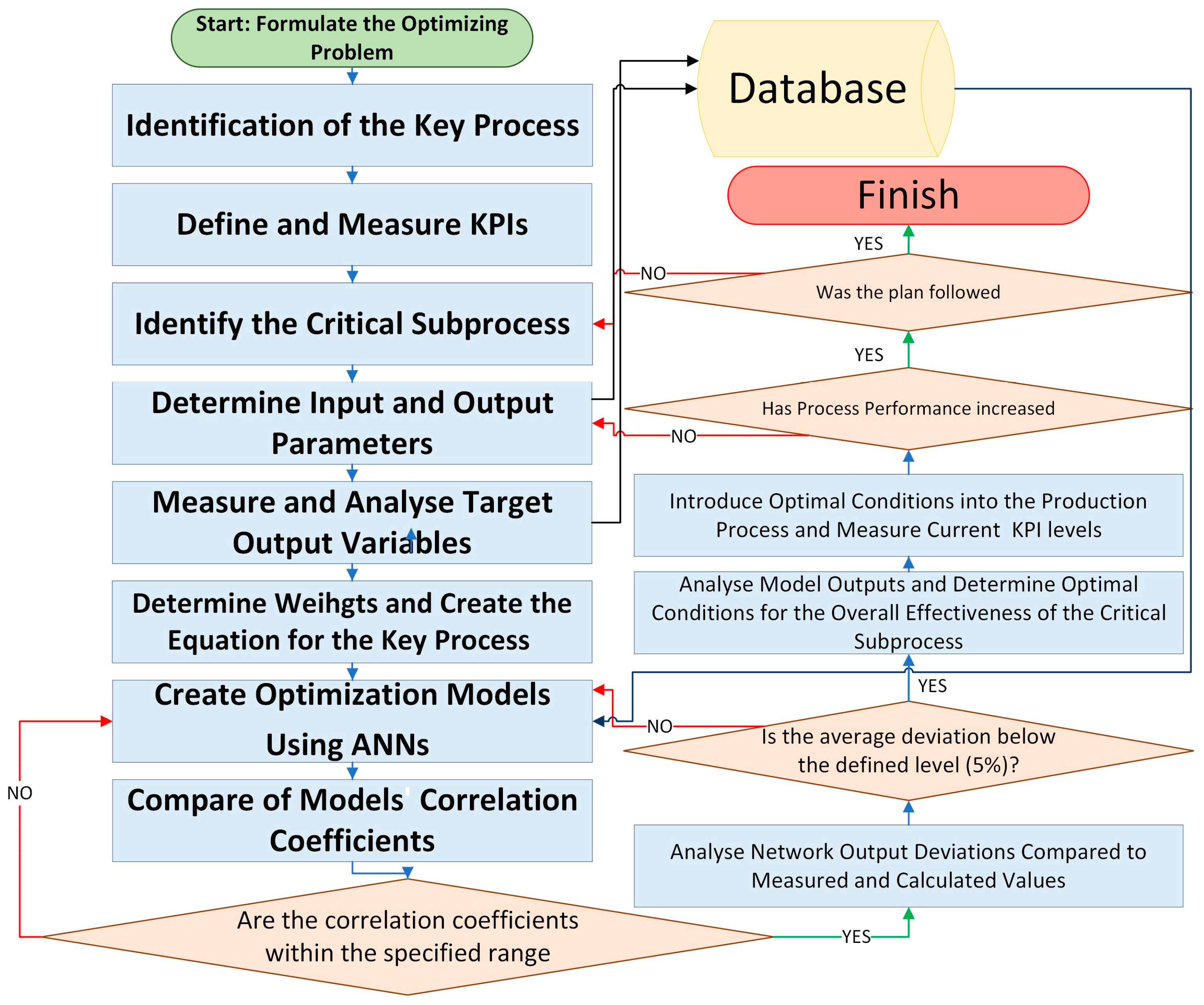
4. Results
- 1.
- Identification of the Key Process:
- Identification of Critical Success Factors (CSFs) linked to the company’s mission, vision, and strategic goals;
- Identification of Key Performance Indicators (KPIs) linked to CSFs;
- Identification of corresponding processes linked to KPIs.
- 2.
- Identification of the key subprocessThe key process can be identified by using the following steps:
- Determining the contribution margins for individual products;
- Determining the share of each product in total sales;
- Using ABC analysis to identify significant, less significant, and insignificant products based on the Pareto principle.
- 3.
- Measuring identified KPIsThe most important prerequisite for effective measurement is the establishment of target values for the identified indicators. Another key aspect is determining the optimal number of these indicators to avoid overwhelming management with too many metrics. However, it is generally impossible to define an optimal number, as it depends on the complexity of production, the company’s size, and the number of business partners.
- 4.
- Identification of the Critical Subprocess: The critical subprocess is one with the highest occurrence of errors and defects. It is important to note that errors in the initial stages of production carry greater weight, as they lead to additional costs for the company either by increasing costs in subsequent processes or through non-quality costs. Another form of cost resulting from errors in the early stages of production includes customer complaints due to hidden defects that are not detected during final inspection and only appear when the product is used.
- 5.
- Determining the Input and Output Parameters of the Critical Subprocess:
- Defining the physical nature of the examined subprocess and its basic technical parameters;
- Defining target variables linked to CSFs that have a technical–economic character.
- 6.
- Measuring the levels of target output variables
- Defining input parameter levels based on information and knowledge gained during the manufacturing process to set up machine-technological equipment, which is essential for determining the level of output variables;
- Another activity includes establishing relationships for calculating target variables.
- 7.
- Determining Weights of Output Parameters:
- Determining the importance of individual output parameters by defining weight coefficients concerning the company’s mission, vision, strategy, and defined CSFs;
- Creating an equation for the manufacturing subprocess.
- 8.
- Creating Models Using Artificial Neural Networks (ANNs):
- Setting input and output variables;
- Defining the training and testing sets;
- Determining the number of hidden neural layers and the type of neural network;
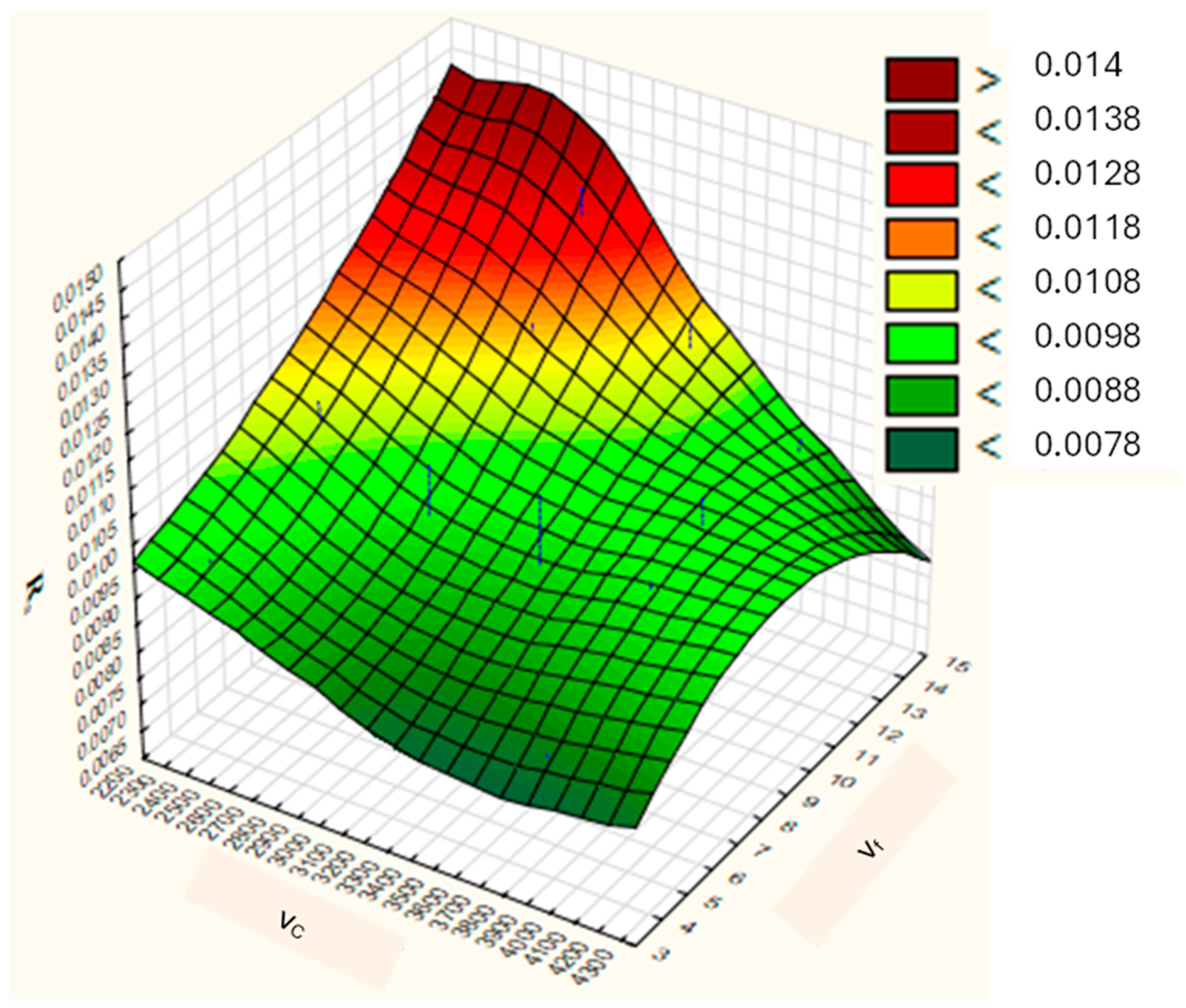
- Creating individual models for each target variable and a comprehensive model based on the defined equation of the manufacturing process, followed by analyzing correlation coefficients, deviations, and least squares graphs to identify the most suitable models and determine optimal conditions.
- 9.
- Control and Feedback:This is one of the most important activities of the model, requiring a focus on continuous improvement. If the subprocess meets the established goals or optimal KPI values, it is necessary to identify the next critical subprocess. If all critical subprocesses within the production of the key product are optimized, the optimization process is complete, but attention should then shift to the production of the next product.
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Georgieva, D.V.; Neykov, N.; Barčić, A.P.; Ćurić, P.; Klarić, K. Participation of Bulgarian furniture manufacturing in global and local value chains as a factor supporting their innovation activities. Sustainability 2023, 15, 13260. [Google Scholar] [CrossRef]
- Potkány, M.; Musa, H.; Schmidtová, J.; Bařinová, D. How do high-performance manufacturing enterprises differ from others with respect to the essence and use of controlling? J. Int. Stud. 2023, 16, 193–207. [Google Scholar] [CrossRef]
- Paranitharan, K.P.; Ramesh Babu, T.; Pal Pandi, A.; Jeyathilagar, D. An empirical validation of integrated manufacturing business excellence model. Int. J. Adv. Manuf. Technol. 2017, 92, 2569–2591. [Google Scholar] [CrossRef]
- Elstermann, M.; Fleischmann, A. Modeling complex process systems with subject-oriented means. In Proceedings of the ACM on Human-Computer Interaction, Seville, Spain, 26–29 June 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Pagan, N.; Baumann, J.; Elokda, E.; Pasquale, G.; Bolognani, S.; Hann’ak, A. A Classification of Feedback Loops and Their Relation to Biases in Automated Decision-Making Systems. In Proceedings of the ACM Conference on Equity and Access in Algorithms, Mechanisms, and Optimization, Boston, MA, USA, 30 October–1 November 2023; pp. 1–14. [Google Scholar] [CrossRef]
- Knyazeva, H. System Theory Approach as a Basis of Strategic Management. Foresight STI Gov. 2020, 4, 6–8. [Google Scholar] [CrossRef]
- Czapla, A. Complexity Theory in Management. Management 2019, 20, 321–330. [Google Scholar] [CrossRef]
- Heik, D.; Ghofrani, J.; Reichelt, D. Adaptive Management Shell for Mapping the Process Capability of Manufacturing Components: A Systematic Mapping Study. In Proceedings of the IEEE International Conference on Industrial Informatics, Warwick, UK, 20–23 July 2020; Volume 1, pp. 7–14. [Google Scholar] [CrossRef]
- Groover, M.P. Fundamentals of Modern Manufacturing: Materials, Processes, and Systems, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. Function-transformation methods for multi-objective optimization. Eng. Optim. 2005, 37, 551–570. [Google Scholar] [CrossRef]
- Amouzgar, K.; Bandaru, S.; Andersson, T.; Ng, A.H.C. Metamodel-based multi-objective optimization of a turning process by using finite element simulation. Eng. Optim. 2020, 52, 1261–1278. [Google Scholar] [CrossRef]
- Yin, R. Process Manufacturing Industry and Process Engineering. In Metallurgical Process Engineering; Springer: Berlin/Heidelberg, Germany, 2011; pp. 25–46. [Google Scholar] [CrossRef]
- Sujová, E.; Vysloužilová, D.; Koleda, P.; Gajdzik, B. Research on the Evaluation of the Efficiency of Production Processes Through the Implementation of Key Performance Indicators. Manag. Syst. Prod. Eng. 2023, 31, 404–410. [Google Scholar] [CrossRef]
- Svobodová, Ľ.; Janků, L.S. Method for Automatic Furniture Placement Based on Simulated Annealing and Genetic Algorithm. In Proceedings of the Advances and Trends in Artificial Intelligence, IEA/AIE, Kuala Lumpur, Malaysia, 9–12 June 2021; Fujita, H., Selamat, A., Lin, J.C.W., Ali, M., Eds.; Springer: Cham, Switzerland, 2021; pp. 480–491. [Google Scholar] [CrossRef]
- Tarigan, U.; Siregar, I.; Siregar, K.; Tarigan, U.P.P. Production scheduling using ant colony optimization in furniture industry. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1122, 012056. [Google Scholar] [CrossRef]
- Wang, G.; Gu, L.; Yun, D. Corrigendum: Preliminary Multi-Physics Performance Analysis and Design Evaluation of UO2 Fuel for LBE-Cooled Subcritical Reactor of China Initiative Accelerator Driven System. Front. Energy Res. 2022, 9, 732801. [Google Scholar] [CrossRef]
- Srivastav, B. The novel Artificial Neural Network assisted models: A review. OSF Preprints. [Preprint]. March 2021 [Cited January 2024]. Available online: https://mpra.ub.uni-muenchen.de/106499/1/MPRA_paper_106499.pdf (accessed on 3 December 2024).
- Rathi, N.; Rathi, N. An application of ann for modeling and optimisation of process parameters of manufacturing process: A review. Int. J. Appl. Sci. Technol. 2020, 4, 127–134. [Google Scholar] [CrossRef]
- Quintana, G.; Rudolf, T.; Ciurana, J.; Brecher, C. Surface roughness prediction through internal kernel information and external accelerometers using artificial neural networks. J. Mech. Sci. Technol. 2011, 25, 2877–2886. [Google Scholar] [CrossRef]
- Madić, M.; Marinković, V.; Radovanović, M. Mathematical modeling and optimization of surface roughness in turning of polyamide based on artificial neural network. Mechanics 2012, 18, 574–581. [Google Scholar] [CrossRef][Green Version]
- Bedelean, B.; Ispas, M.; Răcășan, S.; Baba, M. Optimization of Wood Particleboard Drilling Operating Parameters by Means of the Artificial Neural Network Modeling Technique and Response Surface Methodology. Forests 2022, 7, 1045. [Google Scholar] [CrossRef]
- Huang, J. An Evaluation Model for Green Manufacturing Quality of Children’s Furniture Based on Artificial Intelligence. Int. J. Des. Nat. Ecodyn. 2020, 15, 921–930. [Google Scholar] [CrossRef]
- Bibaud-Alves, J.; Thomas, P.; Haouzi, H. Demand Forecasting using Artificial Neuronal Networks and Time Series: Application to a French Furniture Manufacturer Case Study. In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), Vienna, Austria, 17–19 October 2019; SCITEPRESS: Setúbal, Portugal, 2019; pp. 502–507. [Google Scholar] [CrossRef]
- Rosienkiewicz, M.; Kowalski, A.; Helman, J.; Zbieć, M. Development of Lean Hybrid Furniture Production Control System based on Glenday Sieve, Artificial Neural Networks and Simulation Modeling. Drv. Ind. 2018, 69, 163–173. [Google Scholar] [CrossRef]
- Sujová, A.; Simanová, Ľ.; Marcineková, K. Sustainable Process Performance by Application of Six Sigma Concepts: The Research Study of Two Industrial Cases. Sustainability 2016, 8, 260. [Google Scholar] [CrossRef]
- Singh, A.; Jain, R.; Singh, B.; Meena, M.L. Ergonomic Evaluation and Work Table Design for Wood Furniture Manufacturing Industry. In Ergonomics for Improved Productivity; Springer: Singapore, 2021; pp. 383–390. [Google Scholar] [CrossRef]
- Ratnasingam, J. Production Flow in Furniture Manufacturing. Design Science and Innovation; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Fernando, S.; Gunasekara, C.; Shahpasandi, A.; Nguyen, K.; Sofi, M.; Setunge, S.; Mendis, P.; Rahman, M.T. Sustainable Cement Composite Integrating Waste Cellulose Fibre: A Comprehensive Review. Polymers 2023, 15, 520. [Google Scholar] [CrossRef] [PubMed]
- Smardzewski, J.; Krzyżaniak, Ł.; Wojciechowski, K.W.; Peliński, K.; Tretiakov, K.V.; Narojczyk, J.W. Bending Performance and Failure Behavior of Wooden Sandwich Panels with Corrugated Cores. Phys. Status Solidi B 2022, 259, 2200423. [Google Scholar] [CrossRef]
- Xiao, J.; Wu, Y.; Xie, K.; Hu, Q. Managing the e-commerce disruption with IT-based innovations. Inf. Manag. 2019, 56, 122–139. [Google Scholar] [CrossRef]
- Emmadi, L.; Varaprasad, R.; Venkataraman, H. Analysis of SDN based IIoT networks Targeting Automation Processes in Smart Factory Environments. In Proceedings of the 10th IEEE International Conference on Communication Systems and Network Technologies (CSNT), Bhopal, India, 5–6 June 2021; IEEE: New York, NY, USA, 2021; pp. 465–472. [Google Scholar] [CrossRef]
- Al-Fedaghi, S.; Aldamkhi, G. Conceptual Modeling of an IP Phone Communication System: A Case Study. Int. J. Interdiscip. Telecommun. Netw. 2021, 13, 83–94. [Google Scholar] [CrossRef]
- Anbarasi, M.; Kumar, S. The Impact of Effective Relationship Between Production and Sales. J. Comput. Theor. Nanosci. 2020, 17, 1781–1785. [Google Scholar] [CrossRef]
- Simanová, Ľ.; Gejdoš, P. The Use of Statistical Quality Control Tools to Quality Improving in the Furniture Business. Procedia Econ. Financ. 2015, 34, 276–283. [Google Scholar] [CrossRef]
- Sankhye, S.; Hu, G. Machine Learning Methods for Quality Prediction in Production. Logistics 2020, 4, 35. [Google Scholar] [CrossRef]
- Kulcsár, T.; Tímár, I. Mathematical optimization and engineering applications. Math. Model. Comput. 2016, 3, 59–78. [Google Scholar] [CrossRef]
- Tatsienko, V.; Shatko, D.; Bakanov, A. Optimization of a technological process based on time of its key operations. Vestn. Kuzbass State Tech. Univ. 2020, 1, 12–19. [Google Scholar] [CrossRef]
- Kulcsár, T.; Tímár, I. Mathematical optimization in design-Overview and application. Acta Tech. Corviniensis Bull. Eng. 2012, 5, 21. [Google Scholar]
- Ahmed, S.; Arora, R. Quality characteristics optimization in CNC end milling of A36 K02600 using Taguchi’s approach coupled with artificial neural network and genetic algorithm. Int. J. Syst. Assur. Eng. Manag. 2019, 10, 676–695. [Google Scholar] [CrossRef]
- Tamang, S.; Chandrasekaran, M. Integrated optimization methodology for intelligent machining of inconel 825 and its shop-floor application. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 865–877. [Google Scholar] [CrossRef]
- Fusek, M.; Halama, R. MKP a MHP. [Finite Element Method-FEM and Boundary Element Method-BEM]. Ph.D. Dissertation, Technical University of Ostrava, Plzeň, Czech Republic, University of West Bohemia, Ostrava, Czech Republic, 2011. Available online: https://www.scribd.com/document/630403530/mkp-mhp-interaktivne (accessed on 3 December 2024).
- Shein, A.I.; Zemtsova, O.G. Analytical solution of optimization problem of stability of frame systems. IOP Conf. Ser. Mater. Sci. Eng. 2018, 463, 042065. [Google Scholar] [CrossRef]
- Lahiri, D.; Nag, M.; Mukherjee, D.; Garai, S.; Banerjee, R.; Ray, R.R. Recent trends in approaches for optimization of process parameters for the production of microbial cellulase from wastes. Environ. Sustain. 2021, 4, 273–284. [Google Scholar] [CrossRef]
- Mukherjee, I.; Ray, P.K. A review of optimization techniques in metal cutting process. Comput. Ind. Eng. 2006, 50, 15–34. [Google Scholar] [CrossRef]
- Tsai, M.-H.; Lee, J.-N.; Tsai, H.-D.; Shie, M.-J.; Hsu, T.-L.; Chen, H.-S. Applying a neural network to predict surface roughness and machining accuracy in the milling of SUS304. Electronics 2023, 12, 981. [Google Scholar] [CrossRef]
- Boyko, N.; Lukash, O. Methodology for estimating the cost of construction equipment based on the analysis of important characteristics using machine learning methods. J. Eng. 2023, 2023, 8833753. [Google Scholar] [CrossRef]
- Liu, J.; Qi, Y.; Tao, J.; Tao, T. Analysis of the performance of machine learning models in predicting the severity level of large-truck crashes. Future Transp. 2022, 2, 939. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Shen, W. A review of ensemble learning algorithms used in remote sensing applications. Appl. Sci. 2022, 12, 8654. [Google Scholar] [CrossRef]
- Helder, M.A.; Rodrigo, S.B.; Kunst, R.; Elvis, F.B.; Pesenti, G.C.; Barbosa, J.L.V. Data science methods and tools for industry 4.0: A systematic literature review and taxonomy. Sensors 2023, 23, 5010. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Li, P.; Qian, S.; Quan, H.; Miao, J.; Liu, M.; Hu, Y.; Memetimin, E. Path Planning Technique for Mobile Robots: A Review. Machines 2023, 11, 980. [Google Scholar] [CrossRef]
- Kedir, N.; Nguyen, P.H.D.; Pérez, C.; Ponce, P.; Aminah, R.F. Systematic literature review on fuzzy hybrid methods in photovoltaic solar energy: Opportunities, challenges, and guidance for implementation. Energies 2023, 16, 3795. [Google Scholar] [CrossRef]
- Para, J.; Javier, D.S.; Nebro, A.J. Energy-aware multi-objective job shop scheduling optimization with metaheuristics in manufacturing industries: A critical survey, results, and perspectives. Appl. Sci. 2022, 12, 1491. [Google Scholar] [CrossRef]
- Parham, D.P.; Aser, A.A.; Nazzal, M.A.; Darras, B.M. An industry 4.0 technology selection framework for manufacturing systems and firms using fuzzy AHP and fuzzy TOPSIS methods. Systems 2023, 11, 192. [Google Scholar] [CrossRef]
- Vamvakas, D.; Michailidis, P.; Korkas, C.; Kosmatopoulos, E. Review and evaluation of reinforcement learning frameworks on smart grid applications. Energies 2023, 16, 5326. [Google Scholar] [CrossRef]
- Matsuzaka, Y.; Yashiro, R. AI-based computer vision techniques and expert systems. AI 2023, 4, 289. [Google Scholar] [CrossRef]
- Fowler, W.; Ting, J.; Meng, S.; Li, L.; Tirrell, M. Integrating Systems Thinking into Teaching Emerging Technologies. J. Chem. Educ. 2019, 96, 2805–2813. [Google Scholar] [CrossRef]
- Papakitsos, E.; Makrygiannis, P.; Mavrakis, A. A Study on Applications of Systems Engineering to Holistic Didactics. Mod. Perspect. Lang. Lit. Educ. 2021, 9, 36–52. [Google Scholar] [CrossRef]
- Monat, J.; Amissah, M.; Gannon, T. Practical Applications of Systems Thinking to Business. Systems 2021, 8, 14. [Google Scholar] [CrossRef]
- Iacovidou, E.; Hahladakis, J.; Purnell, P. A systems thinking approach to understanding the challenges of achieving the circular economy. Environ. Sci. Pollut. Res. Int. 2020, 28, 24785–24806. [Google Scholar] [CrossRef] [PubMed]
- Mishra, B.; Kumar, N.; Mukhtar, M. Systems Biology and Machine Learning in Plant-Pathogen Interactions. Mol. Plant-Microbe Interact. MPMI 2019, 32, 45–55. [Google Scholar] [CrossRef]
- Bui, H.; Galanou, E. Translation of systems thinking to organizational goals: A systematic review. J. Gen. Manag. 2022, 47, 233–245. [Google Scholar] [CrossRef]
- Sarker, I.H. AI-based modeling: Techniques, applications and research issues towards automation, intelligent and smart systems. SN Comput. Sci. 2022, 3, 158. [Google Scholar] [CrossRef] [PubMed]
- Nayernia, H.; Bahemia, H.; Papagiannidis, S. A Systematic Review of the Implementation of Industry 4.0 from the Organisational Perspective. Int. J. Prod. Res. 2021, 60, 1–32. [Google Scholar] [CrossRef]
- Al-Surmi, A.; Bashiri, M.; Koliousis, I. AI based decision making: Combining strategies to improve operational performance. Int. J. Prod. Res. 2021, 60, 4464–4486. [Google Scholar] [CrossRef]
- Dora, M.A.; Kumar, S.K.; Mangla, A.; Pant, A.; Kamal, M.M. Critical success factors influencing artificial intelligence adoption in food supply chains. Int. J. Prod. Res. 2021, 60, 1959665. [Google Scholar] [CrossRef]
- Kusumastuti, Y.; Eliyana, A.; Wahyudin, F.; Abdurahman, T.; Sari, P. Leading business amidst the pandemic: The application of systems thinking. Syst. Rev. Pharm. 2020, 11, 1754–1757. [Google Scholar]
- Plowman, D.; Baker, L.; Beck, T.; Kulkarni, M.; Solansky, S.; Travis, D. Radical Change Accidentally: The Emergence and Amplification of Small Change. Acad. Manag. J. 2007, 50, 515–543. [Google Scholar] [CrossRef]
- Bal, B.C.; Gündeş, Z. Surface roughness of medium-density fiberboard processed with CNC machine. Measurement 2020, 153, 107421. [Google Scholar] [CrossRef]
- Wei, W.; Li, Y.; Xue, T.; Tao, S.; Mei, C.; Zhou, W.; Wang, T. The research progress of machining mechanisms in milling wood-based materials. BioResources 2018, 13, 2139–2149. [Google Scholar] [CrossRef]
- Yasir, M.; Ginta, T.L.; Ariwahjoedi, B.; Alkali, A.U.; Danish, M. Effect of cutting speed and feed rate on surface roughness of AISI 316l SS using end-milling. ARPN J. Eng. Appl. Sci. 2016, 11, 2496–2500. Available online: https://www.researchgate.net/publication/309579527_Effect_of_cutting_speed_and_feed_rate_on_surface_roughness_of_AISI_316l_SS_using_end-milling (accessed on 8 January 2024).
- European Committee for Standardization. Standards EN 622 Fibreboards Specifications. 2009. Available online: https://standards.globalspec.com/std/1252786/en-622-5 (accessed on 3 December 2024).
- Novák, V.; Rousek, M.; Kopecký, Z. Assessment of wood surface quality obtained during high-speed milling by use of non-contact method. Drv. Ind. 2011, 62, 105–113. [Google Scholar] [CrossRef]
- Revankar, G.D.; Shetty, R.; Rao, S.S.; Gaitonde, V.N. Analysis of surface roughness and hardness in titanium alloy machining with polycrystalline diamond tool under different lubricating modes. Mater. Res. 2014, 17, 1010–1022. [Google Scholar] [CrossRef]
- Mori, M.; Furuta, M.; Nakai, T.; Fukaya, T.; Liu, J.; Yamazaki, K. High-speed machining of titanium by new PCD tools. SAE Trans. 1999, 108, 682–688. [Google Scholar] [CrossRef]
- Bai, Q.; Yao, Y.; Chen, S. Research and development of polycrystalline diamond woodworking tools. Int. J. Refract. Met. Hard Mater. 2002, 20, 395–400. [Google Scholar] [CrossRef]
- Rangone, A.; Mella, P. Obstacles to Managing Dynamic Systems. The Systems Thinking Approach. Int. J. Bus. Soc. Sci. 2019, 10, 24–41. [Google Scholar] [CrossRef]
- Ganesan, H.; Mohankumar, G. Optimization of Machining Techniques in CNC Turning Centre Using Genetic Algorithm. Arab. J. Sci. Eng. 2013, 38, 1529–1538. [Google Scholar] [CrossRef]
- Al-Aomar, R.; Al-Okaily, A. A GA-based parameter design for single machine turning process with high-volume production. Comput. Ind. Eng. 2006, 50, 317–337. [Google Scholar] [CrossRef]
- Adu-Amankwa, K.; Attia, A.; Janardhanan, M.; Patel, I. A predictive maintenance cost model for CNC SMEs in the era of industry 4.0. Int. J. Adv. Manuf. Technol. 2019, 104, 3567–3587. [Google Scholar] [CrossRef]
- Kumar, D.; Karwasra, K.; Soni, G. Bibliometric analysis of artificial neural network applications in materials and engineering. Mater. Today Proc. 2020, 28, 1629–1634. [Google Scholar] [CrossRef]
- Alexa, O.; Ilie, C.O.; Vilau, R.; Marinescu, M.; Truta, M. Using Neural Networks to Modeling Vehicle Dynamics. Appl. Mech. Mater. 2014, 659, 133–138. [Google Scholar] [CrossRef]
- Sapuan, S.; Mujtaba, I. Composite Materials Technology: In Neural Network Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar] [CrossRef]

| I. Expert Systems and Knowledge-based Systems | |
| Ontologies and Knowledge | Domain, Upper and Task Ontologies Knowledge Representation Techniques (Semantic Networks, Frames, Description Logistic) Knowledge Modeling Approaches (Conceptual and Rule-based Modeling) |
| Expert Systems | Diagnostic Prescriptive Predictive |
| Rule-Based Systems | Rule Refinement Rule-based Machine Learning |
| II. Machine Learning | |
| a. Supervised Learning | |
| Regression Analysis | Linear Polynomial Ridge Lasso Support Vector Bayesian |
| Classification | Decision Trees Random Forest Support Vector Machines k-Nearest Neighbors Naïve Bayes Logistic Regression Discriminant Analysis |
| b. Unsupervised Learning | |
| Clustering | K-Means Hierarchical Clustering Density-Based Spatial Clustering of Applications with Noise Gaussian Mixture Models |
| Dimensionality Reduction | Principal Component Analysis Singular Value Decomposition t-Distributed Stochastic Neighbor Embedding |
| Association Rule Learning | Apriori algorithm Eclat algorithm FP-Growth algorithm |
| Anomaly Detection | Isolation Forest One-Class SVM Local Outlier Factor |
| c. Ensemble Methods | |
| Averaging Methods | Bagging (Bootstrap Aggregating) Random Forest |
| Boosting Methods | Adaptive Boosting Gradient Boosting Machines eXtreme Gradient Boosting Light Gradient Boosting CatBoost |
| d. Neural Networks | |
| Artificial Neural Networks | Multi-layer Perceptrons Deep Neural Networks Recurrent Neural Networks Convolutional Neural Networks Long Short-Term Memory Autoencoders Feedforward Networks |
| Deep Reinforcement Learning | Reinforcement Learning with Neural Networks Q-Learning with Deep Q-Networks Proximal Policy Optimization Actor-Critic Methods |
| Parameter: | Spindle Speed | Cutting Speed | Feed Rate |
|---|---|---|---|
| No. | [rev.min−1] | [m.min−1] | [m.min−1] |
| 1. | 10,000 | 2419.03 | 4.00 |
| 2. | 12,000 | 2902.83 | 4.00 |
| 3. | 14,000 | 3386.64 | 4.00 |
| 4. | 16,000 | 3870.44 | 4.00 |
| 5. | 18,000 | 4354.25 | 4.00 |
| 6. | 10,000 | 2419.03 | 8.00 |
| 7. | 12,000 | 2902.83 | 8.00 |
| 8. | 14,000 | 3386.64 | 8.00 |
| 9. | 16,000 | 3870.44 | 8.00 |
| 10. | 18,000 | 4354.25 | 8.00 |
| 11. | 10,000 | 2419.03 | 10.00 |
| 12. | 12,000 | 2902.83 | 10.00 |
| 13. | 14,000 | 3386.64 | 10.00 |
| 14. | 16,000 | 3870.44 | 10.00 |
| 15. | 18,000 | 4354.25 | 10.00 |
| 16. | 18,000 | 4354.25 | 12.00 |
| 17. | 18,000 | 4354.25 | 14.00 |
| 18. | 12,000 | 2902.83 | 12.00 |
| 19. | 12,000 | 2902.83 | 14.00 |
| 20. | 14,000 | 3386.64 | 12.00 |
| 21. | 14,000 | 3386.64 | 14.00 |
| 22. | 16,000 | 3870.44 | 12.00 |
| 23. | 16,000 | 3870.44 | 14.00 |
| LPM 4 | MITUTOYO SJ-210 | Median | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| 1. | 9.926 | 10.155 | 9.385 | 9.04 | 9.58 | 9.245 | 9.483 |
| 2. | 8.535 | 9.194 | 8.337 | 9.59 | 8.5214 | 8.679 | 8.607 |
| 3. | 7.791 | 8.035 | 8.449 | 7.907 | 7.958 | 7.266 | 7.933 |
| 4. | 8.094 | 9.061 | 7.755 | 8.364 | 7.996 | 8.542 | 8.229 |
| 5. | 8.62 | 8.045 | 9.878 | 9.337 | 8.324 | 8.892 | 8.756 |
| 6. | 8.883 | 11.254 | 10.786 | 11.208 | 9.856 | 10.987 | 10.887 |
| 7. | 9.009 | 10.656 | 12.241 | 11.459 | 9.456 | 10.127 | 10.392 |
| 8. | 10.486 | 11.155 | 10.865 | 10.567 | 10.257 | 10.366 | 10.527 |
| 9. | 8.541 | 9.49 | 11.123 | 10.666 | 9.254 | 9.842 | 9.666 |
| 10. | 9.095 | 10.068 | 8.833 | 8.197 | 8.951 | 9.012 | 8.982 |
| 11. | 10.107 | 11.656 | 10.021 | 13.927 | 11.246 | 10.899 | 11.073 |
| 12. | 9.225 | 9.181 | 10.575 | 10.357 | 9.587 | 9.46 | 9.524 |
| 13. | 8.368 | 11.683 | 9.196 | 8.83 | 9.257 | 8.622 | 9.013 |
| 14. | 8.478 | 11.036 | 10.462 | 10.765 | 8.752 | 10.254 | 10.358 |
| 15. | 10.032 | 11.605 | 11.355 | 10.54 | 11.245 | 10.822 | 11.034 |
| 16. | 7.76 | 9.014 | 9.84 | 9.1 | 8.002 | 7.892 | 8.508 |
| 17. | 7.85 | 9.601 | 7.659 | 9.379 | 8.569 | 8.262 | 8.416 |
| 18. | 11.25 | 12.621 | 9.335 | 9.74 | 11.367 | 12.606 | 11.309 |
| 19. | 12.478 | 12.427 | 14.995 | 13.687 | 13.953 | 12.606 | 13.147 |
| 20. | 9.533 | 8.215 | 9.864 | 11.271 | 9.659 | 10.337 | 9.762 |
| 21. | 11.284 | 10.423 | 11.388 | 10.982 | 11.321 | 12.898 | 11.303 |
| 22. | 9.262 | 9.232 | 8.619 | 8.539 | 9.163 | 11.889 | 9.198 |
| 23. | 9.854 | 9.772 | 10.128 | 10.181 | 9.822 | 9.561 | 9.838 |
| V | E | TM | TL(PCD) | CI(PCD) | CNI | CS | Ra | |
|---|---|---|---|---|---|---|---|---|
| No. | [m3] | [W] | [min] | [min] | [€] | [€] | [%] | [mm] |
| 1. | 102.48 | 210.27 | 0.517 | 240.66 | 0.76 | 0.41 | 74.65 | 9.483 |
| 2. | 204.96 | 210.27 | 0.517 | 163.64 | 1.12 | 0.05 | 79.83 | 8.607 |
| 3. | 307.44 | 210.27 | 0.517 | 118.10 | 1.56 | 0.05 | 84.58 | 7.933 |
| 4. | 409.92 | 210.27 | 0.517 | 89.04 | 2.06 | 0.04 | 87.91 | 8.229 |
| 5. | 512.40 | 210.27 | 0.517 | 69.40 | 2.65 | 0.04 | 90.32 | 8.756 |
| 6. | 614.88 | 159.40 | 0.392 | 240.66 | 0.38 | 0.12 | 63.34 | 10.887 |
| 7. | 717.36 | 159.40 | 0.392 | 163.64 | 0.56 | 0.04 | 71.76 | 10.392 |
| 8. | 819.84 | 159.40 | 0.392 | 118.10 | 0.78 | 0.04 | 77.88 | 10.527 |
| 9. | 922.32 | 159.40 | 0.392 | 89.04 | 1.03 | 0.04 | 82.36 | 9.666 |
| 10. | 1024.80 | 159.40 | 0.392 | 69.40 | 1.32 | 0.05 | 85.70 | 8.982 |
| 11. | 1127.28 | 149.22 | 0.367 | 240.66 | 0.31 | 0.12 | 59.44 | 11.073 |
| 12. | 1229.76 | 149.22 | 0.367 | 163.64 | 0.45 | 0.05 | 68.30 | 9.524 |
| 13. | 1332.24 | 149.22 | 0.367 | 118.10 | 0.62 | 0.04 | 74.91 | 9.013 |
| 14. | 1434.72 | 149.22 | 0.367 | 89.04 | 0.83 | 0.04 | 79.84 | 10.358 |
| 15. | 1537.20 | 149.22 | 0.367 | 69.40 | 1.06 | 0.04 | 83.56 | 11.034 |
| 16. | 1639.68 | 142.44 | 0.350 | 69.40 | 0.88 | 0.12 | 81.52 | 8.508 |
| 17. | 1742.16 | 137.60 | 0.338 | 69.40 | 0.76 | 0.04 | 79.58 | 8.416 |
| 18. | 1844.64 | 142.44 | 0.350 | 163.64 | 0.37 | 0.04 | 65.17 | 11.309 |
| 19. | 1947.12 | 137.60 | 0.338 | 163.64 | 0.32 | 0.04 | 62.31 | 13.147 |
| 20. | 2049.60 | 142.44 | 0.350 | 118.10 | 0.52 | 0.05 | 72.16 | 9.762 |
| 21. | 2152.08 | 137.60 | 0.338 | 118.10 | 0.44 | 0.13 | 69.61 | 11.303 |
| 22. | 2254.56 | 142.44 | 0.350 | 89.04 | 0.69 | 0.04 | 77.47 | 9.198 |
| 23. | 2357.04 | 137.60 | 0.338 | 89.04 | 0.59 | 0.17 | 75.23 | 9.838 |
| No. | Ra | Ra net | Deviation Ra |
|---|---|---|---|
| 1. | 9.483 | 8.775 | 7.46% |
| 2. | 8.607 | 8.415 | 2.23% |
| 3. | 7.933 | 8.258 | −4.10% |
| 4. | 8.229 | 8.179 | 0.60% |
| 5. | 8.756 | 8.134 | 7.10% |
| 6. | 10.887 | 10.743 | 1.32% |
| 7. | 10.392 | 10.827 | −4.19% |
| 8. | 10.527 | 10.147 | 3.61% |
| 9. | 9.666 | 9.582 | 0.87% |
| 10. | 8.982 | 9.251 | −3.00% |
| 11. | 11.073 | 10.940 | 1.20% |
| 12. | 9.524 | 9.534 | −0.11% |
| 13. | 9.013 | 9.330 | −3.52% |
| 14. | 10.358 | 10.200 | 1.52% |
| 15. | 11.034 | 10.987 | 0.42% |
| 16. | 8.508 | 8.705 | −2.31% |
| 17. | 8.416 | 8.974 | −6.63% |
| 18. | 11.309 | 11.258 | 0.45% |
| 19. | 13.147 | 13.336 | −1.44% |
| 20. | 9.762 | 9.939 | −1.82% |
| 21. | 11.303 | 10.884 | 3.70% |
| 22. | 9.198 | 9.462 | −2.88% |
| 23. | 9.838 | 9.902 | −0.65% |
| 2.66% | |||
| No. | CO | CO net | Deviation CO |
|---|---|---|---|
| 1. | 1.2 | 0.91 | 11.42% |
| 2. | 1.41 | 1.34 | 4.78% |
| 3. | 1.84 | 1.86 | −1.36% |
| 4. | 2.35 | 2.36 | −0.49% |
| 5. | 2.93 | 2.76 | 5.85% |
| 6. | 0.60 | 0.62 | −2.20% |
| 7. | 0.78 | 0.78 | 0.67% |
| 8. | 1.00 | 1.3 | −2.82% |
| 9. | 1.25 | 1.31 | −4.25% |
| 10. | 1.54 | 1.55 | −0.51% |
| 11. | 0.51 | 0.57 | −10.50% |
| 12. | 0.66 | 0.67 | −1.27% |
| 13. | 0.83 | 0.83 | −0.24% |
| 14. | 1.3 | 1.3 | 0.63% |
| 15. | 1.27 | 1.20 | 4.95% |
| 16. | 1.8 | 1.8 | 0.45% |
| 17. | 0.95 | 0.96 | −0.86% |
| 18. | 0.57 | 0.61 | −5.74% |
| 19. | 0.51 | 0.57 | −10.65% |
| 20. | 0.72 | 0.73 | −0.96% |
| 21. | 0.64 | 0.66 | −3.16% |
| 22. | 0.89 | 0.87 | 1.66% |
| 23. | 0.78 | 0.79 | −0.83% |
| 3.31% | |||
| No. | TM | TM net | Deviation TM |
|---|---|---|---|
| 1. | 0.517 | 0.527 | −2.05% |
| 2. | 0.517 | 0.517 | −0.09% |
| 3. | 0.517 | 0.515 | 0.31% |
| 4. | 0.517 | 0.519 | −0.36% |
| 5. | 0.517 | 0.526 | −1.77% |
| 6. | 0.392 | 0.391 | 0.28% |
| 7. | 0.392 | 0.393 | −0.37% |
| 8. | 0.392 | 0.392 | −0.21% |
| 9. | 0.392 | 0.392 | −0.06% |
| 10. | 0.392 | 0.392 | −0.19% |
| 11. | 0.367 | 0.362 | 1.30% |
| 12. | 0.367 | 0.359 | 2.04% |
| 13. | 0.367 | 0.359 | 2.06% |
| 14. | 0.367 | 0.362 | 1.17% |
| 15. | 0.367 | 0.365 | 0.43% |
| 16. | 0.35 | 0.353 | −0.72% |
| 17. | 0.338 | 0.35 | −3.51% |
| 18. | 0.35 | 0.352 | −0.44% |
| 19. | 0.338 | 0.351 | −3.73% |
| 20. | 0.35 | 0.35 | 0.13% |
| 21. | 0.338 | 0.349 | −3.12% |
| 22. | 0.35 | 0.348 | 0.44% |
| 23. | 0.338 | 0.347 | −2.75% |
| 1.20% | |||
| Parameter | Training Power | Test Power |
|---|---|---|
| Ra | 0.983539 | 0.731064 |
| CO | 0.997696 | 0.998569 |
| TM | 0.996817 | 0.996756 |
| Total | 0.992684 | 0.908797 |
| vc | Revolution | vf | Ra | cat. 1 | NO | cat. 1 | TM | cat. 1 |
|---|---|---|---|---|---|---|---|---|
| [m.min−1] | [m.min−1] | [µm] | Ra | [€] | NO | [min] | Tm | |
| 4240.87 | 17,531 | 3.00 | 7.507 | VL | 3.03 | VH | 0.566 | VH |
| 4354.25 | 18,000 | 3.00 | 7.510 | VL | 3.13 | VH | 0.568 | VH |
| 4127.48 | 17,063 | 3.00 | 7.573 | VL | 2.92 | VH | 0.564 | VH |
| 4014.10 | 16,594 | 3.00 | 7.658 | VL | 2.81 | VH | 0.561 | VH |
| 3900.72 | 16,125 | 3.00 | 7.710 | VL | 2.70 | VH | 0.561 | VH |
| 3787.34 | 15,656 | 3.00 | 7.751 | VL | 2.58 | VH | 0.560 | VH |
| 3673.96 | 15,188 | 3.00 | 7.826 | VL | 2.45 | H | 0.559 | VH |
| 4240.87 | 17,531 | 3.63 | 7.918 | VL | 2.79 | VH | 0.538 | H |
| 4354.25 | 18,000 | 3.63 | 7.934 | VL | 2.92 | VH | 0.540 | H |
| 3560.58 | 14,719 | 3.00 | 7.937 | VL | 2.31 | H | 0.558 | VH |
| 2200.00 | 9095 | 9.32 | 11.144 | MH | 0.53 | VL | 0.371 | VL |
| 2200.00 | 9095 | 8.68 | 10.871 | MH | 0.53 | VL | 0.382 | VL |
| 2200.00 | 9095 | 9.95 | 11.420 | MH | 0.54 | VL | 0.362 | VL |
| 2200.00 | 9095 | 8.05 | 10.601 | MH | 0.54 | VL | 0.395 | L |
| 2313.38 | 9563 | 9.95 | 11.319 | MH | 0.55 | VL | 0.361 | VL |
| 2313.38 | 9563 | 9.32 | 11.042 | MH | 0.55 | VL | 0.370 | VL |
| 2200.00 | 9095 | 10.58 | 11.699 | H | 0.55 | VL | 0.356 | VL |
| 2200.00 | 9095 | 7.42 | 10.333 | M | 0.55 | VL | 0.410 | L |
| 2313.38 | 9563 | 10.58 | 11.600 | H | 0.56 | VL | 0.355 | VL |
| 2313.38 | 9563 | 8.68 | 10.770 | MH | 0.56 | VL | 0.381 | VL |
| 3673.96 | 15,188 | 12.47 | 10.066 | M | 0.77 | VL | 0.345 | VL |
| 3787.34 | 15,656 | 12.47 | 9.963 | M | 0.80 | VL | 0.345 | VL |
| 3560.58 | 14,719 | 12.47 | 10.176 | M | 0.73 | VL | 0.345 | VL |
| 3900.72 | 16,125 | 12.47 | 9.849 | M | 0.84 | VL | 0.345 | VL |
| 3447.20 | 14,250 | 12.47 | 10.328 | M | 0.70 | VL | 0.345 | VL |
| 3333.81 | 13,782 | 12.47 | 10.553 | M | 0.67 | VL | 0.345 | VL |
| 3787.34 | 15,656 | 13.11 | 9.935 | M | 0.79 | VL | 0.345 | VL |
| 3673.96 | 15,188 | 13.11 | 10.082 | M | 0.75 | VL | 0.345 | VL |
| 4014.10 | 16,594 | 12.47 | 9731 | M | 0.88 | VL | 0.345 | VL |
| 2540.14 | 10,501 | 12.47 | 12,479 | H | 0.60 | VL | 0.345 | VL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marcineková, K.; Janáková Sujová, A. Multi-Objective Optimization of Manufacturing Process Using Artificial Neural Networks. Systems 2024, 12, 569. https://doi.org/10.3390/systems12120569
Marcineková K, Janáková Sujová A. Multi-Objective Optimization of Manufacturing Process Using Artificial Neural Networks. Systems. 2024; 12(12):569. https://doi.org/10.3390/systems12120569
Chicago/Turabian StyleMarcineková, Katarína, and Andrea Janáková Sujová. 2024. "Multi-Objective Optimization of Manufacturing Process Using Artificial Neural Networks" Systems 12, no. 12: 569. https://doi.org/10.3390/systems12120569
APA StyleMarcineková, K., & Janáková Sujová, A. (2024). Multi-Objective Optimization of Manufacturing Process Using Artificial Neural Networks. Systems, 12(12), 569. https://doi.org/10.3390/systems12120569







