Layout Planning of a Basic Public Transit Network Considering Expected Travel Times and Transportation Efficiency
Abstract
:1. Introduction
1.1. Literature Review
1.2. Objective and Contribution
2. Notations, Assumptions, Problem Description, and Solution Framework
2.1. Planning Objective
2.2. Constraints
2.3. Planning Model Building
2.4. Solution Framework for BPTN Layout Planning
3. Analysis of Expected Transit Flow Distribution
3.1. Impedance Setting
3.2. ETFD Analysis for Different Types of Transit Systems
- (1)
- Capacity-free ETFD analysis
- (2)
- Capacity-constrained ETFD analysis
- (3)
- Cooperative ETFD analysis
4. Objective–Subjective Weighting Approach, Path Selection, and TGS
4.1. Generation of Candidate Path Set
4.2. Objective–Subjective Integrated Weighting Approach and Path Selection
4.2.1. Objective Weighting
4.2.2. Subjective Weighting
4.2.3. Path Selection
4.3. Topology Graph Simplification (TGS)
5. Case Study
5.1. Test Network, Calculation Scenarios, and Algorithm Parameter Settings
5.2. Comparison of Results in Different Scenarios
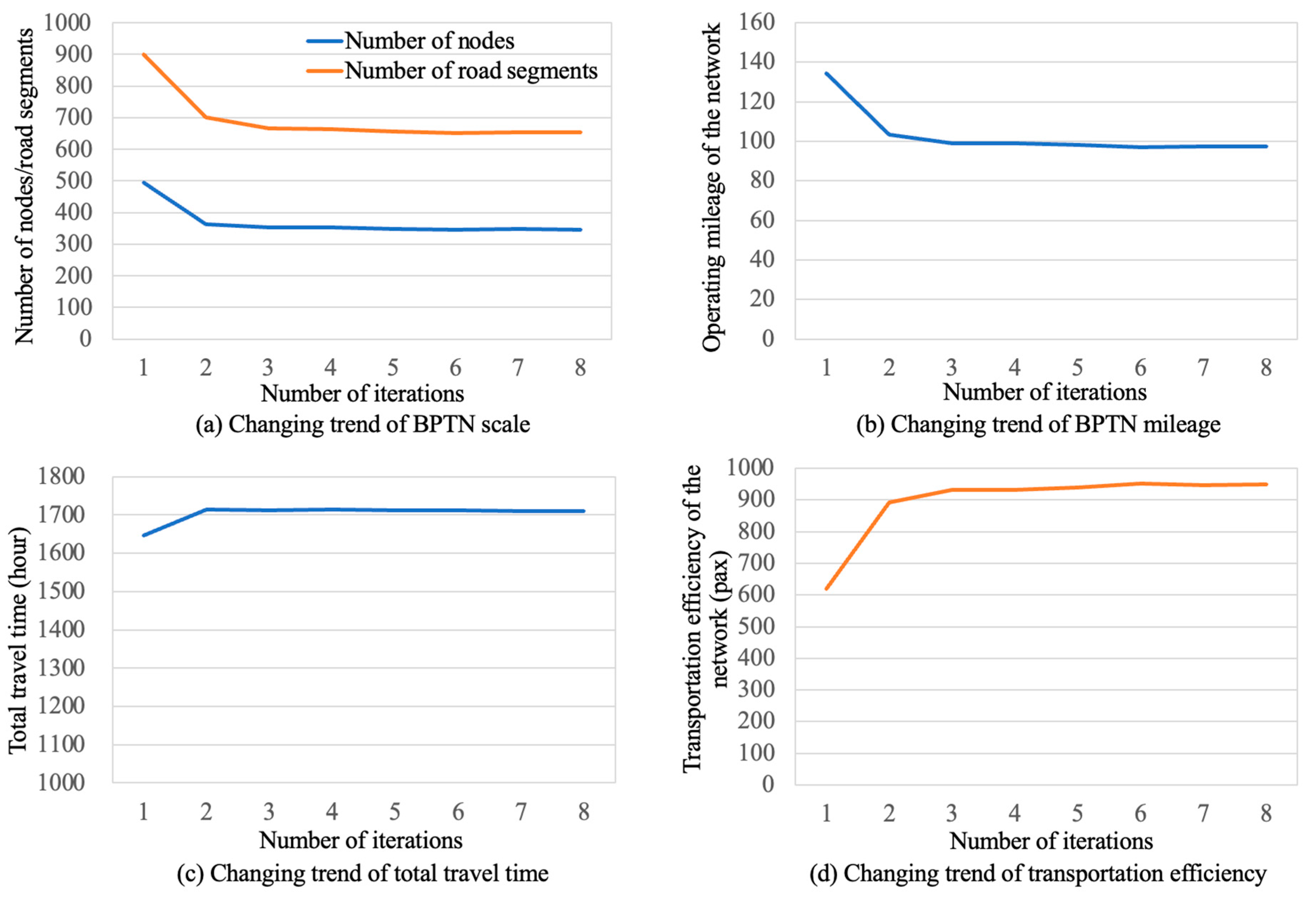
5.3. Analysis of the Computational Process
5.4. BPTN Layouts Under Different Demand Structures
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ceder, A.; Wilson, N.H.M. Bus network design. Transp. Res. Part B Methodol. 1986, 20, 331–344. [Google Scholar] [CrossRef]
- Baaj, M.H.; Mahmassani, H.S. An AI-based approach for transit route system planning and design. J. Adv. Transp. 1991, 25, 187–209. [Google Scholar] [CrossRef]
- Arbex, R.O.; da Cunha, C.B. Efficient transit network design and frequencies setting multi-objective optimization by alternating objective genetic algorithm. Transp. Res. Part B Methodol. 2015, 81, 355–376. [Google Scholar] [CrossRef]
- Liang, M.; Wang, W.; Dong, C.; Zhao, D. A cooperative coevolutionary optimization design of urban transit network and operating frequencies. Expert Syst. Appl. 2020, 160, 113736. [Google Scholar] [CrossRef]
- Ahern, Z.; Paz, A.; Corry, P. Approximate multi-objective optimization for integrated bus route design and service frequency setting. Transp. Res. Part B Methodol. 2022, 155, 1–25. [Google Scholar] [CrossRef]
- Cai, J.; Li, Z.; Long, S. Integrated Optimization of Route and Frequency for Rail Transit Feeder Buses under the Influence of Shared Motorcycles. Systems 2024, 12, 263. [Google Scholar] [CrossRef]
- Li, S.; Liang, Q.; Han, K.; Wen, K. An SD-LV Calculation Model for the Scale of the Urban Rail Transit Network. Systems 2024, 12, 233. [Google Scholar] [CrossRef]
- Mylonakou, M.; Chassiakos, A.; Karatzas, S.; Liappi, G. System dynamics analysis of the relationship between urban transportation and overall citizen satisfaction: A case study of Patras city, Greece. Systems 2023, 11, 112. [Google Scholar] [CrossRef]
- Christofides, N. Graph Theory: An Algorithmic Approach (Computer Science and Applied Mathematics); Academic Press, Inc.: New York, NY, USA, 1975. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability; W H Freeman: New York, NY, USA, 1979. [Google Scholar]
- Golden, B.L.; Raghavan, S.; Wasil, E.A. (Eds.) The Vehicle Routing Problem: Latest Advances and New Challenges; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 43. [Google Scholar]
- Diestel, R. Graph Theory; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- O’Kelly, M.E. The Location of Interacting Hub Facilities. Transp. Sci. 1986, 20, 92–106. [Google Scholar] [CrossRef]
- Vuchic, V.R. Urban Transit: Operations, Planning, and Economics; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Newell, G.F. Some issues relating to the optimal design of bus routes. Transp. Sci. 1979, 13, 20–35. [Google Scholar] [CrossRef]
- Daganzo, C.F. Structure of competitive transit networks. Transp. Res. Part B Methodol. 2010, 44, 434–446. [Google Scholar] [CrossRef]
- Thompson, G.L.; Matoff, T.G. Keeping Up with the Joneses: Radial vs. Multidestinational Transit in Decentralizing Regions. J. Am. Plan. Assoc. 2003, 69, 296–312. [Google Scholar] [CrossRef]
- Nourbakhsh, S.M.; Ouyang, Y. A structured flexible transit system for low demand areas. Transp. Res. Part B Methodol. 2012, 46, 204–216. [Google Scholar] [CrossRef]
- Chen, M.; Wu, F.; Yin, M.; Xu, J. Impact of road network topology on public transportation development. Wirel. Commun. Mob. Comput. 2021, 2021, 6209592. [Google Scholar] [CrossRef]
- Zhang, M. Travel choice with no alternative: Can land use reduce automobile dependence? J. Plan. Educ. Res. 2006, 25, 311–326. [Google Scholar] [CrossRef]
- Wong, R.C.P.; Szeto, W.Y.; Yang, L.; Li, Y.C.; Wong, S.C. Elderly users’ level of satisfaction with public transport services in a high-density and transit-oriented city. J. Transp. Health 2017, 7, 209–217. [Google Scholar] [CrossRef]
- De Bona, A.A.; de Oliveira Rosa, M.; Fonseca, K.V.O.; Lüders, R. A reduced model for complex network analysis of public transportation systems. Phys. A Stat. Mech. Its Appl. 2021, 567, 125715. [Google Scholar] [CrossRef]
- Bontorin, S.; Cencetti, G.; Gallotti, R.; Lepri, B.; De Domenico, M. Emergence of complex network topologies from flow-weighted optimization of network efficiency. Phys. Rev. X 2024, 14, 021050. [Google Scholar] [CrossRef]
- Polimeni, A.; Vitetta, A. Network design and vehicle routing problems in road transport systems: Integrating models and algorithms. Transp. Eng. 2024, 16, 100247. [Google Scholar] [CrossRef]
- Yujing, W.; Yi, D.; Fu, R.; Ruoxin, Z.; Pei, W.; Tian, D.; Qingyun, D. Analysing the spatial configuration of urban bus networks based on the geospatial network analysis method. Cities 2020, 96, 102406. [Google Scholar]
- Shanmukhappa, T.; Ho, I.W.H.; Tse, C.K. Spatial analysis of bus transport networks using network theory. Phys. A Stat. Mech. Its Appl. 2018, 502, 295–314. [Google Scholar] [CrossRef]
- Tian, Y.; Chen, H.; Xiao, D. The layout method for town public transit network based on TOD. In Proceedings of the International Conference on Transportation Engineering, Chengdu, China, 25–27 July 2009; pp. 1963–1968. [Google Scholar]
- Badia, H.; Estrada, M.; Robusté, F. Competitive transit network design in cities with radial street patterns. Transp. Res. Part B Methodol. 2014, 59, 161–181. [Google Scholar] [CrossRef]
- Fan, W.; Mei, Y.; Gu, W. Optimal design of intersecting bimodal transit networks in a grid city. Transp. Res. Part B Methodol. 2018, 111, 203–226. [Google Scholar] [CrossRef]
- Manual, H.C. Highway Capacity Manual; The National Academies Press: Washington, DC, USA, 2000; Volume 2, p. 1. [Google Scholar]
- Vuchic, V.R. Urban Transit Systems and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Vince, A. A framework for the greedy algorithm. Discret. Appl. Math. 2002, 121, 247–260. [Google Scholar] [CrossRef]
- Li, H.; Mao, B.; Bertini, R.L. Evaluating the impacts of bus facility design features on transit operations in Beijing, China: A simulation approach. In Proceedings of the 87th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 13–17 January 2008. [Google Scholar]
- Deng, T.; Nelson, J.D. Bus Rapid Transit implementation in Beijing: An evaluation of performance and impacts. Res. Transp. Econ. 2013, 39, 108–113. [Google Scholar] [CrossRef]
- Spiess, H. Conical volume-delay functions. Transp. Sci. 1990, 24, 153–158. [Google Scholar] [CrossRef]
- Bell, M.G. Alternatives to Dial’s logit assignment algorithm. Transp. Res. Part B Methodol. 1995, 29, 287–295. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Zhao, D.; Jin, K. A Revised Logit Model for Stochastic Traffic Assignment with a Relatively Stable Dispersion Parameter. IEEE Intell. Transp. Syst. Mag. 2021, 14, 92–104. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Lee, C.K. A multiple-path routing strategy for vehicle route guidance systems. Transp. Res. Part C Emerg. Technol. 1994, 2, 185–195. [Google Scholar] [CrossRef]
- Park, D. Multiple Path-Based Vehicle Routing in Dynamic and Stochastic Transportation Networks. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 1998. [Google Scholar]
- Yen, J.Y. Finding the k shortest loopless paths in a network. Manag. Sci. 1971, 17, 712–716. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of entropy weight method in decision-making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Cheng, Q.Y. Structure entropy weight method to confirm the weight of evaluating index. Syst. Eng. Theory Pract. 2010, 30, 1225–1228. [Google Scholar]
- Chen, P. Effects of the entropy weight on TOPSIS. Expert Syst. Appl. 2021, 168, 114186. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Bilga, P.S.; Singh, J.; Singh, S.; Scutaru, M.-L.; Pruncu, C.I. Revealing the benefits of entropy weights method for multi-objective optimization in machining operations: A critical review. J. Mater. Res. Technol. 2021, 10, 1471–1492. [Google Scholar] [CrossRef]











| Transit System Type | Hierarchy of Roads | Highest Design Speed | Average Operating Speed |
|---|---|---|---|
| Subway and light rail | Rail transit segments | 80 km/h | 50 km/h |
| BRT | Express and trunk roads | 45 km/h | 30 km/h |
| Regular bus | Urban secondary and branch roads | 25 km/h | 20 km/h |
| Local bus | Suburban roads | 20 km/h | 15 km/h |
| Application Scenarios | ETFD Analysis Methods | Assignment Approaches | Service Targets |
|---|---|---|---|
| Integrated transportation network without rail transit | Capacity-free ETFD analysis | Shortest-path assignment | Recognition of transit corridors for rail transit systems |
| Capacity-constrained ETFD analysis | Shortest-path incremental assignment | BRT systems | |
| Multi-path incremental assignment | Regular and local bus systems | ||
| Integrated transportation network with existing rail transit | Cooperative ETFD analysis | Shortest-path incremental assignment | BRT systems |
| Multi-path incremental assignment | Regular and local bus systems |
| Scenarios | Description | Algorithm and Parameter Settings |
|---|---|---|
| Scenario 1 | Remove rail transit lines to identify urban transit corridors | Capacity-free ETFD analysis Shortest-path assignment Subjective weight control parameter |
| Scenario 2 | Remove rail transit lines to optimize the BPTN layout for regular bus systems | Capacity-constrained ETFD analysis Multi-path incremental assignment Subjective weight control parameter |
| Scenario 3 | Optimize the BPTN layout for BRT systems to cooperate the rail transit system | Cooperative ETFD analysis Shortest-path incremental assignment Subjective weight control parameter |
| Scenario 4 | Optimize the BPTN layout for regular bus systems to cooperate the rail transit system | Cooperative ETFD analysis Multi-path incremental assignment Subjective weight control parameter |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, M.; Wang, W.; Chao, Y.; Dong, C. Layout Planning of a Basic Public Transit Network Considering Expected Travel Times and Transportation Efficiency. Systems 2024, 12, 550. https://doi.org/10.3390/systems12120550
Liang M, Wang W, Chao Y, Dong C. Layout Planning of a Basic Public Transit Network Considering Expected Travel Times and Transportation Efficiency. Systems. 2024; 12(12):550. https://doi.org/10.3390/systems12120550
Chicago/Turabian StyleLiang, Mingzhang, Wei Wang, Ye Chao, and Changyin Dong. 2024. "Layout Planning of a Basic Public Transit Network Considering Expected Travel Times and Transportation Efficiency" Systems 12, no. 12: 550. https://doi.org/10.3390/systems12120550
APA StyleLiang, M., Wang, W., Chao, Y., & Dong, C. (2024). Layout Planning of a Basic Public Transit Network Considering Expected Travel Times and Transportation Efficiency. Systems, 12(12), 550. https://doi.org/10.3390/systems12120550






