Modeling a Green and Reliable Intermodal Routing Problem for Food Grain Transportation Under Carbon Tax and Trading Regulations and Multi-Source Uncertainty
Abstract
1. Introduction
2. Problem Definition
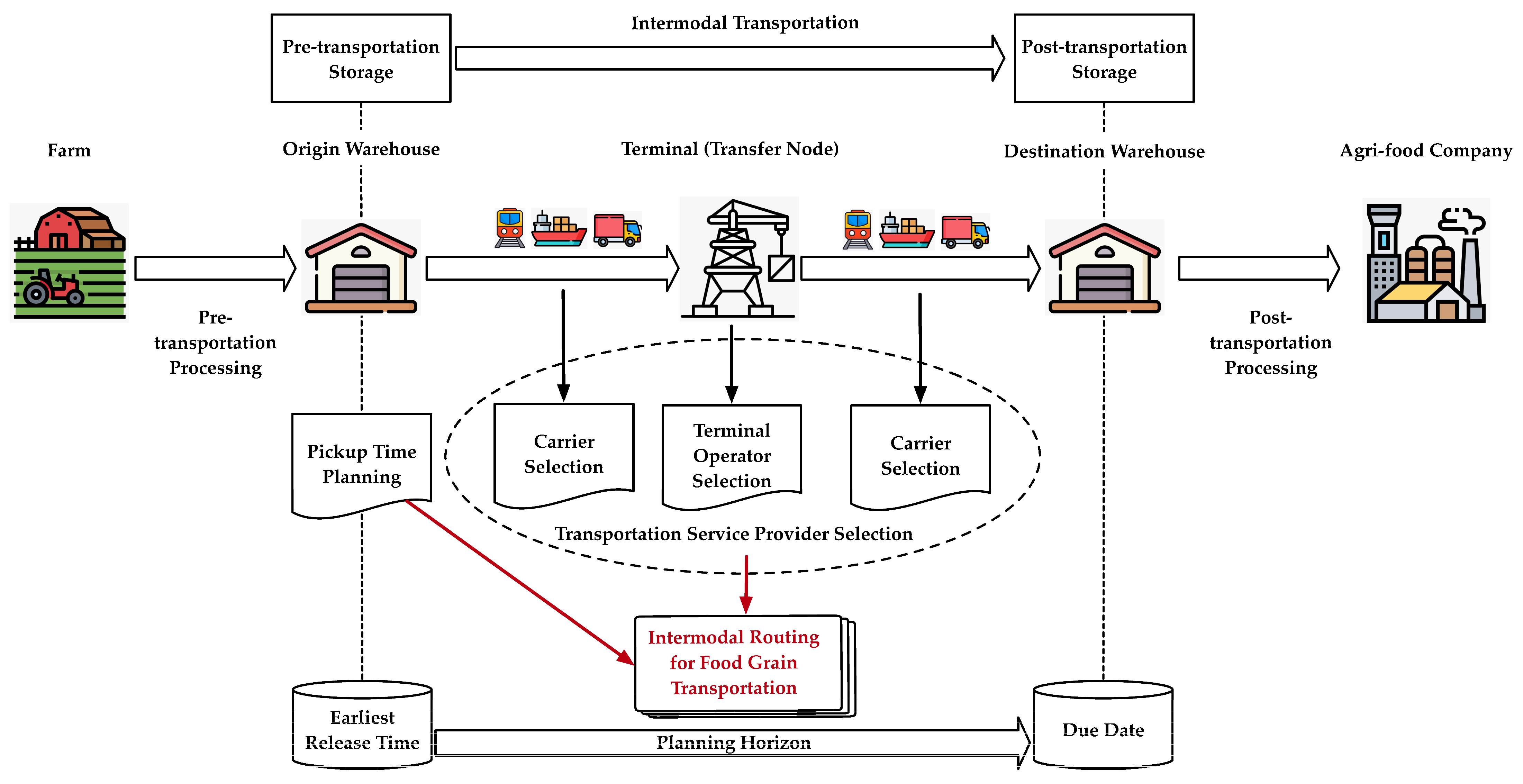
2.1. Scenario Description
2.2. Objective Formulation
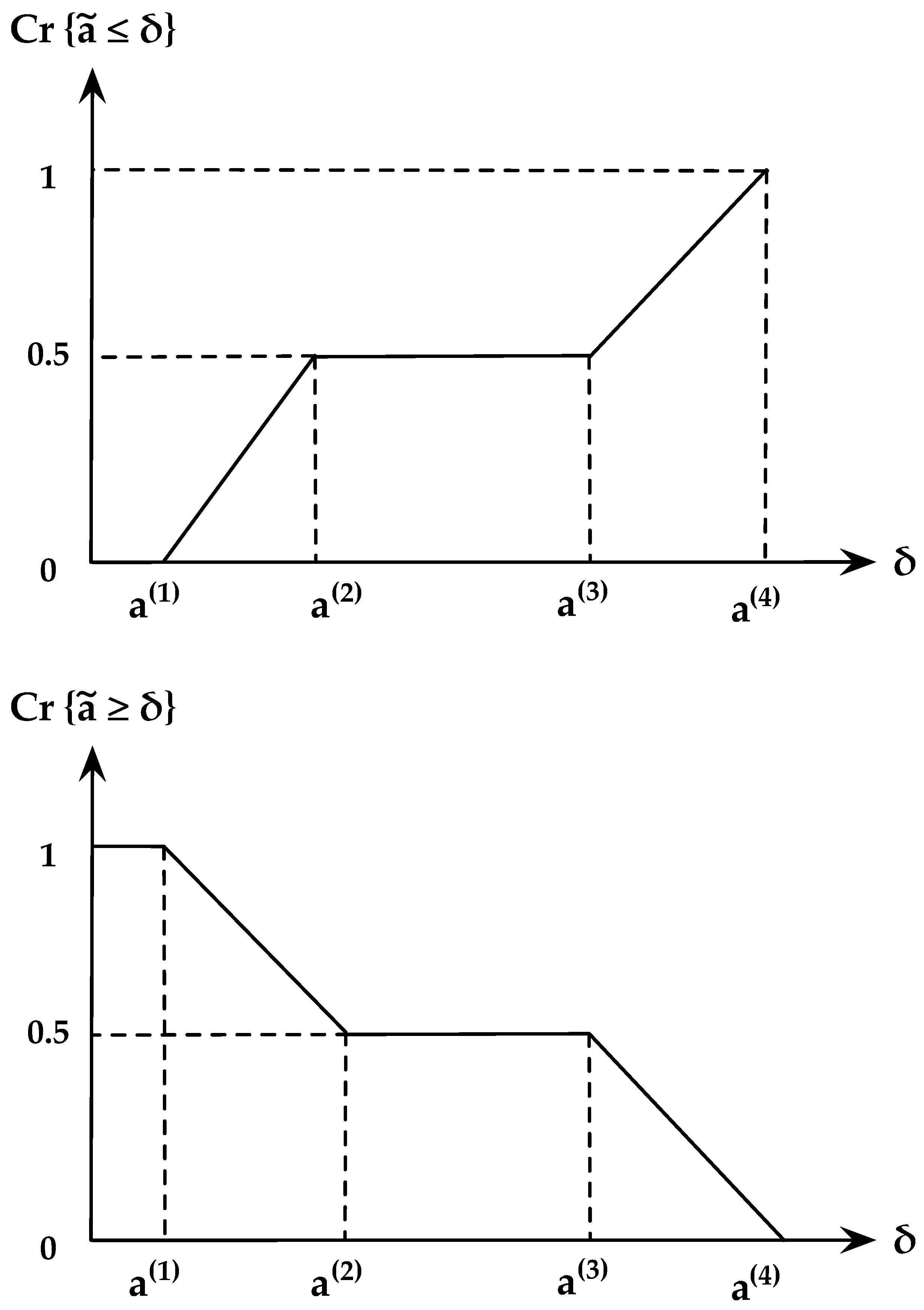
2.3. Multi-Source Uncertainty Modeling
3. Problem Modeling
3.1. Symbol Defination
3.2. Mathematical Model
4. A Two-Stage Solution Method
4.1. Stage I: Model Defuzzification
4.2. Stage II: Model Linearization
5. Numerical Case Study
5.1. Numerical Case Design
5.2. Sensitivity Analysis
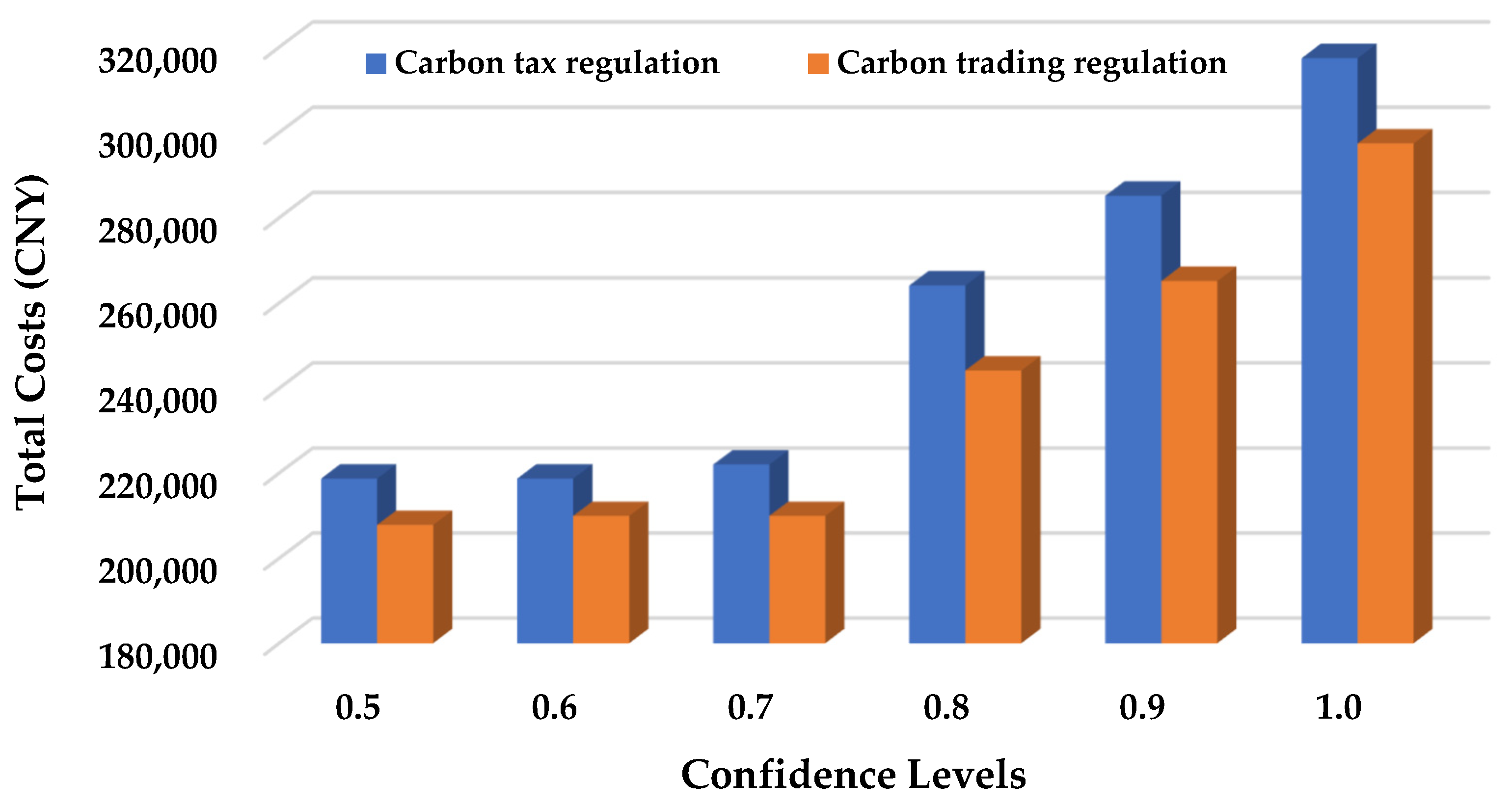
5.2.1. Sensitivity Analysis Concerning Confidence Levels
5.2.2. Sensitivity Analysis Concerning Wastage Threshold
5.3. Comparison Between Carbon Tax and Trading Regulations
5.4. Verificatin of Feasibility of Carbon Tax and Trading Regulations
5.5. Managerial Implications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Liu, X.; Xu, Y. Analysis of dynamic changes and main obstacle factors of grain supply and demand balance in northwest China. Sustainability 2023, 15, 10835. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y. Reflections on China’s food security and land use policy under rapid urbanization. Land Use Policy 2021, 109, 105699. [Google Scholar] [CrossRef]
- Wu, B.R.; Wang, L. Forecasting grain yield in China using attention-based ADE-Bi-IndRNN model. Oper. Res. Manag. Sci. 2024, 33, 102–107. [Google Scholar]
- Sun, X.; Sun, J.Q. Study on the overall safe and green development of logistics and supply chain of China‘s North-to-South food grain transportation. J. Commer. Econ. 2023, 2023, 76–79. [Google Scholar]
- Wan, M.; Kuang, H.B.; Jia, P.; Yu, F.P.; Ma, Q.L.; Zhang, Y.G.; Zhao, S.E. Integrated optimization of grain loading strategies and transportation routes considering losses. J. Transp. Syst. Eng. Inf. Technol. 2024. Available online: https://link.cnki.net/urlid/11.4520.U.20240725.1530.004 (accessed on 4 November 2024).
- Gonzales, D.; Searcy, E.M.; Ekşioğlu, S.D. Cost analysis for high-volume and long-haul transportation of densified biomass feedstock. Transp. Res. Part A Policy Pract. 2013, 49, 48–61. [Google Scholar] [CrossRef]
- Soliani, R.D. Logistics and transportation in Brazilian agribusiness: The flow of grain production. J. Econ. Bus. Manag. 2022, 10, 210–219. [Google Scholar] [CrossRef]
- Li, J.; Jing, K.; Khimich, M.; Shen, L. Optimization of green containerized grain supply chain transportation problem in Ukraine considering disruption scenarios. Sustainability 2023, 15, 7620. [Google Scholar] [CrossRef]
- de Faria, C.H.F.; Almeida, J.F.F.; Pinto, L.R. Simulation–optimisation approach for sustainable planning of intermodal logistics in the Brazilian grain export industry. Decis. Anal. J. 2024, 10, 100388. [Google Scholar] [CrossRef]
- Fuller, S.; Paggi, M. Efficient interfacing of the truck-to-ship intermodal grain transfer system: Port of Houston. J. Agric. Appl. Econ. 1979, 11, 95–100. [Google Scholar] [CrossRef]
- Lee, E. Spatial analysis for an intermodal terminal to support agricultural logistics: A case study in the upper great plains. Manag. Res. Rev. 2015, 38, 299–319. [Google Scholar] [CrossRef]
- Gronalt, M.; Schultze, R.C.; Posset, M. Intermodal transport—Basics, structure, and planning approaches. In Sustainable Transportation and Smart Logistics; Elsevier: Amsterdam, The Netherlands, 2019; pp. 123–149. [Google Scholar]
- Pencheva, V.; Asenov, A.; Sladkowski, A.; Ivanov, B.; Georgiev, I. Current issues of multimodal and intermodal cargo transportation. In Modern Trends and Research in Intermodal Transportation; Springer: Berlin/Heidelberg, Germany, 2022; pp. 51–124. [Google Scholar]
- Pang, Y.; Pan, S.; Ballot, E. Robust optimization for perishable product distribution under uncertainty of multimodal transportation services. IFAC-WorksOnLine 2023, 56, 7620–7625. [Google Scholar] [CrossRef]
- Nourbakhsh, S.M.; Bai, Y.; Maia, G.D.; Ouyang, Y.; Rodriguez, L. Grain supply chain network design and logistics planning for reducing post-harvest loss. Biosyst. Eng. 2016, 151, 105–115. [Google Scholar] [CrossRef]
- An, K.; Ouyang, Y. Robust grain supply chain design considering post-harvest loss and harvest timing equilibrium. Transp. Res. Part E Logist. Transp. Rev. 2016, 88, 110–128. [Google Scholar] [CrossRef]
- Mogale, D.G.; Kumar, S.K.; Tiwari, M.K. Green food supply chain design considering risk and post-harvest losses: A case study. Ann. Oper. Res. 2020, 295, 257–284. [Google Scholar] [CrossRef]
- Gupta, M.; Kaur, H.; Singh, S.P. Multi-echelon agri-food supply chain network design integrating operational and strategic objectives: A case of public distribution system in India. Ann. Oper. Res. 2021, 1–58. [Google Scholar] [CrossRef]
- Taşkıner, T.; Bilgen, B. Optimization models for harvest and production planning in agri-food supply chain: A systematic review. Logistics 2021, 5, 52. [Google Scholar] [CrossRef]
- Maiyar, L.M.; Thakkar, J.J. Robust optimisation of sustainable food grain transportation with uncertain supply and intentional disruptions. Int. J. Prod. Res. 2020, 58, 5651–5675. [Google Scholar] [CrossRef]
- Maiyar, L.M.; Thakkar, J.J. Environmentally conscious logistics planning for food grain industry considering wastages employing multi objective hybrid particle swarm optimization. Transp. Res. Part E Logist. Transp. Rev. 2019, 127, 220–248. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Y.; Xiao, Y.; Mo, W.; Xiao, Y.; Wang, J. Optimization of multimodal paths for oversize and heavyweight cargo under different carbon pricing policies. Sustainability 2024, 16, 6588. [Google Scholar] [CrossRef]
- Zhang, X.; Yuan, X.M.; Jiang, Y.D. Optimization of multimodal transportation under uncertain demand and stochastic carbon trading price. Syst. Eng.-Theory Pract. 2021, 41, 2609–2620. [Google Scholar]
- Cheng, X.Q.; Jin, C.; Yao, G.Q.; Wang, C. Research on robust optimization for route selection problem in multimodal transportation under the cap and trade policy. Chin. J. Manag. Sci. 2021, 29, 82–90. [Google Scholar]
- Cheng, X.Q.; Jin, C.; Wang, C.; Mamatok, Y. Impacts of different low-carbon policies on route decisions in intermodal freight transportation: The case of the west river region in China. In Proceedings of the International Forum on Shipping, Ports and Airports (IFSPA), Hong Kong Polytechnic University, Hong Kong, China, 20–24 May 2019. [Google Scholar]
- Wang, S.; Zhang, Q.; Wang, W. The impact of carbon abatement policies on port intermodal freight transportation routing and cost. In Proceedings of the 3rd International Conference on Electrical and Information Technologies for Rail Transportation (EITRT) 2017: Transportation, Changsha, China, 20–22 October 2017; Springer: Singapore, 2018; pp. 689–699. [Google Scholar]
- Grossmann, I.E.; Apap, R.M.; Calfa, B.A.; García-Herreros, P.; Zhang, Q. Recent advances in mathematical programming techniques for the optimization of process systems under uncertainty. Comput. Chem. Eng. 2016, 91, 3–14. [Google Scholar] [CrossRef]
- Delbart, T.; Molenbruch, Y.; Braekers, K.; Caris, A. Uncertainty in intermodal and synchromodal transport: Review and future research directions. Sustainability 2021, 13, 3980. [Google Scholar] [CrossRef]
- Lu, K.; Liao, H.; Zavadskas, E.K. An overview of fuzzy techniques in supply chain management: Bibliometrics, methodologies, applications and future directions. Technol. Econ. Dev. Econ. 2021, 27, 402–458. [Google Scholar] [CrossRef]
- Castaneda, J.; Ghorbani, E.; Ammouriova, M.; Panadero, J.; Juan, A.A. Optimizing transport logistics under uncertainty with simheuristics: Concepts, review and trends. Logistics 2022, 6, 42. [Google Scholar] [CrossRef]
- Tian, W.; Cao, C. A generalized interval fuzzy mixed integer programming model for a multimodal transportation problem under uncertainty. Eng. Optim. 2017, 49, 481–498. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Yang, K.; Jiang, L. Uncertain programming model for the cross-border multimodal container transport system based on inland ports. Axioms 2023, 12, 132. [Google Scholar] [CrossRef]
- Fazayeli, S.; Eydi, A.; Kamalabadi, I.N. Location-routing problem in multimodal transportation network with time windows and fuzzy demands: Presenting a two-part genetic algorithm. Comput. Ind. Eng. 2018, 119, 233–246. [Google Scholar] [CrossRef]
- Wang, C.N.; Dang, T.T.; Le, T.Q.; Kewcharoenwong, P. Transportation optimization models for intermodal networks with fuzzy node capacity, detour factor, and vehicle utilization constraints. Mathematics 2020, 8, 2109. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Q.; Ma, L.; Zhang, Z. Sparrow search algorithm with adaptive t distribution for multi-objective low-carbon multimodal transportation planning problem with fuzzy demand and fuzzy time. Expert Syst. Appl. 2024, 238, 122042. [Google Scholar] [CrossRef]
- Huang, Y.; Li, T.; Ma, L. A multi-objective multimodal transportation route planning model considering fuzzy node loads. Int. J. Innov. Comput. Inf. Control 2024, 20, 1331–1350. [Google Scholar]
- Li, X.; Sun, Y.; Qi, J.; Wang, D. Chance-constrained optimization for a green multimodal routing problem with soft time window under twofold uncertainty. Axioms 2024, 13, 200. [Google Scholar] [CrossRef]
- Sun, Y. Fuzzy approaches and simulation-based reliability modeling to solve a road-rail intermodal routing problem with soft delivery time windows when demand and capacity are uncertain. Int. J. Fuzzy Syst. 2020, 22, 2119–2148. [Google Scholar] [CrossRef]
- Sun, Y.; Yu, N.; Huang, B. Green road–rail intermodal routing problem with improved pickup and delivery services integrating truck departure time planning under uncertainty: An interactive fuzzy programming approach. Complex Intell. Syst. 2022, 8, 1459–1486. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, F.Y.; Yuan, X.M.; Zhang, H.Y. Low-carbon multimodal transportation path optimization under dual uncertainty of demand and time. Sustainability 2021, 13, 8180. [Google Scholar] [CrossRef]
- Flodén, J.; Bärthel, F.; Sorkina, E. Transport buyers choice of transport service–A literature review of empirical results. Res. Transp. Bus. Manag. 2017, 23, 35–45. [Google Scholar] [CrossRef]
- Maiyar, L.M.; Thakkar, J.J. Modelling and analysis of intermodal food grain transportation under hub disruption towards sustainability. Int. J. Prod. Econ. 2019, 217, 281–297. [Google Scholar] [CrossRef]
- Wan, S.P.; Dong, J.Y. Possibility linear programming with trapezoidal fuzzy numbers. Appl. Math. Model. 2014, 38, 1660–1672. [Google Scholar] [CrossRef]
- Ebrahimnejad, A.; Tavana, M. A novel method for solving linear programming problems with symmetric trapezoidal fuzzy numbers. Appl. Math. Model. 2014, 38, 4388–4395. [Google Scholar] [CrossRef]
- Asghari, M.; Fathollahi-Fard, A.M.; Mirzapour Al-E-Hashem, S.M.J.; Dulebenets, M.A. Transformation and linearization techniques in optimization: A state-of-the-art survey. Mathematics 2022, 10, 283. [Google Scholar] [CrossRef]
- Xiong, G.; Wang, Y. Best routes selection in multimodal networks using multi-objective genetic algorithm. J. Comb. Optim. 2014, 28, 655–673. [Google Scholar] [CrossRef]
- Anghinolfi, D.; Paolucci, M.; Sacone, S.; Siri, S. Integer programming and ant colony optimization for planning intermodal freight transportation operations. In Proceedings of the 2011 IEEE International Conference on Automation Science and Engineering, Shanghai, China, 10–12 June 2011; IEEE: New York, NY, USA, 2011; pp. 214–219. [Google Scholar]
- Xu, J.; Zhou, X. Approximation based fuzzy multi-objective models with expected objectives and chance constraints: Application to earth-rock work allocation. Inf. Sci. 2013, 238, 75–95. [Google Scholar] [CrossRef]
- Kundu, P.; Kar, S.; Maiti, M. Multi-objective multi-item solid transportation problem in fuzzy environment. Appl. Math. Model. 2013, 37, 2028–2038. [Google Scholar] [CrossRef]
- Dong, H.; Wu, Y. Green closed-loop supply chain network based on PIWOA multi-objective fuzzy optimal design. Ind. Eng. J. 2020, 24, 27. [Google Scholar]
- Zheng, Y.; Liu, B. Fuzzy vehicle routing model with credibility measure and its hybrid intelligent algorithm. Appl. Math. Comput. 2006, 176, 673–683. [Google Scholar] [CrossRef]
- Xie, Y.; Lu, W.; Wang, W.; Quadrifoglio, L. A multimodal location and routing model for hazardous materials transportation. J. Hazard. Mater. 2012, 227, 135–141. [Google Scholar] [CrossRef]
- Zandkarimkhani, S.; Mina, H.; Biuki, M.; Govindan, K. A chance constrained fuzzy goal programming approach for perishable pharmaceutical supply chain network design. Ann. Oper. Res. 2020, 295, 425–452. [Google Scholar] [CrossRef]
- Afify, B.; Soeanu, A.; Awasthi, A. Separation linearization approach for the capacitated facility location problem under disruption. Expert Syst. Appl. 2021, 169, 114187. [Google Scholar] [CrossRef]
- Wu, X.; Wu, Y.; Cheng, X.; Cheng, C.; Li, Z.; Wu, Y. A mixed-integer linear programming model for hydro unit commitment considering operation constraint priorities. Renew. Energy 2023, 204, 507–520. [Google Scholar] [CrossRef]
- Sun, Y.; Lang, M. Bi-objective optimization for multi-modal transportation routing planning problem based on Pareto optimality. J. Ind. Eng. Manag. 2015, 8, 1195–1217. [Google Scholar] [CrossRef]
- Jiang, Q.W.; Lin, Y.; Feng, F.L. Research on multimodal transport path optimization problem considering carbon tax value changes under fuzzy time. J. Ind. Technol. Econ. 2020, 39, 81–88. [Google Scholar]
- Sun, Y.; Yu, N.; Wang, D.Z.; Chen, W.J. Study on the bi-objective optimization for the multimodal routing problem with multiple time windows. Railw. Transp. Econ. 2021, 43, 82–89. [Google Scholar]
- Yuan, X.M.; Jiang, Y.D.; Zhang, X. Research on robust optimization of interval-based fuzzy multimodal transport paths under low-carbon policies. Ind. Eng. Manag. 2021, 26, 134–141. [Google Scholar]
- Li, Y.L.; Lv, Y.B. Study on economy of multi-modal transport considering carbon emission and time cost. China Transp. Rev. 2023, 45, 143–147. [Google Scholar]
- Sun, Y.; Zhang, C.; Sun, G. An Interval fuzzy programming approach to solve a green intermodal routing problem for timber transportation under uncertain information. Forests 2024, 15, 2003. [Google Scholar] [CrossRef]
- Azadi, A.H.S.; Khalilzadeh, M.; Antucheviciene, J.; Heidari, A.; Soon, A. A sustainable multi-objective model for capacitated-electric-vehicle-routing-problem considering hard and soft time windows as well as partial recharging. Biomimetics 2024, 9, 242. [Google Scholar] [CrossRef]
- Zhang, K.; He, F.; Zhang, Z.; Lin, X.; Li, M. Multi-vehicle routing problems with soft time windows: A multi-agent reinforcement learning approach. Transp. Res. Part C Emerg. Technol. 2020, 121, 102861. [Google Scholar] [CrossRef]
- Taş, D.; Jabali, O.; Van Woensel, T. A vehicle routing problem with flexible time windows. Comput. Oper. Res. 2014, 52, 39–54. [Google Scholar] [CrossRef]
- Guo, N.; Qian, B.; Shen, Y.Q.; Na, J.; Hu, R.; Geng, Y. Hyper-heuristic ant colony optimization algorithm for green two-echelon multi-period vehicle routing problem with flexible time windows. Control Decis. 2024. [Google Scholar] [CrossRef]
- Li, D.; Gan, M.; Qiao, Y.; Ou, Q.; Liu, X. A MINP model and hybrid heuristic algorithm for railway cold chain service network design problem: A case study of China. Int. J. Prod. Res. 2024, 1–22. [Google Scholar] [CrossRef]
- Wang, S.; Tao, F.; Shi, Y. Optimization of location–routing problem for cold chain logistics considering carbon footprint. Int. J. Environ. Res. Public Health 2018, 15, 86. [Google Scholar] [CrossRef] [PubMed]
- Dalman, H.; Güzel, N.; Sivri, M. A fuzzy set-based approach to multi-objective multi-item solid transportation problem under uncertainty. Int. J. Fuzzy Syst. 2016, 18, 716–729. [Google Scholar] [CrossRef]
- Chen, S.M. Evaluating weapon systems using fuzzy arithmetic operations. Fuzzy Sets Syst. 1996, 77, 265–276. [Google Scholar] [CrossRef]
- Akther, T.; Ahmad, S.U. A computational method for fuzzy arithmetic operations. Daffodil Int. Univ. J. Sci. Technol. 2009, 4, 18–22. [Google Scholar] [CrossRef]
- Patra, K. Fuzzy risk analysis using a new technique of ranking of generalized trapezoidal fuzzy numbers. Granul. Comput. 2022, 7, 127–140. [Google Scholar] [CrossRef]
- Peykani, P.; Hosseinzadeh Lotfi, F.; Sadjadi, S.J.; Ebrahimnejad, A.; Mohammadi, E. Fuzzy chance-constrained data envelopment analysis: A structured literature review, current trends, and future directions. Fuzzy Optim. Decis. Mak. 2022, 21, 197–261. [Google Scholar] [CrossRef]


| Types of Food Grains | Grain-Producing Areas | Freight Volumes (10 Thousand Ton) | Transportation Modes | Destinations |
|---|---|---|---|---|
| Corn | Heilongjiang, Jilin, Liaoning, and Inner Mongolia | 14,000 | Road, rail, and rail–sea intermodal transportation | North China, Sichuan, Chongqing, Guangdong, Guangxi, and coastal regions |
| Huang-Huai Plain | 2000 | Water, road, and rail transportation | Hunan, Hubei, and Hunan-Jiangxi region | |
| Japonica rice | Northeast China | 1500~1600 | Rail, and rail–sea intermodal transportation | North China, East China, Southeast China, and Northwest China |
| Jiangsu | 600~700 | Water, road, and rail transportation | Middle and lower Yangtze River reaches, and Jiangsu-Zhejiang region | |
| Non-glutinous rice | Yangtze River basin | 1600 | Water, road, and rail transportation | Guangdong, Guangxi, Zhejiang, and Fujian |
| Transportation Modes | (CNY/TEU) | (CNY/(TEU·km)) | (km/h) | (kg/(TEU·km)) | (%/100 km) |
|---|---|---|---|---|---|
| Rail | 500 | 2.03 | (50, 55, 60, 65) | (0.060, 0.075, 0.085, 0.105) | (0.030, 0.040, 0.045, 0.055) |
| Road | 15 | 8 | (50, 60, 70, 80) | (2.150, 2.350, 2.550, 2.650) | (0.040, 0.055, 0.065, 0.080) |
| Water | 950 | 0 | (20, 25, 30, 40) | (0.075, 0.085, 0.105, 0.115) | (0.035, 0.045, 0.060, 0.075) |
| Transfer Types | (CNY/TEU) | (min/TEU) | (kg/TEU) | (%) |
|---|---|---|---|---|
| Rail—Road | 5 | (2.0, 2.6, 3.5, 4.4) | (4.05, 4.65, 5.10, 6.05) | (0.05, 0.15, 0.25, 0.40) |
| Rail—Water | 7 | (4.0, 5.3, 6.0, 7.5) | (5.30, 5.85, 6.10, 6.60) | (0.15, 0.25, 0.40, 0.55) |
| Road—Water | 10 | (3.0, 4.5, 6.5, 8.0) | (5.20, 5.70, 6.20, 6.50) | (0.10, 0.20, 0.45, 0.60) |
| Parameters | (TEU) | (CNY/TEU) | (CNY/(TEU·h)) | (CNY/(TEU·h)) | ||
|---|---|---|---|---|---|---|
| Values | (25, 28, 31, 35) | 50,000 | 8:00 a.m. on day 1 | 5:00 p.m. on day 3 | 30 | 10 |
| Number of Variables | Number of Integer Variables | Number of Constraints | Number of Nonzeros | Solver State |
|---|---|---|---|---|
| 1794 | 569 | 1033 | 10,854 | Global Optimum |
| Wastage Thresholds | 1.0% | 1.5% | 2.0% | 2.5% | 3.0% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Regulations | Tax | Trading | Tax | Trading | Tax | Trading | Tax | Trading | Tax | Trading | |
| Confidence levels | 0.5 | 7963 | 15,975 | 8278 | 13,558 | 8728 | 13,558 | 8728 | 13,558 | 8728 | 13,558 |
| 0.6 | 7963 | 10,118 | 8278 | 13,613 | 8728 | 13,613 | 8728 | 13,613 | 8728 | 13,613 | |
| 0.7 | 8282 | 12,180 | 9084 | 13,613 | 9084 | 13,613 | 9084 | 13,613 | 9084 | 13,613 | |
| 0.8 | 12,776 | 12,776 | 10,373 | 10,373 | 17,607 | 17,607 | 10,706 | 10,706 | 10,706 | 10,750 | |
| 0.9 | — | — | — | — | 27,267 | 27,267 | 20,436 | 20,436 | 17,406 | 17,406 | |
| 1.0 | — | — | — | — | — | — | — | — | 28,197 | 28,197 | |
| Wastage Thresholds | 1.0% | 1.5% | 2.0% | 2.5% | 3.0% | |
|---|---|---|---|---|---|---|
| Confidence levels | 0.5 | 7963 | 6510 | 5575 | 5575 | 5575 |
| 0.6 | 7963 | 6510 | 6231 | 6231 | 6231 | |
| 0.7 | 8282 | 6510 | 6510 | 6510 | 6510 | |
| 0.8 | 12,776 | 10,373 | 10,029 | 8892 | 8663 | |
| 0.9 | — | — | 26,178 | 14,978 | 14,749 | |
| 1.0 | — | — | — | — | 28,179 | |
| Wastage Thresholds | 1.0% | 1.5% | 2.0% | 2.5% | 3.0% | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Regulations | Tax | Trading | Tax | Trading | Tax | Trading | Tax | Trading | Tax | Trading | |
| Confidence levels | 0.5 | 0 | 50.2 | 21.4 | 52.0 | 36.2 | 58.9 | 36.1 | 58.9 | 36.1 | 58.9 |
| 0.6 | 0 | 21.3 | 21.4 | 52.2 | 28.6 | 54.2 | 28.6 | 54.2 | 28.6 | 54.2 | |
| 0.7 | 0 | 32.0 | 28.3 | 52.2 | 28.3 | 52.2 | 28.3 | 52.2 | 28.3 | 52.2 | |
| 0.8 | 0 | 0 | 0 | 0 | 43.0 | 43.0 | 16.9 | 16.9 | 19.1 | 19.4 | |
| 0.9 | — | — | — | — | 4.0 | 4.0 | 26.7 | 26.7 | 15.3 | 15.3 | |
| 1.0 | — | — | — | — | — | — | — | — | 0.1 | 0.1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, C.; Chen, A.; Sun, G. Modeling a Green and Reliable Intermodal Routing Problem for Food Grain Transportation Under Carbon Tax and Trading Regulations and Multi-Source Uncertainty. Systems 2024, 12, 547. https://doi.org/10.3390/systems12120547
Sun Y, Zhang C, Chen A, Sun G. Modeling a Green and Reliable Intermodal Routing Problem for Food Grain Transportation Under Carbon Tax and Trading Regulations and Multi-Source Uncertainty. Systems. 2024; 12(12):547. https://doi.org/10.3390/systems12120547
Chicago/Turabian StyleSun, Yan, Chen Zhang, Ailing Chen, and Guohua Sun. 2024. "Modeling a Green and Reliable Intermodal Routing Problem for Food Grain Transportation Under Carbon Tax and Trading Regulations and Multi-Source Uncertainty" Systems 12, no. 12: 547. https://doi.org/10.3390/systems12120547
APA StyleSun, Y., Zhang, C., Chen, A., & Sun, G. (2024). Modeling a Green and Reliable Intermodal Routing Problem for Food Grain Transportation Under Carbon Tax and Trading Regulations and Multi-Source Uncertainty. Systems, 12(12), 547. https://doi.org/10.3390/systems12120547






