Development of a Forecasting Framework Based on Advanced Machine Learning Algorithms for Greenhouse Gas Emissions
Abstract
1. Introduction
2. Materials and Methods
2.1. Machine Learning Algorithms
2.1.1. Multiple Linear Regression
2.1.2. Random Forest Regression
2.1.3. K-Nearest Neighbor Regression
2.1.4. XGBoost Regression
2.1.5. Support Vector Regression
2.1.6. Multilayer Perceptron Regression
2.2. Performance Evaluation
3. Data Description
4. Results and Discussion
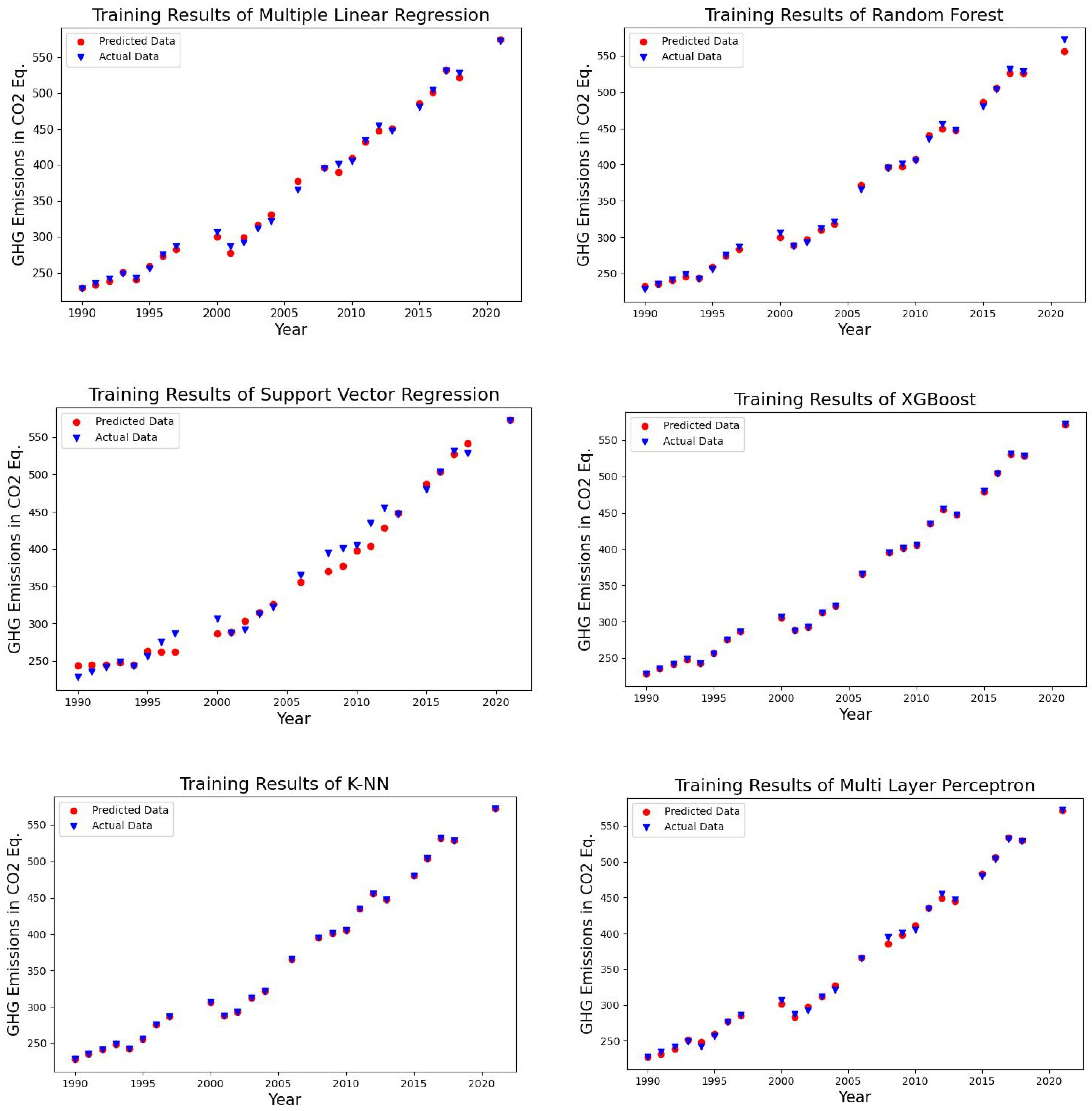
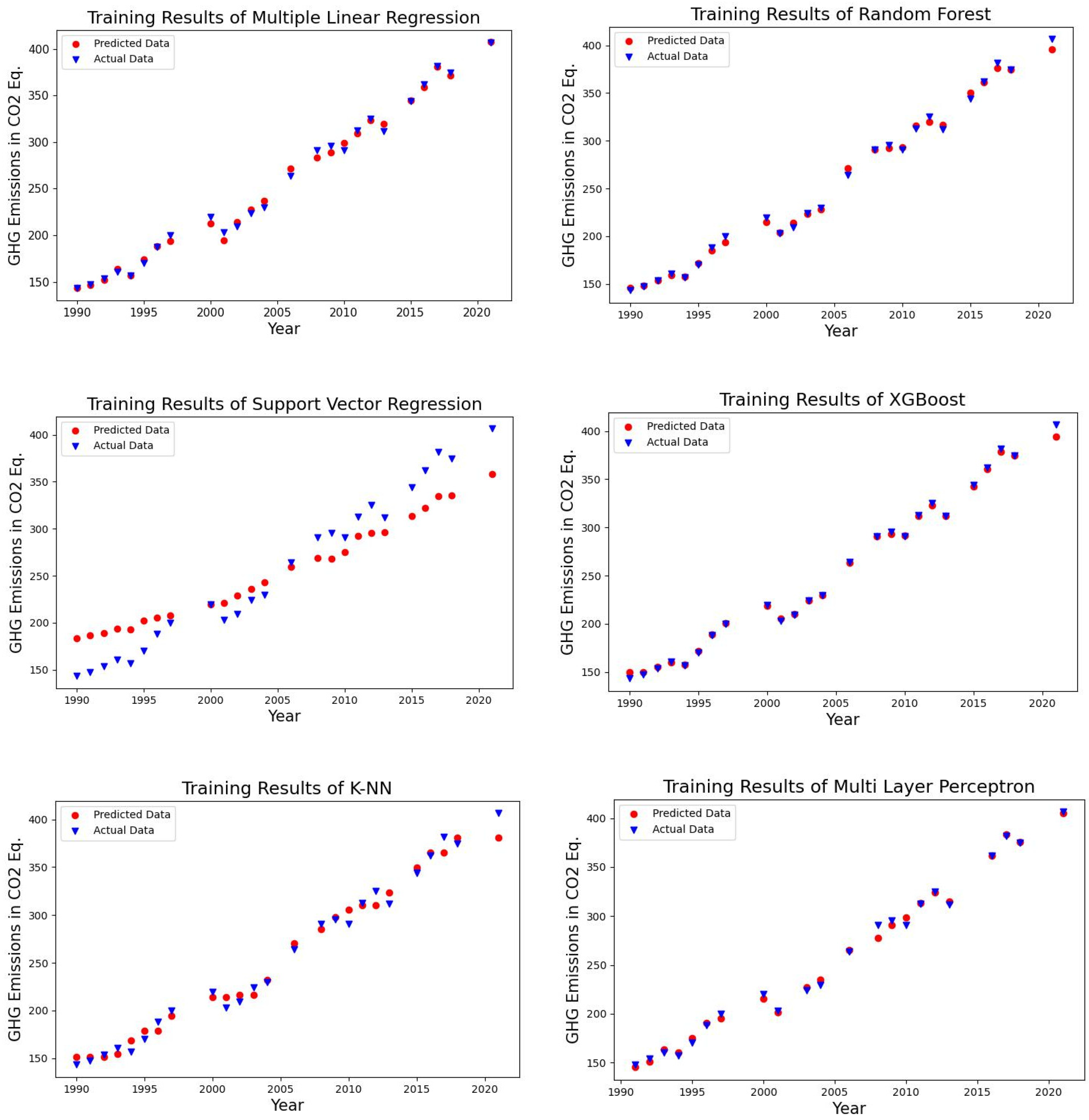
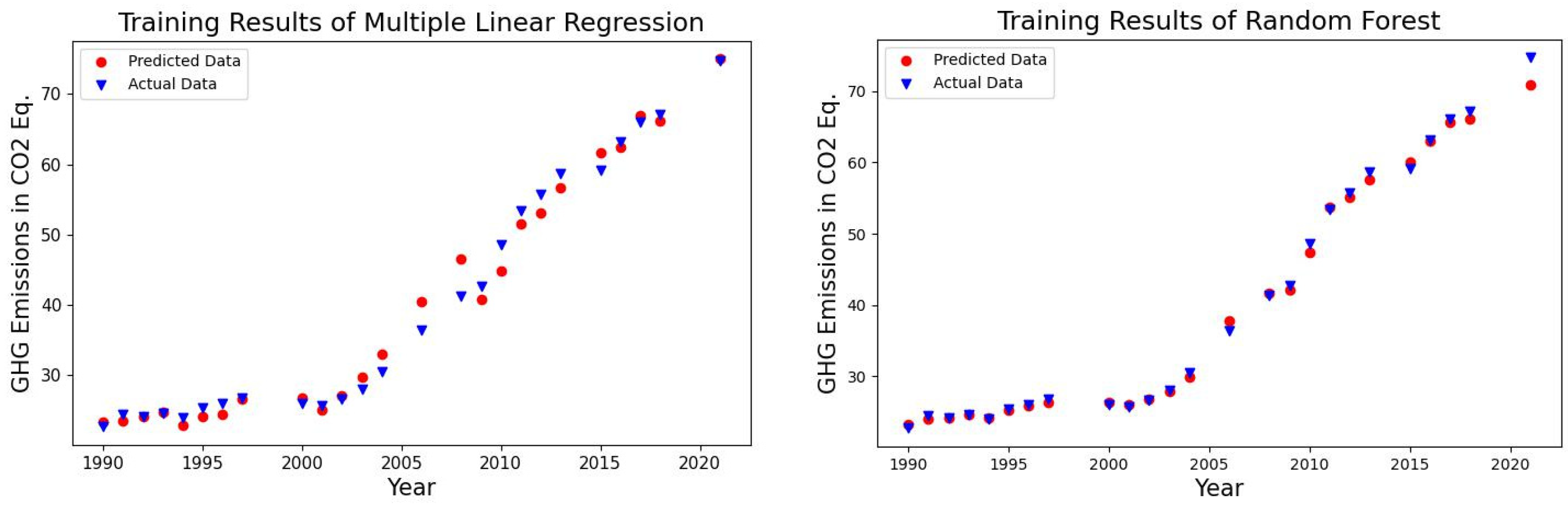
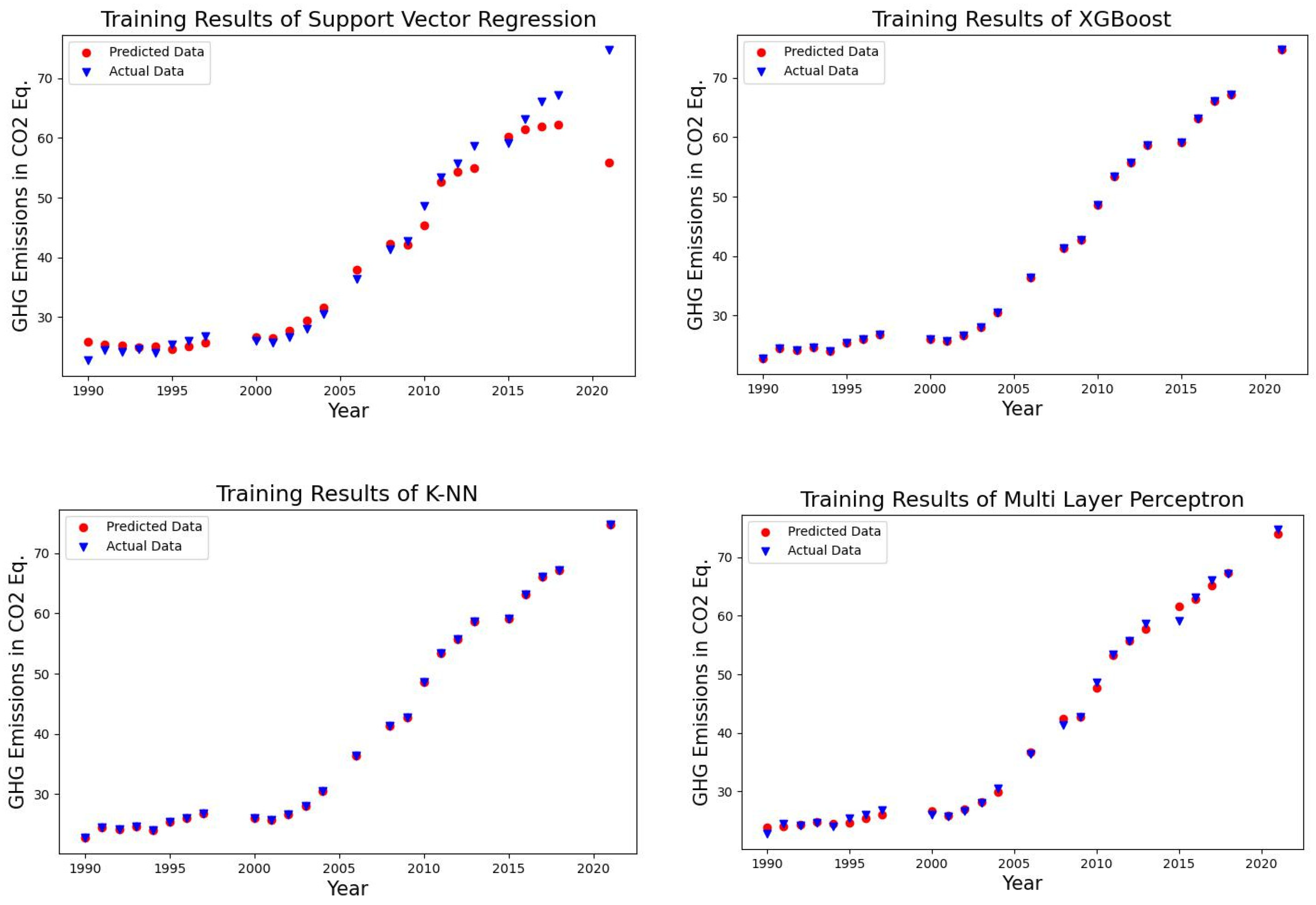
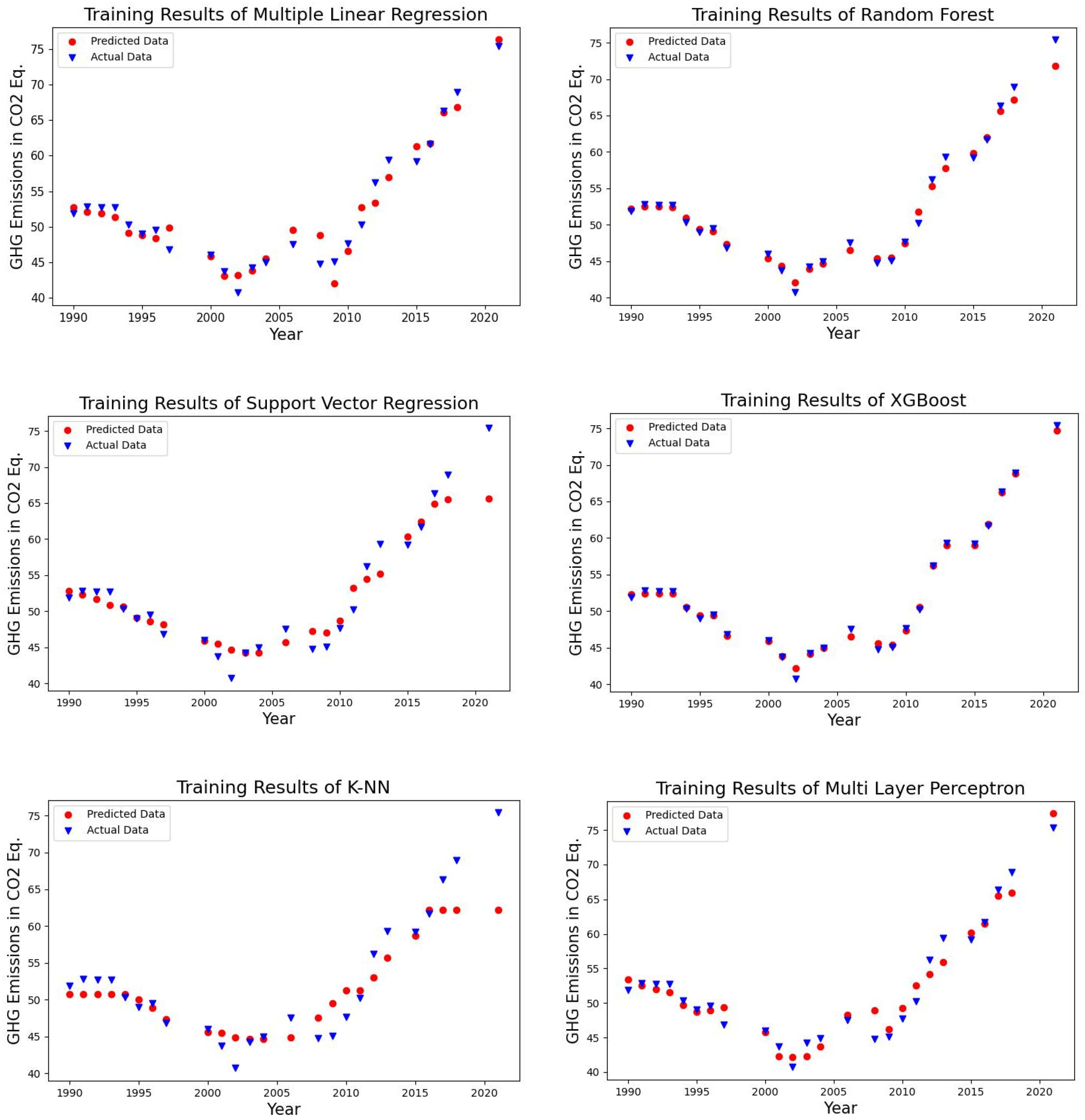
4.1. Forecasting Results of the Algorithms
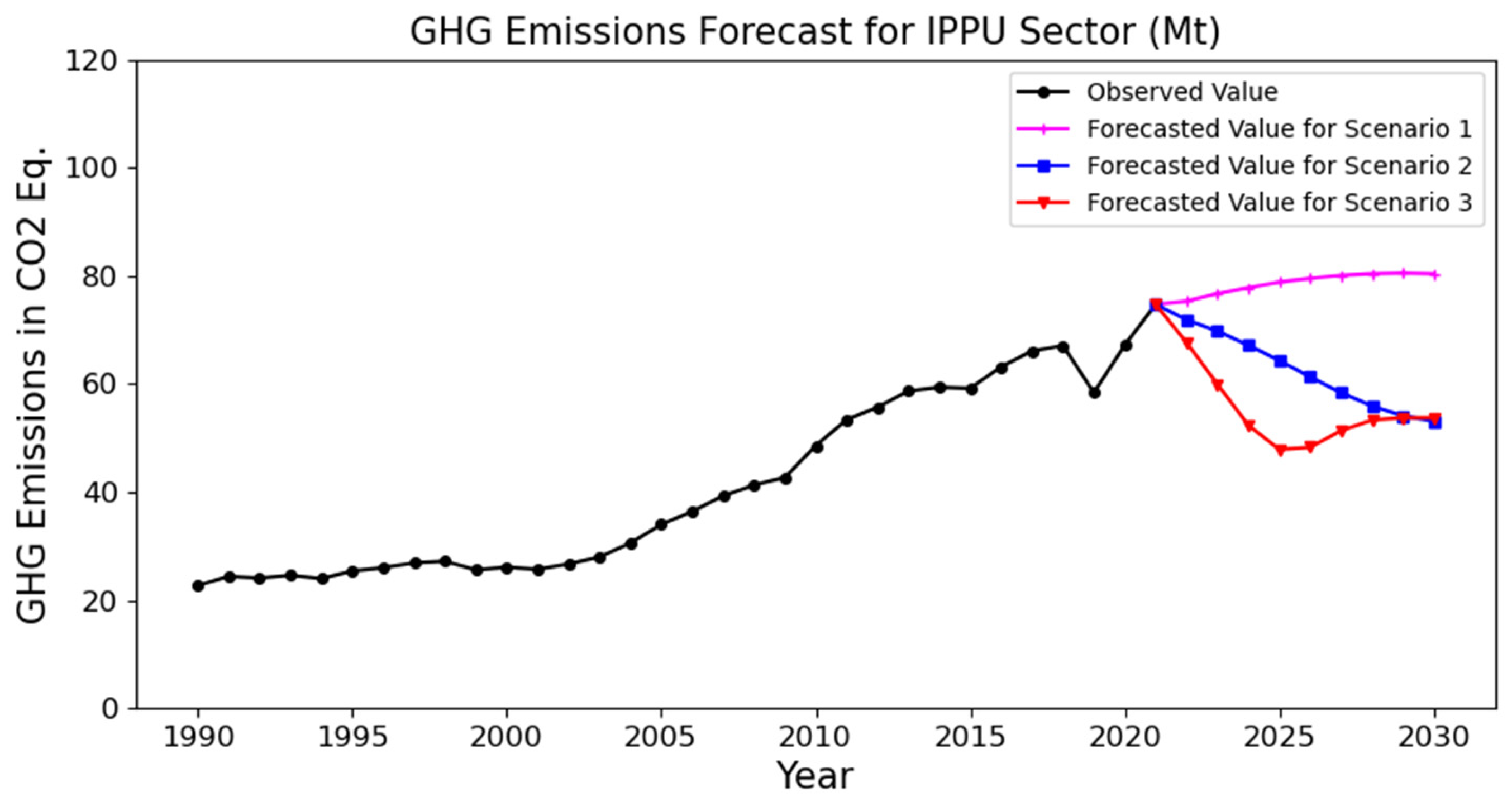
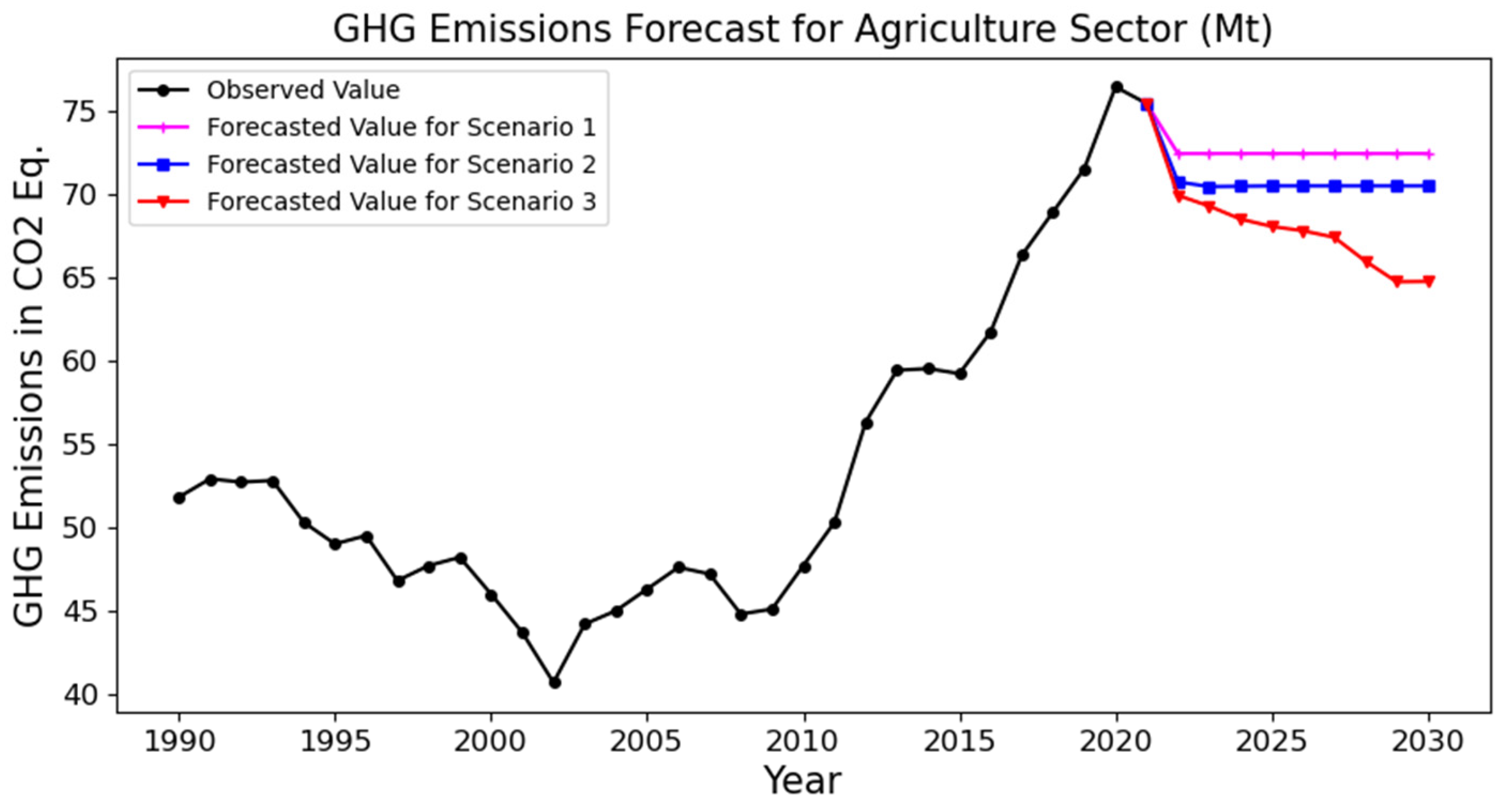
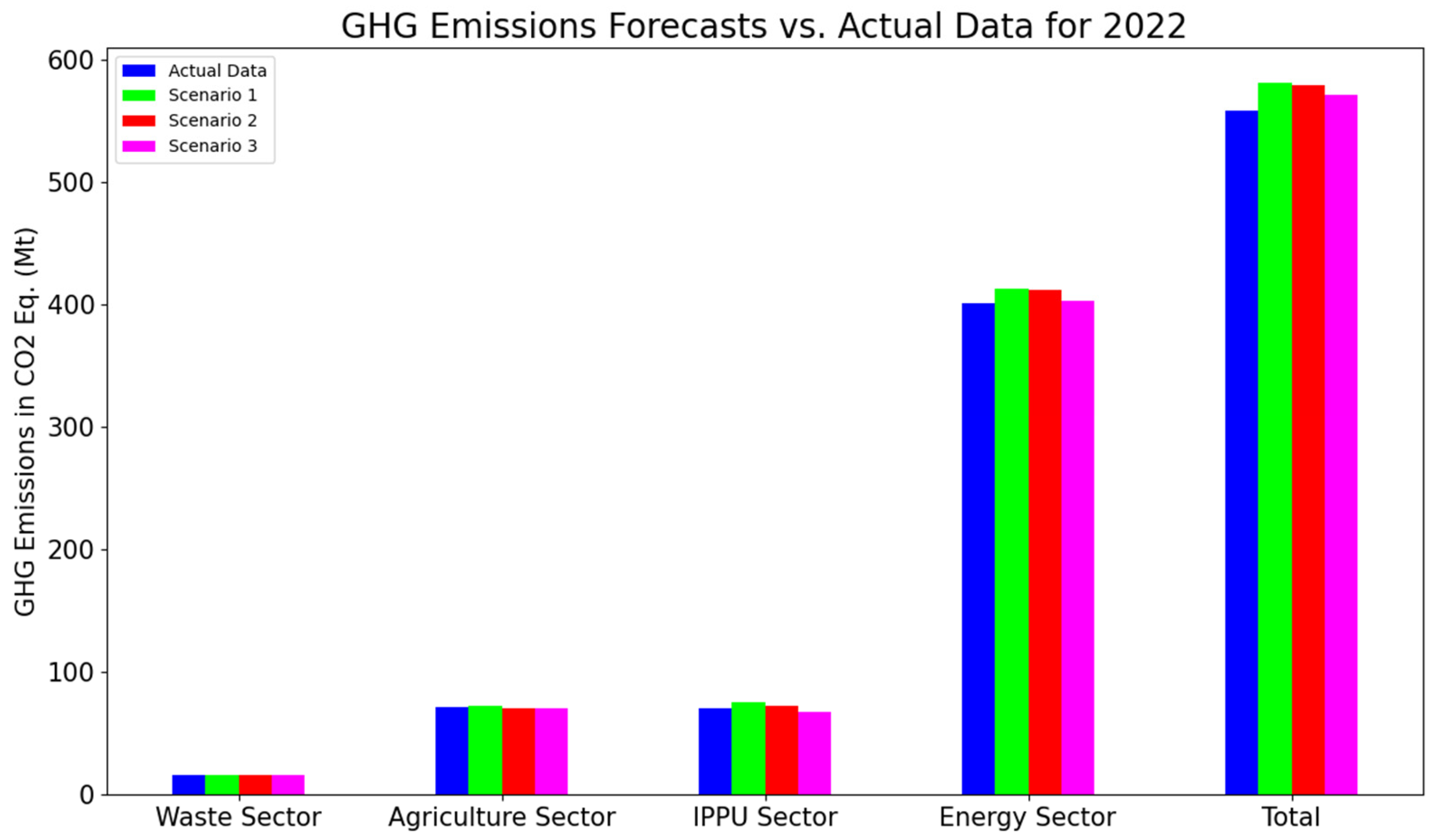
4.2. Scenario Analysis
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ho, W.T.; Yu, F.W. Optimal selection of predictors for greenhouse gas emissions forecast in Hong Kong. J. Clean. Prod. 2022, 370, 133310. [Google Scholar] [CrossRef]
- Unites Nations Climate Change. What Is the United Nations Framework Convention on Climate Change? Available online: https://unfccc.int/process-and-meetings/what-is-the-united-nations-framework-convention-on-climate-change (accessed on 22 July 2024).
- Unites Nations Climate Change. The Paris Agreement. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 22 July 2024).
- Rogelj, J.; Elzen, M.; Höhne, N.; Fransen, T.; Fekete, H.; Winkler, H.; Schaeffer, R.; Sha, F.; Riahi, K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 °C. Nature 2016, 534, 631–639. [Google Scholar] [CrossRef] [PubMed]
- Kayakuş, M.; Terzioğlu, M.; Erdoğan, D.; Zetter, S.A.; Kabas, O.; Moiceanu, G. European Union 2030 Carbon Emission Target: The Case of Turkey. Sustainability 2023, 15, 13025. [Google Scholar] [CrossRef]
- Ministry of Environment, Urbanization and Climate Change-Directorate of Climate Change. Climate Change Mitigation Strategy and Action Plan 2024–2030. Available online: https://iklim.gov.tr/en/action-plans-i-121 (accessed on 22 July 2024).
- Turkish Statistics Institute. Greenhouse Gas Emissions Statistics, 1990–2022. Available online: https://data.tuik.gov.tr/Bulten/Index?p=Greenhouse-Gas-Emissions-Statistics-1990-2022-53701 (accessed on 22 July 2024).
- Zhao, K.; Yu, S.; Wu, L.; Wu, X.; Wang, L. Carbon emissions prediction considering environment protection investment of 30 provinces in China. Environ. Res. 2024, 244, 117914. [Google Scholar] [CrossRef] [PubMed]
- Ayvaz, B.; Kusakci, A.O.; Gül, T.T. Energy-related CO2 emission forecast for Turkey and Europe and Eurasia A discrete grey model approach. Grey Syst. Theory Appl. 2017, 7, 437–454. [Google Scholar]
- Şahin, U. Forecasting of Turkey’s greenhouse gas emissions using linear and nonlinear rolling metabolic grey model based on optimization. J. Clean. Prod. 2019, 239, 118079. [Google Scholar] [CrossRef]
- Li, K.; Pingping Xiong, P.; Wu, Y.; Dong, Y. Forecasting greenhouse gas emissions with the new information priority generalized accumulative grey model. Sci. Total Environ. 2022, 807, 150859. [Google Scholar] [CrossRef]
- Ding, S.; Hu, J.; Lin, Q. Accurate forecasts and comparative analysis of Chinese CO2 emissions using a superior time-delay grey model. Energy Econ. 2023, 126, 107013. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Saifoddin, A.; Shirmohammadi, R.; Aslani, A. Forecasting of CO2 emissions in Iran based on time series and regression analysis. Energy Rep. 2019, 5, 619–631. [Google Scholar] [CrossRef]
- Karakurt, I.; Aydin, G. Development of regression models to forecast the CO2 emissions from fossil fuels in the BRICS and MINT countries. Energy 2023, 263, 125650. [Google Scholar] [CrossRef]
- Ozdemir, M.; Pehlivan, S.; Melikoglu, M. Estimation of greenhouse gas emissions using linear and logarithmic models: A scenario-based approach for Turkiye’s 2030 vision. Energy Nexus 2024, 13, 100264. [Google Scholar] [CrossRef]
- Bakay, M.S.; Agbulut, Ü. Electricity production based forecasting of greenhouse gas emissions in Turkey with deep learning, support vector machine and artificial neural network algorithms. J. Clean. Prod. 2021, 285, 125324. [Google Scholar] [CrossRef]
- Akyol, M.; Uçar, E. Carbon footprint forecasting using time series data mining methods: The case of Turkey. Environ. Sci. Pollut. Res. 2021, 28, 38552–38562. [Google Scholar] [CrossRef] [PubMed]
- Agbulut, Ü. Forecasting of transportation-related energy demand and CO2 emissions in Turkey with different machine learning algorithms. Sustain. Prod. Consum. 2022, 29, 141–157. [Google Scholar] [CrossRef]
- AlKheder, S.; Almusalam, A. Forecasting of carbon dioxide emissions from power plants in Kuwait using United States Environmental Protection Agency, Intergovernmental panel on climate change, and machine learning methods. Renew. Energy 2022, 191, 819–827. [Google Scholar] [CrossRef]
- Kumari, S.; Singh, S.K. Machine learning-based time series models for effective CO2 emission prediction in India. Environ. Sci. Pollut. Res. 2023, 30, 116601–116616. [Google Scholar] [CrossRef]
- Giannelos, S.; Bellizio, F.; Goran Strbac, G.; Zhang, T. Machine learning approaches for predictions of CO2 emissions in the building sector. Electr. Power Syst. Res. 2024, 235, 110735. [Google Scholar] [CrossRef]
- Javanmard, M.E.; Tang, Y.; Wang, Z.; Tontiwachwuthikul, P. Forecast energy demand, CO2 emissions and energy resource impacts for the transportation sector. Appl. Energy 2023, 338, 120830. [Google Scholar] [CrossRef]
- Faruque, M.O.; Rabby, M.A.J.; Hossain, M.A.; Islam, M.R.; Rashid, M.M.U.; Muyeen, S.M. A comparative analysis to forecast carbon dioxide emissions. Energy Rep. 2022, 8, 8046–8060. [Google Scholar] [CrossRef]
- Ozcan, T.; Konyalioglu, A.K.; Beldek, T. Deep Learning Based Models for the CO2 emission forecasting in Turkey. In Proceedings of the Tenth International Conference on Environmental Management, Engineering, Planning & Economics, Skiathos Island, Greece, 5–9 June 2023. [Google Scholar]
- Gloria, B.; Höhn, B. Picture This: A Deep Learning Model for Operational Real Estate Emissions. J. Sus. Real Estate 2023, 15, 2251982. [Google Scholar] [CrossRef]
- Sangeetha, A.; Amudha, T. A novel bio-inspired framework for CO2 emission forecast in India. Procedia Comput. Sci. 2018, 125, 367–375. [Google Scholar] [CrossRef]
- Bahmani, M.; GhasemiNejad, A.; Robati, F.N.; Zarin, N.A. A novel approach to forecast global CO2 emission using Bat and Cuckoo optimization algorithms. MethodsX 2020, 7, 100986. [Google Scholar] [CrossRef] [PubMed]
- Ene Yalçın, S. A Forecasting System for Carbon Dioxide Emissions. In Proceedings of the 3rd International Conference on Applied Engineering and Natural Sciences, Konya, Turkey, 20–23 July 2022. [Google Scholar]
- Arık, O.A.; Canbulut, G.; Köse, E. Metaheuristic Algorithms to Forecast Future Carbon Dioxide Emissions of Turkey. Turk. J. Forecast. 2024, 8, 23–39. [Google Scholar] [CrossRef]
- Belbute, J.M.; Pereira, A.M. Reference forecasts for CO2 emissions from fossil-fuel combustion and cement production in Portugal. Energy Policy 2020, 144, 111642. [Google Scholar] [CrossRef]
- Yadav, A.; Gyamfi, B.A.; Asongu, S.A.; Behera, D.K. The role of green finance and governance effectiveness in the impact of renewable energy investment on CO2 emissions in BRICS economies. J. Environ. Manag. 2024, 358, 120906. [Google Scholar] [CrossRef]
- Bennedsen, M.; Hillebrand, E.; Koopman, S.J. Modeling, forecasting, and nowcasting U.S. CO2 emissions using many macroeconomic predictors. Energy Econ. 2021, 96, 105118. [Google Scholar] [CrossRef]
- Zhou, Z.-H. Machine Learning; Springer Nature Singapore Pte Ltd.: Singapore, 2021. [Google Scholar]
- Baek, J.; O’Connell, A.M.; Parker, K.J. Improving breast cancer diagnosis by incorporating raw ultrasound parameters into machine learning. Mach. Learn. Sci. Technol. 2022, 3, 045013. [Google Scholar] [CrossRef]
- Sergio, W.L.; Ströele, V.; Dantas, M.; Braga, R.; Macedo, D.D. Enhancing well-being in modern education: A comprehensive eHealth proposal for managing stress and anxiety based on machine learning. Internet Things 2024, 25, 101055. [Google Scholar] [CrossRef]
- Gan, L.; Wang, H.; Yang, Z. Machine learning solutions to challenges in finance: An application to the pricing of financial products. Technol. Forecast. Soc. Change 2020, 153, 119928. [Google Scholar] [CrossRef]
- Magdalena-Benedicto, R.; Pérez-Díaz, S.; Costa-Roig, A. Challenges and Opportunities in Machine Learning for Geometry. Mathematics 2023, 11, 2576. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Wei, J.; Chu, X.; Sun, X.-Y.; Kun Xu, K.; Deng, H.-X.; Chen, J.; Wei, Z.; Lei, M. Machine learning in materials science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Waqar, A. Intelligent decision support systems in construction engineering: An artificial intelligence and machine learning approaches. Expert Syst. Appl. 2024, 249, 123503. [Google Scholar] [CrossRef]
- Mello, R.F.; Ponti, M.A. Machine Learning a Practical Approach on the Statistical Learning Theory; Springer Nature: Cham, Switzerland, 2018. [Google Scholar]
- Jo, T. Machine Learning Foundations Supervised, Unsupervised, and Advanced Learning; Springer Nature: Cham, Switzerland, 2021. [Google Scholar]
- Olsen, A.A.; McLaughlin, J.E.; Harpe, S.E. Using multiple linear regression in pharmacy education scholarship. Curr. Pharm. Teach. Learn. 2020, 12, 1258–1268. [Google Scholar] [CrossRef]
- Vukovic, D.B.; Spitsina, L.; Gribanova, E.; Spitsin, V.; Lyzin, I. Predicting the Performance of Retail Market Firms: Regression and Machine Learning Methods. Mathematics 2023, 11, 1916. [Google Scholar] [CrossRef]
- Wang, C.; Lia, M.; Yan, J. Forecasting carbon dioxide emissions: Application of a novel two-stage procedure based on machine learning models. J. Water Clim. Change 2023, 14, 477–493. [Google Scholar] [CrossRef]
- Sotiropoulou, K.F.; Vavatsikos, A.P.; Botsaris, P.N. A hybrid AHP-PROMETHEE II onshore wind farms multicriteria suitability analysis using kNN and SVM regression models in northeastern Greece. Renew. Energy 2024, 221, 119795. [Google Scholar] [CrossRef]
- Sumayli, A. Development of advanced machine learning models for optimization of methyl ester biofuel production from papaya oil: Gaussian process regression (GPR), multilayer perceptron (MLP), and K-nearest neighbor (KNN) regression models. Arab. J. Chem. 2023, 16, 104833. [Google Scholar] [CrossRef]
- Sun, X.; Opulencia, M.J.C.; Alexandrovich, T.P.; Khan, A.; Algarni, M.; Abdelrahman, A. Modeling and optimization of vegetable oil biodiesel production with heterogeneous nano catalytic process: Multi-layer perceptron, decision regression tree, and K-Nearest Neighbor methods. Environ. Technol. Innov. 2022, 27, 102794. [Google Scholar] [CrossRef]
- Trizoglou, P.; Liu, X.; Lin, Z. Fault detection by an ensemble framework of Extreme Gradient Boosting (XGBoost) in the operation of offshore wind turbines. Renew. Energy 2021, 179, 945–962. [Google Scholar] [CrossRef]
- Kıyak, B.; Oztop, H.F.; Ertam, F.; Aksoy, I.G. An intelligent approach to investigate the effects of container orientation for PCM melting based on an XGBoost regression model. Eng. Anal. Bound. Elem. 2024, 161, 202–213. [Google Scholar] [CrossRef]
- Pramanik, P.; Jana, R.K.; Ghosh, I. AI readiness enablers in developed and developing economies: Findings from the XGBoost regression and explainable AI framework. Technol. Forecast. Soc. Change 2024, 205, 123482. [Google Scholar] [CrossRef]
- Wen, L.; Cao, Y. Influencing factors analysis and forecasting of residential energy related CO2 emissions utilizing optimized support vector machine. J. Clean. Prod. 2020, 250, 119492. [Google Scholar] [CrossRef]
- Jin, H.; Kim, Y.-G.; Jin, Z.; Rushchitc, A.A.; Al-Shati, A.S. Optimization and analysis of bioenergy production using machine learning modeling: Multi-layer perceptron, Gaussian processes regression, K-nearest neighbors, and Artificial neural network models. Energy Rep. 2022, 8, 13979–13996. [Google Scholar] [CrossRef]
- Jeong, S.; Lim, J.; Hong, S.I.; Kwon, S.C.; Shim, J.Y.; Yoo, Y.; Cho, H.; Lim, S.; Kim, J. A framework for environmental production of textile dyeing process using novel exhaustion-rate meter and multi-layer perceptron-based prediction model. Process Saf. Environ. Prot. 2023, 175, 99–110. [Google Scholar] [CrossRef]
- Xu, R.; Yang, X. Machine learning optimization for catalytic desulfurization of petroleum: Multi-layered perceptron, Multi Task Lasso, and Gaussian process regression models. J. Mol. Liq. 2024, 400, 124508. [Google Scholar] [CrossRef]
- Ene, S.; Öztürk, N. Grey modelling based forecasting system for return flow of end-of-life vehicles. Technol. Forecast. Soc. Change 2017, 115, 155–166. [Google Scholar] [CrossRef]
- Lewis, C.D. Industrial and Business Forecasting Methods; Butterworths-Heinemann: London, UK, 1982. [Google Scholar]







| Dataset | Average | Min | Max | Standard Deviation |
|---|---|---|---|---|
| Year | 2005.5 | 1990 | 2021 | 9.380 |
| Population | 69,201,210 | 54,324,140 | 84,147,320 | 8,955,316 |
| GDP per capita (TRY) | 17,109.515 | 7.24 | 86,231.420 | 20,811.961 |
| Final energy consumption (PJ) | 2972.531 | 1691 | 4820 | 937.311 |
| Renewable energy consumption (PJ) | 274.500 | 217 | 322 | 37.053 |
| Industry production index variables (2021 = 100) | 49.322 | 23.280 | 100 | 22.772 |
| GHG emissions in CO2 eq. (Mt) | 371.425 | 228 | 572 | 106.297 |
| GHG emissions in CO2 eq. for the energy sector (Mt) | 261.695 | 143.147 | 406.472 | 80.735 |
| GHG emissions in CO2 eq. for the IPPU sector (Mt) | 41.043 | 22.691 | 74.715 | 16.953 |
| GHG emissions in CO2 eq. for the agricultural sector (Mt) | 53.277 | 40.708 | 76.437 | 9.599 |
| GHG emissions in CO2 eq. for the waste sector (Mt) | 15.407 | 10.315 | 18.434 | 2.562 |
| Algorithms | MSE | MAE | RMSE | MAPE % | R2 |
|---|---|---|---|---|---|
| Multiple linear regression | 32.279 | 5.155 | 5.681 | 1.391 | 0.996 |
| Random forest regression | 69.716 | 6.955 | 8.350 | 1.665 | 0.992 |
| Support vector regression | 771.655 | 25.593 | 27.779 | 6.373 | 0.915 |
| XGBoost regression | 159.023 | 9.301 | 12.610 | 2.468 | 0.982 |
| kNN regression | 234.900 | 11.657 | 15.326 | 2.715 | 0.974 |
| Multilayer perceptron regression | 245.362 | 12.263 | 15.664 | 2.677 | 0.973 |
| Algorithms | MSE | MAE | RMSE | MAPE % | R2 |
|---|---|---|---|---|---|
| Multiple linear regression | 63.977 | 6.508 | 7.999 | 2.239 | 0.986 |
| Random forest regression | 67.510 | 6.704 | 8.216 | 2.252 | 0.985 |
| Support vector regression | 445.461 | 18.568 | 21.106 | 6.159 | 0.904 |
| XGBoost regression | 99.512 | 7.927 | 9.976 | 2.745 | 0.979 |
| kNN regression | 152.716 | 10.267 | 12.358 | 3.574 | 0.967 |
| Multilayer perceptron regression | 129.589 | 10.059 | 11.384 | 3.401 | 0.972 |
| Algorithms | MSE | MAE | RMSE | MAPE % | R2 |
|---|---|---|---|---|---|
| Multiple linear regression | 13.611 | 2.889 | 3.689 | 6.623 | 0.945 |
| Random forest regression | 11.364 | 2.120 | 3.371 | 4.485 | 0.954 |
| Support vector regression | 8.264 | 2.030 | 2.875 | 3.862 | 0.966 |
| XGBoost regression | 13.270 | 2.391 | 3.643 | 5.298 | 0.946 |
| kNN regression | 24.894 | 2.877 | 4.989 | 5.208 | 0.899 |
| Multilayer perceptron regression | 17.755 | 2.657 | 4.214 | 5.188 | 0.928 |
| Algorithms | MSE | MAE | RMSE | MAPE % | R2 |
|---|---|---|---|---|---|
| Multiple linear regression | 29.191 | 3.882 | 5.403 | 6.175 | 0.789 |
| Random forest regression | 10.299 | 2.216 | 3.209 | 3.426 | 0.926 |
| Support vector regression | 18.638 | 2.814 | 4.317 | 4.184 | 0.865 |
| XGBoost regression | 10.781 | 2.370 | 3.284 | 3.709 | 0.922 |
| kNN regression | 43.440 | 4.470 | 6.591 | 6.796 | 0.686 |
| Multilayer perceptron regression | 18.355 | 3.246 | 4.284 | 5.103 | 0.868 |
| Algorithms | MSE | MAE | RMSE | MAPE % | R2 |
|---|---|---|---|---|---|
| Multiple linear regression | 0.392 | 0.586 | 0.626 | 3.567 | 0.831 |
| Random forest regression | 0.086 | 0.238 | 0.293 | 1.529 | 0.963 |
| Support vector regression | 0.166 | 0.299 | 0.407 | 1.850 | 0.928 |
| XGBoost regression | 0.203 | 0.321 | 0.451 | 2.159 | 0.912 |
| kNN regression | 0.090 | 0.209 | 0.300 | 1.251 | 0.961 |
| Multilayer perceptron regression | 0.264 | 0.439 | 0.513 | 2.652 | 0.886 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ene Yalçın, S. Development of a Forecasting Framework Based on Advanced Machine Learning Algorithms for Greenhouse Gas Emissions. Systems 2024, 12, 528. https://doi.org/10.3390/systems12120528
Ene Yalçın S. Development of a Forecasting Framework Based on Advanced Machine Learning Algorithms for Greenhouse Gas Emissions. Systems. 2024; 12(12):528. https://doi.org/10.3390/systems12120528
Chicago/Turabian StyleEne Yalçın, Seval. 2024. "Development of a Forecasting Framework Based on Advanced Machine Learning Algorithms for Greenhouse Gas Emissions" Systems 12, no. 12: 528. https://doi.org/10.3390/systems12120528
APA StyleEne Yalçın, S. (2024). Development of a Forecasting Framework Based on Advanced Machine Learning Algorithms for Greenhouse Gas Emissions. Systems, 12(12), 528. https://doi.org/10.3390/systems12120528





