Quality Improvement Decisions in Service Supply Chains with Collaborative and Free-Riding Behaviors

Abstract

The dominant position of a member within a service supply chain plays a crucial role in fostering a willingness to improve service quality. Consequently, this study examines a service supply chain comprising a supplier and an integrator, aiming to investigate the influence of four different power structures, namely, supplier-led, integrator-led, supplier–integrator power balance, and supplier–integrator centralized decision, on the decision-making process for service quality improvement by members. The findings highlight that the optimal willingness to improve service quality in a service supply chain is not necessarily infinitely close to 100%, and is influenced by factors such as revenue share, cost, effect, and dominant position. In cases where the collaborative improvement effect is weak, even the dominant member may display a limited willingness, rendering centralized decision-making meaningless. If the collaborative improvement effect surpasses the combined independent improvement effects, the dominant position can help strengthen willingness, although it may not always result in higher profits. Conversely, a power-balanced scenario can be advantageous in achieving the highest profit for the entire supply chain.

1. Introduction

The past few decades have witnessed a boom in the service industry, which is a major contributor to the GDP in many countries and regions [1,2]. Definitely, service firms need to transact with their suppliers and serve their downstream customers, and outsourcing services has become increasingly common [3]. Lu et al. [4] highlight the importance of achieving integration. Stank et al. [5] assert that close relationship among trading partners is important. Similar research conclusions can be found in He et al. [6], Wu et al. [7], and so on. In practice, DBS Bank engaged IBM for 10 years to carry out repair and restoration of servers in its two data centers [8]. Maersk recognizes the value of business collaboration and cooperation with other members. Collaborative efforts between Maersk Line located in Copenhagen, Denmark, APM Terminals located in The Hague, Netherlands, Hamburg Süd located in Hamburg, Germany, and Damco located in Copenhagen, Denmark have elevated operational efficiency and profitability. Additionally, the development of the digital container logistics platform TradeLens by Maersk and IBM has significantly improved response speed and efficiency for all parties involved. Through collaboration with Microsoft Enterprise Services, Maersk has enhanced the performance and scalability of its data center. Likewise, Shandong Iron and Steel Group Co., Ltd. has implemented various measures in collaborative management between upstream and downstream firms to enhance customer demand response speed and drive industrial upgrading.

The above examples demonstrate that the effect of collaborative management surpasses the effect of independent behavior by one party. Most companies acknowledge the importance of collaborative behavior during cooperation. However, there are also quite a few cases where the upstream and downstream fail to collaborate and result in adverse consequences. In March of 2023, the Sina Black Cat Complaint Platform was flooded with complaints about MyGym, including difficulties in obtaining refunds and the sudden closure of offline stores without providing refunds. The underlying cause of these issues lies in MyGym’s failure, as a service integrator, to fulfill its operational guidance and supervisory management responsibilities for its franchise stores. This incident highlights the importance of collaborative efforts between upstream and downstream firms in managing service quality, as relying solely on one side may not be sufficient to improve customer satisfaction. Similar incidents, such as the unfortunate case of Ctrip Parent-Child Nursery School in 2017 due to a lack of collaborative management and the COVID-19 outbreak at Nanjing Lukou Airport in 2021 resulting from neglect in supervising cleaning work, further emphasize the significance of collaborative management and behavior.

A natural question arises as to why some fail to implement collaborative management. It is essential to question whether collaborative management always leads to higher service quality. In reality, the collaborative improvement effect (CIE) may be lower than the independent improvement effect (IIE). For instance, in procurement services, manufacturers prioritize ‘no corruption’ and meticulously follow bidding procedures, while suppliers focus on competitive pricing. Unfortunately, this often compromises the quality of procurement services, sacrificing product and service excellence to compensate for the reduced cost. Consequently, a new question arises: under what circumstances can collaborative management enhance service quality? Public opinion has mentioned the issue of cost, and the aforementioned effect and efficiency concerns are also key factors. Cost and effect are essentially ability-related factors that influence the willingness of service supply chain members.

We focus our investigation on the issue of service quality improvement, which encompasses both collaborative and independent behaviors. Consequently, it is crucial to delve into the improvement willingness of upstream and downstream members, which is closely related to their abilities. These abilities primarily involve the cost and effect of service quality improvement. Higher (lower) costs indicate greater (lesser) difficulty in achieving improvement. The effect primarily refers to the marginal revenue generated by enhancing service quality. As evidenced by the analyzed cases, collaborative behavior holds significant importance. Roels et al. [9] assume that if one member makes efforts to improve quality, the other member will do the same. However, this is not always the case, as observed in the aforementioned examples. Both members can collaborate on quality improvement, or it may transpire that only one party invests in quality enhancement while the other acts as a free-rider. Liu et al. [10] assert that manufacturers often exert insufficient effort, while customer firms exert excessive effort, leading to efficiency losses in the entire supply chain. This parallels the situations mentioned in the previous cases. Any improvement in quality from a member of the supply chain generates marginal revenue for both parties. Consequently, free-riders may emerge, exhibiting a lack of willingness to improve quality. Clearly, free-riding is detrimental in the long run, as exemplified by the case of Nanjing Lukou Airport. Hence, several questions arise: If we define willingness as a viable change from 0 to 1, does the optimal willingness equal 1 or infinitely approach 1? What factors influence the willingness to improve service quality?

Furthermore, it is common for one member of the service supply chain to hold a dominant position while the other member assumes a subordinate role. Does this dominant position impact willingness? The case of Maersk Company provides examples that highlight the pivotal role of the dominant position in implementing collaborative measures. For instance, MyGym, as an internationally renowned integrator, occupies a dominant position in the service supply chain compared to its franchisees. However, its negligent management has resulted in the paralysis of its offline franchisees. This illustrates the significant influence of the dominant position on the willingness to improve service quality. Moreover, the dominant position also affects a partner’s ability to attain profits [11,12]. In the context of the service chain, how does the dominant position influence the willingness to enhance quality? Does it also contribute to higher profitability? Should a centralized approach yield better results than a decentralized situation dominated by one party?

In this paper, we focus on a service supply chain as the subject of our research and quantify the willingness of supply chain members to improve service quality using probability. A few examples of service supply chains can be found in

Table 1. Service supply chains.

No.	Service Supplier	Service Contents	Service Integrator	Customers
1	Huaxiaozhu Taxi	Ride hailing service	Didi Taxi	Customers
	Xiaoju Charging	Charging service
	Enjoy Road Travel	Call forwarding service
2	MEGA	Emotional Class	MyGym	Parents
	ABK	Arts Class
	Music Together	Music Class
3	Child-carer Training Centre	Child-carer Training Service	Nursery schools	Parents
	Daily necessities companies	Daily necessities
	Hospitals	Neonatal and maternal medical examination
4	Beijing Yingtai Knight Technology Development Co., Ltd.	Logistics information management System	P.G.LOGISTICS GROUP CO., LTD	Procter&Gamble, Philips, Unilever, et al.
	Cainiao Network Technology Co., Ltd.	Warhouse management
	Suncontractors	Transports, packages, delivery, etc.
5	China Hainan Airlines	Air tickets	Ctrip.com	Customers
	All Seasons Hotel	Hotel service
	BeMyGuest	Travel service in Singapore
6	IBM	Infrastructure management	Allianz Life Insurance Company	Customers
	ACS	Data management system
	Hewlett-Packard	Website services

, in which some are product service supply chains, and the others are service supply chains only, according to the definition of service supply chains by Wang et al. [13]. To clarify what a service chain is, we list three suppliers with different kinds of service contents for each service integrator, as in Table 1. This looks like a distributed supply chain. However, without loss of generality, we will focus on the supply chain with one supplier and one integrator. Additionally, this paper does not focus on a certain specific industry and is applicable in both service-only and product service supply chains.

By considering the probabilities and marginal revenues associated with the collaborative improvement effect (CIE) and independent improvement effects (IIEs), we calculate the expected return of the supply chain and allocate it between the two members. The difference between revenue and cost is referred to as the net profit of quality improvement. We consider this distribution because revenue and quality improvement exhibit a mutually reinforcing relationship. Additionally, we perform numerical experiments and analysis based on our models and solutions to examine the impact of various relevant parameters or factors on decisions and profits. These findings provide valuable insights and guidance for service firms aiming to enhance their service quality.

This paper makes several significant contributions. Firstly, it uses probability as a measure of willingness to improve quality, which differs from the existing research that either treats service level as a variable or establishes a service level evaluation index system. This paper also investigates the impact of both positive and negative synergies by examining the gap between collaborative improvement effects (CIE) and independent improvement effects (IIEs), providing a quantitative analysis of free-riding behavior. While Liu et al. [14] also discuss probability, their focus is on efforts to prevent followers from violating social responsibility. Secondly, previous studies have often been limited to a single dimension, i.e., cost–benefit analysis, or have focused on the share of benefits among upstream and downstream firms in the supply chain and their effects. This paper, on the other hand, integrates factors such as revenue share, cost, and effect under different power structures to explore their influences on quality improvement decisions. Moreover, unlike previous studies, the dominant position in this paper does not necessarily lead to increased profits. Its positive role depends on the relationship between CIE and the sum of two IIEs. Thirdly, the models and conclusions presented in this paper have broad applicability as they are not limited to any specific industry and are relevant to both product service supply chains and pure service supply chains, such as logistics service supply chains, infant and child service supply chains, and elderly service supply chains. When the transfer payment is zero, the scope of the application extends beyond upstream and downstream firms. For instance, the problem of service collaboration between two different suppliers can draw upon the ideas and methods presented in this paper.

The remaining sections of this paper are as follows. Section 2 provides a literature review. Section 3 gives the related descriptions, including assumptions and sign notations. Section 4 proposes four types of models to make decisions about improving service quality, gives the corresponding solutions, and compares the results under different power structures. Section 5 demonstrates the numerical examples and analyzes the decisions and profits to highlight the influences of improvement cost, improvement effect, revenue share, and dominant position. Section 6 concludes the paper based on the model solutions and numerical results.

2. Literature Review

2.1. Service Quality

The literature on service quality can be broadly categorized into three main areas: understanding the concept of service quality, identifying the factors that influence it, and developing measurement methods to assess it [15]. Furthermore, some of the literature has examined the classification of different definitions and measurement approaches [16,17,18]. Additionally, numerous studies have investigated control models to manage service quality [19,20]. However, the majority of the literature investigates service quality or takes it as a decision variable in quantitative models. Compared with previous studies, we introduce the concept of probability to describe the willingness to improve service quality, in which service quality itself is not a decision variable but is discussed from a quantitative point. Furthermore, we examine the decision-making process raised by different dominators, offering unique insights into this area of research.

2.2. Service Supply Chains

A significant body of the literature has been dedicated to the study of service supply chains, encompassing various aspects. Some researchers give the definitions of service supply chains [21,22,23], while others focus on exploring the differences between manufacturing and service supply chains [13]. Furthermore, the literature on service supply chains can be reviewed from the following two perspectives. From the perspective of research method, diverse approaches have been used in previous studies, such as literature reviews [13,24,25], case studies [26,27], empirical research [28,29], and mathematical models based on game theory [23,30]. Moreover, the previous literature covers a wide range of issues from the perspective of research contents, including the alignment of supply and demand [19], operations management [31], specific industries such as tourism [27], commerce, and digital trade [32,33], and information technology [22]. However, few of them have discussed the willingness and behaviors of quality improvement. To fill this gap, our study proposes mathematical models considering collaborative and free-riding behaviors to examine decisions on service quality issues.

2.3. Service Quality Decisions Based on Different Supply Chain Power Structures

A member in a dominant position possesses the authority to exert control over other members [14]. Existing studies predominantly examine leadership within the context of supply chain channel coordination and introduce various contracts to maximize overall benefits [14,34]. When it comes to quality issues in product service supply chains, which encompass both products and professional services [13,35,36], several noteworthy findings have emerged. For instance, Liu et al. [37] reveal that when manufacturers choose to build their platforms instead of using third-party platforms, they can obtain higher service levels and obtain conditions for improving service levels when using third-party platforms, while Zhai et al. [38] explore the influence of demand disruptions on the service level. Zhan et al. [39] compare and analyze the optimal service quality level under decentralized decision-making and centralized decision-making in the dual-channel supply chain and conclude that further coordination is necessary. Wang et al. [40] realize the optimization of a dual-channel supply chain considering service quality by using a wholesale price contract. Furthermore, Gong et al. [41] consider the impact of consumer free-riding and reverse benefit-sharing ratio on service decision-making in a dual-channel supply chain. Sun et al. [42] discuss these issues from other perspectives. Notably, logistics service supply chains have received more attention in these studies [19,43,44]. In the realm of service-only supply chains, numerous studies have explored centralized and decentralized decision-making across different service industries [40].

However, few of them explicitly focus on quality issues, and most of the studies focus on service level or quality decision-making [8,10,39,41,45,46]. The above literature aims to compare the differences in service levels or service quality between centralized and decentralized decision-making, encompassing two types of power structures. Most of the mentioned studies consider the leader–follower relationship based on the Stackelberg game, while only Liu et al. [46] consider the converse dominant relations and situations where two members possess equal power. Existing studies primarily focus on power structures within manufacturing supply chains [47,48]. They reveal that dominance plays a crucial role in profitability [11], and power strategies are closely related to supply chain members’ performance [38,46]. In this paper, we examine four power structures of service supply chains: supplier dominance, integrator dominance, equal power between two members, and joint centralized decision-making by both members.

In fact, there is some research directly related to this paper. For example, Roels et al. [8] incorporate vendor and buyer service efforts into the Cobb–Douglas function to determine outputs. Similarly, Dey et al. [45] use the Cobb–Douglas function in a contract-theoretic model. The application of the Cobb–Douglas function in service supply chains is considered a classic approach. However, Roels et al. [8] assume that if one member makes efforts to improve quality, the other member will also make efforts. On the other hand, Dey et al. [45] provide profit functions for the upstream and downstream members based on the effort level of the upstream member but do not consider the downstream member’s effort level. Liu et al. [46] conceptualize the service level as a variable and discuss pricing and power distribution strategies under different leader–follower relationships, with the power distribution ratio treated as a decision variable.

Differently, this paper examines not only collaborative behaviors but also free-riding behaviors, even though collaboration may not always occur. In other words, we consider revenue distribution between two members, similar to the power distribution discussed by Liu et al. [46], but we incorporate it as an exogenous decision variable within the revenue function [41]. In the research of Roels et al. [8], revenue distribution between two members is also considered, while the share is treated as a decision variable. This is different from our assumption that it is an exogenous variable, and we further explore decision-making under four power structures. Roels et al. [8], Dey et al. [45], and Liu et al. [10] introduce transfer payment as a coordinating mechanism, sometimes denoted as a fixed value and sometimes varying with time, effort level, or other variables. In this paper, we focus on decisions under different power structures, considering transfer payment as a fixed component to indicate the interaction between the upstream and downstream members. Furthermore, cost functions in the above-listed works utilize linear functions [8], power functions [8,46], or exponential functions [45]. Nevertheless, we introduce two distinct parameters to represent the members’ marginal costs by using a quadratic function [39,40].

2.4. Literature Summary

Overall, the existing literature can be summarized in the following three areas. Firstly, traditional revenue functions mostly consider demand quantity and price, and some describe member outputs using performance-based evaluations, utility functions, and joint production functions such as the Cobb–Douglas function. These approaches often assume that both service providers and buyers exert efforts together and overlook the scenario of free-riding, where one member benefits from the other’s service quality improvement without making efforts of its own. Secondly, most studies focus on coordinating behaviors in service supply chains through various mechanisms. However, if the ability to improve quality does not change, the behavior cannot fundamentally change either. The improvement ability is an important aspect that deserves attention, but few studies have explored it in depth. The improvement ability is associated with factors, such as improvement effect, improvement cost, and efficiency in this paper. Thirdly, while many studies have examined sharing strategies, such as revenue-sharing, profit-sharing, and cost-sharing, few have investigated the combined influence of sharing strategies and improvement ability factors. In this paper, we introduce probability to express willingness and free-riding behavior in the expected revenue function. The distribution of revenue between two members is directly linked to improvement incentives. Specifically, we combine incentives and the ability to analyze decisions regarding improvement willingness and the profits obtained from quality improvement behaviors. Lastly, the power structure has received significant attention in supply chain studies, particularly in manufacturing chains. However, only a few studies have discussed the power structure in service supply chains and its impact on service levels. This paper emphasizes the influence of the customer improvement effort (CIE) and the internal improvement effort (IIE) on service levels. Several papers connected to our study are cited in

Table 2. The contribution of the most related papers.

Literature	Service Quality Improvement	Improvement Effect	Improvement Cost	Sharing Strategies	Improvement Ability	Power Structure	Free-Riding Behaviors
Roels et al. [8]	✓	✓	✓	✓			✓
Liu et al. [10]	✓		✓	✓			✓
Fang et al. [11]				✓		✓
Liu et al. [14]				✓		✓
Qin et al. [19]	✓	✓	✓			✓
Jin et al. [34]				✓		✓
Liu et al. [35]	✓			✓		✓
Feng et al. [36]				✓		✓
Liu et al. [37]	✓	✓	✓		✓	✓
Zhai et al. [38]	✓		✓			✓
Zhan et al. [39]	✓	✓	✓		✓
Wang et al. [40]	✓	✓	✓	✓	✓
Gong et al. [41]	✓		✓	✓			✓
Sun et al. [42]				✓			✓
Chen et al. [44]	✓
Dey et al. [45]				✓
Liu et al. [46]						✓
Shang et al. [47]				✓		✓
Li et al. [48]						✓
This paper	✓	✓	✓	✓	✓	✓	✓

so that we can compare them and more clearly demonstrate our contributions.

3. Problem Descriptions

As discussed by Seth et al. [16], service quality can also be modeled using gap analysis, similar to the model proposed by Parasuraman et al. [49]. Taking inspiration from this perspective, a bidirectional study can help achieve the fundamental objective of the service supply chain. In line with the rationale presented in the gap analysis, albeit with some differences, this paper assumes that chain members must make decisions regarding whether and to what degree they will improve service quality. In this context, consider a service supply chain comprising a supplier and an integrator, where the supplier exerts efforts to reduce the quality gap, while the integrator exerts reverse efforts, as depicted in Figure 1.

Regarding the bidirectional nature, taking pure service supply chains as an example, the provision of service by the supply chain and the consumption of service by consumers often occur at the same time or even in the same space. The process of service provision requires consumers’ participation, and some basic information or materials of consumers need to be provided to service integrators and suppliers. Moreover, the transmission of information and materials is, to some extent, a reverse flow process. For example, the cooperation process between a third-party testing center and a hospital requires the physical participation of the testing subjects, and their basic information, sample materials such as blood to be tested, and even the testing subjects themselves undergo reverse flow in the service supply chain. It is obvious that when consumers participate, the service truly occurs and triggers revenue, and this revenue is generated through collaboration. Generally, the service provider and integrator usually sign agreements to consider revenue sharing, and when the sharing ratio is appropriate, it will be an incentive for both parties. In addition, the bidirectional nature also includes cooperation between the downstream integrator and upstream supplier. When the supplier plans to improve service quality, the integrator should cooperate as a partner, and the degree of cooperation is worth exploring, as it has a significant impact on improving the overall revenue of the chain. The degree of cooperation is essentially the willingness to exert efforts to improve service quality. Of course, we rule out situations where the members have the ability but deliberate lack of cooperation, because the premise of cooperating as partners in a chain is to become better. Since they form a chain like a union, there is no reason to deliberately not improve, unless there are difficulties with regard to ability or the results are not good enough. However, it is important to note that they may not necessarily collaborate in improving quality.

The degree of cooperation or willingness to improve may be described in practice as “somewhat cooperative (somewhat willing)”, “quite cooperative (very willing)”, “especially cooperative (especially willing)”, etc. In view of this, this paper characterizes the degree of cooperation or willingness to improve as a variable from 0 to 1, where 0 represents without any degree of cooperation or willingness, and 1 represents 100% cooperation or 100% willingness. In fact, the willingness here can also be seen as a probability, that is, the possibility of being willing to cooperate with a relative high degree. A lower possibility indicates a lower degree of cooperation, while a higher possibility indicates a stronger degree of cooperation.

We assume that the integrator chooses a level of willingness $a$ to improve service quality, specifically manifested as optimizing the production process and manufacturing process. The supplier’s willingness is denoted as $b$, which can be manifested as providing technical support or establishing a more complete quality management system. The levels a and b are chosen on the scale of (0, 1). It is obvious that the willingness variables satisfy the following conditions: both variables cannot take the value of 0 or 1. Cooperation between upstream and downstream members of a supply chain is a game problem, and the equilibrium game strategy can be divided into two situations:

Case 1 The game has optimal pure strategies. There may be four optimal pure strategies (see

Table 3. Game with optimal pure strategy between the integrator and supplier.

		The Supplier
		To improve	Not to improve
The integrator	To improve	(I)	(III)
	Not to improve	(II)	(IV)

): (I) Both parties are 100% committed to quality improvement, perhaps due to policy reasons, because the industry is in a growth phase, or because both parties are very certain about the benefits of improving service quality. For example, the Introduction of this paper mentions Shandong Iron and Steel Group Co., Ltd. has implemented various measures in collaborative management between upstream and downstream firms to enhance customer demand response speed and drive industrial upgrading. (II) The integrator firmly refuses to make any quality improvements, but the supplier will definitely improve service quality. This may be because the integrator has already developed relatively maturely, while the supplier has multiple competitors. In order to win a competitive position, it will definitely insist on improving service quality. For example, in the cooperation between the Taobao platform and its logistics service providers, if logistics service providers abandon quality improvement, they will face a serious decline in orders. (III) The integrator resolutely carries out quality improvement, but the supplier absolutely does not carry out any improvements. This may be because as a downstream member, the integrator needs to collaborate with more than one supplier. Only by adhering to quality improvement can they do a good job in collaboration and present better services to consumers. For example, Zhongdamen International Logistics Company continuously improves the quality of cross-border e-commerce services. (IV) Integrators and suppliers insist on not improving service quality. This may be because some industries have developed very maturely, achieving standardization of service quality, and there is no need for service quality improvement in a short period. For example, cooperation between fast-food enterprises such as McDonald’s, KFC, Pizzahut, and their suppliers.

Case2 The game does not have any optimal pure strategies, but it has an optimal mixed strategy. As shown in

Table 4. Game with optimal mixed strategy between the integrator and supplier.

			The Supplier
			$b$	$1-b$
			To improve	Not to improve
The integrator	$a$	To improve	$\alpha$	$\gamma$
	$1-a$	Not to improve	$\beta$	0

, the integrator chooses the strategy of ‘improve’ and that of ‘not improve’ based on a probability $a$ and $1-a$, while the supplier chooses the strategy of ‘improve’ and that of ‘not improve’ based on a probability $b$ and $1-b$. As for cooperation between the integrator and the supplier in the service supply chain, the probability of collaborating to improve service quality is $ab$, and the revenue generated by the behavior is $a$. The probability of only the supplier making improvements is $(1-a)b$, and the resulting revenue is $\beta$. The probability of only the integrator making improvement is $a(1-b)$, generating revenue $\gamma$. The probability of neither party making quality improvements is $(1-a)(1-b)$, and there will be no revenue at all.

Obviously, this paper aims to study the optimal mixed strategy. Although we do not strictly indicate which type of service supply chain is being studied, it is not appropriate to study the cooperation and sharing strategies on pure service supply chains by simply applying the existing research theories and methods of manufacturing supply chains or manufacturing-related service supply chains, and these need to be explored separately. Instead, in terms of quality improvement, the model and approach discussed in this paper can also be applied to the research of both types of service supply chains. This is the basic starting point of this study. In addition, in the current economic environment, high-quality development has become a national strategy, and that of the manufacturing industry has received widespread attention from the theoretical and practical fields. However, the attention of high-quality development in the service industry is insufficient, and specifically, issues such as how to improve service quality itself, how to motivate service supply chain members to improve service quality, and what are the key factors that restrict service quality improvement urgently need to be addressed. Therefore, this paper chooses quality improvement in service supply chains as the research object, aiming to clarify the factors that affect the willingness to improve service quality, explore how these factors affect the willingness of supply chain members, and provide valuable decision-making suggestions to the industry and even the government.

Based on the previous description (refer to Fan et al. [50], Gu et al. [51], and Xing et al. [52]), we set the corresponding costs as $1/2{\eta }_i{a}^2$ and $1/2{\eta }_s{b}^2$ where ${\eta }_i$ and ${\eta }_s$ are the rate of change of marginal cost to improve service quality for the integrator and supplier, respectively. The expected total revenue of the final quality improvement is described as $R=\alpha ab+\beta (1-a)b+\gamma a(1-b)$. This function means that high-quality service requires the joint efforts of upstream and downstream enterprises. If only upstream or downstream enterprises improve service quality, the service that consumers ultimately experience is discounted, which affects their purchasing intention and leads to less supply chain profit. For example, when consumers shop on the Tmall platform but fail to receive timely delivery from third-party logistics companies, the consumer experience is not good, which affects their willingness to purchase again, and thus, the chain revenue is different.

Bidirectional nature also includes cooperation between the downstream integrator and upstream supplier. When the supplier plans to improve service quality, the integrator should cooperate as a partner. The integrator makes decisions with the goal of maximizing profits, making it difficult to achieve an idealized state of service supply chain decision-making. When the integrator benefits from the service quality improvement efforts of the supplier, the supplier will inevitably adjust the degree of service quality improvement efforts, thereby promoting the optimization of the service supply chain. Based on this, the incentive mechanism of transfer payments is an important way to encourage the supplier to strengthen its efforts in improving service quality. Transfer payment refers to a coordination contract for the transfer of funds between members of the supply chain. Qi et al. [53] argue that constructing a reasonable transfer payment contract can achieve Pareto optimality. Furthermore, Wang et al. [54] point out that transfer payment contracts constructed considering altruistic preferences will make the operation of low-carbon e-commerce closed-loop supply chains more effective. The existence of fixed costs has created a risk-sharing mechanism between upstream and downstream enterprises. Even if market demand fluctuates greatly, upstream enterprises can still obtain certain income security through fixed fees. Therefore, in this paper, we assume that the upstream service supplier charges a one-time transfer payment fee T to the downstream service integrator, treating the transfer payment as a fixed component to reflect the interaction between upstream and downstream members.

We consider that the integrator and supplier receive a share of the total revenue from quality improvement in proportions $\lambda$ and $1-\lambda$, $\lambda$ is related to industry competition and corporate social status and is assumed to be exogenous to simplify the model. It is obvious that the integrator and supplier will receive $\lambda R$ and $(1-\lambda )R$ when considering different power structures. More symbols are shown in

Table 5. Symbols and notations.

Symbols	Notations
$a$	Integrator’s willingness to improve service quality
b	Supplier’s willingness to improve service quality
$\alpha$	Effect of collaborative quality improvement of two members
$\beta$	Effect of independent quality improvement of supplier
$\gamma$	Effect of independent quality improvement of integrator
$\lambda$	Revenue share of the integrator
$1-\lambda$	Revenue share of the supplier
${\eta }_i$	The rate of change of marginal cost to improve service quality for the integrator
${\eta }_s$	The rate of change of marginal cost to improve service quality for the supplier
$T$	The transfer payment from the downstream service integrator to the upstream service supplier
${\pi }_i$	Integrator’s profit from quality improvement
${\pi }_s$	Supplier’s profit from quality improvement
$\pi$	Total profit of the integrator and supplier
${\pi }_c$	Total profit of supply chain in centralized decision
$ID$	The situation that integrator works as a leader in quality improvement
$SD$	The situation that supplier works as a leader in quality improvement
$SP$	The situation that the integrator and supplier are power-balanced
$C$	The situation that integrator and supplier make a centralized decision

.

4. Models and Solutions Based on Different Power Structures

This section considers the willingness decisions of the service supply chain under the four power structures, namely, supplier-led, integrator-led, supplier–integrator power balance, and supplier–integrator centralized decision. The proofs of the theorems and propositions are illustrated in Appendix B.

4.1. Supplier Dominates

When the service provider dominates, it first shows its willingness to improve service quality. For example, a logistics service provider can signal the willingness to improve service quality through information system upgrades. Its integrator observes these signals and improves service quality through measures such as employee training. Under the gross revenue allocation structure, the profits of the integrator and supplier are described as

$$\begin{array}{l}\underset{a}{Max} {\pi }_{i(SD)}=\lambda [\alpha ab+\beta (1-a)b+\gamma a(1-b)]-{\displaystyle \frac{1}{2}}{\eta }_i{a}^2-T\\ \underset{b}{Max} {\pi }_{s(SD)}=(1-\lambda )[\alpha ab+\beta (1-a)b+\gamma a(1-b)]-{\displaystyle \frac{1}{2}}{\eta }_s{b}^2+T\end{array}$$

The decision model when the supplier dominates is thus as follows:

$$\begin{array}{r}\underset{b}{Max} {\pi }_{s(SD)}=(1-\lambda )[\alpha ab+\beta (1-a)b+\gamma a(1-b)]-{\displaystyle \frac{1}{2}}{\eta }_s{b}^2+T\\ subject \mathrm{to} \underset{a}{Max} {\pi }_{i(SD)}=\lambda [\alpha ab+\beta (1-a)b+\gamma a(1-b)]-{\displaystyle \frac{1}{2}}{\eta }_i{a}^2-T\end{array}$$

Firstly, we need to assume the supplier has shown its willingness and focus on the maximization of the integrator’s profit. The specific optimization results of the integrator are described in Theorem 1.

Theorem 1.

The profit function of the integrator has a maximum value, and the optimal decision result is

$$a={\displaystyle \frac{\lambda [\alpha -(\beta +\gamma )]b+\lambda \gamma }{{\eta }_i}}$$

For simplification, here, we call $\alpha <\beta +\gamma$ as ‘1 + 1 < 2’, which specifically means that CIE is less than the sum of IIEs; for the same reason, $\alpha >\beta +\gamma$ is named ‘1 + 1 > 2’, indicating that CIE is greater than the sum of IIEs. It can be seen from Theorem 1 that when a supplier is dominant, its willingness does not always have a positive effect on the integrator. For example, when 1 + 1 < 2, it will have a negative effect. When the supplier’s willingness to improve is a fixed positive value, the greater the CIE, the stronger the integrator’s willingness to improve. When 1 + 1 > 2, both the revenue share and the supplier’s individual improvement effect have positive incentives for the integrator.

We then optimize the supplier’s quality improvement profit, the model is as below:

$$\underset{b}{Max} {\pi }_{s(SD)}=(1-\lambda )[{\displaystyle \frac{b\beta (\lambda A+{\eta }_i)}{{\eta }_i}}+{\displaystyle \frac{A\gamma \lambda (b-1)-A\alpha b\lambda }{{\eta }_i}}]-{\displaystyle \frac{1}{2}}{\eta }_s{b}^2+T$$

The corresponding optimization results of the supplier are described in Theorem 2.

Theorem 2.

When the second derivative is less than zero, that is $2\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2<{\eta }_i{\eta }_s$, the supplier’s profit function can be maximized, and the optimal willingness to improve service quality is

$$b_{SD}={\displaystyle \frac{2\gamma (1-\lambda )\lambda [\alpha -(\beta +\gamma )]+(1-\lambda )\beta {\eta }_i}{{\eta }_i{\eta }_s-2\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2}}.$$

According to the optimal decision in Theorem 2, we can obtain the final optimal results as follows.

$$\begin{array}{l}{a}_{SD}={\displaystyle \frac{\gamma \lambda M+\lambda (1-\lambda )[\alpha -(\beta +\gamma )]N}{M{\eta }_i}},\\ {\pi }_{i(SD)}=\lambda R-{\displaystyle \frac{{\lambda }^2{S}^2}{2{\eta }_i}}-T,\\ {\pi }_{s(SD)}=(1-\lambda )R-{\displaystyle \frac{{\eta }_s{(\lambda -1)}^2{N}^2}{2M^2}}+T.\end{array}$$

The undefined symbols appearing in the above expressions are described in Appendix A. It is easy to see from Theorem 2 that the stronger the CIE, the more willing the supplier is to make quality improvements.

4.2. Integrator Dominates

When the service integrator dominates, it first shows its willingness to improve service quality. For example, Shandong Iron and Steel strived to build an industrial collaborative information management platform, and then, upstream suppliers were promoted to improve supply efficiency and quality. The decision model when the integrator dominates is thus as follows:

$$\begin{array}{c}\underset{a}{Max} {\pi }_{i(ID)}=\lambda [\alpha ab+\beta (1-a)b+\gamma a(1-b)]-{\displaystyle \frac{1}{2}}{\eta }_i{a}^2-T\\ subject \mathrm{to} \underset{b}{Max} {\pi }_{s(ID)}=(1-\lambda )[\alpha ab+\beta (1-a)b+\gamma a(1-b)]-{\displaystyle \frac{1}{2}}{\eta }_s{b}^2+T\end{array}$$

Theorem 3.

When the integrator takes the lead, the supplier’s profit always has a maximum value, and the integrator achieves a maximum value when the second derivative is less than zero, that is$2\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2<{\eta }_i{\eta }_s$. The optimal corresponding decisions are

$$\begin{array}{l}{a}_{ID}={\displaystyle \frac{2\beta (1-\lambda )\lambda [\alpha -(\beta +\gamma )]+\gamma \lambda {\eta }_s}{{\eta }_i{\eta }_s-2\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2}},\\ b_{ID}={\displaystyle \frac{(\lambda -1)[\lambda N^{\prime }(\beta +\gamma -\alpha )-\beta M^{\prime }]}{M^{\prime }{\eta }_s}}\end{array}$$

The integrator and supplier’s profit from quality improvement are independent as

$$\begin{array}{l}{\pi }_{i(ID)}=\lambda R^{\prime }-{\displaystyle \frac{{\eta }_i{\lambda }^2{N}^{\prime 2}}{2M^{\prime 2}}}-T,\\ {\pi }_{s(ID)}=(1-\lambda )R^{\prime }-{\displaystyle \frac{{(\lambda -1)}^2{S}^{\prime 2}}{2{\eta }_s}}+T.\end{array}$$

Similarly, Theorem 3 reveals that the stronger the CIE, the stronger the willingness of the dominant integrator.

4.3. Supplier and Integrator with Same Power

When two members are power-balanced, their decisions are optimized independently and then simultaneously. For example, Toyota Motor Corporation has established long-term stable and equal cooperative relations with its suppliers to jointly improve product and service quality. Upstream suppliers strive to improve production processes, and Toyota also provides technical support and training. The cooperation between upstream and downstream when the powers are balanced promotes the improvement of the quality of products and services. The decision model when the supplier and integrator has the same power is as follows:

$$\left\{\begin{array}{l}\underset{a}{Max} {\pi }_{i(SP)}=\lambda [\alpha ab+\beta (1-a)b+\gamma a(1-b)]-{\displaystyle \frac{1}{2}}{\eta }_i{a}^2-T\\ \underset{b}{Max} {\pi }_{s(SP)}=(1-\lambda )[\alpha ab+\beta (1-a)b+\gamma a(1-b)]-{\displaystyle \frac{1}{2}}{\eta }_s{b}^2+T\end{array}\right.$$

The optimal decision and profit of the integrator and supplier are described in Theorem 4.

Theorem 4.

When the integrator and supplier are power-balanced, the optimal decisions are

$$\begin{array}{l}{a}_{SP}={\displaystyle \frac{\beta (1-\lambda )\lambda [\alpha -(\beta +\gamma )]+\lambda {\eta }_s\gamma }{{\eta }_i{\eta }_s-\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2}},\\ b_{SP}={\displaystyle \frac{(1-\lambda )\beta {\eta }_i+\gamma \lambda (1-\lambda )[\alpha -(\beta +\gamma )]}{{\eta }_i{\eta }_s-\lambda (\lambda -1){[\alpha -(\beta +\gamma )]}^2}}.\end{array}$$

The two supply chain members’ profits are

$$\begin{array}{l}{\pi }_{i(SP)}=\lambda R^{″}-{\displaystyle \frac{{\eta }_i{\lambda }^2{X}^2}{2Z^2}}-T,\\ {\pi }_{s(SP)}=(1-\lambda )R^{″}-{\displaystyle \frac{{\eta }_s{(\lambda -1)}^2{Y}^2}{2Z^2}}+T.\end{array}$$

When two members are power-balanced, there is an obvious symmetrical relationship between the integrator and the supplier’s willingness in decision-making expressions, and both of them continue to improve as CIE increases. The power-balance situation does not mean that the revenue share must be equal, and the fifty-five share does not necessarily bring the strongest willingness to improve.

4.4. Centralized Decision

In the case of centralized decision-making, the integrator and supplier make decisions from the overall situation to maximize the profit of the whole supply chain. The specific model is as follows:

$$\underset{a,b}{Max} {\pi }_c=a\alpha b+\beta (1-a)b+\gamma a(1-b)-{\displaystyle \frac{1}{2}}{\eta }_i{a}^2-{\displaystyle \frac{1}{2}}{\eta }_s{b}^2$$

The corresponding results are given in Theorem 5.

Theorem 5.

In centralized decision-making, if the quality improvement cost and effect meet the condition that ${\eta }_i{\eta }_s>{[\alpha -(\beta +\gamma )]}^2$, the overall profit of the supply chain changes concavely concerning the willingness of the integrator and the supplier to improve the quality of service, with a maximum value. The optimal results are as below:

$$\begin{array}{l}{a}_C={\displaystyle \frac{\beta [\alpha -(\beta +\gamma )]+{\eta }_s\gamma }{{\eta }_i{\eta }_s-{[\alpha -(\beta +\gamma )]}^2}},\\ b_C={\displaystyle \frac{\gamma [\alpha -(\beta +\gamma )]+\beta {\eta }_i}{{\eta }_i{\eta }_s-{[\alpha -(\beta +\gamma )]}^2}},\\ {\pi }_c={\displaystyle \frac{\alpha UV}{W^2}}-{\displaystyle \frac{{\eta }_s{V}^2+{\eta }_i{U}^2}{2W^2}}-{\displaystyle \frac{\beta (U/W+1)V+\gamma (V/W+1)U}{W}}.\end{array}$$

After the centralized decision, we will not discuss the redistribution of profit between the integrator and supplier here. Readers can refer to Shang and Yang [55].

It can be seen from Theorem 5 that the centralized decision result has nothing to do with the revenue share. When 1 + 1 > 2, the centralized decision result is greater than that in other situations if we pay attention to the expression of the numerator and denominator. In addition, the willingness will increase as CIE increases.

4.5. Comparisons about Optimal Results among Different Power Structures

In order to compare the decisions made under various power structures and the profit of each member, we have organized the results of Section 4.1, Section 4.2, Section 4.3 and Section 4.4 and presented them in

Table 6. Comparisons of optimal results among different power structures.

Optima	Supplier Dominates	Integrator Dominates	Power-Balanced	Centralized Decision
$a$	${\displaystyle \frac{\lambda \gamma {\eta }_s+\lambda (1-\lambda )\beta [\alpha -(\beta +\gamma )]}{{\eta }_i{\eta }_s-2\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2}}$	${\displaystyle \frac{2\beta (1-\lambda )\lambda [\alpha -(\beta +\gamma )]+\gamma \lambda {\eta }_s}{{\eta }_i{\eta }_s-2\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2}}$	${\displaystyle \frac{\beta (1-\lambda )\lambda [\alpha -(\beta +\gamma )]+\lambda {\eta }_s\gamma }{{\eta }_i{\eta }_s-\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2}}$	${\displaystyle \frac{\beta [\alpha -(\beta +\gamma )]+{\eta }_s\gamma }{{\eta }_i{\eta }_s-{[\alpha -(\beta +\gamma )]}^2}}$
$b$	${\displaystyle \frac{(1-\lambda )2\gamma \lambda [\alpha -(\beta +\gamma )]+(1-\lambda )\beta {\eta }_i}{{\eta }_i{\eta }_s-2\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2}}$	${\displaystyle \frac{(1-\lambda )\lambda \gamma [\alpha -(\beta +\gamma )]+(1-\lambda )\beta {\eta }_i}{{\eta }_i{\eta }_s-2\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2}}$	${\displaystyle \frac{(1-\lambda )\beta {\eta }_i+\gamma \lambda (1-\lambda )[\alpha -(\beta +\gamma )]}{{\eta }_i{\eta }_s-\lambda (1-\lambda ){[\alpha -(\beta +\gamma )]}^2}}$	${\displaystyle \frac{\gamma [\alpha -(\beta +\gamma )]+\beta {\eta }_i}{{\eta }_i{\eta }_s-{[\alpha -(\beta +\gamma )]}^2}}$
${\pi }_i$	$\lambda R-{\displaystyle \frac{{\lambda }^2{S}^2}{2{\eta }_i}}-T$	$\lambda R^{\prime }-{\displaystyle \frac{{\eta }_i{\lambda }^2{N}^{\prime 2}}{2M^{\prime 2}}}-T$	$\lambda R^{\prime \prime }-{\displaystyle \frac{{\eta }_i{\lambda }^2{X}^2}{2Z^2}}-T$	-
${\pi }_s$	$(1-\lambda )R-{\displaystyle \frac{{\eta }_s{(\lambda -1)}^2{N}^2}{2M^2}}+T$	$(1-\lambda )R^{\prime }-{\displaystyle \frac{{(\lambda -1)}^2{S}^{\prime 2}}{2{\eta }_s}}+T$	$(1-\lambda )R^{\prime \prime }-{\displaystyle \frac{{\eta }_s{(\lambda -1)}^2{Y}^2}{2Z^2}}+T$	-
$\pi$	$R-{\displaystyle \frac{{\lambda }^2{S}^2}{2{\eta }_i}}-{\displaystyle \frac{{\eta }_s{(\lambda -1)}^2{N}^2}{2M^2}}$	$R^{\prime }-{\displaystyle \frac{{(\lambda -1)}^2{S}^{\prime 2}}{2{\eta }_s}}-{\displaystyle \frac{{\eta }_i{\lambda }^2{N}^{\prime 2}}{2M^{\prime 2}}}$	$R^{\prime \prime }-{\displaystyle \frac{{\eta }_i{\lambda }^2{X}^2}{2Z^2}}-{\displaystyle \frac{{\eta }_s{(\lambda -1)}^2{Y}^2}{2Z^2}}$	${\displaystyle \frac{2[\alpha -(\beta +\gamma )]UV-({\eta }_s{V}^2+{\eta }_i{U}^2)}{2W^2}}-{\displaystyle \frac{\beta V+\gamma U}{W}}$

. After comparison and analysis, we obtain a relationship between decision-making and profits among different power structures, as described in Propositions 1–5.

Proposition 1.

Regarding the supplier and integrator’s willingness in each situation, we have the following results: 

(i) 

If $(1-\lambda )\beta {\eta }_i\le \lambda \gamma {\eta }_s+\lambda (1-\lambda )\delta (\beta -2\gamma )$, $a_{SD}\ge b_{SD}$. If $(1-\lambda )\beta {\eta }_i>\lambda \gamma {\eta }_s+\lambda (1-\lambda )\delta (\beta -2\gamma )$, $a_{SD}<b_{SD}$.

(ii) 

If $(1-\lambda )\beta {\eta }_i\le \gamma \lambda {\eta }_s+\lambda (1-\lambda )\delta (2\beta -\gamma )$, $a_{ID}\ge b_{ID}$. If $(1-\lambda )\beta {\eta }_i>\gamma \lambda {\eta }_s+\lambda (1-\lambda )\delta (2\beta -\gamma )$, $a_{ID}<b_{ID}$.

(iii) 

If $(1-\lambda )\beta {\eta }_i\le \lambda \gamma {\eta }_s+\lambda (1-\lambda )\delta (\beta -\gamma )$, $a_{SP}\ge b_{SP}$. If $(1-\lambda )\beta {\eta }_i>\lambda \gamma {\eta }_s+\lambda (1-\lambda )\delta (\beta -\gamma )$, $a_{SP}<b_{SP}$.

(iv) 

If $\beta {\eta }_i\le {\eta }_s\gamma +\delta (\beta -\gamma )$, $a_C\ge b_C$. If $\beta {\eta }_i>{\eta }_s\gamma +\delta (\beta -\gamma )$, $a_C<b_C$.

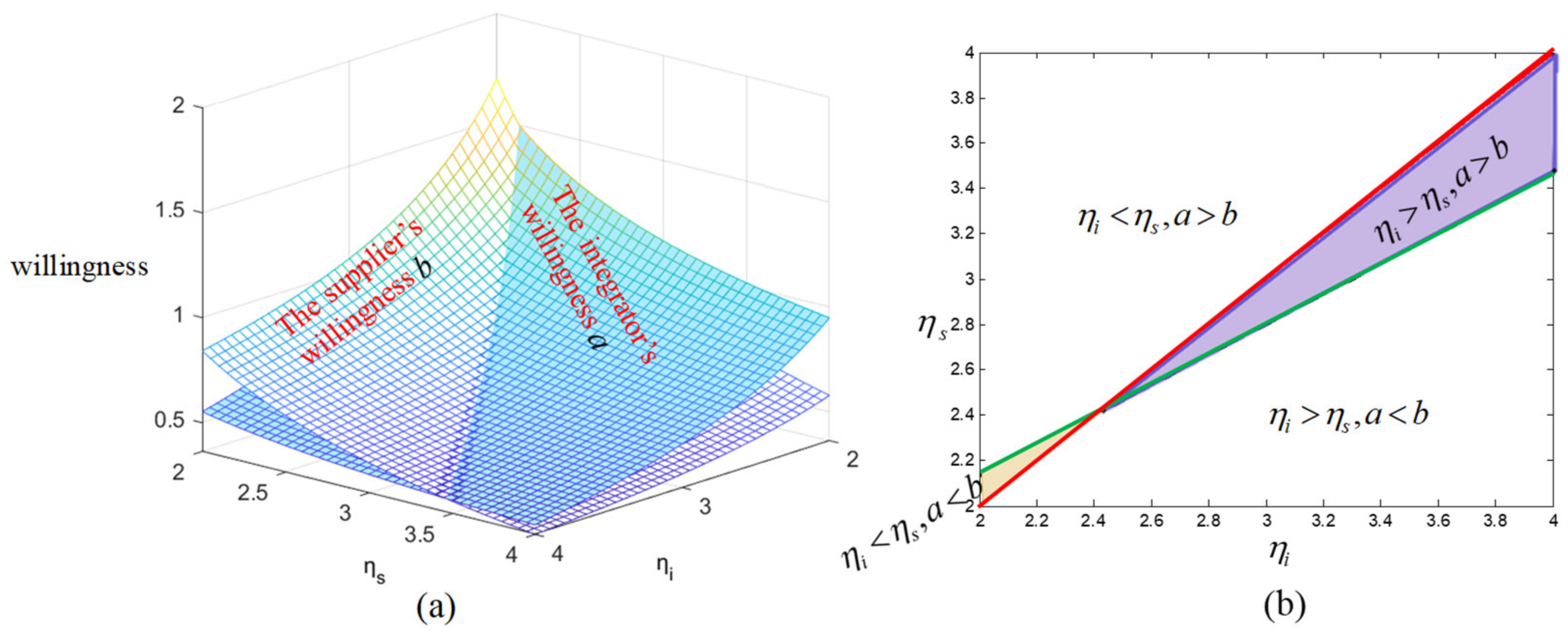
Proposition 1 reveals that the willingness of a dominant member is not necessarily higher than that of a subordinate one, and the relationship depends on $\beta$, $\gamma$, ${\eta }_i$, ${\eta }_s$ and $\lambda$; especially when $\delta =\alpha -(\beta +\gamma )=0$, it is completely determined by the relationship between $(1-\lambda )\beta {\eta }_i$ and $\lambda \gamma {\eta }_s$. When $(1-\lambda )\beta {\eta }_i\le \lambda \gamma {\eta }_s$, the integrator’s willingness is stronger, and on the contrary, the supplier’s willingness is stronger. This does not seem to have a certain relationship with who is dominant. For the revenue share, it is easy to find that there will be $a<b$ if $0\le \lambda <\beta {\eta }_i/(\beta {\eta }_i+\gamma {\eta }_s)$ and $a\ge b$ if $1-\lambda \le \gamma {\eta }_s/(\beta {\eta }_i+\gamma {\eta }_s)$. It indicates that when the revenue share is lower than a certain threshold, it will stimulate the supply chain member to make quality improvements, and the member with a higher revenue share has a weaker willingness. Extending this discussion to centralized decision-making, we find $\beta {\eta }_i>\gamma {\eta }_s\iff \beta /{\eta }_s>\gamma /{\eta }_i$ incurs $b>a$ and $\beta {\eta }_i<\gamma {\eta }_s\iff \beta /{\eta }_s<\gamma /{\eta }_i$ makes $a\ge b$. If we regard $\beta /{\eta }_s$, $\gamma /{\eta }_i$ the input–output efficiency of the supplier and the integrator, we will find that the member with a higher input–output efficiency has a stronger willingness, and the member with a lower input-output efficiency has a weaker willingness.

Proposition 2.

The following conclusions are based on $\delta =\alpha -(\beta +\gamma )>0$

(i) 

${\displaystyle \frac{\partial a_{SD}}{\partial \alpha }}>0$, ${\displaystyle \frac{\partial b_{SD}}{\partial \alpha }}>0$, ${\displaystyle \frac{\partial a_{ID}}{\partial \alpha }}>0$, ${\displaystyle \frac{\partial b_{ID}}{\partial \alpha }}>0$, ${\displaystyle \frac{\partial a_{SP}}{\partial \alpha }}>0$, ${\displaystyle \frac{\partial b_{SP}}{\partial \alpha }}>0$, ${\displaystyle \frac{\partial a_C}{\partial \alpha }}>0$, ${\displaystyle \frac{\partial b_C}{\partial \alpha }}>0$.

(ii) 

If ${\displaystyle \frac{\alpha -\gamma }{2}}\le \beta \le \alpha -\gamma$, there will be ${\displaystyle \frac{\partial a_{SD}}{\partial \beta }}\le 0$, ${\displaystyle \frac{\partial a_{ID}}{\partial \beta }}\le 0$, ${\displaystyle \frac{\partial a_{SP}}{\partial \beta }}\le 0$, ${\displaystyle \frac{\partial a_C}{\partial \beta }}\le 0$. If ${\eta }_i<\gamma \lambda$, there will be ${\displaystyle \frac{\partial b_{ID}}{\partial \beta }}\le 0$, ${\displaystyle \frac{\partial b_{ID}}{\partial \beta }}\le 0$, ${\displaystyle \frac{\partial b_{SP}}{\partial \beta }}\le 0$, ${\displaystyle \frac{\partial b_C}{\partial \beta }}\le 0$.

(iii) 

If ${\eta }_s<(1-\lambda )\beta$, there will be ${\displaystyle \frac{\partial a_{SD}}{\partial \gamma }}\le 0$, ${\displaystyle \frac{\partial a_{ID}}{\partial \gamma }}\le 0$, ${\displaystyle \frac{\partial a_{SP}}{\partial \gamma }}\le 0$, ${\displaystyle \frac{\partial a_C}{\partial \gamma }}\le 0$. If ${\displaystyle \frac{\alpha -\beta }{2}}\le \gamma \le \alpha -\beta$, there will be ${\displaystyle \frac{\partial b_{ID}}{\partial \gamma }}\le 0$, ${\displaystyle \frac{\partial b_{ID}}{\partial \gamma }}\le 0$, ${\displaystyle \frac{\partial b_{SP}}{\partial \gamma }}\le 0$, ${\displaystyle \frac{\partial b_C}{\partial \gamma }}\le 0$.

(iv) 

${\displaystyle \frac{\partial a_{SD}}{\partial {\eta }_i}}\le 0$, ${\displaystyle \frac{\partial a_{ID}}{\partial {\eta }_i}}\le 0$, ${\displaystyle \frac{\partial a_{SP}}{\partial {\eta }_i}}\le 0$, ${\displaystyle \frac{\partial a_C}{\partial {\eta }_i}}\le 0$, ${\displaystyle \frac{\partial b_{SD}}{\partial {\eta }_i}}\le 0$, ${\displaystyle \frac{\partial b_{ID}}{\partial {\eta }_i}}\le 0$, ${\displaystyle \frac{\partial b_{SP}}{\partial {\eta }_i}}\le 0$, ${\displaystyle \frac{\partial b_C}{\partial {\eta }_i}}\le 0$.

(v) 

${\displaystyle \frac{\partial a_{SD}}{\partial {\eta }_s}}\le 0$, ${\displaystyle \frac{\partial a_{ID}}{\partial {\eta }_s}}\le 0$, ${\displaystyle \frac{\partial a_{SP}}{\partial {\eta }_s}}\le 0$, ${\displaystyle \frac{\partial a_C}{\partial {\eta }_s}}\le 0$, ${\displaystyle \frac{\partial b_{SD}}{\partial {\eta }_s}}\le 0$, ${\displaystyle \frac{\partial b_{ID}}{\partial {\eta }_s}}\le 0$, ${\displaystyle \frac{\partial b_{SP}}{\partial {\eta }_s}}\le 0$, ${\displaystyle \frac{\partial b_C}{\partial {\eta }_s}}\le 0$.

(vi) 

If $\lambda \le 1/2$, there will be ${\displaystyle \frac{\partial a_{SD}}{\partial \lambda }}>0$, ${\displaystyle \frac{\partial a_{ID}}{\partial \lambda }}>0$, ${\displaystyle \frac{\partial a_{SP}}{\partial \lambda }}>0$. If $\lambda >1/2$, there will be ${\displaystyle \frac{\partial b_{SD}}{\partial \lambda }}>0$, ${\displaystyle \frac{\partial b_{ID}}{\partial \lambda }}>0$, ${\displaystyle \frac{\partial b_{SP}}{\partial \lambda }}>0$. $a_C$ and $b_C$ remain unchanged when $\lambda$ changes.

The conclusions of Proposition 2 do not mean that there will be completely opposite results when $\delta \le 0$. In fact, when $\lambda (1-\lambda )\beta {\eta }_i{\eta }_s+2\beta {\lambda }^2{(1-\lambda )}^2{\delta }^2+4{\lambda }^2(1-\lambda )\gamma {\eta }_s\delta \ge 0$, we can judge ${\displaystyle \frac{\partial a_{SD}}{\partial \alpha }}\ge 0$ and vice versa. Similarly, the positive or negative effects of other parameters on supply chain members’ willingness also have preconditions for their existence, which can be seen from the proof process of Proposition 2. This means that the influence of each parameter on the willingness of supply chain members is not strictly monotonous, but there are one or more inflection points. $\delta >0$ is only a special case, but Proposition 2 shows that 1 + 1 > 2 is critical to the willingness of the supplier and the integrator to improve quality. When 1 + 1 > 2, the influence of the parameter $\alpha$, ${\eta }_i$, and ${\eta }_s$ on the willingness of each member is strictly monotonous, and the influence of the parameter $\lambda$ is also strictly monotonous, but simple conditions need to be met. Under this premise, the two members’ willingness under each power structure is positively correlated with $\alpha$, and negatively correlated with parameters ${\eta }_i$ and ${\eta }_s$. It can be seen from this that the willingness of supply chain members should start by enhancing the collaborative effect and reducing the cost. The influence of $\beta$ and $\gamma$ on two members’ willingness may be positive or negative, which shows that the impact of $\beta$ and $\gamma$ on willingness is not stable. Furthermore interesting is that when $\lambda \le 1/2$, the increase in $\lambda$ risks the integrator and makes the integrator more proactive in quality improvement; when $\lambda >1/2$, the supplier’s revenue share is already lower than 50%, and if it continues to increase, the supplier will be less willing to make quality improvements. Additionally, none of these conclusions seem to have changed because of the dominance of supply chain members.

Proposition 3.

If $\delta =\alpha -\left(\beta +\gamma \right)>0$, there must be $a_{SP}\le a_{SD}\le a_{ID}<a_C$ and $b_{SP}\le b_{ID}\le b_{SD}<b_C$.

Proposition 3 reveals that, whether 1 + 1 > 2 is crucial for willingness decisions. If there is 1 + 1 > 2, the willingness under centralized decision-making is the greatest. Regarding the integrator or the supplier, the willingness with a clear dominant position is greater than that when two members are power-balanced. With regard to the member in a dominant position, its willingness is greater than that when it is subordinate.

Proposition 4.

The integrator’s profits satisfy

(i) 

${\pi }_{i(SD)}\ge {\pi }_{i(ID)}\ge {\pi }_{i(SP)}$ if there are $\delta >0$ and $6{\gamma }^2{\delta }^4{\lambda }^2(1-\lambda ){\phi }_1+(1-\lambda ){\beta }^2{\delta }^2{\eta }_i^2{\phi }_2\ge {\delta }^2\lambda {\eta }_i{\eta }_s{\gamma }^2{\phi }_3+2\beta \gamma {\eta }_i\delta {\phi }_2{\phi }_4$.

(ii) 

${\pi }_{i(ID)}\le {\pi }_{i(SD)}\le {\pi }_{i(SP)}$ when the following conditions are satisfied simultaneously.

$$\begin{array}{l}\beta {\delta }^2(1-\lambda )(2\beta {\eta }_i{\eta }_s{\phi }_1+3\beta {\lambda }^3{\delta }^2{\eta }_i^2+2\lambda \gamma \delta {\eta }_s{\phi }_7)+2\gamma \delta {\eta }_s^2(\lambda \gamma \delta {\phi }_5+\beta {\eta }_i^2{\eta }_s)\le \lambda {\delta }^2[{\lambda }^2{\gamma }^2{\delta }^2{\phi }_5+2\lambda \delta \beta \gamma {\eta }_i{\phi }_5+2{\eta }_i^3{\eta }_s{\beta }^2+2{\beta }^2{\lambda }^2{(1-\lambda )}^3{\delta }^4]\\ {\delta }^2(1-\lambda )(6{\gamma }^2{\delta }^2{\lambda }^2{\phi }_1+{\beta }^2{\eta }_i^2{\phi }_2)\le \gamma \delta {\eta }_i(\delta \lambda {\eta }_s\gamma {\phi }_3+2\beta {\phi }_2{\phi }_4).\end{array}$$

Proposition 4 reveals that when 1 + 1 > 2, the profit of the integrator in a subordinate position is greater than that in a dominant position, and the dominant position does not bring more profit. Under appropriate conditions, the integrator’s profit in the power-balanced situation is greater than those of the other two power structures, but it may also be lower than those of the other two situations.

Proposition 5.

The supplier’s profits under different power structures satisfy the following relationships:

(i) 

If $\delta >0$ and $3\lambda {\gamma }^2{\delta }^2{\eta }_s+6\gamma \beta {\eta }_i{\eta }_s\delta \le 2(1-\lambda ){\beta }^2{\delta }^2{\eta }_i$, there will be ${\pi }_{s(SP)}\le {\pi }_{s(SD)}\le {\pi }_{s(ID)}$.

(ii) 

If $3\lambda {\gamma }^2{\delta }^2{\eta }_s+6\gamma \beta {\eta }_i{\eta }_s\delta \ge 2(1-\lambda ){\beta }^2{\delta }^2{\eta }_i$ and $(1-\lambda ){\beta }^2{\eta }_i^2{\delta }^2{\phi }_5\ge 2\beta \gamma {\eta }_i\delta {\phi }_1{\phi }_6+\lambda {\gamma }^2{\delta }^2{\phi }_1{\phi }_5+\lambda (1-\lambda )\gamma {\eta }_i{\eta }_s{\delta }^3(\lambda \gamma \delta +2\beta {\eta }_i)$, there will be ${\pi }_{s(SP)}\le {\pi }_{s(ID)}\le {\pi }_{s(SD)}$.

(iii) 

If $\delta >0$ and $(1-\lambda ){\beta }^2{\eta }_i^2{\delta }^2{\phi }_5\le 2\beta \gamma {\eta }_i\delta {\phi }_1{\phi }_6$, there will be ${\pi }_{s(ID)}\le {\pi }_{s(SP)}\le {\pi }_{s(SD)}$.

Proposition 5 indicates that when 1 + 1 > 2, the profit of the supplier in a dominant position is always greater than the corresponding profit in the power-balanced situation, but the supplier led by the integrator can also obtain a higher profit than other situations under appropriate conditions. The relationship between the supplier’s profits in the two situations of the integrator with a dominant position and power is not necessary, and various possibilities may exist.

5. Numerical Examples and Analysis

The service industry plays a crucial role in driving global economic growth. According to the World Bank, the service industry’s added value accounted for more than 60% of global GDP in 2022 and continued to rise. Service quality, as the core of service supply chain management, has always been highly valued by consumers and businesses alike. However, not all enterprises exhibit a high willingness to improve service quality, which can lead to quality incidents, as discussed in the introduction. This emphasizes the importance of service quality management for both upstream and downstream enterprises in the supply chain, and the collaborative and independent improvement efforts of chain members can be influenced by their position within the supply chain. For instance, companies like SAP and service integrators such as Accenture, Deloitte, and Capgemini have established close partnerships to enhance customer service across various industries [31]. As the world’s third-largest independent software supplier, SAP imposes stringent controls on its partners’ service aspects, continuously monitoring and evaluating their performance. Accenture, the world’s largest listed consulting company, collaborates with SAP on multiple innovative initiatives, providing customers with industry-leading solutions. Each year, over 50,000 SAP experts deliver project services to customers worldwide. Another example is MyGym, a leading company in the industry, which rigorously selects franchisees and carries out supervision and management to maintain service quality. However, MyGym’s failure to effectively manage service quality resulted in damage to its reputation and a decline in performance. Considering the importance of synergies, studying the impact of power structures and related parameters on service quality improvement decisions and members’ profits is crucial. This section combines practical background information and utilizes MATLAB 9.12 software to assign values to each parameter for subsequent numerical analysis. The dominant position, revenue function, and game process exhibit symmetry. For instance, MyGym, as an internationally renowned integrator, occupies a dominant position in the service supply chain compared to its franchisees. SAP, as the world’s third-largest independent software supplier, occupies a dominant position in the service supply chain compared to its integrators. So it is important to consider symmetry when assigning parameters. For example, refer to Liu et al. [14], after setting ${\eta }_i=3.5, {\eta }_s=4$, we also need to consider ${\eta }_i=4, {\eta }_s=3.5$. Similarly, both $\lambda =0.6$ and $\lambda =0.4$ need to be analyzed.

5.1. Effect of Collaborative Quality Improvement

In order to clearly analyze the impact of CIE on the willingness and profit, we will consider four power structures, discuss various combinations of cost and revenue share in each structure, and examine how decisions and profit change with $\alpha$. The combinations can be simplified into two categories: the difficulty of improvement is small and the share is high, and the difficulty of improvement is big but the share is low. We take into account the influence of symmetry and dominance and then subdivide it into four categories.

• Analysis of willingness to improve quality

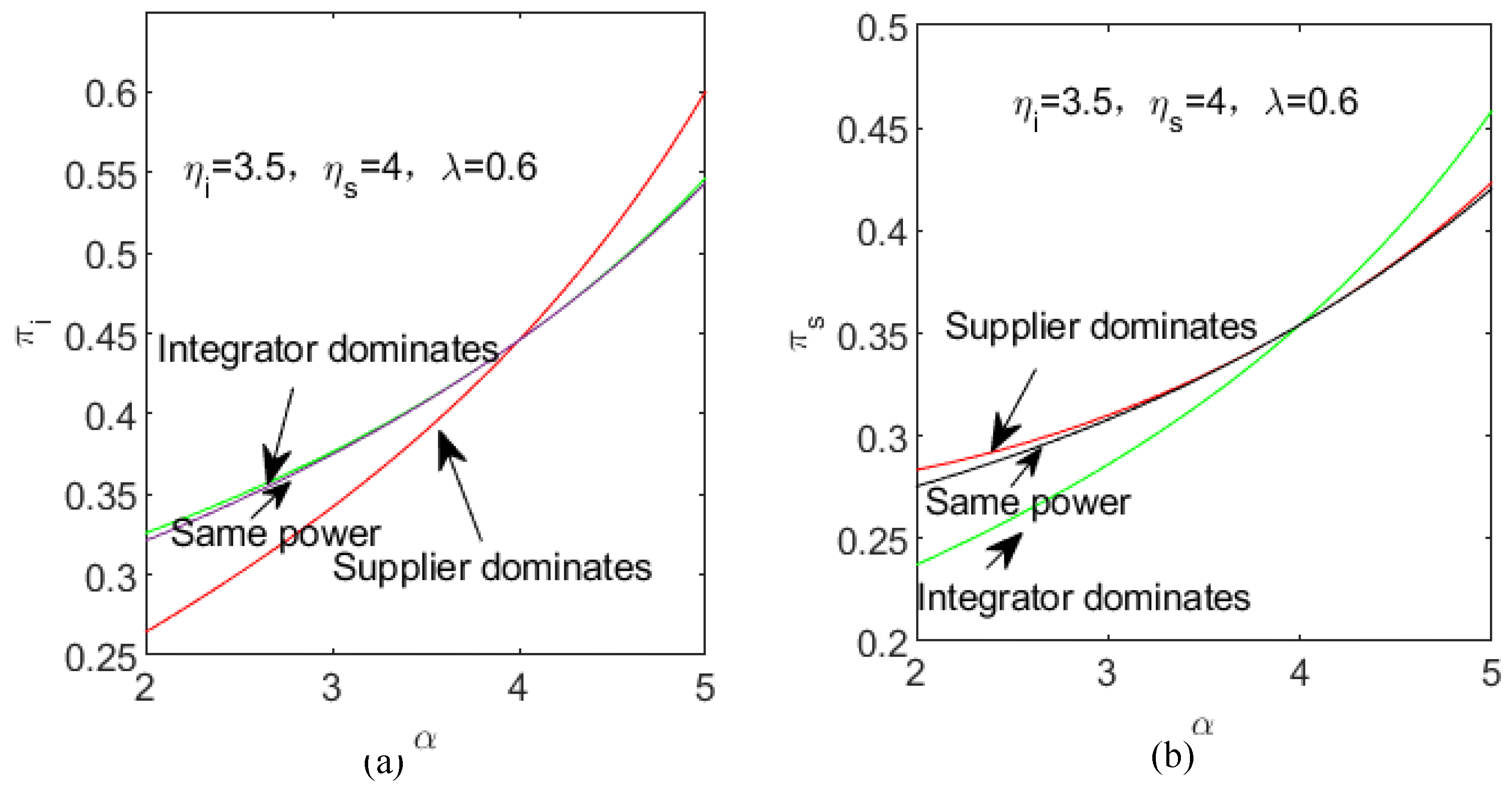
There is a Chinese saying: Everybody’s business is nobody’s business. It reveals that hitch-hiking is human nature. Nevertheless, whether 1 + 1 > 2 has an important impact on their willingness and profits. Here, we especially focus on the willingness of the dominant supplier when $\alpha \in [1,5]$. The trend is different when $\alpha \in [1,5]$. For example, in centralized decisions, the willingness is not always higher than that of other power structures, as shown in Figure 2a. When $\alpha \le 0.64$, $b_{SD}\le b_c\le b_{SP}$. When $0.64<\alpha <0.725$, $b_{SP}\le b_c\le b_{ID}$. When $\alpha \ge 0.725$, the centralized decision has an absolute advantage. Therefore, when CIE is too poor, centralized decisions will be meaningless; for the dominant supplier, under the pressure of high cost and low $\lambda$, it has no willingness at all. Although the integrator still has the willingness to improve under the incentive of a high revenue share, after observing the supplier’s “lying flat” posture as a dominant player, the willingness is slowly declining, and then, the improvement of service quality will become meaningless. In practice, if $\alpha$ is too poor, supply chain members will look for new partners. Then, we focus on $\alpha \ge 2$ in the following discussion. As shown in Figure 2b, the supplier’s willingness has changed from a negative value to a positive one and will continue to increase. Here, $\alpha \ge 2$ means CIE is at least greater than one of the two IIEs. In addition, $\alpha \in [2,5]$ includes both the case of $\alpha \le \beta +\gamma$ and the case of $\alpha >\beta +\gamma$, as shown in Figure 2a,b. The two members’ willingness in various situations can be seen in

Table A1. Willingness to improve service quality under different power structures.

Power Structures	Parameters	$\mathit{a}$	$\mathit{b}$	$\mathit{a}$	$\mathit{b}$	$\mathit{a}$	$\mathit{b}$	$\mathit{a}$	$\mathit{b}$
Supplier dominates	α	${\eta }_i=3.5,{\eta }_s=4,\lambda =0.6$		${\eta }_i=3.5,{\eta }_s=4,\lambda =0.4$		${\eta }_i=4,{\eta }_s=3.5,\lambda =0.6$		${\eta }_i=4,{\eta }_s=3.5,\lambda =0.4$
	3	0.32	0.136	0.201	0.24	0.275	0.166	0.172	0.284
	3.5	0.329	0.167	0.213	0.268	0.285	0.196	0.184	0.311
	4	0.343	0.2	0.229	0.3	0.3	0.229	0.2	0.343
	4.5	0.363	0.236	0.248	0.337	0.32	0.265	0.219	0.38
Integrator dominates	α	${\eta }_i=3.5,{\eta }_s=4,\lambda =0.6$		${\eta }_i=3.5,{\eta }_s=4,\lambda =0.4$		${\eta }_i=4,{\eta }_s=3.5,\lambda =0.6$		${\eta }_i=4,{\eta }_s=3.5,\lambda =0.4$
	3	0.284	0.172	0.166	0.275	0.24	0.201	0.136	0.32
	3.5	0.311	0.184	0.196	0.285	0.268	0.213	0.167	0.329
	4	0.343	0.2	0.229	0.3	0.3	0.229	0.2	0.343
	4.5	0.38	0.219	0.265	0.32	0.337	0.248	0.236	0.363
Nobody dominates	α	${\eta }_i=3.5,{\eta }_s=4,\lambda =0.6$		${\eta }_i=3.5,{\eta }_s=4,\lambda =0.4$		${\eta }_i=4,{\eta }_s=3.5,\lambda =0.6$		${\eta }_i=4,{\eta }_s=3.5,\lambda =0.4$
	3	0.314	0.169	0.198	0.27	0.27	0.198	0.169	0.314
	3.5	0.327	0.184	0.212	0.284	0.284	0.212	0.184	0.327
	4	0.343	0.2	0.229	0.3	0.3	0.229	0.2	0.343
	4.5	0.362	0.218	0.247	0.319	0.319	0.247	0.218	0.362
Centralized decision	α	${\eta }_i=3.5,{\eta }_s=4,\lambda =0.6$		${\eta }_i=3.5,{\eta }_s=4,\lambda =0.4$		${\eta }_i=4,{\eta }_s=3.5,\lambda =0.6$		${\eta }_i=4,{\eta }_s=3.5,\lambda =0.4$
	3	0.462	0.385	0.462	0.385	0.385	0.462	0.385	0.462
	3.5	0.509	0.436	0.509	0.436	0.436	0.509	0.436	0.509
	4	0.571	0.5	0.571	0.5	0.5	0.571	0.5	0.571
	4.5	0.655	0.582	0.655	0.582	0.582	0.655	0.582	0.655

of Appendix C. As shown in Figure 2a, when $\alpha \ge 2$, the willingness of each member increases with $\alpha$, and the changes are slightly weaker, except under centralized decisions. We also find that $a_{ID}\le a_{SP}\le a_{SD}$ and $b_{SD}\le b_{SP}\le b_{ID}$, which means the willingness under a power-balanced situation is neither bad nor good. In the centralized decision, it is higher than that under other three power structures. When 1 + 1 < 2, even as a dominant member, its willingness is low; when 1 + 1 > 2, the dominant position has a considerable impact, as Proposition 3 states.

2.

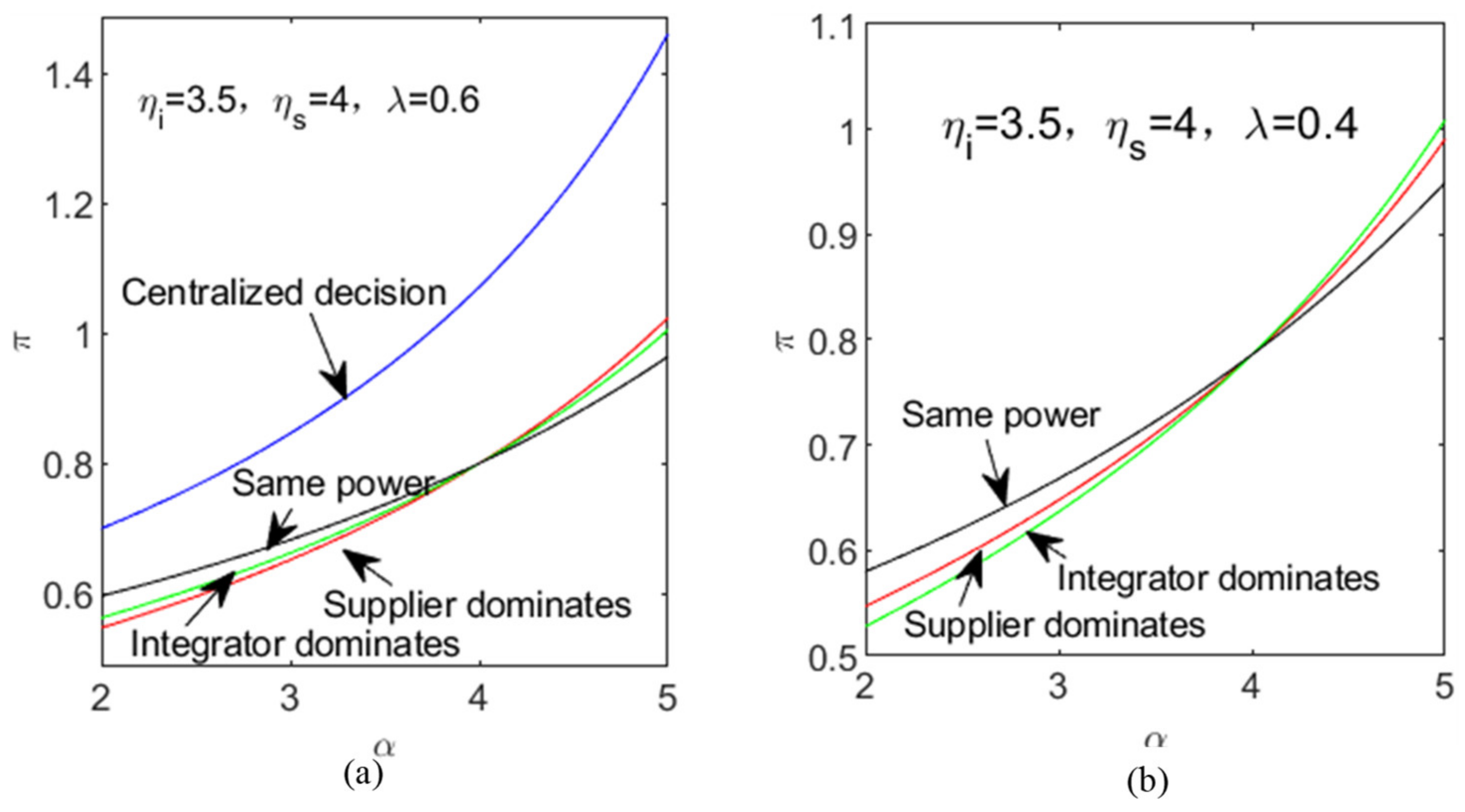
Profit analysis

It seems that the dominant position does not have the absolute advantage of winning profits (see Table A1 in Appendix C), and the decline in costs does not bring absolute increases in profits. The revenue share is an exception. This conclusion holds for the first three power structures. Obviously, the cost and revenue share structure have no effect on the profit in centralized decisions, but α has an obvious positive correlation with the profit. The changes in the profit of the supplier and the integrator can be seen in Figure 3a,b, and we find that the total profit of the chain will achieve a relatively larger value if the member with low difficulty and a high revenue share is dominant.

The profit of the integrator and supplier in the four power structures increases with $\alpha$ continuously. When 1 + 1 < 2, the profit is closely related to its dominant position. When 1 + 1 > 2, the profit changes as Propositions 4 and 5 state. There is no absolute correlation between the profit and its dominant position. However, the final profit has a close relationship with the revenue share.

For the whole chain, the profit in each structure shows a convex upward trend with $\alpha$, and centralized decisions are significantly better than other ones. As shown in Figure 4a, if 1 + 1 < 2, when the integrator is dominant, the profit is higher than the other two structures, the latter two are relatively close to each other, and both are significantly smaller than the former. If 1 + 1 > 2, the situation is absolutely reversed. The reason may be the lower cost. However, when 1 + 1 > 2 and $\alpha \ge 4$, the member with high cost takes the lead, its corresponding overall chain profit will be higher than the other two structures. This means that if the member who has more difficulties takes the lead, it is more conducive for the whole chain to gain a higher profit.

A member whose service quality is more difficult to improve but has a larger revenue share will generally have a higher willingness than the other one. The detail about two members’ respective profits will not be repeated here and can be found in

Table A2. Profits of supply chain and two members under different power structures.

Power Structures	Parameters	${\mathit{\pi }}_{\mathit{i}}$	${\mathit{\pi }}_{\mathit{s}}$	$\mathit{\pi }$	${\mathit{\pi }}_{\mathit{i}}$	${\mathit{\pi }}_{\mathit{s}}$	$\mathit{\pi }$	${\mathit{\pi }}_{\mathit{i}}$	${\mathit{\pi }}_{\mathit{s}}$	$\mathit{\pi }$	${\mathit{\pi }}_{\mathit{i}}$	${\mathit{\pi }}_{\mathit{s}}$	$\mathit{\pi }$
Supplier dominates	α	${\eta }_i=3.5,{\eta }_s=4,\lambda =0.6$			${\eta }_i=3.5,{\eta }_s=4,\lambda =0.4$			${\eta }_i=4,{\eta }_s=3.5,\lambda =0.6$			${\eta }_i=4,{\eta }_s=3.5,\lambda =0.4$
	3	0.342	0.31	0.652	0.263	0.385	0.648	0.35	0.286	0.637	0.286	0.376	0.662
	3.5	0.389	0.33	0.719	0.294	0.417	0.711	0.398	0.307	0.705	0.317	0.408	0.725
	4	0.446	0.354	0.8	0.331	0.454	0.786	0.454	0.331	0.786	0.354	0.446	0.8
	4.5	0.514	0.385	0.899	0.377	0.5	0.877	0.523	0.362	0.885	0.4	0.491	0.891
Integrator dominates	α	${\eta }_i=3.5,{\eta }_s=4,\lambda =0.6$			${\eta }_i=3.5,{\eta }_s=4,\lambda =0.4$			${\eta }_i=4,{\eta }_s=3.5,\lambda =0.6$			${\eta }_i=4,{\eta }_s=3.5,\lambda =0.4$
	3	0.376	0.286	0.662	0.286	0.35	0.637	0.385	0.263	0.648	0.31	0.342	0.652
	3.5	0.408	0.317	0.725	0.307	0.398	0.705	0.417	0.294	0.711	0.33	0.389	0.719
	4	0.446	0.354	0.8	0.331	0.454	0.786	0.454	0.331	0.786	0.354	0.446	0.8
	4.5	0.491	0.4	0.891	0.362	0.523	0.885	0.5	0.377	0.877	0.385	0.514	0.899
Nobody dominates	α	${\eta }_i=3.5,{\eta }_s=4,\lambda =0.6$			${\eta }_i=3.5,{\eta }_s=4,\lambda =0.4$			${\eta }_i=4,{\eta }_s=3.5,\lambda =0.6$			${\eta }_i=4,{\eta }_s=3.5,\lambda =0.4$
	3	0.375	0.308	0.683	0.285	0.383	0.668	0.383	0.285	0.668	0.308	0.375	0.683
	3.5	0.408	0.329	0.737	0.306	0.416	0.722	0.416	0.306	0.722	0.329	0.408	0.737
	4	0.446	0.354	0.8	0.331	0.454	0.786	0.454	0.331	0.786	0.354	0.446	0.8
	4.5	0.49	0.384	0.875	0.361	0.499	0.86	0.499	0.361	0.86	0.384	0.49	0.875
Centralized decision	α	${\eta }_i=3.5,{\eta }_s=4,\lambda =0.6$			${\eta }_i=3.5,{\eta }_s=4,\lambda =0.4$			${\eta }_i=4,{\eta }_s=3.5,\lambda =0.6$			${\eta }_i=4,{\eta }_s=3.5,\lambda =0.4$
	3	Undefined		0.846	Undefined		0.846	Undefined		0.846	Undefined		0.846
	3.5			0.945			0.945			0.945			0.945
	4			1.071			1.071			1.071			1.071
	4.5			1.236			1.236			1.236			1.236

in Appendix C. If 1 + 1 < 2, the profit in a power-balanced situation will be higher than the other two dominant cases, and if 1 + 1 > 2, the result is the opposite, and this balanced situation becomes the most unfavorable. In the two dominant situations, if 1 + 1 < 2, the member can benefit from the dominant position and higher cost. When 1 + 1 > 2, the situation is the opposite, see Figure 4b.

5.2. Quality Improvement Decisions and Profits with Uniformly Reduced Costs

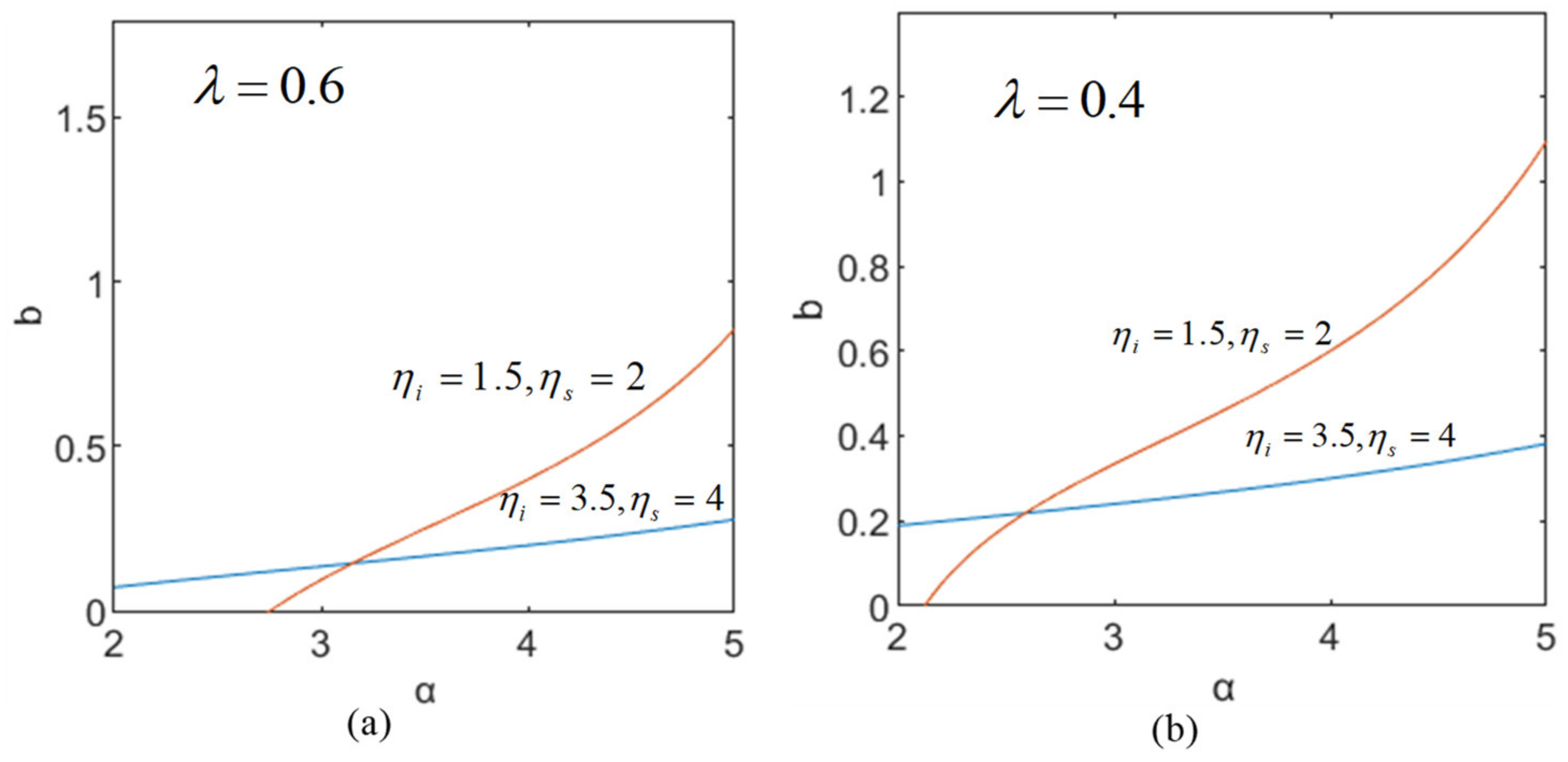
As mentioned in Proposition 2, the cost has a significant impact on the willingness, but this correlation is not necessary. Figure 5a,b show the respective effects of cost when the supplier dominates. In most cases, the willingness may be stronger if the cost is low. However, the purple and light yellow areas in Figure 5b show a few opposite results. When the rate of change in the marginal cost of the integrator is less than that of the supplier, the integrator’s willingness to improve service quality may be lower than the supplier’s willingness to improve service value. When the marginal cost change rate of the supplier is smaller than that of the integrator, the supplier’s willingness to improve service quality may also be lower than the integrator’s willingness to improve service value. Then, we take these results as a benchmark to analyze the impact of the unified cost reduction. It is found that the uniform decrease in cost is still beneficial for increasing the members’ willingness, and it also incurs an increase in profit, see Table A1 and

Table A3. Willingness to improve quality and corresponding profits with costs reduces uniformly.

Power Structures	Decisions	$\mathit{a}$	$\mathit{b}$	${\mathit{\pi }}_{\mathit{i}}$	${\mathit{\pi }}_{\mathit{s}}$	$\mathit{\pi }$	$\mathit{a}$	$\mathit{b}$	${\mathit{\pi }}_{\mathit{i}}$	${\mathit{\pi }}_{\mathit{s}}$	$\mathit{\pi }$
Supplier dominates	α	${\eta }_i=1.5,{\eta }_s=2,\lambda =0.6$					${\eta }_i=1.5,{\eta }_s=2,\lambda =0.4$
	3.0	0.762	0.095	0.550	0.648	1.197	0.444	0.333	0.415	0.733	1.148
	3.5	0.750	0.250	0.722	0.700	1.422	0.472	0.458	0.534	0.842	1.376
	4.0	0.800	0.400	0.960	0.800	1.760	0.533	0.600	0.693	1.000	1.693
	4.5	0.917	0.583	1.330	0.967	2.297	0.639	0.792	0.939	1.242	2.181
	α	${\eta }_i=2,{\eta }_s=1.5,\lambda =0.6$					${\eta }_i=2,{\eta }_s=1.5,\lambda =0.4$
	3.0	0.524	0.254	0.579	0.521	1.100	0.286	0.571	0.539	0.686	1.224
	3.5	0.542	0.389	0.760	0.589	1.349	0.333	0.667	0.644	0.800	1.444
	4.0	0.600	0.533	1.000	0.693	1.693	0.400	0.800	0.800	0.960	1.760
	4.5	0.708	0.722	1.368	0.856	2.224	0.500	1.000	1.050	1.200	2.250
Integrator dominates	α	${\eta }_i=1.5,{\eta }_s=2,\lambda =0.6$					${\eta }_i=1.5,{\eta }_s=2,\lambda =0.4$
	3.0	0.571	0.286	0.686	0.539	1.224	0.254	0.524	0.521	0.579	1.100
	3.5	0.667	0.333	0.800	0.644	1.444	0.389	0.542	0.589	0.760	1.349
	4.0	0.800	0.400	0.960	0.800	1.760	0.533	0.600	0.693	1.000	1.693
	4.5	1.000	0.500	1.200	1.050	2.250	0.722	0.708	0.856	1.368	2.224
	α	${\eta }_i=2,{\eta }_s=1.5,\lambda =0.6$					${\eta }_i=2,{\eta }_s=1.5,\lambda =0.4$
	3.0	0.333	0.444	0.733	0.415	1.148	0.095	0.762	0.648	0.550	1.197
	3.5	0.458	0.472	0.842	0.534	1.376	0.250	0.750	0.700	0.722	1.422
	4.0	0.600	0.533	1.000	0.693	1.693	0.400	0.800	0.800	0.960	1.760
	4.5	0.792	0.639	1.242	0.939	2.181	0.583	0.917	0.967	1.330	2.297
Nobody dominates	α	${\eta }_i=1.5,{\eta }_s=2,\lambda =0.6$					${\eta }_i=1.5,{\eta }_s=2,\lambda =0.4$
	3.0	0.696	0.261	0.676	0.625	1.301	0.406	0.478	0.506	0.716	1.222
	3.5	0.735	0.327	0.797	0.694	1.491	0.463	0.531	0.585	0.837	1.422
	4.0	0.800	0.400	0.960	0.800	1.760	0.533	0.600	0.693	1.000	1.693
	4.5	0.898	0.490	1.193	0.958	2.151	0.626	0.694	0.849	1.232	2.081
	α	${\eta }_i=2,{\eta }_s=1.5,\lambda =0.6$					${\eta }_i=2,{\eta }_s=1.5,\lambda =0.4$
	3.0	0.478	0.406	0.716	0.506	1.222	0.261	0.696	0.625	0.676	1.301
	3.5	0.531	0.463	0.837	0.585	1.422	0.327	0.735	0.694	0.797	1.491
	4.0	0.600	0.533	1.000	0.693	1.693	0.400	0.800	0.800	0.960	1.760
	4.5	0.694	0.626	1.232	0.849	2.081	0.490	0.898	0.958	1.193	2.151
Centralized decision	α	${\eta }_i=1.5,{\eta }_s=2$					${\eta }_i=2,{\eta }_s=1.5$
	3.0	0.5	1	Undefined		1.5	1	0.5	Undefined		1.5
	3.5	0.727	1.091			1.818	1.091	0.727			1.818
	4.0	1.000	1.333			2.333	1.333	1.000			2.333
	4.5	1.455	1.818			3.273	1.818	1.455			3.273

in Appendix C. Furthermore, in Figure 5a, as costs decrease, willingness increases, but the rate of willingness increase gradually slows down. This is because as service quality gradually improves, the additional benefits (such as customer satisfaction, market share growth, etc.) brought by each unit of service quality increase will gradually decrease, while the marginal cost of each unit of service quality increase will increase. This means that although initially investing resources to improve service quality can bring significant returns, the growth rate of these returns will gradually slow down over time. Therefore, although the willingness of enterprises to improve service quality is still increasing, their growth rate will slow down due to diminishing marginal utility.

Low cost does not necessarily bring higher willingness when $\alpha \le 3.15$, see Figure 6a. The reason may be that the supplier has observed that $\alpha$ is becoming greater so that 1 + 1 > 2. Even if the cost is high, its willingness will increase. When the cost keeps rising, the impact of $\alpha$ is not obvious. It has an important relationship with $\lambda$. When $\lambda =0.4$, both the law and trend are the same, but the turning point is earlier, see Figure 6b, and other cost structures also appear similar. For the subordinate integrator, no matter what the value $\lambda$ is, the low cost will definitely enhance the willingness, see Figure 7a,b. If two members are power-balanced, low cost is advantageous. This is also true for centralized decisions. Therefore, when the dominant relationship is clear, the uniform reduction in cost will absolutely enhance the willingness of the subordinate member, but the willingness of the dominant one depends more on $\alpha$ and $\lambda$.

5.3. Impact of the Ratio of Independent Effect over Cost

Assuming that the efficiency of quality improvement is described by the ratio of effect to cost, we consider four situations as shown in

Table 7. Different cases about efficiency of two members.

Members	Case I $\begin{array}{l}\mathit{\beta }=2, {\mathit{\eta }}_{\mathit{i}}=3.5,\\ \mathit{\gamma }=2.5, {\mathit{\eta }}_{\mathit{s}}=4\end{array}$	Case II $\begin{array}{l}\mathit{\beta }=2, {\mathit{\eta }}_{\mathit{i}}=4,\\ \mathit{\gamma }=2.5, {\mathit{\eta }}_{\mathit{s}}=3.5\end{array}$	Case III $\begin{array}{l}\mathit{\beta }=2.5, {\mathit{\eta }}_{\mathit{i}}=3.5,\\ \mathit{\gamma }=2, {\mathit{\eta }}_{\mathit{s}}=4\end{array}$	Case IV $\begin{array}{l}\mathit{\beta }=2.5, {\mathit{\eta }}_{\mathit{i}}=4,\\ \mathit{\gamma }=2, {\mathit{\eta }}_{\mathit{s}}=3.5\end{array}$
Integrator	0.714	0.625	0.571	0.5
Supplier	0.5	0.571	0.625	0.714

.

The improvement efficiency of the integrator continues to decline, and that of the supplier continues to rise. Correspondingly, the willingness of the integrator continues to decline, and that of the supplier continues to increase. As shown in Figure A1 in Appendix D, it means that there is a clear positive correlation between efficiency and willingness. However, the change in profit is not always like this. As shown in Figure A2 in Appendix D, even if the supplier’s willingness continues to increase, its profit is going down. However, the results of the integrator are on the contrary. The total profit of the chain has not increased due to the increase in the efficiency of the dominant player, as shown in Figure A3 in Appendix D. These analyses are based on $\lambda =0.5$. If $\lambda =0.6$, the total profit will be greatest when the integrator is most efficient. If $\lambda =0.4$, the total profit will be the largest when the supplier is most efficient. In addition, the willingness, the profit of each member, and the total chain profit all increase with $\alpha$, that is, the influence of CIE is more prominent.

6. Conclusions

6.1. Conclusions

This paper employs probability to characterize the willingness to improve service quality in a service supply chain, aiming to examine the significance of collaborative improvement and the potential factors contributing to free-riding behavior. By analyzing the solutions of the game model and conducting numerical experiments under various power structures, we make several noteworthy findings. Firstly, the existence of a turning point has a substantial impact on decision-making and profit, determining whether the combined effort of both members exceeds their individual efforts. Additionally, the influence of the dominant position is subject to changes at these turning points. Secondly, the optimal willingness to maximize profit is consistently less than 1, indicating that moderate levels of effort yield the highest returns. Thirdly, the role of revenue sharing is evident as it positively motivates upstream and downstream members to enhance service quality. Lower improvement costs do not necessarily translate into higher willingness, but they do facilitate greater profitability. Moreover, improvement efficiency has a positive effect on willingness, but its impact on profit is not always definitive. Lastly, the overall profit of the supply chain exhibits close ties to system consistency. The detailed conclusions are elaborated below:

(1)

When the collaborative improvement effect (CIE) of the two members is poor, centralized decision-making becomes insignificant. In such cases, a phenomenon may arise where the willingness of the dominant member initially remains quite low, approximately zero, but gradually increases, while the willingness of the non-dominant member shows a downward trend. This finding differs from that of Roles et al. [8], which suggests that the buyer is more inclined to exert high efforts when the vendor does the same. However, when CIE is relatively larger, regardless of the power structure, the willingness of supply chain members increases along with CIE, leading to an increase in individual and overall chain profits. Moreover, the willingness of each member in centralized decision-making is higher than in other power structures. A stronger independent quality improvement effect results in a higher willingness to improve. If the CIE and both independent improvement effects (IIEs) satisfy the condition 1 + 1 > 2, the willingness to improve quality under centralized decision-making surpasses that under other power structures. Specifically, when it comes to the integrator or the supplier, having a clear dominant position leads to a greater improvement willingness compared to situations where the two members have balanced power. The dominant position has a positive effect on increasing willingness. However, it is important to note that a dominant position does not necessarily guarantee higher profits. This finding diverges from the perspective of Fang et al. [11], which suggests that dominance influences a partner’s ability to achieve profits, with retailers benefiting from the absence of a dominant manufacturer, while manufacturers prefer a dominant scenario. It also differs from the conclusion of Liu et al. [43], which proposes that the dominant supply chain member in a decentralized manufacturing supply chain tends to gain more profit. Although Fang et al. [11] and Liu et al. [43] focus on the manufacturing supply chain, and Liu et al. [46] focus on the service supply chain, there are differences between their findings. For instance, Liu et al. [46] reveal that the allocation of control power leading to higher profits depends on the service level. The provider gains more profit when in a dominant position with a low service level, while it gains more profit in a subordinate position when the service level exceeds a certain threshold. Both conclusions revolve around a critical point, but the specific context differs, and the critical point pertains to different aspects. However, they share the common understanding that a dominant position does not necessarily result in higher profits.

(2)

A uniform decrease in costs has a significant impact on profits. When a chain member with low improvement difficulty and a high revenue share holds a dominant position, it tends to contribute to the largest overall profit for the chain to some extent. However, when the collaborative improvement effect (CIE) is not obvious, low cost does not necessarily result in a higher willingness to improve service quality. This can be seen as an explanation for the lack of coordination between Nanjing Lukou Airport and the cleaning company. In the case of the airport, where market demand and revenue are relatively stable, the quality of cleaning services and customer feedback usually have little impact on their profits, which means that collaborative improvement efforts yield weak results. As a result, when the cleaning company reduced costs and downsized its staff to increase profits, the airport did not exhibit a stronger willingness to improve. Without the pandemic, cost reduction would have resulted in higher profits. However, under the unique circumstances of the epidemic, it led to significant losses. If collaborative behavior can yield more apparent effects, such as when the government and media frequently praise or provide material rewards, and when collaborative management and optimized operations can uniformly reduce costs, the willingness to improve services would increase. For example, the collaboration between ASUS and Dell in procurement services has successfully reduced costs and increased efficiency, leading to a stronger willingness to improve. As the conclusion of this paper, when the CIE is evident and continues to increase, low cost brings about a higher willingness to improve service quality. However, when the cost is already high, even if the CIE continues to increase, the willingness to improve does not change significantly. When there is a clear dominant relationship between the two members, a uniform reduction in costs will undoubtedly increase the willingness of the subordinate member, but the change in the willingness of the dominant member depends more on the CIE and revenue share. When the revenue share is much higher, low cost holds an absolute advantage.

(3)

There is a clear positive correlation between improvement efficiency and improvement willingness, but this does not always result in changes in profits. Even if supply chain members continue to increase their willingness to improve, their profits may exhibit a downward trend, and the overall profit of the supply chain is not solely determined by the efficiency of the leading member. However, if the member with a higher revenue share is also more efficient in quality improvement, the overall profit of the supply chain can achieve greater value.

(4)

For the entire supply chain, if 1 + 1 < 2, the total profit of the chain is highest when the two members are power-balanced. However, if the member who faces greater difficulty in improvement takes the dominant position, the profit obtained is higher than when the member with less difficulty leads. On the other hand, when 1 + 1 > 2 and the difficulty in improvement becomes more apparent, the power-balanced situation becomes the least favorable. Even if the revenue share is low, the quality improvement led by the member with less difficulty is more likely to increase the overall profit of the chain. A higher revenue share has a greater potential to incentivize chain members to improve service quality and obtain more profits. When the member with a high revenue share takes the dominant position, the chain’s profit can achieve a larger value.

In summary, we provide the following answers to the question of how to prevent free-riding behavior. Firstly, it is essential to continuously strengthen CIE in the cooperation between upstream and downstream firms. The more apparent the effect, the stronger the willingness and the higher the profitability. Secondly, increasing the revenue share is a relatively reliable approach. Thirdly, the dominant position should be given sufficient opportunities to fulfill its role, particularly in the case of 1 + 1 > 2. Fourthly, implementing unified cost reduction through collaborative efforts is highly necessary.

6.2. Impliactions and Limitations

Based on the research findings of this paper, we propose some management insights, some for the government and some for enterprises:

Firstly, the effectiveness of cooperation. The government should help establish some public platforms to disclose information on the reputation and qualifications of service enterprises, in order to facilitate their selection of partners and avoid situations where the cooperation effect is poor or even not cooperative. At the same time, in the dimension of service quality, a black- and white-list system should be gradually established. For enterprises with outstanding cooperation effects and forming a reputation for service quality, the government could issue quality awards to encourage them. Warnings and punishments shall be given to enterprises with poor cooperation results that result in quality accidents. In addition, the government can provide subsidies and convenience to service enterprises in the fields of block chain, Internet of Things, and big data to improve their informatization level, reduce information asymmetry, and strengthen cooperation effectiveness.

Secondly, cost. Benchmark enterprises, industry associations, and governments should showcase more successful service quality improvement projects, advocating that although service quality improvement requires a higher initial cost, it will ultimately lead to a significant decrease in operating costs, which is beneficial for enterprises to obtain long-term profits. At the same time, the government could assist in promoting the standardized development of the service industry, gradually deepening the quality management system of the manufacturing industry into the service industry, promoting the standardization of service quality management, and avoiding service costs as obstacles to service quality improvement.

Thirdly, revenue sharing. The government should provide subsidies to some key service industries, avoiding no service quality improvement due to revenue sharing issues, which may affect service experience and happiness index. For example, in industries such as early education, elderly care, and public libraries, appropriate subsidies play a crucial role in improving service quality and helping to enhance social welfare. For example, some elderly care institutions have improved their information technology level, care service level, and elderly health level based on government subsidies, becoming industry benchmarks and providing templates for the development of the elderly care industry.

Fourth, dominant position. Although centralized decision-making and leadership may not always have a crucial impact, their impact on partners cannot be underestimated. Industry associations and governments should guide benchmark enterprises to continue to play a demonstrative role, share their experience, and even management models in improving service quality, and better strengthen the industry’s willingness to improve service quality.

Fifth, consumer preferences for service quality. Improving service quality is not only driven by the willingness of the supply side itself, but also by the demand side’s preference for service quality. If consumers are willing to pay higher prices for high-quality services, the enthusiasm of service providers to improve service quality will also be enhanced. Therefore, businesses and governments could stimulate the public’s demand for high-quality services through some consumer subsidies. In addition, industry associations can establish a standardized service quality evaluation system to target and improve service quality based on consumer preferences.

However, this paper does have some limitations. For instance, it does not consider the impact of collaborative behavior on market demand, the proportion of revenue as an endogenous variable is not thoroughly studied, and the role of transfer payments in decision-making is not adequately reflected. In the future, it would be valuable to delve into these perspectives to further investigate the enhancement of service quality.