Optimizing Multi-Stage Project Portfolio Selection Considering Integrating Lifecycle and Interactions
Abstract
1. Introduction
- Considering the full project lifecycle: Incorporating the construction timeline of each project into the selection process ensures completion within planned schedules, enabling more efficient resource allocation.
- Considering project interactions: Our method accounts for the complex interactions that may arise between projects. By evaluating the effects of these interactions, we gain a clearer understanding of the portfolio’s overall value, risks, and other key factors.
- Refined selection method: We introduce a new decision-making framework that assesses solution quality based on the specific characteristics of the solution set, providing decision-makers with more objective and informed outcomes.
2. Literature Review
2.1. Project Portfolio Selection
2.2. Decision Criteria in Portfolio Selection
2.3. Scheduling Constraints in Project Portfolio Selection
2.4. Interaction Modeling in Project Portfolio Selection
2.5. Findings of the Literature Review
- A comprehensive approach is proposed, which integrates project interactions, multi-objective optimization, and refined solution selection.
- A new heuristic algorithm is proposed, which combines the advantages of the two algorithms for a more efficient solution.
- A new scheme refinement selection method is proposed, which mines the ranking rules based on the features of the schemes and avoids the subjective preference in the decision of multiple schemes.
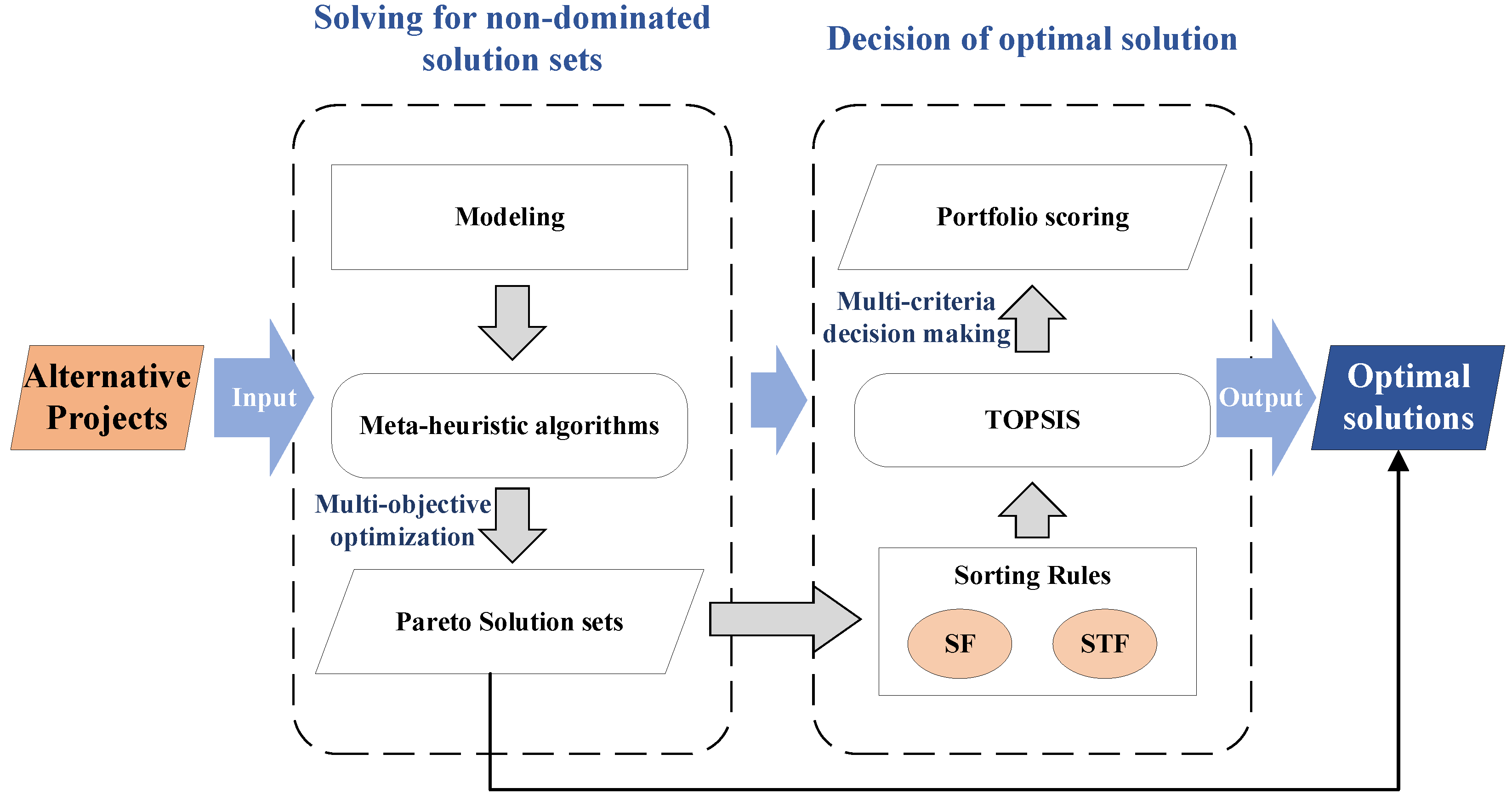
3. Model Formulation
3.1. Notations
3.2. Decision Variable
3.3. Objective Function
3.4. Solving Algorithm
3.4.1. Population Initialization
3.4.2. Decode
3.4.3. Determine if Ended
- The number of iterations reaches the specified algebra;
- Some individuals in the current population have attained a satisfactory value for each objective function;
- After iteration of the specified algebra, the non-inferior solution set does not change.
3.4.4. Non-Dominant Rank Sorting
3.4.5. Elite Population Division
3.4.6. Mutation
3.4.7. Crossover
3.4.8. Select
4. Decision-Making Method
4.1. Decision-Making Indicators
- Projects that appear more frequently than others in different non-dominated sets are likely to perform better and should receive more attention.
- Project interactions that are frequently activated are considered to help the project portfolio achieve higher benefits.
4.1.1. Selected Frequency (SF)
4.1.2. Selected Together Frequency (STF)
4.2. Decision-Making Method Using TOPSIS
4.2.1. Normalization
4.2.2. Determine Ideal Solutions
4.2.3. Distance to the Ideal Solution
4.2.4. Calculate the Optimal Solution for All Time Phases
5. Example Analysis
5.1. Data Instruction
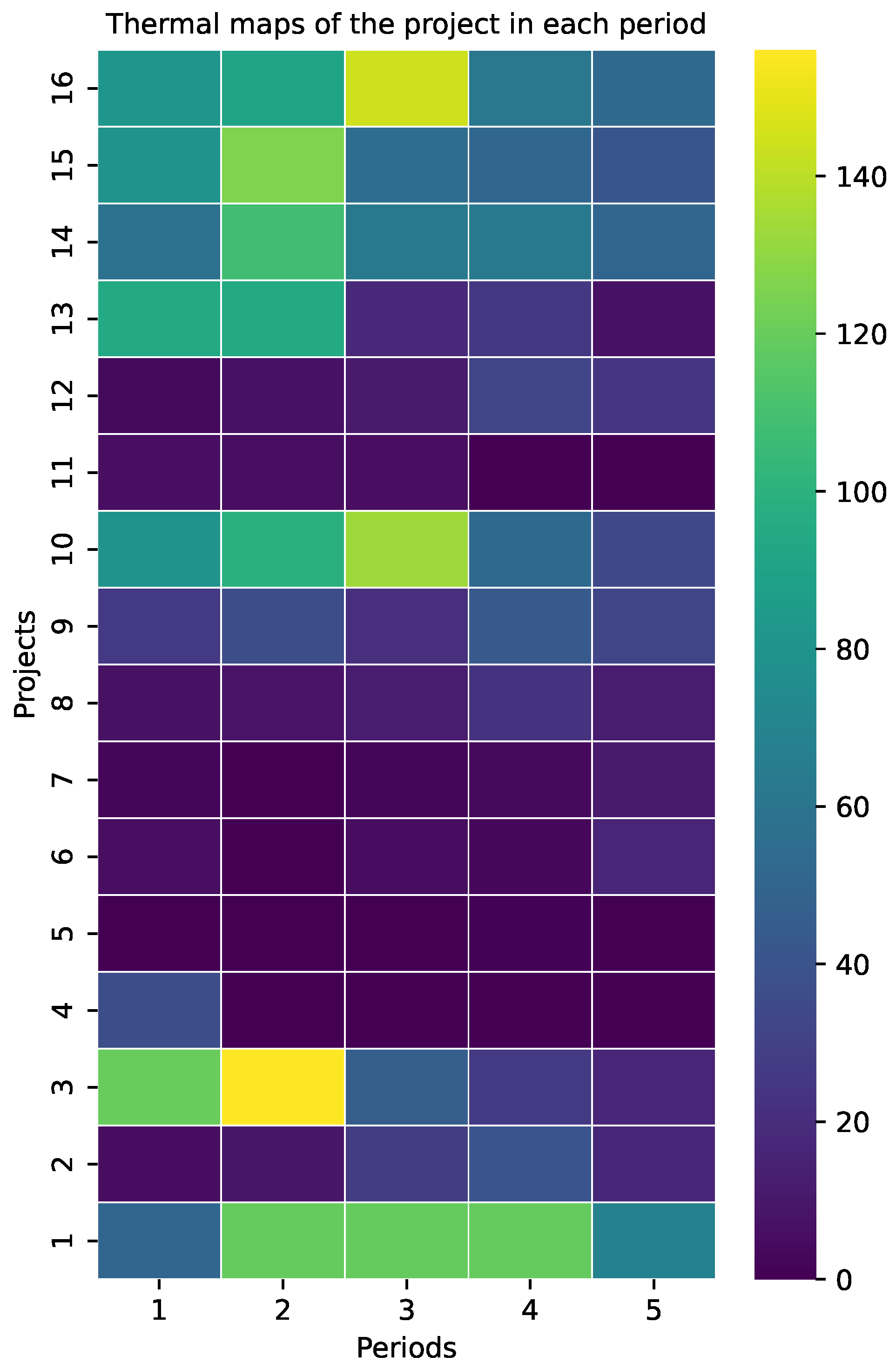
5.2. Results
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Basic Project Data
| Project | Cost (USD 1M) | Annual Cost (USD 1M) | ||||
|---|---|---|---|---|---|---|
| P1 | 48 | 11.0064 | 12.2688 | 12.36 | 12.3648 | 0 |
| P2 | 38 | 18.6998 | 19.3002 | 0 | 0 | 0 |
| P3 | 40 | 23.82 | 16.18 | 0 | 0 | 0 |
| P4 | 43 | 43 | 0 | 0 | 0 | 0 |
| P5 | 35 | 35 | 0 | 0 | 0 | 0 |
| P6 | 25 | 25 | 0 | 0 | 0 | 0 |
| P7 | 26 | 26 | 0 | 0 | 0 | 0 |
| P8 | 41 | 18.532 | 22.468 | 0 | 0 | 0 |
| P9 | 53 | 23.4578 | 29.5422 | 0 | 0 | 0 |
| P10 | 81 | 17.6337 | 30.7395 | 32.6349 | 0 | 0 |
| P11 | 97 | 29.7402 | 32.7569 | 34.5029 | 0 | 0 |
| P12 | 51 | 22.848 | 28.152 | 0 | 0 | 0 |
| P13 | 89 | 89 | 0 | 0 | 0 | 0 |
| P14 | 78 | 39 | 39 | 0 | 0 | 0 |
| P15 | 97 | 44.8043 | 52.1957 | 0 | 0 | 0 |
| P16 | 90 | 24.174 | 31.914 | 33.912 | 0 | 0 |
| Project | Value (USD 1M) | Annual Value (USD 1M) | ||||
|---|---|---|---|---|---|---|
| P1 | 113 | 12.43 | 28.2161 | 35.3125 | 37.0414 | 0 |
| P2 | 77 | 34.7578 | 42.2422 | 0 | 0 | 0 |
| P3 | 78 | 36.7926 | 41.2074 | 0 | 0 | 0 |
| P4 | 67 | 67 | 0 | 0 | 0 | 0 |
| P5 | 19 | 19 | 0 | 0 | 0 | 0 |
| P6 | 54 | 54 | 0 | 0 | 0 | 0 |
| P7 | 67 | 67 | 0 | 0 | 0 | 0 |
| P8 | 73 | 31.7477 | 41.2523 | 0 | 0 | 0 |
| P9 | 76 | 32.376 | 43.624 | 0 | 0 | 0 |
| P10 | 148 | 40.3744 | 51.0452 | 56.5804 | 0 | 0 |
| P11 | 114 | 24.1338 | 44.9274 | 44.9388 | 0 | 0 |
| P12 | 105 | 42.105 | 62.895 | 0 | 0 | 0 |
| P13 | 34 | 34 | 0 | 0 | 0 | 0 |
| P14 | 88 | 44 | 44 | 0 | 0 | 0 |
| P15 | 105 | 52.5 | 52.5 | 0 | 0 | 0 |
| P16 | 111 | 22.6995 | 41.6805 | 46.62 | 0 | 0 |
| Project | (year) | Annual Risk | ||||
|---|---|---|---|---|---|---|
| P1 | 4 | 0.1 | 0.2 | 0.1 | 0.05 | 0 |
| P2 | 2 | 0.13 | 0.16 | 0 | 0 | 0 |
| P3 | 2 | 0.11 | 0.15 | 0 | 0 | 0 |
| P4 | 1 | 0.18 | 0 | 0 | 0 | 0 |
| P5 | 1 | 0.15 | 0 | 0 | 0 | 0 |
| P6 | 1 | 0.19 | 0 | 0 | 0 | 0 |
| P7 | 1 | 0.33 | 0 | 0 | 0 | 0 |
| P8 | 2 | 0.23 | 0 | 0 | 0 | 0 |
| P9 | 2 | 0.22 | 0 | 0 | 0 | 0 |
| P10 | 3 | 0.1 | 0.1 | 0.1 | 0 | 0 |
| P11 | 3 | 0.1 | 0.1 | 0.2 | 0 | 0 |
| P12 | 2 | 0.1 | 0.15 | 0 | 0 | 0 |
| P13 | 2 | 0.03 | 0 | 0 | 0 | 0 |
| P14 | 2 | 0.1 | 0 | 0 | 0 | 0 |
| P15 | 2 | 0.1 | 0 | 0 | 0 | 0 |
| P16 | 3 | 0.1 | 0 | 0.14 | 0 | 0 |
| Project | Benefit Synergy | Cost Synergy | Risk Synergy | Schedule Synergy |
|---|---|---|---|---|
| P1 | P2 0.0389 P3 0.0939 | P2 -0.0979 | P2 0.0389 P3 0.0939 | / |
| P2 | P1 0.087 | P1 -0.041 | P1 0.087 | / |
| P3 | P1 0.0924 P6 -0.1 P10 0.0683 P14 0.0975 | P6 0.05 P10 0.064 P14 -0.0844 | P1 0.0924 P10 0.0683 P14 0.0975 | / |
| P4 | / | / | / | P3 |
| P5 | / | / | / | / |
| P6 | P2 -0.1 P12 0.097 | P2 0.04 P12 0.0595 | P2 -0.1 P12 0.097 | / |
| P7 | P13 -0.1 | P13 0.1 | P13 -0.1 | / |
| P8 | / | / | / | P4 |
| P9 | / | / | / | / |
| P10 | P3 0.0734 | P3 -0.086 | P3 0.0734 | P6 |
| P11 | / | / | / | / |
| P12 | P6 0.0495 | P6 -0.0399 | P6 0.0495 | / |
| P13 | P7 -0.08 | P7 0.1 | P7 -0.08 | / |
| P14 | P3 0.0368 | P3 -0.0941 | P3 0.0368 | P3 |
| P15 | / | / | / | / |
| P16 | / | / | / | / |
Appendix B. The Results of Project Selection in Different Periods





References
- Korotkov, V.; Wu, D. Evaluating the quality of solutions in project portfolio selection. Omega 2020, 91, 102029. [Google Scholar] [CrossRef]
- Kyle, R.H.; Ruhul, A.S. Evolutionary and Memetic Computing for Project Portfolio Selection and Scheduling; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Artūras, P.; Kristina, Č.; Aldona, J.; Pavlo, M.; Olegas, P. Algorithm for the assessment of heavyweight and oversize cargo transportation routes. J. Bus. Econ. Manag. 2017, 18, 1098–1114. [Google Scholar]
- Khorshidian, H.; Akbarpour, S.M.; Fatemi, G. An intelligent truck scheduling and transportation planning optimization model for product portfolio in a cross-dock. J. Intell. Manuf. 2019, 30, 163–184. [Google Scholar] [CrossRef]
- Tao, Y.; Luo, X.; Wu, Y.; Zhang, L.; Liu, Y.; Xu, C. Portfolio selection of power generation projects considering the synergy of project and uncertainty of decision information. Comput. Ind. Eng. 2023, 175, 108896. [Google Scholar] [CrossRef]
- Mohagheghi, V.; Mousavi, S.M.; Vahdani, B. A new multi-objective optimization approach for sustainable project portfolio selection: A real world application under interval-valued fuzzy environment. Iran. J. Fuzzy Syst. 2016, 13, 41–68. [Google Scholar]
- Abbasi, D.; Ashrafi, M.; Ghodsypour, S.H. A multi objective-BSC model for new product development project portfolio selection. Expert Syst. Appl. 2020, 162, 113757. [Google Scholar] [CrossRef]
- Fabián, D.; Franco, Q.; Óscar, C.V. The knapsack problem with scheduled items. Electron. Notes Discret. Math. 2018, 69, 293–300. [Google Scholar]
- Heidenberger, K.; Stummer, C. Research and development project selection and resource allocation: A review of quantitative modelling approaches. Int. J. Manag. Rev. 1999, 1, 197–224. [Google Scholar] [CrossRef]
- Khadija, B.; Laila, K. Project portfolio selection: Multi-criteria analysis and interactions between projects. Int. J. Comput. Sci. Issues 2014, 11, 134–143. [Google Scholar]
- Bai, L.; Zheng, K.; Wang, Z.; Liu, J. Service provider portfolio selection for project management using a BP neural net- work. Ann. Oper. Res. 2022, 308, 41–62. [Google Scholar] [CrossRef]
- David, S. Continuous-time formulations for multi-mode project scheduling. Comput. Oper. Res. 2023, 152, 106147. [Google Scholar]
- Ding, H.; Zhuang, C.; Liu, J. Extensions of the resource- constrained project scheduling problem. Autom. Constr. 2023, 153, 104958. [Google Scholar] [CrossRef]
- Song, S.; Yang, F.; Xia, Q. Multi-criteria project portfolio selection and scheduling problem based on acceptability analysis. Comput. Ind. Eng. 2019, 135, 793–799. [Google Scholar] [CrossRef]
- Wang, C.; Chen, W. A fuzzy model for R&D project portfolio selection. In Proceedings of the 2011 International Conference on Information Management, Innovation Management, and Industrial Engineering, Shenzhen, China, 26–27 November 2011; Volume 1, pp. 100–104. [Google Scholar]
- Tavana, M.; Khanjani, S.; Di, C. A chance-constrained portfolio selection model with random-rough variables. Neural Comput. Appl. 2019, 31, 931–945. [Google Scholar] [CrossRef]
- Carlsson, C.; Fuller, R.; Heikkilä, M.; Majlender, P. A fuzzy approach to R&D project portfolio selection. Int. J. Approx. Reason. 2007, 44, 93–105. [Google Scholar]
- Teller, J. Portfolio risk management and its contribution to project portfolio success: An investigation of organization, process, and culture. Proj. Manag. J. 2013, 44, 36–51. [Google Scholar] [CrossRef]
- Saeed, M.A.; Tabassum, H.; Zahid, M.M.; Jiao, Y.; Nauman, S. Organizational flexibility and project portfolio performance: The roles of environmental uncertainty and innovation capability. Eng. Manag. J. 2022, 34, 249–264. [Google Scholar] [CrossRef]
- Souza, D.G.B.; Silva, C.E.S.; Soma, N.Y. Selecting Projects on the Brazilian R&D Energy Sector: A Fuzzy-Based Approach for Criteria Selection. IEEE Access 2020, 8, 50209–50225. [Google Scholar]
- Archer, N.; Ghasemzadeh, F. Project portfolio selection and management. In The Wiley Guide to Project, Program & Portfolio Management; Morris, P., Pinto, J.K., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2007; pp. 94–112. [Google Scholar]
- Chao, R.O.; Kavadias, S. R&D intensity and the new product development portfolio. IEEE Trans. Eng. Manag. 2013, 60, 664–675. [Google Scholar]
- Mogbojuri, A.O.; Olanrewaju, O.A. Goal programming and genetic algorithm in multiple objective optimization model for project portfolio selection: A review. Niger. J. Technol. 2022, 41, 862–869. [Google Scholar] [CrossRef]
- Chen, R.; Liang, C.; Gu, D. IT project portfolio scheduling and multi-skilled staff assignment with ant colony optimization algorithm. Unpublished work. 2016. [Google Scholar]
- Mercangoz, B.A. Particle swarm algorithm: An application on portfolio optimization. In Metaheuristic Approaches to Portfolio Optimization; IGI Global: Hershey, PA, USA, 2019; pp. 27–59. [Google Scholar]
- Nielsen, M.K.J.; Jacobsen, A.M.S.Ø.; Carstensen, J.L.; Toft Nielsen, M.; Tambo, T. Industrial R&D project portfolio selection method using a multi-objective optimization program: A conceptual quantitative framework. J. Ind. Eng. Manag. 2024, 17, 217–234. [Google Scholar]
- Alinezhad, R.; Ansari, R.; Mahdikhani, M.; Banihashemi, S.A. Multi-phase projects selection and scheduling problem: A multi-objective optimization approach. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 2575–2591. [Google Scholar] [CrossRef]
- Ghanbari, M.; Jaber Olaikhan, A.A.; Skitmore, M. Enhancing project portfolio selection for construction holding firms: A multi-objective optimization framework with risk analysis. Eng. Constr. Archit. Manag. 2024. ahead of print. [Google Scholar] [CrossRef]
- Chen, H.; Li, X.; Lu, X.; Sheng, N.; Zhou, W.; Geng, H.; Yu, S. A multi-objective optimization approach for the selection of overseas oil projects. Comput. Ind. Eng. 2021, 151, 106977. [Google Scholar] [CrossRef]
- Beşikci, U.; Bilge, Ü.; Ulusoy, G. Multi-mode resource constrained multi-project scheduling and resource portfolio problem. Eur. J. Oper. Res. 2015, 240, 22–31. [Google Scholar] [CrossRef]
- Laslo, Z. Project portfolio management: An integrated method for resource planning and scheduling to minimize planning/scheduling-dependent expenses. Int. J. Proj. Manag. 2010, 28, 609–618. [Google Scholar] [CrossRef]
- Pérez, F.; Gómez, T.; Caballero, R.; Liern, V. Project portfolio selection and planning with fuzzy constraints. Technol. Forecast. Soc. Chang. 2018, 131, 117–129. [Google Scholar] [CrossRef]
- RezaHoseini, A.; Ghannadpour, S.F.; Hemmati, M. A comprehensive mathematical model for resource-constrained multi-objective project portfolio selection and scheduling considering sustainability and projects splitting. J. Clean. Prod. 2020, 269, 122073. [Google Scholar] [CrossRef]
- Trappey, C.V.; Trappey, A.J.C.; Chiang, T.A.; Kuo, J.Y. A strategic product portfolio management methodology considering R&D resource constraints for engineering-to-order industries. Int. J. Technol. Manag. 2009, 48, 258–276. [Google Scholar]
- Bai, L.; Zhang, K.; Shi, H.; An, M.; Han, X. Project portfolio resource risk assessment considering project interdependency by the fuzzy Bayesian network. Complexity 2020, 2020, 5410978. [Google Scholar] [CrossRef]
- Moon, Y.; Yao, T. A robust mean absolute deviation model for portfolio optimization. Comput. Oper. Res. 2011, 38, 1251–1258. [Google Scholar] [CrossRef]
- Smith-Perera, A.; García-Melón, M.; Poveda-Bautista, R.; Pastor-Ferrando, J.-P. A Project Strategic Index proposal for portfolio selection in electrical company based on the Analytic Network Process. Renew. Sustain. Energy Rev. 2010, 14, 1569–1579. [Google Scholar] [CrossRef]
- Long, L.D.; Ohsato, A. Fuzzy critical-chain method for project scheduling under resource constraints and uncertainty. Int. J. Proj. Manag. 2008, 26, 688–698. [Google Scholar] [CrossRef]
- Ghomi, S.M.T.F.; Ashjari, B. A simulation model for multi-project resource allocation. Int. J. Proj. Manag. 2002, 20, 127–130. [Google Scholar] [CrossRef]
- Baker, N.; Freeland, J. Recent advances in R&D benefit measurement and project selection methods. Manag. Sci. 1975, 21, 1164–1175. [Google Scholar]
- Pendharkar, P.C.; Rodger, J.A. Information technology capital budgeting using a knapsack problem. Int. Trans. Oper. Res. 2010, 13, 333–351. [Google Scholar] [CrossRef]
- Killen, C.P. Evaluation of project interdependency visualizations through decision scenario experimentation. Int. J. Proj. Manag. 2013, 31, 804–816. [Google Scholar] [CrossRef]
- Lopes, Y.G.; Almeida, A.T.D. Assessment of synergies for selecting a project portfolio in the petroleum industry based on a multi-attribute utility function. J. Pet. Sci. Eng. 2015, 126, 131–140. [Google Scholar] [CrossRef]
- Eilat, H.; Golany, B.; Shtub, A. Constructing and evaluating balanced portfolios of R&D projects with interactions: A DEA based methodology. Eur. J. Oper. Res. 2006, 172, 1018–1039. [Google Scholar]
- Zorluoğlu, Ö.Ş.; Kabak, Ö. An interactive multi-objective programming approach for project portfolio selection and scheduling. Comput. Ind. Eng. 2022, 169, 108191. [Google Scholar] [CrossRef]
- Liesiö, J.; Kee, T.; Malo, P. Modeling project interactions in multiattribute portfolio decision analysis: Axiomatic foundations and practical implications. Eur. J. Oper. Res. 2024, 316, 988–1000. [Google Scholar] [CrossRef]
- Wei, H.; Niu, C.; Xia, B.; Dou, Y.; Hu, X. A refined selection method for project portfolio optimization considering project interactions. Expert Syst. Appl. 2020, 142, 112952. [Google Scholar] [CrossRef]
- Wang, L.; Qian, C.; Goh, M. Integrated Approach for Project Risk Assessment and Evaluation under Risk Interactions. IEEE Trans. Eng. Manag. 2022, 71, 2418–2429. [Google Scholar] [CrossRef]
- Su, G.; Hastak, M.; Deng, X.; Khallaf, R. Risk Sharing Strategies for IPD Projects: Interactional Analysis of Participants’ Decision-Making. J. Manag. Eng. 2021, 37, 04020101. [Google Scholar] [CrossRef]
- Amir, F.F.; Hosein, D.; Kaveh, K.D.; Amir, H.S.; Mehdi, H. A framework for interactive risk assessment in projects: Case study of oil and gas megaprojects in presence of sanctions. J. Model. Manag. 2022, 17, 569–600. [Google Scholar]
- Zhao, J.; Guo, P.; Pan, N. Optimisation of Project Portfolio Risk Measurement and Selection Based on Interaction Effects. Oper. Res. Manag. 2011, 20, 120–126. [Google Scholar]
- Wang, J.; Guo, P.; Zhao, J. R&D Project Portfolio Robustness Risk Measurement and Selection Model. Oper. Res. Manag. 2017, 26, 140–148. [Google Scholar]
- Pinheiro, P.R.; Amaro, J.B.; Saraiva, R.D. A random-key genetic algorithm for solving the nesting problem. Int. J. Comput. Integr. Manuf. 2016, 29, 1159–1165. [Google Scholar] [CrossRef]
- Igor, M.; Gabriel, S.; Glaydston, M.R.; Israel, M.; Pedro, H.G. A Hybrid BRKGA Approach for the Multiproduct Two Stage Capacitated Facility Location Problem. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022. [Google Scholar]
- Mojtaba, G.; Mohsen, Z.; Pavel, T.; Amir, Z.; Eva, T. A hybridizing-enhanced differential evolution for optimization. PeerJ Comput. Sci. 2023, 9, e1420. [Google Scholar]
- Pelc, K.I. Research and development project selection. R D Manag. 1998, 28, 53–54. [Google Scholar]
- Thiele, B.; Ryan, M.; Abbasi, A. Developing a dataset of real projects for portfolio, program and project control management research. Data Brief 2020, 34, 106659. [Google Scholar] [CrossRef] [PubMed]
- Harrison, K.R.; Elsayed, S.M.; Garanovich, I.L.; Weir, T.; Boswell, S.G.; Sarker, R.A. Generating datasets for the project portfolio selection and scheduling problem. Data Brief 2022, 42, 108208. [Google Scholar] [CrossRef] [PubMed]








| Parameters | Meaning |
|---|---|
| i | Project i |
| Whether project i is selected or not | |
| t | Time period t |
| The stage at which project i is located | |
| The duration of project i | |
| Whether project i is selected within the time period t | |
| The k phase of project i within the time phase t | |
| q | The qth value function |
| The value of the qth value in stage t | |
| Interaction benefit r is active or not in period t | |
| Interaction effects of projects i and j on benefits | |
| Interaction effects of projects i and j on costs | |
| Interaction effects of projects i and j on technology | |
| The value of the qth benefit achieved by project i at time stage t at carried out time k | |
| The value of the qth benefit of project i at time stage tat carried out time k, achieved through the interaction effect | |
| Combined interaction coefficients for projects i and j | |
| Lower limit of resource consumption per time period | |
| Upper limit of resource consumption per time period | |
| Lower limit on the number of simultaneous projects per time period | |
| Upper limit on the number of simultaneous projects per time period | |
| Combined interaction coefficients for projects i and j |
| Algorithm | BRK-NSDE | BRKGA | NSGA |
|---|---|---|---|
| Solution time | 70 s | 102 s | 67 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, B.; Dou, Y.; Chen, Z. Optimizing Multi-Stage Project Portfolio Selection Considering Integrating Lifecycle and Interactions. Systems 2024, 12, 414. https://doi.org/10.3390/systems12100414
Qiu B, Dou Y, Chen Z. Optimizing Multi-Stage Project Portfolio Selection Considering Integrating Lifecycle and Interactions. Systems. 2024; 12(10):414. https://doi.org/10.3390/systems12100414
Chicago/Turabian StyleQiu, Biaobiao, Yajie Dou, and Ziyi Chen. 2024. "Optimizing Multi-Stage Project Portfolio Selection Considering Integrating Lifecycle and Interactions" Systems 12, no. 10: 414. https://doi.org/10.3390/systems12100414
APA StyleQiu, B., Dou, Y., & Chen, Z. (2024). Optimizing Multi-Stage Project Portfolio Selection Considering Integrating Lifecycle and Interactions. Systems, 12(10), 414. https://doi.org/10.3390/systems12100414






