Optimistic Third-Party Sellers in E-Commerce Supply Chains

Abstract

This paper investigates the effects of optimism in an e-commerce supply chain where two third-party sellers offer substitutable products through a shared e-commerce platform. In this context, optimism is defined as a cognitive bias in which third-party sellers underestimate the probability of encountering low market potential. We present a game-theoretic model to characterize the equilibrium strategies of both the platform and the sellers. Our analysis reveals that when both sellers exhibit optimism bias, this bias invariably leads to lower expected profits for them. However, seller optimism can benefit both the platform and the whole system. That is, as sellers become more biased, the profits of the platform and the entire supply chain increase. Moreover, when a biased seller competes with a sophisticated one, unilateral optimism can result in a win–lose outcome in which the optimistic seller benefits from her bias at the expense of her sophisticated rival. Indeed, we demonstrate that optimism can confer a competitive advantage in a duopoly, allowing the more biased seller to earn higher profits than its less biased competitor—even if the latter is unbiased or sophisticated. Our work sheds light on the conditions under which optimism bias may have detrimental or beneficial impacts on e-commerce supply chain operations.

1. Introduction

Optimism refers to a cognitive bias where people overestimate the probability of positive outcomes and underestimate the likelihood of negative events in the future. This psychological phenomenon is exemplified by smokers who often believe they are less susceptible to lung cancer or other smoking-related diseases compared to their peers, as documented by [1]. Recognized as one of the most prevalent and persistent cognitive biases in psychology and behavioral economics [2], optimism bias has been observed across various domains, including finance [3], insurance [4], and medicine [5], which highlights its pervasive nature in human decision-making processes.

Interestingly, this optimism has also been observed anecdotally among third-party sellers in e-commerce supply chains. E-commerce platforms such as Amazon, eBay, and Alibaba enable third-party sellers—including manufacturers, brand holders, and suppliers—to market their products directly to consumers via online marketplaces. These sellers often maintain an overly positive outlook on their business prospects, which can lead to overinvestment or continued investment in less promising aspects of their operations. A 2020 survey highlighted this phenomenon, revealing that a striking 97% of Amazon’s third-party sellers were planning to expand their businesses1. However, only 62% reported an actual increase in profits that year2. This disparity between expectations and reality became even more pronounced in 2022. Despite growing concerns about inflation impacting consumer spending and increasing business costs for Amazon sellers, 95% still planned to enlarge their ventures on the platform3. Alarmingly, the proportion of sellers who successfully boosted their profits that year plummeted to just 30%4.

The trend of optimism is not unique to Amazon third-party sellers; it extends to other online platforms as well. For instance, on Alibaba’s Taobao and Tmall, a survey of nearly 24,000 merchants revealed that over 66% expressed optimism about their business prospects for the remainder of the year, with 14% even anticipating rapid growth in sales or profits5. However, the reality often fell short of these expectations. Many of these optimistic respondents ultimately faced long-term profit losses, beleaguered by pandemic-related challenges like decreased customer orders, delivery delays, and restricted cash flows. This discrepancy between expectation and reality aligns with a well-documented phenomenon in the academic literature: optimism bias among entrepreneurs and executives. Numerous studies provide substantial evidence supporting this claim, e.g., [6,7,8]. In the specific context of e-commerce, Ref. [9] observes that entrepreneurs operating in highly uncertain environments tend to be overly optimistic about their chances of success.

Optimism bias among third-party sellers has been both empirically validated through academic research and observed anecdotally in practical settings. This stark contrast between sellers’ optimistic outlook and the challenging economic realities they face underscores the potential risks associated with unchecked optimism in the e-commerce sector. For example, optimism bias may result in an overestimation of consumer demand, potentially causing an accumulation of excessive inventory. Such misjudgments can have serious financial implications, tying up capital in unsold stock and escalating storage costs, which may ultimately erode profits.

However, the perspective on optimism bias is not uniformly negative among third-party sellers. Some believe that while this bias can indeed lead to adverse outcomes, it may also offer certain benefits, particularly when facing fierce competition and existential threats. This viewpoint is exemplified by an executive from a third-party seller on Inspur iGo, a prominent online platform in China, who stated, “This is not the first time our growth has hinged on our response to a challenging business environment, and we remain optimistic about maintaining and seizing business opportunities during the downturn. […] Our management philosophy embraces ’irrational optimism’ regarding what we can achieve”. This stance suggests that maintaining an unwavering belief in eventual success, despite challenging circumstances, may contribute to a company’s resilience. Some optimistic companies appear more likely to persist and potentially thrive in highly competitive markets, using their positive outlook as a strategic asset.

While optimism bias has been extensively studied in fields such as psychology and entrepreneurship, its effects on decision-making and competition within e-commerce platforms remain underexplored. In fact, e-commerce supply chains operate in dynamic, highly competitive environments where cognitive biases, such as optimism, can significantly affect strategic behavior, market outcomes, and platform dynamics. For example, optimism bias can influence sellers’ decisions, such as inventory, pricing, and investment, potentially leading to both positive and negative outcomes for the supply chain. Therefore, understanding these effects is crucial for platforms, sellers, and policymakers. Our research aims to fill this gap by exploring several critical questions:

• How does optimism bias influence third-party sellers’ behaviors?
• Is optimism bias universally detrimental to the members of the e-commerce supply chain and the overall supply chain?
• Can optimism bias potentially provide third-party sellers with a competitive advantage in fierce market competition?

This study aims to assess the direct impact of seller optimism on e-commerce supply chain efficiency, offering insights that can improve decision-making and strategy in e-commerce.

To this end, we present a game-theoretic model that introduces the notion of optimism bias into an e-commerce supply chain. In this model, two third-party sellers offer substitutable products to consumers through a common online platform. The platform sets a commission rate, earning a fixed percentage of the sellers’ sales revenues for facilitating each transaction. At the commencement of the selling season, each third-party seller determines its product order quantities without precise knowledge of consumer demand, which is governed by the random market size. Given that sellers on an e-commerce platform make strategic decisions while anticipating the actions of their competitors, this game-theoretic model allows us to describe the competitive dynamics, and to explore how their strategic decisions evolve in equilibrium. By using a game-theoretic approach, we can capture the impact of optimism bias on the equilibrium outcomes and illustrate how this bias influences the competitive landscape.

In the face of this uncertainty, third-party sellers are susceptible to optimism bias, leading them to underestimate the likelihood of encountering a low market size. Note that the opposite of optimism bias is pessimism bias, where individuals regard themselves as worse off than others. While pessimism bias could theoretically influence seller behavior, it is less prevalent in competitive e-commerce settings, where competition typically requires a positive outlook to justify the risks and investments involved. Furthermore, optimism and pessimism biases do not necessarily have symmetric effects. Optimism bias tends to amplify competitive behavior, driving overordering and more aggressive strategies, while pessimism bias, in contrast, could lead to risk aversion or market exit, which are not the primary focus of our study. Therefore, we maintain that the primary focus of our current study is on optimism bias due to its practical relevance and its stronger presence in competitive e-commerce environments.

We study two distinct scenarios regarding the platform’s commission rate: (1) an exogenous commission rate and (2) endogenous strategic commission decisions. In the first scenario, the online platform’s commission rate is exogenous. In the second scenario, the platform can strategically set its commission rate. This approach allows us to isolate the effects of optimism bias under different commission rate conditions and to evaluate the platform’s role in shaping market outcomes. Our analysis offers a novel perspective by focusing on how optimism bias alters competitive dynamics between biased and sophisticated sellers, and how platforms can strategically respond to this bias. This contributes to both the academic literature and practical insights for managing e-commerce supply chains in the presence of cognitive biases. Below, we highlight the main findings.

(1) Exogenous commission rate. First, our findings reveal that both sellers suffer from optimism bias; the more severe the bias, the lower the performance of the seller. Notably, the repercussions of one seller’s optimism bias extend beyond self-impact, negatively affecting its rival as well. This phenomenon can be explained by the distortion of ordering decisions caused by optimism bias. Sellers under the influence of this cognitive bias tend to maintain higher stock levels than what would be optimal under realistic market conditions. Consequently, this overordering leads to a dual negative effect: 1. Self-harm: The biased seller incurs unnecessary inventory costs and potential losses from unsold stock. 2. Harm to the rival: Excessive inventory in the market can lead to increased competition and potential price pressures, adversely affecting the competing seller.

Second, contrary to conventional wisdom, we find that moderate levels of optimism can confer a competitive advantage. Specifically, when both sellers exhibit relatively low levels of optimism bias, the more biased seller can, surprisingly, outperform its less biased or even entirely unbiased competitor. Furthermore, our study demonstrates that even seller sophistication—characterized by an absence of bias and full awareness of a competitor’s optimism bias—may not be sufficient to counteract the competitive edge provided by optimism bias. In scenarios where a biased seller competes against a sophisticated seller, we observe the potential for a win–lose outcome in which optimism bias can benefit the biased seller at the expense of the sophisticated seller, despite the latter’s presumed advantages in market understanding and strategic positioning. This unexpected finding challenges the conventional wisdom about the uniformly detrimental nature of cognitive biases in business decision-making.

The complex interplay between optimism bias and seller performance can be attributed to two contrasting effects on the biased seller: 1. Distortion Effect: Optimism bias leads to suboptimal (increased) ordering decisions, potentially resulting in reduced profitability. 2. Competitive Advantage Effect: Paradoxically, this increased inventory commitment inadvertently causes its sophisticated competitor to reduce its order quantity, effectively mitigating market competition. The ultimate outcome of this dynamic hinges on the magnitude of the biased seller’s optimism. When the optimism bias is relatively modest, the competitive advantage effect can outweigh the distortion effect, allowing the biased seller to derive a net benefit from its own cognitive bias.

(2) Endogenous commission rate. First, while the optimistic seller consistently underperforms compared to its unbiased counterpart in terms of profitability, our analysis uncovers an unexpected positive externality: the platform itself can benefit from sellers’ optimism bias. Specifically, we demonstrate a positive correlation between the degree of seller optimism and platform performance. This unanticipated advantage can be attributed to the following mechanism: optimism bias distorts sellers’ inventory decisions, prompting them to place larger orders than what would be considered theoretically optimal. While this overordering tendency is detrimental to the seller’s individual performance, it simultaneously drives an increase in the overall volume of product sales. Consequently, the e-commerce platform, which typically earns a commission on each transaction, experiences a boost in revenue as a result of the increased sales volume.

Second, our research yields a surprising and counterintuitive finding: seller optimism can enhance the overall performance of the entire supply chain when the platform employs an endogenous commission rate strategy. This implies that the benefits accrued by the platform due to optimism bias can outweigh the potential harm inflicted on third-party sellers. To contextualize this result, consider the following scenario: in a hypothetical centralized system, an unbiased planner coordinates the actions of sellers and the platform to maximize aggregate profits. If this central planner were removed, allowing sellers and the platform to make independent decisions, the sellers would typically underorder, resulting in suboptimal system-wide performance. However, our analysis reveals that if optimistic sellers replace unbiased ones in this decentralized setting, the entire supply chain might actually benefit, contingent on the degree of optimism bias present. The underlying mechanism for this unexpected result can be explained as follows: seller optimism tends to drive higher inventory levels, which serves as a counterbalance to the natural tendency towards underordering in decentralized systems. This compensatory effect can potentially elevate order quantities closer to the optimal levels that would be achieved under centralized planning. Consequently, the presence of optimism bias can, under certain conditions, lead to improved overall system performance.

Third, to enhance the credibility and reliability of our findings, we conducted additional robustness tests through extended modeling analyses. A key component of this extended analysis involved examining a new model variant: the case of a sophisticated platform. In this scenario, the platform possesses the ability to anticipate and account for the sellers’ optimism bias in its decision-making process. Our analysis reveals that as competing sellers exhibit increased levels of bias, a sophisticated platform would respond by elevating its commission rate. Despite this strategic adjustment by the platform, our results consistently demonstrate that biased sellers continue to place larger orders compared to their unbiased counterparts. More significantly, our core findings remain robust even within this more complex model extension. Specifically, we demonstrate that optimism bias can act as a positive force for the platform, but it is detrimental to third-party sellers. Moreover, we find that the benefit optimism bias brings to the platform may outweigh the harm it causes to the seller. Consequently, the whole system (including the platform and sellers) may benefit from optimism bias, even if sellers face negative outcomes. The persistence of these key results underscores the fundamental nature of the relationships we have identified.

The rest of this paper is organized as follows. In Section 2, we review the relevant literature and highlight our main contributions. Section 3 presents the basic analytical model for the e-commerce supply chain. In Section 4, we introduce optimism bias by assuming the commission rate is exogenous and common knowledge. In Section 5, we extend our analysis to the case with an endogenous commission rate. Section 6 tests the robustness of our main findings by considering the case of a sophisticated platform. Finally, Section 7 concludes the paper and provides managerial insights.

2. Literature Review and Our Contributions

Our research lies at the intersection of two significant streams of the literature: optimism bias and e-commerce supply chain. To the best of our knowledge, this study represents the first attempt to bridge these two distinct areas by investigating the profound impact of seller optimism on e-commerce supply chain management. By exploring this novel connection, we aim to contribute valuable insights into both fields and offer a fresh perspective on the dynamics of e-commerce supply chain.

2.1. Optimism Bias

Optimism bias, one of the most prevalent and robust cognitive biases documented in psychology and behavioral economics, has been extensively studied over the past few decades [10]. This bias manifests in various aspects of human behavior and decision-making. For example, Ref. [11] demonstrated that the majority of college students underestimated their chances of developing a drinking problem or getting divorced while overestimating their likelihood of owning a home and living past 80. These findings highlight the pervasive nature of optimism bias in personal life projections. In the realm of decision-making and project management, Refs. [12,13] incorporated optimism into their research models. Their studies revealed that optimism bias can explain the well-known “planning fallacy” in project management, where individuals tend to underestimate the time needed to complete a task. Furthermore, Ref. [14] shows that as team size increases, individuals increasingly underestimate the time required to complete tasks, suggesting that optimism bias can be even more pronounced within group dynamics.

The previous literature on optimism bias focuses on examining its effects on decision-making in business and competitive environments. For example, Ref. [15] examined how the heterogeneity of reference effects influences a newsvendor’s decision-making process in a competitive setting, thus revealing that more optimistic newsvendors tend to disregard their rivals’ behavior. In controlled laboratory experiments, Ref. [16] utilized a simple supplier scorecard mechanism to reward suppliers who reached preset performance thresholds. They observed that suppliers often performed better than expected due to their over-optimism about reward chances, illustrating how optimism bias can sometimes lead to improved performance outcomes. Ref. [17] explored the impact of investor optimism regarding risk on the market incentives of P2P lending platforms to report information, shedding light on the role of optimism in financial decision-making. Other researchers have expanded the scope to examine the impact of optimism on sustainable supply chains [18,19,20], entry strategies [21,22], and product design [23]. In competitive contexts, Ref. [24] shows that overoptimism can result in participants underestimating competition and overestimating their abilities, which can lead to losses. By contrast, Ref. [25] investigated the impact of optimism in a duopoly setting, suggesting that a win–win outcome can prevail in scenarios of unilateral optimism.

These studies above focused on individual decision-making in isolated settings, rather than in dynamic, multi-agent environments like e-commerce supply chain contexts. In fact, while previous studies on optimism bias often focused on its effects in entrepreneurial or investment contexts, few have explored how optimism bias affects strategic interactions between competing sellers on shared e-commerce platforms. Our study uniquely contributes by modeling these interactions in a game-theoretic framework, allowing us to capture the complex dynamics of competition influenced by biased perceptions.

2.2. E-Commerce Supply Chains

Our research also contributes to the extensive literature that focuses on exploring critical operational issues in e-commerce supply chain operations, including information sharing [26,27], logistics service sharing [28,29], financing sellers via platforms [30,31], the use of advanced techniques [32,33], and supply chain serviceability [34]. Within this broad domain, one prominent stream of research focuses on the strategic interactions between online platforms and third-party sellers, exploring the complex dynamics that shape the e-commerce ecosystem. For example, Ref. [35] examined the impact of an e-commerce platform’s encroachment decisions on the sales efforts of online sellers. Ref. [36] investigated the optimal bundling strategy for an e-commerce platform involving independent sellers’ products. This study offers important insights into how platforms can leverage product combinations to enhance overall market performance and seller engagement. Ref. [37] explored scenarios where third-party sellers possess superior demand information. Their work highlights the importance of information asymmetry in platform–seller relationships and its implications for market dynamics.

Another significant stream of e-commerce research focuses on the optimal sales formats employed by online platforms, primarily comparing agency selling and reselling models. These studies have explored the impact of upstream competition [38,39,40,41], downstream competition [42,43], or a combination of both [44,45,46]. For example, Ref. [40] demonstrated that competing platforms’ preferences for selling formats depend on the role of third-party information, particularly in quality or fit dimensions. Ref. [41] investigated the optimal mode for intermediaries in an e-tailing channel comprising two competing sellers and an e-commerce marketplace. Ref. [47] examined the spillover effect on third-party sellers’ product offerings and retailers’ platform openness decisions, shedding light on the broader ecosystem impacts of platform strategies. Other studies have explored factors beyond competition that may impact the preference of reselling and agency selling models, such as new-media advertising [48], platform owner’s entry [49], and the coexistence of self-operated and third-party online channels [50].

A growing body of literature focuses on the implications of behavioral biases in decision-making within e-commerce contexts. For example, Ref. [51] explored the impact of regret bias on SMEs in e-commerce supply chains and investigated the applications and implications of AI in managing regret bias. Ref. [52] analyzed the impacts of follower manufacturers’ fairness concern behavior on e-commerce supply chains. Recent years have witnessed more research in risk preference, which relates to an individual’s tolerance or aversion to uncertainty, where a risk-seeking individual may choose uncertain outcomes with the potential for higher rewards, while a risk-averse individual prefers outcomes with less uncertainty. For example, Ref. [53] examined the impacts of business owners’ risk preferences on e-business adoption.

In our paper, we examine a prevalent yet understudied cognitive bias in e-commerce supply chains, namely optimism bias. Optimism bias refers to a cognitive bias where individuals overestimate favorable outcomes or underestimate risks, often leading to decision-making based on overly positive expectations about future events. In this sense, optimism bias influences the perceived probability of success or favorable outcomes, while risk preference affects how individuals weigh potential payoffs given their understanding of the risks. As a result, we contribute to the existing literature by demonstrating how our model adds to the understanding of cognitive biases in competitive environments, as opposed to simply reflecting differences in risk tolerance.

2.3. Contributions

Building upon the existing literature, our research makes three significant contributions to the understanding of optimism bias in e-commerce supply chains: 1. Bilateral Optimism and Its Broader Impact: When both sellers exhibit optimism bias, we uncover a nuanced dynamic. Although this bias invariably leads to self-harm and rival-harm for the sellers themselves, it can paradoxically benefit the platform and the supply chain as a whole. This finding challenges conventional wisdom and highlights the complex interplay between individual biases and system-wide outcomes in e-commerce ecosystems. 2. Asymmetric Optimism and Competitive Dynamics: In scenarios where a biased seller competes against a sophisticated seller, we observe a win–lose situation. Contrary to what one might expect, the biased seller often benefits at the expense of the sophisticated seller. While previous studies have found that optimism bias can lead to suboptimal decision-making, our model shows that in certain competitive scenarios, optimism bias can give a biased seller a competitive advantage over a sophisticated seller. 3. Optimism as a Competitive Edge: We demonstrate that in direct competition between two biased sellers, the more biased seller can gain an advantage over its less biased competitor. This holds true provided that the optimism bias in both sellers is not excessively severe. Furthermore, our research reveals that even when an unbiased decision-maker possesses full knowledge of a rival’s optimism, this information alone is insufficient to neutralize the competitive advantage conferred by optimism bias.

These findings challenge conventional wisdom about the universally detrimental nature of cognitive biases in business settings. By elucidating the complex effects of optimism bias on competitive dynamics and overall market outcomes, our work paves the way for more nuanced strategies in managing and leveraging cognitive biases within e-commerce supply chains.

3. The Model

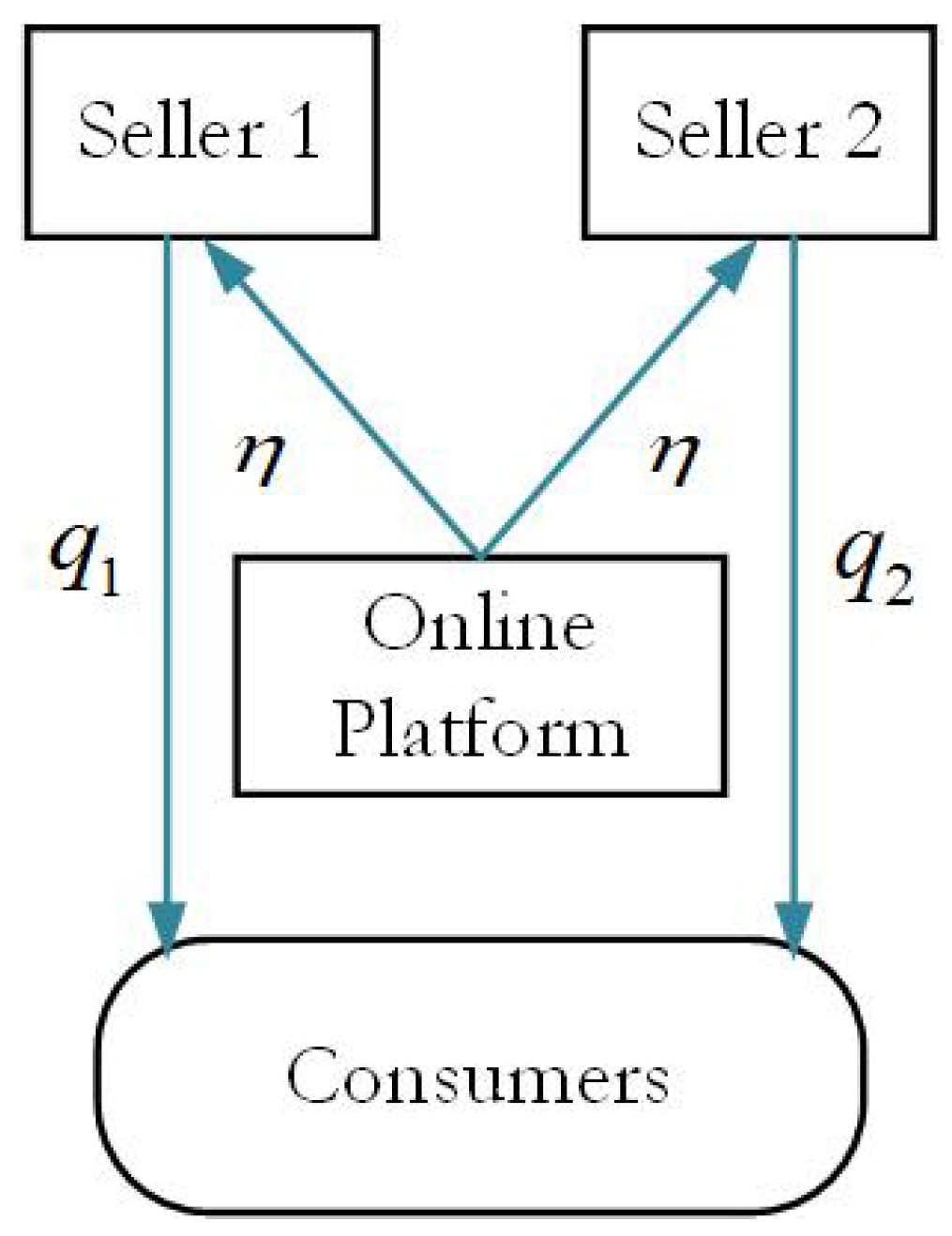
We consider a stylized e-commerce supply chain, as shown in Figure 1, consisting of two third-party sellers (referred to as “she”) selling their partially substitutable products through a common online platform (referred to as “he”). We use $i=1,2$ to denote the set of sellers and refer to the product sold by seller i as product i. Each seller i independently places an order $q_i$ at a common unit cost $c(\ge 0)$. The platform receives a commission proportional to each seller’s revenue at a rate of $\eta \in (0,1)$; the proportion of revenue each seller retains is $1-\eta$. We assume that the commission rate $\eta$ is identical for both sellers.

Given that the products are substitutable, the price of product i is represented by a linear inverse demand function:

$$p_i=\alpha -q_i-\gamma q_j,$$

(1)

where $\alpha >0$ represents the market potential (size) and $\gamma \in (0,1)$ denotes the degree of substitutability of the products. A larger $\gamma$ indicates a higher degree of substitution and a higher intensity of quantity competition. This form of inverse demand function is extensively used in the operations management [27,54], marketing [55], and economics [56,57] literature.

To account for variations in market size, we assume that $\alpha$ is random, taking either of two values: ${\alpha }_l(>0)$ and ${\alpha }_h(\ge {\alpha }_l)$ with probabilities $\lambda$ and $1-\lambda$, respectively, where $\lambda \in [0,1]$. Here, ${\alpha }_l$ and ${\alpha }_h$ represent a bad market and a good market, respectively. This description of variations in market size captures the basic notion of uncertainty well and has been widely used in the operations literature [58]. Let $\overline{\alpha }:=(1-\lambda ){\alpha }_h+\lambda {\alpha }_l$ be the mean of the market potential. In (1), the random $\alpha$ is the theoretical price ceiling (the highest possible price). We assume ${\alpha }_l>c$ to avoid trivial cases, ensuring the seller can make a positive profit even in a bad market. One can view $\overline{\alpha }-c$ as the (expected) margin potential. We define $v:=(\overline{\alpha }-c)/\overline{\alpha }$ as the relative margin potential (RMP). A higher RMP indicates either a lower ordering cost c or a higher market potential $\overline{\alpha }$.

Given the order quantities ($q_1,q_2$), the expected profit for seller i is, for $i=1,2$,

$${\pi }_i(q_1,q_2):=(1-\eta )(\overline{\alpha }-q_i-\gamma q_j)q_i-c{q}_i.$$

(2)

With the exogenous commission rate $\eta$, Lemma 1 summarizes the (unbiased) equilibrium order quantities ($q_1^{*},q_2^{*}$). These results are documented in [59].

Lemma 1

([59]). For a given η, the equilibrium ordering quantities ($q_1^{*},q_2^{*}$) for the unbiased seller system exist and are unique. Moreover, they are identical, and $q^{*}:=q_1^{*}=q_2^{*}$ is given by

$$q^{*}:=\left\{\begin{array}{cc}{\displaystyle \frac{\overline{\alpha }\left(1-\eta \right)-c}{(2+\gamma )\left(1-\eta \right)}}\hfill & if \eta <v\hfill \\ 0\hfill & if \eta \ge v.\hfill \end{array}\right.$$

(3)

Moreover, we have $\partial q^{*}/\partial \eta \le 0$, $\partial q^{*}/\partial \gamma \le 0$, and $\partial q^{*}/\partial \overline{\alpha }\ge 0$.

Lemma 1 indicates that when the commission rate is higher than the RMP, i.e., $\eta \ge v$, it is unprofitable for third-party sellers to place orders. Moreover, the equilibrium order quantity $q^{*}$ decreases with the commission rate $\eta$. Intuitively, as the commission rate decreases, the seller has more incentive to increase her inventory level because she can retain a higher share of the sales revenues. In a similar vein, with more intense competition (larger demand mean), the equilibrium order quantity would be lower (higher) than before.

4. Optimistic Sellers

We now introduce the notion of optimism bias into this setting. In this context, seller i exhibits optimism bias by placing an order as though the likelihood of market potential being low is ${\widehat{\lambda }}_i$ rather than $\lambda$, where

$${\widehat{\lambda }}_i:={\kappa }_i·\lambda$$

(4)

for ${\kappa }_i\in [0,1]$. Accordingly, let $\widehat{\alpha }\left({\kappa }_i\right):=(1-{\kappa }_i\lambda ){\alpha }_h+{\kappa }_i\lambda {\alpha }_l$ be seller i’s subjective mean of market size. Consistent with the literature, e.g., [18,19,21,25], we model optimism as a cognitive bias that causes sellers to believe they are less likely to experience a bad market. In other words, seller i is optimistic about the market in the sense that she overestimates the mean of market size, i.e., $\widehat{\alpha }\left({\kappa }_i\right)\ge \overline{\alpha }$.

The parameter ${\kappa }_i$ can be interpreted as the level of seller i’s optimism. ${\kappa }_i=1$ indicates that seller i is not biased at all. If ${\kappa }_i<1$, then seller i is unrealistically optimistic because she underestimates the probability of experiencing low market potential, i.e., ${\widehat{\lambda }}_i<\lambda$. The lower the value of ${\kappa }_i$, the more biased seller i. In the extreme case, ${\kappa }_i=0$ means that seller i is infinitely optimistic, behaving as though the market potential is constant and equal to its high state ${\alpha }_h$. Define $\widehat{v}\left({\kappa }_i\right):=(\widehat{\alpha }\left({\kappa }_i\right)-c)/\widehat{\alpha }\left({\kappa }_i\right)$ as seller i’s subjective RMP. Note that (optimistic) seller i overestimates the RMP, i.e., $\widehat{v}\left({\kappa }_i\right)\ge v$, because she overestimates the market size.

In defining the game between competitive sellers, we follow [58] by assuming that each seller has no foresight of her competitor’s optimism bias. In other words, each seller behaves as if the other behaves in the same way. Thus, given the commission rate $\eta$, biased seller i behaves as though her game with her rival satisfies the following equation for $i=1,2$:

$$\underset{q_i}{max}\{(1-\eta )(\widehat{\alpha }\left({\kappa }_i\right)-q_i-\gamma q_j)q_i-c{q}_i\}.$$

Proposition 1.

For a given η, seller i with optimism parameter ${\kappa }_i$ orders a quantity ${\widehat{q}}_i\left({\kappa }_i\right)$ as follows for $i=1,2$:

$${\widehat{q}}_i\left({\kappa }_i\right):=\left\{\begin{array}{cc}{\displaystyle \frac{\widehat{\alpha }\left({\kappa }_i\right)\left(1-\eta \right)-c}{(2+\gamma )\left(1-\eta \right)}}\hfill & if \eta <\widehat{v}\left({\kappa }_i\right)\hfill \\ 0\hfill & if \eta \ge \widehat{v}\left({\kappa }_i\right).\hfill \end{array}\right.$$

(5)

Moreover, ${\widehat{q}}_i\left({\kappa }_i\right)$ decreases with ${\kappa }_i$.

Proposition 1 extends the standard structural properties established in Lemma 1 to the case of optimistic sellers. The fundamental structural properties observed in unbiased ordering operations remain unchanged despite the sellers’ change in ordering policy due to optimism bias. Moreover, Proposition 1 indicates that when unbiased seller i (${\kappa }_i=1$) has no incentive to place an order due to the excessively high commission rate ($\eta \ge v$), biased seller i (${\kappa }_i<1$) may order the product if the commission rate is lower than the subjective RMP ($\eta <\widehat{v}\left({\kappa }_i\right)$). Intuitively, optimism bias causes sellers to overestimate the probability of profiting from ordering activity, thus inducing them to place an order. Furthermore, the more optimistic seller i is about the market, the more she orders the product. In other words, the biased seller always over-orders relative to the unbiased seller, i.e., ${\widehat{q}}_i\left({\kappa }_i\right)\ge q^{*}$.

Albeit counterintuitive, Proposition 1 is consistent with the empirical and theoretical observations. For example, sellers often overestimate future demand for their products, leading to overordering or stocking higher levels of inventory than required6. In a similar vein, Ref. [15] theoretically demonstrates that optimistic newsvendors frequently overorder and maintain higher inventory levels than necessary. The observations help validate our model.

Next, we investigate the impact of optimism bias on the seller’s performance. To this end, we assume that $\eta <v$ in order to avoid trivial cases with a zero order quantity. Given $({\widehat{q}}_1,{\widehat{q}}_2)$, the resulting expected profit for seller i is ${\widehat{\pi }}_i({\kappa }_i,{\kappa }_j):={\pi }_i({\widehat{q}}_i,{\widehat{q}}_j)$ for $i,j=1,2$.

Proposition 2.

Seller i’s profit ${\widehat{\pi }}_i({\kappa }_i,{\kappa }_j)$ is increasing in the parameters ${\kappa }_i$ and ${\kappa }_j$.

Proposition 2 indicates that optimism bias always drags down the seller’s performance, aligning with our intuition that cognitive bias leads to self-harm. Intuitively, optimism bias induces the seller to make suboptimal decisions (increasing the order quantity), thereby harming herself. Moreover, optimism bias in one seller also harms her rival’s performance. In fact, bilateral optimism leads to a lose–lose situation, where optimism bias in one seller results in self-harm and rival-harm. For insight, optimism bias in one seller leads to a higher order quantity, thereby lowering the retail price of the product and consequently hurting the rival. Taken together, both sellers’ shared optimism distorts ordering decisions and intensifies quantity competition between them, resulting in neither seller benefiting from this bilateral optimism.

A natural question arising from Proposition 2 is to what extent one seller’s optimism negatively affects her performance as well as that of her rival. To address this question, we assume that ${\kappa }_1<{\kappa }_2$, without loss of generality. Proposition 3 reveals that the less biased seller does not necessarily gain an advantage in competition with the more biased seller, particularly when the aggregate optimism bias of both sellers is relatively low.

Proposition 3.

Define $m:=2-{\displaystyle \frac{\gamma (2+\gamma )q^{*}}{({\alpha }_h-{\alpha }_l)\lambda }}$. The more biased seller earns less profit than the less biased seller if ${\kappa }_1+{\kappa }_2<m$ but earns more profit than the less biased seller if ${\kappa }_1+{\kappa }_2>m$. That is, ${\widehat{\pi }}_1({\kappa }_1,{\kappa }_2)>{\widehat{\pi }}_2({\kappa }_1,{\kappa }_2)\iff {\kappa }_1+{\kappa }_2>m$.

Ref. [60] empirically showed that optimistic individuals tend to put in more effort, achieve higher earnings, and have a greater likelihood of succeeding in areas like sports, business, and politics. In addition, optimism fuels the implementation of the strategy, such as aggressive marketing or expansion, which temporarily outpaces more conservative competitors7. In this light, Proposition 3 indicates that optimism can also be a competitive advantage in e-commerce practice. For illustration, we plot the profits of seller 1 and seller 2 in Figure 2. As per this figure, the more biased seller (seller 1) earns a higher expected profit than its less biased competitor (seller 2) if both sellers are not too biased (${\kappa }_1+{\kappa }_2>m$). For example, in Figure 2a, we keep ${\kappa }_2=1$ and vary ${\kappa }_1$ from 0 to 1. We observe that the more biased seller earns more profit than the unbiased seller when the aggregate optimism of two sellers is relatively slight (${\kappa }_1+1>m\simeq 1.11$). As ${\kappa }_1$ further decreases, seller 1 becomes more biased and ultimately loses her competitive advantage. For example, in Figure 2d, we keep ${\kappa }_2=0.5$ and vary ${\kappa }_1$ from 0 to 0.5. We observe that a comparatively lower bias level always provides a performance guarantee—${\widehat{\pi }}_1({\kappa }_1,{\kappa }_2)<{\widehat{\pi }}_2({\kappa }_1,{\kappa }_2)$—because the aggregate optimism bias across both sellers is relatively high (${\kappa }_1+{\kappa }_2\le 1<m$).

For insight, consider the case in which ${\kappa }_1={\kappa }_2$. In this case, both sellers maintain identical order quantities, each capturing fifty percent of the system’s expected profit. However, as seller 1 becomes more biased (${\kappa }_1$ decreases), seller 1’s order quantity would be larger than that of seller 2. Consequently, seller 1’s effective revenue becomes stochastically larger, resulting in a higher expected profit compared to her competitor. In light of this, Proposition 3 demonstrates a crucial point: the negative impact of a seller’s optimism on her own performance may be less severe than the damage it inflicts on her competitor’s performance. This insight reveals an intriguing dynamic in competitive e-commerce markets where optimism bias can inadvertently confer a relative advantage.

Next, we demonstrate that the advantage attributed to optimism in Proposition 3 is robust, persisting even when the biased seller’s competitor is sophisticated. We define a sophisticated seller as one who is unbiased and fully cognizant of her rival’s optimism bias. This sophistication implies that the seller can accurately anticipate her rival’s ordering behavior and incorporate this knowledge into her own decision-making process. Without loss of generality, we assume that seller 2 is sophisticated while seller 1 is biased. Thus, the equilibrium order quantity of seller 1 is ${\widehat{q}}_1\left({\kappa }_1\right)$, as shown in Proposition 1. Anticipating seller 1’s ordering strategy ${\widehat{q}}_1\left({\kappa }_1\right)$, sophisticated seller 2’s problem is to set the order quantity $q_2$ to maximize her equilibrium expected profit: ${\pi }_2({\widehat{q}}_1,q_2)$. Thus, seller 2’s equilibrium order quantity is

$$q_2^f\left({\kappa }_1\right)={\displaystyle \frac{[\overline{\alpha }-\gamma {\widehat{q}}_1\left({\kappa }_1\right)](1-\eta )-c}{2(1-\eta )}}.$$

(6)

Note that (6) is the best-response function that gives the sophisticated seller’s optimal order quantity as a function of seller 1’s optimism level ${\kappa }_1$, indicating that the more biased seller 1 is, the less seller 2 will order. Intuitively, the sophisticated seller foresees that the biased rival will increase the stocking level, thereby ordering less to prevent the marginal revenue from diminishing.

Given ${\kappa }_1$, the expected profit of the biased seller is ${\widehat{\pi }}_b\left({\kappa }_1\right):={\pi }_1({\widehat{q}}_1,q_2^f)$, and the expected profit of the sophisticated seller is ${\widehat{\pi }}_f\left({\kappa }_1\right):={\pi }_2({\widehat{q}}_1,q_2^f)$. Next, we study how optimism bias affects the performance of both the biased and sophisticated sellers.

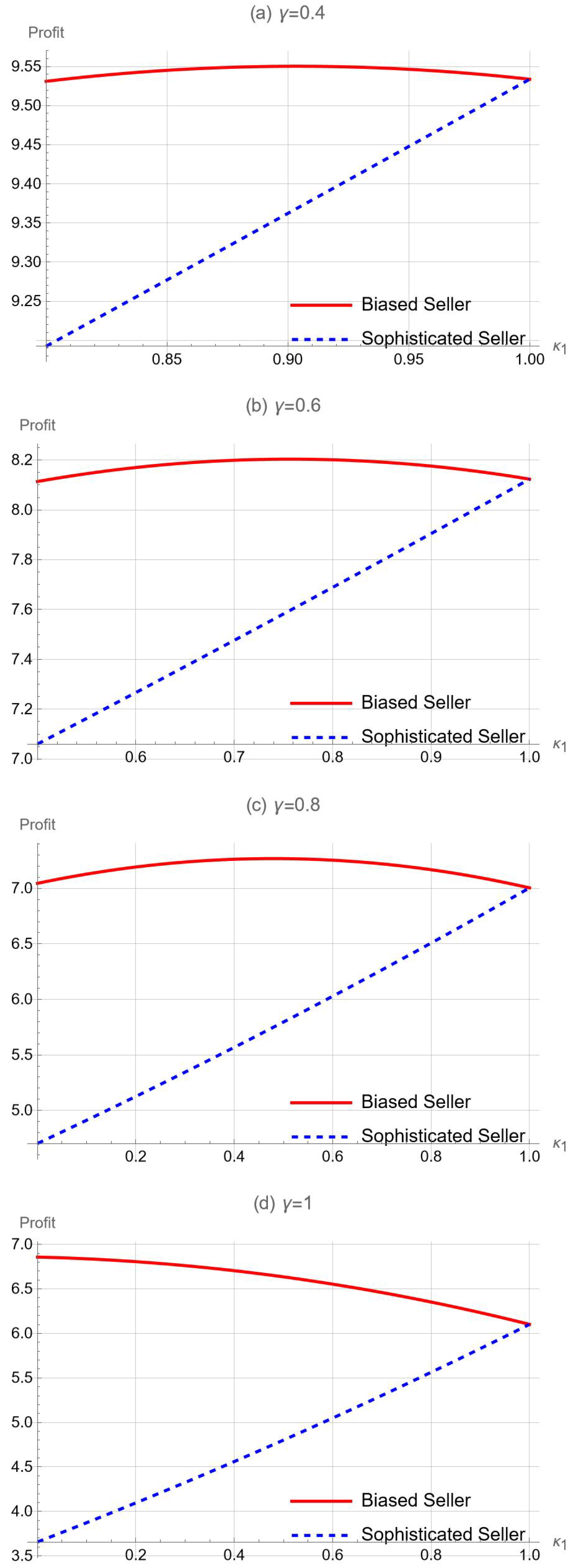
Proposition 4.

When a biased seller competes with a sophisticated seller, there exists a threshold $\overline{m}\in (0,1)$ such that the biased seller’s profit ${\widehat{\pi }}_b$ decreases with ${\kappa }_1$ in the region ${\kappa }_1\in (\overline{m},1)$, while the sophisticated seller’s profit ${\widehat{\pi }}_f$ increases with ${\kappa }_1$ in the same region.

In contrast to Proposition 2, Proposition 4 indicates that the biased seller can benefit from optimism bias, particularly when optimism bias is relatively low (${\kappa }_1>\overline{m}$). Interestingly, in such cases, the sophisticated seller suffers rather than benefits from her rival’s optimism bias, even though she can perfectly foresee the rival’s ordering strategy and accordingly choose the optimal order quantity. For illustration, we plot how ${\widehat{\pi }}_b$ and ${\widehat{\pi }}_f$ change with respect to ${\kappa }_1$ in Figure 3. As per this figure, when ${\kappa }_1=1$, the biased seller obtains the same profit as her sophisticated competitor. As optimism bias becomes more severe (${\kappa }_1$ decreases), the biased seller’s profit can increase even though the sophisticated seller’s profit always decreases. Consequently, Figure 3 demonstrates that a sophisticated seller may not gain any advantage in competition with a biased seller. For example, the sophisticated seller earns less profit than her competitor at any level of optimism bias, as shown in Figure 3c,d.

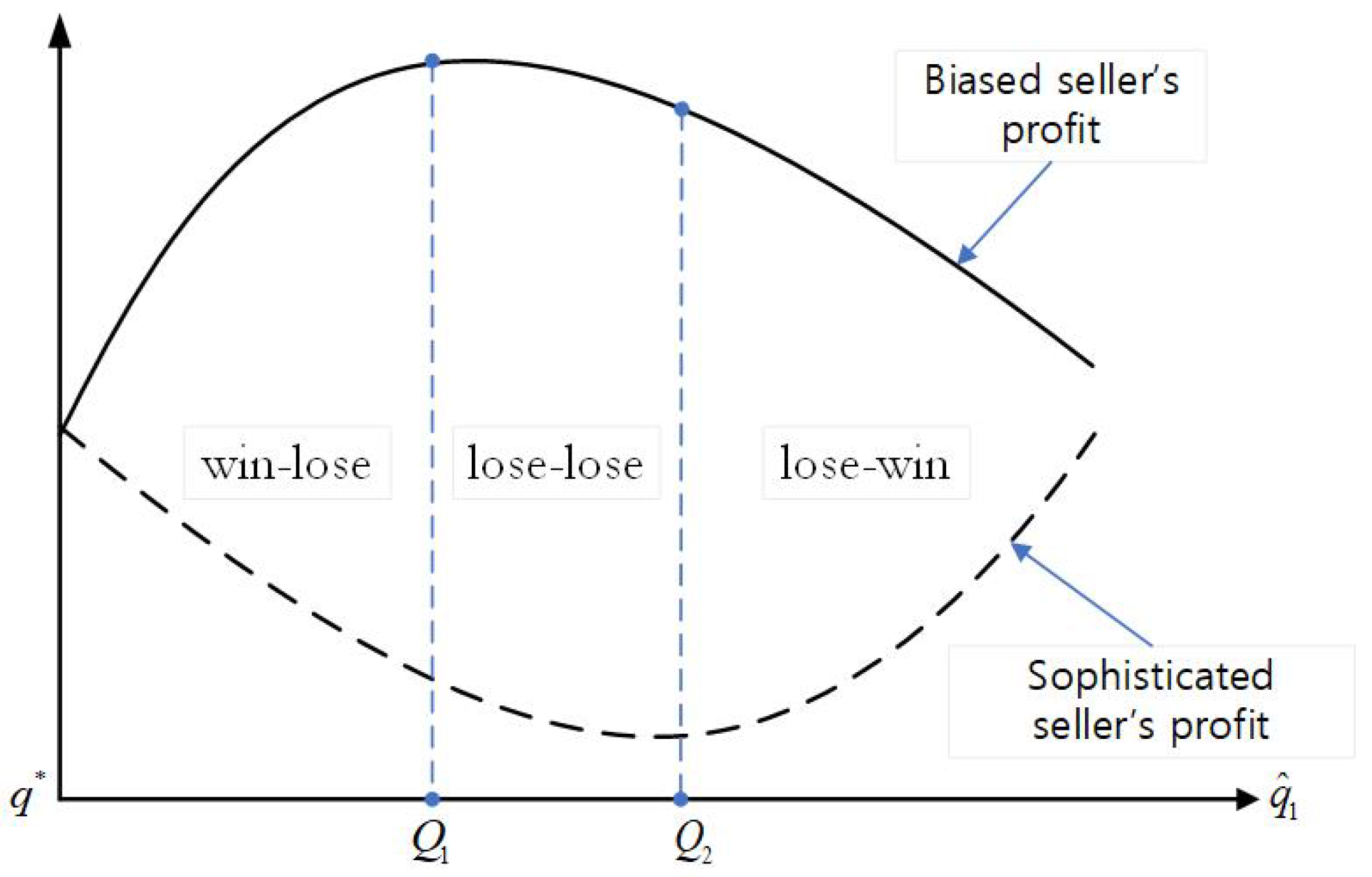
To understand and explore the intuition behind Proposition 4, we plot how ${\widehat{\pi }}_b$ and ${\widehat{\pi }}_f$ change with ${\widehat{q}}_1$ in Figure 4. Recall that ${\widehat{q}}_1({\kappa }_1=1)=q^{*}$ and ${\widehat{q}}_1$ increases as optimism bias becomes more severe (${\kappa }_1$ decreases). As shown in this figure, optimism bias never benefits both the biased and sophisticated seller simultaneously. Specifically, when ${\widehat{q}}_1<Q_1={\displaystyle \frac{(4-{\gamma }^2)q^{*}}{4-2{\gamma }^2}}$, the expected profit of the biased seller increases as ${\widehat{q}}_1$ increases; that is, the biased seller benefits from her own bias. Conversely, this bias leads to lower performance for the sophisticated competitor. When ${\widehat{q}}_1>Q_2={\displaystyle \frac{(2+\gamma )q^{*}}{\gamma }}$, optimism bias is detrimental (beneficial) to the biased (sophisticated) seller. When $Q_1<{\widehat{q}}_1<Q_2$, a lose–lose outcome prevails. The underlying reason why unilateral optimism can benefit the biased seller but hurt the sophisticated competitor lies in the effect of optimism on the sellers’ ordering decisions and resulting marginal revenues.

Specifically, optimism has two effects on the biased seller’s performance. The first (direct) effect is negative because a more severe optimism bias exacerbates the distortion in the seller’s ordering decision, consistent with Proposition 2. The second (indirect) effect is that optimism bias leads the biased seller to choose a higher inventory level, which induces her sophisticated competitor to lower the inventory level, thus alleviating market competition. Therefore, the indirect effect of optimism bias on the biased seller’s performance is positive. When the degree of optimism is relatively low (the value of ${\kappa }_1$ is relatively large), the indirect effect is significant enough to outweigh the direct effect. As a result, optimism bias ultimately benefits the biased seller, but it does so at the expense of the sophisticated seller.

5. Strategic Platform

In this section, we examine the case in which the platform can strategically adjust the commission rate $\eta$ to maximize his expected profit. The interaction between the sellers and the platform is represented as a two-step game: (1) the platform announces a commission rate $\eta$; (2) given $\eta$, each seller determines the order quantity. We assume that the online platform is unbiased and unaware of the sellers’ optimism bias. Thus, by anticipating that the equilibrium order quantity of each seller for a given $\eta$ is $q^{*}\left(\eta \right)$, the platform’s problem in the first stage is equivalent to setting the commission rate $\eta$ to maximize his expected profit:

$${\pi }_P(\eta ,q^{*}):=2\eta [\overline{\alpha }-q^{*}\left(\eta \right)-\gamma q^{*}\left(\eta \right)]q^{*}\left(\eta \right).$$

(7)

Given (7), Ref. [59] established the (unbiased) equilibrium commission rate ${\eta }^{*}$, as documented in Lemma 2.

Lemma 2

([59]). Define

$$F\left(\eta \right):=-c^2\left(1+\gamma \right)\left(1+\eta \right)+\gamma \overline{\alpha }c\left(1-\eta \right)+{\overline{\alpha }}^2{\left(1-\eta \right)}^3.$$

(8)

Thus, the commission rate in equilibrium ${\eta }^{*}\in (0,v)$ is uniquely determined by $F\left({\eta }^{*}\right)$=0. Moreover, ${\eta }^{*}$ increases with γ and $\overline{\alpha }$, and decreases with c.

Lemma 2 indicates that a higher intensity of competition (greater $\gamma$) compels the platform to charge a higher commission rate, consistent with specific observations. For example, the commissions on Amazon, eBay, and Walmart for books, which have greater substitutability, range from 12% to 15%, much higher than those for consumer electronics, where commissions rarely exceed 8%8. In a similar vein, greater cost-efficiency (smaller c) or higher market potential (greater $\overline{\alpha }$) means greater relative margin potential, leading to the increasing profit of sellers. So, the platform charges a higher commission to extract additional revenue.

Note that the equilibrium commission rate is smaller than the RMP, i.e., ${\eta }^{*}<v$. Therefore, the fundamental structural properties of how optimism bias affects sellers’ performance, as observed in the case of an exogenous commission rate, remain unchanged. Next, we analytically explore how seller optimism affects the platform’s performance. For simplicity, we focus on the case of symmetric optimism by assuming a common optimism level $\kappa$ for the two competing sellers, i.e., $\kappa ={\kappa }_1={\kappa }_2$. Let $\widehat{q}\left(\kappa \right)={\widehat{q}}_1\left(\kappa \right)={\widehat{q}}_2\left(\kappa \right)$. Thus, given the biased order quantity $\widehat{q}\left(\kappa \right)$ and the equilibrium commission rate ${\eta }^{*}$, the platform’s ensuing expected profit is ${\widehat{\pi }}_P\left(\kappa \right):={\pi }_P({\eta }^{*},\widehat{q}\left(\kappa \right))$.

Proposition 5.

When both sellers are characterized by the optimism parameter κ, there exists a threshold $m^P\in (0,1)$ such that the platform’s profit ${\widehat{\pi }}_P$ decreases with κ over the region of $\kappa \in (m^P,1)$.

Proposition 5 indicates that optimism bias can benefit the online platform, even though this bias always drags down the sellers’ performance (as shown in Proposition 2). For an illustration, we plot ${\widehat{\pi }}_P$ in Figure 5. As per this figure, the platform’s profit decreases with $\kappa$, indicating that any level of seller optimism can benefit the platform.

To put this in perspective, recall that a biased seller always overorders relative to an unbiased seller. Optimism bias induces sellers to make suboptimal decisions, harming themselves. However, this bias increases the inventory level, thereby increasing revenue from product sales and benefiting the platform. As a result, a win–lose outcome can prevail, where the seller suffers, but the platform benefits from optimism bias.

Proposition 5 prompts a crucial question: can optimism bias benefit the platform to such an extent that it enhances the performance of the entire supply chain, encompassing both the platform and competing sellers? Given our previous observations, we are particularly intrigued by the impact of seller optimism on the total profit of the entire supply chain, ${\widehat{\pi }}_e:={\widehat{\pi }}_1+{\widehat{\pi }}_2+{\widehat{\pi }}_P$.

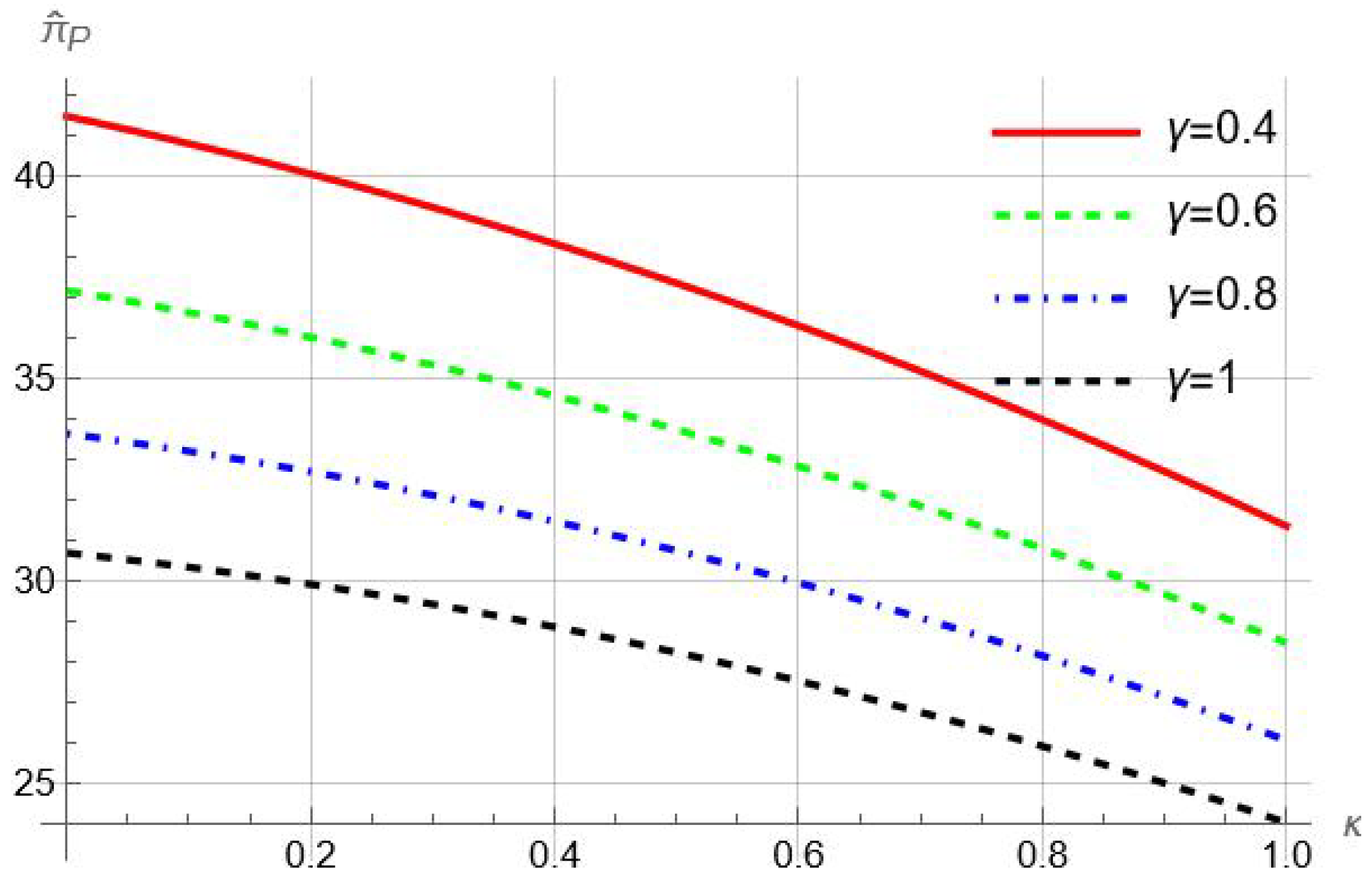
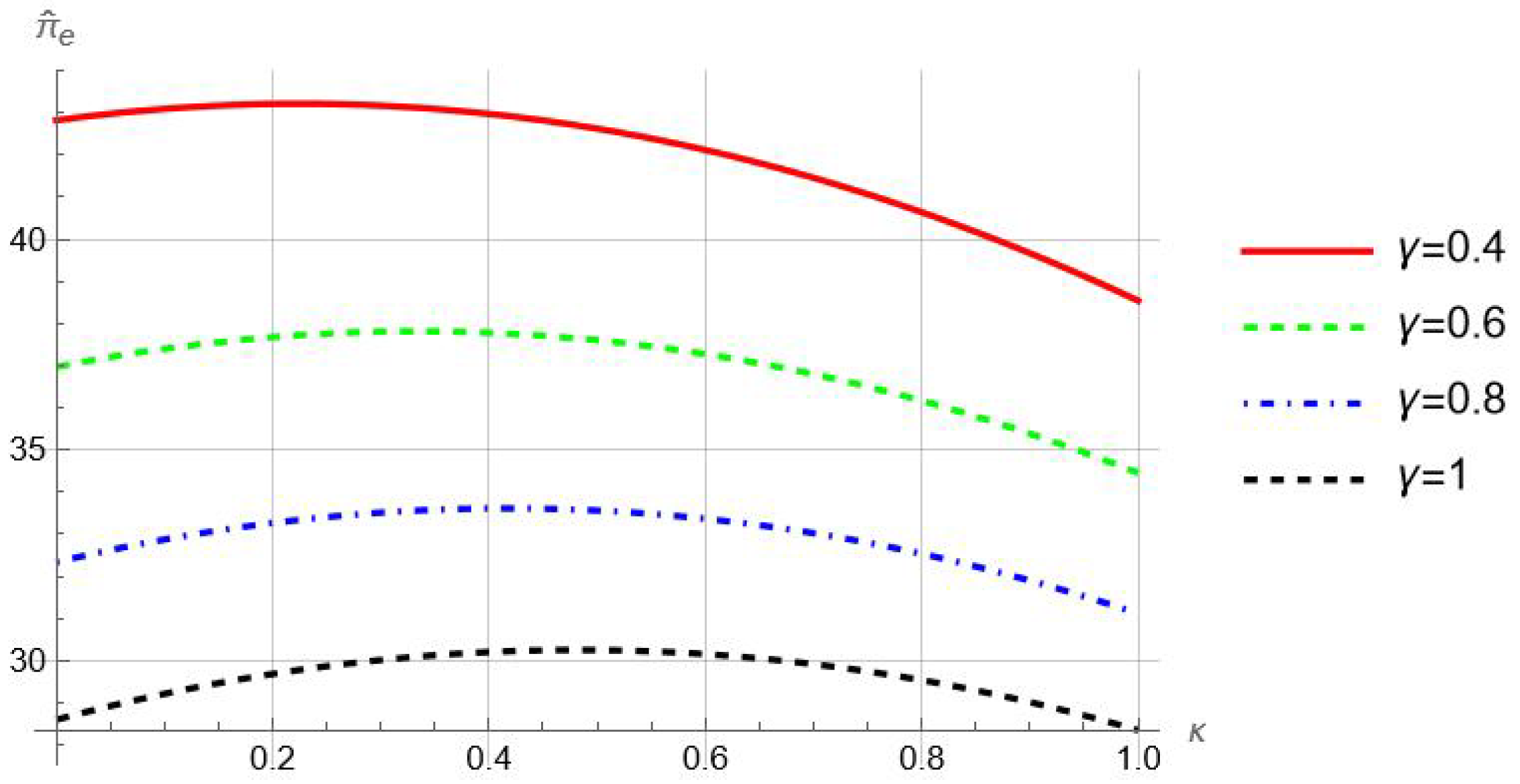
Proposition 6.

When both sellers are characterized by the optimism parameter κ, there exists a threshold $m^e\in (0,1)$ such that the system’s total profit ${\widehat{\pi }}_e$ decreases with κ over the region $\kappa \in (m^e,1)$.

Proposition 6 indicates that seller optimism can improve system-wide performance within a certain range of optimism levels. For an illustration, we plot how ${\widehat{\pi }}_e$ changes with $\kappa$ in Figure 6. As shown, the entire supply chain’s performance can improve as seller optimism becomes more severe (as $\kappa$ decreases), especially when optimism bias is relatively low. Recall that while optimism bias always hurts third-party sellers (Proposition 2), it can benefit the online platform (Proposition 5). The enhanced system-wide performance demonstrated by Proposition 6 indicates that optimism bias can bring more benefits to the platform than the harm it causes to the sellers.

For insight, we consider a hypothetical centralized system in which the platform and sellers are centrally coordinated to maximize the aggregate profit of the entire system. The expected profit of such a system is $\Pi :=\left(1-\lambda \right)\left[\left({\alpha }_h-q\right)q-cq\right]+\lambda \left[\left({\alpha }_l-q\right)q-cq\right]$. This centralized system can be viewed as a first-best benchmark. The optimal order quantity for each seller in this scenario is $q^f=(\overline{\alpha }-c)/2$. Accordingly, we refer to $q^f$ as the first-best order quantity.

The performance of the entire supply chain depends on the relationship between the biased order quantity $\widehat{q}\left(\kappa \right)$ and the first-best benchmark $q^f$. The closer the value of $\widehat{q}\left(\kappa \right)$ is to $q^f$, the better the performance of the whole channel. Since third-party sellers only receive a portion of the sales revenue, the unbiased seller tends to underorder relative to the first-best order quantity, i.e., $\widehat{q}(\kappa =1)<q^f$, making the whole system worse off. However, optimism bias leads to a higher order quantity, thereby pulling the order quantity closer to the first-best level. In other words, optimism can alleviate the underordering resulting from decentralization to a certain extent, thus mitigating the detrimental impact of decentralization on supply chain performance. If this is the case, the entire supply chain ultimately benefits from seller optimism.

6. Robustness Check: Sophisticated Platform

To evaluate the robustness of our main findings, we extend our analysis to the case of a sophisticated platform, which is unbiased and fully aware of the sellers’ optimism bias. In practice, online platforms may have the expertise to identify third-party sellers due to advanced technology and expert human reviews. Sophistication implies that the platform can anticipate the sellers’ stocking behaviors and factor them into its decision-making process. Thus, accounting for the sellers’ order quantities in equilibrium $\widehat{q}\left(\kappa \right)$, the sophisticated platform’s problem is equivalent to choosing the commission rate $\eta$ that maximizes his expected profit ${\pi }_P(\eta ,\widehat{q})$. Lemma 3 establishes the equilibrium commission rate of the sophisticated platform with relatively low product substitutability.

Lemma 3.

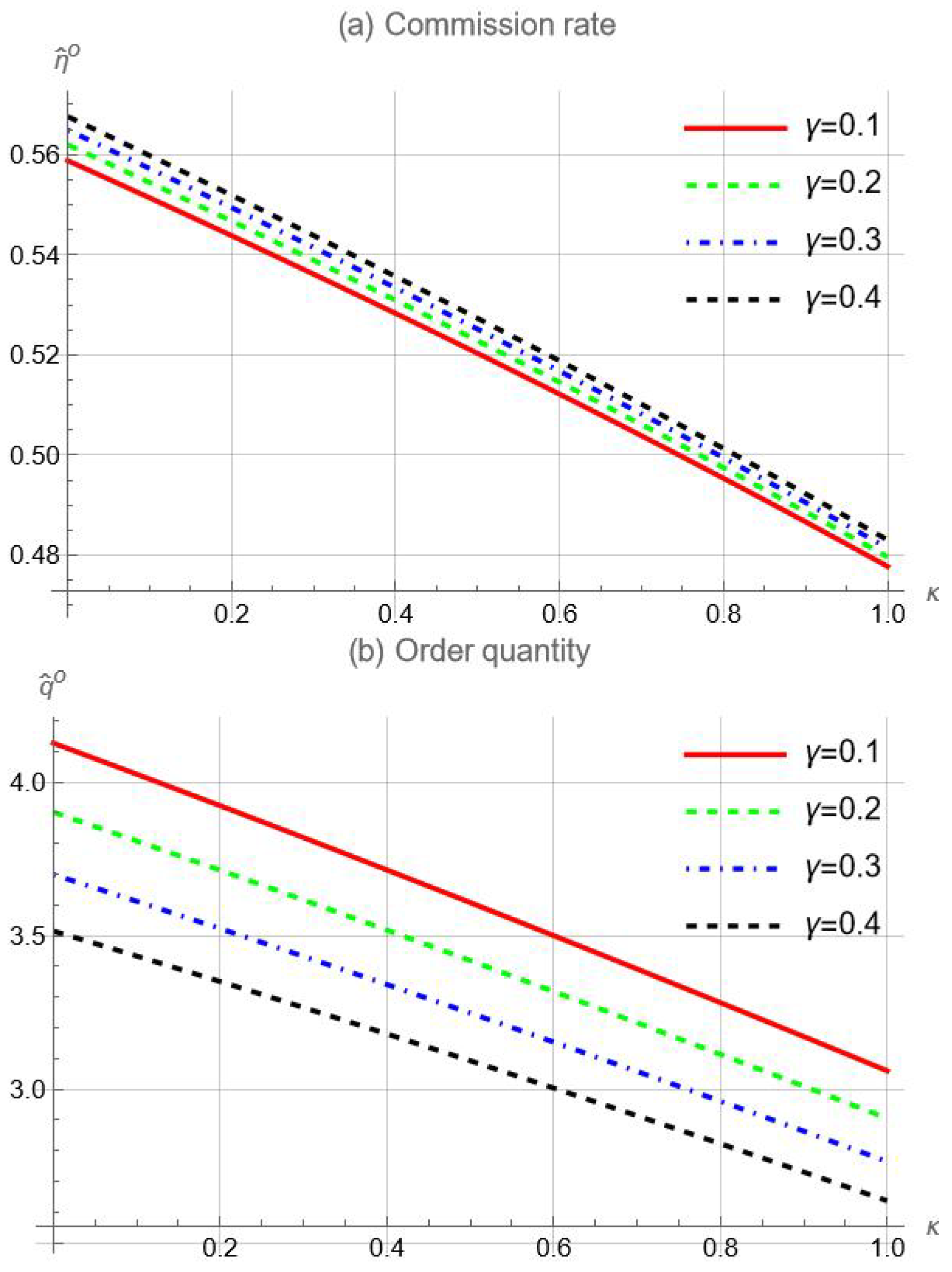
If $(2+\gamma )\lambda <1$, then the sophisticated platform’s equilibrium commission rate ${\widehat{\eta }}^o\left(\kappa \right)\in (0,v)$ is uniquely determined by

$$\begin{array}{cc}\hfill {\displaystyle \frac{c^2\left(1+\eta \right)(1+\gamma )}{{\left(1-\eta \right)}^3}}& =\widehat{\alpha }\left(\kappa \right)\left[{\alpha }_h\left(1+\left(-2+\gamma \left(-1+\kappa \right)+\kappa \right)\lambda \right)+{\alpha }_l\left(2+\gamma \left(1-\kappa \right)-\kappa \right)\lambda \right]\hfill \\ \hfill & +{\displaystyle \frac{c\left[-\left(2+\gamma \right)\overline{\alpha }+2\left(1+\gamma \right)\widehat{\alpha }\left(\kappa \right)\right]}{{\left(1-\eta \right)}^2}}.\hfill \end{array}$$

(9)

For illustration, we plot how the equilibrium commission rate changes with respect to the optimism parameter $\kappa$ in Figure 7a. In this figure, we let $\gamma \in \{0.1,0.2,0.3,0.4\}$ to ensure that $(2+\gamma )\lambda <1$. As per this figure, the sophisticated platform increases the commission rate as the seller’s optimism bias intensifies. Intuitively, the sophisticated platform anticipates the seller’s tendency to order more inventory due to her optimism bias, which results in higher revenue for the platform. Therefore, the platform sets a higher commission rate to capture a portion of the additional revenue generated by the seller’s stocking behavior.

Given ${\widehat{\eta }}^o$, seller i’s order quantity is, for $i=1,2$,

$${\widehat{q}}^o:={\displaystyle \frac{[{\alpha }_h(1-\kappa \lambda )+{\alpha }_l\kappa \lambda ](1-{\widehat{\eta }}^o)-c}{(2+\gamma )(1-{\widehat{\eta }}^o)}}.$$

(10)

Figure 7b further indicates that the seller’s order quantity decreases with the parameter $\kappa$, suggesting that the seller would increase her stock level as optimism bias becomes more severe. For insight, two drivers are at play regarding the impact of $\kappa$ on the seller’s stock level. The first driver, a direct effect of $\kappa$, is that optimism bias increases the inventory level. The second driver is indirect: as per Lemma 3, severe optimism bias leads to a higher commission rate, which, in turn, results in a lower stock level, according to (10). Overall, the direct driver outweighs the indirect driver, resulting in the biased seller still overordering relative to the unbiased seller, even when the platform is sophisticated.

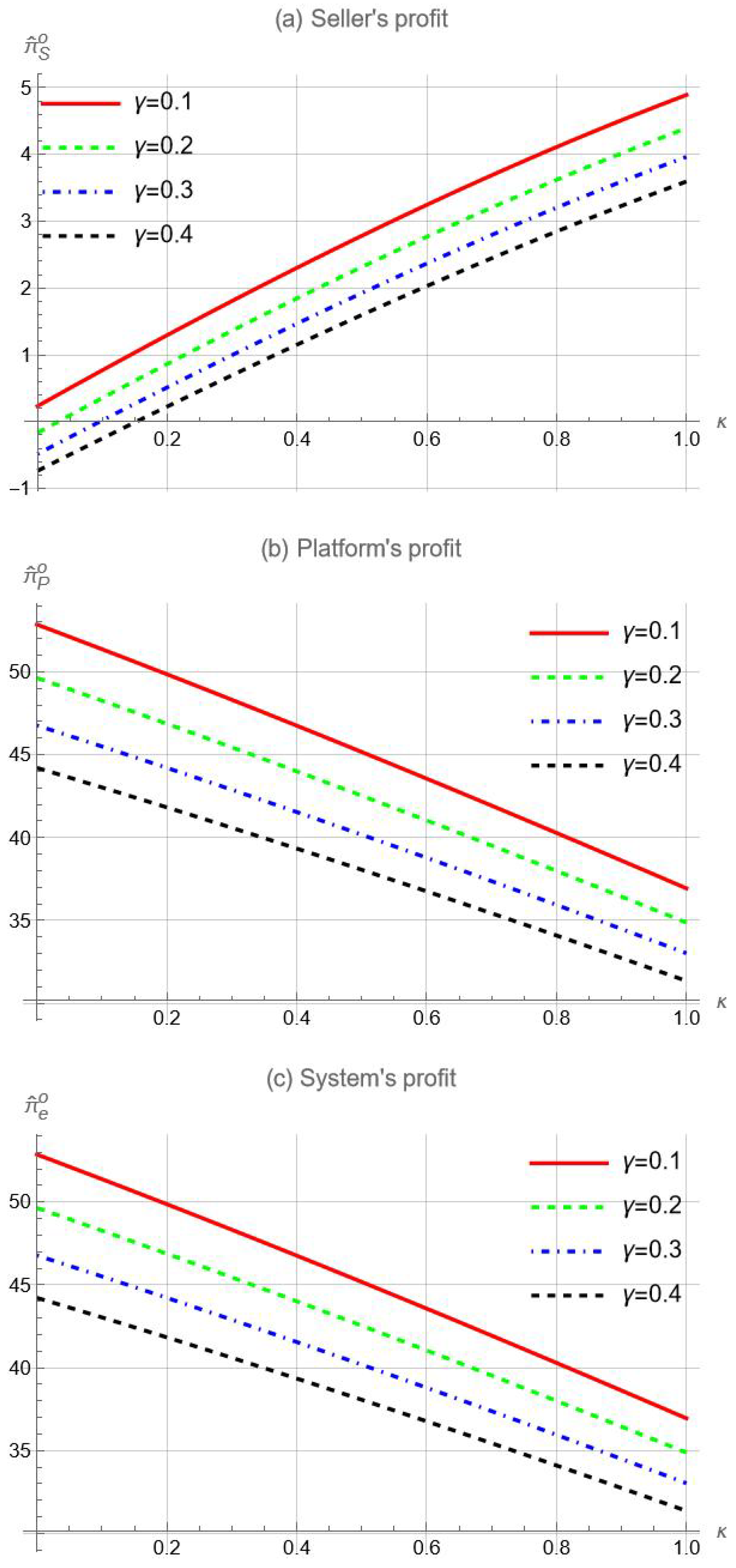
Given ${\widehat{\eta }}^o$ and ${\widehat{q}}^o$, let ${\widehat{\pi }}_s^o:={\pi }_1({\widehat{\eta }}^o,{\widehat{q}}^o)={\pi }_2({\widehat{\eta }}^o,{\widehat{q}}^o)$ represent each seller’s resulting profit, and ${\widehat{\pi }}_P^o:={\pi }_P({\widehat{\eta }}^o,{\widehat{q}}^o)$ represent the platform’s resulting profit. Consequently, the total profit of the entire supply chain is ${\widehat{\pi }}_e^o:=2{\widehat{\pi }}_s^o+{\widehat{\pi }}_P^o$. In the case of a sophisticated platform, it is challenging to analytically examine the impacts of seller optimism due to the difficulty of obtaining a closed-form solution for the equilibrium commission rate of the sophisticated platform (see Proof of Lemma 3 in the Appendix A). Therefore, we resort to conducting numerical experiments to gain more insights. Our numerical analysis shows that our main findings continue to hold even when the platform is sophisticated. Specifically, optimism bias can act as a positive force for the platform and the entire system, but it is detrimental to third-party sellers, as shown in Figure 8.

For insight, optimism bias forces the seller to make non-optimal decisions (increasing the order quantity), thereby harming herself. Furthermore, the commission rate set by the sophisticated platform increases due to the seller’s optimism bias, leading to a lower share of the sales revenue for the seller and further reducing her profit. In summary, optimism bias harms the sellers. On the other hand, the increase in order quantity and commission rate benefits the platform, making seller optimism a positive force for the performance of the sophisticated platform. Additionally, seller optimism can mitigate the impact of order distortion caused by decentralization, leading to improved performance of the entire channel.

7. Conclusions, Managerial Insights, and Possible Implementations

This paper investigates the effects of seller optimism within an e-commerce supply chain consisting of two competing third-party sellers and an online platform. In this context, sellers are prone to optimism bias, as they tend to underestimate the likelihood of encountering low market potential in the future. To explore these dynamics, we present a game-theoretic model that characterizes the equilibrium strategies of both the platform and the sellers involved.

Our findings reveal potential positive outcomes stemming from seller optimism. Specifically, we demonstrate that both the platform and the entire channel can benefit from seller optimism, particularly when this bias is relatively low. Interestingly, we find that optimism bias does not inevitably lead to self-harm for sellers. In a scenario where a biased seller competes with a sophisticated counterpart, unilateral optimism can result in a win–lose outcome, benefiting the optimistic seller at the expense of its sophisticated rival. The advantages of optimism lie, in part, in motivating a biased seller to maintain higher inventory levels. This, in turn, compels the sophisticated competitor to reduce the inventory, thereby mitigating quantity competition in the market. However, when both sellers exhibit optimism bias, its positive effect dissipates, leaving both worse off in equilibrium.

Finally, we demonstrate that optimism bias can provide a competitive edge in a duopoly, even if the less biased seller is unbiased or sophisticated. While optimism can lead to a competitive advantage under certain conditions, it also carries significant risks. In fact, overly optimistic sellers may overestimate demand, leading to excessive inventory, higher costs, and ultimately failure. Therefore, this advantage is not guaranteed and can be context-dependent.

7.1. Managerial Insights

In light of our theoretical exploration of the impact of seller optimism in e-commerce supply chains, our results offer two crucial managerial insights for firms adopting strategies in response to optimism bias.

First, since previous research has emphasized that optimism bias may cause people to make decisions with negative outcomes for themselves or others, various approaches have been proposed to overcome optimism bias, such as taking an outside view and a post mortem approach [61]. In this sense, our study offers the following strategic recommendations for sellers adopting strategies in response to this bias. Specifically, the seller is encouraged to carry out mitigation programs in scenarios without a sophisticated competitor. In contrast, if the competitor is sophisticated, initiating programs to overcome optimism may adversely affect the seller’s performance, particularly when optimism bias is already low. In fact, even if the competitor is not sophisticated, complete elimination of optimism bias may not be entirely wise. This is because excessively eliminating optimism bias could cause the seller to lose their competitive advantage.

Second, our analysis presents an interesting dynamic between third-party sellers and an online platform, revealing that a moderate optimism can potentially bring positive effects to the online platform and the entire e-commerce supply chain. Furthermore, even if the platform could recognizing sellers’ optimism bias when setting commission rates, a win–win dynamic emerges in the supply chain—that is, both the platform and the whole system can benefit from seller optimism, especially when the degree of optimism is relatively low.

7.2. Possible Implementations

The managerial insights above provide real-world management strategies that e-commerce platforms and sellers could adopt:

• The third-party sellers should carefully evaluate the advantages and timing of implementing optimism mitigation strategies. Specifically, if the competitor is sophisticated, the seller should not initiating such programs to reduce optimism. Instead, if competitor sophistication is achieved, our findings advocate for reducing severe optimism to a lower, more manageable level, which emerges as a more optimal strategy for the seller.
• The online platform can strategically leverage the sellers’ optimism. Specifically, when seller optimism is moderate, platform operators should foster this optimism by offering positive reinforcement, information, and incentives. In addition, it is crucial to monitor the level of optimism to prevent it from escalating excessively, as this could result in heightened competition and reduced customer satisfaction, ultimately harming the platform. Therefore, striking the right balance in fostering and managing seller optimism is key to maximizing the platform’s benefits while mitigating potential risks.
• Government agencies and other external bodies aiming to boost supply chain performance by addressing optimism bias should consider a two-pronged approach. When seller optimism is high, encourage third-party sellers to implement mitigation strategies to prevent potential negative consequences of excessive overconfidence. Conversely, when seller optimism is low, foster a culture that promotes positive overconfidence by providing support and resources that help sellers leverage their optimism constructively. This balanced approach can help external entities guide sellers towards a level of optimism that contributes positively to the supply chain’s overall performance.

The effective application of our study’s managerial insights in addressing seller optimism critically hinges on the ability to accurately gauge the extent of such optimism. For instance, third-party sellers exhibiting significant optimism should consider implementing mitigation programs. Furthermore, if platforms can precisely measure a seller’s degree of optimism, they can strategically leverage this information to enhance overall performance. Consequently, the capacity to accurately assess a manager’s level of optimism is paramount for the successful implementation of our research findings.

Researchers typically measure optimism bias through two determinants of risk: absolute risk and comparative risk; see, e.g., [62,63]. Recognizing that optimism is a persistent and stable cognitive bias, managers can employ these established measures to assess its degree. By accurately identifying and quantifying optimism, businesses can tailor their strategies more effectively, potentially mitigating risks and capitalizing on opportunities presented by optimism bias. In this light, understanding optimism degrees can be instrumental in making informed decisions in response to optimism bias for optimal performance enhancement.

7.3. Future Research

Future research could productively explore several avenues. Future studies could investigate how optimism bias might manifest differently across various platform models, such as direct sales platforms versus marketplace models with third-party sellers. Each platform type may have different competitive dynamics, and understanding how optimism bias interacts with these factors would provide deeper insights. Second, our analytical framework is currently confined to a one-period game, not accounting for a dynamic, multi-period environment. Future research could explore the behavioral impacts of optimism bias in the long run, including its effect on seller sustainability and platform evolution. Third, while our focus has been on seller optimism, a prevalent and challenging issue in e-commerce, other behavioral biases, also deserves attention. Future research could develop a more comprehensive behavioral framework, integrating biases such as overconfidence, loss aversion, and optimism bias. These would allow for a richer analysis of how different cognitive biases interact and influence market outcomes, potentially leading to new insights on how sellers strategize in competitive e-commerce environments. In a similar vein, future studies might delve into the effects of optimism among platform operators due to the fact that optimism bias is prevalent among entrepreneurs and executives, including those managing platforms. This could further complicate the interactions between sellers and platforms, opening new avenues for research.

Overall, we envision our paper as a foundational contribution to the evolving field of bias-related e-commerce research, paving the way for a more comprehensive understanding of how cognitive biases impact decision-making and performance in digital marketplaces.