A Study on the Heterogeneity of China’s Provincial Economic Growth Contribution to Carbon Emissions
Abstract
1. Introduction
2. Literature Review
3. Research Data and Methodology
3.1. Variables and Interpretation
- (i)
- (ii)
- Independent variables: Per capita GDP (denoted as GDP) and the proportion of GDP contributed by tertiary industry (denoted as TR). In the context of China, many studies have verified that GDP contributes to carbon emissions [14,15,16,17,18]. However, we believe that this contribution is not constant over time and varies among provinces, and is likely closely related to TR. Therefore, we chose GDP as an indicator of economic growth, while TR served as a direct descriptive variable capturing the heterogeneity in the contribution of economic growth to carbon emissions. In Section 3.2, we elaborate on this process in detail. These data were obtained from the China Statistical Yearbook.
- (iii)
- Control variables: Per capita disposable income (denoted as DI), financial interrelation ratio (denoted as FIR), financial efficiency (denoted as FE), mileage of highways (denoted as MH), afforestation area (denoted as AFF), per capita fixed asset investment (denoted FI), per capita fixed asset investment in the state-owned energy industry (denoted as EFI), per capita technology market transaction volume (denoted TM), patents for inventions authorized per 10k persons (denoted PA), size of population(PO), and urbanization rate (denoted UR). The data of FIR and FE were obtained from the China Financial Yearbook and the remaining data were retrieved from the national data website (https://data.stats.gov.cn/, accessed on 22 August 2024), as well as the China Statistical Yearbook.
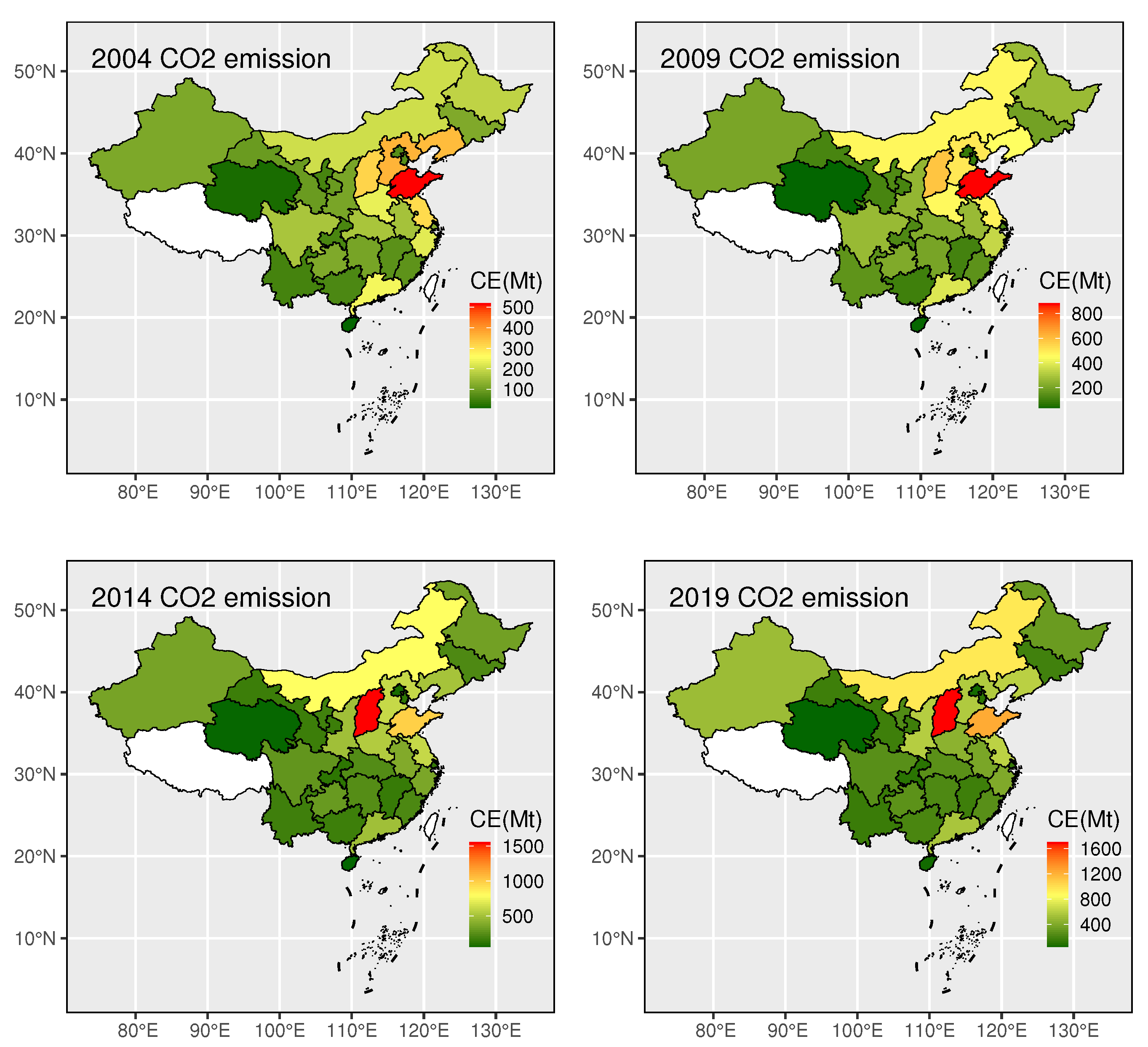
3.2. Analysis of Carbon Dependence Heterogeneity and Spatial Spillover Effects of Carbon Emissions
4. Model Construction and Empirical Analysis
4.1. Model Building
4.2. Methods of Estimation
4.3. Empirical Result Analysis
4.3.1. Empirical Analysis of Spatial Spillover Effects
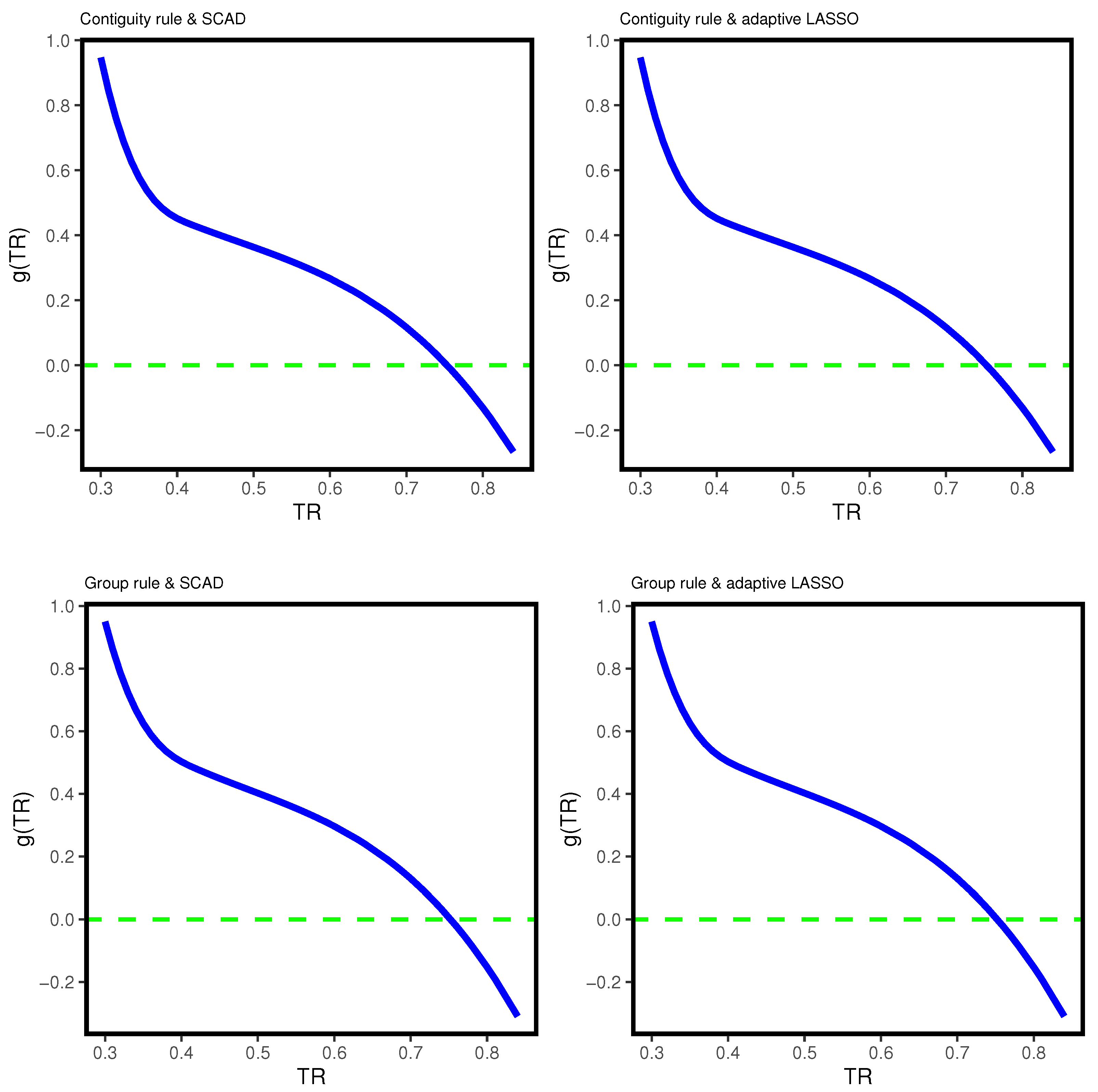
4.3.2. Analysis of Heterogeneity in Provincial Economic Growth Contributions to Carbon Emissions
- (i)
- “Strong dependency” stage: When TR , and the coefficient of per capita GDP is greater than 0.4.
- (ii)
- “Weak dependency” stage: When TR , with the coefficient of per capita GDP is approximately between 0.2 and 0.4.
- (iii)
- “Economic carbon peak” stage: When TR , indicating a per capita GDP coefficient of less than 0.2.
4.3.3. Analysis of Other Factors
5. Conclusions and Policy Suggestions
5.1. Main Conclusions
5.2. Policy Suggestions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jalil, A.; Mahmud, S.F. Environment Kuznets curve for CO2 emissions: A cointegration analysis for China. Energy Policy 2009, 37, 5167–5172. [Google Scholar] [CrossRef]
- Liu, H.; Yan, Q.; Sun, Y. Environmental Kuznets curve of CO2 emissions in China-empirical estimation based on time Series and panel Data. Forum Sci. Technol. China 2009, 180, 108–113. (In Chinese) [Google Scholar]
- Tapio, P. Towards a theory of decoupling: Degrees of decoupling in the EU and the case of road traffic in Finland between 1970 and 2001. Transp. Policy 2005, 12, 137–151. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Y.Z.; Wang, R.; Zhang, J.; Peng, J. The decoupling relationship of carbon emissions in Chinese counties and the evolution of its spatio-temporal characteristics. Resour. Sci. 2022, 44, 744–755. (In Chinese) [Google Scholar]
- Hu, H.; Zuo, W.; Xu, S. Study on the decoupling effect and driving factors of carbon emissions from transportation and energy in the Yangtze River Economic Zone. Resour. Environ. Yangtze River Basin 2022, 31, 862–877. (In Chinese) [Google Scholar]
- Dietz, T.; Rosa, E.A. Effects of population and affluence on CO2 emissions. Proc. Natl. Acad. Sci. USA 1997, 94, 175–179. [Google Scholar] [CrossRef]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Shi, A. The impact of population pressure on global carbon dioxide emissions, 1975–1996: Evidence from pooled cross-country data. Ecol. Econ. 2003, 44, 29–42. [Google Scholar] [CrossRef]
- Cole, M.A.; Neumayer, E. Examining the Impact of Demographic Factors on Air Pollution. Popul. Environ. 2004, 26, 5–21. [Google Scholar] [CrossRef]
- Fan, Y.; Liu, L.; Wu, G.; Wei, Y. Analyzing impact factors of CO2 emissions using the STIRPAT model. Environ. Impact Assess. Rev. 2006, 26, 377–395. [Google Scholar] [CrossRef]
- Haseeb, M.; Haseeb, S.; Azam, M. Rural-urban transformation, energy consumption, economic growth, and CO2 emissions using STRIPAT model for BRICS countries. Environ. Prog. Sustain. Energy 2017, 36, 523–531. [Google Scholar] [CrossRef]
- Khan, K.; Su, C.W. Urbanization and carbon emissions: A panel threshold analysis. Environ. Sci. Pollut. Res. 2021, 28, 26073–26081. [Google Scholar] [CrossRef]
- Li, H.; Mu, H.; Zhang, M.; Li, N. Analysis on influence factors of China’s CO2 emissions based on Path-STIRPAT model. Energy Policy 2011, 39, 6906–6911. [Google Scholar] [CrossRef]
- Zhu, Q.; Peng, X. The impacts of population change on carbon emissions in China during 1978–2008. Environ. Impact Assess. Rev. 2012, 36, 1–8. [Google Scholar] [CrossRef]
- Li, H.; Mu, H.; Zhang, M.; Gui, S. Analysis of regional difference on impact factors of China’s energy—Related CO2 emissions. Energy 2012, 39, 319–326. [Google Scholar] [CrossRef]
- Liu, R.; Fang, Y.; Peng, S.; Benani, N.; Wu, X.; Chen, Y.; Wang, T.; Chai, Q.; Yang, P. Study on factors influencing carbon dioxide emissions and carbon peak heterogenous pathways in Chinese provinces. J. Environ. Manag. 2024, 365, 121667. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, X. An empirical study on the influencing factors of China’s carbon emissions–Based on fixed-effects panel quantile regression model. J. Shanxi Univ. Soc. Sci. 2021, 44, 86–96. (In Chinese) [Google Scholar]
- Li, J.; Huang, X.; Yang, H.; Chuai, X.; Wu, C. Convergence of carbon intensity in the Yangtze River Delta, China. Habitat Int. 2017, 60, 58–68. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Yang, H.; Chuai, X.; Yang, H. The impact of land urbanization on carbon dioxide emissions in the Yangtze River Delta, China: A multiscale perspective. Cities 2021, 116, 103275. [Google Scholar] [CrossRef]
- Wang, P.; Wu, W.; Zhu, B.; Wei, Y. Examining the impact factors of energy-related CO2 emissions using the STIRPAT model in Guangdong Province, China. Appl. Energy 2013, 106, 65–71. [Google Scholar] [CrossRef]
- Shi, K.; Yu, B.; Zhou, Y.; Chen, Y.; Yang, C.; Chen, Z.; Wu, J. Spatiotemporal variations of CO2 emissions and their impact factors in China: A comparative analysis between the provincial and prefectural levels. Appl. Energy 2019, 233, 170–181. [Google Scholar] [CrossRef]
- Qi, H.; Shen, X.; Long, F. Research on spatio-temporal pattern and influencing factors of carbon emissions in Zhejiang Province counties. Resour. Environ. Yangtze River Basin 2023, 32, 821–831. (In Chinese) [Google Scholar]
- Chen, B.; Zhang, L. Analysis of the influence of financial development on carbon emissions under the dynamic space perspective. Soft Sci. 2014, 28, 140–144. (In Chinese) [Google Scholar]
- Du, J.; Sun, X.; Cao, R.; Zhang, Z. Statistical inference for partially linear additive spatial autoregressive models. Spat. Stat. 2018, 25, 52–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, D. Estimation of semi-parametric varying-coefficient spatial panel data models with random-effects. J. Stat. Plan. Inference 2015, 159, 64–80. [Google Scholar] [CrossRef]
- Tian, R.; Xia, M.; Xu, D. Profile quasi-maximum likelihood estimation for semiparametric varying-coefficient spatial autoregressive panel models with fixed effects. Stat. Pap. 2024; published online. [Google Scholar]
- Shan, Y.; Liu, J.; Liu, Z.; Xu, X.; Shao, S.; Wang, P.; Guan, D. New provincial CO2 emission inventories in China based on apparent energy consumption data and updated emission factors. Appl. Energy 2016, 184, 742–750. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, D.; Zheng, H.; Ou, J.; Li, Y.; Meng, J.; Mi, Z.; Liu, Z.; Zhang, Q. China CO2 emission accounts 1997–2015. Sci. Data 2018, 5, 170201. [Google Scholar] [CrossRef]
- Shan, Y.; Huang, Q.; Guan, D.; Hubacek, K. China CO2 emission accounts 2016–2017. Sci. Data 2020, 7, 54. [Google Scholar] [CrossRef]
- Guan, Y.; Shan, Y.; Huang, Q.; Wang, D.; Hubacek, K. Assessment to China’s Recent Emission Pattern Shifts. Earth’s Future 2021, 9, 1–13. [Google Scholar] [CrossRef]
- Zhang, Y. The impact of financial development on carbon emissions: An empirical analysis in China. Energy Policy 2011, 39, 2197–2203. [Google Scholar] [CrossRef]
- Pesaran, M.H. Estimation and Inference in Large Heterogeneous Panels with a Multifactor Error Structure. Econometrica 2006, 74, 967–1012. [Google Scholar] [CrossRef]
- Pesaran, M.H. A simple panel unit root test in the presence of cross-section dependence. J. Appl. Econom. 2007, 22, 265–312. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the LASSO. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zou, H. The Adaptive Lasso and Its Oracle Properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Cheng, S. A penalized quasi-maximum likelihood method for variable selection in the spatial autoregressive model. Spat. Stat. 2018, 25, 86–104. [Google Scholar] [CrossRef]
- Xia, M.; Zhang, Y.; Tian, R. Variable selection of high-dimensional spatial autoregressive panel models with fixed effects. J. Math. 2023, 2023, 9837117. [Google Scholar] [CrossRef]



| Primary Indicators | Sub Indicators | Unit | Symbol |
|---|---|---|---|
| Carbon emission | - | million tons | CE |
| Economic growth | Per capita GDP | 10k Yuan | GDP |
| Industrial structure | The proportion of the GDP contributed by the tertiary industry | - | TR |
| Wealth | Per capita disposable income | 10k Yuan | DI |
| Per capita fixed asset investment | 10k Yuan | FI | |
| Finance | Financial interrelation ratio | - | FIR |
| Financial efficiency | - | FE | |
| Transportation | Mileage of highways | 10k km | MH |
| Greening level | Afforestation area | 1000 acres | AFF |
| Technology | Per capita fixed asset investment in the state-owned energy industry | 10k Yuan | EFI |
| Per capita technology market transaction volume | 10k Yuan | TM | |
| Patents for inventions authorized per 10k persons | items per 10k persons | PA | |
| Population | Size of population | 10k persons | PO |
| Urbanization rate | - | UR |
| Indicators | Unit | Mean | Standard Deviation | Maximum | Minimum |
|---|---|---|---|---|---|
| CE | million tons | 312.442 | 263.806 | 1700.040 | 7.550 |
| GDP | 10k Yuan | 3.012 | 1.895 | 11.524 | 0.424 |
| TR | - | 0.439 | 0.093 | 0.840 | 0.300 |
| DI | 10k Yuan | 1.703 | 0.741 | 5.261 | 0.722 |
| FI | 10k Yuan | 2.101 | 1.261 | 6.500 | 0.222 |
| FIR | - | 3.026 | 1.067 | 7.552 | 1.445 |
| FE | - | 0.763 | 0.124 | 1.244 | 0.455 |
| MH | 10k km | 13.008 | 7.561 | 33.710 | 0.780 |
| AFF | 1000 acres | 192.216 | 168.761 | 861.900 | 0.710 |
| EFI | 10k Yuan | 0.074 | 0.067 | 0.406 | 0.013 |
| TM | 10k Yuan | 0.061 | 0.193 | 1.852 | 0.000 |
| PA | items per 10k persons | 1.176 | 2.507 | 24.259 | 0.024 |
| PO | 10k persons | 4469.157 | 2684.577 | 11,521.000 | 539.000 |
| UR | - | 0.539 | 0.143 | 0.900 | 0.263 |
| Variables | Level | First-Order Difference | ||
|---|---|---|---|---|
| p-Value | Stationarity | p-Value | Stationarity | |
| ln CE | >0.1 | not stationary | <0.01 | stationary |
| ln GDP | >0.1 | not stationary | 0.011 | stationary |
| ln TR | >0.1 | not stationary | 0.048 | stationary |
| ln DI | >0.1 | not stationary | <0.01 | stationary |
| ln FI | >0.1 | not stationary | 0.073 | stationary |
| ln FIR | >0.1 | not stationary | <0.01 | stationary |
| ln FE | >0.1 | not stationary | <0.01 | stationary |
| ln MH | <0.01 | stationary | <0.01 | stationary |
| ln AFF | >0.1 | not stationary | <0.01 | stationary |
| ln EFI | >0.1 | not stationary | <0.01 | stationary |
| ln TM | >0.1 | not stationary | <0.01 | stationary |
| ln PA | >0.1 | not stationary | <0.01 | stationary |
| ln PO | >0.1 | not stationary | 0.097 | stationary |
| ln UR | >0.1 | not stationary | <0.01 | stationary |
| Estimator | Indicator | Contiguity Rule | Group Rule | ||
|---|---|---|---|---|---|
| Adaptive LASSO | SCAD | Adaptive LASSO | SCAD | ||
| - | 0.0260 | 0.0263 | 0.0257 | 0.0258 | |
| (0.0018) | (0.0018) | (0.0017) | (0.0017) | ||
| - | 0.2892 | 0.2660 | 0.2513 | 0.2644 | |
| (0.0225) | (0.0346) | (0.0294) | (0.0578) | ||
| ln DI | 0.0336 | 0 | 0.1157 | 0.1301 | |
| (0.0033) | (-) | (0.0019) | (0.0273) | ||
| ln FI | 0 | 0 | 0 | 0 | |
| (-) | (-) | (-) | (-) | ||
| ln FIR | 0.3586 | 0.3837 | 0.3410 | 0.3600 | |
| (0.0215) | (0.0834) | (0.0302) | (0.0845) | ||
| ln FE | −0.1781 | −0.2082 | −0.142 | −0.0015 | |
| (0.0118) | (0.0195) | (0.0129) | (−0.0004) | ||
| ln MH | −0.0710 | 0 | −0.1029 | −0.1142 | |
| (−0.0062) | (-) | (0.0125) | (0.0213) | ||
| ln AFF | −0.0657 | −0.0559 | −0.0713 | −0.0746 | |
| (0.0043) | (0.0018) | (0.0068) | (0.0104) | ||
| ln EFI | 0 | 0 | 0 | 0 | |
| (-) | (-) | (-) | (-) | ||
| ln TM | 0 | −0.0045 | −0.0155 | −0.0143 | |
| (-) | (0.0005) | (0.0019) | (0.0012) | ||
| ln PA | 0 | 0 | 0 | 0 | |
| (-) | (-) | (-) | (-) | ||
| ln PO | 1.1827 | 1.2072 | 0.8170 | 0.8472 | |
| (0.0728) | (0.2266) | (0.0690) | (0.2300) | ||
| ln UR | 0 | 0 | 0 | 0 | |
| (-) | (-) | (-) | (-) | ||
| R-squred | - | 0.9618 | 0.9614 | 0.9623 | 0.9621 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, R.; Xia, M.; Zhang, Y.; Xu, D.; Lu, S. A Study on the Heterogeneity of China’s Provincial Economic Growth Contribution to Carbon Emissions. Systems 2024, 12, 391. https://doi.org/10.3390/systems12100391
Tian R, Xia M, Zhang Y, Xu D, Lu S. A Study on the Heterogeneity of China’s Provincial Economic Growth Contribution to Carbon Emissions. Systems. 2024; 12(10):391. https://doi.org/10.3390/systems12100391
Chicago/Turabian StyleTian, Ruiqin, Miaojie Xia, Yuqi Zhang, Dengke Xu, and Shan Lu. 2024. "A Study on the Heterogeneity of China’s Provincial Economic Growth Contribution to Carbon Emissions" Systems 12, no. 10: 391. https://doi.org/10.3390/systems12100391
APA StyleTian, R., Xia, M., Zhang, Y., Xu, D., & Lu, S. (2024). A Study on the Heterogeneity of China’s Provincial Economic Growth Contribution to Carbon Emissions. Systems, 12(10), 391. https://doi.org/10.3390/systems12100391






