1. Introduction
With the rapid development of artificial intelligence, information processing has become more complex and diversified in meeting the actual needs of decision-making evaluations. Natural language processing is an important part of artificial intelligence. How human cognition information is processed will affect the evaluation results of multi-criteria decision-analysis (MCDA) problems. Risk analysis is the first step in identifying a potential accident scenario [
1]. The failure modes and effects analysis (FMEA) method, which originated in the US military in the 1960s, is a preventive risk-assessment tool widely used for qualitative assessment in MCDA. The risk-priority number (RPN) approach in FMEA is mainly used for ranking possible risk-failure items. The RPN approach is a natural language-processing method which uses the product of the three risk-assessment factors—severity (
S), occurrence (
O), and detection (
D)—to calculate the RPN value. The risk factors
S,
O, and
D use a semantic term set of 1 to 10 to represent the level of risk. Many scholars have combined FMEA and different algorithms to deal with issues related to risk assessment in different industries. For example, Chang et al. [
2] combined the hesitant fuzzy linguistic-term sets and the ordered weighted geometric operator to process the risk-assessment problems of extreme low-k dielectric integration. Aydin et al. [
3] combined the best-worst method and the picture fuzzy set–based approach to solving the risk-assessment problems of the oil and gas industry. Huang et al. [
4] combined interactive multi-criteria decision-making and the probabilistic linguistic term-sets method to process the risk-assessment problems of enterprise architecture and information systems. To this day, many scholars have extended the application of the FMEA method to solve decision-related issues in many different industries, such as aircraft maintenance and repair [
5], zero-carbon measures [
6], the self-service electric car [
7], high temperature superconducting devices [
8], clean energy development [
9], the lead-acid battery [
10], and risk analysis of submarine pipelines [
11]. Although the typical RPN approach is simple to calculate and widely used in different fields, it cannot effectively deal with fuzzy information (FI), intuitionistic FI, and Pythagorean FI, which are types of human cognitive information.
To grasp uncertain information in daily life, Atanassov [
12] first introduced the concepts of intuitionistic fuzzy sets (IFSs). The characterized IFSs use membership grade (MG) and non-membership grade (NMG) to describe fuzzy phenomena in daily life, limiting the sum of MG and NMG to less than or equal to 1. As an extension of the original fuzzy set and IFS, the Pythagorean fuzzy set (PFS) can provide a larger solution space and better deal with uncertain information and FI when solving practical MCDA problems. Meanwhile, the characterized PFSs use the MG and the NMG to describe fuzzy phenomena in daily life, limiting the square sum of MG and NMG to less than or equal to 1. To this day, PFSs have been widely used in many different industries and fields, such as cotton fabric selection [
13], security threats of computers [
14], childhood cancer risk assessment [
15], lean manufacturing [
16], internet finance service [
17], and sustainable supplier evaluation problems [
18].
The key point of MCDA problems lies in the way multiple criteria are evaluated. Many scholars use different research methods to solve complex MCDA problems, such as the combined compromise solution (CoCoSo) method [
19], simple weighted sum product (simple WISP) method [
20], soft analytic network process method [
21], neutrosophic set method [
22], analytical hierarchy-process (AHP) method [
23], the Serbian term ‘VlseKriterijumska Optimizacija I Kompromisno Resenje’ (VIKOR) method [
24], multiobjective optimization by ratio analysis plus the full multiplicative form (MULTIMOORA) method [
25], and so on. The relative weight consideration of risk-assessment factors is the main key to influencing the risk-ranking results of the basic elements of risk failure. However, the typical RPN method ignores the weight considerations between different risk-assessment factors, resulting in incorrect evaluation results. In order to effectively handle the weight considerations between different risk-assessment factors of MCDA problems, Yazdani et al. [
19] first proposed the concept of the CoCoSo method, which uses the arithmetic weighted sum, the geometric weighted sum, and three different appraisal score strategies for ranking possible alternatives. Bouraima et al. [
26] combined the interval rough number, stepwise weight assessment ratio analysis, and the CoCoSo method to perform the sustainable transportation assessment of railway systems in West Africa. Extending the concept of the CoCoSo method, Zafaranlouei et al. [
27] combined the base-criterion method and the fuzzy Z-numbers method to solve the problem of sustainable waste management. Chang [
28] combined the CoCoSo method, subjective-objective weights consideration, and the 2-tuple linguistic representation method to handle supplier-selection issues. To this day, the CoCoSo method has been extended to handle MCDA problems in different domains, such as railway transportation systems [
26], doctor selection [
29], risk assessment of gas pipeline construction [
30], third-party reverse logistics [
31], and the application of unmanned aerial vehicles in traffic management [
32].
When risk-assessment operations are performed, cognitive information provided by experts is sometimes hesitant. However, the conventional risk-evaluation approach cannot handle hesitant cognitive information. To effectively overcome the limitation of the conventional risk-evaluation approach—such as the inability to handle FI, intuitionistic FI, and Pythagorean FI of human cognitive information, ignoring the relative-weight considerations between evaluation criteria, and the inability to process hesitant information from experts—this paper introduced a novel PFS-based risk-ranking method to handle human cognitive information in MCDA problems. The proposed PFS-based risk-ranking method uses the PFS method to simultaneously process complete information, FI, intuitionistic FI, and Pythagorean FI. For the risk-assessment factor consideration, the proposed PFS-based risk-ranking method uses the CoCoSo approach to consider the relative weight between risk-assessment factors. In processing hesitant information, the maximum operator, average operator, and minimum operator of the hesitation-interval value are used to calculate the risk-failure item ranking of different operators.
The remainder of this paper is structured as follows. In
Section 2, we briefly review and introduce the basic concepts and operation rules related to IFSs, PFSs, and the CoCoSo method.
Section 3 discusses the PFS-based risk-ranking approach for handling human cognitive information in risk-assessment problems. In
Section 4, a practical healthcare waste-hazards risk-ranking example is used to illustrate the calculation process of the proposed risk-ranking method based on PFS and verify the effectiveness and correctness of the proposed method.
Section 5 summarizes the conclusions and provides suggestions for future research.
3. Proposed Novel Pythagorean Fuzzy Set–Based Risk-Ranking Method
Accurate risk assessment results use limited resources to prevent the occurrence of possible malfunctioning projects, ensuring that the product or system achieves the expected function. Risk-assessment problems are considered multi-expert and MCDA problems. The processing method of human cognitive information is a key problem in risk assessment, influencing the risk-ranking results. Due to its simple calculation, the RPN approach is the most widely used risk-assessment method. However, it can only handle complete information from experts and cannot handle FI, intuitionistic FI, and Pythagorean FI provided by experts. In addition, the RPN approach cannot handle hesitant information from experts and process the relative weight between possible evaluation criteria. These gaps can lead to incorrect risk-ranking results. To ensure correct and effective processing of risk ranking problems, this paper integrates PFSs and the CoCoSo method in handling human cognitive information. PFSs can process human cognitive information from a wide range of MCDA problems, unlike IFSs and typical fuzzy sets. The proposed novel PFS-based risk-ranking method uses the CoCoSo method to consider the relative weight of possible evaluation criteria. In dealing with hesitant information provided by experts, the proposed method uses the maximum operator, average operator, and minimum operator of the hesitation-interval value to perform calculations of different operators.
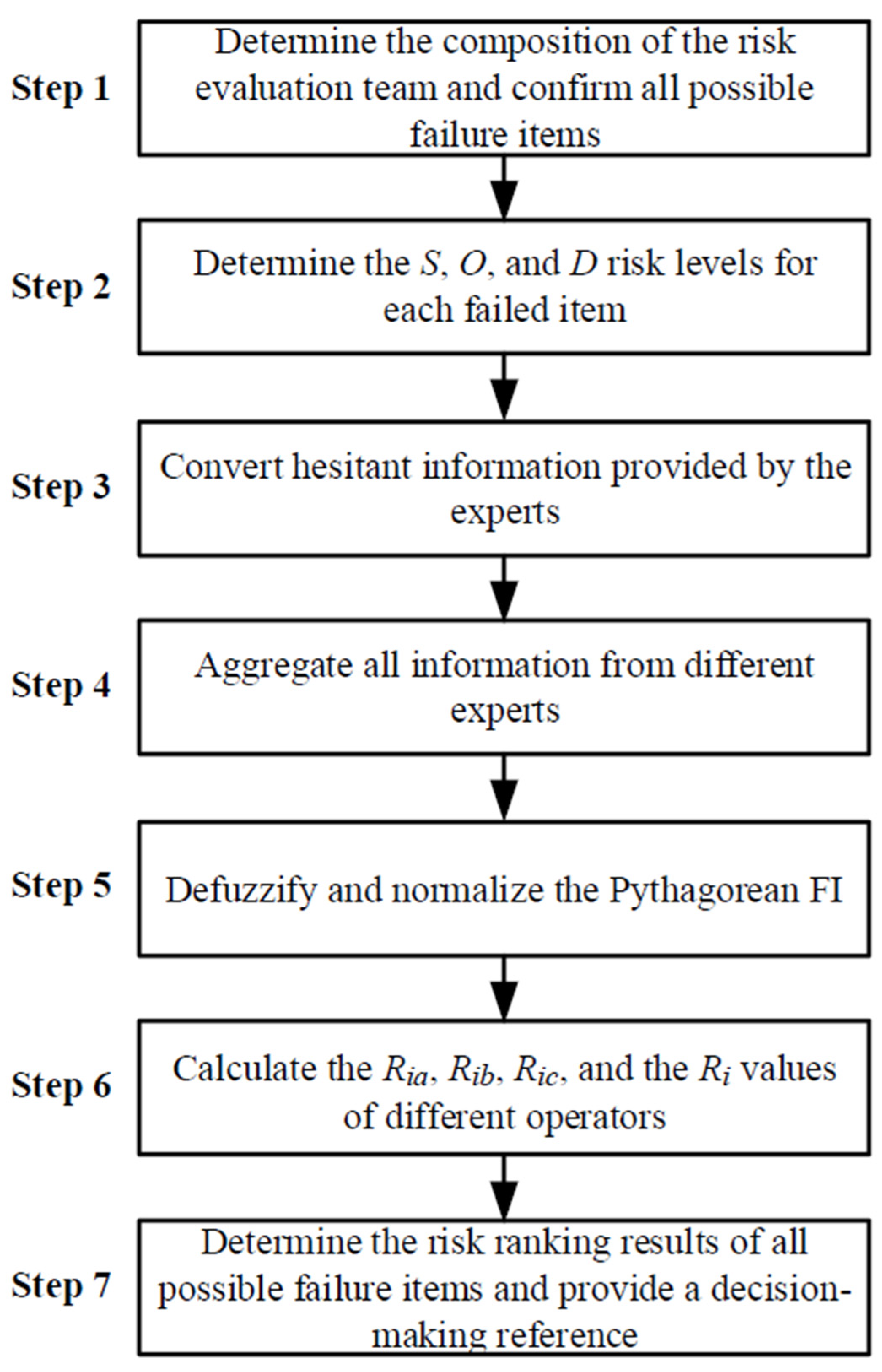
The proposed novel PFS-based risk-ranking method calculation has 7 steps; the flowchart is presented in
Figure 1.
According to the expertise and experience of the experts, form a cross-disciplinary risk-evaluation team in which team members can discuss all possible failure items together.
Each expert determines the risk levels of the three risk factors (
S,
O, and
D) for each failed item based on their past experience. The conversion between the risk levels, linguistic terms, and the PFN is shown in
Table 1.
For example, in
Table 1, an expert determines the risk level of the risk factors (
S,
O, and
D) as s1, for which the corresponding linguistic term is extremely very low (EVL). Then the corresponding PFN is (0.05, 1.00).
To deal with the hesitation information that experts provide, use the maximum operator, average operator, and minimum operator of the hesitation-interval value to replace the original hesitant information.
Use Equation (11) to aggregate all information from different experts.
Use Equation (12) to defuzzify the initial PFS decision matrix. Then, use Equations (15) and (16) to normalize the PFS decision matrix.
Based on the maximum operator, average operator, and minimum operator, use Equations (19)–(22) to calculate the , , , and the values for the different operators, respectively.
The values from large to small indicate the results of the risk ranking of all possible failure projects. This risk-ranking result provides a reference for decision-making.
Figure 1.
The flowchart of the proposed novel PFS-based risk-ranking method.
Figure 1.
The flowchart of the proposed novel PFS-based risk-ranking method.
5. Conclusions
How human cognitive information is processed is a key issue in risk assessment. With the advent of artificial intelligence, processing human cognitive information has become more important because it will directly affect the results of decision-making evaluations. Because the typical RPN method is relatively simpler to calculate than other risk-assessment methods, it is currently the most widely used risk-assessment tool. However, the typical RPN method is also accompanied by many limitations, such as the inability to handle FI, intuitionistic FI, and Pythagorean FI of human cognition. Further, the RPN method cannot process the relative weights between evaluation criteria, which may lead to biased evaluation results.
Therefore, to strengthen the ability of risk assessments, this paper integrates the PFSs and the CoCoSo method to process the risk-ranking problems of potential failure items. PFSs provide a wider solution space than the original fuzzy set and IFSs and can comprehensively deal with all kinds of uncertain information in real life. The CoCoSo method can consider different weight-calculation approaches to handle the relative weights between different risk-assessment factors. In dealing with hesitation information provided by experts, the maximum operator, average operator, and minimum operator are applied to compute the risk-ranking results of all possible failure projects. This risk-ranking result provides a reference for decision-making.
The proposed novel Pythagorean fuzzy set–based risk-ranking method contains the following advantages:
- (1)
The proposed method can simultaneously process complete information, FI, intuitionistic FI, and Pythagorean FI.
- (2)
The proposed method can handle hesitant cognitive information.
- (3)
The proposed method takes into account the relative weights of risk-assessment factors.
Although the proposed novel Pythagorean fuzzy set-based risk-ranking method can effectively handle human cognitive information in risk-assessment problems, however, the proposed method still has the limitation that it cannot handle the incomplete information provided by experts. Future research directions can expand upon the discussion of how to deal with the incomplete information provided by experts. Subsequent researchers can extend the proposed method to deal with decision-making issues in different fields, such as green energy planning, investment selection, performance evaluation, reliability evaluation, and supplier selection. They can also use different algorithms to calculate the subjective and objective weights between evaluation criteria and explore the influence of different combinations of subjective and objective weights on the evaluation results.