Evaluation of Enterprise Decarbonization Scheme Based on Grey-MEREC-MAIRCA Hybrid MCDM Method
Abstract
1. Introduction
2. Literature Review
2.1. Enterprise Decarbonization
2.2. MEREC with Related MCDM Methods
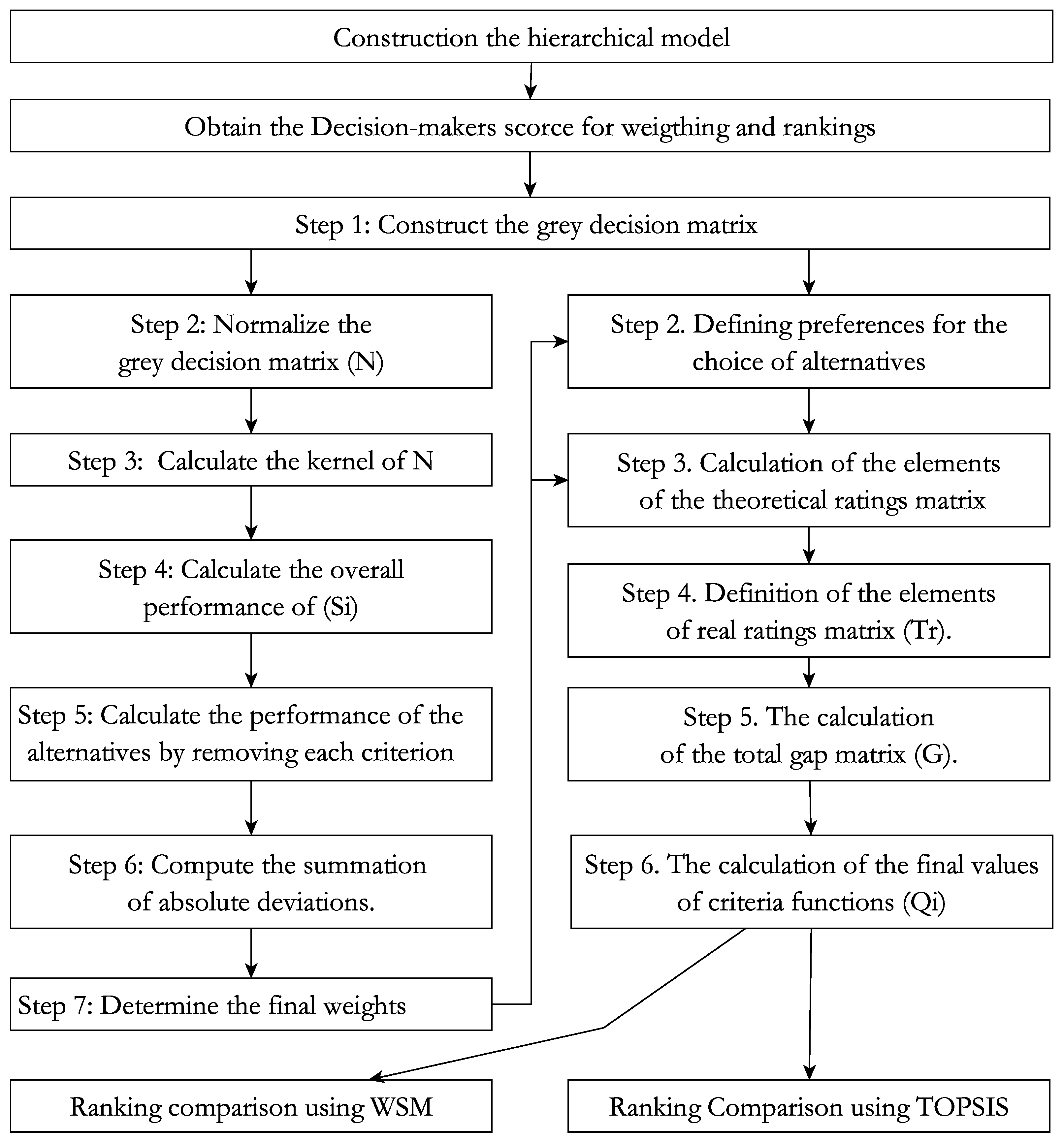
3. Methodology
3.1. Evaluation Criteria
3.1.1. Carbon Emission ()
3.1.2. Energy Efficiency ()
3.1.3. Technological Advancement ()
3.1.4. Environment Management ()
3.1.5. Corporate Social Responsibility ()
3.2. Grey-MEREC
- Addition:
- Subtraction:
- Multiplication:
- Division: .
- The local weights are calculated using Equation (7).
- The effective weight is obtained by multiplying the local weight of the first-level criteria with the local weight of the second-level criteria. Equation (8) represents this calculation.
3.3. Grey-MAIRCA
4. Result and Analysis
4.1. Grey-MEREC for Group DM Weighting
4.2. Grey-MAIRCA for Ranking Enterprise
4.3. Comparison of Using the Weighted Sum Model and TOPSIS
4.3.1. WSM for Ranking Enterprise
4.3.2. TOPSIS for Ranking Enterprise
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARAS | Additive Ratio Assessment |
| AROMAN | A Ranking Order Method Accounting for Two-Step Normalization |
| BESS | Battery Energy Storage Systems |
| CoCoSo | Combined Compromise Solution |
| COPRAS | COmplex PRoportional ASsessment of alternatives |
| CPT | Cumulative Prospect Theory |
| CRITIC | Criteria Importance Through the Inter-criteria Correlation |
| DMs | Decision-Makers |
| DNMA | Double Normalization-Based Multiple Aggregation |
| EAMR | Evaluation by an Area-based Method of Ranking |
| EVs | Electric Vehicles |
| GRA | Grey Relational Analysis |
| GST | Grey System Theory |
| MAIRCA | Multi-Attribute Ideal-Real Comparative Analysis |
| MARCOS | Measurement Alternatives and |
| Ranking according to the Compromise Solution | |
| MCDM | Multi-Criteria Decision Making |
| MEREC | Method based on the Removal Effects of Criteria |
| MULTIMOORA | Multiplicative Multi-Objective Optimization by Ratio Analysis |
| NETs | Negative Emission Technologies |
| PWA | Power Weighted Average |
| q-ROFS | Q-Rung Orthopair Fuzzy Set |
| SMART | Simple Multi-Attribute Rating Technique Extended to Ranking |
| SSD | Solid-State Drive |
| SVNN | Single-Valued Neutrosophic |
| SWARA | Stepwise Weight Analysis Ratio Assessment |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
| WASPAS | Weighted Aggregated Sum Product Assessment |
| VIKOR | VIseKriterijumska Optimizacija I Kompromisno Resenje |
| (Multicriteria Optimization and Compromise Solution) |
References
- Chen, T.; Yu, J.; Keyes, N. China’s Transition to a Low-Carbon Economy and Climate Resilience Needs Shifts in Resources and Technologies. 2023. Available online: https://www.worldbank.org/en/news/press-release/2022/10/12/china-s-transition-to-a-low-carbon-economy-and-climate-resilience-needs-shifts-in-resources-and-technologies (accessed on 25 June 2023).
- Alinezhad, A.; Khalili, J. New Methods and Applications in Multiple Attribute Decision Making (MADM); International Series in Operations Research & Management Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 277. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Hashemi-Madani, F.S.; Forghani, A. Comparison of Compensatory and Non-Compensatory Multi Criteria Decision Making Models in Water Resources Strategic Management. Water Resour. Manag. 2017, 31, 3745–3759. [Google Scholar] [CrossRef]
- Esangbedo, M.O.; Che, A. Grey Weighted Sum Model for Evaluating Business Environment in West Africa. Math. Probl. Eng. 2016, 2016, 3824350. [Google Scholar] [CrossRef][Green Version]
- Douissa, M.R.; Jabeur, K. A Non-Compensatory Classification Approach for Multi-Criteria ABC Analysis. Soft Comput. 2020, 24, 9525–9556. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Chitsaz, N.; Randhir, T.O. Non-Compensatory Decision Model for Incorporating the Sustainable Development Criteria in Flood Risk Management Plans. SN Appl. Sci. 2020, 2, 6. [Google Scholar] [CrossRef]
- Dotoli, M.; Epicoco, N.; Falagario, M. Multi-Criteria Decision Making Techniques for the Management of Public Procurement Tenders: A Case Study. Appl. Soft Comput. 2020, 88, 106064. [Google Scholar] [CrossRef]
- Deng, J. The Primary Methods of Grey System Theory; Huazhong University of Science and Technology Press: Wuhan, China, 2005. [Google Scholar]
- Cao, Q.; Esangbedo, M.O.; Bai, S.; Esangbedo, C.O. Grey SWARA-FUCOM Weighting Method for Contractor Selection MCDM Problem: A Case Study of Floating Solar Panel Energy System Installation. Energies 2019, 12, 2481. [Google Scholar] [CrossRef]
- Esangbedo, M.O.; Xue, J.; Bai, S.; Esangbedo, C.O. Relaxed Rank Order Centroid Weighting MCDM Method With Improved Grey Relational Analysis for Subcontractor Selection: Photothermal Power Station Construction. In IEEE Transactions on Engineering Management; IEEE: Piscataway, NJ, USA, 2022; pp. 1–18. [Google Scholar] [CrossRef]
- Esangbedo, M.O.; Bai, S. Scaling Foreign-Service Premium Allowance Based on SWARA and GRA with Grey Numbers. J. Grey Syst. 2020, 32, 38–58. [Google Scholar]
- Zhou, H.; Ping, W.; Wang, Y.; Wang, Y.; Liu, K. China’s Initial Allocation of Interprovincial Carbon Emission Rights Considering Historical Carbon Transfers: Program Design and Efficiency Evaluation. Ecol. Indic. 2021, 121, 106918. [Google Scholar] [CrossRef]
- Xu, J.; Cao, J.; Wang, Y.; Shi, X.; Zeng, J. Evolutionary Game on Government Regulation and Green Supply Chain Decision-Making. Energies 2020, 13, 620. [Google Scholar] [CrossRef]
- Yi, Y.; Li, J. The Effect of Governmental Policies of Carbon Taxes and Energy-Saving Subsidies on Enterprise Decisions in a Two-Echelon Supply Chain. J. Clean. Prod. 2018, 181, 675–691. [Google Scholar] [CrossRef]
- Zhang, H.; Li, P.; Zheng, H.; Zhang, Y. Impact of Carbon Tax on Enterprise Operation and Production Strategy for Low-Carbon Products in a Co-Opetition Supply Chain. J. Clean. Prod. 2021, 287, 125058. [Google Scholar] [CrossRef]
- Rockström, J.; Gaffney, O.; Rogelj, J.; Meinshausen, M.; Nakicenovic, N.; Schellnhuber, H.J. A Roadmap for Rapid Decarbonization. Science 2017, 355, 1269–1271. [Google Scholar] [CrossRef]
- Griscom, B.W.; Adams, J.; Ellis, P.W.; Houghton, R.A.; Lomax, G.; Miteva, D.A.; Schlesinger, W.H.; Shoch, D.; Siikamäki, J.V.; Smith, P.; et al. Natural Climate Solutions. Proc. Natl. Acad. Sci. USA 2017, 114, 11645–11650. [Google Scholar] [CrossRef] [PubMed]
- Davis, S.J.; Lewis, N.S.; Shaner, M.; Aggarwal, S.; Arent, D.; Azevedo, I.L.; Benson, S.M.; Bradley, T.; Brouwer, J.; Chiang, Y.M.; et al. Net-Zero Emissions Energy Systems. Science 2018, 360, eaas9793. [Google Scholar] [CrossRef]
- Minx, J.C.; Lamb, W.F.; Callaghan, M.W.; Fuss, S.; Hilaire, J.; Creutzig, F.; Amann, T.; Beringer, T.; Garcia, W.d.O.; Hartmann, J.; et al. Negative Emissions—Part 1: Research Landscape and Synthesis. Environ. Res. Lett. 2018, 13, 063001. [Google Scholar] [CrossRef]
- Creutzig, F.; Roy, J.; Lamb, W.F.; Azevedo, I.M.L.; Bruine de Bruin, W.; Dalkmann, H.; Edelenbosch, O.Y.; Geels, F.W.; Grubler, A.; Hepburn, C.; et al. Towards Demand-Side Solutions for Mitigating Climate Change. Nat. Clim. Chang. 2018, 8, 260–263. [Google Scholar] [CrossRef]
- Zvezdov, D.; Hack, S. Carbon Footprinting of Large Product Portfolios. Extending the Use of Enterprise Resource Planning Systems to Carbon Information Management. J. Clean. Prod. 2016, 135, 1267–1275. [Google Scholar] [CrossRef]
- Ma, Y.; Tao, P. A Perspective on Management Myopia: The Impact of Digital Transformation on Carbon Emission Intensity. Sustainability 2023, 15, 9417. [Google Scholar] [CrossRef]
- Grubler, A.; Wilson, C.; Bento, N.; Boza-Kiss, B.; Krey, V.; McCollum, D.L.; Rao, N.D.; Riahi, K.; Rogelj, J.; De Stercke, S.; et al. A Low Energy Demand Scenario for Meeting the 1.5 °C Target and Sustainable Development Goals without Negative Emission Technologies. Nat. Energy 2018, 3, 515–527. [Google Scholar] [CrossRef]
- Wu, B.; Liu, P.; Xu, X. An Evolutionary Analysis of Low-Carbon Strategies Based on the Government–Enterprise Game in the Complex Network Context. J. Clean. Prod. 2017, 141, 168–179. [Google Scholar] [CrossRef]
- Fan, L.; Xu, J. Authority–Enterprise Equilibrium Based Mixed Subsidy Mechanism for Carbon Reduction and Energy Utilization in the Coalbed Methane Industry. Energy Policy 2020, 147, 111828. [Google Scholar] [CrossRef]
- Qu, X.; Sun, X. How to Improve the Function of Government Carbon Tax in Promoting Enterprise Carbon Emission Reduction: From the Perspective of Three-Stage Dynamic Game. Environ. Sci. Pollut. Res. 2022, 29, 31348–31362. [Google Scholar] [CrossRef]
- Geng, J.; Ji, M.; Yang, L. Role of Enterprise Alliance in Carbon Emission Reduction Mechanism: An Evolutionary Game Analysis. Int. J. Environ. Res. Public Health 2022, 19, 11368. [Google Scholar] [CrossRef]
- Gell, M. Carbon-Constrained Health Care Enterprise. J. Eval. Clin. Pract. 2010, 16, 220–227. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Dai, A.; Zhao, D.; Song, Q. Identifying the Influence Factors on Low-Carbon Behavior of Employees from Petrochemical Enterprise under “Carbon Neutrality”. Environ. Dev. Sustain. 2022, 1–22. [Google Scholar] [CrossRef]
- Sindhwani, R.; Singh, P.L.; Behl, A.; Afridi, M.S.; Sammanit, D.; Tiwari, A.K. Modeling the Critical Success Factors of Implementing Net Zero Emission (NZE) and Promoting Resilience and Social Value Creation. Technol. Forecast. Soc. Chang. 2022, 181, 121759. [Google Scholar] [CrossRef]
- Ayan, B.; Abacıoğlu, S.; Basilio, M.P. A Comprehensive Review of the Novel Weighting Methods for Multi-Criteria Decision-Making. Information 2023, 14, 285. [Google Scholar] [CrossRef]
- Tian, G.; Lu, W.; Zhang, X.; Zhan, M.; Dulebenets, M.A.; Aleksandrov, A.; Fathollahi-Fard, A.M.; Ivanov, M. A Survey of Multi-Criteria Decision-Making Techniques for Green Logistics and Low-Carbon Transportation Systems. Environ. Sci. Pollut. Res. 2023, 30, 57279–57301. [Google Scholar] [CrossRef] [PubMed]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of Objective Weights Using a New Method Based on the Removal Effects of Criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Simic, V.; Gokasar, I.; Deveci, M.; Svadlenka, L. Mitigating Climate Change Effects of Urban Transportation Using a Type-2 Neutrosophic MEREC-MARCOS Model. In IEEE Transactions on Engineering Management; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Deveci, M.; Gokasar, I.; Mishra, A.R.; Rani, P.; Ye, Z. Evaluation of Climate Change-Resilient Transportation Alternatives Using Fuzzy Hamacher Aggregation Operators Based Group Decision-Making Model. Eng. Appl. Artif. Intell. 2023, 119, 105824. [Google Scholar] [CrossRef]
- Nicolalde, J.F.; Cabrera, M.; Martinez-Gomez, J.; Salazar, R.B.; Reyes, E. Selection of a Phase Change Material for Energy Storage by Multi-Criteria Decision Method Regarding the Thermal Comfort in a Vehicle. J. Energy Storage 2022, 51, 104437. [Google Scholar] [CrossRef]
- Mishra, A.R.; Tripathi, D.K.; Cavallaro, F.; Rani, P.; Nigam, S.K.; Mardani, A. Assessment of Battery Energy Storage Systems Using the Intuitionistic Fuzzy Removal Effects of Criteria and the Measurement of Alternatives and Ranking Based on Compromise Solution Method. Energies 2022, 15, 7782. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Saha, A.; Hezam, I.M.; Cavallaro, F.; Chakrabortty, R.K. An Extended DNMA-based Multi-Criteria Decision-Making Method and Its Application in the Assessment of Sustainable Location for a Lithium-Ion Batteries? Manufacturing Plant. Heliyon 2023, 9, e14244. [Google Scholar] [CrossRef] [PubMed]
- Ul Haq, R.S.; Saeed, M.; Mateen, N.; Siddiqui, F.; Naqvi, M.; Yi, J.B.; Ahmed, S. Sustainable Material Selection with Crisp and Ambiguous Data Using Single-Valued Neutrosophic-MEREC-MARCOS Framework. Appl. Soft Comput. 2022, 128, 109546. [Google Scholar] [CrossRef]
- Mishra, A.R.; Saha, A.; Rani, P.; Hezam, I.M.; Shrivastava, R.; Smarandache, F. An Integrated Decision Support Framework Using Single-Valued-MEREC-MULTIMOORA for Low Carbon Tourism Strategy Assessment. IEEE Access 2022, 10, 24411–24432. [Google Scholar] [CrossRef]
- Jahan, A.; Edwards, K.L. A State-of-the-Art Survey on the Influence of Normalization Techniques in Ranking: Improving the Materials Selection Process in Engineering Design. Mater. Des. 2015, 65, 335–342. [Google Scholar] [CrossRef]
- Gardziejczyk, W.; Zabicki, P. Normalization and Variant Assessment Methods in Selection of Road Alignment Variants–Case Study. J. Civ. Eng. Manag. 2017, 23, 510–523. [Google Scholar] [CrossRef]
- Brauers, W.; Zavadskas, E. The MOORA Method and Its Application to Privatization in a Transition Economy. Control Cybern. 2006, 35, 445–469. [Google Scholar]
- Zavadskas, E.K.; Turskis, Z. A New Logarithmic Normalization Method in Games Theory. Informatica 2008, 19, 303–314. [Google Scholar] [CrossRef]
- Ivanovic, B.; Saha, A.; Stevic, Z.; Puska, A.; Zavadskas, E.K. Selection of Truck Mixer Concrete Pump Using Novel MEREC DNMARCOS Model. Arch. Civ. Mech. Eng. 2022, 22, 173. [Google Scholar] [CrossRef]
- Hezam, I.M.; Mishra, A.R.; Rani, P.; Cavallaro, F.; Saha, A.; Ali, J.; Strielkowski, W.; Streimikiene, D. A Hybrid Intuitionistic Fuzzy-MEREC-RS-DNMA Method for Assessing the Alternative Fuel Vehicles with Sustainability Perspectives. Sustainability 2022, 14, 5463. [Google Scholar] [CrossRef]
- Bošković, S.; Švadlenka, L.; Jovčić, S.; Dobrodolac, M.; Simić, V.; Bacanin, N. An Alternative Ranking Order Method Accounting for Two-Step Normalization (AROMAN)—A Case Study of the Electric Vehicle Selection Problem. IEEE Access 2023, 11, 39496–39507. [Google Scholar] [CrossRef]
- Trung, D.D.; Thinh, H.X. A Multi-Criteria Decision-Making in Turning Process Using the MAIRCA, EAMR, MARCOS and TOPSIS Methods: A Comparative Study. Adv. Prod. Eng. Manag. 2021, 16, 443–456. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Le, X.H.; Nguyen, T.T.; Tran, Q.H.; Vu, N.P. A Comparative Study on Multi-Criteria Decision-Making in Dressing Process for Internal Grinding. Machines 2022, 10, 303. [Google Scholar] [CrossRef]
- Le, H.A.; Hoang, X.T.; Trieu, Q.H.; Pham, D.L.; Le, X.H. Determining the Best Dressing Parameters for External Cylindrical Grinding Using MABAC Method. Appl. Sci. 2022, 12, 8287. [Google Scholar] [CrossRef]
- Esangbedo, M.O.; Abifarin, J.K. Cost and Quality Optimization Taguchi Design with Grey Relational Analysis of Halloysite Nanotube Hybrid Composite: CNC Machine Manufacturing. Materials 2022, 15, 8154. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, P.; Zavadskas, E.K.; Stevic, Z.; Vujovic, V. A New Joint Strategy for Multi-Criteria Decision-Making: A Case Study for Prioritizing Solid-State Drive. Int. J. Comput. Commun. Control 2022, 17. [Google Scholar] [CrossRef]
- Chaurasiya, R.; Jain, D. A New Algorithm on Pythagorean Fuzzy-Based Multi-Criteria Decision-Making and Its Application. Iran. J. Sci.-Technol.-Trans. Electr. Eng. 2023, 47, 871–886. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M. Assessment of Distribution Center Locations Using a Multi-Expert Subjective–Objective Decision-Making Approach. Sci. Rep. 2021, 11, 19461. [Google Scholar] [CrossRef]
- Yu, Y.; Wu, S.B.; Yu, J.X.; Xu, Y.; Song, L.; Xu, W.P. A Hybrid Multi-Criteria Decision-Making Framework for Offshore Wind Turbine Selection: A Case Study in China. Appl. Energy 2022, 328, 120173. [Google Scholar] [CrossRef]
- Yu, Y.; Wu, S.B.; Yu, J.X.; Chen, H.C.; Zeng, Q.Z.; Xu, Y.; Ding, H.Y. An Integrated MCDM Framework Based on Interval 2-Tuple Linguistic: A Case of Offshore Wind Farm Site Selection in China. Process Saf. Environ. Prot. 2022, 164, 613–628. [Google Scholar] [CrossRef]
- Narayanamoorthy, S.; Parthasarathy, T.N.; Pragathi, S.; Shanmugam, P.; Baleanu, D.; Ahmadian, A.; Kang, D. The Novel Augmented Fermatean MCDM Perspectives for Identifying the Optimal Renewable Energy Power Plant Location. Sustain. Energy Technol. Assess. 2022, 53, 102488. [Google Scholar] [CrossRef]
- Gligoric, Z.; Gligoric, M.; Miljanovic, I.; Lutovac, S.; Milutinovic, A. Assessing Criteria Weights by the Symmetry Point of Criterion (Novel SPC Method)-Application in the Efficiency Evaluation of the Mineral Deposit Multi-Criteria Partitioning Algorithm. CMES-Comput. Model. Eng. Sci. 2023, 136, 955–979. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Saha, A.; Hezam, I.M.; Pamucar, D. Fermatean Fuzzy Heronian Mean Operators and MEREC-based Additive Ratio Assessment Method: An Application to Food Waste Treatment Technology Selection. Int. J. Intell. Syst. 2022, 37, 2612–2647. [Google Scholar] [CrossRef]
- Miskic, S.; Tadic, S.; Stevic, A.; Krstic, M.; Roso, V. A Novel Hybrid Model for the Evaluation of Industry 4.0 Technologies’ Applicability in Logistics Centers. J. Math. 2023, 2023, 3532862. [Google Scholar] [CrossRef]
- Simic, V.; Ivanovic, I.; Doric, V.; Torkayesh, A.E. Adapting Urban Transport Planning to the COVID-19 Pandemic: An Integrated Fermatean Fuzzy Model. Sustain. Cities Soc. 2022, 79, 103669. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M. Sustainable Supplier Selection and Order Allocation Using an Integrated ROG-Based Type-2 Fuzzy Decision-Making Approach. Mathematics 2023, 11, 2014. [Google Scholar] [CrossRef]
- Deveci, M.; Mishra, A.R.; Gokasar, I.; Rani, P.; Pamucar, D.; Ozcan, E. A Decision Support System for Assessing and Prioritizing Sustainable Urban Transportation in Metaverse. IEEE Trans. Fuzzy Syst. 2023, 31, 475–484. [Google Scholar] [CrossRef]
- Liu, S.; Yang, Y.; Forrest, J. Grey Data Analysis; Computational Risk Management; Springer: Singapore, 2017. [Google Scholar] [CrossRef]
- Esangbedo, M.O.; Bai, S. Grey regulatory focus theory weighting method for the multi-criteria decision-making problem in evaluating university reputation. Symmetry 2019, 11, 230. [Google Scholar] [CrossRef]
- Pamucar, D.S.; Tarle, S.P.; Parezanovic, T. New Hybrid Multi-Criteria Decision-Making DEMATEL-MAIRCA Model: Sustainable Selection of a Location for the Development of Multimodal Logistics Centre. Econ. Res.-Ekon. Istraživanja 2018, 31, 1641–1665. [Google Scholar] [CrossRef]
- Sałabun, W.; Urbaniak, K. A New Coefficient of Rankings Similarity in Decision-Making Problems. In Lecture Notes in Computer Science, Proceedings of the Computational Science–ICCS 2020, Amsterdam, The Netherlands, 3–5 June 2020; Krzhizhanovskaya, V.V., Závodszky, G., Lees, M.H., Dongarra, J.J., Sloot, P.M.A., Brissos, S., Teixeira, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 632–645. [Google Scholar] [CrossRef]



| Weighing | Evaluation | Uncertainty | Applications | Researchers |
|---|---|---|---|---|
| Methods | Methods | Methods | ||
| MEREC | DNMARCOS | – | Truck mixer concrete pump | Ivanovic et al. [45] |
| MEREC | MULTIMOORA | Fermatean fuzzy set | Renewable energy power plant location | Narayanamoorthy et al. [57] |
| MEREC | MULTIMOORA | Single-Valued Neutrosophic Set (SVNS) | low-carbon tourism strategies) | Mishra, Saha, et al. [40] |
| MEREC | MARCOS | SVNS | Aircraft Sustainable material selection | Ul Haq et al. [39] |
| MEREC | Symmetry point of Criterion | – | Mineral deposit | Gligoric et al. [58] |
| MEREC | MABAC | Cylinder dressing parameter setting | Le et al. [50] | |
| MEREC | MARCOS | Fuzzy | Industry 4.0 in logistics center | Miskic et al. [60] |
| MEREC | CoCoSo | Fermatean Fuzzy Model | Urban transportation plan | Simic et al. [61] |
| MEREC | SMART, WASPAS | ROG for interval type-2 fuzzy sets (IFS) | Supplier selection and order allocation | Keshavarz-Ghorabaee [62] |
| MEREC, Rank Sum (RS) | DNMA | Intuitionistic Fuzzy set | Alternative fuel vehicle | Hezam et al. [46] |
| MEREC, RS | MARCOS | IFS | Battery Energy Storage Systems | Mishra et al. [37] |
| MEREC SWARA | DNMA | SVNS | Locations selection for lithium-ion batteries factory | Mishra et al. [38] |
| MEREC, SWARA | WASPAS | – | Detergent and hygienic product distribution center | Keshavarz-Ghorabaee [54] |
| SWARA, MEREC | Weighted Sum Product Method | Q-rung orthopair fuzzy set | Sustainable public transportation | Deveci et al. [63] |
| MEREC, SWARA | MARCOS | Pythagorean fuzzy method | Hospital management system | Chaurasiya & Jain [53] |
| PWA, SWARA II, MEREC | CPT & CoCoSo | Interval 2-tuple linguistic | offshore wind urbine selection | Yu et al. [55] |
| Entropy, MEREC | TOPSIS, EAMR, MAIRCA, MARCOS | – | Turning process | Trung & Thinh [48] |
| Entropy, MEREC | VIKOR, COPRAS, TOPSIS | – | Thermal Material selection for vehicle | Nicolalde et al. [36] |
| Entropy, MEREC | TOPSIS, MARCOS, EAMR | – | Dressing process for Internal grinding | Nguyen et al. [49] |
| Entropy, MEREC | ARAS | Fermatean fuzzy | food waste treatment technology selection | Rani et al. [59] |
| Entropy MEREC, CRITIC | MARCOS | – | SSD assessment | Kumar et al. [52] |
| Decision- | Criteria (m)/ | … | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Makers | Companies | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | … | (19) |
| 85 | 82 | 80 | 76 | 66 | 66 | 90 | 78 | 79 | 69 | 60 | … | 88 | ||
| 99 | 85 | 75 | 78 | 66 | 66 | 89 | 73 | 75 | 66 | 62 | … | 98 | ||
| 92 | 79 | 79 | 68 | 73 | 67 | 92 | 77 | 80 | 74 | 65 | … | 69 | ||
| 94 | 77 | 86 | 76 | 68 | 68 | 82 | 82 | 80 | 73 | 67 | … | 92 | ||
| 97 | 83 | 87 | 85 | 67 | 72 | 96 | 86 | 79 | 68 | 70 | … | 99 | ||
| 94 | 80 | 79 | 92 | 72 | 70 | 84 | 70 | 75 | 62 | 62 | … | 94 | ||
| 88 | 80 | 85 | 85 | 75 | 75 | 80 | 90 | 84 | 90 | 85 | … | 80 | ||
| 97 | 95 | 80 | 90 | 95 | 90 | 80 | 95 | 99 | 95 | 90 | … | 95 | ||
| 97 | 95 | 90 | 95 | 86 | 95 | 90 | 80 | 98 | 95 | 95 | … | 87 | ||
| 95 | 95 | 95 | 95 | 95 | 90 | 95 | 85 | 96 | 95 | 90 | … | 88 | ||
| 88 | 95 | 90 | 95 | 87 | 90 | 85 | 95 | 97 | 95 | 95 | … | 84 | ||
| 86 | 85 | 80 | 75 | 89 | 85 | 90 | 85 | 88 | 90 | 90 | … | 93 | ||
| 80 | 70 | 80 | 75 | 82 | 77 | 85 | 77 | 85 | 80 | 86 | … | 73 | ||
| 83 | 73 | 75 | 80 | 75 | 85 | 80 | 75 | 80 | 75 | 83 | … | 76 | ||
| 77 | 78 | 82 | 85 | 78 | 80 | 88 | 80 | 79 | 85 | 72 | … | 80 | ||
| 79 | 80 | 77 | 81 | 83 | 79 | 78 | 83 | 73 | 82 | 79 | … | 82 | ||
| 80 | 81 | 79 | 77 | 82 | 90 | 72 | 85 | 90 | 79 | 77 | … | 79 | ||
| 81 | 85 | 80 | 88 | 81 | 83 | 77 | 88 | 82 | 81 | 76 | … | 89 | ||
| 88 | 83 | 80 | 77 | 100 | 67 | 66 | 66 | 90 | 66 | 77 | … | 83 | ||
| 89 | 84 | 77 | 79 | 67 | 78 | 77 | 64 | 77 | 68 | 78 | … | 89 | ||
| 90 | 79 | 78 | 88 | 79 | 84 | 86 | 63 | 79 | 70 | 77 | … | 93 | ||
| 79 | 85 | 85 | 80 | 81 | 82 | 87 | 60 | 69 | 80 | 80 | … | 89 | ||
| 69 | 78 | 86 | 78 | 77 | 80 | 80 | 71 | 80 | 83 | 85 | … | 79 | ||
| 92 | 80 | 83 | 81 | 73 | 75 | 79 | 80 | 81 | 81 | 82 | … | 73 | ||
| 80 | 80 | 80 | 80 | 70 | 60 | 80 | 70 | 70 | 80 | 80 | … | 60 | ||
| 80 | 90 | 60 | 70 | 70 | 100 | 70 | 90 | 80 | 100 | 70 | … | 70 | ||
| 80 | 80 | 70 | 90 | 90 | 70 | 60 | 90 | 90 | 100 | 80 | … | 80 | ||
| 80 | 90 | 90 | 80 | 80 | 90 | 90 | 90 | 90 | 90 | 70 | … | 80 | ||
| 90 | 90 | 80 | 90 | 70 | 90 | 90 | 90 | 80 | 70 | 80 | … | 90 | ||
| 80 | 90 | 60 | 60 | 60 | 100 | 80 | 70 | 80 | 60 | 90 | … | 80 | ||
| 97 | 78 | 68 | 85 | 67 | 78 | 76 | 68 | 86 | 67 | 87 | … | 96 | ||
| 80 | 90 | 80 | 90 | 90 | 100 | 80 | 90 | 90 | 90 | 100 | … | 80 | ||
| 98 | 95 | 98 | 98 | 97 | 99 | 95 | 96 | 96 | 97 | 97 | … | 97 | ||
| 87 | 94 | 92 | 90 | 86 | 93 | 97 | 88 | 88 | 87 | 85 | … | 84 | ||
| 75 | 88 | 79 | 86 | 85 | 83 | 84 | 86 | 86 | 88 | 85 | … | 86 | ||
| 80 | 86 | 83 | 84 | 70 | 80 | 70 | 70 | 90 | 80 | 90 | … | 90 |
| Index (m) | Companies/Criteria | ||||||
|---|---|---|---|---|---|---|---|
| 1 | [80, 97] | [80, 99] | [80, 98] | [79, 95] | [69, 97] | [80, 94] | |
| 2 | [78, 83] | [84, 95] | [79, 95] | [77, 95] | [78, 95] | [80, 90] | |
| 3 | [68, 85] | [60, 80] | [70, 98] | [85, 95] | [79, 90] | [60, 83] | |
| 4 | [76, 85] | [70, 90] | [68, 98] | [76, 95] | [78, 95] | [60, 92] | |
| 5 | [66, 100] | [66, 95] | [73, 97] | [68, 95] | [67, 87] | [60, 89] | |
| 6 | [60, 78] | [66, 100] | [67, 99] | [68, 93] | [72, 90] | [70, 100] | |
| 7 | [66, 90] | [70, 89] | [60, 95] | [82, 97] | [80, 96] | [70, 90] | |
| 8 | [66, 90] | [64, 95] | [63, 96] | [60, 90] | [71, 95] | [70, 85] | |
| 9 | [70, 90] | [75, 99] | [79, 98] | [69, 96] | [79, 97] | [75, 90] | |
| 10 | [66, 90] | [66, 100] | [70, 100] | [73, 95] | [68, 95] | [60, 90] | |
| 11 | [60, 87] | [62, 100] | [65, 97] | [67, 90] | [70, 95] | [62, 90] | |
| 12 | [70, 97] | [80, 100] | [80, 97] | [79, 97] | [84, 90] | [80, 93] | |
| 13 | [63, 88] | [61, 90] | [66, 100] | [66, 96] | [66, 100] | [60, 80] | |
| 14 | [69, 87] | [66, 95] | [60, 99] | [65, 100] | [67, 90] | [60, 95] | |
| 15 | [60, 98] | [70, 85] | [60, 99] | [79, 98] | [60, 93] | [60, 85] | |
| 16 | [70, 89] | [80, 92] | [80, 98] | [88, 95] | [80, 93] | [80, 95] | |
| 17 | [60, 86] | [60, 87] | [70, 98] | [80, 98] | [70, 86] | [75, 92] | |
| 18 | [78, 90] | [70, 96] | [77, 99] | [60, 98] | [68, 95] | [60, 92] | |
| 19 | [60, 96] | [70, 98] | [69, 97] | [80, 92] | [79, 99] | [73, 94] |
| Correlation | Grey-MEREC-MAIRCA | WSM | TOPSIS | |
|---|---|---|---|---|
| Grey-MEREC-MAIRCA | Spearman’s rho | – | ||
| Kendall’s Tau B | – | |||
| Weighted Correlation () | – | |||
| WS-Coefficient | – | |||
| WSM | Spearman’s rho | 0.943 | – | |
| Kendall’s Tau B | 0.867 | – | ||
| Weighted Correlation () | 0.902 | – | ||
| WS-Coefficient | 0.885 | – | ||
| TOPSIS | Spearman’s rho | 0.886 | 0.943 | – |
| Kendall’s Tau B | 0.733 | 0.867 | – | |
| Weighted Correlation () | 0.976 | 0.927 | – | |
| WS-Coefficient | 0.989 | 0.958 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esangbedo, M.O.; Tang, M. Evaluation of Enterprise Decarbonization Scheme Based on Grey-MEREC-MAIRCA Hybrid MCDM Method. Systems 2023, 11, 397. https://doi.org/10.3390/systems11080397
Esangbedo MO, Tang M. Evaluation of Enterprise Decarbonization Scheme Based on Grey-MEREC-MAIRCA Hybrid MCDM Method. Systems. 2023; 11(8):397. https://doi.org/10.3390/systems11080397
Chicago/Turabian StyleEsangbedo, Moses Olabhele, and Mingcheng Tang. 2023. "Evaluation of Enterprise Decarbonization Scheme Based on Grey-MEREC-MAIRCA Hybrid MCDM Method" Systems 11, no. 8: 397. https://doi.org/10.3390/systems11080397
APA StyleEsangbedo, M. O., & Tang, M. (2023). Evaluation of Enterprise Decarbonization Scheme Based on Grey-MEREC-MAIRCA Hybrid MCDM Method. Systems, 11(8), 397. https://doi.org/10.3390/systems11080397









