Scheduling Complex Cyber-Physical Systems with Mixed-Criticality Components
Abstract
1. Introduction
- (1)
- We propose a new system goal for complex CPSs, called component-MC schedulability, which considers the balance between resource efficiency and safety assurance under component-based MC systems.
- (2)
- Under the component-MC schedulability, we propose a new scheduling framework called component-based MC scheduling with dynamic resource allocation (CMC-DRA), for component-based MC systems. In the framework, we develop scheduling semantics and a mode-switching algorithm for the CMC-DRA framework.
- (3)
- We derive an online schedulability analysis of CMC-DRA for runtime scenarios. We also derive an offline feasibility analysis of the CMC-DRA.
- (4)
- We evaluate the effectiveness of the CMC-DRA scheme through randomly generated synthetic workloads compared to the existing approaches.
2. Background
2.1. System Model
- Component Model. As Figure 1 illustrates, we consider a component-based system with multiple MC components: . Each MC component is characterized by component interface and component workload , where is a set of tasks: .
- Task Model. For simplicity, we consider dual criticality levels: HC and LC. We define an MC task model: task is characterized by , where represents the minimum inter-job separation time, is a low-criticality worst-case execution time (LO-WCET), indicates a high-criticality WCET (HI-WCET), is the task criticality level ( or ), and denotes the isolation property ( or ). Task has a relative deadline equal to . Given conservative assumptions for HI-WCETs, we assume that .
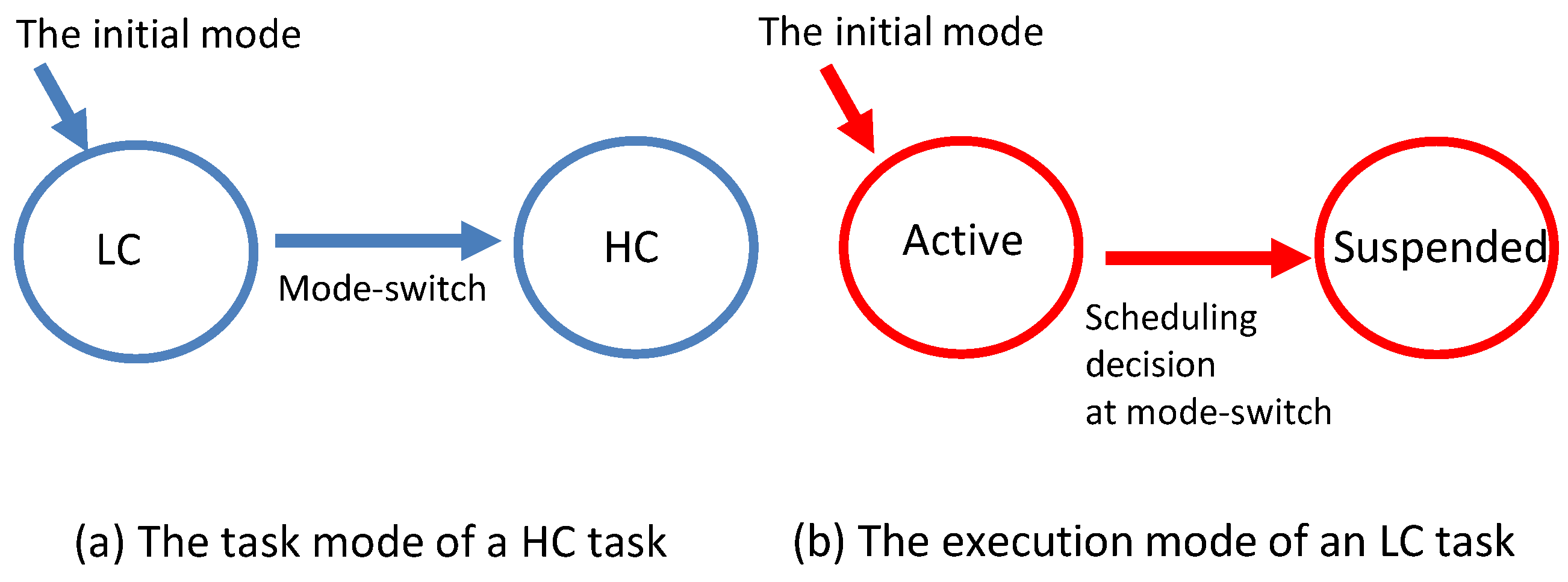
- Behavior Model. We consider the behavioral model of HC and LC tasks in runtime scheduling. Each task has a task mode (denoted as ) indicating its behavior. For HC tasks, we assume some degree of uncertainty about each job’s execution time. A job demonstrates LC behavior if the job completes within its LO-WCET or exhibits HC behavior otherwise. Task is in LC mode () if it does not show HC behavior and in HC mode () otherwise.
- System Goal. In existing MC systems, MC schedulability is defined as follows: for a given MC task set, the system is MC-schedulable if
- HC tasks are always schedulable, and
- LC tasks are schedulable if no mode-switch occurs.
- Comp-MC-A: HC tasks are always schedulable;
- Comp-MC-B: LC tasks are schedulable if no mode-switch occurs; and
- Comp-MC-C: The schedulability of isolated LC tasks is unaffected by the behavior outside the component.
2.2. Review of MC Scheduling Algorithms
- (1)
- Scheduling policy: Initially, all LC tasks start in active mode. All HC tasks except HC-mode-preferred tasks start in LC mode (HC-mode-preferred HC tasks are enforced to execute consistently in HC mode). The deadline-based scheduler assigns the highest priority to the task with the earliest effective deadline: For an HC task, the scheduler executes the task based on its VD if it is in LC mode and based on its real deadline otherwise. For an LC task, the scheduler executes the task based on its real deadlines.
- (2)
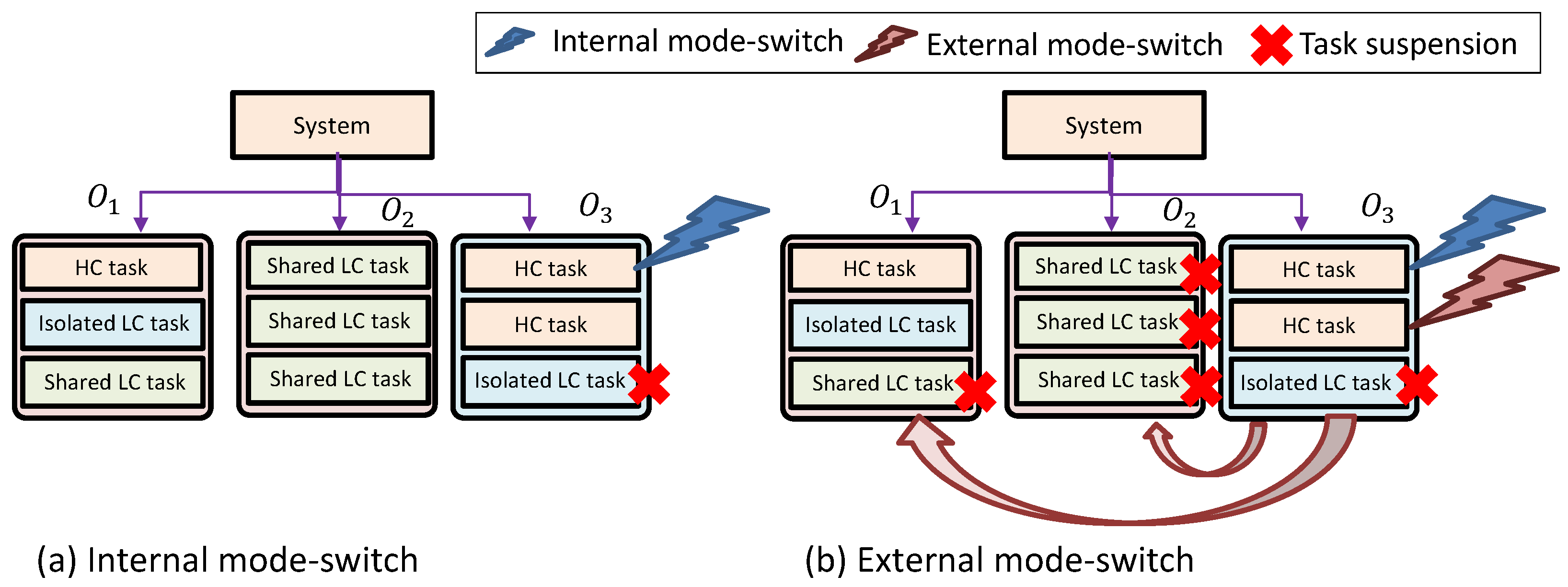
- Mode-switching algorithm: When an HC task mode-switches from LC to HC, the scheduler may suspend LC tasks due to the increased resource demand of the HC task (the increased upper bound of task execution time from LO-WCET to HI-WCET). Based on an online schedulability test (presented later), the scheduler chooses to suspend LC tasks.
- : LC mode, HC task set (),
- : HC mode, HC task set () including the mode-switching task,
- : active LC task set (), and
- : suspended LC task set () including LC tasks that are being suspended at a mode-switch.
3. Component-Based Mixed-Criticality Scheduling Framework
3.1. Challenges and Approaches
3.2. Process Overview
3.3. The CMC-DRA Scheduling Algorithm
3.3.1. CMC-DRA Component Resource Manager
- (1)
- Mandatory resource adjustment: This step is vital to guarantee the component-MC schedulability of a component.
- (a)
- If the mandatory component resources () exceed the previously assigned component resource (), we increase from to .
- (b)
- If the available resources () are smaller than the mandatory component resource, the mode-switch is changed to external (Figure 3b). For the external mode-switch, the component resource manager should request the component’s resource deficiency () from the system resource manager: .
- (2)
- Optional resource adjustment (if ): This step is optional to reduce the suspension of LC tasks. We increase by .
- (1)
- Find a component s.t. and .
- (a)
- can reduce its component resources from to . We let be the maximum possible resource donation: .
- (b)
- If , we reduce the component resources of maximally and update .
- (c)
- Otherwise, we reduce the component resources of only by and update .
- (2)
- Repeat the above procedure until . A feasible system passing the offline feasibility test (which will be presented in Section 3.4) must be terminated.
3.3.2. CMC-DRA Mode-Switching Algorithm
3.4. Schedulability Analysis of CMC-DRA
3.4.1. Online Schedulability Analysis
3.4.2. Offline Feasibility Analysis and Interface Computation
4. Evaluation
4.1. Simulation Setup
- (1)
- Component utilization, , is a real number drawn from the range .
- (2)
- The ratio of isolated tasks over total LC tasks, , is a real number drawn from the range .
- (3)
- For a task ,
- -
- Task utilization, , is a real number drawn from the range .
- -
- The ratio of , , is a real number drawn from the range .
- -
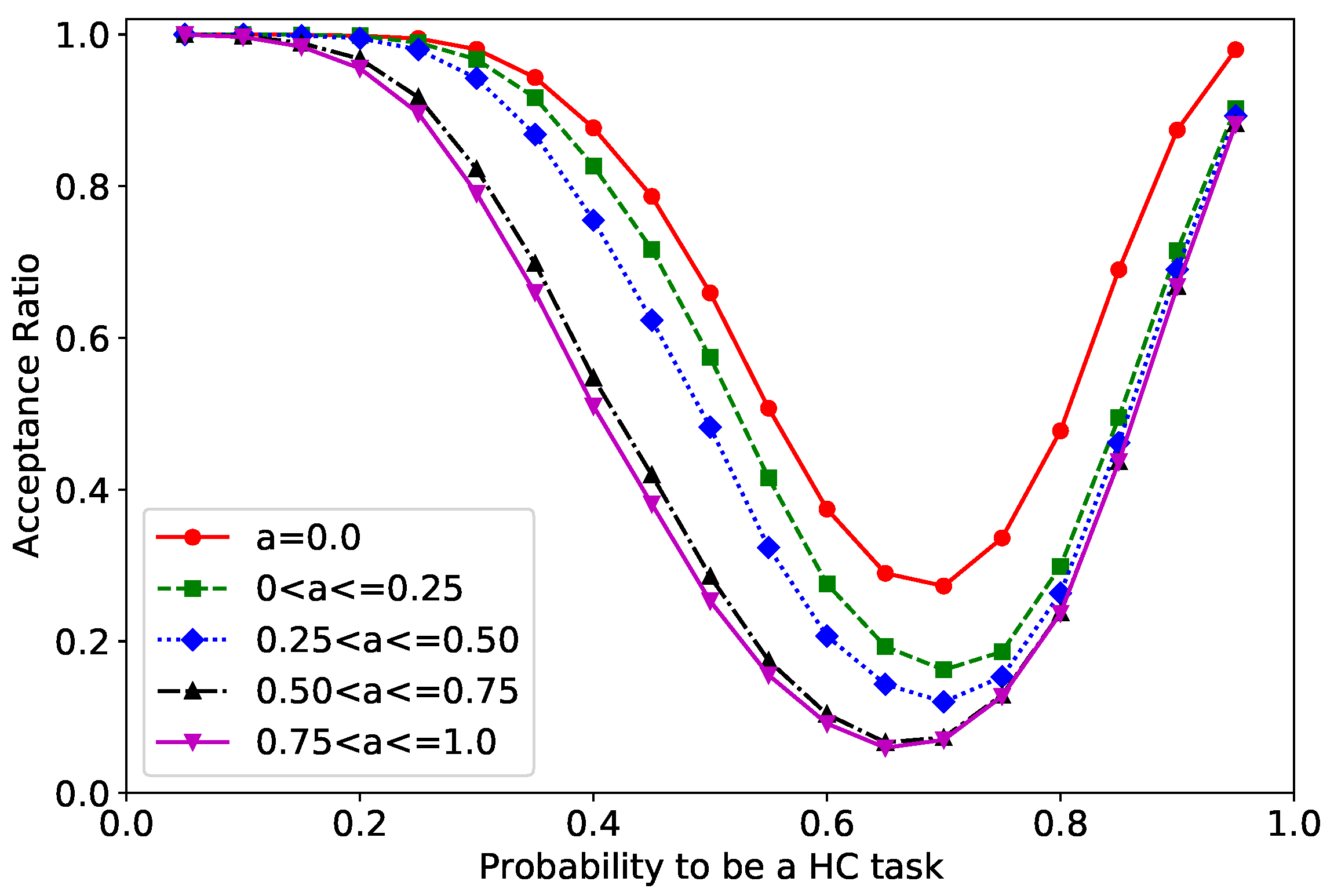
- The probability that the task is an HC task, , is a real number from the range [0, 1]. If (default value of is 0.5), set . Otherwise, set .
- (4)
- We repeat the steps to generate a task in the component until exceeds . Then, we discard the task added last.
4.2. Simulation Results
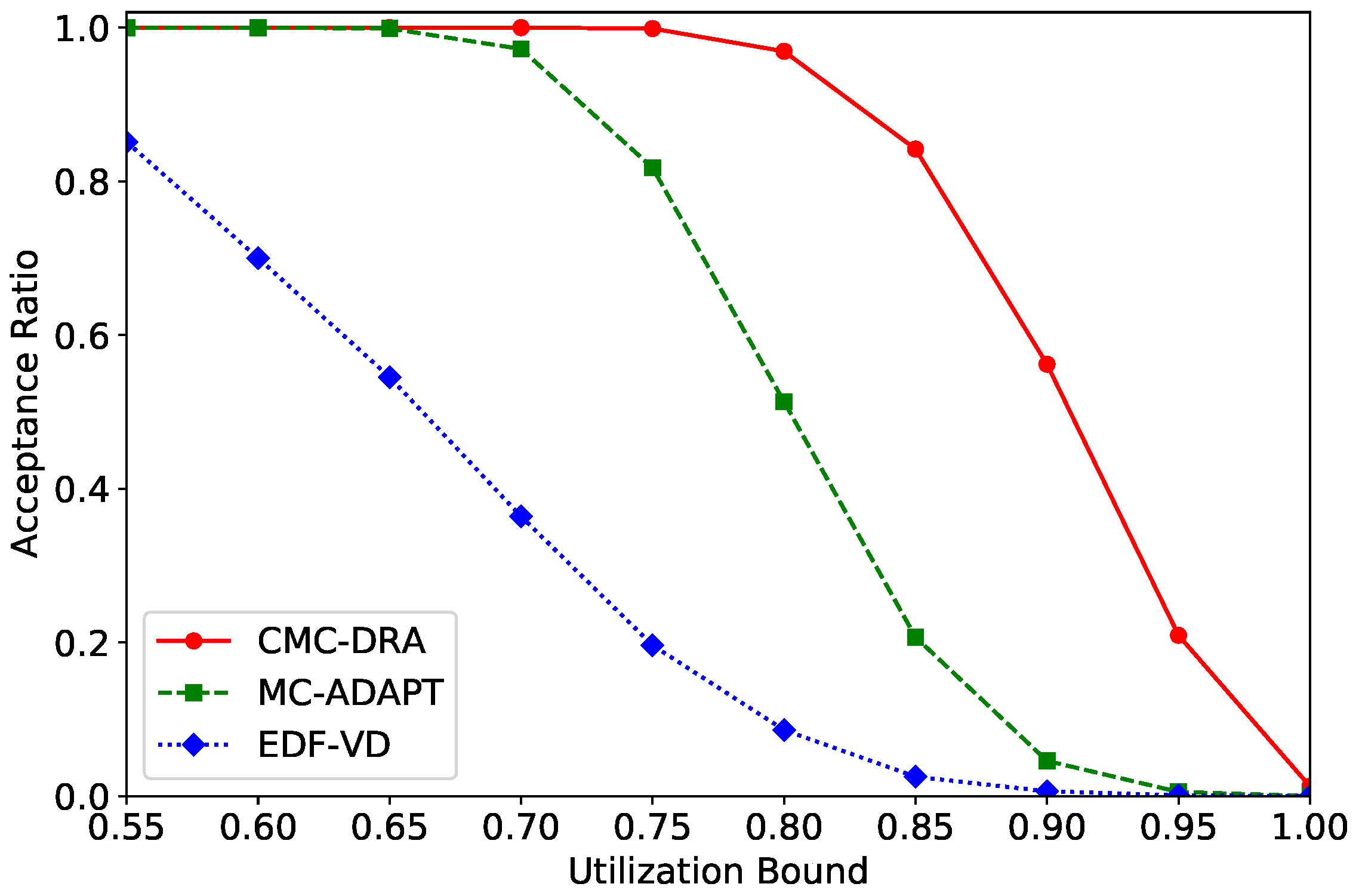
4.2.1. System Feasibility for Scheduling Algorithms
- (1)
- A variant of the MC-ADAPT scheduling algorithm [18] for component-based systems: When a mode-switch occurs in a component, the algorithm selectively suspends LC tasks in the component. The mode-switch does not propagate to other components.
- (2)
- A variant of the EDF-VD scheduling algorithm [15] for component-based systems: When a mode-switch happens in a component, the algorithm suspends all LC tasks in the component. The mode-switch does not propagate to other components.
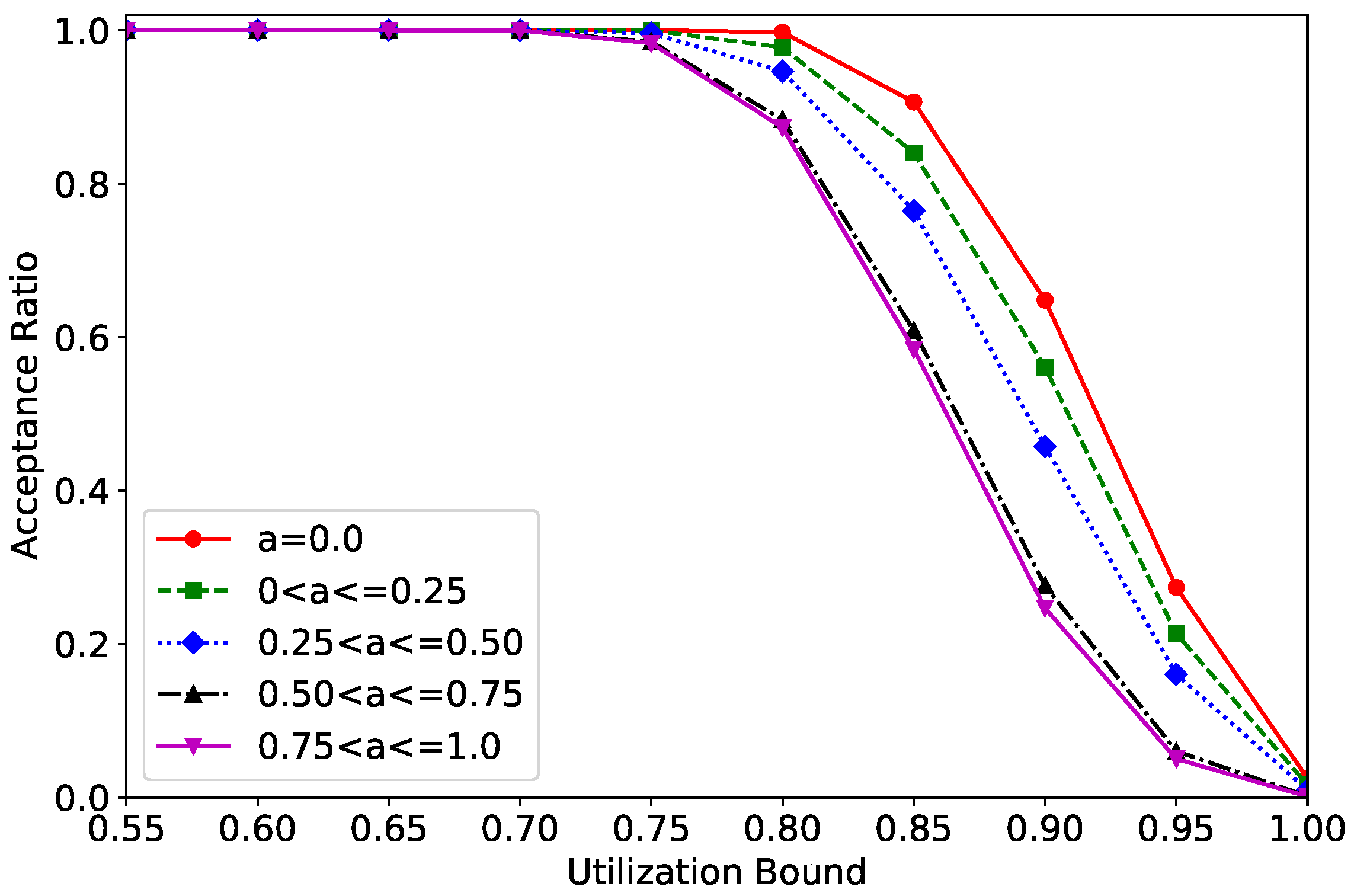
4.2.2. System Feasibility for Alpha Parameters
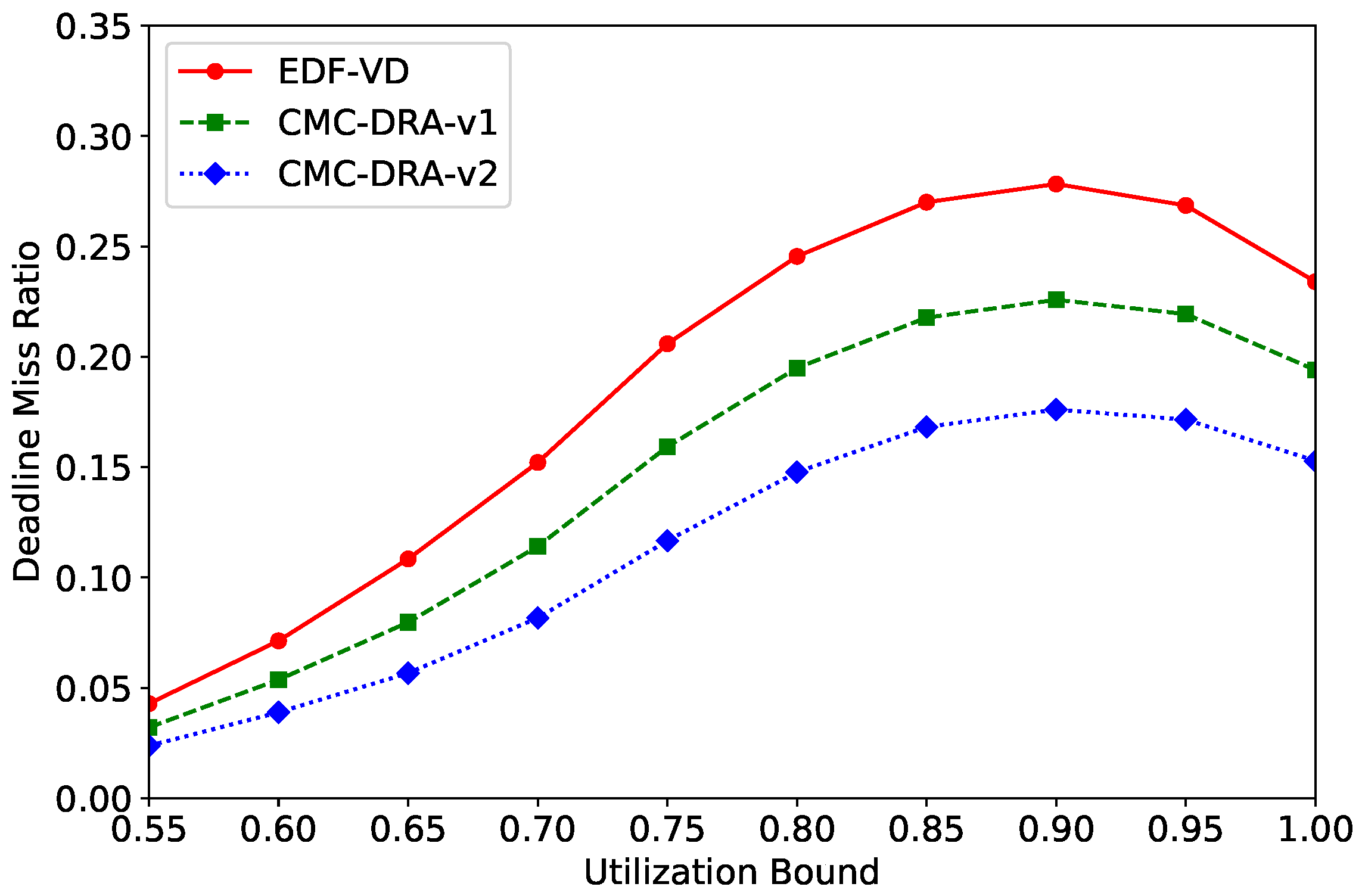
4.2.3. Runtime Performance (Deadline Miss Ratio of LC Tasks)
- (1)
- The EDF-VD scheduling algorithm [15] is a non-component-based MC scheduling algorithm suspending all LC tasks at any mode-switch.
- (2)
- The CMC-DRA-v1 scheduling algorithm is a simplified version of the CMC-DRA algorithm without considering the component state and resource manager. At the mode-switch in a component, the algorithm suspends all LC tasks in the mode-switching component and suspends all shared LC tasks in other components.
- (3)
- The CMC-DRA-v2 scheduling algorithm is the proposed CMC-DRA algorithm, which strictly follows Section 3.3.
5. Discussion
5.1. Implementation in Autonomous Driving Mini Vehicles
5.2. Implementation with Virtualization Platforms
5.3. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notation
| An MC component | |
| The workload of component (a set of tasks ) | |
| An MC task =(, , , , ) | |
| Task period of | |
| LO-WCET of | |
| HI-WCET of | |
| Task criticality of ( or ) | |
| Isolation property for LC tasks (true or false) | |
| The set of tasks in all components in the system | |
| A set of tasks whose task criticality is : | |
| A set of tasks whose task criticality is : | |
| A set of LC tasks whose isolation property is true: | |
| A set of LC tasks whose isolation property is false: | |
| Task mode of indicating runtime task behavior | |
| LC mode HC task set | |
| HC mode HC task set | |
| Active LC task set | |
| Suspended LC task set | |
| S | System state indicating runtime state of the system: |
| x | A system-wide virtual deadline tuning parameter |
| HC-mode-preferred tasks | |
| Component state indicating runtime state of component : | |
| Current component state of | |
| Initial component state of | |
| The worst-case component state of when external mode-switches but no internal mode-switches occur | |
| The worst-case component state of when internal mode-switches occur | |
| Component resource indicating proportional share of the system resource for component | |
| The minimum component resource to schedule when | |
| The previously assigned component resource of | |
| The maximum possible resource donation of | |
| The minimum component resource to schedule when | |
| The minimum component resource to schedule when | |
| The minimum component resource to schedule when | |
| Resource demand of over time interval length t | |
| The mandatory component resource to schedule for component-MC schedulability | |
| The optional component resource to reduce the suspension of LC tasks in | |
| The remaining system resource that is not distributed to any component | |
| The deficiency of component resource to provide the mandatory component resource |
Appendix A
- Case 1 ( is ). We show that the collective demands over are equal to or less than :which is equal to or less than by Equation (4) with .
- Case 2 ( is not ). Assume that the current component state is transited from a feasible component state ( is also a feasible system state) by one mode-switch. Let be the mode-switching job of task before time and be the release time of . Let be on . Task denotes the HC task which the latest mode-switching job before belongs to.We only need to show that the collective demands over are equal to or less than . Since is a feasible component state, we have for any t. We calculate the collective demand by dividing the cases depending on .
- Case 2-A. (). The collective demand is calculated as
- Case 2-B. (). The collective demand is calculated as
References
- Henzinger, T.; Matic, S. An Interface Algebra for Real-Time Components. In Proceedings of the 12th IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS’06), San Jose, CA, USA, 4–7 April 2006; pp. 253–266. [Google Scholar] [CrossRef]
- Prisaznuk, P. Integrated modular avionics. In Proceedings of the Aerospace and Electronics Conference, NAECON 1992, Dayton, OH, USA, 18–22 May 1992; Volume 1, pp. 39–45. [Google Scholar] [CrossRef]
- ARINC653—An Avionics Standard for Safe, Partitioned Systems; Wind River Systems/IEEE Seminar. 2008. Available online: https://docplayer.net/287772-Arinc-653-an-avionics-standard-for-safe-partitioned-systems.html (accessed on 20 February 2023).
- Abeni, L.; Balsini, A.; Cucinotta, T. Container-Based Real-Time Scheduling in the Linux Kernel. SIGBED Rev. 2019, 16, 33–38. [Google Scholar] [CrossRef]
- Cucinotta, T.; Abeni, L.; Marinoni, M.; Balsini, A.; Vitucci, C. Reducing Temporal Interference in Private Clouds through Real-Time Containers. In Proceedings of the 2019 IEEE International Conference on Edge Computing (EDGE), Milan, Italy, 8–13 July 2019; IEEE Computer Society: Los Alamitos, CA, USA, 2019; pp. 124–131. [Google Scholar] [CrossRef]
- ISO/DIS 26262-1; Road Vehicles Functional Safety Part 1 Glossary. Technical Report; ISO: Geneva, Switzerland, 2009.
- Gall, H. Functional safety IEC 61508/IEC 61511 the impact to certification and the user. In Proceedings of the AICCSA, IEEE Computer Society, Doha, Qatar, 31 March–4 April 2008; pp. 1027–1031. [Google Scholar]
- AUTOSAR. AUTomotive Open System Architecture. Available online: www.autosar.org (accessed on 29 April 2023).
- Ren, J.; Phan, L.T.X. Mixed-Criticality Scheduling on Multiprocessors Using Task Grouping. In Proceedings of the 2015 27th Euromicro Conference on Real-Time Systems (ECRTS), Lund, Sweden, 8–10 July 2015; pp. 25–34. [Google Scholar] [CrossRef]
- Gu, X.; Easwaran, A.; Phan, K.M.; Shin, I. Resource Efficient Isolation Mechanisms in Mixed-Criticality Scheduling. In Proceedings of the 2015 27th Euromicro Conference on Real-Time Systems (ECRTS), Lund, Sweden, 8–10 July 2015; pp. 13–24. [Google Scholar] [CrossRef]
- Burns, A.; Baruah, S. Towards A More Practical Model for Mixed Criticality Systems. In Proceedings of the First Workshop of Mixed Criticality Systems (WMC 2013), Vancouver, BC, Canada, 3–6 December 2013; pp. 1–6. [Google Scholar]
- Vestal, S. Preemptive Scheduling of Multi-criticality Systems with Varying Degrees of Execution Time Assurance. In Proceedings of the 28th IEEE International Real-Time Systems Symposium, RTSS 2007, Tucson, AZ, USA, 3–6 December 2007; pp. 239–243. [Google Scholar] [CrossRef]
- Burns, A.; Davis, R.I. A Survey of Research into Mixed Criticality Systems. ACM Comput. Surv. 2017, 50, 1–37. [Google Scholar] [CrossRef]
- Baruah, S.; Burns, A.; Davis, R. Response-Time Analysis for Mixed Criticality Systems. In Proceedings of the 2011 IEEE 32nd Real-Time Systems Symposium (RTSS), Vienna, Austria, 29 November–2 December 2011; pp. 34–43. [Google Scholar] [CrossRef]
- Baruah, S.; Bonifaci, V.; D’Angelo, G.; Li, H.; Marchetti-Spaccamela, A.; van der Ster, S.; Stougie, L. The Preemptive Uniprocessor Scheduling of Mixed-Criticality Implicit-Deadline Sporadic Task Systems. In Proceedings of the 2012 24th Euromicro Conference on Real-Time Systems (ECRTS), Pisa, Italy, 11–13 July 2012; pp. 145–154. [Google Scholar]
- Guan, N.; Ekberg, P.; Stigge, M.; Yi, W. Effective and Efficient Scheduling of Certifiable Mixed-Criticality Sporadic Task Systems. In Proceedings of the 2011 IEEE 32nd Real-Time Systems Symposium (RTSS), Vienna, Austria, 29 November–2 December 2011; pp. 13–23. [Google Scholar] [CrossRef]
- Huang, P.; Kumar, P.; Stoimenov, N.; Thiele, L. Interference Constraint Graph—A new specification for mixed-criticality systems. In Proceedings of the 2013 IEEE 18th Conference on Emerging Technologies Factory Automation (ETFA), Cagliari, Italy, 10–13 September 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Lee, J.; Chwa, H.S.; Phan, L.T.X.; Shin, I.; Lee, I. MC-ADAPT: Adaptive Task Dropping in Mixed-Criticality Scheduling. ACM Trans. Embed. Comput. Syst. 2017, 16, 163:1–163:21. [Google Scholar] [CrossRef]
- Chen, G.; Guan, N.; Hu, B.; Yi, W. EDF-VD Scheduling of Flexible Mixed-Criticality System with Multiple-Shot Transitions. IEEE Trans.-Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 2393–2403. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J. MC-FLEX: Flexible Mixed-Criticality Real-Time Scheduling by Task-Level Mode Switch. IEEE Trans. Comput. 2022, 71, 1889–1902. [Google Scholar] [CrossRef]
- Lackorzyński, A.; Warg, A.; Völp, M.; Härtig, H. Flattening Hierarchical Scheduling. In Proceedings of the Tenth ACM International Conference on Embedded Software; EMSOFT’12. ACM: New York, NY, USA, 2012; pp. 93–102. [Google Scholar] [CrossRef]
- Lackorzynski, A.; Völp, M.; Warg, A. Flat but Trustworthy: Security Aspects in Flattened Hierarchical Scheduling. SIGBED Rev. 2014, 11, 8–12. [Google Scholar] [CrossRef]
- Deos: A Time & Space Partitioned DO-178 Level A Certifiable RTOS. Available online: http://www.ddci.com/products_deos.php (accessed on 29 April 2023).
- O’Kelly, M.; Zheng, H.; Karthik, D.; Mangharam, R. F1TENTH: An Open-source Evaluation Environment for Continuous Control and Reinforcement Learning. In Proceedings of the NeurIPS 2019 Competition and Demonstration Track; Escalante, H.J., Hadsell, R., Eds.; PMLR: Vancouver, BC, Canada, 2020; Volume 123, pp. 77–89. [Google Scholar]
- Kang, W.; Chung, S.; Kim, J.Y.; Lee, Y.; Lee, K.; Lee, J.; Shin, K.G.; Chwa, H.S. DNN-SAM: Split-and-Merge DNN Execution for Real-Time Object Detection. In Proceedings of the 2022 IEEE 28th Real-Time and Embedded Technology and Applications Symposium (RTAS), Milano, Italy, 4–6 May 2022; pp. 160–172. [Google Scholar] [CrossRef]
- Cinque, M.; Cotroneo, D.; De Simone, L.; Rosiello, S. Virtualizing mixed-criticality systems: A survey on industrial trends and issues. Future Gener. Comput. Syst. 2022, 129, 315–330. [Google Scholar] [CrossRef]
- Struhár, V.; Behnam, M.; Ashjaei, M.; Papadopoulos, A.V. Real-Time Containers: A Survey. In Proceedings of the 2nd Workshop on Fog Computing and the IoT (Fog-IoT 2020); Cervin, A., Yang, Y., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2020; Volume 80, pp. 7:1–7:9. [Google Scholar] [CrossRef]

| EDF-VD | CMC-DRA-v1 | CMC-DRA-v2 | |
|---|---|---|---|
| Total simulation time | 737,419 ms | 769,343 ms | 731,906 ms |
| Simulation time per each workload | 16.387 ms | 17.097 ms | 16.265 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Koh, K. Scheduling Complex Cyber-Physical Systems with Mixed-Criticality Components. Systems 2023, 11, 281. https://doi.org/10.3390/systems11060281
Lee J, Koh K. Scheduling Complex Cyber-Physical Systems with Mixed-Criticality Components. Systems. 2023; 11(6):281. https://doi.org/10.3390/systems11060281
Chicago/Turabian StyleLee, Jaewoo, and Keumseok Koh. 2023. "Scheduling Complex Cyber-Physical Systems with Mixed-Criticality Components" Systems 11, no. 6: 281. https://doi.org/10.3390/systems11060281
APA StyleLee, J., & Koh, K. (2023). Scheduling Complex Cyber-Physical Systems with Mixed-Criticality Components. Systems, 11(6), 281. https://doi.org/10.3390/systems11060281