A Hybrid Metaheuristic Solution Method to Traveling Salesman Problem with Drone

Abstract

The challenging idea of using drones in last-mile delivery systems of logistics addresses a new routing problem referred to as the traveling salesman problem with drone (TSP-D). TSP-D aims to construct a route to deliver parcels to a set of customers by either a truck or a drone, thereby minimizing operational costs. Since TSP-D is considered NP-hard, using metaheuristics is one of the most promising solutions. This paper presents a hybrid metaheuristic solution method of TSP-D based on two state-of-the-art algorithms: the genetic algorithm and ant colony optimization algorithm. Heuristics in TSP-D literature are based on two consequent decisions: truck routing and drone assignment. Unlike those in the existing literature, the proposed metaheuristic constructs both truck and drone routes simultaneously. Additionally, to the best of our knowledge, we introduce for the first time a solution method on the basis of an ant colony optimization approach to TSP-D. Additionally, we propose a binary pheromone framework for both drone and truck, diverging from the traditional pheromone structure. Computational experiments indicate that the proposed hybrid metaheuristic algorithm is able to generate optimal routes for provided instances of TSP-D benchmarking. In addition, the algorithm improves the best-known solutions of some instances found by rival heuristics.

1. Introduction

Technical developments in last-mile delivery systems in logistics over recent years have resulted in enhanced use of unmanned air vehicles (UAVs), frequently referred to as drones, in numerous regions. The innovative idea of using drones in delivery arrived and began to draw attention on an international level when some of the primary online retailers announced their drone-integrated delivery processes. Using drones in last-mile parcel delivery is challenging, as they are faster than ground vehicles and are not affected by traffic conditions in city centers. Moreover, in recent years, people’s consumption patterns have indicated that purchasing preferences are more inclined toward online shopping. Considering this rapid trade and the increasing number of online retailers, delivery speed is of great importance. Hence, fast delivery is a competitive factor for retailers, and combining the high capacity of trucks with the speed advantage of drones is challenging.

This idea purports to address a new routing problem with drones, referred to as Traveling Salesman Problem with Drone (TSP-D), a variant of the well-known traveling salesman problem (TSP). Prompted by the last-mile delivery process, Murray and Chu [1] produced the first study that introduced the routing problem of a drone incorporated with a truck, calling it the Flying Sidekick-Traveling Salesman Problem (FSTSP), and Agatz et al. [2] presented a TSP-D much like the FSTSP. The TSP-D aims to construct a route to deliver parcels to a given set of customer locations by either a truck or a drone, minimizing operational costs, which are generally considered to be greater, the longer the total completion time of the tour. The basic distinction between these two variants of drone-aided parceling problems is that TSP-D lets the truck visit a customer more than once in order to meet the drone, whereas trucks and drones can serve just one customer location without returning to the same node in FSTSP. 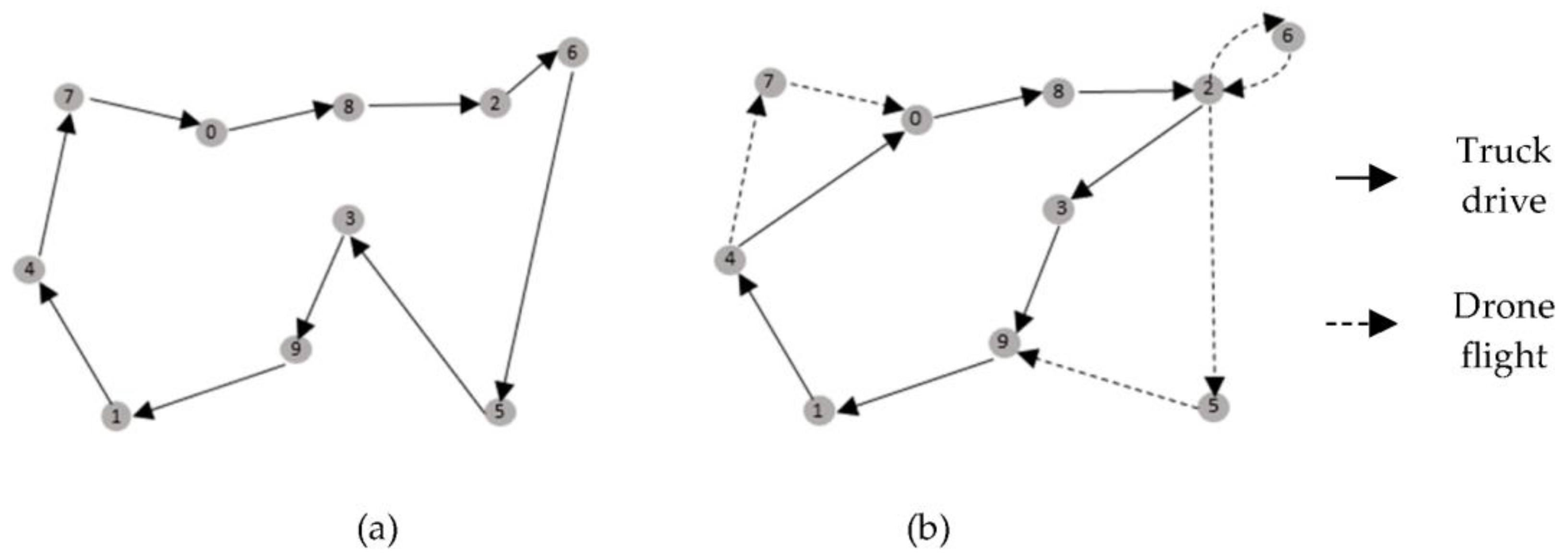Figure 1 denotes a TSP solution versus a TSP-D solution for a customer number of 9, where customer 0 is the depot. As seen in TSP-D tour representation, by serving some customer locations with the drone instead of the truck, the total distance of the truck’s travel can be reduced. With this parallelization of drone delivery tasks, the completion time of the tour can also be decreased.

TSP-D is a combinatorial optimization problem considered in NP-hard. Exact solution methods for this class of problems based on integer programming are solvable only for small-sized instances within a limited time. To obtain solutions within a reasonable computation time for larger-scaled optimization problems, heuristic algorithms are broadly applied. Heuristic algorithms proposed for traditional TSP solutions are divided into two classes: classical heuristics and metaheuristics [3]. Classical heuristics consists of the route construction and route improvement stages. These heuristics proposed in TSP-D solutions also consist of two stages: first, merging a TSP route, and then gradually assigning drone nodes to this route. We see that these kinds of classical heuristic algorithms have been primarily considered in most of the TSP-D studies reviewed. Comparably, metaheuristic methods have rarely been studied thus far in TSP-D (see Section 2). Motivated by the limited number of studies in the area, a metaheuristic approach is considered to for developing TSP-D. The presented metaheuristic solution approach in this paper is a combination of a well-known genetic algorithm (GA) and an ant colony optimization (ACO)-inspired algorithm: the genetic algorithm with ant search-based solution method (GA-AS).

GA and ACO are population search-based metaheuristics; they generate a wide number of random solutions to explore promising regions of solution space simultaneously. Whereas classical heuristics searches begin with a single solution and use broadly neighborhood search rules, we would rather apply a population-based searching approach to TSP-D (which is rarely presented), and present a comparison to those with single solution-based searching heuristics, using neighborhood procedure.

GA is a robust technique that can adapt easily to any kind of problem instance, evaluate any kind of objective function, and is applicable for wide variety of optimization problems; a limitation on GA is that it may need to be coupled with a local search method [4]. With this in mind, we considered a hybridized application of GA. The ACO algorithm is also widely used in NP-hard problems, more particularly in traditional TSP, resulting in promising solutions. Because it was the first problem the ACO algorithm attempted to solve, TSP is crucial to ACO [5]. The following factors are some of those that led to the selection of ACO to be applied to TSP-D: (i) TSP-D can be adapted to the ant behavior metaphor relatively easily, and is well-suited to the features of ACO; (ii) traditional TSP is the one most studied on ACO algorithms, with encouraging results [6]; and (iii) ACO implementation in TSP-D has not yet been studied in the existing literature.

The main contributions of this paper are as follows:

• Heuristic methods in the TSP-D solution literature are based on two separate decisions: truck routing (route construction) and drone assignment (route improvement). A traditional TSP route is constructed at the first step, in which drones are neglected, and then drone nodes are determined by using heuristics to obtain a TSP-D route. Unlike the TSP-D literature, both truck and drone routes are developed simultaneously with the proposed GA-AS algorithm.
• The binary pheromone framework in GA-AS is presented differently from the traditional pheromone structure of ACO. TSP-D consists of two different types of vehicles, and thus two different paths appear in a route: truck paths and drone paths. Each vehicle lays down its own type of pheromone along the paths by using binary pheromone formulations in the proposed algorithm.

The remaining parts of the paper are structured as follows: Section 2 discusses the works related to TSP-D, based on heuristic solution approaches. Section 3 defines the proposed hybrid metaheuristic GA-AS. Section 4 reports the experimental results and Section 5 concludes the paper.

2. Related Works

In this section, in alignment with the scope of this paper, we focused on TSP-D studies in the literature, addressing routing with a single truck and a single drone, and reviewing solutions and approaches presented for these. The existing solutions to TSP-D in the literature can be reviewed as exact methods and heuristic/metaheuristic methods. Exact methods solve the problem by using integer linear programming (ILP) formulations which generate optimal solutions for limited-sized instances. Considering the problem is NP-hard, to reach feasibly good solutions for larger-sized instances heuristic/metaheuristic methods have been presented in the current reviewed literature that follows.

The two works [1,2] are the first presentation of FSTSP and TSP-D, and serve as the basis for various extensions of drone-aided truck delivery problems in the literature. The basic distinction between these two variants is that TSP-D allows more than one visit to the customer to meet the drone, whereas trucks and drones can serve just one customer without returning the same node in FSTSP. The authors also presented a mathematical formulation of these problems. Ref. [5] proposed a mixed ILP formulation that solved problem instances with as many as ten customers while requiring numerous hours. In order to generate better solutions, they also presented a heuristic approach and benchmark instances. Ref. [6] proposed an integer linear programming formulation that is capable of solving instances with up to just 10 customers in 1 h. They also presented two heuristics based on local search techniques and new benchmarking instances.

Exact solution approaches based on ILP formulations of the problem [7,8,9] are able to solve small-sized instances optimally. In [10], the authors, much like in the first introduced TSP-D, extended their work by presenting a dynamic programming model solvable for larger-sized instances. Yurek and Ozmutlu [11] proposed an iterative optimization algorithm based on decomposition, producing a better computational time. Several studies [12,13,14] can be viewed as exact solutions to the problem.

Regarding the computational limitations of exact solutions, heuristic approaches are generally used to achieve feasible solutions to larger-sized instances of TSP-D. Heuristics are commonly classified as classical heuristics and metaheuristics. Classical heuristic algorithms consisting of route construction and route improvement stages have been used in most of the TSP-D studies reviewed. As well as the first proposed TSP-D heuristic by Agatz et al. [2] consists of a route-first, cluster-second approach. A truck route is constructed, in which drones are neglected at the first step, generally by using the Concorde solver, which finds a traditional TSP tour; then, drone nodes are generally determined using neighborhood search heuristics. Ponza [15] implemented a heuristic approach in his thesis to the FSTSP solution based on simulated annealing. Ha et al. [16] considered a different objective of the problem, aiming to reduce operational costs and to reduce the truck waiting time for the drone; consequently, two heuristic approaches were developed. TSP-LS uses local search procedures after an optimal truck route is found as a TSP tour; GRASP selects drone nodes to set up a TSP-D solution from a TSP tour in the construction step. They concluded through computational tests that GRASP obtained better solutions in terms of quality than TSP-LS. Marinelli et al. [17] modified this GRASP, considering a new assumption that the drone can launch and meet the truck along an arc, not just on a customer node. Freitas and Penna [18] presented a heuristic named HGVNS based on a neighborhood search to add drone deliveries after an optimal TSP tour found by a mixed ILP solution. Almuhaideb et al. [19] also followed a route-first, partition-second procedure in their study, and proposed a GRASP that includes two variants used as a local search procedure: hill-climbing and simulated annealing. Gozalez et al. [20] described a greedy heuristic working through an iterative procedure based on simulated annealing, allowing multiple drone visits between consequent rendezvous nodes, and also considering battery limitations that were not formulated before. Baniasadi et al. [21] considered a clustered generalized TSP as an extended variant of TSP, and proposed a transformation model. They also adapted their model to drone-assisted delivery problems. They separated the problem nodes into clusters and subclusters, in which the truck just visits one node in a subcluster, while drones visit every other node. This presents a disparate solution method to the problem.

Heuristic approaches are primarily considered in most TSP-D studies, while metaheuristics have rarely been studied so far in TSP-D. Ha et al. [22] introduced a hybrid genetic algorithm named HGA, which includes the use of a genetic algorithm and local search procedure combined to solve TSP-D, considering two objectives: min-cost and min-time. The genetic algorithm has an education step to improve the solution quality by exploring neighborhoods. HGA outperforms the previously proposed GRASP and existing methods. Another genetic algorithm implemented in TSP-D is the work of Ferrandez et al. [23], wherein a genetic algorithm was used to solve a TSP route for a truck, and a K-means algorithm was used to determine drone launch nodes. Finally, Tong et al. [24] also worked with a metaheuristic as a modification of the traditional tabu search algorithm. They changed the neighborhood structure of the tabu search, which extends the search range. The waiting times of trucks at launch nodes were also considered in their model.

Drone-aided routing problems, of which TSP-D is a variant, have some other variants, for instance, problems extended by the use of multiple drones and/or multiple trucks [25,26,27,28], or parallel drone scheduling problems [29,30]. We also refer interested readers to the surveys of Macrina et al. [31] and Otto et al. [32] for a comprehensive literature review of drone-aided routing problems with some other variants and solution methods.

As a consequence of reviewing the literature, it can be seen up to now that heuristic approaches are primarily focused on TSP-D studies, because ILP solutions call for significant computational times. Researchers have tried to generate solutions to instances involving many more nodes, attempting to solve them within an acceptable computation time. An additional factor is that metaheuristics are rarely studied in comparison with classical heuristics.

Another significant inference is that most of the heuristic algorithms mentioned here in TSP-D literature solve the problem in two stages: first, route construction, and second, route improvement. These algorithms consist of an improvement stage starting from a traditional TSP tour. Route construction is the first step to obtaining a traditional TSP tour using a Concorde solver or a heuristic algorithm. Route improvement consists of determining the drone nodes on the route to finalize it as a TSP-D tour. These improvements are generally based on neighborhood search procedures.

To the best of our knowledge, a method that constructs truck and drone routes in a single stage has not previously appeared in the current literature. Considering the use of such an algorithm, optimization can be simultaneously held on the route, while determining truck and drone nodes at the same time. As opposed to staggered algorithms, it could not be more appropriate for a problem of this nature.

3. The Genetic Algorithm with Ant Search-Based Solution Method to TSP-D

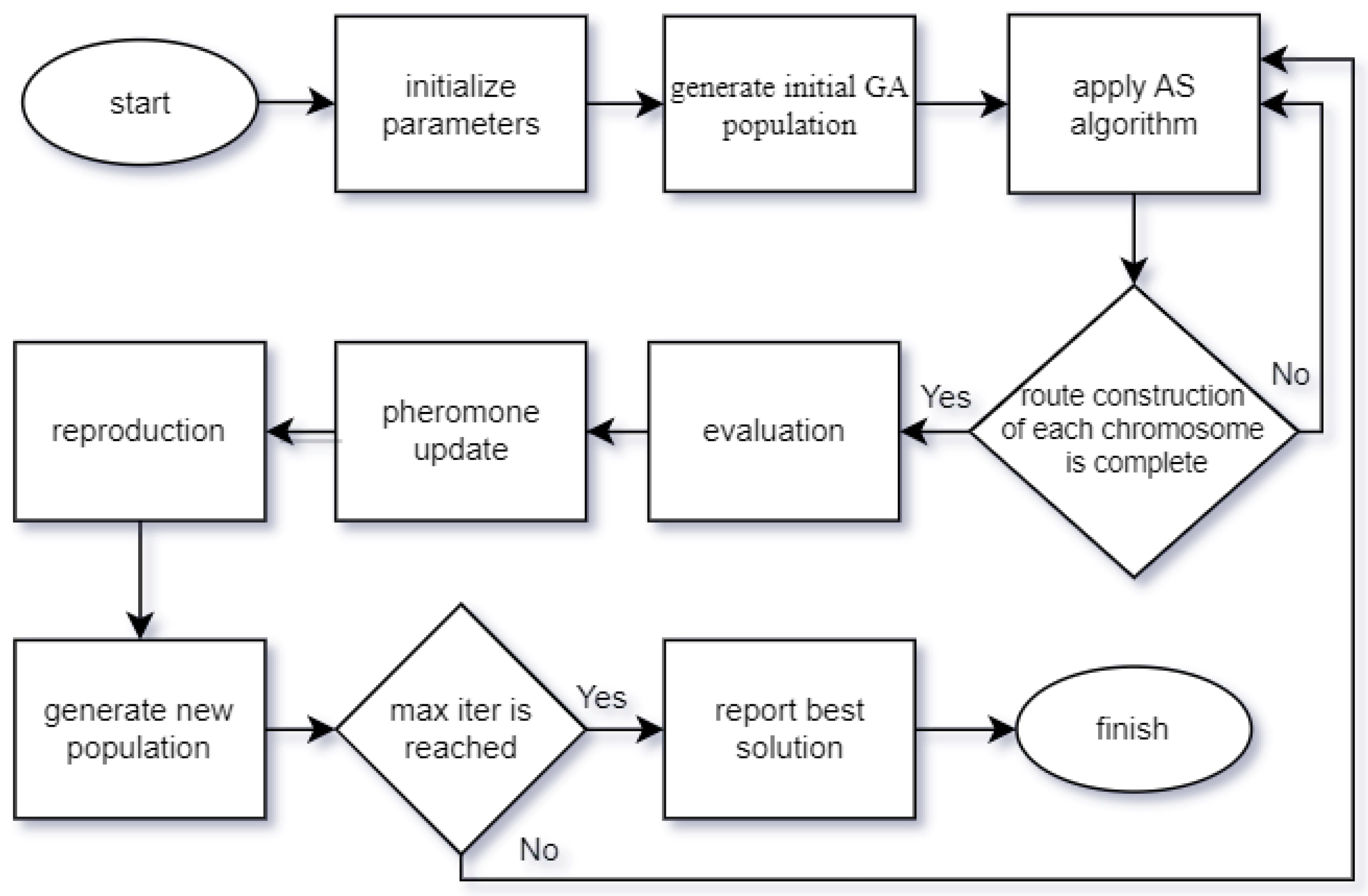
Here, we described a metaheuristic method to solve TSP-D based on the GA which works in parallel with an ant search (AS) procedure inspired by the traditional ACO algorithm that we call the genetic algorithm with ant search-based solution (GA-AS). The framework follows the classical GA optimization steps, whereas a new searching procedure inspired by ACO has been developed. The GA generates solutions and determines truck and drone delivery nodes, whereas the AS algorithm finds out the min-cost TSP-D routes. The proposed AS algorithm uses a new procedure based on a binary pheromone formulation variously from the pheromone structure of classical ant colony optimization. The framework of the proposed GA-AS is described in Algorithm 1.

Algorithm 1: The GA-AS algorithm

1: Initialize Population 2: iter = 0 3: for (iter < maxiter) 4:    gpop = 0; 5:    Generate truckphmtrx and dronephmtrx 6:    for (gpop = 0, gpop < maximum number of population, gpop++) 7:     Select the chromosome (gpop) 8:     Apply AS algorithm (gpop, truckphmtrx and dronephmtrx) 9:     Generate the route and fitness of each chromosome 10:    end 11:    for (until the max number of crossover) 12:     Select the parents P1 and P2 13:     Generate offspring individual O from P1 and P2 14:     Replace unwilling chromosome with offspring O 15:    end 16:    for (until the max number of mutation) 17:     Select the random allele on the chromosome 18:     Mutate the selected allele 19:    end 20:    update truckphmtrx and dronephmtrx 21: end

In detail, at the beginning, the algorithm initializes the genetic population (line 1), and each chromosome in the GA population goes through the AS algorithm to be constructed as the TSP-D route (line 8). The AS algorithm will be defined exhaustively in Section 3.2. Each chromosome is evaluated in line 9 to obtain a fitness value corresponding to its tour cost. In line 12, chromosomes are selected to be parents for reproduction via the roulette wheel method. Lines 13 to 18 present the reproduction part of GA, consisting of the crossover and mutation processes; elitism is also applied to the population (line 14). Child chromosomes after the reproduction part generate the new population of GA, and the algorithm returns to line 2. The algorithm repeats until the given maximum number of iterations is reached. At the end, the algorithm returns the solution found with min-cost. All the processes of the proposed algorithm will be explained in detail through the following sections. In addition, the given diagram in Figure 2 displays the flow of the algorithm.

3.1. Solution Representation in GA

The representation of the genetic solution is the main decision component of our GA, because choosing the right encoding greatly affects the performance of the algorithm. Encoding each solution represents a unique and feasible random point in the solution space of the problem.

Binary representation is applied for our GA, wherein each chromosome is encoded as a string of bits. Alleles on the chromosome can take the value of 0 or 1, and thus many possible solution representations may be generated using a small number of alleles. In our solution representation with a binary encoded chromosome, 0 represents any customer node that will be served by truck; 1 represents any customer node that will be served by drone. Figure 3 illustrates this solution representation for a randomly generated string in our GA. The length of the chromosome is equal to the total number of customer nodes (n) in the problem. Each gen location I of chromosomes corresponds to the customer node i, where i is from 1 to n. There, two separate arrays are generated in the algorithm to determine whether customers will be served by a truck or drone: truck delivery node (TD) and drone delivery node (DD) arrays. In a random chromosome generated by GA, if gen location i takes the value of 0, the customer node i will be served by a truck, and node i will be added to the TDarray; otherwise, it will be added to the DDarray. In this step of the algorithm, the chromosome determines only truck deliveries and drone deliveries, as the customer node id’s representation does not contain the delivery sequence.

3.2. Ant Search Algorithm (AS)

The AS step of the algorithm GA-AS constructs TSP-D routes corresponding to delivery types of nodes determined by GA. The AS algorithm transforms each chromosome solution of GA into a feasible TSP-D solution. The following parts describe the ant search procedure of the algorithm in detail.

3.2.1. Supportive Structure for AS Procedure

We first decided to separate the transportation types in a TSP-D route. TSP-D acknowledges that a path between two customer nodes may be taken in three ways: by truck alone, by drone alone, or by a truck with a drone standing on it. Figure 4 shows a TSP-D route with all possible transportation types. The route’s construction will be based on these types of transportation. We define four transportation types on the TSP-D route, as explained below.

• Type 1: (truck alone) The truck moves from customer i alone, takes path ij and serves customer j alone; meanwhile, the drone is having its own sortie to serve another customer node.
• Type 2: (drone alone) The drone has a sortie between customer i and j, serves customer j alone, and lands on another (rendezvous) node to meet the truck again.
• Type 3: (truck and drone together) A path ij is taken by a truck carrying a drone on top. A truck moves from customer i to serve customer j. Delivery will be completed by a truck while the drone will be standing by.
• Type 4: (drone with return) The drone sortie follows the i-j-i path. A drone is located on top of a truck at node i, launches from i to serve customer j alone, and returns to its launch node i to land on a truck.

* If a node with type 1 will be a rendezvous node in the algorithm, then its type will transform into type 3.

3.2.2. Solution Representation in AS

An array is generated for thte candidate solution in the AS algorithm, which represents a TSP-D route. The elements of the array consist of a customer node id, which is placed, respectively, in the visiting sequence. The first and last element of the array belong to the depot (0). Each element of the array also has a label which represents its transportation type. An example of a solution array in AS, the transformation of a GA solution to a TSP-D route, and the corresponding graph is illustrated in Figure 5.

3.2.3. Two-Pheromone Framework of AS

AS initializes N numbers of ant at each iteration, which is equal to a number of individuals in each GA population. For k = 1,..,N, each ant k is assigned to chromosome k generated in GA step. Thereby, each ant k in AS also uses the information in TDarray k and DDarray k.

Our AS, out of the classical framework of ACO, has two separate pheromones, one for the drone and the other for the truck. Therefore, two pheromone matrices are generated in the algorithm. One is the truck pheromone (P_t) matrix and one is the drone pheromone (P_d) matrix for nxn size of each, where n is the number of customer nodes. $P_{t_{ij}}$ value gives the current pheromone amount on the truck path between node i and node j; $P_{d_{ij}}$ value gives the current pheromone amount on the drone path between node i and node j (i = 1,..,n; j = i,..,n for each). $P_{t_{ij}}$ and $P_{d_{ij}}$ values are used in the selection process, as will be defined in the following section. At the beginning of the first iteration in the AS algorithm, 1/n is assigned to each $P_{t_{ij}}$ and $P_{d_{ij}}$ value, and at the end of each iteration will be updated by a defined formula which will be presented in Section 3.4.

3.2.4. Restrictions on Selection

An ant is located at the depot at the beginning of the route’s construction, and selects its next visiting node using a probability function until all customer nodes are sequenced. There are some restrictions on the selection of the next visiting node j from the located node i, which depend on the transportation type of node i. Choosing the next node is restricted due to which vehicle was used in the last transportation. For instance, if a node is served by a truck alone, transportation to the next node can only be taken by a truck again. All these restrictions are given below.

• If node i is type 1, then node j may only be one of: type 1 or type 3.
• If node i is type 2, then node j may only be type 3.
• If node i is type 3, then node j may only be one of: type 3, type 2 or type 4.
• If node i is type 4, then node j may only be one of: type3 or type 2.

Ant k, located at node i, selects the next node j to construct a TSP-D route in the AS algorithm. To select the next visiting node j in the route, at first, possible paths from nodes i to j should be determined. Possible paths are generated according to the transportation type of node i as defined in the following requisites.

• If the transportation type of node i is type 3 or type 2 or type 4, the next node j may become either a truck node and drone node; this means any unsequenced node from TDarray and DDarray is a candidate node to be j. All unsequenced drone paths and truck paths from i to j should be determined for evaluation.
• If the transportation type node i is type 1, the next node j may become a truck node or rendezvous node; this means any unsequenced node from only TDarray may become j. Only possible truck paths should be determined for evaluation.

After determining candidate nodes for j, each should be evaluated through a selection mechanism to determine which one will be selected as the next node in the TSP-D route. This selection mechanism of route construction is described in Section 3.2.5.

3.2.5. Selection Mechanism

Ant k located at node i chooses the next visiting customer node j proportional to the pheromone amount and distance of the path between i and j. For each candidate path from i to j, a selection value ${\mathsf{\upsilon }}_{ij}$ is computed as defined in Equation (1). Recalling, if customer j belongs to the truck deliveries array determined before by the GA, the truck pheromone amount $P_{t_{ij}}$ is taken into calculation; otherwise, the drone pheromone amount $P_{d_{ij}}$ is taken. d_ij gives the Euclidian distance between i and j. α and β are pre-given parameters regulating how much the pheromone amount and distance will influence the selection of the next node in the calculation.

$${\upsilon }_{ij}=\left\{\begin{array}{c}{P_{t_{ij}}}^{\propto }\times {\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d_{ij}$}\right.}^{\beta },j\in TDarray\\ {P_{d_{ij}}}^{\propto }\times {\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d_{ij}$}\right.}^{\beta },j\in DDarray\end{array}\right.$$

(1)

After assigning ${\upsilon }_{ij}$ for each possible path ij, the probability of node j becoming the next customer node is computed as in Equation (2) by using the probability equation; each possible node j has a value between 0–1 to be used in the selection. At this step, the algorithm generates a random number r between 0–1, and takes the cumulative sum S of all probabilities until S ≥ r; for $p\left(i,j\right),\mathrm{t}\mathrm{h}\mathrm{e}$ value of path ij wherein S exceeds r. j is chosen to be the next node in the sequence.

$$p\left(i,j\right)=\frac{{\upsilon }_{ij}}{\sum {\upsilon }_{ij}}$$

(2)

The algorithm repeats this framework until all customer nodes have been ordered in a solution array k, which is the TSP-D route solution corresponding to chromosome k. N number of solution arrays are generated corresponding to N number of individuals in a GA population, which forms one iteration of the algorithm.

3.3. Individual Evaluation

Customer locations are given as an input data matrix consisting of the x- and y- coordinates of each customer node. The coordinate matrix is transformed to a distance matrix d, where each d_ij is the Euclidean distance between the customer nodes i and j. Using the fact that the speed of the truck TS and speed of the drone DS differs, instead of accounting costs in terms of distance traveled, costs are specified over the time traveled. Two separate cost matrices, truck cost matrix TC and drone cost matrix DC, are identified, wherein $T_{C_{ij}}$ gives the total delivery time of the truck launching from customer i and arriving to customer j. $D_{C_{ij}}$ is the total sortie time of the drone launching from customer i and landing to customer j. These values computed as in Equations (3) and (4), respectively.

$$T_{C_{ij}}=\frac{d_{ij}}{T_S}$$

(3)

$$D_{C_{ij}}=\frac{d_{ij}}{D_S}$$

(4)

The objective function of the problem, which is to be optimized, is also used to evaluate individuals. Our objective is to minimize the total delivery time required to serve all customers, where the depot is both the starting and finishing node. According to our objective function, each P_k, after sequencing as a TSP-D tour by AS, obtains an evaluation value denoted as fitness measurement $f_k$. To measure the fitness of each P_k, the total cost (${TCost}_{P_k}$) of the TSP-D tour must be computed as the total delivery time of the sequenced nodes in chromosome k. The total cost is calculated as follows. At the beginning, the truck where and drone are located together at the depot, node i = 0 for the depot and i = 1, …, n, where n is the number of customers. Let customer i be a launch node and customer j be the next visiting node in the sequence. If node j is a type 3 or type 1 node, then $T_{C_{ij}}$ is added to ${TCost}_{P_k}$; if node j is a type 4 node, then sortie time $D_{C_{ij}}$ is multiplied by two and added to ${TCost}_{P_k}$; if node j is a rendezvous node, then the maximum of $T_{C_{ij}}$ and $D_{C_{ij}}$ is added to ${TCost}_{P_k}$. Then, the fitness value is calculated for each individual by Equation (5).

$$f_k=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${TCost}_{P_k}$}\right.$$

(5)

3.4. Pheromone Update

At the end of each AS iteration, the pheromone amount on path ij will be changed after all ants have completed their tours. This change is called the pheromone update, and it takes two forms: pheromone deposit and pheromone evaporation. Proportionally to the appearance frequency of path ij as an edge of the tour in solution array k, the pheromone amount will be deposited. The deposited pheromone amount on a path ij depends on how much path ij is taken by ant k. Evaporation is a decrease in the amount of pheromone on path ij at iteration t, while the pheromone amount at iteration t + 1 is updated using an evaporation constant e, where 0 < e < 1. As we established a two-pheromone framework in the algorithm, the pheromone amounts also need to be updated in two cases, for both truck paths and drone paths, separately.

If path ij belongs to solutionarray k and if the node j belongs to TDarray, this means path ij is taken by the truck. Thus, the pheromone amount on the truck path ij ($P_{t_{ij}}$) should be updated by the formula given in Equation (6).

$$P_{t_{ij}}\left(t+1\right)=P_{t_{ij}}\left(t\right)e+\sum _{k=1}^N∆P_{t_{ij}}^k$$

(6)

$∆P_{t_{ij}}^k$ refers to the change in pheromone amount on the truck path ij at the current iteration and computed by Equation (7), which is inversely proportional to the total cost of the tour found in solutionarray k, denoted as the fitness of individual k and formulated as ${f_k=1/TCost}_{P_k}$ before.

$$∆P_{t_{ij}}^k=\left\{\begin{array}{cc}{f}_k,& \hfill j\in TDarrayandpathij\in {solutionarray}_k\\ 0,& \hfill otherwise\end{array}\right.$$

(7)

If path ij belongs to solutionarray k, and if node j belongs to DDarray, then path ij will be taken by the drone. Thus, the pheromone amount on the drone path ij ($P_{d_{ij}}$) should be updated by the formula given in Equations (8) and (9).

$$P_{d_{ij}}\left(t+1\right)=P_{d_{ij}}\left(t\right)e+\sum _{k=1}^N∆P_{d_{ij}}^k$$

(8)

$$∆P_{d_{ij}}^k=\left\{\begin{array}{cc}{f}_k,\hfill & \hfill j\in DDarrayandpathij\in {solutionarray}_k\\ 0,\hfill & \hfill otherwise\end{array}\right.$$

(9)

3.5. Parent Selection

The selection operator of GA processes is characteristically similar to natural selection in biological systems. Individuals in the population reach different levels of fitness, and the selection mechanism drives the search for better solutions by preferring individuals with higher fitness. In each iteration of our GA, individuals are selected to the mating pool to become a parent by the roulette wheel method, which is a selection method proportionate to fitness. The least fit individuals also have a chance of being selected as a parent in this scheme, which provides genotypic diversity, thereby preventing the convergence of the algorithm. Each individual P_k in the population contains N number of members, and obtains a probability of selection proportional to its fitness over the total fitness of the population. The fitness probability is assigned to each individual P_k by the given formula in Equation (10).

$${p(f}_k)=\frac{f_k}{\sum _{k=1}^N{f}_k}$$

(10)

Once parent chromosomes are selected for reproduction, they are replaced in the newly generated population by their offspring, which allows the loss of super-fit individuals by crossover, and the possibility of replacing them with inferior solutions. Keeping the k-number of best-fitted members in the current population and copying them directly to the new population without undergoing reproduction, known as elitism, is applied in our GA.

3.6. Crossover and Mutation

After randomly choosing two parents from the mating pool, a crossover operator is applied to reproduction in the algorithm. The method to be used in this operator differs by problem type. As usual, the solution of TSP by GA, as a combinatorial optimization problem, has to be represented by permutation encoding of strings. Thus, it drives the necessity to develop appropriate crossover and mutation operators. With a difference in our GA for TSP-D, the specific use of binary coding removes this need and also exerts a better computational effort. An often-used crossover method for GAs, the single-point crossover, is applied to our binary strings. A single point on the binary string is chosen randomly and is called a crossover point. The gene sequence of the first parent chromosome before this crossover point and the gene sequence of the second parent chromosome after the crossover point are copied directly as they are, and the first offspring is generated. The second offspring is generated using the same crossover point and only changing the gene sequence of parents. After crossover, offspring are subjected to a mutation, wherein we applied single-bit mutation for binary represented strings, inversing a bit from 0 to 1 or 1 to 0. Arrays of truck delivery nodes and drone delivery nodes are also updated, corresponding to newly generated chromosomes.

4. Experimental Results and Discussions

This section presents computational experiments to evaluate the performance of the proposed algorithm GA-AS. The GA-AS was implemented in Visual Studio C++, and experiments were run on an Intel Core i7 processor with 4.00 GHz and 16 GB RAM.

Since the TSP-D has been recently studied, commonly used benchmarking instances for problems with optimal solutions are not available in the literature. Yet, Bouman et al. [33] provided a set of test data to TSP-D containing a set of instances with different numbers of customers (n) in the range of 5 to 250, and 10 different instances for each problem size n. We experimented on the second type of instance provided in [33], the so-called single-center. Distances between a pair of locations are computed as Euclidian distances. The alpha value indicates the relative speed of the drone/truck. As a default, alpha = 2 is assumed, meaning the drone is two times faster than the truck. Each location is eligible to be serviced by both the drone and truck. The service time of the vehicles and the launch time of the drones are set to 0. Drone endurance is assumed to be infinite. Experiments in sections are organized as follows. In Section 4.1, we first determined the algorithm parameters before conducting experiments. In Section 4.2, the GA-AS was primarily evaluated on a small-sized problem; then, in Section 4.3, the GA-AS was compared with three rival existing algorithms in the context of larger-sized problems.

4.1. Parameter Setting

Prior to the computational testing of the algorithm, we first carried out a design of experiment to determine the best values of the GA-AS parameters using the Taguchi method. The different parameter values used to experiment are classified as parameter levels and given in

Table 1. Parameter levels for experimental design.

Parameter	Level 1	Level 2	Level 3
Crossover rate	0.6	0.7	0.8
Mutation rate	0.1	0.2	0.3
Evaporation constant	0.5	0.7	0.9
α	1	2	3
β	3	4	5

. The levels were determined according to the references of [34,35]. Each GA population size was set to 100, and each run consists of 1000 iterations of the algorithm. Any increase in them only incurs additional computational time due to experimental trials.

The “singlecenter-62-n20” problem from [33] was used in the parameter-setting experiments. The results of the experimental design are evaluated through S/N ratios obtained using the Taguchi analysis. The highest S/N value indicates the best level of parameters to be used. Figure 6 graphically presents the effects of the parameter values. Considering the results of the analysis, the parameters of the GA-AS algorithm are set as reported in

Table 2. Parameter set of GA-AS.

Parameter	Value
Crossover rate	0.8
Mutation rate	0.3
Evaporation constant	0.9
α	1
β	5

.

4.2. Results of GA-AS on Small-Sized Instances

Bouman et al. provided a set of instances in [33] with optimal solutions given only for problems with a maximum of nine customers (n = 9). The data set contains ten different instances for each problem, and size n indicates the customer numbers. There are a total of 50 single-center instances where alpha = 2 is used to test GA-AS in this section.

Table 3. Results of GA-AS for Bouman et al. [33] instances.

Instance	n	IP	GA-AS	%GAP	Instance	n	IP	GA-AS	%GAP
1	5	154.26	154.26	0.00	26	7	98.71	98.77	0.06
2	5	140.54	140.54	0.00	27	7	177.86	177.10	0.43
3	5	52.67	52.92	0.46	28	7	169.77	170.97	0.71
4	5	108.94	108.94	0.00	29	7	193.34	193.34	0.00
5	5	122.15	122.15	0.00	30	7	177.10	177.10	0.00
6	5	162.22	162.22	0.00	31	8	155.20	155.48	0.18
7	5	133.95	133.95	0.00	32	8	107.20	107.20	0.00
8	5	81.50	81.50	0.00	33	8	172.85	177.06	2.44
9	5	143.15	143.15	0.00	34	8	226.91	226.91	0.00
10	5	140.40	140.40	0.00	35	8	188.46	188.46	0.00
11	6	128.01	128.01	0.00	36	8	181.37	181.37	0.00
12	6	125.94	125.94	0.00	37	8	134.62	134.62	0.00
13	6	215.91	215.91	0.00	38	8	286.71	286.71	0.00
14	6	119.24	147.71	23.87	39	8	181.07	181.07	0.00
15	6	169.62	169.62	0.00	40	8	214.90	217.51	1.21
16	6	117.84	117.84	0.00	41	9	116.93	116.93	0.00
17	6	263.03	263.03	0.00	42	9	316.25	318.84	0.82
18	6	258.65	258.65	0.00	43	9	226.28	238.26	5.29
19	6	188.80	188.80	0.00	44	9	228.28	233.03	2.08
20	6	122.17	122.17	0.00	45	9	279.66	279.66	0.00
21	7	208.34	208.34	0.00	46	9	214.02	216.19	1.01
22	7	178.38	178.38	0.00	47	9	277.73	282.98	1.89
23	7	116.24	116.24	0.00	48	9	200.95	200.96	0.00
24	7	152.59	152.59	0.00	49	9	349.49	349.49	0.00
25	7	130.50	130.50	0.00	50	9	196.84	196.84	0.00

presents the numerical results of the experiments. Instances used in experiments are given in the first column. The instance size is represented by column “n”. The values reported in the column “GA-AS” are the best value of the objective function in terms of time (secs) obtained over 30 runs of the algorithm for each instance. The optimal solution of each problem instance is presented in column “IP”. These optimal solutions provided in [33] have been solved by using the IP formulation of the problem. The column “GAP%” computes the percentage difference between the best-found solution of GA-AS and the optimal solution of that problem instance.

As for numerical results, the performance of the GA-AS algorithm is successful in its ability to find optimal solutions, which are provided only for small-sized instances. GA-AS found the optimal solutions in 37 out of the 50 problem instances tested, and obtained acceptably close to optimal results in the remaining instances. Experiments demonstrated that GA-AS can generate optimal TSP-D tours in instances tested with an average of 0.80% gap, compared to IP solutions of these instances.

4.3. Results of Comparison with Rival Algorithms

Here, we present an evaluation of the GA-AS’s performance over larger-sized problem instances in [33], in which optimal solutions for instances bigger than n = 9 are not provided; thus, our algorithm was compared with the best-found solutions of three rival algorithms: LS [2], HGVNS [18], and two variants of the GRASP algorithm presented in [19].

The experiment used a total of 40 problem instances with n sizes of 10, 20, 50, and 75 customers, where each size contains 10 different instance sets.

Table 4. Results of GA-AS in larger-sized instances from Bouman et al. [33], and comparison among rival algorithms [2,18,19].

n	LS [2]	HGVNS [18]	GRASP-HCLS [19]	GRASP-SA [19]	GA-AS
10	278.22	291.36	287.13	295.49	263.50
20	384.87	364.08	416.47	428.09	399.73
50	554.58	593.54	617.43	723.88	649.61
75	741.38	754.43	861.21	1030.92	978.25

presents the best-found solution values of each referenced algorithm. The reported results in the table present the mean value of the best-found solutions obtained over 10 problem instances of each n-sized problem type. We also report the computation time of the proposed GA-AS algorithm for each tested n-size of problem instances in

Table 5. Computation time of the GA-AS algorithm on different n-sizes of instances.

n	Time (Sec.)	n	Time (Sec.)
5	0.45	10	1.64
6	0.61	20	6.65
7	0.91	50	74.91
8	1.09	75	197.27
9	1.36

.

The proposed GA-AS algorithm outperformed four algorithms and improved the best-found solution in the n = 10-sized problem instances. The GA-AS algorithm obtained better results than the best-found solutions of the GRASP-SA variant on overall instances, and performed better than the GRASP algorithm in instances in which n = 20. We observed that GA-AS is an efficient algorithm in smaller-sized instances, whereas it obtains worse or close results in larger-sized ones. We were not able to separately compare solutions of each ten instances in each n problem set, owing to relevant studies presenting their solutions over average values instead of presenting each independently. Otherwise, we would provide more specific results and a more intense analysis of the performance of the algorithm.

5. Conclusions

In this study, we addressed the TSP-D and presented a hybrid metaheuristic solution method based on two state-of-the-art algorithms, the genetic algorithm and ant colony optimization algorithm, named GA-AS. Unlike heuristics, metaheuristic methods have rarely been studied so far in TSP-D; we proposed this algorithm to contribute to the literature’s appraisal of the problem. TSP-D heuristic solutions almost wholly consist of truck routing and drone assignment decisions carried out separately. A traditional TSP route is constructed before drone nodes are determined by a heuristic to obtain the TSP-D tour. The main contribution of this study presents a varying solution method, where the GA-AS simultaneously constructs a TSP-D tour while two algorithms determine the truck and drone nodes. In addition, we may state that ant colony optimization has herein been applied for the first time to solving TSP-D, as the GA-AS uses it in its searching methodology. Finally, a binary pheromone framework in GA-AS is implemented differently from the traditional pheromone structure of the ant colony algorithm.

Numerical experiments have demonstrated that the proposed metaheuristic algorithm can generate optimal TSP-D routes for provided instances with solutions. In addition, the algorithm improved the best-known solutions of some instances found by state-of-the-art heuristics in the literature. Overall, we indicate that the proposed metaheuristic method is comparable with classical heuristics in TSP-D solutions. Furthermore, the proposed method still has the potential for performance improvement in larger-sized instances. We limited this study on TSP-D by working with a single truck and a single drone; in further studies, the algorithm may be extended in order to implement it in delivery problems dealing with multiple drones and trucks. Another limitation of this study is that the battery recharge time is negligible, and the drone’s endurance is set to infinite. Further studies may consider the remaining battery charge and drone endurance.