Prediagnosis of Disease Based on Symptoms by Generalized Dual Hesitant Hexagonal Fuzzy Multi-Criteria Decision-Making Techniques
Abstract
:1. Introduction
1.1. Motivation of the Study
1.2. Research Outline
- For pre-diagnosis of the diseases, pick the disorders that are caused by viruses, have many overlapping symptoms, and have been scientifically identified.
- Identifying the symptoms of different diseases and comparative studies on signs with slight differences.
- Develop a comparative matrix based on criteria and alternatives for the Generalized Dual Hesitant Hexagonal fuzzy number by the decision-makers (DMs) to capture all the ambiguity, hesitancy, and vagueness.
- Calculate the criteria weight using the MCDM method FCRITIC. According to decision experts, this part identifies which symptoms are more severe and dangerous than others.
- Rank the diseases by FWASPAS and FCoCoSo, two MCDM methods for pre-diagnosis and early treatment. The two approaches mentioned above are considered concurrently for robustness and to ensure the consistency of our ranking.
- We conducted sensitivity and comparative analyses to check the result’s vagueness and unbiasedness. It demonstrates that how internally consistent our results are.
1.3. Structure of the Paper
2. Literature Review
3. Preliminaries
3.1. Fuzzy Set Theory
3.1.1. Generalized Fuzzy Number
- 1.
- is continuous, ,
- 2.
- for all ,
- 3.
- is monotonically increasing on and ,
- 4.
- for all ,
- 5.
- is monotonically decreasing on and ,
- 6.
- for all .
3.1.2. Hesitant Fuzzy Number
3.1.3. Dual Hesitant Fuzzy Number
- (a).
- for all
- (b).
- where and
3.1.4. Basic Operation of DHFS
- A.
- Complement of
- B.
- Union of and
- C.
- Intersection of and
- D.
- Addition of and
- E.
- Multiplication of and
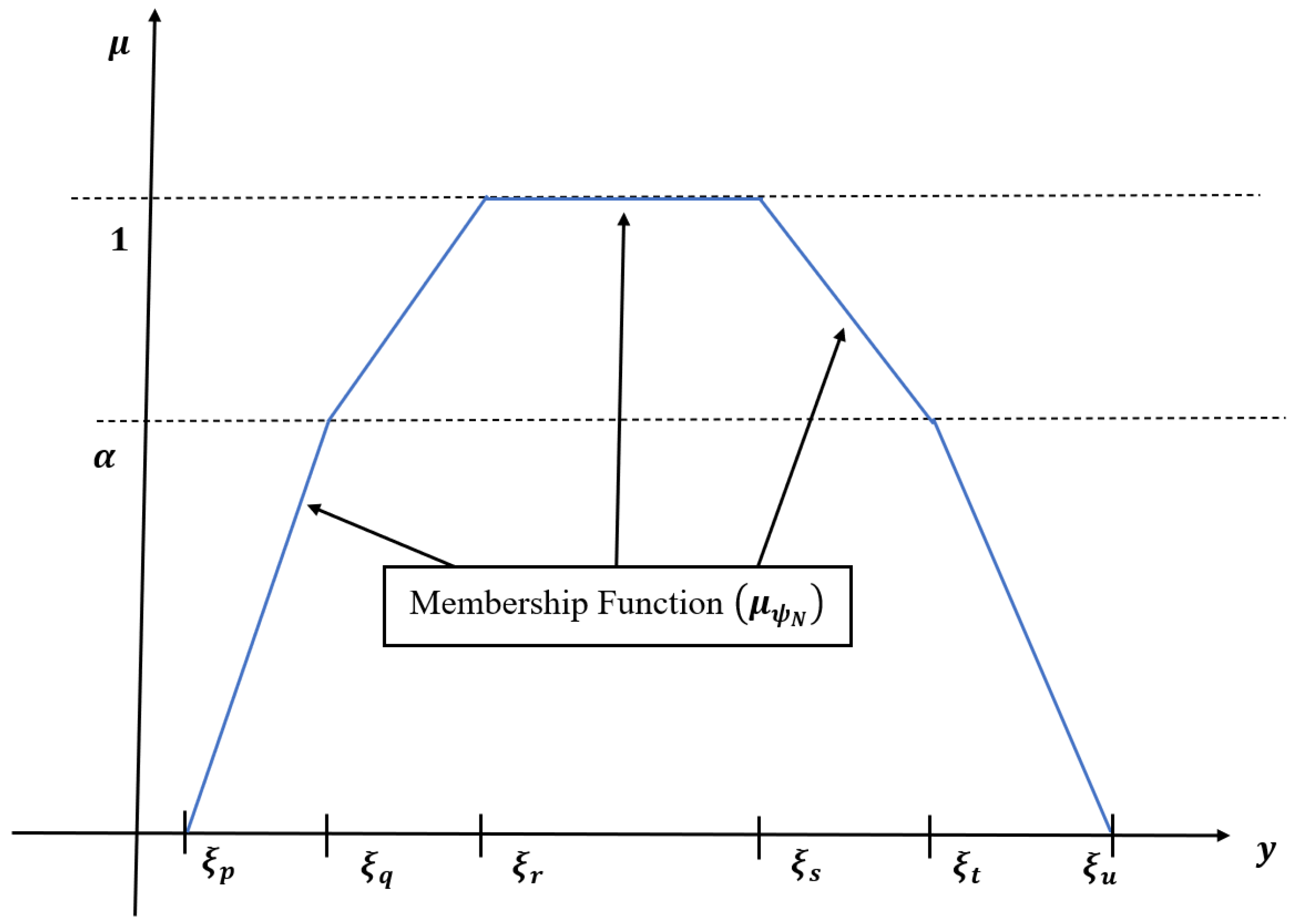
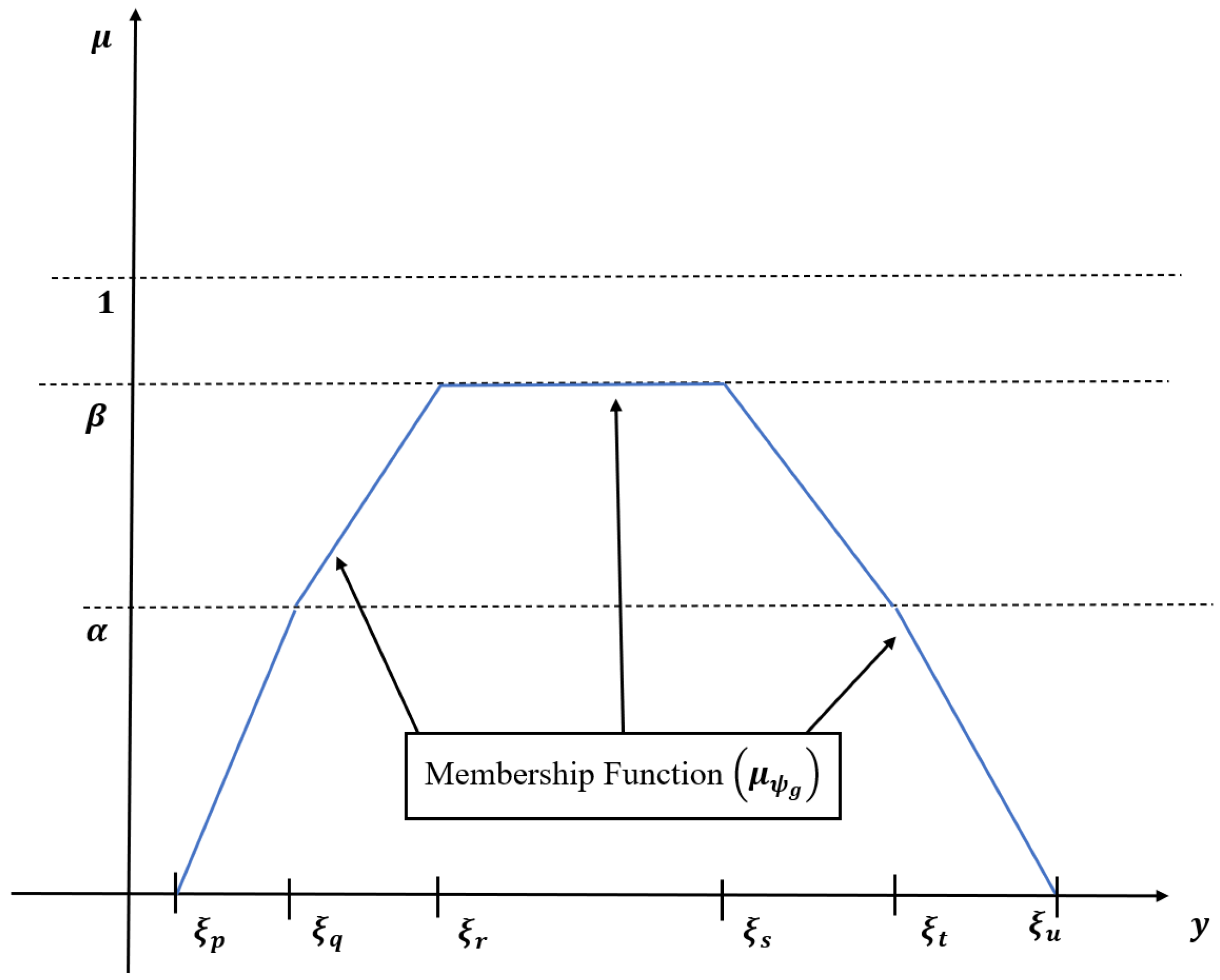
3.2. Hexagonal Fuzzy Number
- then hexagonal fuzzy number becomes trapezoidal fuzzy number.
- then hexagonal fuzzy number becomes trapezoidal fuzzy number.
- then hexagonal fuzzy numbers are not restructured.
3.2.1. Arithmetic Operation on
- 1.
- Addition:
- 2.
- Subtraction:
- 3.
- Multiplication:
- 4.
- Scalar Multiplication:
- 5.
- Division:
- 6.
- Inverse:
3.2.2. Generalised Hexagonal Fuzzy Set
- If then the becomes a zero set.
- If and then the becomes generalised trapezoidal fuzzy set .
- If and then the becomes trapezoidal fuzzy set .
- If and with then the unchanged.
- If and with then the becomes generalised trapezoidal fuzzy set .
- If and then the becomes hexagonal fuzzy set.
- If then the becomes trapezoidal fuzzy set .
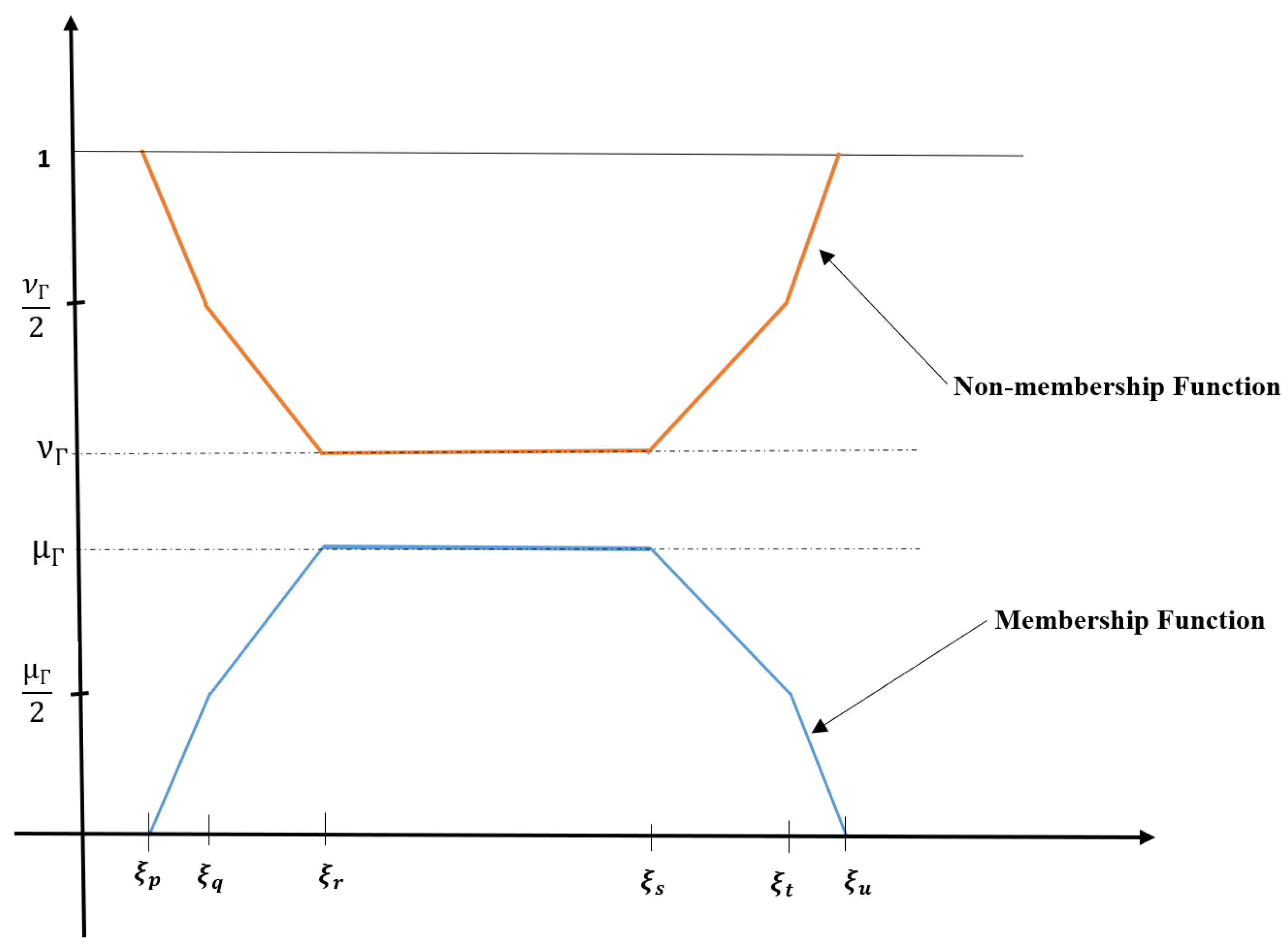
3.3. Generalized Hexagonal Dual Hesitant Fuzzy Set
3.3.1. Hexagonal Dual Hesitant Fuzzy Set
3.3.2. Hexagonal Dual Hesitant Fuzzy Number (
3.3.3. Generalized Hesitant Fuzzy Number ()
3.3.4. Generalized Hexagonal Fuzzy Number
3.4. Generalized Dual Hesitant Hexagonal Fuzzy Number
3.4.1. Benefits of Rather than
- (A)
- may represent membership degrees that are positive or negative, whereas fuzzy sets can only do so for positive membership degrees. This makes it possible for to represent scenarios when one element is uncertain and potentially not a set member.
- (B)
- The uncertainty and hesitancy of a decision-maker can be better captured by than , producing more precise and dependable outcomes.
- (C)
- Decision-makers can make better decisions with access to more complete and accurate information from .
- (D)
- When handling uncertain or missing data, delivers additional flexibility, which can result in more reliable and adaptable decision-making systems.
3.4.2. Benefits of Rather than
- (a)
- provides a more accurate and improved representation of uncertainty and ambiguous information than fuzzy sets. It can also represent the degree of hesitation in decision-making.
- (b)
- For handling ambiguous or missing data, provides greater flexibility. Under a single framework, it enables the representation of several kinds of uncertainty, including randomness, fuzziness, and incompleteness.
- (c)
- provides a clear and intuitive interpretation of each element’s membership and non-membership degrees, making it easy for decision-makers to understand and use and allowing for more informed and reliable decision-making.
3.5. Arithmetic Operation of
3.5.1. Arithmetic Operation of (1st Type):
- A.
- Addition of two s:
- B.
- Subtraction of two s:
- C.
- Scalar multiplication of :where be a scalar.
- D.
- Multiplication of two s:
- E.
- Division of two s:
- F.
- Inverse of :
- G.
- Power (scalar) of :
3.5.2. Arithmetic Operation of (2nd Type)
- A.
- Addition of two s:
- B.
- Subtraction of two s:
- C.
- Scalar multiplication of :where be a scalar.
- D.
- Multiplication of two s:
- E.
- Division of two s:
- F.
- Inverse of :
- G.
- Power (scalar) of :
3.6. De-Fuzzification of Generalized Dual Hesitant Hexagonal Fuzzy Number
- (I)
- Generalized dual hesitant hexagonal fuzzy numbers are a complex type of fuzzy number that can better represent uncertain or ambiguous information. We can obtain more accurate and precise defuzzification results by developing a new de-fuzzification method specifically for this type of fuzzy number.
- (II)
- With this defuzzification procedure, the de-fuzzified value is often between the six numbers of a hexagonal fuzzy number for any .
- (III)
- This new de-fuzzification method can be applied to various applications in different fields, such as engineering, finance, and economics, where generalized dual hesitant hexagonal fuzzy numbers are commonly used.
- (IV)
- The new de-fuzzification technique can be changed and adjusted to accommodate various fuzzy number types or problem domains. More versatility and adaptation in particular situations are possible because of this flexibility.
- (V)
- Creating a novel de-fuzzification approach can enhance the study of fuzzy sets and fuzzy logic since it can provide a unique perspective and methods for accessing ambiguous or uncertain data.
4. Multi-Criteria Decision Making Methodology
4.1. The Fuzzy Criteria Importance through Inter-Criteria Correlation (FCRITIC) Method
- A:
- Formulate a decision matrix in terms of Generalized Dual Hesitant Hexagonal Fuzzy Number ():Decision matrix given by DMs are asi.e.,whereare kth DMs ratting in , given on alternatives with respect to criteria . Here, criteria and alternative . Additionally, consider, hesitant variable .
- B:
- Aggregation of decisions of DMs assigned in Equation (40) on using the following equationwhere for all and .The aggregated decision results of the K decision makers are obtained by the Equation (41). Therefore, the aggregating decision matrix iswherehere, and with .
- C:
- De-fuzzify the decision matrix :De-fuzzify the decision matrix by the de-fuzzified formula and convert second type number to crisp number by the Equation (37). Now the de-fuzzifies decision matrix is formed aswhere is the de-fuzzifies value of number .
- D:
- Normalize the decision matrixThen, find the normalized decision matrix from the de-fuzzifies decision matrix , using the following formula:where
- E:
- Calculate the standard deviation for each criteria by the equation, as follows:where is the population mean, n is size of the population (i.e., number of criteria) and .
- F:
- Find the linear correlation coefficient between the criteria and . Determine the symmetric matrix of with elements which is the linear correlation coefficient between the vectors and and correlation coefficient criteria to criteria denoted by .
- G:
- Measure of the conflict created by the criteria:In this step, we have to calculate the measure of the conflict created by the criterion with respect to the decision situation defined by the rest of criteria.
- H:
- Determining the quantity of the information in relation to each criteria bywhere criteria .
- I:
- Determining the objective weights:Calculate the weight of the criteria denoted by and defined as follows:Finally, Equation (50) gives the criteria weight of each criteria .
4.2. The Fuzzy Weighted Aggregated Sum Product Assessment (FWASPAS) Approach
- A.
- Develop the decision matrix with respect to :
- B.
- Aggregation of DMs opinion:All ratings assigned by DMs on K decision matrices are aggregated by the Equation (41) and make a single decision matrix , shown in the previous section.
- C.
- Normalize the aggregated decision matrix :The aggregated decision matrix shown in the Equation (42) where every entry are of the second type appear in Equation (43). Then, normalize the decision matrix by normalizing every element. Normalized is denoted by and describe as follows:whereThen, the normalized decision matrix () is shown as
- D.
- Weight of the criteria:Criteria weights are calculated by the FCRITIC method in previous section by the Equation (50) and criteria weights are .
- E.
- Weighted Sum Normalized Decision Matrix:Find out the weighted sum normalized decision matrix by the formulawhere scalar multiplication of of the second type obeys the Equation (31).
- F.
- De-fuzzify the weighted sum normalized decision matrix :De-fuzzify matrix by the Equation (37) and update the decision matrix as
- G.
- Weighted Sum model (WSM):Determine the weighted sum model where as follows
- H.
- Weighted Product Normalized Decision Matrix:Find out the weighted product normalized decision matrix by the equationHere the scalar power of of the second type is obtained by the Equation (32).
- I.
- De-fuzzifies the weighted product normalized decision matrix :De-fuzzifies the matrix by the Equation (37) and renovate the decision matrix as
- J.
- Weighted Product model (WPM):Formulate the weighted product model where as follows
- K.
- Evaluate :Now, the Weighted Aggregated Sum Product Assessment (WASPAS) model value which is a unique combination of WSM and WPM is calculated as followswhere , is the coefficient of combined optimally. If the Weighted Sum Model and Weighted Product Model approaches have equal effect on the combined optimality criteria, then consider .
- L.
- Ranking the alternativeThe alternatives are ordered based on the value of the Equation (60), where are alternatives numbers. The alternative with the largest value is the best alternative and ranks first.
4.3. The Fuzzy Combined Compromise Solution (FCoCoSo) Approach
- 1.
- Build up the decision matrix on :Decision matrix constructed by DMs is shown in step “A” of Section 4.1. Decision matrix shown in Equation (38) with every entry are formed like Equation (40).
- 2.
- Aggregation of DMs opinion:Aggregate the K decision matrix in a single decision matrix by Equation (41).
- 3.
- Normalization of the decision matrix :
- 4.
- Weight of the criteria:Obtain weight of the criteria using FCRITIC method in the Section 4.1. Criteria weights are denoted by and described in Equation (50).
- 5.
- Weighted Sum model (WSM):In FWASPAS method (Section 4.2), calculated WSM data using the Equation (56).
- 6.
- Weighted Product Model (WPM):Similar way, from FWASPAS method (in Section 4.2) obtain WPM data applying Equation (59).
- 7.
- 8.
- Finally, rank the alternatives obtained based on the value ofwhere , and are taken form previous steps. Here, alternative numbers are .Rank alternatives based on values in increasing order.
4.4. Pseudo Code Depicting the Empirical Study Application
5. Brief Discussion of Alternative Diseases
5.1. Malaria
5.2. Influenza
5.3. Typhoid
5.4. Dengue
5.5. Monkey Pox
5.6. Ebola
5.7. Pneumonia
6. Symptom of Disease and Model Setup
7. Data Collection
- DM1: MD-Internal Medicine, MBBS General Physician
- DM2: MBBS, MD-Medicine, MD-USC, California, General Physician
- DM3: MBBS, MD-Pediatrics, MRCP (UK), Diploma in Child Health (DCH), Pediatrician
8. Numerical Description
Computational Complexity
- For the FCRITIC method, the K decision matrices have entries. Then, the aggregated decision matrix has operations. To de-fuzzifies the decision matrix, another operation are conducted. Normalizing the decision matrix calculation are performed. Calculate the standard division by n number of operations. We performed operation to find the correlation coefficients. To measure the conflict created by the criteria, operations are conducted. Finally, obtain the criteria weight by conducted operations. Total operations performed for the FCRITIC method are .
- For the FWASPAS technique, from the FCRITIC method, we already obtain aggregated decision matrix. Then, normalize the aggregated decision matrix by conducting operations. Another calculations was performed to the weighted sum decision matrix. To de-fuzzified the weighted sum decision matrix operations operated and weighted sum value calculated by m operations. Similarly, finding to weighted product decision matrix, de-fuzzification, and weighted product value , , and m operations performed, respectively. Finally, to rank the alternatives operations are conducted. Then, the total calculations conducted for the FWASPAS method are .
- For the FCoCoSo method, form the FCRITIC and the FWASPAS methods, we already obtain weighted sum value and weighted product value. Then, to calculate , and values operations conducted. Finally, to rank the alternatives on the basis of operations. Total calculation conducted for the FCoCoSo method are .
- For FCRITIC, number of calculation are .
- For FWASPAS, number of operations are .
- For FCoCoSo, number of operations are .
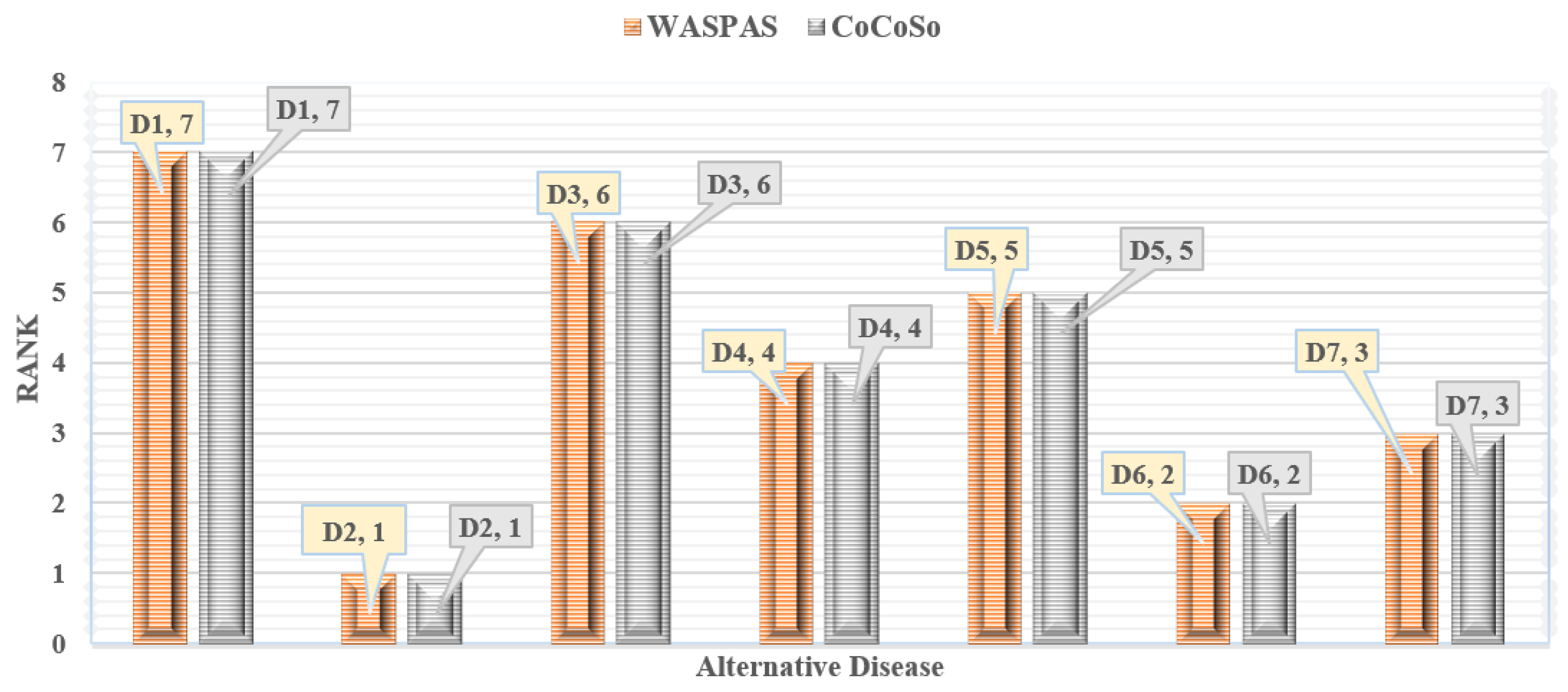
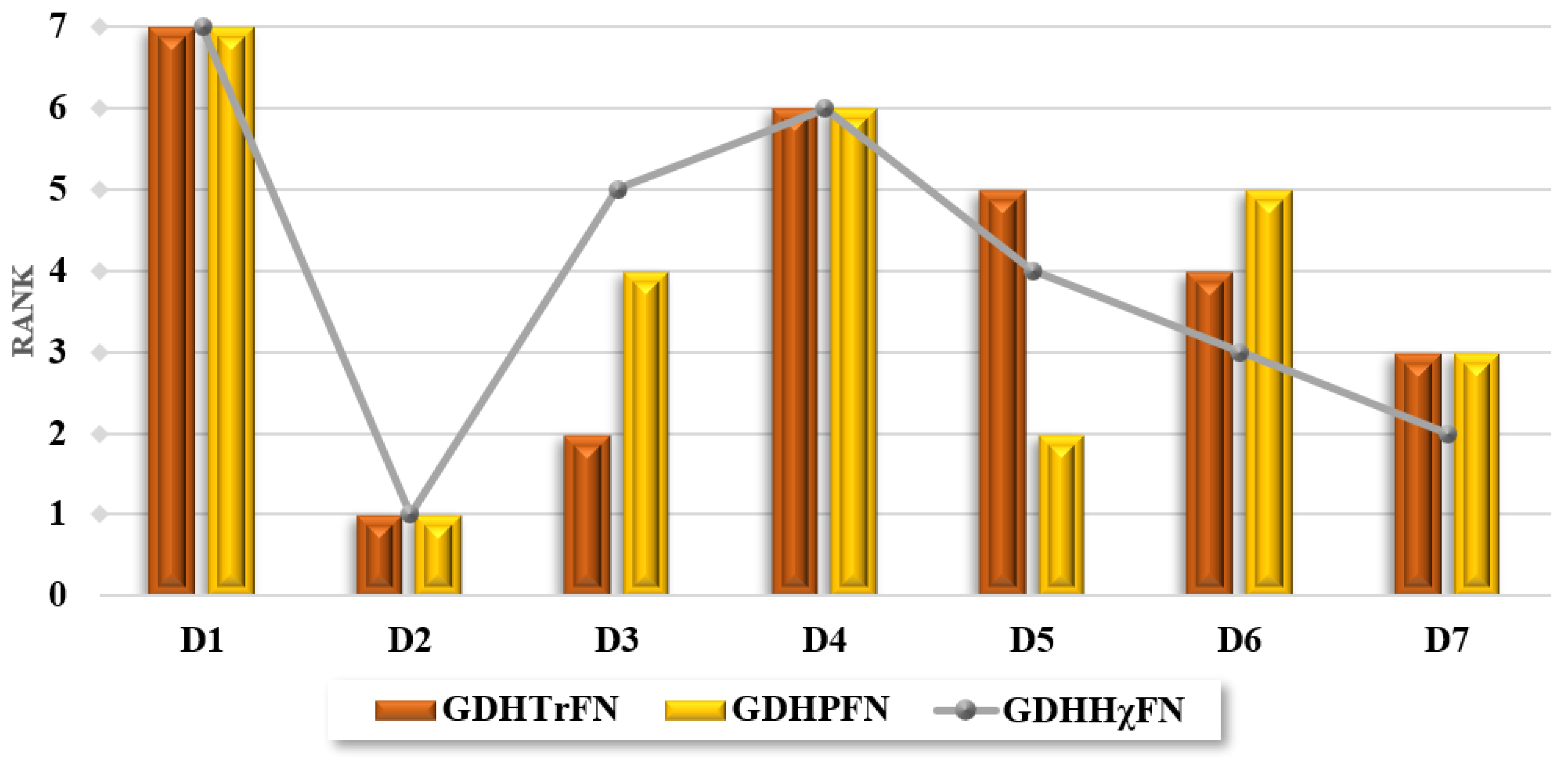
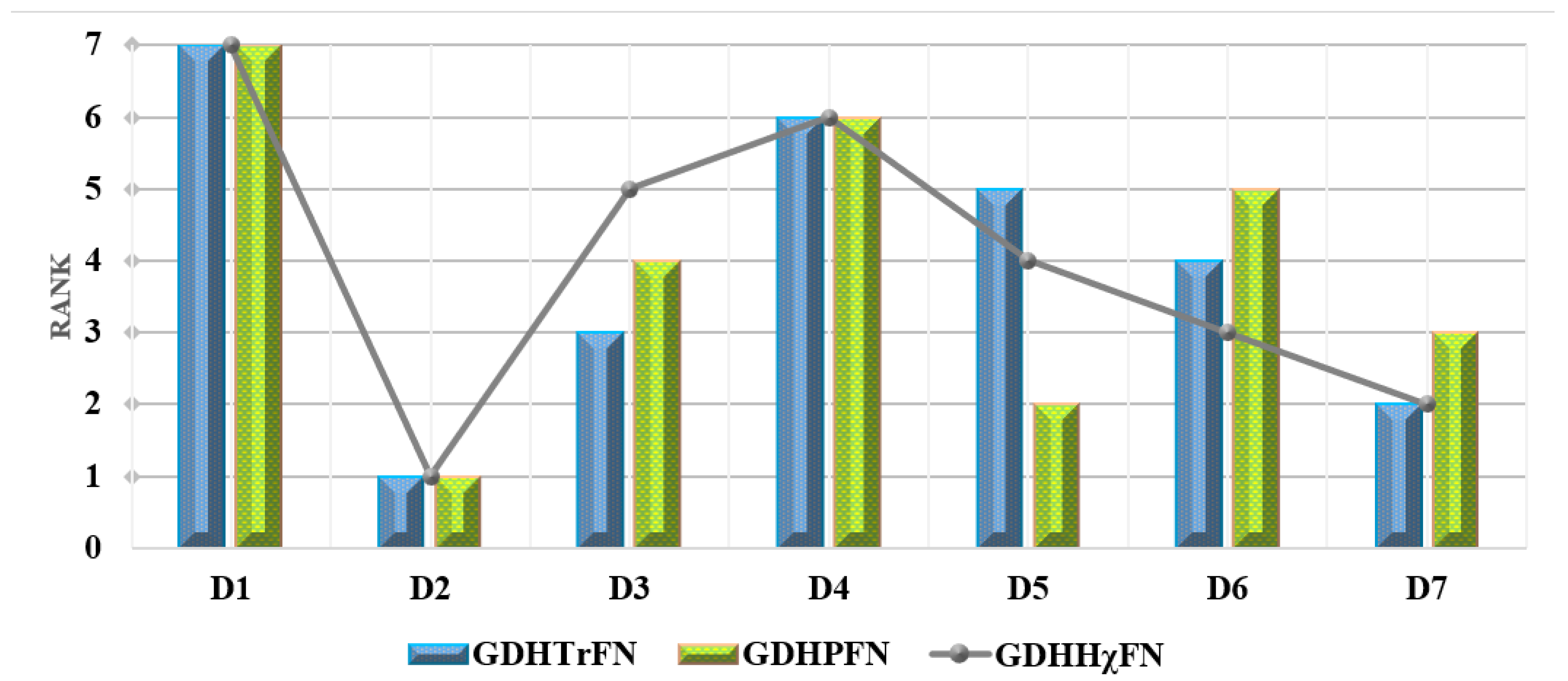
9. Sensitivity Analysis and Comparative Analysis
9.1. Sensitivity Analysis
9.2. Comparative Analysis
10. Practical Implications
11. Conclusions and Future Research Extension
11.1. Summary of Study and Contributions
- (a)
- In order to compare each , we have first proposed a new defuzzification technique for a and modified the arithmetic operation of first type and second type.
- (b)
- Then, we develop an aggregation formula to combine more than one decision matrix.
- (c)
- Here, we have used the FCRITIC approach to determine the weight of the criteria (symptom).
- (d)
- We have applied the FWASPAS and FCoCoSo methods simultaneously to determine the rank of the alternatives (Disease).
- (e)
- Finally, we conducted a comparative analysis using two alternative fuzzy numbers, and .
11.2. The Crucial Findings
11.3. The Restriction and Directions for Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, B.; Yun, Y.S. The generalized trapezoidal fuzzy sets. J. Chungcheong Math. Soc. 2011, 24, 253–266. [Google Scholar]
- Deli, I. A TOPSIS method by using generalized trapezoidal hesitant fuzzy numbers and application to a robot selection problem. J. Intell. Fuzzy Syst. 2020, 38, 779–793. [Google Scholar] [CrossRef]
- Chen, S.J.; Chen, S.M. Fuzzy risk analysis based on similarity measures of generalized fuzzy numbers. IEEE Trans. Fuzzy Syst. 2003, 11, 45–56. [Google Scholar] [CrossRef]
- Xu, P.; Su, X.; Wu, J.; Sun, X.; Zhang, Y.; Deng, Y. A note on ranking generalized fuzzy numbers. Expert Syst. Appl. 2012, 39, 6454–6457. [Google Scholar] [CrossRef]
- Li, G.; Kou, G.; Lin, C.; Xu, L.; Liao, Y. Multi-attribute decision making with generalized fuzzy numbers. J. Oper. Res. Soc. 2015, 66, 1793–1803. [Google Scholar] [CrossRef]
- Chen, T.Y. Multiple criteria group decision-making with generalized interval-valued fuzzy numbers based on signed distances and incomplete weights. Appl. Math. Model. 2012, 36, 3029–3052. [Google Scholar] [CrossRef]
- Pedrycz, W. On generalized fuzzy relational equations and their applications. J. Math. Anal. Appl. 1985, 107, 520–536. [Google Scholar] [CrossRef] [Green Version]
- Keikha, A. Generalized hesitant fuzzy numbers and their application in solving MADM problems based on TOPSIS method. Soft Comput. 2022, 26, 4673–4683. [Google Scholar] [CrossRef]
- Wan, S.; Dong, J.; Chen, S.M. Fuzzy best-worst method based on generalized interval-valued trapezoidal fuzzy numbers for multi-criteria decision-making. Inf. Sci. 2021, 573, 493–518. [Google Scholar] [CrossRef]
- Song, Y.; Hu, J. Vector similarity measures of hesitant fuzzy linguistic term sets and their applications. PLoS ONE 2017, 12, E0189579. [Google Scholar] [CrossRef] [Green Version]
- Liao, H.; Xu, Z.; Zeng, X.J.; Merigó, J.M. Qualitative decision making with correlation coefficients of hesitant fuzzy linguistic term sets. Knowl.-Based Syst. 2015, 76, 127–138. [Google Scholar] [CrossRef]
- Mardani, A.; Saraji, M.K.; Mishra, A.R.; Rani, P. A novel extended approach under hesitant fuzzy sets to design a framework for assessing the key challenges of digital health interventions adoption during the COVID-19 outbreak. Appl. Soft Comput. 2020, 96, 106613. [Google Scholar] [CrossRef]
- Ghorui, N.; Ghosh, A.; Mondal, S.P.; Bajuri, M.Y.; Ahmadian, A.; Salahshour, S.; Ferrara, M. Identification of dominant risk factor involved in spread of COVID-19 using hesitant fuzzy MCDM methodology. Results Phys. 2021, 21, 103811. [Google Scholar] [CrossRef]
- Ali, W.; Shaheen, T.; Haq, I.U.; Toor, H.G.; Akram, F.; Jafari, S.; Uddin, M.Z.; Hassan, M.M. Multiple-Attribute Decision Making Based on Intuitionistic Hesitant Fuzzy Connection Set Environment. Symmetry 2023, 15, 778. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, Y.; Huang, J.; Wei, J.; Herrera-Viedma, E. Social network clustering and consensus-based distrust behaviors management for large-scale group decision-making with incomplete hesitant fuzzy preference relations. Appl. Soft Comput. 2022, 117, 108373. [Google Scholar] [CrossRef]
- Aikhuele, D.O.; Odofin, S. A generalized triangular intuitionistic fuzzy geometric averaging operator for decision-making in engineering and management. Information 2017, 8, 78. [Google Scholar] [CrossRef] [Green Version]
- Rajendran, C.; Ananthanarayanan, M. Fuzzy criticalpath method with hexagonal and generalised hexagonal fuzzy numbers using ranking method. Int. J. Appl. Eng. Res. 2018, 13, 11877–11882. [Google Scholar]
- Ritmak, N.; Rattanawong, W.; Vongmanee, V. The dynamic evaluation model of health sustainability under MCDM benchmarking health indicator standards. Int. J. Environ. Res. Public Health 2022, 20, 259. [Google Scholar] [CrossRef]
- Mumtaz, A. Prioritizing and overcoming barriers to e-health use among elderly people: Implementation of the analytical hierarchical process (AHP). J. Healthc. Eng. Hindawi 2022, 2022, 7852806. [Google Scholar] [CrossRef] [PubMed]
- Yas, Q.M.; Adday, B.N.; Abed, A.S. Evaluation multi diabetes mellitus symptoms by integrated fuzzy-based MCDM approach. Turk. J. Comput. Math. Educ. 2021, 12, 4069–4082. [Google Scholar]
- Yildirim, F.S.; Sayan, M.; Sanlidag, T.; Uzun, B.; Ozsahin, D.U.; Ozsahin, I. Comparative evaluation of the treatment of COVID-19 with multi-criteria decision-making techniques. J. Healthc. Eng. Hindawi 2021, 2021, 8864522. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Tsai, J.F.; Dang, T.T.; Lin, M.H.; Pham, H.A.; Nguyen, K.A. A hybrid spherical fuzzy MCDM approach to prioritize governmental intervention strategies against the COVID-19 pandemic: A case study from Vietnam. Mathematics 2021, 9, 2626. [Google Scholar] [CrossRef]
- Addy, M.; Chaudhuri, A.K.; Das, A. Role of data mining techniques and MCDM model in detection and severity monitoring to serve as precautionary methodologies against ‘Dengue’. In Proceedings of the International Conference on Computer Science, Engineering and Applications (ICCSEA), Gunupur, India, 13–14 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Mohammed, M.A.; Abdulkareem, K.H.; Al-Waisy, A.S.; Mostafa, S.A.; Al-Fahdawi, S.; Dinar, A.M.; Alhakami, W.; Baz, A.; Al-Mhiqani, M.N.; Alhakami, H.; et al. Benchmarking methodology for selection of optimal COVID-19 diagnostic model based on entropy and TOPSIS methods. IEEE Access 2020, 8, 99115–99131. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Gamal, A.; Manogaran, G.; Son, L.H.; Long, H.V. A novel group decision making model based on neutrosophic sets for heart disease diagnosis. Multimed. Tools Appl. 2020, 79, 9977–10002. [Google Scholar] [CrossRef]
- Sharawat, K.; Dubey, S.K. Diet recommendation for diabetic patients using MCDM approach. Adv. Intell. Syst. Comput. 2018, 624, 239–246. [Google Scholar] [CrossRef]
- Basanta, H.; Huang, Y.P.; Lee, T.T. Intuitive IoT-based H2U healthcare system for elderly people. In Proceedings of the 13th International Conference on Networking, Sensing, and Control (ICNSC), Mexico City, Mexico, 28–30 April 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Uzoka, F.M.; Nwokoro, C.; Obot, O.; Ekpenyong, M.; Udo, A.I.A.; Akinnuwesi, B. Analytic hierarchy process model for the diagnosis of typhoid fever. In Proceedings of the Future Technologies Conference (FTC), Vancouver, Canada, 21–23 October 2022; pp. 341–358. [Google Scholar] [CrossRef]
- Fantini, J.; Chahinian, H.; Yahi, N. A vaccine strategy based on the identification of an annular ganglioside binding motif in Monkeypox virus protein E8L. Viruses 2022, 14, 2531. [Google Scholar] [CrossRef]
- Kaler, J.; Hussain, A.; Flores, G.; Kheiri, S.; Desrosiers, D. Monkeypox: A comprehensive review of transmission, pathogenesis, and manifestation. Cureus 2022, 14, e26531. [Google Scholar] [CrossRef]
- Nakasi, R.; Mwebaze, E.; Zawedde, A. Mobile-aware deep learning algorithms for malaria parasites and white blood cells localization in thick blood smears. Algorithms 2021, 14, 17. [Google Scholar] [CrossRef]
- Abodayeh, K.; Raza, A.; Rafiq, M.; Arif, M.S.; Naveed, M.; Zeb, Z.; Abbas, S.Z.; Shahzadi, K.; Sarwar, S.; Naveed, Q.; et al. Analysis of pneumonia model via efficient computing techniques; Computers, Materials & Continua. Mater. Contin. 2021, 70, 6073–6088. [Google Scholar] [CrossRef]
- Bhuju, G.; Phaijoo, G.R.; Gurung, D.B. Fuzzy approach analyzing SEIR-SEI dengue dynamics. Biomed Res. Int. 2020, 2020, 1508613. [Google Scholar] [CrossRef]
- Nathan, A.M.; Teh, C.S.J.; Jabar, K.A.; Teoh, B.T.; Tangaperumal, A.; Westerhout, C.; Zaki, R.; Eg, K.P.; Thavagnanam, S.; Bruyne, J.A.D. Bacterial pneumonia and its associated factors in children from a developing country: A prospective cohort study. PLoS ONE 2020, 15, e0228056. [Google Scholar] [CrossRef] [PubMed]
- Modibbo, U.M.; Heman, E.D.; Hafisu, R. Multi-criteria decision analysis for malaria control strategies using analytic hierarchy process: A case of Yola North local government area, Adamawa state Nigeria. Amity J. Comput. Sci. (Ajcs) 2019, 3, 43–50. [Google Scholar]
- Samanlioglu, F. Evaluation of influenza intervention strategies in Turkey with fuzzy AHP-VIKOR. J. Healthc. Eng. 2019, 2019, 9486070. [Google Scholar] [CrossRef] [Green Version]
- Majid, N.A.; Nazi, N.M.; Mohamed, A.F. Distribution and spatial pattern analysis on dengue cases in Seremban district, Negeri Sembilan, Malaysia. Sustainability 2019, 11, 3572. [Google Scholar] [CrossRef] [Green Version]
- Martin, N.; Ritha, W.; Vinoline, I.A.; Selvi, P. Analysis of the risk of ebola disease: Fuzzy VIKOR method based on the possibility theory. Int. J. Manag. Appl. Sci. 2019, 5, 37–40. [Google Scholar]
- Gbadamosi, B.; Ojo, M.M.; Oke, S.I.; Matadi, M.B. Qualitative analysis of a dengue fever model. Math. Comput. Appl. 2018, 23, 33. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.Y.; Eun, S.J.; Park, D.K. Malaria vulnerability map mobile system development using GIS-based decision-making technique. Locat.-Based Mob. Mark. Innov. 2018, 2018, 8436210. [Google Scholar] [CrossRef] [Green Version]
- Tilahun, G.T.; Makinde, O.D.; Malonza, D. Modelling and optimal control of typhoid fever disease with cost-effective strategies. Comput. Math. Methods Med. 2017, 2017, 2324518. [Google Scholar] [CrossRef] [Green Version]
- Kourtis, A.P.; Appelgren, K.; Chevalier, M.S.; McElroy, A. Ebola virus disease focus on children. Pediatr. Infect. Dis. J. 2015, 34, 893–897. [Google Scholar] [CrossRef] [Green Version]
- Dewan, A.M.; Corner, R.; Hashizume, M.; Ongee, E.T. Typhoid fever and its association with environmental factors in the Dhaka metropolitan area of Bangladesh: A spatial and time-series approach. PLoS Neglected Trop. Dis. 2013, 7, e1998. [Google Scholar] [CrossRef] [Green Version]
- Araz, O.M. Integrating complex system dynamics of pandemic influenza with a multi-criteria decision making model for evaluating public health strategies. J. Syst. Sci. Syst. Eng. 2013, 22, 319–339. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, J.; Zhang, G. Combining one class classification models for avian influenza outbreaks. In Proceedings of the Symposium on Computational Intelligence in Multicriteria Decision-Making (MDCM), Paris, France, 11–15 April 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Attaluri, P.K.; Chen, Z.; Weerakoon, A.M.; Lu, G. Integrating decision tree and hidden markov model (HMM) for subtype prediction of human influenza a virus. In Cutting-Edge Research Topics on Multiple Criteria Decision Making; Springer: Berlin/Heidelberg, Germany, 2009; Volume 35, pp. 52–58. [Google Scholar] [CrossRef]
- Sindhu, M.S.; Rashid, T. Selection of alternative based on linear programming and the extended fuzzy TOPSIS under the framework of dual hesitant fuzzy sets. Soft Comput. 2023, 27, 1985–1996. [Google Scholar] [CrossRef]
- Ismael, S.F.; Alias, A.H.; Zaidan, A.A.; Zaidan, B.B.; Alsattar, H.A.; Qahtan, S.; Albahri, O.S.; Talal, M.; Alamoodi, A.H.; Mohammed, R.T. Toward sustainable transportation: A pavement strategy selection based on the extension of dual-hesitant fuzzy multicriteria decision-making methods. IEEE Trans. Fuzzy Syst. 2023, 31, 380–393. [Google Scholar] [CrossRef]
- Kang, D.; Anuja, A.; Narayanamoorthy, S.; Gangemi, M.; Ahmadian, A. A dual hesitant q-rung orthopair enhanced MARCOS methodology under uncertainty to determine a used PPE kit disposal. Environ. Sci. Pollut. Res. 2022, 29, 89625–89642. [Google Scholar] [CrossRef]
- Calache, L.D.D.R.; Camargo, V.C.B.; Osiro, L.; Carpinetti, L.C.R. A genetic algorithm based on dual hesitant fuzzy preference relations for consensus group decision making. Appl. Soft Comput. 2022, 121, 108778. [Google Scholar] [CrossRef]
- Ni, Y.; Zhao, H.; Xu, Z.; Wang, Z. Multiple attribute decision-making method based on projection model for dual hesitant fuzzy set. Fuzzy Optim. Decis. Mak. 2022, 21, 263–289. [Google Scholar] [CrossRef]
- Guirao, J.L.G.; Sindhu, M.S.; Rashid, T.; Kashif, A. Multiple criteria decision-making based on vector similarity measures under the framework of dual hesitant fuzzy sets. Discret. Dyn. Nat. Soc. 2020, 2020, 1425487. [Google Scholar] [CrossRef]
- Garg, H.; Kaur, G. Quantifying gesture information in brain hemorrhage patients using probabilistic dual hesitant fuzzy sets with unknown probability information. Comput. Ind. Eng. 2020, 140, 106211. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, Z.; Wang, H. The strategy selection problem on artificial intelligence with an integrated VIKOR and AHP method under probabilistic dual hesitant fuzzy information. IEEE Access 2019, 7, 103979–103999. [Google Scholar] [CrossRef]
- Chen, H.; Xu, G.; Yang, P. Multi-attribute decision-making approach based on dual hesitant fuzzy information measures and their applications. Mathematics 2019, 7, 786. [Google Scholar] [CrossRef] [Green Version]
- Narayanamoorthy, S.; Ramya, L.; Baleanu, D.; Kureethara, J.V.; Annapoorani, V. Application of normal wiggly dual hesitant fuzzy sets to site selection for hydrogen underground storage. Int. J. Hydrogen Energy 2019, 44, 28874–28892. [Google Scholar] [CrossRef]
- Liu, P.; Cheng, S. Interval-valued probabilistic dual hesitant fuzzy sets for multi-criteria group decision-making. Int. J. Comput. Intell. Syst. 2019, 12, 1393–1411. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.; Xu, Z.; Zhao, H.; Su, Z. Probabilistic dual hesitant fuzzy set and its application in risk evaluation. Knowl.-Based Syst. 2017, 127, 16–28. [Google Scholar] [CrossRef]
- Deli, I.; Karaaslan, F. Generalized trapezoidal hesitant fuzzy numbers and their applications to multi criteria decision-making problems. Soft Comput. 2021, 25, 1017–1032. [Google Scholar] [CrossRef]
- Sultan, A.; Sałabun, W.; Faizi, S.; Ism, M. Hesitant fuzzy linear regression model for decision making. Symmetry 2021, 13, 1846. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Güler, M. A combined hesitant fuzzy MCDM approach for supply chain analytics tool evaluation. Appl. Soft Comput. 2021, 112, 107812. [Google Scholar] [CrossRef]
- Farid, H.M.A.; Riaz, M. Some generalized q-rung orthopair fuzzy Einstein interactive geometric aggregation operators with improved operational laws. Int. J. Intell. Syst. 2021, 36, 7239–7273. [Google Scholar] [CrossRef]
- Zulqarnain, R.M.; Saeed, M.; Ali, B.; Abdal, S.; Saqlain, M.; Ahamad, M.I.; Zafar, Z. Generalized fuzzy TOPSIS to solve multi-criteria decision-making problems. J. New Theory 2020, 32, 40–50. [Google Scholar]
- Yue, Q.; Zhang, L. Two-sided matching for hesitant fuzzy numbers in smart intelligent technique transfer. Mech. Syst. Signal Process. 2020, 139, 106643–106653. [Google Scholar] [CrossRef]
- Garg, H.; Keikha, A.; Nehi, H.M. Multiple-attribute decision-making problem using TOPSIS and choquet integral with hesitant fuzzy number information. Math. Probl. Eng. 2020, 2020, 9874951. [Google Scholar] [CrossRef]
- Zhong, Y.; Guo, X.; Gao, H.; Qin, Y.; Huang, M.; Luo, X. A new multi-criteria decision-making method based on Pythagorean hesitant fuzzy Archimedean Muirhead mean operators. J. Intell. Fuzzy Syst. 2019, 37, 5551–5571. [Google Scholar] [CrossRef] [Green Version]
- Garg, H.; Arora, R. Dual hesitant fuzzy soft aggregation operators and their application in decision-making. Cogn. Comput. 2018, 10, 769–789. [Google Scholar] [CrossRef]
- Faizi, S.; Rashid, T.; Sałabun, W.; Zafar, S.; Wątróbski, J. Decision making with uncertainty using hesitant fuzzy sets. Int. J. Fuzzy Syst. 2018, 20, 93–103. [Google Scholar] [CrossRef] [Green Version]
- Faizi, S.; Sałabun, W.; Rashid, T.; Watrobski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Liang, D.; Xu, Z. The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy sets. Appl. Soft Comput. 2017, 60, 167–179. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, Z.; Wang, H. Dual hesitant fuzzy VIKOR method for multi-criteria group decision making based on fuzzy measure and new comparison method. Inf. Sci. 2017, 388–389, 1–16. [Google Scholar] [CrossRef]
- Khan, M.S.A.; Abdullah, S.; Ali, A.; Siddiqui, N.; Amin, F. Pythagorean hesitant fuzzy sets and their application to group decision making with incomplete weight information. J. Intell. Fuzzy Syst. 2017, 33, 3971–3985. [Google Scholar] [CrossRef]
- Wang, L.; Shen, Q.; Zhu, L. Dual hesitant fuzzy power aggregation operators based on Archimedean t-conorm and t-norm and their application to multiple attribute group decision making. Appl. Soft Comput. 2016, 38, 23–50. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues Lima, F., Jr.; Osiro, L.; Carpinetti, L.C.R. A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. Appl. Soft Comput. 2014, 21, 194–209. [Google Scholar] [CrossRef]
- Zadeh, L.A. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 28–44. [Google Scholar] [CrossRef] [Green Version]
- Rajaprakash, S.; Ramalingam, P.; Purangan, J. Intuitionistic fuzzy analytical hierarchy process with fuzzy Delphi method. Glob. J. Pure Appl. Math. 2011, 11, 1677–1697. [Google Scholar]
- Ma, X.; Fei, Q.; Qin, H.; Li, H.; Chen, W. A new efficient decision making algorithm based on interval-valued fuzzy soft set. Appl. Intell. 2021, 51, 3226–3240. [Google Scholar] [CrossRef]
- Ma, X.; Qin, H.; Abawajy, J.H. Interval-valued intuitionistic fuzzy soft sets based decision-making and parameter reduction. IEEE Trans. Fuzzy Syst. 2022, 30, 357–369. [Google Scholar] [CrossRef]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the International Conference on Fuzzy Systems, Jeju, Republic of Korea, 20–24 August 2009; pp. 1378–1382. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Torra, V.; Xu, Z.; Herrera, F. Hesitant fuzzy sets: State of the art and future directions. Int. J. Intell. Syst. 2014, 29, 495–524. [Google Scholar] [CrossRef]
- Chen, N.; Xu, Z.; Xia, M. Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis. Appl. Math. Model. 2013, 37, 2197–2211. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z.; Xia, M. Dual hesitant fuzzy sets. J. Appl. Math. 2012, 2012, 879629. [Google Scholar] [CrossRef] [Green Version]
- Tyagi, S.K. Correlation coefficient of dual hesitant fuzzy sets and its applications. Appl. Math. Model. 2015, 39, 7082–7092. [Google Scholar] [CrossRef]
- Gazi, K.H.; Mondal, S.P.; Chatterjee, B.; Ghorui, N.; Ghosh, A.; De, D. A new synergistic strategy for ranking restaurant locations: A decision-making approach based on the hexagonal fuzzy numbers. Rairo Oper. Res. 2023, 57, 571–608. [Google Scholar] [CrossRef]
- Rajarajeswari, P.; Sudha, A.S.; Karthika, R. A new operation on hexagonal fuzzy number. International Journal of Fuzzy Logic Sys. 2013, 3, 15–26. [Google Scholar]
- Nayagam, V.L.G.; Murugan, J. Hexagonal fuzzy approximation of fuzzy numbers and its applications in MCDM. Complex Intell. Syst. 2021, 7, 1459–1487. [Google Scholar] [CrossRef]
- Nayagam, V.L.G.; Murugan, J.; Suriyapriya, K. Hexagonal fuzzy number inadvertences and its applications to MCDM and HFFLS based on complete ranking by score functions. Comput. Appl. Math. 2020, 39, 323. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, S.C.; Öztaysi, B. Present worth analysis using hesitant fuzzy sets. In Proceedings of the 16th World Congress of the International Fuzzy Systems Association (IFSA), Gijon, Spain, 30 June–3 July 2015; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 255–259. [Google Scholar] [CrossRef] [Green Version]
- Sangeetha, K.; Parimala, M. On solving a fuzzy game problem using hexagonal fuzzy numbers. Mater. Today Proc. 2021, 47, 2102–2106. [Google Scholar] [CrossRef]
- Jangid, V.; Kumar, G. Hexadecagonal fuzzy numbers: Novel ranking and defuzzification techniques for fuzzy matrix game problems. Fuzzy Inf. Eng. 2022, 14, 84–122. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The CRITIC method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Kasim, M.M.; Hamid, R.; Ghazali, M.F. A modified CRITIC method to estimate the objective weights of decision criteria. Symmetry 2021, 13, 973. [Google Scholar] [CrossRef]
- Rudnik, K.; Bocewicz, G.; Kucińska-Landwójtowicz, A.; Czabak-Górska, I.D. Ordered fuzzy WASPAS method for selection of improvement projects. Expert Syst. Appl. 2021, 169, 114471. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevi cius, A. Optimization of weighted aggregated sum product assessment. Elektron. Elektrotechnika 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Zavadskas, E.K.; Turskis, Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2019, 57, 2501–2519. [Google Scholar] [CrossRef]
- Luo, F.; Luo, X. Intelligent disease prediagnosis only based on symptoms. J. Healthc. Eng. 2021, 2021, 9963576. [Google Scholar] [CrossRef]
- Alzahrani, F.A.; Ghorui, N.; Gazi, K.H.; Giri, B.C.; Ghosh, A.; Mondal, S.P. Optimal site selection for women university using neutrosophic multi-criteria decision making approach. Buildings 2023, 13, 152. [Google Scholar] [CrossRef]




| Authors | Citation | Years | MCDM Methods | Application Area |
|---|---|---|---|---|
| Ritmak, N. et al. | [18] | 2023 | AHP and TOPSIS | Health sustainability model |
| Mumtaz, A. | [19] | 2022 | AHP | Prioritizing and overcoming barriers to e-health |
| Yas, Q. M. et al. | [20] | 2021 | TOPSIS | Evaluation of multi diabetes mellitus symptoms |
| Yildirim, F. S. et al. | [21] | 2021 | PROMETHEE and VIKOR | Treatment of COVID-19 |
| Nguyen, P.H. et al. | [22] | 2021 | SF-AHP and FWASPAS | COVID-19 Pandemic |
| Addy, M. et al. | [23] | 2020 | MCDM | Detection and severity monitoring to serve for Dengue |
| Mohammed, M. A. et al. | [24] | 2020 | Entropy and TOPSIS | Selection of optimal COVID-19 diagnostic model |
| Abdel-Basset, M. et al. | [25] | 2020 | N-MCDM | Heart disease diagnosis |
| Sharawat, K. et al. | [26] | 2018 | AHP and TOPSIS | Diet recommendation for diabetic patients |
| Basanta, H. et al. | [27] | 2016 | AHP | IoT-based H2U healthcare system |
| This paper | 2023 | FCRITIC, FWASPAS, FCoCoSo | Diagnosis of a patient |
| Authors | Citation | Year | Types of Diseases | Optimization Techniques |
|---|---|---|---|---|
| Faith-Michael Uzoka et al. | [28] | 2022 | Typhoid | AHP |
| Jacques Fantini et al. | [29] | 2022 | Monkeypox | – |
| Jasndeep Kaler et al. | [30] | 2022 | Monkeypox | – |
| Rose Nakasi et al. | [31] | 2021 | Malaria | Faster R-CNN and SSD MobileNet |
| Abodayeh, K. et al. | [32] | 2021 | Pneumonia | Euler, Runge–Kutta and non-standard finite difference technique |
| Madhumita Addy et al. | [23] | 2020 | Dengue | MCDM |
| G. Bhuju et al. | [33] | 2020 | Dengue | Fuzzy SEIR-SEI |
| Anna Marie Nathan et al. | [34] | 2020 | Pneumonia | – |
| Umar M. Modibbo et al. | [35] | 2019 | Malaria | AHP |
| Funda Samanlioglu | [36] | 2019 | Influenza | AHP and VIKOR |
| Nuriah Abd Majid et al. | [37] | 2019 | Dengue | Spatial Mean Center, Standard Distant and Standard Deviational Ellipse |
| Nivetha Martin et al. | [38] | 2019 | Ebola | Fuzzy VIKOR |
| Gbadamosi, B. et al. | [39] | 2018 | Dengue | Disease-Free Equilibrium (DFE) |
| Jung-Yoon Kim et al. | [40] | 2018 | Malaria | AHP and PROMETHEE |
| Tilahun, G. T. et al. | [41] | 2017 | Typhoid | Disease-Free Equilibrium (DFE) |
| Athena P. Kourtis et al. | [42] | 2015 | Ebola | – |
| Ashraf M. Dewan et al. | [43] | 2013 | Typhoid | Spatial analysis and Cluster mapping |
| Ozgur Maraz | [44] | 2013 | Influenza | AHP |
| Jie Zhang et al. | [45] | 2011 | Influenza | One class classification model |
| Pavan K. Attaluri et al. | [46] | 2009 | Influenza | Hidden Markov Model |
| This paper | 2023 | 7 diseases | FCRITIC, FWASPAS, FCoCoSo |
| Authors | Citation | Year | Application Area | Methodology |
|---|---|---|---|---|
| Sindhu et al. | [47] | 2023 | Selection of alternative based on linear programming | Fuzzy TOPSIS |
| S. F. Ismael et al. | [48] | 2023 | A Pavement Strategy Selection | DH-FWZIC, DH-FDOSM |
| Daekook Kang et al. | [49] | 2022 | determine a used PPE kit disposal | MARCOS |
| Verma et al. | [50] | 2022 | Consensus group decision-making | A genetic algorithm based |
| Ni, Y. et al. | [51] | 2022 | Product marketing | Dual hesitant MADM |
| Guirao et al. | [52] | 2020 | Multiple Criteria Decision-Making Based on Vector Similarity Measures | Linear programming |
| Garg et al. | [53] | 2020 | Quantifying gesture information in brain hemorrhage patients | Entropy |
| Z. Ren et al. | [54] | 2019 | The Strategy Selection Problem on Artificial Intelligence | VIKOR, AHP |
| Huiping Chen et al. | [55] | 2019 | Dual Hesitant Fuzzy Information Measures and Their Applications | Entropy |
| Narayanamoorthy, S. et al. | [56] | 2019 | Site selection for hydrogen underground storage | VIKOR |
| Liu et al. | [57] | 2019 | Risk Evaluation | Three phased MCGDM |
| Hao, Z. et al. | [58] | 2017 | Risk evaluation | PDHFs MCDM |
| This paper | 2023 | Prediagnosis of disease based on symptoms | FCRITIC, FWASPAS, and FCoCoSo |
| Authors | Year | Hesitant Type | Optimization Methods | Applications | |
|---|---|---|---|---|---|
| Deli, I. et al. | [59] | 2021 | Generalized Trapezoidal Hesitant Fuzzy Numbers (GTHFN) | Ranking method of GTHFN | Best option to invest an investment company |
| Sultan, A. et al. | [60] | 2021 | Triangular hesitant fuzzy set | TOPSIS | Determine the business chain for most revenue |
| Büyüközkan, G. et al. | [61] | 2021 | Hesitant fuzzy linguistic term set | AHP and MULTIMOORA | Supply chain analysis on logistics services |
| Farid, H.M.A. et al. | [62] | 2021 | q-rung orthopair fuzzy numbers | Gq-ROFEIWG | Determine its upcoming year’s strategy on multinational corporation |
| Zulqarnain, R.M. et al. | [63] | 2020 | Generalized triangular fuzzy number (GTFN) | TOPSIS | Garments industry hire a supplier |
| Yue, Q. et al. | [64] | 2020 | Hesitant fuzzy number (HFN) | Two-sided matching (TsM) method | Smart intelligent technique transfer |
| Garg, H. et al. | [65] | 2020 | Generalized trapezoidal hesitant fuzzy number (GTHFN) | TOPSIS and Choquet integral (CI) | Artificial numerical example |
| Zhong, Y. et al. | [66] | 2019 | Pythagorean hesitant fuzzy set | MCDM method based on the PHFAMM and WPHFAMM operators | Green supply chain management |
| Garg, H. et al. | [67] | 2018 | Dual hesitant fuzzy soft set | Aggregation operator | Monsoon rains in river catchments |
| Faizi, S. et al. | [68] | 2018 | L–R-type generalized fuzzy numbers | COMET | Electrical resistance |
| Faizi, S. et al. | [69] | 2017 | L-R-type generalized fuzzy numbers | Characteristic Objects Method (COMET) | Production on mobile factory |
| Liang, D. et al. | [70] | 2017 | Hesitant Pythagorean fuzzy sets | TOPSIS | Energy development strategy |
| Zhiliang, R. et al. | [71] | 2017 | Dual hesitant fuzzy set | VIKOR | Smartphone design firms to increasing profit |
| Khan, M.S.A. et al. | [72] | 2017 | Pythagorean hesitant fuzzy set | MADM on Pythagorean hesitant fuzzy information | Choose the best option of investment company |
| Wang, L. et al. | [73] | 2016 | Dual hesitant fuzzy set | Power aggregation operator | Urban traffic route choices |
| This paper | 2023 | Generalized dual hesitant hexagonal fuzzy set | FCRITIC, FWASPAS, and FCoCoSo | Prediagnosis of disease based on symptoms |
| Kahram- an, G. et al. [89] | Rajend- ran, C. et al. [17] | Sangee- tha K. et al. [90] | Jangid, V. et al. [91] | Proposed Model | |
|---|---|---|---|---|---|
| Equation (24) | Equation (4) | Equation (6) | Equation (40) | Equation (33) | |
| Linguistic Terms | (2nd Type) | De-Fuzzified Value |
|---|---|---|
| Strongly Significant (SSG) | ||
| Highly Significant (HSG) | ||
| More Significant (MSG) | ||
| Significant (SG) | ||
| Less Significant (LSG) | ||
| Below Significant (BSG) | ||
| Weakly Significant (WSG) |
| Criteria | Fever | Body Ache | Fatigue | Chills | SOB | Nausea | Vomiting | Diarrhea | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Alternative | ||||||||||
| DM 1 | SSG | LSG | LSG | MSG | WSG | BSG | LSG | SG | ||
| SSG | HSG | SG | LSG | SG | SG | LSG | HSG | |||
| SSG | SG | WSG | MSG | WSG | HSG | LSG | BSG | |||
| SSG | LSG | WSG | MSG | WSG | HSG | LSG | BSG | |||
| SG | SG | BSG | MSG | HSG | HSG | BSG | WSG | |||
| SSG | HSG | LSG | LSG | BSG | BSG | HSG | SG | |||
| SSG | LSG | BSG | SG | HSG | SG | LSG | WSG | |||
| Criteria | Fever | Body Ache | Fatigue | Chills | SOB | Nausea | Vomiting | Diarrhea | ||
| Alternative | ||||||||||
| DM 2 | HSG | LSG | LSG | SG | WSG | LSG | LSG | MSG | ||
| SSG | HSG | MSG | LSG | SG | SG | BSG | SSG | |||
| HSG | MSG | WSG | MSG | WSG | MSG | SG | BSG | |||
| HSG | SG | WSG | HSG | WSG | HSG | BSG | LSG | |||
| SG | SG | WSG | SG | HSG | HSG | LSG | WSG | |||
| SSG | MSG | LSG | LSG | BSG | SG | HSG | MSG | |||
| HSG | SG | BSG | SG | SSG | SG | SG | WSG | |||
| Criteria | Fever | Body Ache | Fatigue | Chills | SOB | Nausea | Vomiting | Diarrhea | ||
| Alternative | ||||||||||
| DM 3 | HSG | LSG | LSG | HSG | WSG | BSG | BSG | SG | ||
| SSG | HSG | SG | LSG | MSG | SG | SG | HSG | |||
| SSG | SG | WSG | HSG | WSG | SSG | LSG | LSG | |||
| SSG | LSG | BSG | MSG | BSG | HSG | SG | BSG | |||
| SG | SG | LSG | MSG | HSG | HSG | BSG | WSG | |||
| SSG | HSG | LSG | LSG | BSG | WSG | MSG | SG | |||
| SSG | BSG | SG | SG | HSG | SG | SG | WSG | |||
| Criteria | Fever | Body Ache | Fatigue | Chills | SOB | Nausea | Vomiting | Diarrhea |
|---|---|---|---|---|---|---|---|---|
| Weight | 0.10781 | 0.11548 | 0.10293 | 0.16443 | 0.14482 | 0.11271 | 0.09636 | 0.15546 |
| Alternative | WSM | WPM | WASPAS | Ranking |
|---|---|---|---|---|
| 0.11443 | 3.84640 | 4.79597 | 7 | |
| 0.14261 | 4.87374 | 4.94932 | 1 | |
| 0.12596 | 4.14258 | 4.84629 | 5 | |
| 0.12660 | 4.11709 | 4.84148 | 6 | |
| 0.12949 | 4.22887 | 4.85601 | 4 | |
| 0.13054 | 4.35577 | 4.87842 | 3 | |
| 0.13559 | 4.42553 | 4.88686 | 2 |
| Alternative | Ranking | ||||
|---|---|---|---|---|---|
| 0.12820 | 2.00000 | 0.78958 | 1.55978 | 7 | |
| 0.16237 | 2.51340 | 1.00000 | 1.96700 | 1 | |
| 0.13816 | 2.17778 | 0.85092 | 1.69061 | 5 | |
| 0.13736 | 2.17675 | 0.84597 | 1.68578 | 6 | |
| 0.14107 | 2.23108 | 0.86883 | 1.72940 | 4 | |
| 0.14521 | 2.27323 | 0.89434 | 1.77012 | 3 | |
| 0.14763 | 2.33555 | 0.90925 | 1.81015 | 2 |
| Alternative | WASPAS | CoCoSo |
|---|---|---|
| 6 | 6 | |
| 1 | 1 | |
| 5 | 5 | |
| 7 | 7 | |
| 4 | 4 | |
| 2 | 2 | |
| 3 | 3 |
| Alternative | WASPAS | CoCoSo |
|---|---|---|
| 7 | 7 | |
| 1 | 1 | |
| 6 | 6 | |
| 4 | 4 | |
| 5 | 5 | |
| 2 | 2 | |
| 3 | 3 |
| Alternative | WASPAS | CoCoSo |
|---|---|---|
| 3 | 4 | |
| 1 | 2 | |
| 5 | 5 | |
| 4 | 3 | |
| 7 | 7 | |
| 2 | 1 | |
| 6 | 6 |
| Alternatives | ||||||
|---|---|---|---|---|---|---|
| WASPAS | CoCoSo | WASPAS | CoCoSo | WASPAS | CoCoSo | |
| 7 | 7 | 7 | 7 | 7 | 7 | |
| 1 | 1 | 1 | 1 | 1 | 1 | |
| 2 | 3 | 4 | 4 | 5 | 5 | |
| 6 | 6 | 6 | 6 | 6 | 6 | |
| 5 | 5 | 2 | 2 | 4 | 4 | |
| 4 | 4 | 5 | 5 | 3 | 3 | |
| 3 | 2 | 3 | 3 | 2 | 2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Momena, A.F.; Mandal, S.; Gazi, K.H.; Giri, B.C.; Mondal, S.P. Prediagnosis of Disease Based on Symptoms by Generalized Dual Hesitant Hexagonal Fuzzy Multi-Criteria Decision-Making Techniques. Systems 2023, 11, 231. https://doi.org/10.3390/systems11050231
Momena AF, Mandal S, Gazi KH, Giri BC, Mondal SP. Prediagnosis of Disease Based on Symptoms by Generalized Dual Hesitant Hexagonal Fuzzy Multi-Criteria Decision-Making Techniques. Systems. 2023; 11(5):231. https://doi.org/10.3390/systems11050231
Chicago/Turabian StyleMomena, Alaa Fouad, Shubhendu Mandal, Kamal Hossain Gazi, Bibhas Chandra Giri, and Sankar Prasad Mondal. 2023. "Prediagnosis of Disease Based on Symptoms by Generalized Dual Hesitant Hexagonal Fuzzy Multi-Criteria Decision-Making Techniques" Systems 11, no. 5: 231. https://doi.org/10.3390/systems11050231







