The Reform of Curricula in the Spanish University System: How Well Matched Are New Bachelor’s Degrees to Jobs
Abstract
1. Introduction
2. Background
2.1. Educational Mismatch among University Graduates: Theoretical Explanations
2.2. Educational Mismatch among University Graduates: Empirical Evidence
3. Methods
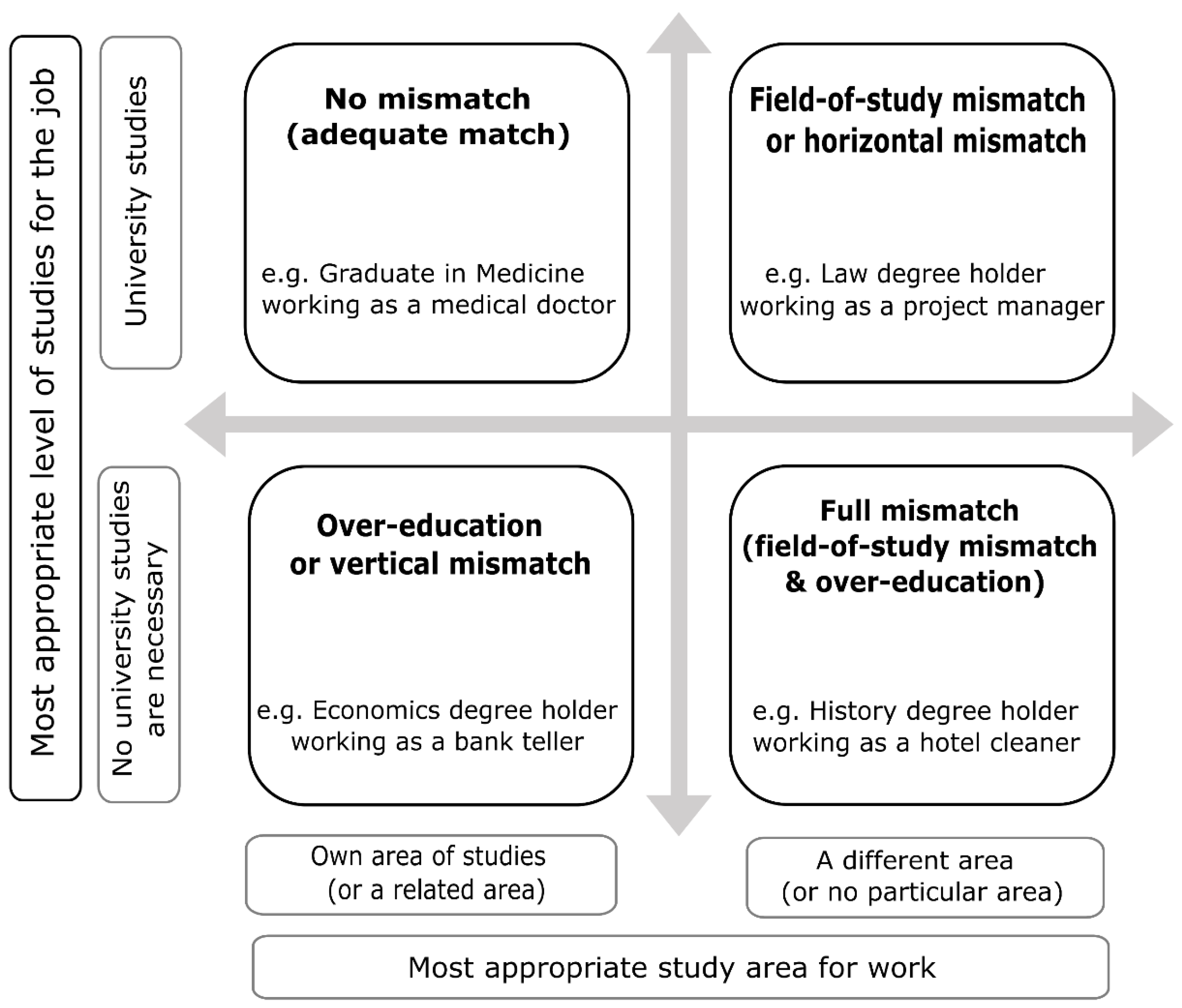
3.1. Educational Mismatch Measurement: Subjective Self-Assessment
Incidence of Educational Mismatch
3.2. Modeling the Education–Job Match
3.2.1. The Econometric Model
3.2.2. A Multinomial Logit Model of the Probability of Education–Employment Matching
3.2.3. Estimation Results
3.2.4. Tests for the Multinomial Logistic Regression Model
4. The Education–job Matching Process
4.1. A Binomial Probit Model with Sample Selection
4.2. Estimation Results
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Salas-Velasco, M. The technical efficiency performance of the higher education systems based on data envelopment analysis with an illustration for the Spanish case. Educ. Res. Policy Pract. 2020, 19, 159–180. [Google Scholar] [CrossRef]
- Meliciani, V.; Radicchia, D. Overeducation and Overskill in the Italian Labour Market: The role of Fields of Study; Working Paper; Birkbeck College, University of London: London, UK, 2016. [Google Scholar]
- Yorke, M.; Harvey, L. Graduate attributes and their development. New Dir. Inst. Res. 2005, 128, 41–58. [Google Scholar] [CrossRef]
- Salas-Velasco, M. Mapping the (mis)match of university degrees in the graduate labor market. J. Labour Mark. Res. 2021, 55, 14. [Google Scholar] [CrossRef]
- Freeman, R. The Overeducated American; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Groot, W.; van den Brink, H.M. Overeducation in the labour market: A meta-analysis. Econ. Educ. Rev. 2000, 19, 149–158. [Google Scholar] [CrossRef]
- Leuven, E.; Oosterbeek, H. Overeducation and mismatch in the labor market. In Handbook of the Economics of Education; Hanushek, E.A., Machin, S., Woessmann, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 4, pp. 283–326. [Google Scholar]
- McGuinness, S. Overeducation in the labour market. J. Econ. Surv. 2006, 20, 387–418. [Google Scholar] [CrossRef]
- Sloane, P.J. Much ado about nothing? What does the overeducation literature really tell us? In Overeducation in Europe; Büchel, F., de Grip, A., Mertens, A., Eds.; Edward Elgar: Cheltenham, UK, 2003; pp. 11–45. [Google Scholar]
- Somers, M.A.; Cabus, S.J.; Groot, W.; van den Brink, H.M. Horizontal mismatch between employment and field of education: Evidence from a systematic literature review. J. Econ. Surv. 2019, 33, 567–603. [Google Scholar] [CrossRef]
- Dolton, P.; Vignoles, A. The incidence and effects of overeducation in the U.K. graduate labour market. Econ. Educ. Rev. 2000, 19, 179–198. [Google Scholar] [CrossRef]
- Verhaest, D.; Sellami, S.; Van der Velden, R. Differences in horizontal and vertical mismatches across countries and fields of study. Int. Labour Rev. 2017, 156, 1–23. [Google Scholar] [CrossRef]
- Sloane, P.J. Overeducation, Skill Mismatches, and Labor Market Outcomes for College Graduates (IZA World of Labor No. 88); Institute for the Study of Labor (IZA): Bonn, Germany, 2014. [Google Scholar]
- Knight, J.B. Job competition, occupational production functions, and filtering down. Oxf. Econ. Pap. 1979, 31, 187–204. [Google Scholar] [CrossRef]
- Zamfir, A.M.; Militaru, E.; Mocanu, C.; Lungu, E.O. School-to-work transition of higher education graduates in four European countries. Comp. A J. Comp. Int. Educ. 2020, 50, 36–52. [Google Scholar] [CrossRef]
- Hadjivassiliou, K.P.; Tassinari, A.; Eichhorst, W.; Wozny, F. Assessing the Performance of School-to-Work Transition Regimes in the EU (IZA Discussion Paper No. 10301); Institute for the Study of Labor (IZA): Bonn, Germany, 2016. [Google Scholar]
- Autor, D. The polarization of job opportunities in the U.S. labor market: Implications for employment and earnings. Community Invest. 2011, 23, 11–16/40–41. [Google Scholar]
- Stiglitz, J.E. The theory of “screening”, education, and the distribution of income. Am. Econ. Rev. 1975, 65, 283–300. [Google Scholar]
- Winkler, D.R. Screening models and education. In Economics of Education: Research and Studies; Psacharopoulos, G., Ed.; Pergamon: Oxford, UK, 1987; pp. 287–291. [Google Scholar]
- Bachan, R. Grade inflation in UK higher education. Stud. High. Educ. 2017, 42, 1580–1600. [Google Scholar] [CrossRef]
- Arcidiacono, P.; Aucejo, E.M.; Hotz, V.J. University differences in the graduation of minorities in STEM fields: Evidence from California. Am. Econ. Rev. 2016, 106, 525–562. [Google Scholar] [CrossRef] [PubMed]
- Diem, A.; Wolter, S.C. Overeducation among Swiss university graduates: Determinants and consequences. J. Labour Mark. Res. 2014, 47, 313–328. [Google Scholar] [CrossRef]
- Spence, M. Job market signaling. Q. J. Econ. 1973, 87, 355–374. [Google Scholar] [CrossRef]
- Spence, A.M. Market Signaling: Informational Transfer in Hiring and Related Screening Process; Harvard University Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Blaug, M. Where are we now in the economics of education? Econ. Educ. Rev. 1985, 4, 17–28. [Google Scholar] [CrossRef]
- Thurow, L.C. Generating Inequality; Basic Books: New York, NY, USA, 1975. [Google Scholar]
- Robst, J. Education and job match: The relatedness of college major and work. Econ. Educ. Rev. 2007, 26, 397–407. [Google Scholar] [CrossRef]
- Doeringer, P.B.; Piore, M.J. Internal Labor Markets and Manpower Analysis; Lexington Books: Lexington, KY, USA, 1971. [Google Scholar]
- Groot, W. Overeducation and the returns to enterprise-related schooling. Econ. Educ. Rev. 1993, 12, 299–309. [Google Scholar] [CrossRef]
- Verdugo, R.R.; Verdugo, N.T. The impact of surplus schooling on earnings: Some additional findings. J. Hum. Resour. 1989, 24, 629–643. [Google Scholar] [CrossRef]
- Kampelmann, S.; Rycx, F. The impact of educational mismatch on firm productivity: Evidence from linked panel data. Econ. Educ. Rev. 2012, 31, 918–931. [Google Scholar] [CrossRef]
- Kiker, B.F.; Santos, M.C.; De Oliveira, M.M. Overeducation and undereducation: Evidence for Portugal. Econ. Educ. Rev. 1997, 16, 111–125. [Google Scholar] [CrossRef]
- Kupets, O. Education-job mismatch in Ukraine: Too many people with tertiary education or too many jobs for low-skilled? J. Comp. Econ. 2016, 44, 125–147. [Google Scholar] [CrossRef]
- Salas-Velasco, M. Propensity for Self-Employment in a Model of Occupational Choice: Evidence from a Cohort of Recent University Graduates in Spain. Sustainability 2023, 15, 3400. [Google Scholar] [CrossRef]
- Green, F.; Henseke, G. Should governments of OECD countries worry about graduate underemployment? Oxf. Rev. Econ. Policy 2016, 32, 514–537. [Google Scholar] [CrossRef]
- Charlot, O.; Decreuse, B. Over-education for the rich, under-education for the poor: A search-theoretic microfoundation. Labour Econ. 2010, 17, 886–896. [Google Scholar] [CrossRef]
- McFadden, D. The measurement of urban travel demand. J. Public Econ. 1974, 3, 303–328. [Google Scholar] [CrossRef]
- Schmidt, P.; Strauss, R.P. The prediction of occupation using multiple logit models. Int. Econ. Rev. 1975, 16, 471–486. [Google Scholar] [CrossRef]
- Hersch, J. Education match and job match. Rev. Econ. Stat. 1991, 73, 140–144. [Google Scholar] [CrossRef]
- McFadden, D.L. Conditional logit analysis of qualitative choice behavior. In Frontiers in Econometrics; Zarembka, P., Ed.; Academic Press: Cambridge, MA, USA, 1974; pp. 105–142. [Google Scholar]
- Bowen, H.P.; Wiersema, M.F. Modeling limited dependent variables: Guidelines for researchers of strategic management. In Research Methodology in Strategy and Management; Ketchen, D.J., Bergh, D., Eds.; JAI/Elsevier Press: Amsterdam, The Netherlands, 2004; Volume 1, pp. 87–134. [Google Scholar]
- McGuinness, S.; Pouliakas, K.; Redmond, P. Skills mismatch: Concepts, measurement and policy approaches. J. Econ. Surv. 2018, 32, 985–1015. [Google Scholar] [CrossRef]
- Rose, S.J. Mismatch: How Many Workers with a Bachelor’s Degree Are Overqualified for Their Jobs? The Urban Institute: Washington, DC, USA, 2017. [Google Scholar]
- Maddala, G.S. Limited-Dependent and Qualitative Variables in Econometrics; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Fagerland, M.W.; Hosmer, D.W. A generalized Hosmer–Lemeshow goodness-of-fit test for multinomial logistic regression models. Stata J. 2012, 12, 447–453. [Google Scholar] [CrossRef]
- Hausman, J.; McFadden, D. Specification tests for the multinomial logit model. Econometrica 1984, 52, 1219–1240. [Google Scholar] [CrossRef]
- Lindsey, C. Probit Model with Sample Selection by Mlexp. The STATA Blog. Available online: https://blog.stata.com/2015/10/22/probit-model-with-sample-selection-by-mlexp/ (accessed on 22 October 2015).
- Van de Ven, W.P.; Van Praag, B.M. The demand for deductibles in private health insurance: A probit model with sample selection. J. Econom. 1981, 17, 229–252. [Google Scholar] [CrossRef]
- Wooldridge, J.M. Introductory Econometrics: A modern Approach, 5th ed.; South-Western (Cengage Learning): Boston, MA, USA, 2012. [Google Scholar]
- Heckman, J.J. Sample selection bias as a specification error. Econometrica 1979, 74, 153–161. [Google Scholar] [CrossRef]
- Organisation for Economic Co-operation and Development. Skills Matter: Further Results from the Survey of Adult Skills. 2016. Available online: https://www.oecd.org/skills/skills-matter-9789264258051-en.htm (accessed on 14 December 2022).
- Jovanovic, B. Job matching and the theory of turnover. J. Political Econ. 1979, 87 Pt 1, 972–990. [Google Scholar] [CrossRef]

| Current Job in 2014 (EILU2014 Survey) (b) | Current Job in 2019 (EILU2019 Survey) (c) | |||
|---|---|---|---|---|
| Freq. | Percent | Freq. | Percent | |
| Educational (mis)match | ||||
| No mismatch | 12,387 | 66.38 | 16,395 | 67.29 |
| Horizontal mismatch | 1379 | 7.39 | 2735 | 11.23 |
| Vertical mismatch | 1725 | 9.24 | 1655 | 6.79 |
| Vertical and horizontal mismatch | 3169 | 16.98 | 3580 | 14.69 |
| Total | 18,660 | 100.00 | 24,365 | 100.00 |
| Pr (Jobmatch = 1) | Pr (Jobmatch = 2) | Pr (Jobmatch = 3) | Pr (Jobmatch = 4) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No Mismatch | Horizontal Mismatch | Vertical Mismatch | Vertical and Horizontal Mismatch | |||||||||
| dy/dx | Std. Err. | dy/dx | Std. Err. | dy/dx | Std. Err. | dy/dx | Std. Err. | |||||
| Bachelor’s degree awarded (1) | ||||||||||||
| Educational Studies | 0.094 | *** | 0.022 | −0.050 | 0.018 | −0.007 | 0.015 | −0.037 | 0.015 | |||
| Teaching | 0.103 | *** | 0.018 | −0.067 | 0.014 | 0.011 | 0.012 | −0.047 | 0.012 | |||
| Fine Arts (2) | −0.132 | 0.020 | 0.032 | ** | 0.014 | 0.050 | *** | 0.013 | 0.050 | *** | 0.013 | |
| Geography and History (3) | −0.117 | 0.026 | 0.074 | *** | 0.016 | −0.061 | 0.024 | 0.103 | *** | 0.015 | ||
| Philosophy | −0.089 | 0.036 | 0.046 | ** | 0.021 | −0.042 | 0.033 | 0.084 | *** | 0.021 | ||
| Foreign Languages (4) | −0.046 | 0.026 | 0.036 | ** | 0.016 | −0.026 | 0.022 | 0.036 | ** | 0.018 | ||
| Language and Literature | 0.047 | 0.030 | −0.020 | 0.020 | −0.064 | 0.030 | 0.038 | ** | 0.019 | |||
| Economics | 0.022 | 0.022 | −0.007 | 0.016 | 0.053 | *** | 0.014 | −0.068 | 0.016 | |||
| Political Sciences | −0.157 | 0.028 | 0.064 | *** | 0.018 | 0.054 | *** | 0.016 | 0.039 | ** | 0.019 | |
| Psychology (5) | −0.006 | 0.021 | 0.001 | 0.016 | 0.001 | 0.015 | 0.004 | 0.015 | ||||
| Sociology | −0.109 | 0.042 | 0.067 | *** | 0.026 | 0.027 | 0.026 | 0.015 | 0.027 | |||
| Finance and Accounting | 0.096 | *** | 0.035 | −0.044 | 0.028 | 0.026 | 0.020 | −0.078 | 0.025 | |||
| Business Administration | 0.058 | *** | 0.019 | −0.038 | 0.014 | 0.059 | *** | 0.012 | −0.079 | 0.013 | ||
| Labor Relations | 0.015 | 0.027 | −0.028 | 0.021 | 0.017 | 0.017 | −0.005 | 0.018 | ||||
| Marketing | −0.038 | 0.024 | 0.029 | 0.016 | 0.042 | *** | 0.015 | −0.033 | 0.017 | |||
| Law | −0.007 | 0.020 | 0.000 | 0.014 | 0.032 | ** | 0.013 | −0.025 | 0.014 | |||
| Biology | −0.008 | 0.026 | −0.035 | 0.020 | 0.051 | *** | 0.015 | −0.008 | 0.018 | |||
| Biomedical and Health Engineering (6) | 0.096 | *** | 0.029 | −0.010 | 0.020 | −0.002 | 0.022 | −0.084 | 0.025 | |||
| Environmental Sciences | −0.079 | 0.025 | 0.057 | *** | 0.016 | 0.016 | 0.017 | 0.006 | 0.017 | |||
| Chemistry | 0.030 | 0.027 | −0.021 | 0.021 | 0.057 | *** | 0.016 | −0.065 | 0.022 | |||
| Geology (7) | −0.072 | 0.029 | 0.016 | 0.021 | 0.010 | 0.021 | 0.046 | ** | 0.019 | |||
| Physics (8) | 0.188 | *** | 0.041 | 0.008 | 0.022 | −0.106 | 0.045 | −0.090 | 0.030 | |||
| Mathematics and Statistics | 0.111 | *** | 0.027 | −0.018 | 0.020 | −0.006 | 0.019 | −0.087 | 0.021 | |||
| Computing | 0.200 | *** | 0.022 | −0.100 | 0.018 | 0.042 | *** | 0.013 | −0.143 | 0.018 | ||
| Chemical Engineering | 0.064 | 0.036 | 0.042 | 0.022 | −0.025 | 0.030 | −0.082 | 0.027 | ||||
| Electric Engineering (9) | 0.176 | *** | 0.034 | −0.012 | 0.023 | −0.012 | 0.024 | −0.151 | 0.030 | |||
| Telecom Engineering | 0.170 | *** | 0.023 | −0.048 | 0.017 | 0.031 | ** | 0.014 | −0.152 | 0.019 | ||
| Industrial Engineering | 0.163 | *** | 0.021 | −0.034 | 0.015 | 0.013 | 0.014 | −0.142 | 0.017 | |||
| Naval and Aeronautical Engineering | 0.178 | *** | 0.035 | −0.018 | 0.023 | −0.002 | 0.024 | −0.158 | 0.032 | |||
| Food Engineering (10) | 0.052 | 0.033 | 0.024 | 0.022 | 0.031 | 0.020 | −0.106 | 0.030 | ||||
| Civil Engineering (11) | 0.089 | *** | 0.022 | 0.019 | 0.015 | −0.033 | 0.017 | −0.075 | 0.016 | |||
| Architecture | 0.072 | *** | 0.022 | −0.021 | 0.016 | −0.009 | 0.016 | −0.042 | 0.016 | |||
| Agricultural Engineering (12) | 0.054 | ** | 0.022 | −0.021 | 0.016 | 0.014 | 0.014 | −0.047 | 0.016 | |||
| Veterinary | 0.312 | *** | 0.042 | −0.089 | 0.031 | −0.131 | 0.045 | −0.093 | 0.027 | |||
| Odontology | 1.715 | *** | 0.066 | 0.308 | *** | 0.069 | −0.758 | 0.023 | −1.265 | 0.033 | ||
| Medicine | 0.641 | *** | 0.061 | −0.200 | 0.051 | −0.090 | 0.034 | −0.351 | 0.069 | |||
| Nursing | 0.413 | *** | 0.028 | −0.081 | 0.020 | −0.064 | 0.019 | −0.268 | 0.027 | |||
| Physiotherapy | 0.216 | *** | 0.031 | −0.028 | 0.023 | −0.079 | 0.027 | −0.109 | 0.024 | |||
| Pharmacy (13) | 0.211 | *** | 0.033 | −0.054 | 0.025 | −0.042 | 0.024 | −0.115 | 0.025 | |||
| Social Work | 0.093 | *** | 0.023 | −0.075 | 0.019 | 0.005 | 0.014 | −0.023 | 0.015 | |||
| Sports Science | −0.031 | 0.025 | −0.029 | 0.020 | 0.045 | *** | 0.015 | 0.016 | 0.017 | |||
| Tourism | −0.126 | 0.025 | 0.013 | 0.017 | 0.092 | *** | 0.014 | 0.021 | 0.016 | |||
| Transport and Services | 0.046 | 0.034 | 0.011 | 0.023 | 0.039 | 0.020 | −0.096 | 0.029 | ||||
| Factors to find the job: theory (b) | 0.194 | *** | 0.005 | −0.031 | 0.004 | −0.015 | 0.003 | −0.148 | 0.004 | |||
| Factors to find the job: practical skills | 0.106 | *** | 0.006 | −0.029 | 0.004 | 0.009 | ** | 0.004 | −0.086 | 0.004 | ||
| Factors to find the job: knowing languages | 0.050 | *** | 0.006 | 0.032 | *** | 0.004 | −0.037 | 0.004 | −0.045 | 0.005 | ||
| Factors to find the job: computer skills | 0.010 | 0.006 | 0.023 | *** | 0.004 | −0.002 | 0.003 | −0.031 | 0.005 | |||
| Factors to find the job: management ability | 0.073 | *** | 0.007 | 0.016 | *** | 0.005 | −0.019 | 0.004 | −0.069 | 0.005 | ||
| Factors to find the job: personal and social skills | −0.031 | 0.008 | 0.007 | 0.006 | 0.001 | 0.005 | 0.022 | *** | 0.006 | |||
| Double university degree (=1 yes) | 0.073 | *** | 0.014 | 0.024 | *** | 0.009 | −0.033 | 0.010 | −0.065 | 0.013 | ||
| Master’s degree (=1 yes) | 0.092 | *** | 0.006 | 0.008 | 0.004 | −0.035 | 0.004 | −0.064 | 0.004 | |||
| Age under 30 years (c) | 0.059 | *** | 0.007 | −0.015 | 0.005 | −0.013 | 0.004 | −0.030 | 0.005 | |||
| Age of 35 or more years | −0.033 | 0.008 | 0.050 | *** | 0.005 | −0.006 | 0.004 | −0.011 | 0.006 | |||
| Private university (=1 yes) | 0.045 | *** | 0.009 | 0.008 | 0.006 | −0.001 | 0.005 | −0.052 | 0.007 | |||
| Gender (=1 male) | 0.003 | 0.006 | 0.008 | 0.004 | −0.008 | 0.003 | −0.003 | 0.004 | ||||
| First Stage: Participation Equation (Probit) | Second Stage: Outcome Equation (Probit) | |||||
|---|---|---|---|---|---|---|
| Coef. | Robust Std. Err. | Coef. | Robust Std. Err. | |||
| Arts and humanities degrees | −0.009 | 0.083 | −0.262 | ** | 0.108 | |
| STEM degrees (a) | −0.013 | 0.052 | 0.252 | *** | 0.088 | |
| Health sciences degrees | −0.100 | 0.073 | 0.304 | ** | 0.130 | |
| Factors to find the job: theory (b) | −0.195 | *** | 0.049 | 0.419 | *** | 0.076 |
| Factors to find the job: practical skills | −0.058 | 0.055 | 0.231 | *** | 0.086 | |
| Factors to find the job: knowing languages | 0.140 | *** | 0.052 | −0.092 | 0.078 | |
| Factors to find the job: computer skills | 0.146 | *** | 0.051 | −0.224 | *** | 0.085 |
| Factors to find the job: management ability | −0.030 | 0.063 | 0.221 | ** | 0.088 | |
| Factors to find the job: personal and social skills | 0.112 | 0.066 | −0.463 | *** | 0.110 | |
| Double university degree (=1 yes) | 0.341 | *** | 0.103 | −0.075 | 0.173 | |
| Master’s degree (=1 yes) | 0.179 | *** | 0.047 | 0.009 | 0.077 | |
| Age under 30 years (c) | 0.029 | 0.062 | −0.113 | 0.098 | ||
| Age of 35 or more years | −0.072 | 0.059 | −0.050 | 0.091 | ||
| Private university (=1 yes) | −0.001 | 0.063 | 0.404 | *** | 0.129 | |
| Gender (=1 male) | 0.216 | *** | 0.046 | −0.257 | *** | 0.070 |
| Recognized disability (d) | 0.325 | ** | 0.163 | |||
| Mother with a university education (=1 yes) | 0.089 | ** | 0.045 | |||
| Constant | −1.910 | *** | 0.178 | 2.046 | 0.099 | |
| Log pseudolikelihood = −2226.32 | Number of obs. = 6933 | Number of obs. = 581 | ||||
| rho = −0.997 [95% Conf. Interval: −1.00, −0.83] | ||||||
| Wald test of indep. eqns. (rho = 0): chi2(1) = 9.55 Prob > chi2 = 0.002 | ||||||
| Wald chi2(15) = 113.13 Prob > chi2 = p < 0.001 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salas-Velasco, M. The Reform of Curricula in the Spanish University System: How Well Matched Are New Bachelor’s Degrees to Jobs. Systems 2023, 11, 200. https://doi.org/10.3390/systems11040200
Salas-Velasco M. The Reform of Curricula in the Spanish University System: How Well Matched Are New Bachelor’s Degrees to Jobs. Systems. 2023; 11(4):200. https://doi.org/10.3390/systems11040200
Chicago/Turabian StyleSalas-Velasco, Manuel. 2023. "The Reform of Curricula in the Spanish University System: How Well Matched Are New Bachelor’s Degrees to Jobs" Systems 11, no. 4: 200. https://doi.org/10.3390/systems11040200
APA StyleSalas-Velasco, M. (2023). The Reform of Curricula in the Spanish University System: How Well Matched Are New Bachelor’s Degrees to Jobs. Systems, 11(4), 200. https://doi.org/10.3390/systems11040200





