Trading Risk Spillover Mechanism of Rare Earth in China: New Perspective Based on Time-Varying Connectedness Approach
Abstract
1. Introduction
2. Model Specification and Estimation
2.1. TVP-VAR-SV Model for Price Dynamics
2.2. Volatility Spillover Measures and Graph Network
2.3. Multivariate Nonlinear Causality and Impulse Response
3. Data
4. Empirical Analysis in China’s Rare Earth Market
4.1. Risk Spillover of China’s Rare Earth Market
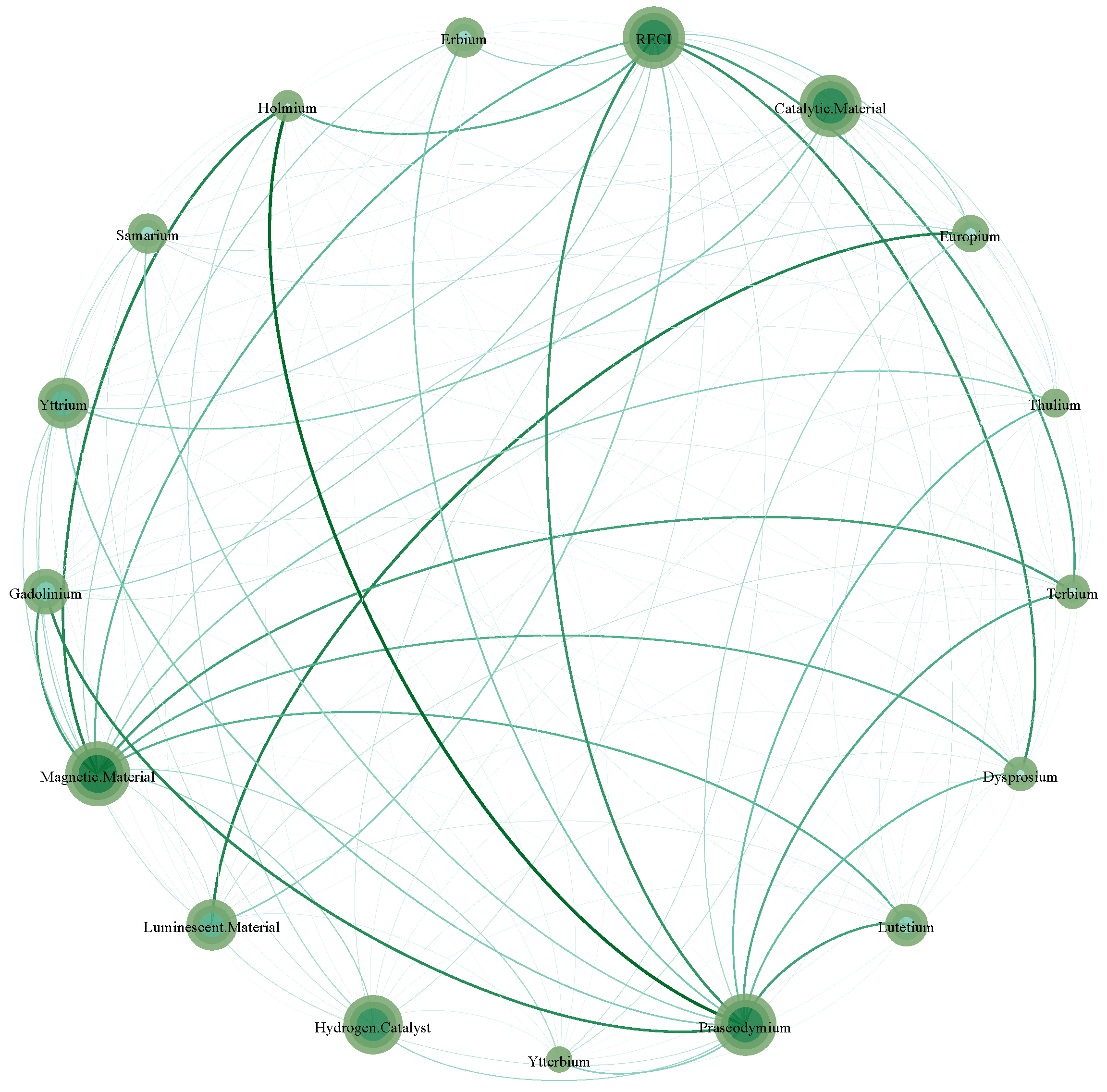
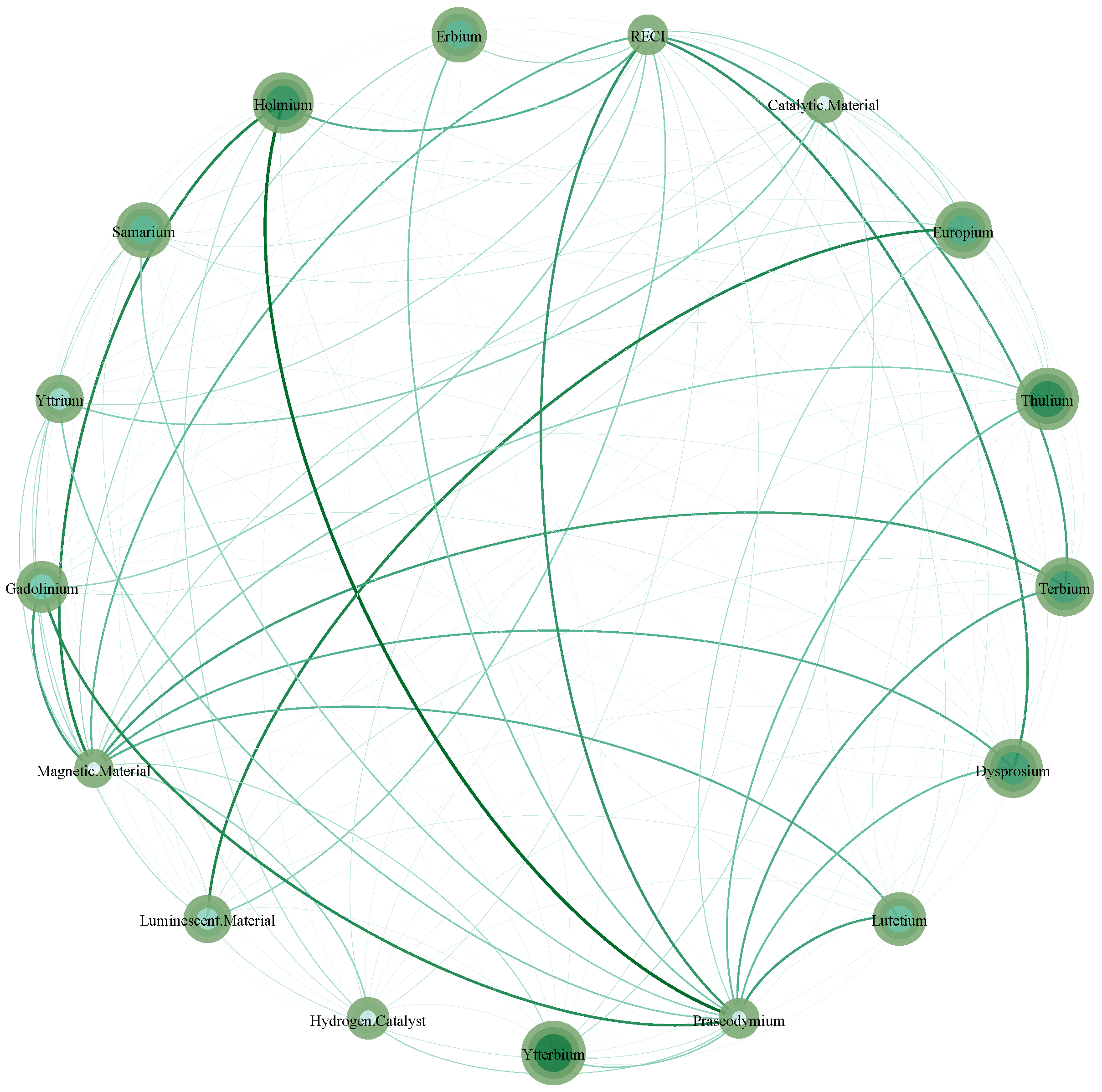
4.2. Bilateral Trading Risk Spillover Complex Network
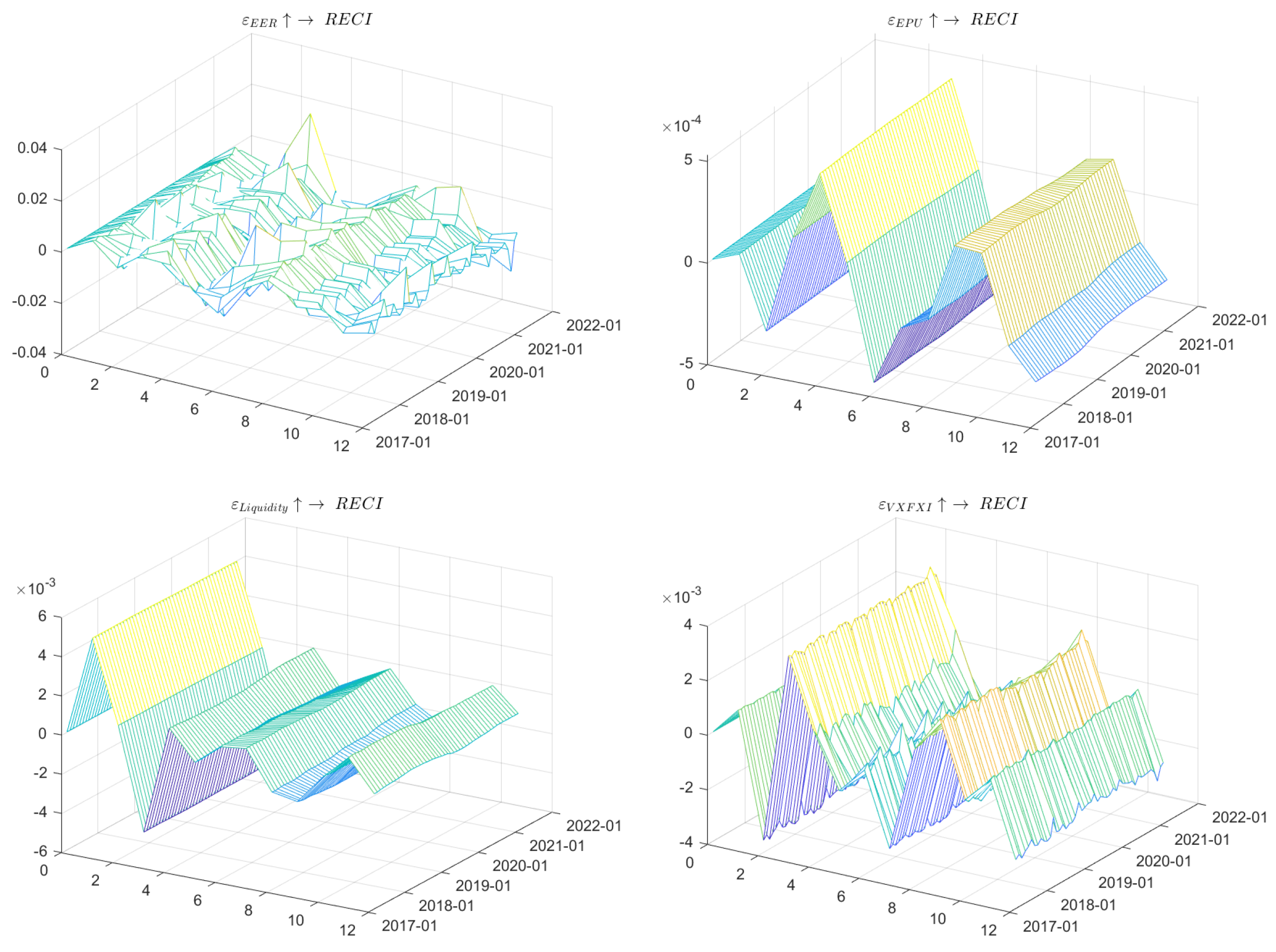
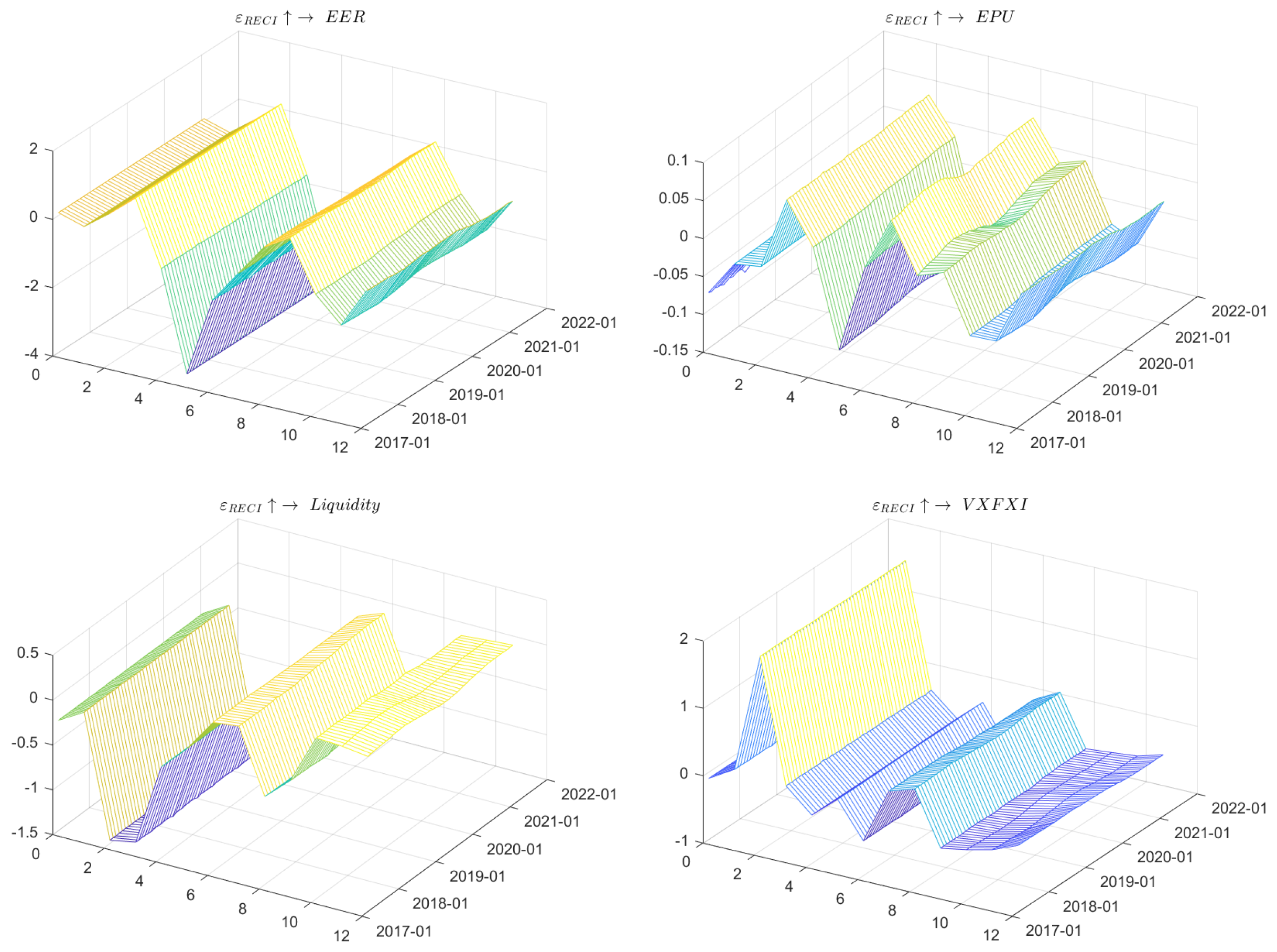
4.3. Risk Spillover Mechanism and Driven Factor Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
- Give the initial value of , , , and ;
- Sample from , subject to the given condition , , and ;Specifically, the observation equation corresponds to the linear Gaussian shocks of equation. For the observable vector , the state vector is and the set of the parameter vector is . We have the following conditional transformation, respectively:Finally, with the mean and derivative of and , the conditional density function can be expressed as:
- Sample from , subject to the given condition , , and ;
- Sample from , subject to the given condition , , and . Specifically, sample the independent identically distributed random variables Q, W, and S from ;
- Sample from , subject to the given condition , , and ;
- Return to 2.
References
- Hossain, M.K.; Rubel, M.H.K.; Akbar, M.A.; Ahmed, M.H.; Haque, N.; Rahman, M.F.; Hossain, J.; Hossain, K.M. A review on recent applications and future prospects of rare earth oxides in corrosion and thermal barrier coatings, catalysts, tribological, and environmental sectors. Ceram. Int. 2022, 48, 32588–32612. [Google Scholar] [CrossRef]
- Shi, Y.; Feng, Y.; Zhang, Q.; Shuai, J.; Niu, J. Does China’s new energy vehicles supply chain stock market have risk spillovers? Evidence from raw material price effect on lithium batteries. Energy 2023, 262, 125420. [Google Scholar] [CrossRef]
- Naeem, M.A.; Yousaf, I.; Karim, S.; Yarovaya, L.; Ali, S. Tail-event driven NETwork dependence in emerging markets. Emerg. Mark. Rev. 2022, 1, 100971. [Google Scholar] [CrossRef]
- Shuai, J.; Peng, X.; Zhao, Y.; Wang, Y.; Xu, W.; Cheng, J.; Wang, J. A dynamic evaluation on the international competitiveness of China’s rare earth products: An industrial chain and tech-innovation perspective. Resour. Policy 2022, 75, 102444. [Google Scholar] [CrossRef]
- Xiao, S.; Geng, Y.; Rui, X.; Su, C.; Yao, T. Behind of the criticality for rare earth elements: Surplus of China’s yttrium. Resour. Policy 2022, 76, 102624. [Google Scholar] [CrossRef]
- Ilankoon, I.M.S.K.; Dushyantha, N.P.; Mancheri, N.; Edirisinghe, P.M.; Neethling, S.J.; Ratnayake, N.P.; Batapola, N.M. Constraints to rare earth elements supply diversification: Evidence from an industry survey. J. Clean. Prod. 2022, 331, 129932. [Google Scholar] [CrossRef]
- Yin, J.N.; Song, X. A review of major rare earth element and yttrium deposits in China. Aust. J. Earth Sci. 2022, 69, 1–25. [Google Scholar] [CrossRef]
- Haq, I.U.; Nadeem, H.; Maneengam, A.; Samantreeporn, S.; Huynh, N.; Kettanom, T.; Wisetsri, W. Do rare earths and energy commodities drive volatility transmission in sustainable financial markets? Evidence from China, Australia, and the US. Int. J. Financ. Stud. 2022, 10, 76. [Google Scholar] [CrossRef]
- Hau, L.; Zhu, H.; Yu, Y.; Yu, D. Time-frequency coherence and quantile causality between trade policy uncertainty and rare earth prices: Evidence from China and the US. Resour. Policy 2022, 75, 102529. [Google Scholar] [CrossRef]
- Hanif, W.; Mensi, W.; Gubareva, M.; Teplova, T. Impacts of COVID-19 on dynamic return and volatility spillovers between rare earth metals and renewable energy stock markets. Resour. Policy 2023, 80, 103196. [Google Scholar] [CrossRef]
- Van de Leur, M.C.; Lucas, A.; Seeger, N.J. Network, market, and book-based systemic risk rankings. J. Bank. Financ. 2017, 78, 84–90. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Measuring financial asset return and volatility spillovers, with application to global equity markets. Econ. J. 2009, 119, 158–171. [Google Scholar] [CrossRef]
- Acharya, V.V.; Volpin, P.F. Corporate governance externalities. Rev. Financ. 2010, 14, 1–33. [Google Scholar] [CrossRef]
- Acharya, V.V.; Pedersen, L.H.; Philippon, T.; Richardson, M. Measuring systemic risk. Rev. Financ. Stud. 2017, 30, 2–47. [Google Scholar] [CrossRef]
- Acharya, V.V.; Engle, R.; Richardson, M. Capital shortfall: A new approach to ranking and regulating systemic risks. Am. Econ. Rev. 2012, 102, 59–64. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef]
- Grant, E.; Yung, J. The double-edged sword of global integration: Robustness, fragility, and contagion in the international firm network. J. Appl. Econom. 2021, 36, 760–783. [Google Scholar] [CrossRef]
- Härdle, W.K.; Wang, W.; Yu, L. Tenet: Tail-event driven network risk. J. Econom. 2016, 192, 499–513. [Google Scholar] [CrossRef]
- Koop, G.; Pesaran, M.H.; Potter, S.M. Impulse response analysis in nonlinear multivariate models. J. Econom. 1996, 74, 119–147. [Google Scholar] [CrossRef]
- Pesaran, H.H.; Shin, Y. Generalized impulse response analysis in linear multivariate models. Econ. Lett. 1998, 58, 17–29. [Google Scholar] [CrossRef]
- Primiceri, G.E. Time varying structural vector autoregressions and monetary policy. Rev. Econ. Stud. 2005, 72, 821–852. [Google Scholar] [CrossRef]
- Nakajima, J. Time-varying parameter VAR model with stochastic volatility: An overview of methodology and empirical applications. Monet. Econ. Stud. 2011, 29, 107–142. [Google Scholar]
- Antonakakis, N.; Chatziantoniou, I.; Gabauer, D. Refined measures of dynamic connectedness based on time-varying parameter vector autoregressions. J. Risk Financ. Manag. 2020, 13, 84. [Google Scholar] [CrossRef]
- Koop, G.; Korobilis, D. Large time-varying parameter VARs. J. Econom. 2013, 177, 185–198. [Google Scholar] [CrossRef]
- Chan, J.C.; Eisenstat, E. Bayesian model comparison for time-varying parameter VARs with stochastic volatility. J. Appl. Econom. 2018, 33, 509–532. [Google Scholar] [CrossRef]
- Barigozzi, M.; Brownlees, C. Nets: Network estimation for time series. J. Appl. Econom. 2019, 34, 347–364. [Google Scholar] [CrossRef]
- Diks, C.; Panchenko, V. A new statistic and practical guidelines for nonparametric Granger causality testing. J. Econ. Dyn. Control 2006, 30, 1647–1669. [Google Scholar] [CrossRef]
- Du, J.; Chen, X.; Gong, J.; Lin, X.; Lai, K.K. Analysis of stock markets risk spillover with copula models under the background of Chinese financial opening. Int. J. Financ. Econ. 2022, 27, 1–23. [Google Scholar] [CrossRef]
- Diks, C.; Wolski, M. Nonlinear granger causality: Guidelines for multivariate analysis. J. Appl. Econom. 2016, 31, 1333–1351. [Google Scholar] [CrossRef]
- Wind Information Technology Co., Ltd. Wind Finaicial Database, Shanghai, China. Available online: https://www.wind.com.cn/ (accessed on 21 March 2023).
- Bank for International Settlements NPO. BIS Financial Database, Basel, Switzerland. Available online: https://www.bis.org/ (accessed on 21 March 2023).
- Li, K. Report on the Work of the Government, Beijing, China. Available online: http://www.gov.cn/zhuanti/2019qglh (accessed on 21 March 2023).
- Hiemstra, C.; Jones, J.D. Testing for linear and nonlinear Granger causality in the stock price-volume relation. J. Financ. 1994, 49, 1639–1664. [Google Scholar]

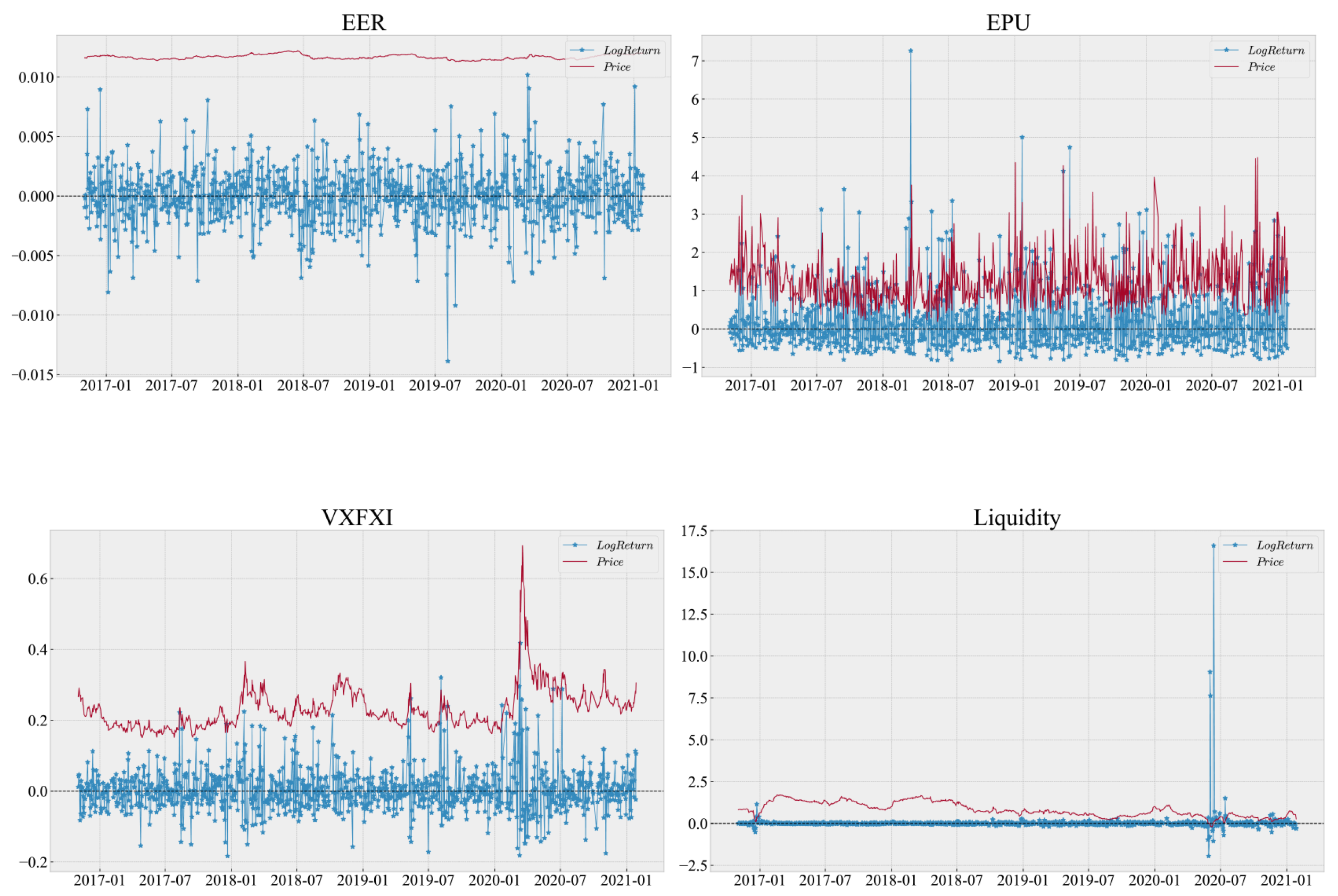

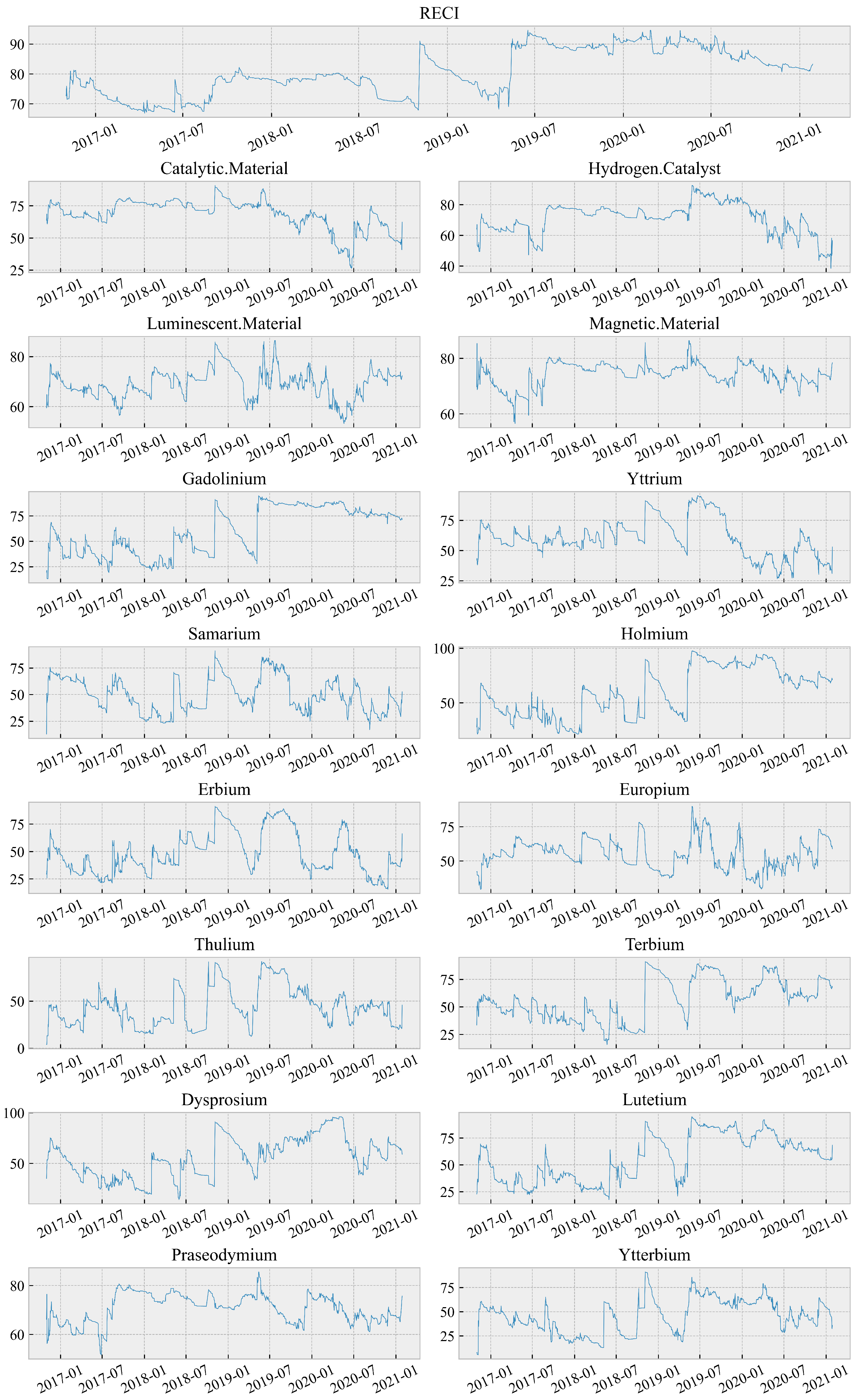
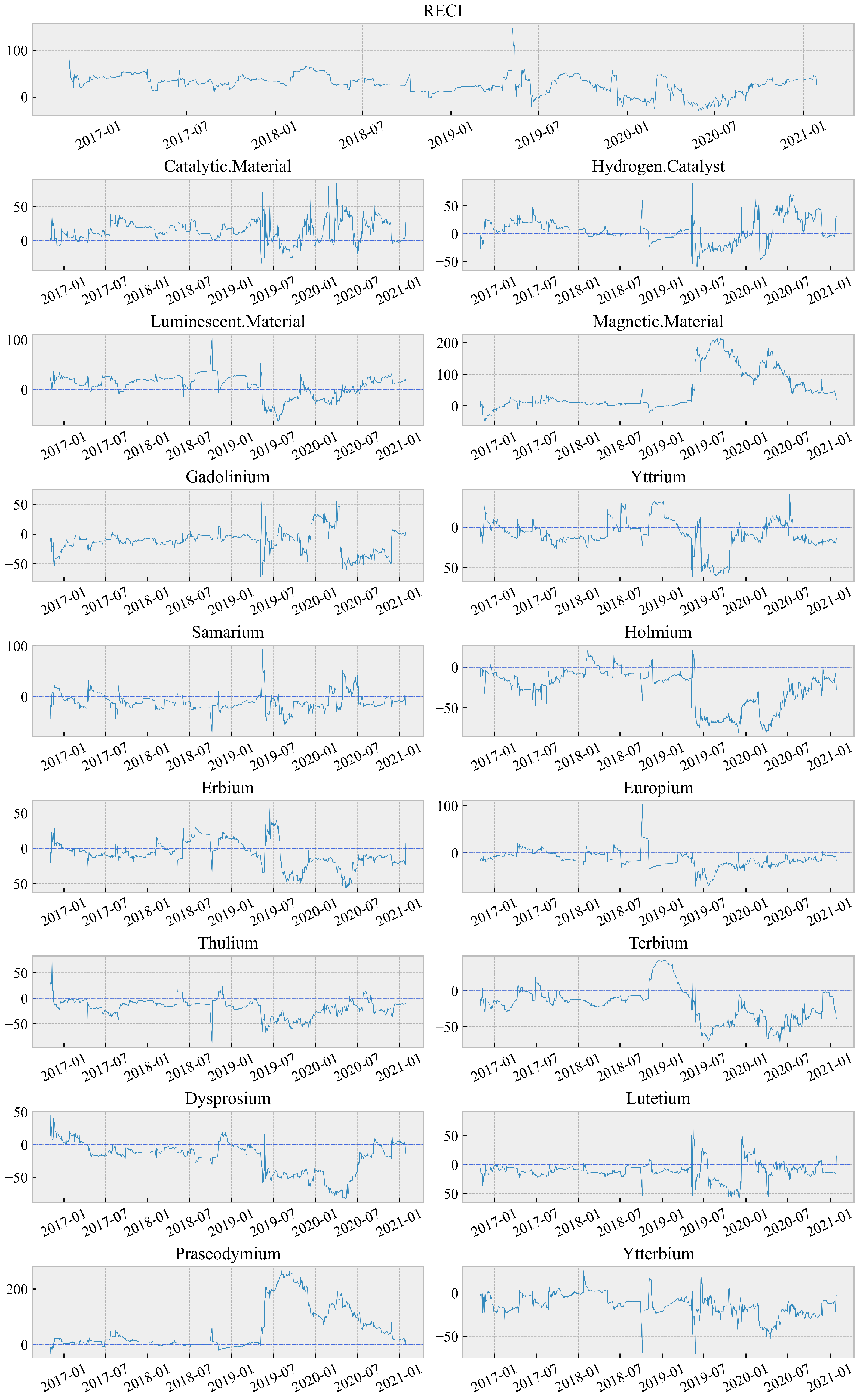
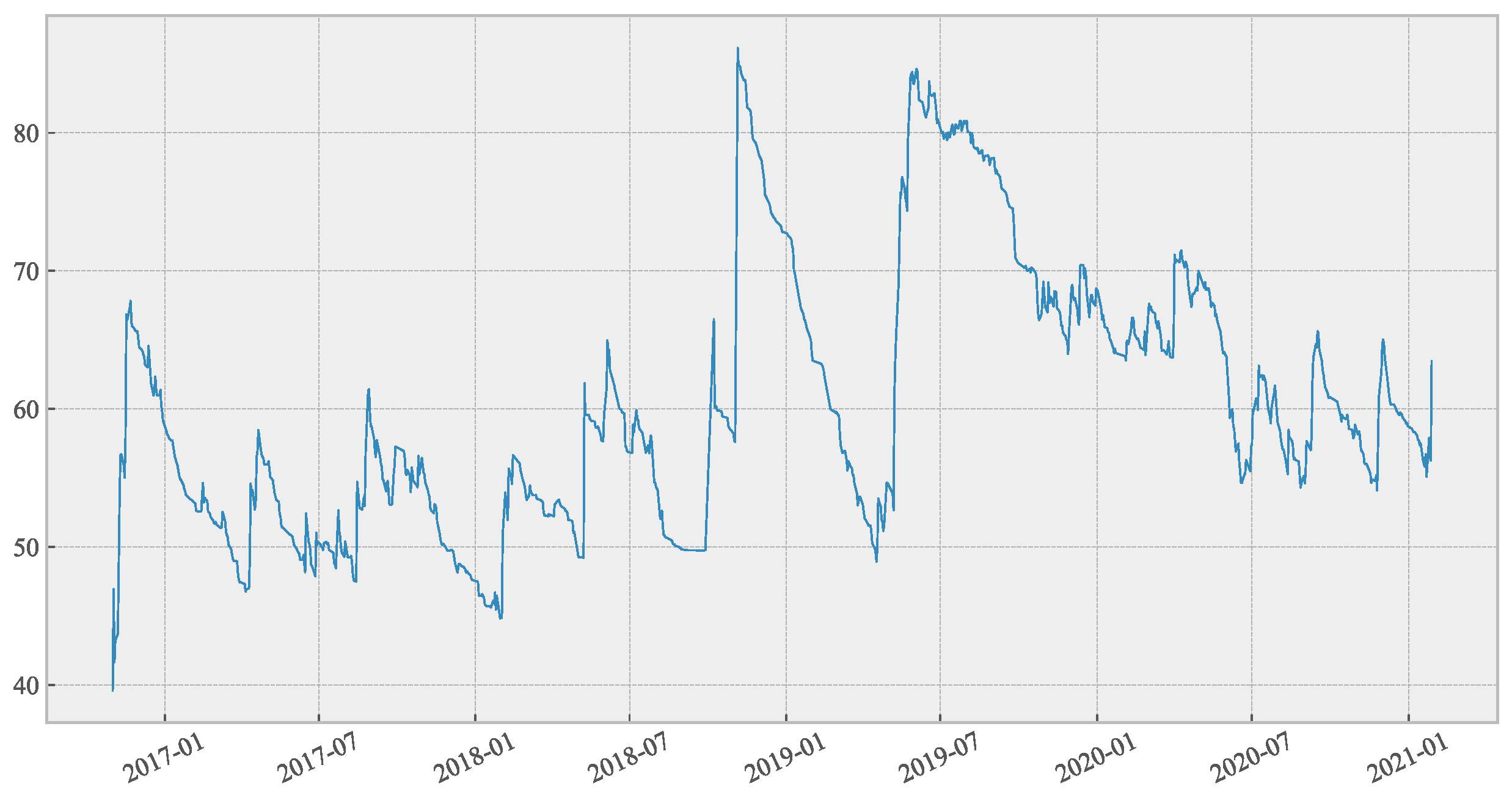
| Name | RECI | Catalysts | Praseodymium | Holmium | VXFXI | EPU | EER | Liquidity | |
|---|---|---|---|---|---|---|---|---|---|
| Info | |||||||||
| Observation | 1249 | 1249 | 1249 | 1249 | 1249 | 1249 | 1249 | 1249 | |
| Frequency | Daily | Daily | Daily | Daily | Daily | Daily | Daily | Daily | |
| Mean | 0.000 | −0.000 | 0.000 | 0.001 | 0.002 | 0.193 | 0.000 | 0.034 | |
| Minimum | −0.040 | −0.045 | −0.095 | −0.105 | −0.184 | −0.839 | −0.014 | −1.951 | |
| Maximum | 0.045 | 0.046 | 0.081 | 0.124 | 0.418 | 7.264 | 0.010 | 16.592 | |
| 1st Quartile | −0.003 | −0.003 | −0.002 | −0.002 | −0.033 | −0.309 | −0.001 | −0.029 | |
| 3rd Quartile | 0.003 | 0.003 | 0.003 | 0.003 | 0.028 | 0.437 | 0.001 | 0.030 | |
| Variance | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.639 | 0.000 | 0.434 | |
| S.D. | 0.007 | 0.010 | 0.013 | 0.015 | 0.063 | 0.800 | 0.002 | 0.659 | |
| Skewness | 0.228 | 0.028 | −0.329 | 0.555 | 1.275 | 2.396 | −0.100 | 19.971 | |
| Kurtosis | 6.732 | 5.447 | 13.417 | 14.309 | 5.103 | 10.150 | 3.002 | 449.406 | |
| J–B | |||||||||
| ARCH-LM | |||||||||
| Q(20) | 19.193 | ||||||||
| ADF(10) | |||||||||
| K–S | 0.022 | 0.038 | 0.019 | 0.020 | 0.017 | 0.015 | 0.030 | 0.014 | |
| Explanation | China’s rare earth composite index | Catalysts index | Rare earth oxides | Rare earth oxides | ETF volatility index of China | Economic policy uncertainty | Effective exchange rate | 3M-Spread of SHIBOR and treasury yield | |
| Source | Wind [31] | Wind [31] | Wind [31] | Wind [31] | Wind [31] | BIS [32] | Du et al. [29] | Wind [31] | |
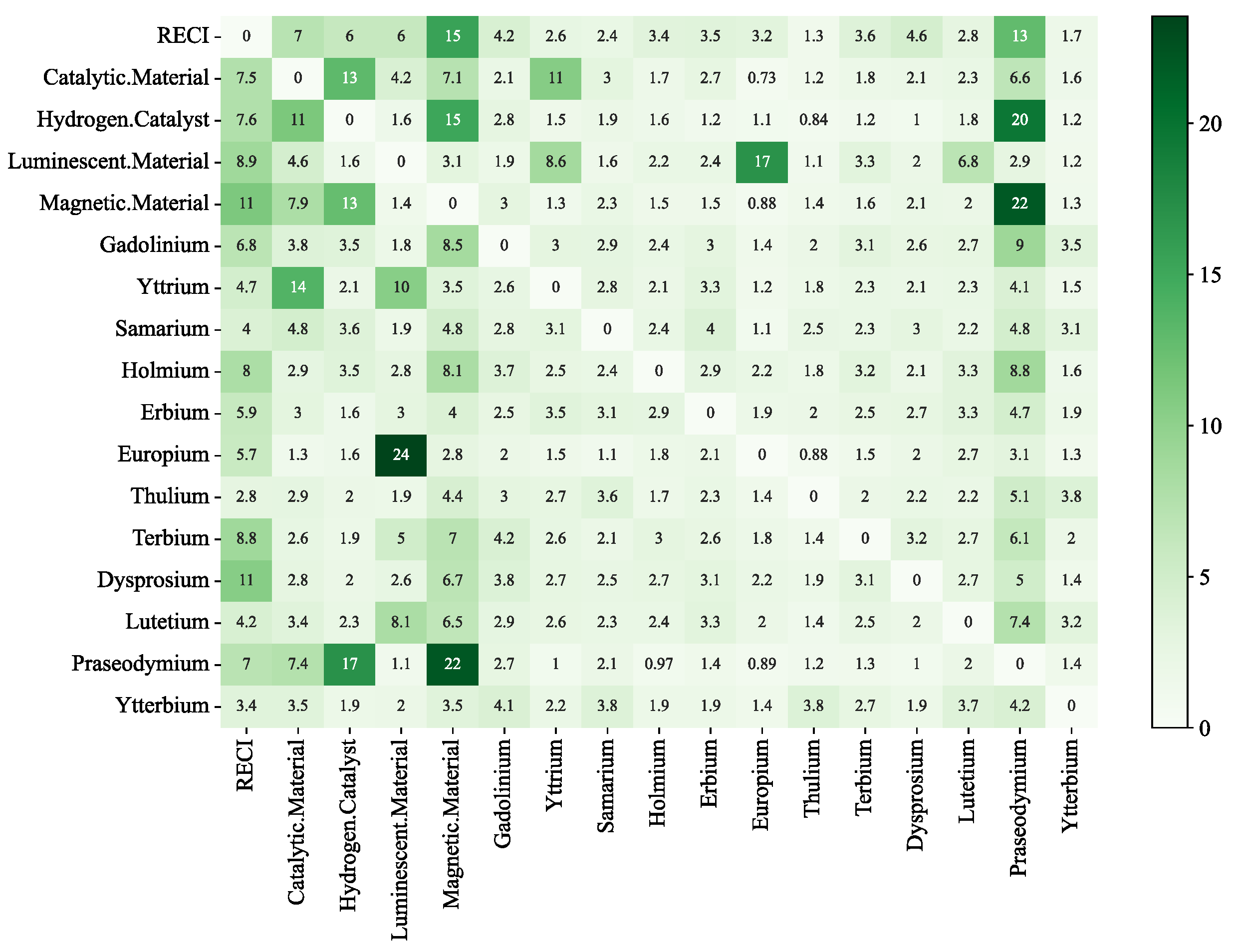
| RECI | Cata. | Hydr. | Lumi. | Magn. | Gado. | Yttr. | Sama. | Holm. | Erbi. | Euro. | Thul. | Terb. | Dysp. | Lute. | Pras. | Ytte. | FROM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RECI | 19.40 | 7.04 | 6.03 | 6.00 | 15.46 | 4.23 | 2.58 | 2.38 | 3.37 | 3.48 | 3.23 | 1.26 | 3.64 | 4.60 | 2.76 | 12.85 | 1.68 | 80.60 |
| Cata. | 7.54 | 31.60 | 13.00 | 4.21 | 7.12 | 2.13 | 10.64 | 3.04 | 1.69 | 2.72 | 0.73 | 1.23 | 1.78 | 2.06 | 2.26 | 6.61 | 1.62 | 68.40 |
| Hydr. | 7.57 | 11.23 | 29.01 | 1.58 | 15.11 | 2.76 | 1.48 | 1.95 | 1.61 | 1.19 | 1.05 | 0.84 | 1.19 | 1.01 | 1.77 | 19.52 | 1.16 | 70.99 |
| Lumi. | 8.91 | 4.62 | 1.60 | 30.80 | 3.11 | 1.89 | 8.61 | 1.55 | 2.25 | 2.38 | 16.92 | 1.14 | 3.30 | 1.97 | 6.84 | 2.85 | 1.25 | 69.20 |
| Magn. | 11.16 | 7.93 | 12.58 | 1.43 | 25.80 | 2.99 | 1.30 | 2.31 | 1.54 | 1.54 | 0.88 | 1.44 | 1.61 | 2.15 | 1.98 | 22.04 | 1.31 | 74.20 |
| Gado. | 6.84 | 3.77 | 3.54 | 1.82 | 8.52 | 39.94 | 2.96 | 2.91 | 2.36 | 2.95 | 1.43 | 2.02 | 3.15 | 2.56 | 2.73 | 9.03 | 3.47 | 60.06 |
| Yttr. | 4.74 | 13.75 | 2.08 | 10.43 | 3.51 | 2.61 | 39.41 | 2.78 | 2.07 | 3.31 | 1.21 | 1.83 | 2.26 | 2.13 | 2.28 | 4.07 | 1.53 | 60.59 |
| Sama. | 4.02 | 4.75 | 3.63 | 1.88 | 4.83 | 2.78 | 3.06 | 49.88 | 2.35 | 3.95 | 1.08 | 2.46 | 2.27 | 2.96 | 2.19 | 4.77 | 3.15 | 50.12 |
| Holm. | 7.98 | 2.94 | 3.54 | 2.83 | 8.09 | 3.71 | 2.50 | 2.36 | 40.11 | 2.86 | 2.23 | 1.76 | 3.24 | 2.11 | 3.32 | 8.81 | 1.62 | 59.89 |
| Erbi. | 5.91 | 3.05 | 1.62 | 2.99 | 4.03 | 2.54 | 3.46 | 3.08 | 2.88 | 51.44 | 1.89 | 1.99 | 2.50 | 2.68 | 3.33 | 4.69 | 1.93 | 48.56 |
| Euro. | 5.71 | 1.30 | 1.65 | 23.54 | 2.79 | 1.98 | 1.53 | 1.15 | 1.83 | 2.09 | 44.99 | 0.88 | 1.47 | 2.00 | 2.67 | 3.13 | 1.27 | 55.01 |
| Thul. | 2.76 | 2.89 | 1.99 | 1.87 | 4.38 | 2.95 | 2.69 | 3.58 | 1.68 | 2.34 | 1.44 | 56.11 | 2.04 | 2.21 | 2.18 | 5.08 | 3.80 | 43.89 |
| Terb. | 8.83 | 2.61 | 1.87 | 4.98 | 6.96 | 4.20 | 2.61 | 2.08 | 2.98 | 2.56 | 1.83 | 1.41 | 43.05 | 3.20 | 2.70 | 6.13 | 2.01 | 56.95 |
| Dysp. | 10.53 | 2.80 | 2.03 | 2.59 | 6.73 | 3.82 | 2.73 | 2.46 | 2.72 | 3.06 | 2.18 | 1.85 | 3.13 | 44.19 | 2.72 | 5.04 | 1.42 | 55.81 |
| Lute. | 4.25 | 3.44 | 2.31 | 8.05 | 6.50 | 2.89 | 2.56 | 2.27 | 2.36 | 3.26 | 2.04 | 1.35 | 2.45 | 1.97 | 43.71 | 7.36 | 3.22 | 56.29 |
| Pras. | 6.97 | 7.43 | 17.10 | 1.15 | 22.10 | 2.71 | 1.00 | 2.08 | 0.97 | 1.41 | 0.89 | 1.18 | 1.27 | 1.04 | 1.99 | 29.32 | 1.39 | 70.68 |
| Ytte. | 3.41 | 3.45 | 1.89 | 2.02 | 3.49 | 4.10 | 2.17 | 3.75 | 1.89 | 1.85 | 1.42 | 3.81 | 2.72 | 1.87 | 3.67 | 4.18 | 54.31 | 45.69 |
| TO | 107.14 | 83.00 | 76.46 | 77.39 | 122.72 | 48.30 | 51.90 | 39.73 | 34.54 | 40.95 | 40.43 | 26.45 | 38.01 | 36.53 | 45.39 | 126.17 | 31.84 | 64.18/60.41 |
| VXFXI | EER | EPU | Liquidity | |
|---|---|---|---|---|
| Panel A (: RECI is not the macroeconomic variables’ nonlinear Granger causality reason) | ||||
| Statistics | 0.5967 | −1.6102 | ||
| p-Value | 0.2753 | 0.0098 | 0.0983 | 0.9463 |
| Panel B (: Macroeconomic variables are not the RECI’s nonlinear Granger causality reason) | ||||
| Statistics | ||||
| p-Value | 0.0002 | 0.0000 | 0.0234 | 0.0781 |
| Mean | S.D. | 95% C.I. | Geweke | Const. | |
|---|---|---|---|---|---|
| 0.0023 | 0.0003 | [0.0018, 0.0029] | 0.6720 | 3.0600 | |
| 0.0023 | 0.0003 | [0.0018, 0.0029] | 0.0040 | 3.7300 | |
| 0.0056 | 0.0016 | [0.0034, 0.0097] | 0.7000 | 32.0000 | |
| 0.0055 | 0.0016 | [0.0034, 0.0094] | 0.7390 | 17.2000 | |
| 0.0022 | 0.0010 | [0.0016, 0.0057] | 0.1240 | 274.9900 | |
| 0.0052 | 0.0017 | [0.0019, 0.0092] | 0.0000 | 94.0100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, R.; Gong, J.; Xia, X. Trading Risk Spillover Mechanism of Rare Earth in China: New Perspective Based on Time-Varying Connectedness Approach. Systems 2023, 11, 168. https://doi.org/10.3390/systems11040168
Ye R, Gong J, Xia X. Trading Risk Spillover Mechanism of Rare Earth in China: New Perspective Based on Time-Varying Connectedness Approach. Systems. 2023; 11(4):168. https://doi.org/10.3390/systems11040168
Chicago/Turabian StyleYe, Rendao, Jincheng Gong, and Xinting Xia. 2023. "Trading Risk Spillover Mechanism of Rare Earth in China: New Perspective Based on Time-Varying Connectedness Approach" Systems 11, no. 4: 168. https://doi.org/10.3390/systems11040168
APA StyleYe, R., Gong, J., & Xia, X. (2023). Trading Risk Spillover Mechanism of Rare Earth in China: New Perspective Based on Time-Varying Connectedness Approach. Systems, 11(4), 168. https://doi.org/10.3390/systems11040168






