A New Lagrangian Problem Crossover—A Systematic Review and Meta-Analysis of Crossover Standards

Abstract

The performance of most evolutionary metaheuristic algorithms relies on various operators. The crossover operator is a standard based on population-based algorithms, which is divided into two types: application-dependent and application-independent crossover operators. In the process of optimization, these standards always help to select the best-fit point. The high efficiency of crossover operators allows engineers to minimize errors in engineering application optimization while saving time and avoiding overpricing. There are two crucial objectives behind this paper; first, we provide an overview of the crossover standards classification that has been used by researchers for solving engineering operations and problem representation. This paper proposes a novel standard crossover based on the Lagrangian Dual Function (LDF) to enhance the formulation of the Lagrangian Problem Crossover (LPX). The LPX for 100 generations of different pairs parent chromosomes is compared to Simulated Binary Crossover (SBX) standards and Blended Crossover (BX) for real-coded crossovers. Three unimodal test functions with various random values show that LPX has better performance in most cases and comparative results in other cases. Moreover, the LPB algorithm is used to compare LPX with SBX, BX, and Qubit Crossover (Qubit-X) operators to demonstrate accuracy and performance during exploitation evaluations. Finally, the proposed crossover stand operator results are demonstrated, proved, and analyzed statistically by the Wilcoxon signed-rank sum test.

1. Introduction

Combinatorial optimization is one of the most widely investigated areas of artificial intelligence. Every year, several research projects focus on issues that arise in this domain. The solution structure, rather than its coding, is utilized by a knowledge-based crossover mechanism for strategic metaheuristic algorithms [1]. Thus, there are several different approaches that researchers have used in the past to solve single or dual problems. However, in the majority of these kinds of applications, research is limited to solve linear programs, quadratic programs, or, more broadly, convex programming issues. Because the primal optimal solution is closely related to the optimal single or dual solution for convex problems, such a study has assisted investigators in better understanding the relationship [2]. Therewith, a set of optimization algorithms influenced by natural events and animal intelligence is characterized as evolutionary nature-inspired metaheuristic algorithms. They are, thus, frequently nature-inspired algorithms, and samples of these evolutionary metaheuristic algorithms are Genetic Algorithm (GA) [3], Artificial Bee Colony [4], Differential Evolution [5], and Learner Performance based Behavior algorithm (LPB) [6]. Therefore, nature-inspired computing is a field of computer science that could be used and shared with an optimization algorithm, computational intelligence, data mining, and machine learning [7].

A problem with a fluctuating objective function is one of the more difficult metaheuristic optimization methods, but it is much more common in real-world search or self-adaptive optimization. The search technique used to solve such problems for optimality must be flexible enough to adjust to the present function [8]. A problem with population-based optimizers is that once the investigation has found a locally optimal solution, there may not be enough diversity to move the search forward to a new, better solution. In many of these circumstances, diversity-preserving strategies such as a high amount of crossover or the use of a clustering operator are required. Therefore, most of the algorithms have been improved and enhanced in the field of metaheuristic optimization by these standard operators [9]. In addition, several effective methods have been developed in this research to improve existing optimizers based on crossing genes between parents. Alternatively, updated standards are always accepted as long as the suggested methods offer novel improvements or comparable results.

When the genetic recombination operator is chosen correctly, crossing genes can match the best-known techniques for a wide range of problems involving restrictions. It would be better to suggest or use the superlative crossover standard to accomplish the goal. The efficiency of this new method could be shown to work for selected features [10]. The motivation behind this paper is the use of conventional techniques and direct search procedures due to the complexity of variables in the problematic domain. Depending on the situation, fixing the problem might involve modifying the basic algorithm, presenting a systematic and comprehensive overview of the meta-analysis, or utilizing innovative metaheuristics. In addition, this paper proposes a novel standard from several strategies linked to mathematical assessments with originally generated methods.

The fundamental goal of this research is to investigate the effectiveness of experience and understanding methods in GAs. This paper is focused on the generation and standards of crossover and how it affects metaheuristic algorithms. Crossover, also known as recombination, is a genetic operator in the special process which is exploited to connect the genetic codes of two parents to make new offspring (children). Further, crossover techniques can be considered to be extremely useful for generating new solutions from a current population stochastically [11]. In many studies, crossover and mutation operators have been associated with GA’s success. Some of them conclude that success rests in both, whether the crossover is performed alone or through mutation or both. Crossover operators play a substantial role in balancing exploitation and exploration, allowing for feature extraction from both chromosomes (parents), with the intention that the developing offspring have beneficial qualities from both chromosomes [12].

Lagrangian Dual Function (LDF) [13] technique can support to exchange genes between chromosomes by locating the replacement chromosome at the highest or lowest point to produce offspring with improved traits. A proposed standard known as Lagrangian Problem Crossover (LPX) is imperative for generating new operators; the crucial characteristic of LPX is that it allows offspring to inherit some characteristics from their parents for finding a new optimal solution in population solution-based metaheuristics. Likewise, depending on the meaning of the worst chromosome for each problem, this point (its worst chromosome) can be chosen on both chromosomes (parents), or by applying crossover between chromosomes to produce the best novel genes. Furthermore, the new operator is identified automatically based on performance ratings and statistical evidence, so the time spent selecting the best operator is taken into account.

The crossover strategy starts with a low value and adjusts it every generation to avoid premature convergence. Moreover, several crossover functions are employed as a strategy to avoid convergence rates. Population (swarm) algorithms are one of the most successful metaheuristics for managing these kinds of numerous case problems. As a result, population-based methods have become one of the most efficient methods for combinatorial function optimization [14]. These techniques operate with several populations of solutions that evolve in tandem with algorithm operation. Accordingly, the following summarizes this paper’s main contributions:

• There are several standard operators used to illustrate how the implementation was conducted and illustrate the mathematical crossover form using small examples and technique operations;
• As a systematic development of previous standards, it has enabled the use of binary form, real-coded form, and ordered-coded form methods;
• Based on LDF, a crossover operator has been proposed that can provide a novel optimum solution for population metaheuristic algorithms that use original metaheuristic optimization;
• The new anticipated LPX is evaluated by comparing it with selected previous tuning methods, a variation on the traditional GA, as discussed in the next sections;
• LPX is compared with other well performing crossover operators using the LPB algorithm as a single objective population-based algorithm and the affected random values and elapsed time are measured;
• The proposed standard operator is statistically analyzed and compared, using nonparametric statistical tests.

The next section describes how this paper is organized; this section is dedicated to discussing related work on crossover standards. Several mathematical crossover standards are presented by thinkable pseudocode in the third section of the paper. The fourth segment examines the novel formula which can be developed as a standard crossover in the future metaheuristic algorithm known as LPX. The fifth section is devoted to proving the heuristic and exploitation crossover results by comparing LPX results with specific real-coded crossover standards. At the end of the paper, the conclusion and novel features are discussed.

2. Crossover Standards Overview

As stated, the paper includes two major subjects. The first part includes a systematic review of crossover standards; the second, a proposed a method to generate novel offspring by generating a newly created evolutionary algorithm.

A systematic review has been performed to assess several efficient methods presented in the research. The reviewed articles, as well as standard sources, were examined using search terms including “crossover standard generation”, “generations of crossover standards of parent chromosomes in evolutionary metaheuristic algorithms”, or “Genetic Algorithm Based on crossover standard generation”. These queries are searched in ScienceDirect, PubMed, and Google Search Engine. These articles and sources were culled to address only crossover standards, evolutionary algorithms, Gas, and crossover operators in GAs. Search dates include up to March 2022. A huge number of articles was retrieved, but in the end, the standard crossover operators were approved by 41 eligible papers.

The second part is the proposed LPX standard which is used as the superlative crossover standard to accomplish the target; the efficiency of this new method might be proved for the feature selection optimization problems. The standard is generated from the mathematical model of the LDF theorem.

Many forms of the crossover have been produced over the years, and comparisons between various types have been proposed. These started with one-point crossover and evolved into a range of ways to cover a variety of conditions, including uniform crossover [15]. To generate improved self-adaptive combinational optimization, a set of assumptions (rules) have been developed to simplify natural/biological events, and these include a list of control parameters to define intensification and diversification rules [16]. The best solution is identified, and other solutions advance toward the most optimal solution according to the given rules. In the stochastic mode, the location of a few solutions can be altered and controlled, such as crossover or mutation operations in several metaheuristic algorithms, which is illustrated in a simple flowchart in Figure 1.

Likewise, several standards for permutation applications, such as the Traveling Salesman Problem (TSP), were defined. There are several ways to approach the TSP using evolutionary algorithms, including binary, route, closeness, ordinal, and vector representations. To reduce the overall distance, the researchers presented a novel crossover operator for the TSP [17]. Another research study confirmed that sequential constructive crossover (SCX) fixed the TSP in 2010. The primary idea behind this strategy is to choose a random point, termed the crossover point; then, before the crossing point, use an SCX technique with improved edges. After the crossover site, the remaining chromosomes are swapped between parents to generate two children; if a chromosome currently exists, it is replaced with an unoccupied chromosome [18].

Ring Crossover was offered as a solution to the recombination problem. Parents were grouped in the design of a ring of this type, and then a cut point was chosen. Parents were grouped in the design of this circle procedure, and then a slice point was selected randomly. The other location was the length of the chromosome; the first offspring develops clockwise from the line (the original cut), and the second offspring evolves counter clockwise. They employed this type of crossover for the aspects mentioned and it outperformed the other types of assessed crossover [19]. Despite that, to prevent creating erroneous solutions, evolutionary algorithms that optimize the ordering of a very large series require specific crossover operators. It is difficult to list all of them. Thus, several standard crossovers have already been documented in

Table 1. Standard crossovers generation.

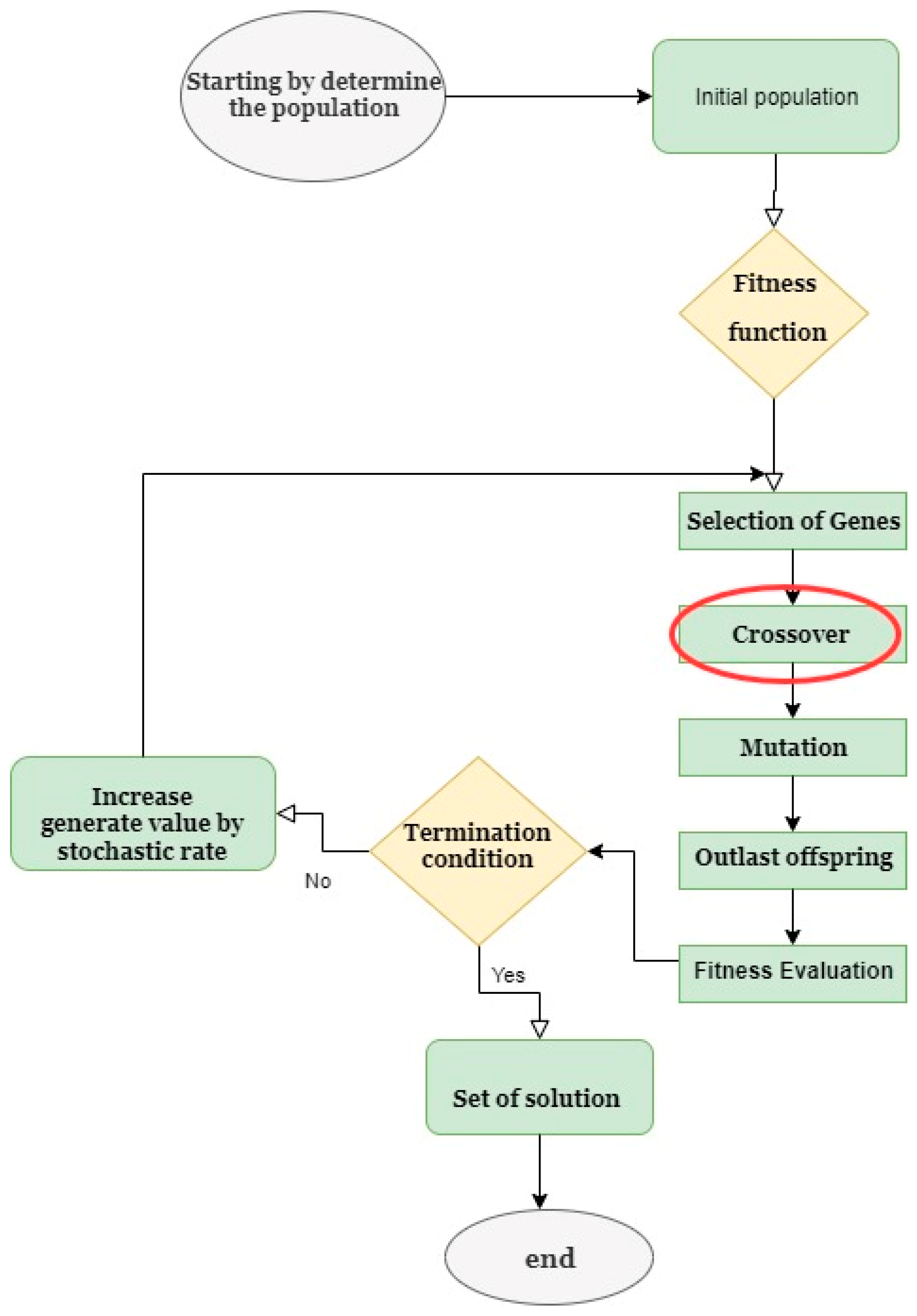
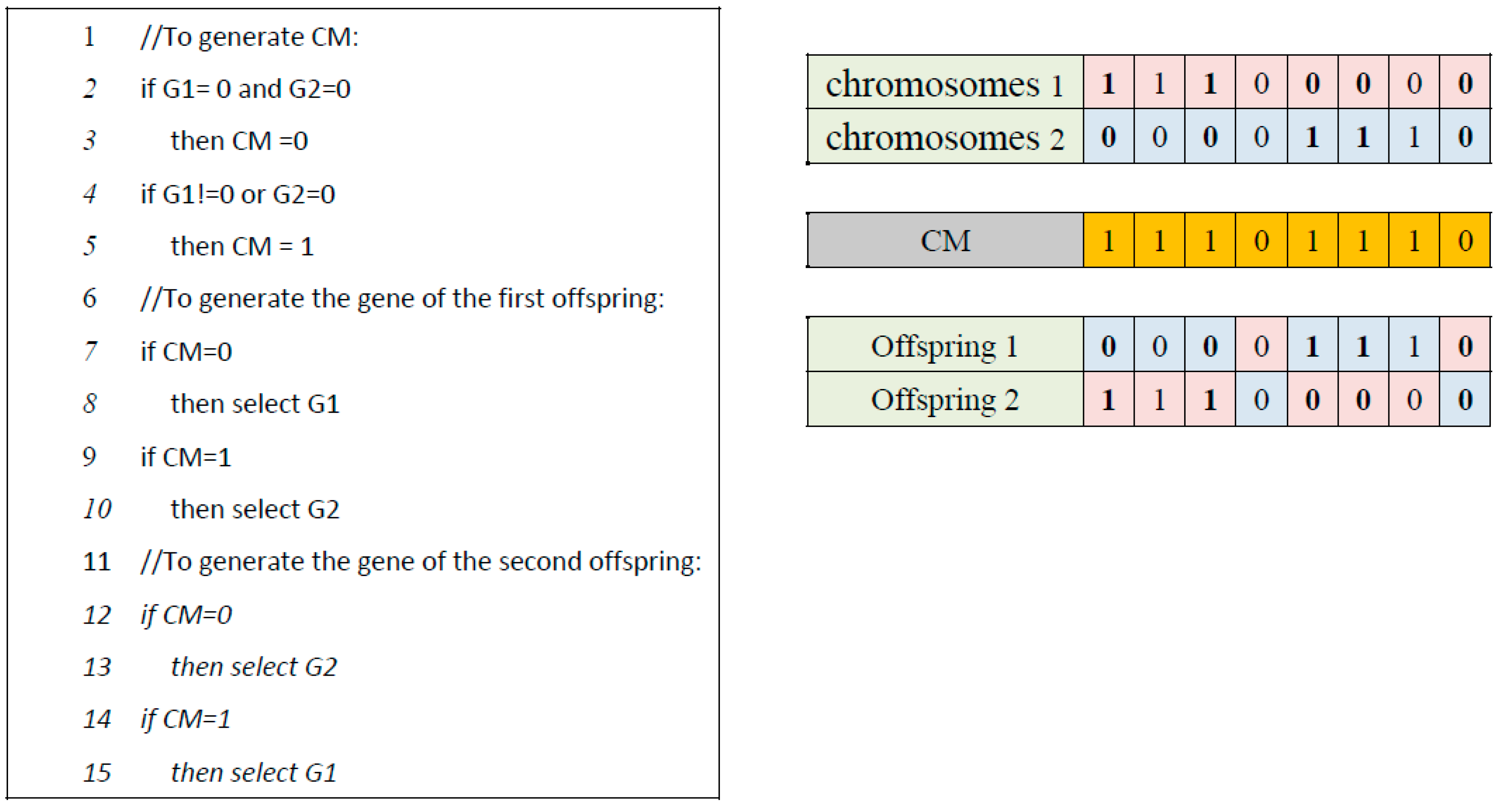
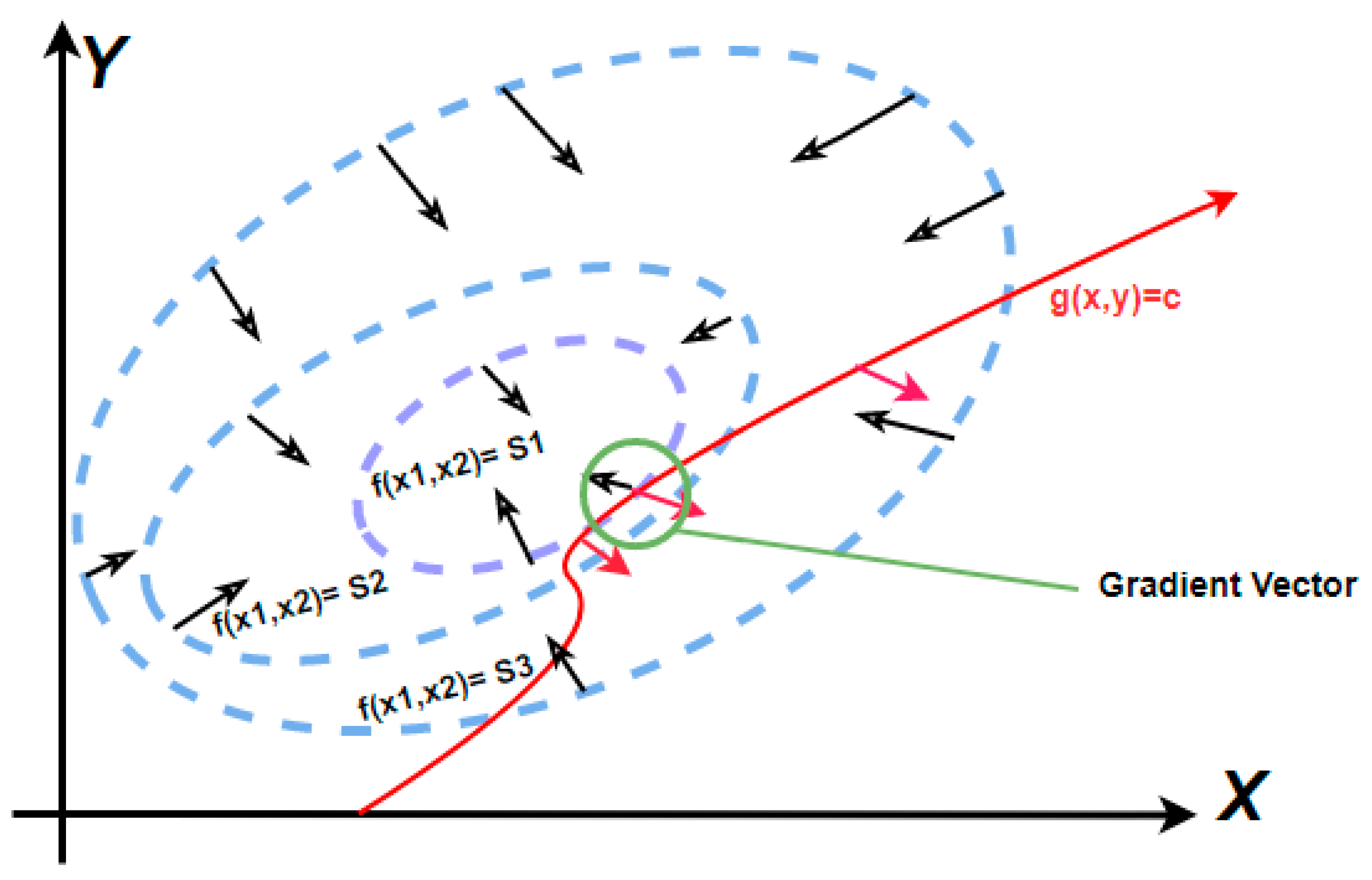
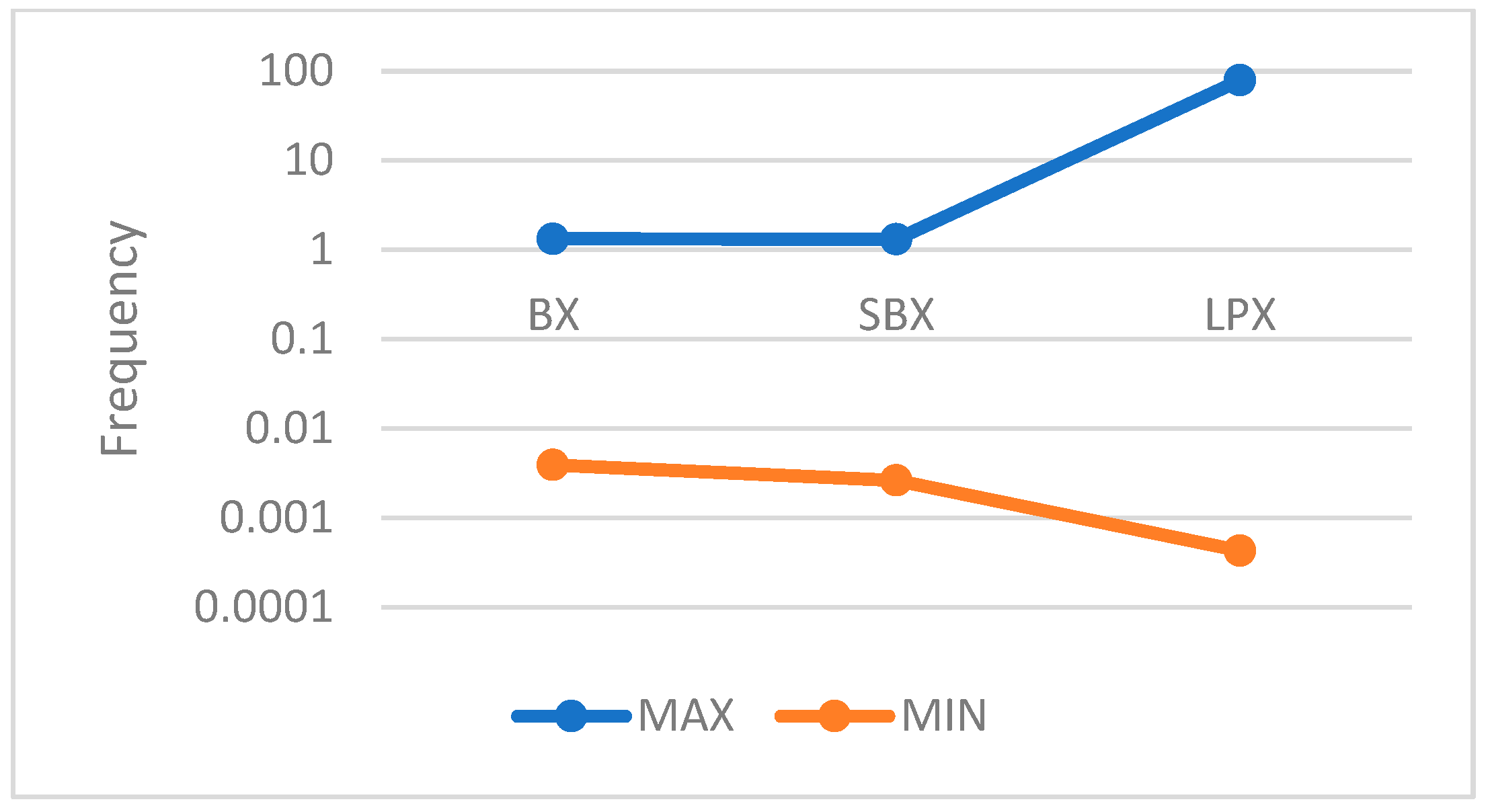
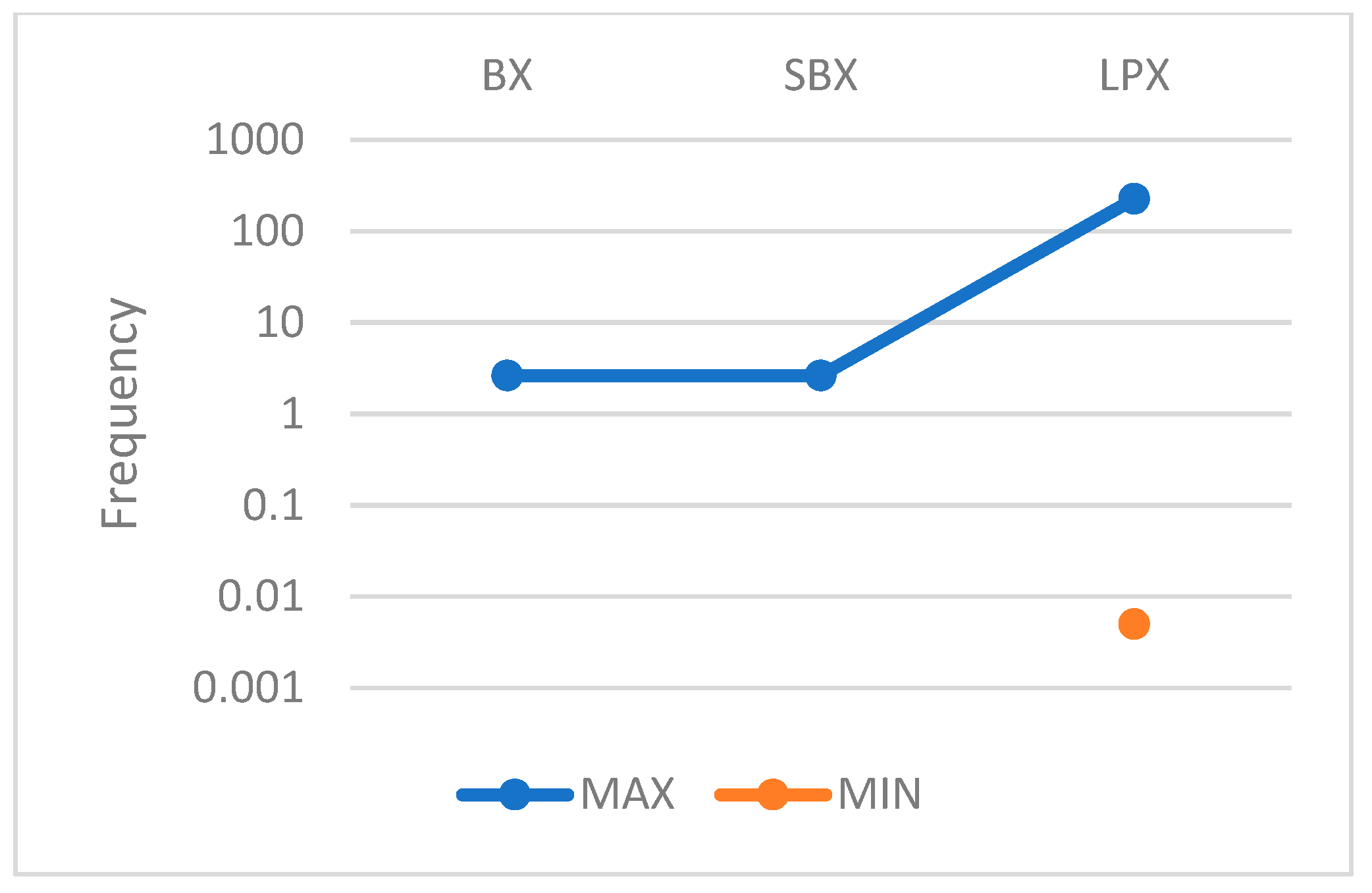
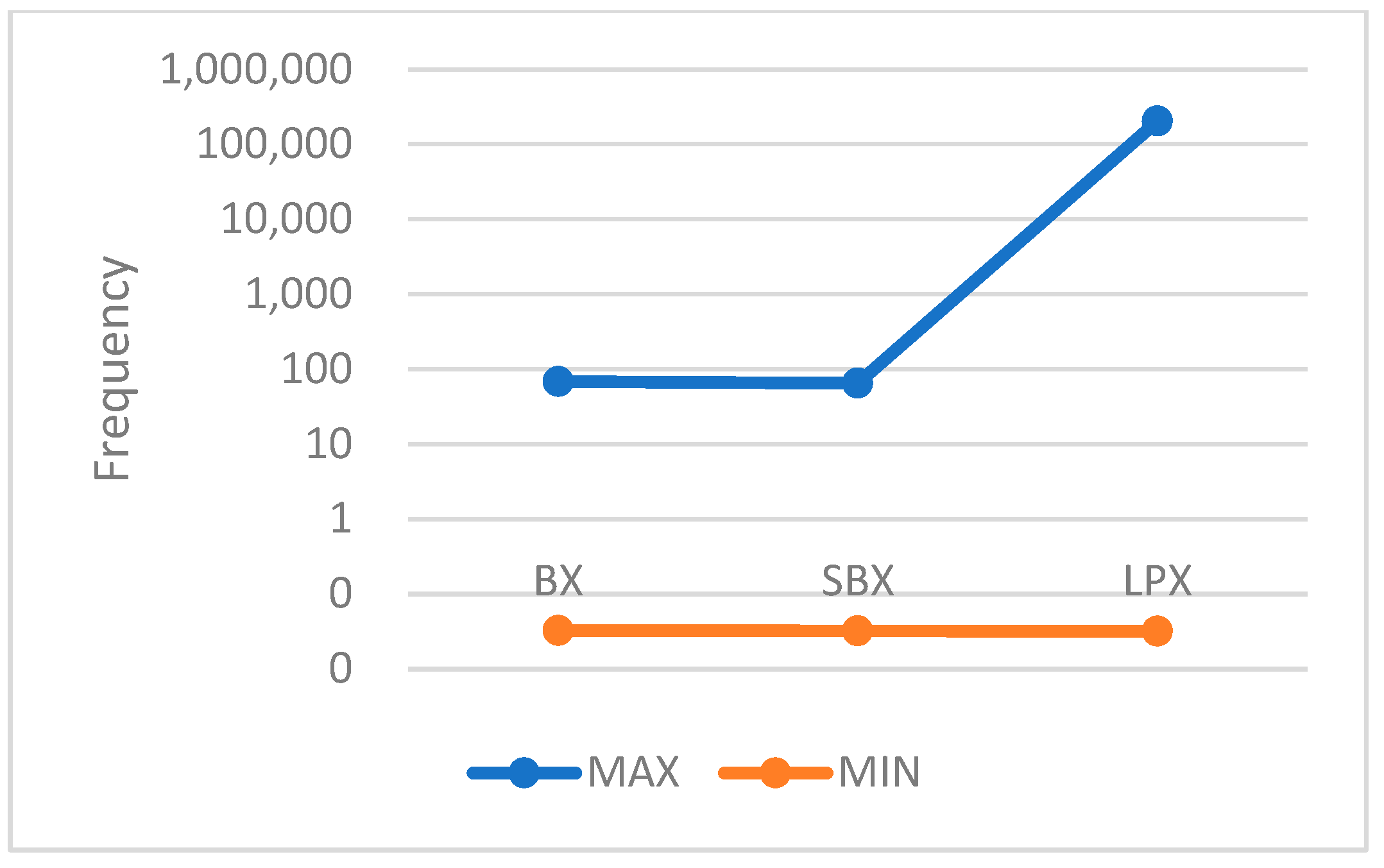
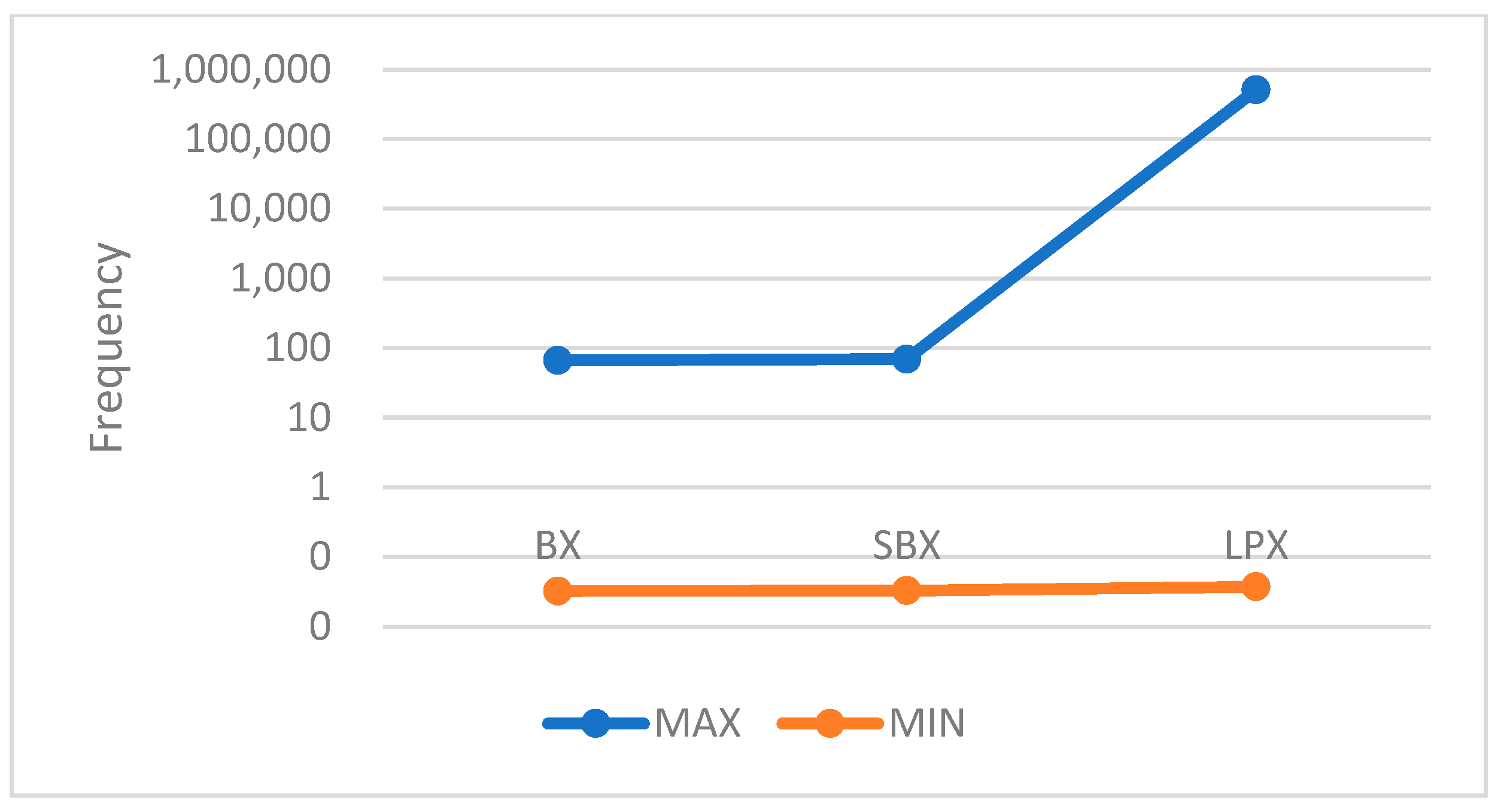
No.	Standard Crossover Operator Name	Initial Abbreviation	Related Work
1	Order Crossover Operator	OX1	[17,20,21]
2	Sequential Constructive crossover	SCX	[18]
3	Order-Based Crossover Operator	OX2-OBX	[20,22]
4	Maximal Preservation Crossover	MPX	[22,23]
5	Alternating Edges Crossover	AEX	[21,23,24]
6	Edge Recombination Crossover	ERX	[20,21]
7	Position-Based Crossover Operator	POS	[20,22,25]
8	Voting Recombination Crossover Operator	VR	[20,22]
9	Alternating Position Crossover Operator	AP	[20,26]
10	Automated Operator Selection	AOS	[27]
11	Complete Sub-tour Exchange Crossover	CSEX	[22,28]
12	Double Masked Crossover	BMX	[22,29]
13	Fuzzy Connectives Based Crossover	FCB	[30,31]
14	Unimodal Normal Distribution Crossover	UNDX	[32,33]
15	Discrete Crossover	DC	[34]
16	Arithmetical Crossover	AC	[19,31,35]
17	Average Bound Crossover	ABX	[36]
19	Heuristic Crossover	HC	[17,37]
20	Parent Centric Crossover	PCX	[22,38]
21	Spin Crossover	SCO	[39]

and each of them has been generated for a specific global solution. However, some of them produced offspring from parents based on real code, whereas others relied on the binary-coded crossover started in the next section.

In application, crossover standards have typically been classified based on the representation of the gene; genetic sequence has been stored in a chromosome represented by a bit matrix or real code in the different algorithms. Crossover strategies for both techniques are popular, and illustrative instances or classes are genetic recombinations, which are thoroughly explained in the following sections. Several current methods ensure that these techniques can be applied to global numerical optimization and current practical problems as a recently proposed meta-heuristic; for example: Slime Mold Algorithm [40], Moth Search Algorithm [41], Hunger Games Search [42], Harris Hawks Optimization [43], and Colony Predation Algorithm [44]. As a result, novel standards should be proposed for evolving evolutionary algorithms.

The capacity of solutions to learn from one another, however, is what gives rise to the intriguing behavior of GAs. Solutions can combine to form offspring for the next generation. Occasionally they will share their poor information, but if we use crossover in conjunction with a harsh selection method, better solutions will emerge; there are many details to crossover with permutations, as in previous population-based algorithms, especially these algorithms based on GA, such as the Quantum-based Avian Navigation Optimizer Algorithm [45]. Thus, we will cover the basic crossover techniques, known as “modification genes”, by Lagrange method techniques. Accordingly,

Table 2. Perfection and shortcomings of crossovers generation.

Perfection of Crossovers Generation

Shortcomings of Crossovers Generation

▪ Through crossover, it is possible to mix incomplete solutions from several competitors. This frequently entails taking a pretty significant step away from either of the parents and can swiftly push one outside of a local optimum; ▪ Crossover is crucial since the tested parents share genetic material, which can result in a more effective solution; ▪ It signifies that even without crossover, the change would be slow, and it would be impossible to push your population over a local optimum; ▪ Without crossover, a population-based algorithm would resemble a search algorithm that uses random numbers, and finding a workable solution would require some luck. However, with crossover, it improves with each iteration while keeping the positive aspects of the previous one [46]; ▪ A high crossover rate causes the genomes in the next generation to be more random. This is because there will be more genomes that are a mix of previous-generation genomes rather than a low crossover rate. The second approach decreases the chance that a very accurate genome will be produced by the crossover operation [47].

▪ To ensure that their representations enable crossover to be reasonable, limited generations should be required for crossover to occur; ▪ An ideal generation is also determined by standard crossover operators. Look at the type of two-point crossovers compared to one-point crossovers. There might be a loss of genetic material from the parent solution in a point crossover or by another standard. As a result, most evaluations depend on complex mathematical models of the new generation [48]; ▪ The actual permutations would be the only additional representations in the second generation. In that situation, the crossover will presumably result in a completely distinct local optimum that is both meaningless and unachievable; ▪ According to several references, single-point crossover results in offspring genomes being less diversified since they are more likely to resemble their parents rather than multi-point which is a hybrid of single-point and uniform [49].

highlights the weak and strong points of crossover operators in metaheuristic population-based algorithms.

3. Mathematical Crossover Standards

In metaheuristic algorithms, the exploration of the optimal solution is based on the generation of new members from existing members. The crossover process facilitates the interchange of genetic code between parents, which results in a higher probability of genes being exceptional to the parents. However, there are numerous crossover techniques recorded in the cited study. Researchers should focus on finding and tackling the question of whether the most effective standard strategy has been improved and adopted. As mentioned, the crossover operator is comparable to multiplication and biological recombination. The data suggest that more than one genome must be selected and that children are produced using the genetic codes (genomes as blue balls on the parents’ chromosomes [50]) and then two more children using two new offspring genes (pink balls). This probabilistic scale is illustrated in Figure 2. Then, the graphic depicts the range of potential offspring in two-dimensional constrained real space between x and y dimensions by generating a box crossover between genes and new offspring.

Typically, the crossover is used in metaheuristic algorithms with a significant probability, particularly in a GA, as challenging in real-coded crossovers [51]. Consequently, the goal of establishing crossover likelihood is to prevent gene loss from the parents, even if the offspring are not better than the parents. According to the distribution of crossover standards, Section 3.1 has determined the forms of binary crossover. The Section 3.2 has classified the categories of real-coded or floating-point crossover. In Section 3.3, the form of order-coded crossover is distributed.

3.1. Binary Form Crossover

This section provides a broader collection of crossover operators used in binary representation for metaheuristic algorithms. Improvements to previous results demonstrate that, according to the current challenges, most of these results are effective crossovers. How to implement some types of crossover standards and point out some interesting comparisons between others could also be shown [52]. Traditionally, genetic material has been stored in a gene, which is represented as a bit collection in various techniques. Crossover procedures for bit-order are prominent, and specific examples or categories include genetic manipulation, as explained in the points below.

Binary Single-point crossover [53]: A crossing point in the parent entity string is picked. Apart from that point in the biological sequence, all data transfer between two units, including biological parents and situational bias, is conducted through strings. As indicated in Figure 3, Genes with sub-blocks that include three bits to the right of that point are transferred correspondingly between the two parents. As illustrated by pink and blue color bites, it has generated two new offspring.

Double-point and n-point crossover [53]: two randomly generated locations (strings) or n-point locations on the individual chromosomes are chosen, and the gene code is switched at these locations. As seen in Figure 4, two equally spaced points on the right and left sides are selected on parent chromosomes, then pink color and blue color bits are swapped to perform two single-point crossovers.

Uniform crossover [49] and half-Uniform crossover [54]: such as in the coin-throwing approach, each gene (bit) is drawn randomly from one of the comparable genes in the selected parents. Each genome is addressed separately rather than being separated into segments. In this situation, we just flip a coin to see if each genome is present in the child. The idea may be tossed about to support one parent having more genetic information in their newborn. Figure 5 shows two chromosomes arrayed as a two-dimensional array with bits exchanged in a light blue color and a pink color.

Uniform Crossover with Crossover Mask (UCM) [27]: The matrices are separated into several non-overlapping zones, and the matrix created by the logical operator is known as the crossover mask (CM) generated by pseudocode control. In Figure 6, we present an example and pseudocode to display how the new offspring has spawned between chromosomes and CMs based on these conditions.

Shuffle Crossover (SHX) [55,56]: Initially, we choose a crossover point at random, such as the highlighted line in Figure 7, then mix the gene code of both parents. It should be emphasized that Shuffle chromosomes for the right and left sites are handled independently. A single point of crossing is chosen, which splits the chromosome into two sections, known as schema. Chromosomes are scrambled in each schema by both parents. To produce offspring, schemas are transferred (as in a single crossover).

Three-Parent Crossover (TPX) [57]: According to the prior solution approach, in this kind of operator, there are numerous probability rate algorithms with which to create innovative offspring from three parent genes. In the elucidation example, Figure 8 highlights the problems involved in calculating future generations based on deliberate offspring generated by swapping genes according to the general pseudocode.

3.2. Real-Coded (Floating Point) Form Crossover

The genes are real-valued without encoding or decoding into binary, and the digits are left alone to speed up the process. Nevertheless, it is less logical than binary representation since crossover has demonstrated that floating-point format can function as well as, if not better than, ordinary binary strings. Therefore, there is no reason to be concerned about algorithm efficiency if the floating-point encoding is utilized [51]. Several crossover techniques for real-coded crossovers were developed. The method is based on effectively adjusted real-coded crossover operations that use the likelihood function to create very distinct sequences that may be candidates for alternative solutions [58]. The crossover techniques are described mathematically in the next points.

Real Single-point Crossover (RSPX) [59]: It is marginally comparable with a binary single-point crossover; it could be combined with two chromosomes and use a real number for each gene at the crossover point. It can also be generated for two-point, three-point, and n-point crossovers. As shown in Figure 9, two genes were crossed and real numbers were swapped between them, resulting in two new offspring.

Single arithmetic crossover (SAX) [57]: This standard should be derived from a single genome ($k$), randomly chosen from both chromosomes ($n$). For instance, in Figure 10, $k$= 2 and then we define a random parameter (α = 0.5). We modify the kth gene of chromosome 1 and chromosome 2 to generate offspring by the selected asthmatic formula that is calculated as Equation (1) [60,61].

$${\mathrm{Gene}}_{\mathrm{offspring}\left(\mathrm{n},\mathrm{k}\right)}=\left(1-\mathsf{\alpha }\right)\ast G_{nk}+\mathsf{\alpha }\ast G_{nk}$$

(1)

$${\mathrm{Gene}}_{\mathrm{offspring}\left(\mathrm{n},2\right)}=\left(1-0.5\right)\ast 0.13+0.5\ast 0.94=0.535$$

Whole Arithmetic Crossover (WAX) and Linear Crossover (LX) [62]: The calculations for the whole arithmetic (linear) crossover have been handled for all genes on the chromosome ($n$) with a single similar arithmetic crossover. The calculation is shown in Equation (2) [58], and an example of how to create new offspring can be seen in Figure 11. Despite this, the probability rates are higher since the number of offspring produced will equal the number of chromosomes (genes =$k$). It should be defined as a random parameter ($\alpha$ and $\beta$) and as (${\alpha }_1=0.5$, ${\alpha }_2=1.5,$ ${\alpha }_3=-0.5\dots \dots {\alpha }_m$) and (${\beta }_1=-0.5$, ${\beta }_2=0.5,$ ${\beta }_3=1.5\dots \dots {\beta }_m$) and, for this example, when the numbers of genes (k) equals three. This example calculated and produced three offspring when $k=1$; in consequence, it can be calculated for k numbers. However, Figure 11 just generates three offspring, the generation could be developed by other children according to the $k$ numbers.

$${\mathrm{Gene}}_{\mathrm{offspring}\left(\mathrm{m},\mathrm{n},\mathrm{K}\right)}={\alpha }_m\ast G_{nk}+{\beta }_m\ast G_{nk}$$

(2)

$$\begin{gathered} {\mathrm{Gene}}_{1,\mathrm{n},1}={\alpha }_1\ast G_{11}+{\beta }_1\ast G_{21}={\alpha }_1\ast 0.88+{\beta }_1\ast 0.64=0.12 \\ {\mathrm{Gene}}_{2,\mathrm{n},1}={\alpha }_2\ast G_{11}+{\beta }_2\ast G_{21}={\alpha }_1\ast 0.88+{\beta }_1\ast 0.64=1.64 \\ {\mathrm{Gene}}_{3,\mathrm{n},1}={\alpha }_3\ast G_{11}+{\beta }_3\ast G_{21}={\alpha }_1\ast 0.88+{\beta }_1\ast 0.64=0.52 \end{gathered}$$

Blended Crossover (BX) [50,63]: One of the effective crossovers that improved several algorithms. If the two-parameter values in a pair of chromosomes are $G1$ and $G2$, $G1$ is thus smaller than $G2$, and the blend crossover method produces an offspring option in the range $\left[G1-\alpha \left(G2-G1\right), G2-\alpha \left(G2-G1\right)\right]$. Where $\alpha$ is a constant to be established, the solutions of the offspring do not exceed the scope of the single variable [50,64].

The example is stated in Figure 12 which indicated $k$ number is equal to 2, $G1$ = 0.13 < $G2$ = 0.94, so we calculate the range by $\left[G1 – \alpha \left(G2 – G1\right), G2 – \alpha \left(G2 – G1\right)\right]$; when $\alpha$ = 0.5 the range is [1.345, 0.535] so, we randomly select $G1$ and $G2$ between the range.

If the process was evaluated in the previous range, it could not find a global solution, as documented in several improvement algorithms. According to earlier researchers [50], the condition might be calculated by the updated blend formula. Thus, a novel technique has been developed for the BX standard. The parameter $\mathsf{\gamma }$ must be determined using $\alpha$ and a random integer $r$ in the range limitation between (0.0, 1.0), both of which are excluded from the Equation (3) [65].

$$\mathsf{\gamma }=\left(1+2\mathsf{\alpha }\right)$$

(3)

$Genom{e}_1$ and $Genom{e}_2$ are the offspring solutions which are regulated by the parents as Equations (4) and (5) [65], consecutively:

$${\mathrm{Gene}}_1=\left(1-\mathsf{\gamma }\right)\ast G_1+\mathsf{\gamma }\ast G_2;$$

(4)

$${\mathrm{Gene}}_2=\left(1-\mathsf{\gamma }\right)\ast G_2+\mathsf{\gamma }\ast G_1.$$

(5)

Figure 13 pointed out the example when $k$ (gene) = 2, then identified randomly $\alpha =0.5$ and $r=0.5$, so parameter $\mathsf{\gamma }$ is calculated by Equation (3).

$$\begin{array}{l}\mathsf{\gamma }=\left(1+2\mathsf{\alpha }\right)\ast \mathrm{r}-\mathsf{\alpha }=\left(1+2\ast 0.5\right)\ast 0.5-0.5=\mathbf{0.5}\\ {\mathrm{Gene}}_1=\left(1-\mathsf{\gamma }\right)\ast G_1+\mathsf{\gamma }\ast G_2=\left(1-0.5\right)\ast 0.13+0.5\ast 0.94=\mathbf{0.535}\\ {\mathrm{Gene}}_2=\left(1-\mathsf{\gamma }\right)\ast G_2+\mathsf{\gamma }\ast G_1=\left(1-0.5\right)\ast 0.94+0.5\ast 0.13=\mathbf{0.535}\end{array}$$

Simulated Binary Crossover (SBX) [66,67]: It is preferable and common to implement a standard crossover operation across all standards. Due to these reasons, SBX was applied to the real-coded parameter without any mutation operator, and SBX was also developed based on the single-point crossover [66]. This approach focuses on the probability distribution of obtainable offspring (Gene) by the specified parents (Genes), as shown in Equation (11) [68]. SBX initially computes the number of children using Formulas (6) and (7) [68], or by using Formulas (8) and (9), that enhance the last two formulas by Azevedo [66], which are the most commonly used. The steps to calculate the float number resulting from the crossover are started by fixing a random number µ ~ (0, 1) at first; then, calculate the $\mathsf{\alpha }$ and generate offspring by using $\mathsf{\alpha }$.

$${\mathrm{Gene}}_1=0.5[(1+{\mathsf{\alpha }}_i)G_1+\left(1-{\mathsf{\alpha }}_i\right)G_2]$$

(6)

$${\mathrm{Gene}}_2=0.5[(1-{\mathsf{\alpha }}_i)G_1+\left(1+{\mathsf{\alpha }}_i\right)G_2]$$

(7)

$${\mathrm{Gene}}_1=0.5\left[\left(G_1+G_2\right)-{\mathsf{\alpha }}_i\left|G_2-G_1\right|\right]$$

(8)

$${\mathrm{Gene}}_2=0.5\left[\left(G_1+G_2\right)+{\mathsf{\alpha }}_i\left|G_2-G_1\right|\right]$$

(9)

As a function of (9), Alpha (${\mathsf{\alpha }}_i$) [63] must be calculated as a function of the two previous offspring. H is the index of a user-defined distribution (not negative), which means η is the number of parameters chosen by the user.

$$\mathsf{\alpha }=\left\{\begin{array}{c}{\left(2\mu \right)}^{\frac{1}{\mathsf{\eta }+1}}, if \mu <0.5\\ {\left(\frac{1}{2\left(1-\mu \right)}\right)}^{\frac{1}{\mathsf{\eta }+1}}, otherwise\end{array}\right.$$

(10)

Utilize the probability distributions to compute the function of Alpha (${\mathsf{\alpha }}_i$).

$$\mathsf{\alpha }=\left\{\begin{array}{c}0.5\left(\mathsf{\eta }+1\right){\mathsf{\alpha }}^{\mathsf{\eta }}, if \alpha \le 1 \left(\mathrm{Contracting} \mathrm{Crossover}\right) \\ 0.5\left(\eta +1\right)\frac{1}{{\mathsf{\alpha }}^{\mathsf{\eta }+2}}, otherwise \left(\mathrm{Expanding}\mathrm{Crossover}\right) \end{array}\right.$$

(11)

When selecting the second gene as a parent 1 and 2 from Figure 14 will produce two new offspring genes, we need to find (${\mathsf{\alpha }}_i$) if $\mu =0.4$, and the user chooses two parameters. The calculation is executed as follows:

$$\begin{array}{l}\mathsf{\alpha }={\left(2\ast 0.4\right)}^{\frac{1}{2+1}}=0.928;\\ {\mathrm{Gene}}_1=0.5\left[\left(0.13+0.94\right)-0.928\left|0.94-0.13\right|\right]=0.1592;\\ {\mathrm{Gene}}_2=0.5\left[\left(0.13+0.94\right)+0.928\ast \left|0.94-0.13\right|\right]=0.9108\left(\mathrm{out}\text{-}\mathrm{of}\text{-}\mathrm{range}\mathrm{probability}\mathrm{distribution}\right).\end{array}$$

However, this technique has many advantages, such as a wider range of offspring explored, and results are reliable and often reach global optima. In Figure 15, it is illustrated that sometimes the results of the offspring gene are out of range based on the probability distributions. This is because the new gene’s impact should be bigger than the old gene, but in this case, the updated gene is smaller than the old gene.

3.3. Order-Coded Problem Methods Crossover

Several different crossover operators have been proposed to reproduce either the relative order or the precise organization of chromosomes from the homologous chromosome. The majority of standard-matched crossovers are operators that maintain exact locations [69]. As a result, the following sections focus on the most basic forms of order-coded crossovers.

Partially Mapped Crossover (PMX) [70]: The procedure produces offspring solutions by transferring sub-orders from one genome to the other while maintaining the original sequence (order) with possible several points, as shown in Figure 16. To initiate, we choose a random range of crossovers and produce children by swapping genes. Unselected substrings are then used to identify the mapping relationship at the time of legalization of the resulting offspring [71].

The Cycle Crossover Operator (CX) [17,72]: Determines the number of cycles that exist between two-parent chromosomes. It may be used with numerical strings in which each component appears only once. This assures that each index point in the resultant offspring is filled with a value from one of his parents [73]. Figure 17 shows that the first offspring world is generated by relying on the pseudocode when the random cycle includes {2, 5, 7, 6, 11}.

4. Lagrangian Problem Crossover

Two types of crossover operators have been used in population-based algorithms. The first type is operated with binary numbers, while the other is operated with real numbers. By using real code, the crossover operator is vindicated by most of the algorithms rather faster than by binary code [74,75]. As discussed in the private table, crossover standards have several weak and strong points. As a result, the major motivation for proving the crossover standards is to propose and demonstrate a distinctive crossover technique. Using novel generated algorithms, crossover operators will take on those responsibilities with varying degrees of precision to find global convergence quickly. The suggested technique is based on LDF for gene crossings. Thus, some following points highlight the novel properties of LPX that should be obvious.

▪

When there are limitations on the input values that can be used, the Lagrange multiplier technique can be utilized. This technique is used to determine the maximum or minimum of a multivariable function [76,77];

▪

The main goal is to find locations where the contour lines of the multivariable function and the input space are adjacent to one another [76];

▪

The constrained population-based optimization problem is transformed into an unconstrained problem using the Lagrange multiplier technique [77,78], which provides the optimum solution when used as a point in the crossover standard;

▪

Optimization with the Lagrangian method explores the application of Lagrange multiplier methods to find local and global convergence for Lagrangian methods under constraint minimization and maximization [79];

▪

Based on LDF, LPX attempts to calculate the most appropriate offspring, which often involves taking a fairly significant step away from each parent.

The event points show that the Lagrange multiplier method is used for determining a function of local maxima and local minima with equality constraints or requirements. This issue contains the requirement that one or more equations be exactly solved by the selected variable values [80]. The correlation between the gradient (slope) of the function and the gradients (slopes) of the constraints leads to a natural form of formulation of the global problem, characterized as the Lagrangian Function [81,82]. These points around or near the slopes may have a function to generate new genes within the specific chromosome.

According to Figure 18, there may be an objective function, signified as $f\left(x,y\right),$ which must be optimized while it is subject to the restriction $g\left(x,y\right)=c$. Let us put this problem statement into perspective before delving further into its discussion. The Gradient $\nabla f\left(x,y\right)$ is a vector which, at every position $\left(x,y\right)$, indicates the direction in which $f$ should be increased as effectively as possible. $f$ will rise as long as the stationary point continues to move in that direction, which is the steepest curve in this direction. Any function’s gradient that is calculated at a specific position $\left(x,y\right)$ will always result in a vector that is perpendicular to the contour line that passes through that point. It is worth noting the exploring point must always remain on the constraint curve $g\left(x,y\right)=c$ when ascending this top of the climax point (at Gradient Vector), such as the global point. In other words, the only directions the solution can travel are tangents to this constraint curve. These tangents’ values remain constant throughout the constraint curve $g\left(x,y\right)=c$ because they are orthogonal to the gradient of the limitation function $g$. Then Gradient Vector must track the optimizer’s motion on the surface of $f$ as the optimizer moves along the constraint curve $g\left(x,y\right)=c$. The solution point should continue to raise $f$, even if it is shifted in a direction along the Gradient $\nabla f\left(x,y\right)$ that has a non-trivial component. A gradient can only be shifted orthogonally to the gradient $\nabla f\left(x,y\right)$ once if it moves only in the direction orthogonal to the gradient. In this case, the solution has reached a local maximum. The gradients of $f$ and $g$ are now pointing in the same general direction.

Thus, as illustrated in Figure 18, the restriction $g\left(x,y\right)=c$ appears as a red curve. The blue curves are characteristics $f\left(x_i,y_i\right)$. Because $S1>S2$, the point where the red constraint tangentially contacts a blue curve is the maximum $f\left(x_1,y_2\right)$, which means tangential to $S1$ in the sideways constraint. Moreover, it shows that the assumption that line graphs are tangential has no bearing on the size of any of these gradient vectors, but it is well. When two vectors have the same orientation, we may multiply one by a constant to obtain the other [83]. The Lagrange multiplier works by assuming that the local minimums and maximums along the constraint occur when the constraint is parallel to the contours. This is stated in $S1,S2,S3$.

In each of the above scenarios, assuming the point is on the contour line, Figure 18 shows how to calculate the stationary point of $\mathcal{L}$ given a function $\nabla f\left(x,y\right)=\lambda \nabla g\left(x,y\right)$ and the Lagrange multiplier $\lambda$. Thus, it uses a general method, called the Lagrange multiplier method, as formulated in Equation (12), for solving constrained optimization problems [84,85]. Equation (12) is explained in the following evaluation.

$$\begin{gathered} \mathcal{L}\left(x,y\right)=f\left(x,y\right)-c \\ g\left(x,y\right)=c\mathrm{If}c\mathrm{is}\mathrm{a}\mathrm{constant} \\ \mathcal{L}\left(x,y\right)=f\left(x,y\right)-g\left(x,y\right) \end{gathered}$$

From these points, it is proved that the Lagrange multiplier λ in Equation (12) is improved by maximizing (or minimizing).

$$\mathcal{L}\left(x,y,\lambda \right)=f\left(x,y\right)-\lambda g\left(x,y\right)$$

(12)

Gradient vectors indicate that this model should be fixed to compute many examples and to determine the optimum point. It will, for example, assist with physical routing. It will be used to select the smallest point to find the shortest physical path. However, the Lagrange dual function may be convenient for identifying several global solutions [86]. As such, the LDF theorem depends on real equation samples [87]. To identify several local points, the theorem would be formulated using a novel crossover operator. Thus, each station should generate a gene for offspring from parent chromosome(s). The developed alternative to the Conic Duality theory is called LDF theory. The Lagrangian Duality Problem theory is more applicable to generic nonlinear limitations [88]. From the stationary point in Equation (12), an offspring is derived in Equation (13) using the LDF theorem.

$$\mathrm{Offspring}=\mathcal{L}(x_1,x_{2,}\mathsf{\alpha })=f\left(x_1,x_2\right)-\alpha g\left(x_1,x_2\right)=f\left(x_1,x_2\right)-{{\displaystyle \sum }}_{i=1}^{n=2}{\mathsf{\alpha }\mathrm{g}}_i\left(x_1,x_2\right)$$

(13)

$$\begin{array}{l}\mathrm{For}\mathrm{Offspring}1:f\left(x_1,x_2\right)=\left(x_1-x_2\right){}^2+\left(x_2-1\right){}^2\\ \mathrm{Subject}\mathrm{to}{\mathrm{g}}_1\left(x_1,x_2\right)=x_1+2x_2-1\\ {\mathrm{g}}_2\left(x_1,x_2\right)=2x_1+x_2-1\\ \mathrm{For}\mathrm{Offspring}2:f\left({\mathrm{x}}_2,{\mathrm{x}}_1\right)=\left({\mathrm{x}}_2-{\mathrm{x}}_1\right){}^2+\left({\mathrm{x}}_1-1\right){}^2\\ \mathrm{Subject}\mathrm{to}{\mathrm{g}}_1\left(x_2,x_1\right)=x_2+2x_1-1\\ {\mathrm{g}}_2\left(x_2,x_1\right)=2x_2+x_1-1\end{array}$$

Consequently, it is possible to generate Offspring1 and Offspring2 at the stationary point by including Equation (13) if the Lagrangian Multiplayer has produced a random value for $\left(\mathsf{\alpha }\right)$ in the specified range according to the population-based generations crossover rate. Therefore, we developed Equations (14) and (15).

$$\mathrm{Offspring}1=\left(x_1-x_2\right){}^2+\left(x_2-1\right){}^2-\left(\mathsf{\alpha }\left(x_1+2x_2-1\right)+\mathsf{\alpha }\left(2x_1+x_2-1\right)\right)$$

(14)

$$\mathrm{Offspring}2=\left(x_2-x_1\right){}^2+\left(x_1-1\right){}^2-\left(\mathsf{\alpha }\left(x_2+2x_1-1\right)+\mathsf{\alpha }\left(2x_2+x_1-1\right)\right)$$

(15)

In this case, the proposed standard for this crossover standard (LPX) is the same as the real-coded crossover. It creates offspring solutions by inserting a sub-sequence from one of the genomes into the parent, while the initial order would be as many point states as reasonable, such as in the example calculated by Equations (14) and (15) to generate new offspring, which is illustrated in Figure 19 as a modification sample crossover. While $x_1$ is indicated as Gene two $G_1$ in chromosome one, $x_2$ is indicated as Gene two $G_2$ in chromosome two when the stationary multiplier is defined randomly as ($\mathsf{\alpha }=0.2$). In the next section, the comparison results are improved heuristically and statistically.

5. Results and Discussion

There are several standard benchmark test functions available to evaluate these standard operators and the performance of population-based algorithms. In

Table 3. Three unimodal benchmark test functions [83].

TF	Functions	Range	Dimension
TF1	$F\left(x\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}{x}_i{}^2$	[−100, 100]	10
TF3	$F\left(x\right)={\displaystyle {\displaystyle \sum }_{i=1}^n}{\left({\displaystyle {\displaystyle \sum }_{j=1}^i}{x}_j\right)}^2$	[−100, 100]	10
TF7	$F\left(X\right)={{\displaystyle \sum }}_{i=1}^{n}i{x}_i{}^4+roundom\left[0,1\right]$	[−1.28, 1.28]	10

, three test functions are selected to analyze this newly introduced operator. However, classical test functions are divided into unimodal modal test functions, multimodal test functions, and composite test functions [89]. Each set of these test functions is used to benchmark certain aspects of the algorithm. For determining the exploitation level and convergence of the standards in the population algorithms, we select these three functions from the unimodal test functions. LPX and BX are compared in the first part of this subsection as heuristic evaluation results. The second part compares our standard operator with BX, SBX, and Qubit-X [45,90] operators, while they are tested by LPB as a population-based algorithm as part of exploitation and convergence results. A Wilcoxon Rank Sum test is used to test all results statistically in the last part as statistical evaluation results. To determine the most appropriate solution, all of the results are affected by the random number value. We illustrated the time consumed during processing to execute dynamic cost minimization.

5.1. Heuristic Evaluation Results

Using mathematical comparisons, this evaluation aimed to identify major usability and performance problems with the standard operators. Tests achieved a total of 100 stochastic generations (genes) for different pairs parents (chromosomes) with crossover rate values (α) are 0.3, 0.5, and 0.7. This difference in random values assists newly proposed algorithms in choosing the best range when selecting the values and achieving the best optima rapidly. Several standards have been reviewed in the previous section, but the test focuses on BX and SBX crossovers. As a result, these two standard heuristic results are compared with LPX results. In addition, performance can be measured based on the statistical value produced. Based on the random value, the more significant value is calculated according to the average, indicating a superior outcome [91,92,93]. Based on crossovers, the outcomes of mathematical calculations from chromosome parents are used to generate a gene in chromosomal offspring [94]. The operation of the arithmetic process is found by applying Equations (4) and (5) for BX, Equations (8) and (9) for SBX, and Equations (14) and (15) for LPX.

The test relies on three unimodal functions [95] based on a group of traditional benchmark functions to determine approval for each gene on a chromosome. The three-test equation in the benchmarks for a single variable includes test function one (TF1), test function three (TF3), and test function seven (TF7), as shown in Table 3 [96]. An algorithm must avoid all local optimal solutions to reach the global optimum, and these sample test functions can aid in mapping out a strategy for exploration. The single result has statistically calculated the summation of generation on chromosome parent and then the average (Mean) and standard deviation (STD) have been mentioned to compare all standards relying on alpha value (α) as a random value that will be generated during the steps of the algorithm.

The Lagrangian functions look for new points in complex applications by searching around the largest local optimum. As has been explained earlier, the Lagrange multiplier method in mathematics is a technique for identifying the local maximum or minimum value of an action that is subject to equality requirements. It is subject to the requirement that the exact values of the variables chosen must satisfy one or more equations as has been proved in LPX. Thus,

Table 4. The performance result test for selected crossover standards with LPX.

Standards		BX			SBX			LPX
α	Test Functions	Sum	Mean	STD	Sum	Mean	STD	Sum	Mean	STD
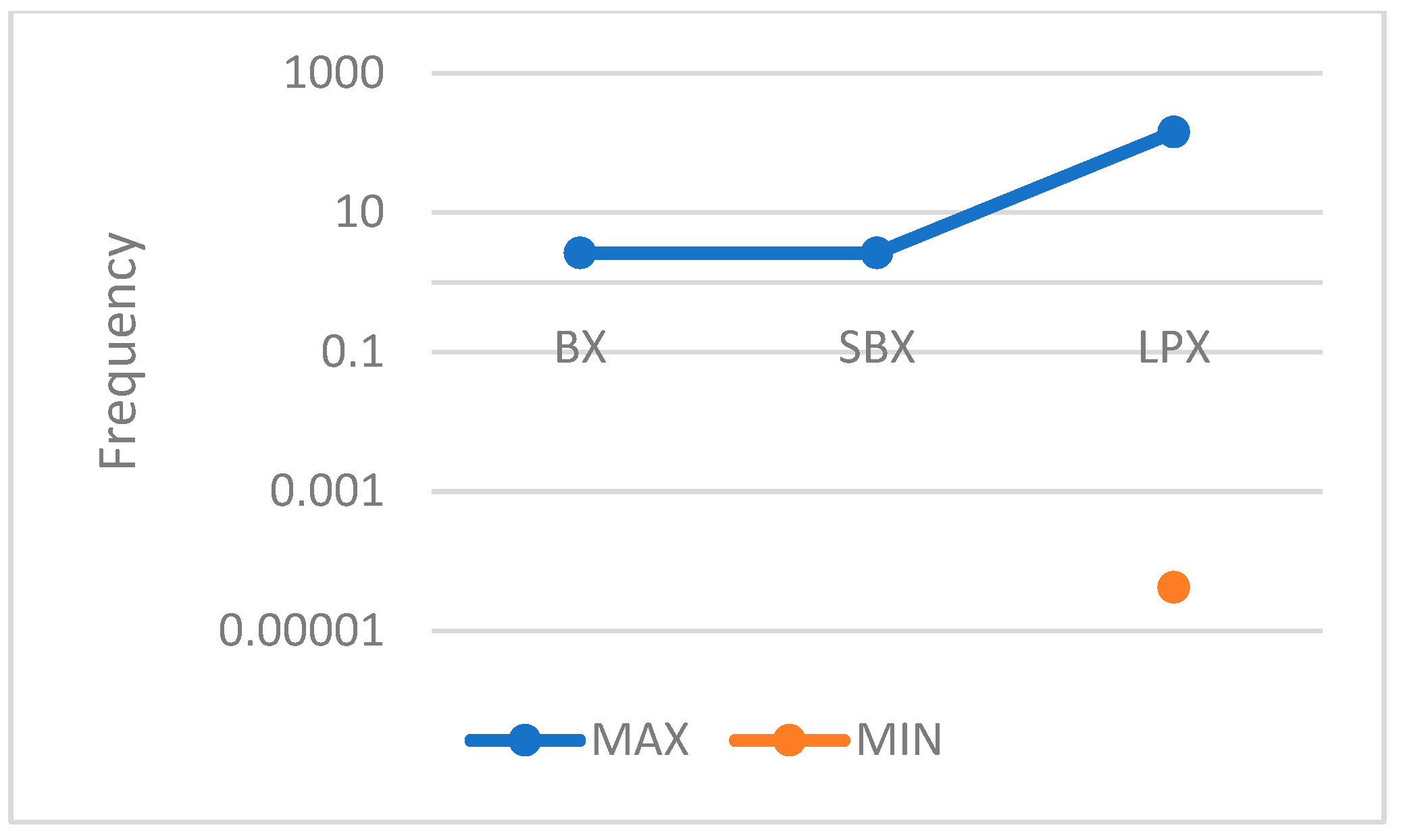
0.2	TF1	42.36	0.42	0.30	31.37	0.31	0.32	1737.56	17.38	17.09
	TF3	60.00	0.60	0.66	60.00	0.60	0.66	3197.01	31.97	31.27
	TF7	779.24	7.79	10.78	487.58	4.88	9.52	1,937,510.53	19,375.11	33,631.08
0.5	TF1	30.00	0.30	0.30	38.58	0.39	0.30	2776.00	27.76	26.17
	TF3	60.00	0.60	0.66	60.00	0.60	0.66	5273.89	52.74	50.06
	TF7	461.88	4.62	9.41	661.72	6.62	10.21	4,348,187.50	43,481.88	64,658.48
0.7	TF1	35.49	0.35	0.31	46.82	0.47	0.30	3648.64	36.49	34.78
	TF3	60.00	0.60	0.66	60.00	0.60	0.66	7019.17	70.19	67.65
	TF7	579.02	5.79	9.88	941.45	9.41	11.81	7,300,002.73	73,000.03	109,185.64

represents the results of the tests of summation, Mean, and STD values for three standard operators by three test functions. For all values of alpha (α), it is found that LPX is more powerful than BX and SBX. Although BX and SBX were reasonable in previous generations, this seems such as a more reasonable option now. In addition, results show that TF7 has high convergence and exploitation for all alpha values. Similarly, LPX could be computed to show the ranking of social classes and stochastically analyze metaheuristic algorithms [97].

Nevertheless, all standards were reasonable according to evolution’s invincible algorithms. Thus, we proved two examples of the maximum and minimum genes on chromosome parents for TF1 for three alpha values. The performance of BX and SBX in TF1 is trivial, but LPX shows slightly better results. Moreover, LPX has demonstrated maximum and minimum gene expression when compared to both BX and SBX standards. Moreover, the process of convergence in LPX revealed that the relationships between generations are higher than the other two crossover standards for all alpha values in TF3, even though it showed the relationship between generations for maximum and minimum gene values based on TF3. Based on TF7 results for all alpha values, LPX has a strangely high result compared to BX and SBX. This is because they have defined and obtained maximum genes and minimum genes. TF7 shows how the chromosome comparative results of the divergent max and min genes are evaluated and highlighted. The frequency of subsequent generations derived from the parent genes is represented on the Y axis in Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27 and Figure 28. This is because there are different max and min genes on each chromosome, which are used to evaluate the comparison results. Ultimately, the heuristic evaluation results indicate that the LPX frequencies are rapidly maximized for these three test functions.

5.2. Exploitation and Convergence Evaluation Results

The effectiveness of the LPX has been assessed using a range of experiments. These studies are designed differently to examine the behaviors of the LPX and reflect both its qualitative and quantitative characteristics. LPX’s exploitation capabilities and convergence behavior for solving problems are demonstrated through a qualitative analysis that employs exploration and average fitness values. For this purpose, we choose the recently developed population algorithm LPB, which is mentioned in the previous section. In the quantitative analysis, the proposed LPX has been compared with other standard crossovers such as BX, SBX, and Qubit-X. We have also selected three classical test functions in Table 3. The effectiveness was evaluated by testing escape ability from local optima, and convergence speed by summing the elapsed time to obtain the fitness point. The novelty of this study lies in its proving the effectiveness of the random value; therefore, three different random values for each test function have been selected. Over 500 iterations, each standard with a different random value is tested with the LPB algorithm, which is executed 30 times using 80 search agents. The sum, STD, and processing time are calculated. The LPX metrics, sum, and STD are rated first or second on almost all three test functions. Due to the results and convergence in the fastest time calculations; thus, bold results are shown in

Table 5. The crossover operator’s comparison results of classical test functions.

Test Fun.	α	LPX			SBX			BX			Qubit-X
		Mean	STD	Time (S.)	Mean	STD	Time (S.)	Mean	STD	Time (S.)	Mean	STD	Time (S.)
TF1	0.2	0.0635	0.0184	141.740	0.01751	0.0236	161.423	0.04428	0.0446	150.384	0.1758	0.0926	144.474
	0.5	0.0680	0.0281	149.798	0.04161	0.0270	162.160	0.04178	0.0323	157.700	0.1411	0.0510	151.992
	0.7	0.0596	0.0279	151.112	0.02959	0.0172	188.501	0.04150	0.0294	163.809	0.1425	0.1045	157.042
TF3	0.2	43.5652	24.8093	159.289	83.37500	59.0221	178.260	41.60497	28.4041	169.970	120.7210	73.2963	164.986
	0.5	40.4260	26.2073	165.144	78.18210	52.1304	161.057	52.58699	37.7840	169.130	175.6268	119.6147	165.608
	0.7	66.7197	58.8220	164.711	85.92191	71.4473	180.216	50.67240	49.2447	167.669	81.3198	52.6167	164.450
TF7	0.2	0.0048	0.0031	143.005	0.01351	0.0188	153.884	0.00624	0.0045	156.457	0.0076	0.0043	160.718
	0.5	0.0049	0.0027	152.029	0.00770	0.0066	164.322	0.00616	0.0029	162.973	0.0094	0.0051	147.530
	0.7	0.0052	0.0033	157.893	0.00773	0.0056	164.504	0.00709	0.0042	163.520	0.0123	0.0064	155.061

. Specifically, the comparison of the LPX standard’s unimodal test functions compared to others at TF7 and all random values showed that LPX had a faster rate of exploitation and convergence. Moreover, the execution time for LPX is marginally faster than TF7 calculations. In addition, if the random value is near (0.5) during TF3, LPX is the most optimal rate of convergence and exploitation.

5.3. Statistical Evaluation Results

The optimization algorithms are stochastic, thus several non-parametric statistical tests, including Wilcoxon signed-rank sum, and analysis of variance (ANOVA) can be used to quantitatively examine the algorithms’ overall performance. Before using a standard to solve optimization problems, its applicability should be determined statistically. The comparison is conducted only between LPX with SBX and LPX with BX standards by the Wilcoxon signed-rank sum test in

Table 6. The Wilcoxon rank sum test (p-value) between crossovers operator for random generations.

Test Functions	α	Standards
		LPX vs. SBX	LPX vs. BX
TF1	0.2	3.6746 × 10−16	5.3124 × 10−16
	0.5	4.7409 × 10−17	4.0951 × 10−17
	0.7	4.7409 × 10−17	3.8618 × 10−17
TF3	0.2	8.5768 × 10−16	8.5768 × 10−16
	0.5	9.5355 × 10−17	9.5355 × 10−17
	0.7	8.2482 × 10−17	8.2482 × 10−17
TF7	0.2	1.6983 × 10−16	2.6103 × 10−16
	0.5	4.0951 × 10−17	3.2378 × 10−17
	0.7	3.2378 × 10−17	2.0802 × 10−17

. The LPX results are considered significant and thus rejected null hypnosis in all statistical tests; all p-value are smaller than 0.05.

Based on

Table 7. The Wilcoxon rank sum test (p-value) between standards for the LPB algorithm.

Test Functions	α	Standards
		LPX vs. SBX	LPX vs. BX	LPX vs. Qubit-X
TF1	0.2	0.000031	0.002415	0.000005
	0.5	0.000241	0.001965	0.000002
	0.7	0.00042	0.015658	0.000031
TF3	0.2	0.002765	0.517048	0.000002
	0.5	0.006836	0.318491	0.000002
	0.7	0.328571	0.393334	0.271155
TF7	0.2	0.000716	0.298944	0.009271
	0.5	0.044919	0.085896	0.000664
	0.7	0.071903	0.057096	0.000058

, the Wilcoxon rank sum test was used to determine the statistical result (p-value) for all crossover operators with LPX. Qubit-X means significant results for all three test functions except TF2 (α = 0.7), which is insignificant and rejects the null hypothesis. Moreover, significant results with SBX have been determined for all test functions for all values without (α = 0.7) for TF3 and TF7. In addition, the significant value of LPX with the BX standard is significant for TF1 for all alpha values. This is due to a lower value than 0.05.

6. Conclusions

In conclusion, the most evolutionary metaheuristic algorithm is based on efficient computation techniques that are applied effectively to different problems. Encoding techniques and standard operators, particularly crossover operators for enhanced metaheuristic optimization, have been responsible for determining their outcomes. In this research, several crossover standards have been collected to assist researchers in obtaining an effective crossover operator and selecting a global solution to the problem. The majority of them were easy to calculate; thus, the calculation was faster, as illustrated. In addition, they allowed for the production of a wide range of offspring from two parameters as determined by two parent values. In addition, the study provided an improved standard option crossover operator to assist in the enhancement of novel mathematical evolutionary algorithms.

In this study, standard crossover operators such as binary-coded crossover, real-coded crossover (floating point), and order-coded problem crossover were mathematically and systematically reviewed. Then, we recommend the optimum crossover standard operator, and LPX has been discovered to be a novel mathematical approach to crossover standards. The LPX is derived from the LDF theorem, which is based on the stationary Lagrange multiplier. Additionally, the capability of the technique was evaluated heuristically for the generation of parent chromosomes and compared with BX and SBX. LPX has the most impressive performance in terms of rate of exploitation and convergence fitness for selected random values. In this manner, these random values assist in selecting the most appropriate range when generating newly developed population-based populations. Moreover, we evaluated LPX results by LPB as a metaheuristic algorithm when LPX, SBX, BX, and Qubit-X were determined by all algorithms. Most test functions have reasonable convergence in the exploitation evaluation for selected random values. Finally, most statistical results for LPX with other standards have proved the significant hypothesis.

In future works, the researcher can evaluate LPX by comparing it with other standardized crossover techniques based on binary form, real-code form, or order-coded problem methods for crossover, and it will be proved by comparison with more test functions such as two-dimensional test functions. LPX may be determined with functional tests that illustrate multimodal test functions and composite test functions. From another perspective, the researchers improved a novel evolutionary metaheuristic algorithm based on populations through single-objective optimization or multi-objective optimization [98,99]. Moreover, LPX equations will be improved based on algorithms such as frequency-modulated synthesis with multi-parent crossover [100] in the Ant Nesting Algorithm [101], Child Drawing Development Optimization [102], and Capuchin Search Algorithm [103]. Thus, LPX asserts that it can deliver the most effective fitness solution. Several research studies by heuristic suggest that large-scale structural optimization, modified to evaluate several strategies pooled with programming techniques, can be used for quantitative appraisal in compliance with enforcement learning [104,105,106]. As a result, LPX might be used for evaluating time-scales in heuristic game problems such as A* or (BA*) search algorithms [107].