Abstract
An underground mine is a very complex production system within the mining industry. Building up the underground mine development system is closely related to the installation of support needed to provide the stability of mine openings. The selection of the type of support system is recognized as a very hard problem and multi-criteria decision making can be a very useful tool to solve it. In this paper we developed a methodology that helps mining engineers to select the appropriate support system with respect to geological conditions and technological requirements. Accordingly, we present a novel hybrid model that integrates the two following decision-making components. First, this study suggests a new approach for calculating the weights of criteria in an objective way named the Modified Preference Selection Index (MPSI) method. Second, the Magnitude of the Area for the Ranking of Alternatives (MARA) method is proposed as a novel multi-criteria decision-making technique for establishing the final rank of alternatives. The model is tested on a hypothetical example. Comparative analysis confirms that the new proposed MPSI–MARA model is a very useful and effective tool for solving different MCDM problems.
1. Introduction
Supporting is one of the most important parts of every underground mine project that needs special attention. It represents the mining activity that is primarily directed at preventing a disastrous mine roof fall. As well as securing roof stability, monitoring and controlling deformations along the underground drifts are extremely important characteristics of every support system technology. Depending on the rock types and geological conditions that govern the deposits, supporting is implemented to a greater or lesser extent. Underground coal mines require extensive utilization of supporting systems, while the application of support in polymetallic deposits is less required.
Since the ore deposits are inclined to surface and are almost exhausted using surface mine technologies, it is necessary to change the exploitation technology by using underground mining technology. The same case applies to coal deposits that are excavated using underground mining methods. Having in mind that the coal is sedimentary rock contained of accompanying soft rocks with low strength, it means that underground objects in coal deposits should be secured from self-destruction. Because of these complex geological conditions, every underground coal mine requires the application of certain support system technologies. Realizing the stability of the underground structures, providing safe workplace conditions for personnel and creating, as much as possible, a longer useful life are essential functions of every support system in an underground coal mine.
In recent years, multi-criteria decision-making (MCDM) methods have experienced increasing application in solving many problems in different fields of research. Economics, mathematics and engineering are just some of the scientific areas where the application of MCDM methods play a vital role in creating a reliable model in the decision-making process. In accordance with that, an enormous number of MCDM methods have been developed for solving such complex problems. With the rapid progress of new MCDM methods, methods for defining the weights of criteria were developed at the same time. It means that the optimal solution largely depends on the weights of criteria. Considering the huge impact on the final results in decision-making process, criteria weight determination is one of the most significant problems in MCDM models.
The MPSI method represents a novel method for determining the weight coefficients in the different MCDM problems in an objective way. This method is based on the traditional Preference Selection Index (PSI) method creating an improved and modified version called the Modified Preference Selection Index (MPSI) method. This modification is quite slight and is only directed at eliminating a certain step from the original PSI method. This minimal modification upgrades the final values of the weight coefficients and makes them closer to values obtained by other objective weighting methods.
The MARA method presents a new multi-criteria decision-making method providing support to decision makers for solving different problems in numerous spheres. This method is based on Magnitude of the Area for the Ranking of Alternatives named the MARA method. The two main functions under the optimal alternative and each alternative are established as the major concepts of this proposed method. Calculating the area under the optimal and each alternative has a pivotal part to play in computing the magnitude of the area that represents the core of this study. The area below the alternative is calculated by definite integration of the linear function over an interval of 0–1. The proposed methodology is easy to understand and is a low time-consumption approach.
The aim of this study is to provide rational assistance to underground mining engineers through the process of support system selection in underground mines. This MCDM model is based on integrating the MPSI method and MARA method as two novel approaches. The MPSI method represents a new technique for evaluating the objective weights of criteria. The MARA method is the new proposed method applied for the ranking of alternatives (support systems in underground mines).
The paper is organized as follows. Firstly, Section 1 provides the Introduction and aim of this paper while the Literature Review is described in Section 2. Then, Section 3 represents a detailed description of the new objective method named MPSI that is used for determining the criteria weights. The novel multi-criteria decision-making method called the MARA method is expressed in Section 4. A comprehensive illustration of the hybrid MPSI–MARA model is demonstrated through the Numerical Example in Section 5, while the validation of the proposed model is verified through the Comparative Analysis in Section 6. Finally, Section 7 deals with the discussion of the proposed methods while concluding considerations and further research are explained in Section 8.
2. Literature Review
Some authors have investigated and estimated different approaches and combined versions of support systems in underground mines as well as in tunnels. Kang [1] analysed the deformations and damage features of coal mine roadways under complex geological and geotechnical characteristics. Additionally, roadway support techniques such as the application of rock bolting, steel arches, grouting and combined support design in coal mines in different countries were analysed. Several case studies have analysed typical support system technologies. In order to better understand the behaviour of support system techniques in coal mines, Mark and Barczak [2] introduced elementary instructions of supporting procedure for mining engineers. The key factors that affect the mine structure such as rock strength, roof span and forces applied to the mine roof were explained. In addition, other significant factors that have an influence on a coal mine roof such as the load-carrying capacity, installation time and quality as well as the ability of the support system to secure skin control were described. Elrawy et al. [3] illustrated the stability evaluation of the underground tunnel in a nickel mine considering of various collapse assessment criteria such as strength of the rock mass, the extent of failure zone and rock mass deformation. They simulated different variants of rock support systems through several cases to select the best one. Putra [4] described the basic concepts of the underground support elements and their selection based on an empirical approach and finite element method. Canbulat and Merwe [5] developed an optimum roof support system methodology based on a stochastic technique and probabilistic approach to input data.
As well as these conventional approaches for supporting in mines, the application of powered roof support mechanisms known as longwall systems is growing rapidly especially in deep coal mines. In the global coal mining industry, a longwall system is recognized as a vital structure for providing protection and safety conditions during the underground mining process. There are many authors who have analysed, investigated, monitored and selected the most efficient longwall system for roof support in underground conditions [6,7,8,9,10].
Numerous researchers have observed and investigated the support design system in underground conditions as a multi-criteria decision-making concept. Rafiee et al. [11] applied the traditional Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method to select the most efficient support system in a Naien water transporting tunnel. They created an initial decision-making matrix considering four alternatives (models of support systems) with respect to five criteria such as the probability of failure, safety factor, cost, applicability factor and displacement. Jalalifear et al. [12] presented an optimum rock bolt system selection for supporting the underground facilities based on a hybrid Analytical Hierarchy Process (AHP)–Entropy–TOPSIS approach. AHP and Entropy methods are used to compute the weights of the total of twenty-six criteria, while the TOPSIS methodology is applied to choose the most preferred rock bolt system design of which there are a total of nine. Shaffiee Haghshenas et al. [13] developed an MCDM model to estimate the most suitable tunnel support system. This methodology is established as a combined version of the FDAHP (Fuzzy Delphi Analytic Hierarchy Process) and ELECTRE (Elimination and Choice Expressing Reality) procedures. Five tunnel support systems with respect to six criteria were used to rank the supporting system and examined through numerical calculation in a case study. Oraee et al. [14] proposed an approach for tunnel support system selection based on the AHP method. Ten alternatives (support systems) and seven criteria such as vertical displacement at point 1, point 2 and point 3, horizontal displacement at point 3, support system costs, support system performance and safety factors are involved in the model. Oraee and Bakhtavar [15] studied the optimum tunnel support system selection using the integration of the AHP, TOPSIS and Preference Ranking Organization METHod for Enrichment Evaluations (PROMETHEE) techniques. To validate the capability of the utilized methods for support system selection, a case study from [14] was implemented. Tajvidi Asr et al. [16] introduced the support system selection in the Beheshtabad tunnel by applying the Simple Additive Weighting (SAW), TOPSIS and Linear Assignment (LA) methods. Six variants of support systems as alternatives with respect to six criteria (cost, safety factor, applicability, installation time, displacement and mechanization) were included in the MCDM process for final ranking. Yavuz et al. [17] presented an optimum support design for a main haulage road in the Western Lignite Corporation (WLC), Tuncbilek, in Turkiye based on the AHP method.
The main and very important part of every MCDM method is assessing the weights of criteria. There are many methods for determining the weights of criteria. All of these methods can be divided into three groups: subjective weighting methods, objective weighting methods and combined weighting methods. Subjective methods for criteria weight determination are based on estimation and opinion by the decision maker. These methods represent the subjective preference by the decision maker of the input data that directly influence the final choice in decision making. There are many subjective weighting methods that have been widely used in various areas such as the Full Consistency Method (FUCOM) [18,19], Step-Wise weight Assessment Ratio Analysis (SWARA) [20,21], PIvot Pairwise RElative Criteria Importance Assessment (PIPRECIA) [22,23], Decision-MAking Trial and Evaluation Laboratory (DEMATEL) [24,25], KEmeny Median Indicator Ranks Accordance (KEMIRA) [26], WEight Balancing Indicator Ranks Accordance (WEBIRA) [27], Simple Multi-Attribute Rating Technique (SMART) [28] and many other methods. Objective methods for criteria weight determination, unlike subjective methods, are based on information from the “raw” input data using mathematical tools for obtaining the criteria weights. These methods exclude any subjective favour and judgement of the decision maker that makes this approach more acceptable and more suitable. Many researchers have applied objective weighting methods in different scientific fields such as Entropy [29,30], CRiteria Importance Through Intercriteria Correlation (CRITIC) [31,32], Standard Deviation (SD) [33,34], Mean Weight (MW) [35,36], Coefficient of Variation (CV) [37], MEthod based on the Removal Effects of Criteria (MEREC) [38,39], LOgarithmic Percentage Change-driven Objective Weighting (LOPCOW) [40], Criteria Impact LOSs (CILOS) [41,42], Integrated Determination Of CRiteria Weight (IDOCRIW) [41,42] and many other methods. Combined methods for criteria weight determination represent the hybrid of subjective and objective methods. These methods take the positive characteristics of the other methods, subjective and objective, and integrate them into one model. There are many authors who have utilized the combined weighting methods [43,44,45,46].
Many authors have applied the PSI method in different scientific disciplines to investigate MCDM problems. Moreover, many authors have used the PSI method combined with other methods under uncertain environments for ranking the alternatives. This method is simple and easy to understand for the decision maker and widely applied in various scientific fields for solving multi-criteria decision-making (MCDM) problems such as: the design stage of the production system life cycle [47], the machining optimization problem [48], the fuel buses selection problem [49], the ranking of the performance factors of a flexible manufacturing system [50], warehouse location for a supermarket [51], natural thermal insulation material selection for the external walls [52], the potential tourism selection of countries [53], the problem of determining laser cutting process conditions [54], machine performance evaluation [55], the problem of human resource management [56], etc. From the very extensive literature review, there are no methods dealing with modified or improved approaches of the PSI method. It was one of the key reasons and main motivations to investigate the original PSI method and to develop a modified application of the PSI method.
In addition to numerous studies implementing the conventional and relatively new MCDM techniques [57,58,59,60], there are many authors who have examined and established an enormous number of MCDM methods that cover uncertain environments creating improved and extended versions of existing MCDM methods [61,62,63,64,65].
3. MPSI Method
In order to calculate the objective weights of criteria, we created a new approach for determining the weight coefficients. We applied well-known Preference Selection Index (PSI) method and made a slight modification of that method. Preference Selection Index (PSI) method was first developed by Maniya and Bhatt [66] as a new type of decision-making method for solving multi-criteria decision-making problems.
MPSI method is based on the degree of the oscillation, i.e., variation in the preference value for each criterion. That variation actually presents the distance between normalized value and mean value per criterion and is expressed by using the Euclidean distance. MPSI method is characterized as a very simple and easy to understand approach for defining the objective weights of criteria. Moreover, this newly developed method is not highly time consuming when calculating the weight coefficients. This makes the MPSI method a greatly flexible and applicable method for solving various different MCDM problems.
This new method is composed of the following steps:
Step 1. Construct the initial decision-making matrix as follows:
where:
represents the vector of corresponding alternatives,
represents the vector of corresponding criteria,
represents the evaluation of the alternative with respect to criterion ,
is the number of alternatives,
is the number of criteria.
Step 2. Form the normalized decision-making matrix as follows:
Depending on criterion tendency, a simple linear normalization technique is used to transform a different input data value into compatible scale, i.e., unity interval .
For beneficial (maximization) criteria:
for non-beneficial (minimization) criteria:
The normalized decision-making matrix is formed as:
where:
represents the normalized value of the corresponding criterion, .
Step 3. Calculate the mean value of the normalized evaluations of criterion and it is calculated with following equation:
Step 4. Calculate the preference variation value as follows:
Step 5. The criteria weights are determined using the following equation:
4. MARA Method
Every decision-making problem consists of two main elements such as alternatives and criteria. Based on these elements, decision maker forms an initial decision-making matrix to choose the best possible alternative as follows:
where:
is a given set of alternatives,
is a given set of criteria,
is the total number of alternatives,
is the total number of criteria,
is an assessment of alternative Ai with respect to a set of criteria.
The procedure of the MARA method is composed of the following steps:
Step 1. Normalization of input data
In this step, the same procedure of normalization of input data is applied as described in Step 2 of the Modified Preference Selection Index (MPSI) method.
Step 2. Weighted normalization
Weighted normalization is based on product of the criterion weight with corresponding normalized value in the following way:
The result of weighted normalization is weighted normalized matrix shown as:
Step 3. Optimal alternative determination
Optimal alternative consists of elements that are determined in the following way:
The final set of the optimal alternative is shown as:
Step 4. Decomposition of the optimal alternative
Decomposition of the optimal alternative represents the division of the optimal alternative into two subsets or two portions. The set can be illustrated as the union of the two subsets:
If characterizes the total number of benefit criteria, then denotes the total number of cost criteria. Accordingly, the optimal alternative is determined as follows:
Step 5. Decomposition of each alternative
As is described in the Step 4, decomposition of each alternative is defined in a similar way:
Step 6. Intensity of the element
For the optimal alternative, intensity of the element can be calculated as:
The intensity for each alternative is computed in the same way as for the optimal alternative:
Step 7. Magnitude of the Area for the Ranking of Alternatives (MARA)
The proposed method is based on the creation of the following two main linear functions.
The first function takes into account the optimal alternative, and it is created through the following two points and . Function is of the linear form as follows:
Analogically, we can create the second function considering the ith alternative by the following way:
Chart of main functions defined by Equations (21) and (22) is represented in Figure 1.
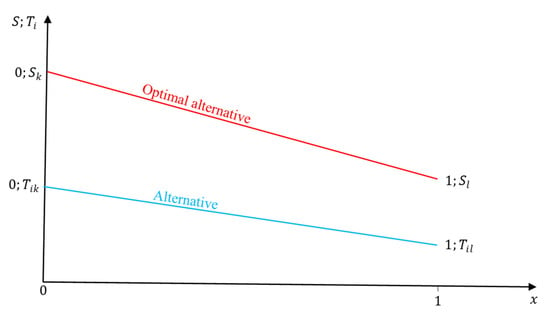
Figure 1.
Function of the optimal and ith alternative.
Area under the optimal alternative is calculated as:
Area under the ith alternative is computed by the following method:
Magnitude of the Area of the ith alternative is represented by the following equation:
Final ranking of the alternatives is determined according to ascending order of .
Figure 2 shows a detailed flow chart of novel hybrid MPSI–MARA model.
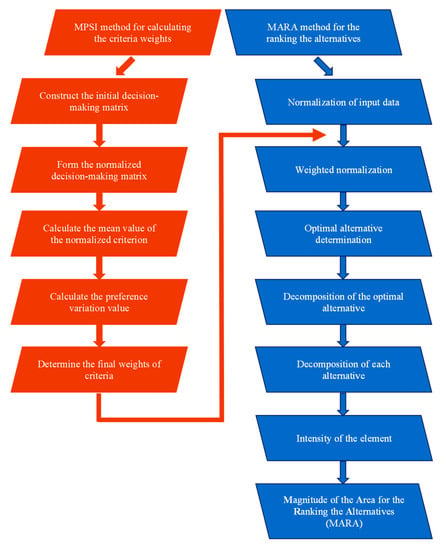
Figure 2.
Hybrid MPSI–MARA model framework.
5. Numerical Example
As the underground support system is one of the key factors in every underground mine, mining engineers must dedicate special attention to its selection. Underground coal mine management is faced with the challenge of selecting the underground support system. The coal deposit has a reserve of approximately 10 million tons of coal. The coal deposit is divided into two zones. Because the first zone of around 6 million tons of coal is almost exhausted, the second zone of approximately 4 million tons should be excavated in the near future. Underground mine engineers have created a mine project where approximately 1200 metres of drifts should be supported. Shotcrete, anchors, wired mesh, steel sets, timber and combination are some of the possible variants of underground support systems that could be used in this coal deposit. It should be noted that the problem is hypothetical.
As we mentioned earlier, mining engineers should select one of the combined support systems that are usually applied. Four alternatives (underground support systems) according to the four criteria are evaluated for this problem. A detailed description of the alternatives and criteria is illustrated below.
5.1. Description of Alternatives
A1—Shotcrete 7–10 cm + anchors + wired mesh
This support system is composed of three basic parts: shotcrete, anchors and wired mesh. Shotcrete is the main component of this system and has the most important role in this support system. It is applied in the form of a layer of a certain thickness on the roof and walls of the underground facilities. Anchors and wired mesh represent the additional structural reinforcement of this system. They are designed to increase the strength and toughness of shotcrete and to prevent the collapse of the underground facilities. Figure 3 shows a graphical visualization of this alternative.
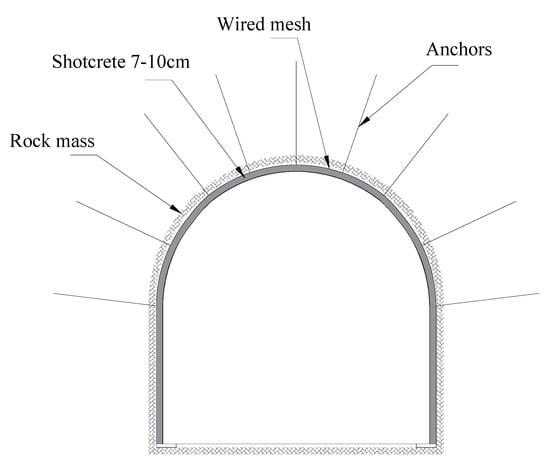
Figure 3.
Illustration of A1.
A2—Shotcrete 10–12 cm + anchors + wired mesh + steel frame
This support system is very similar to the previous system (A1). There are only two small differences between these two support systems. The first small difference refers to the thickness of the layer during the “shotcreting”, while the second difference is reflected in the fact that this system uses a steel frame as additional structural reinforcement. The steel frame is a very significant part of this system, which further increases its support load capacity. In this way, the safety factor of this system is also increased. The only disadvantage of this system is the very long installation time per meter of length. This alternative is graphically represented in Figure 4.
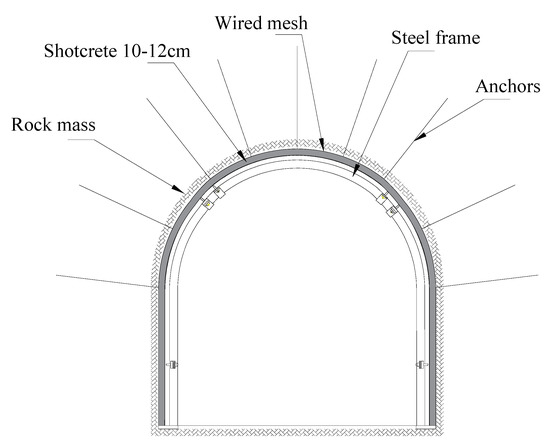
Figure 4.
Illustration of A2.
A3—Steel arches (steel frame + timber)
This support system consists of a steel frame and timber. The steel frame is formed in the shape of an arch and placed in a full drift profile. Timber is used to fill the space between the steel frame and the rock mass mostly in the roof of the underground facility. Since this system is able to support potentially dangerous zones in an underground mine, the required installation time is quite long. Moreover, this system is characterized by high installation costs per meter of length. In Figure 5, steel arches are graphically described.
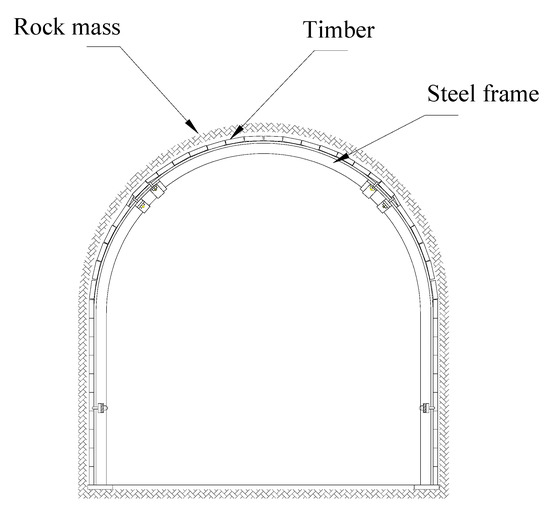
Figure 5.
Illustration of A3.
A4—Steel frame + wired mesh + AT anchors
This support system is designed of a combination of a steel frame, wired mesh and AT anchors. The steel frame provides a secure and stable support predisposed to long-term supporting. The steel frame also ensures a high level of support after significant deformation. The wired mesh is the additional structural reinforcement that protects the employees from small fragments of the mined rock mass and rock samples from the roof. AT (Advanced Technology) anchors represent the system of anchors incorporated into the rock mass. AT anchors are characterized by their quick and easy installation, decreasing the number of employees needed for the development of the drifts and additionally increasing the stability of the underground facility. Combining these three components of support, the load capacity of support is extremely increased. The negative side of this system is the very high installation cost per meter of length. This alternative is clearly illustrated in Figure 6.
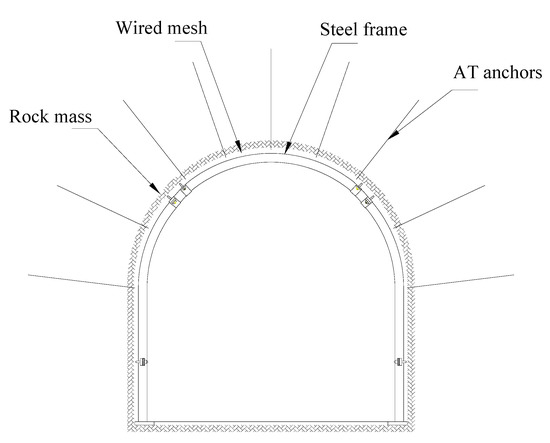
Figure 6.
Illustration of A4.
5.2. Description of Criteria
C1—Installation costs
Installation costs are one of the most significant parameters during the process of support selection in underground mines. It represents the costs that are needed to install the appropriate support system and maintenance costs. Additionally, it includes many types of costs such as capital costs, operating costs, direct and indirect costs, etc. The installation costs are expressed in dollars per meter of length. This criterion should be defined as minimum.
C2—Support load capacity
Support load capacity is a crucial attribute on the basis of which the support system will be selected. It represents the key role in the process of the optimal support system selection in underground mines. In the first row, the support load capacity depends on the ratio between the rock mass and the support system. It means that the stresses and deformations in the rock mass caused by the development of underground facilities have a great impact on the support system. Accordingly, the support load capacity is illustrated as the resistance of the support system to underground pressure. It is expressed in kilopascals. This criterion is characterized as maximum.
C3—Safety factor
Safety factor is a very dominant indicator of the quality of each support system. It indicates how the proposed support system is able to provide stable and secure work conditions in underground mines. It represents a target value of every support system that should be a greater than the target, ensuring the maximum reliability of the system. This criterion should be defined as maximum.
C4—Installation time
Installation time is one of the most important parameters that has a high impact on the support system selection. It is characterized as the time that is needed to install the sections of the support system per meter of length. It has a huge influence on the moment when the exploitation of the ore deposit will be started. Moreover, the final production plan and the final financial results of the project largely depend on this criterion. It is expressed in minutes per meter of length. This criterion tends to be minimum.
The initial decision-making matrix with input data is represented in Table 1. In addition, the tendency of each criterion is shown in Table 1.

Table 1.
Initial decision-making matrix with input data.
Table 2 shows the normalized values of the input data for constructing the normalized decision-making matrix.

Table 2.
The normalized decision-making matrix.
The Modified Preference Selection Index (MPSI) method is applied for assessing the weights of criteria. The weight coefficient of each criterion is represented in Table 3 and Figure 7.

Table 3.
The weights of criteria by MPSI method.
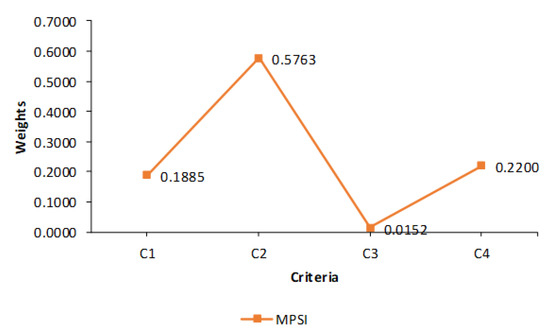
Figure 7.
The weights of criteria obtained by MPSI method.
The weighted normalized decision-making matrix is presented in Table 4.

Table 4.
The weighted normalized decision-making matrix.
Using Equation (11), each element of the optimal alternative is determined. The results are shown in Table 5.

Table 5.
Optimal alternative determination.
In Table 6, decomposition of the optimal alternative is represented.

Table 6.
Decomposition of the optimal alternative.
The decomposition of alternatives is presented in Table 7.

Table 7.
Decomposition of alternatives.
The intensity of the optimal alternative and alternatives is computed by Equations (17)–(20). The results are shown in Table 8.

Table 8.
The intensity of the optimal alternative and alternatives.
Using Equations (21)–(24), we calculated the area under the optimal alternative and alternatives. A brief description of the calculation process is represented for alternative 2 as follows:
The same procedure is valid to the other alternatives.
In Table 9, the values of the area under the optimal alternative and alternatives are shown.

Table 9.
The area under optimal alternative and alternatives.
The Magnitude of the Area of the Alternative is computed by Equation (25). For example, the Magnitude of the Area of alternative 2 is calculated as follows:
The same procedure is valid to other alternatives.
Table 10 and Figure 8 show the Magnitude of the Area of the Alternatives and final ranking of the alternatives, which is determined in ascending order of .

Table 10.
Magnitude of the Area of Alternatives and final ranking of the alternatives.
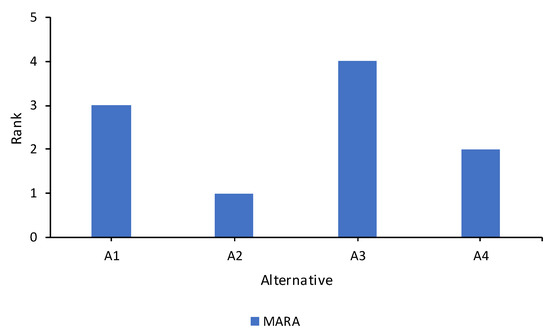
Figure 8.
Final rank of the MARA method.
6. Comparative Analysis
Firstly, we compare the MPSI method with traditional methods for determining the objective weights of criteria, including the Entropy method [67], the MEthod based on the Removal Effects of Criteria (MEREC) method [68], the Coefficient of Variation (CV) method [69] and the CRITIC method [70]. The Entropy, Coefficient of Variation and CRITIC methods use a linear sum normalization procedure, while the MPSI and MEREC methods use a linear max-min normalization technique to evaluate the weights of criteria. The weights of the criteria calculated by each objective weighting method are shown in Table 11 and Figure 9.

Table 11.
The weights of criteria calculated by each objective weighting method.
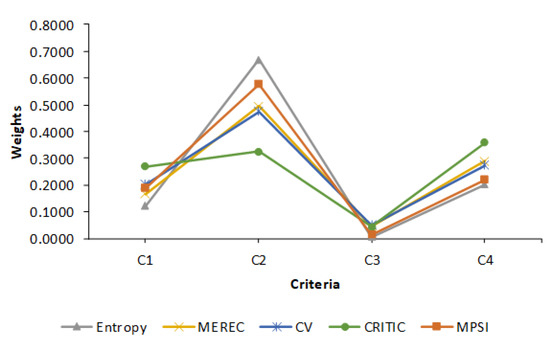
Figure 9.
The weights of criteria obtained by applied methods.
The Spearman’s rank correlation coefficient was used to evaluate the performance of the applied objective weighting methods for defining the weights of criteria. The correlation coefficients are represented in Table 12.

Table 12.
Correlation coefficients of the methods for defining the weights of criteria.
From these obtained results, it is clearly visible that the new MPSI method gives a high degree of correlation with all traditional objective weighting methods. The MPSI method has the strongest correlation with the Entropy method with 0.9894. Additionally, a very high correlation is evident with the Coefficient of Variation (CV) method (0.9837) and MEREC method (0.9732). The correlation coefficient with the CRITIC method is lower than the others with 0.6806 but still high. The average Spearman’s rank correlation coefficient with 0.9067 confirms that the MPSI method stands side by side with the other applied objective weighting methods.
The next phase in the comparative analysis is a comparison procedure of the MARA method with well-known and traditional multi-criteria decision-making methods such as the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method [71], COmplex PRoportional ASsessment (COPRAS) method [72], Simple Additive Weighting (SAW) method [73] and Multi-Attributive Border Approximation area Comparison (MABAC) method [74]. It should be noted that the weights obtained by the MPSI method are used to compute the final rank of alternatives. The final rank of alternatives by the applied MCDM methods is shown in Table 13 and Figure 10.

Table 13.
Final rank of alternatives by applied MCDM methods.
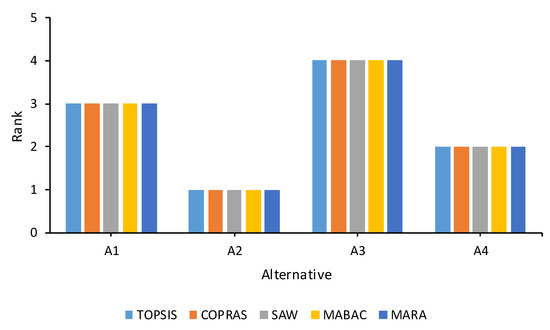
Figure 10.
Chart of the final rank of alternatives.
7. Discussion
In this study, the four possible support systems are determined according to the four adopted attributes. From an extensive numerical and comparative analysis, the importance of the weights of attributes as well as the detailed procedure of ranking the alternatives are clarified. Corresponding to the MPSI method, criterion C2 (support load capacity) with 0.5763 is the most dominant attribute. It is followed by criterion C4 (installation time) with 0.2200, then criterion C1 (installation costs) with 0.1885 and criterion C3 (safety factor) with 0.0152. Regarding the MARA method’s findings, alternative A2 (shotcrete 10–12 cm + anchors + wired mesh + steel frame) occupies the top place with its exceptional performances of supporting. It is followed by alternative A4 (steel frame + wired mesh + AT anchors), then A1 (shotcrete 7–10 cm + anchors + wired mesh) and the last one is A3 (steel arches (steel frame + timber)).
The problem of the support system selection plays a very important role in the optimization process of any underground mine. In order to achieve a positive and profitable final mine production plan, the support system has quite a high impact on the creation of an acceptable technological and economic model. For this purpose, we developed this new hybrid model that helps mining engineers to select the optimal support system. The model is tested on a hypothetical example and shown to be a powerful tool for solving this common problem in an underground coal mine. This new methodology is verified and validated through a comparative analysis with classical MCDM methods, and the results show that the developed model is extremely acceptable and reliable.
This hybrid MPSI–MARA decision-making model introduces a novel methodology to select the optimal support system in an underground mine. This integrated MCDM procedure, which associates two primary phases, the weighting process and the ranking process, provides an effective and flexible tool for solving such complex MCDM problems. Applicability and flexibility to real-life situations, a relatively short time for calculation and simplicity are just some of the positive characteristics that are identified in the developed decision algorithm.
8. Conclusions
Having in mind that the support system selection in underground mines occupies a significant part of every mine project, it must be subjected to a powerful tool for it to be solved. The installation costs, support load capacity, safety factors and installation time are identified as the most dominant attributes for analysing and optimizing the optimal support system selection.
In this paper, we developed a novel hybrid MPSI–MARA approach to select the best support system in underground mines. The MPSI method represents a novel procedure for calculating the weights of the criteria in the different MCDM problems in an objective way. The MARA method is developed as a new method for ranking the alternatives based on the creation of two main linear functions.
The main contribution of this paper is reflected in the fact that two methods that belong to MCDM optimization problems are developed. The first method refers to assigning the weights of criteria in an objective way, while the second method represents a novel approach for the ranking of the alternatives. This innovative model, verified by a great relationship with traditional MCDM methods, contributes to the significant development of numerous scientific disciplines related to MCDM activities such as operational research, artificial intelligence, optimization systems, etc.
The proposed paper offers enormous help for decision makers to overcome this critical problem in the process of underground mine development. Based on this work, mining engineers and mining companies can create a mine project in a much better and easier way. Moreover, they can predict the profitability of the mine production plan considering the installation costs and installation time of each support system. Given the study’s findings, it is clearly visible that the support load capacity represents the most important factor for the support system selection in an underground mine. Since the support load capacity of the support system A2 has the highest value compared to other support systems, there is great potential for it to be selected as the best. Alternative 2 (A2), i.e., the support system composed of shotcrete 10–12 cm + anchors + wired mesh + steel frame, is selected as the best one from the set of possible support systems. The applied decision-making methods produced the same rank order of alternatives. The MARA method is characterized by a high degree of correlation with the compared MCDM methods. The results show that the proposed method is suitable for solving any other MCDM problems. Further research can be directed on the inclusion of an uncertain environment that describes the behaviour of the input data. This would be of great importance in order to obtain a much more reliable and effective final rank of alternatives. Moreover, future studies can focus on incorporating several MCDM methods into the process of the combined MPSI–MARA model. In that way, our new hybrid model would be upgraded and able to solve other complex problems in various research areas.
Author Contributions
Conceptualization, M.G. and Z.G.; methodology, M.G. and Z.G.; validation, S.L., M.N. and Z.L.; formal analysis, S.L. and M.N.; investigation, M.G.; data curation, M.G.; writing—original draft preparation, M.G. and Z.G.; writing—review and editing, M.G. and Z.G.; visualization, S.L., M.N. and Z.L.; supervision, Z.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kang, H. Support technologies for deep and complex roadways in underground coal mines: A review. Int. J. Coal Sci. Technol. 2014, 1, 261–277. [Google Scholar] [CrossRef]
- Mark, C.; Barczak, T.M. Fundamentals of coal mine roof support. New Technology for Coal Mine Roof Support. Proc. NIOSH Open Ind. Brief. 2000, 9453, 23–42. [Google Scholar]
- Abdellah, W.; Abdelhaffez, G.; Saleem, H. Stability assessment of underground openings using different rock support systems. Rud. Zb. 2020, 35, 49–63. [Google Scholar]
- Putra, R.A.M. Underground Support System Determination: A Literature Review. Undergr. Support Syst. Determ. A Lit. Rev. 2021, 83, 14. [Google Scholar]
- Canbulat, I.; Van der Merwe, J.N. Design of optimum roof support systems in South African collieries using a probabilistic design approach. J. S. Afr. Inst. Min. Metall. 2009, 109, 71–88. [Google Scholar]
- Klenowski, G.; McNamara, P. Development of support systems for longwall mining in the Bowen Basin, Central Queensland. In Proceedings of the 2020 Coal Operators’ Conference, Wollongong, Australia, 12–14 February 2020; University of Wollongon Mining Engineering: Wollongong, Australia, 2020. [Google Scholar]
- Szurgacz, D.; Zhironkin, S.; Cehlár, M.; Vöth, S.; Spearing, S.; Liqiang, M. A step-by-step procedure for tests and assessment of the automatic operation of a powered roof support. Energies 2021, 14, 697. [Google Scholar] [CrossRef]
- Prusek, S.; Rajwa, S.; Wrana, A.; Krzemień, A. Assessment of roof fall risk in longwall coal mines. Int. J. Min. Reclam. Environ. 2017, 31, 558–574. [Google Scholar] [CrossRef]
- Wang, D.; Zeng, X.; Wang, G.; Li, R. Adaptability Analysis of Four-Leg Hydraulic Support with Large Mining Height under Impact Dynamic Load. Shock Vib. 2022, 2022, 2168871. [Google Scholar] [CrossRef]
- Yetkin, M.E.; Simsir, F.; Ozfirat, M.K.; Yenice, H.; Ozfirat, P.M. A fuzzy approach to selecting roof supports in longwall mining. S. Afr. J. Ind. Eng. 2016, 27, 162–177. [Google Scholar] [CrossRef][Green Version]
- Rafiee, R.; Ataei, M.; Kamali, M. Probabilistic stability analysis of Naien water transporting tunnel and selection of support system using TOPSIS approach. Sci. Res. Essays 2011, 6, 4442–4454. [Google Scholar]
- Jalalifar, H.; Behaadini, M.; Bazzazi, A.A. The optimum rock bolt support system selection by using AHP-Entropy-TOPSIS method. Ariel 2009, 149, 40–120. [Google Scholar]
- Shaffiee Haghshenas, S.; Mikaeil, R.; Abdollahi Kamran, M.; Shaffiee Haghshenas, S.; Hosseinzadeh Gharehgheshlagh, H. Selecting the Suitable Tunnel Supporting System Using an Integrated Decision Support System, (Case Study: Dolaei Tunnel of Touyserkan, Iran). J. Soft Comput. Civ. Eng. 2019, 3, 51–66. [Google Scholar]
- Oraee, K.; Hosseini, N.; Gholinejad, M. A New Approach for Determination of Tunnel Supporting System Using Analytical Hierarchy Process (AHP). In Proceedings of the 2009 Coal Operators’ Conference, Wollongong, Australia, 12–13 February 2009; The AusIMM Illawarra Branch: Wollongong, Australia, 2009; pp. 78–89. [Google Scholar]
- Hosseini, N.; Oraee, K.; Gholinejad, M. Selection of tunnel support system by using multi criteria decision-making tools. In Proceedings of the 29th International Conference on Ground Control in Mining, Morgantown, WV, USA, 27–29 July 2010; Department of Mining Engineering, College of Engineering and Mineral Resources, West Virginia University: Morgantown, WV, USA, 2010; pp. 1–9. [Google Scholar]
- Tajvidi Asr, E.; Hayaty, M.; Rafiee, R.; Ataie, M.; Jalali, S.E. Selection of optimum tunnel support system using aggregated ranking of SAW, TOPSIS and LA methods. Int. J. Appl. Oper. Res. 2015, 5, 49–63. [Google Scholar]
- Yavuz, M.; Iphar, M.; Once, G. The optimum support design selection by using AHP method for the main haulage road in WLC Tuncbilek colliery. Tunn. Undergr. Space Technol. 2008, 23, 111–119. [Google Scholar] [CrossRef]
- Pamučar, D.; Stević, Ž.; Sremac, S. A New Model for Determining Weight Coefficients of Criteria in MCDM Models: Full Consistency Method (FUCOM). Symmetry 2018, 10, 393. [Google Scholar] [CrossRef]
- Badi, I.; Muhammad, L.J.; Abubakar, M.; Bakır, M. Measuring Sustainability Performance Indicators Using FUCOM-MARCOS Methods. Oper. Res. Eng. Sci. Theory Appl. 2022, 5, 99–116. [Google Scholar] [CrossRef]
- Das, P.P.; Chakraborty, S. SWARA-CoCoSo method-based parametric optimization of green dry milling processes. J. Eng. Appl. Sci. 2022, 69, 35. [Google Scholar] [CrossRef]
- Singh, R.K.; Modgil, S. Supplier selection using SWARA and WASPAS—A case study of Indian cement industry. Meas. Bus. Excell. 2020, 24, 243–265. [Google Scholar] [CrossRef]
- Stanujkic, D.; Zavadskas, E.K.; Karabasevic, D.; Smarandache, F.; Turskis, Z. The use of the pivot pairwise relative criteria importance assessment method for determining the weights of criteria. Rom. J. Econ. Forecast. 2017, 20, 116–133. [Google Scholar]
- Jauković-Jocić, K.; Karabašević, D.; Jocić, G. The use of the PIPRECIA method for assessing the quality of e-learning materials. Ekonomika 2020, 66, 37–45. [Google Scholar] [CrossRef]
- Sharma, M.; Joshi, S.; Kumar, A. Assessing enablers of e-waste management in circular economy using DEMATEL method: An Indian perspective. Environ. Sci. Pollut. Res. 2020, 27, 13325–13338. [Google Scholar] [CrossRef] [PubMed]
- Dwijendra, N.K.A.; Akhmadeev, R.; Tumanov, D.; Kosov, M.; Shoar, S.; Banaitis, A. Modeling social impacts of high-rise residential buildings during the post-occupancy phase using dematel method: A case study. Buildings 2021, 11, 504. [Google Scholar] [CrossRef]
- Krylovas, A.; Zavadskas, E.K.; Kosareva, N.; Dadelo, S. New KEMIRA method for determining criteria priority and weights in solving MCDM problem. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 1119–1133. [Google Scholar] [CrossRef]
- Krylovas, A.; Kosareva, N.; Zavadskas, E.K. WEBIRA-comparative analysis of weight balancing method. Int. J. Comput. Commun. Control 2018, 12, 238–253. [Google Scholar] [CrossRef]
- Oktavianti, E.; Komala, N.; Nugrahani, F. Simple multi attribute rating technique (SMART) method on employee promotions. J. Phys. Conf. Ser. 2019, 1193, 012028. [Google Scholar] [CrossRef]
- Li, X.; Wang, K.; Liu, L.; Xin, J.; Yang, H.; Gao, C. Application of the entropy weight and TOPSIS method in safety evaluation of coal mines. Procedia Eng. 2011, 26, 2085–2091. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Mukhametzyanov, I. Specific character of objective methods for determining weights of criteria in MCDM problems: Entropy, CRITIC and SD. Decis. Mak. Appl. Manag. Eng. 2021, 4, 76–105. [Google Scholar] [CrossRef]
- Singh, T. Optimum design based on fabricated natural fiber reinforced automotive brake friction composites using hybrid CRITIC-MEW approach. J. Mater. Res. Technol. 2021, 14, 81–92. [Google Scholar] [CrossRef]
- Alhabo, M.; Zhang, L. Multi-criteria handover using modified weighted TOPSIS methods for heterogeneous networks. IEEE Access 2018, 6, 40547–40558. [Google Scholar] [CrossRef]
- Nguyen, P.-H.; Tsai, J.-F.; Nguyen, V.-T.; Vu, D.-D.; Dao, T.-K. A Decision Support Model for Financial Performance Evaluation of Listed Companies in The Vietnamese Retailing Industry. J. Asian Financ. Econ. Bus. 2020, 7, 1005–1015. [Google Scholar] [CrossRef]
- Şahin, M. A comprehensive analysis of weighting and multicriteria methods in the context of sustainable energy. Int. J. Environ. Sci. Technol. 2021, 18, 1591–1616. [Google Scholar] [CrossRef] [PubMed]
- Sałabun, W.; Wątróbski, J.; Shekhovtsov, A. Are MCDA Methods Benchmarkable? A Comparative Study of TOPSIS, VIKOR, COPRAS, and PROMETHEE II Methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- El-Santawy, M.F.; Ahmed, A.N. CV-VIKOR: A new approach for allocating weights in multi-criteria decision making problems. Life Sci. J. 2012, 9, 5875–5877. [Google Scholar]
- Ecer, F.; Aycin, E. Novel Comprehensive MEREC Weighting-Based Score Aggregation Model for Measuring Innovation Performance: The Case of G7 Countries. Informatica 2022, 1–31. [Google Scholar] [CrossRef]
- Shanmugasundar, G.; Sapkota, G.; Čep, R.; Kalita, K. Application of MEREC in Multi-Criteria Selection of Optimal Spray-Painting Robot. Processes 2022, 10, 1172. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. A novel LOPCOW-DOBI multi-criteria sustainability performance assessment methodology: An application in developing country banking sector. Omega 2022, 112, 102690. [Google Scholar] [CrossRef]
- Trinkūnienė, E.; Podvezko, V.; Zavadskas, E.K.; Jokšienė, I.; Vinogradova, I.; Trinkūnas, V. Evaluation of quality assurance in contractor contracts by multi-attribute decision-making methods. Econ. Res.-Ekon. Istraživanja 2017, 30, 1152–1180. [Google Scholar] [CrossRef]
- Čereška, A.; Zavadskas, E.K.; Bucinskas, V.; Podvezko, V.; Sutinys, E. Analysis of steel wire rope diagnostic data applying multi-criteria methods. Appl. Sci. 2018, 8, 260. [Google Scholar] [CrossRef]
- Odu, G.O. Weighting methods for multi-criteria decision making technique. J. Appl. Sci. Environ. Manag. 2019, 23, 1449–1457. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, N.; Jing, H.; Meng, B.; Yin, X. A Novel Model of the Ideal Point Method Coupled with Objective and Subjective Weighting Method for Evaluation of Surrounding Rock Stability. Math. Probl. Eng. 2016, 2016, 8935156. [Google Scholar] [CrossRef]
- Pan, X.; Liu, H.; Huan, J.; Sui, Y.; Hong, H. Allocation model of carbon emission permits for the electric power industry with a combination subjective and objective weighting approach. Energies 2020, 13, 706. [Google Scholar] [CrossRef]
- Mahmoody Vanolya, N.; Jelokhani-Niaraki, M. The use of subjective–objective weights in GIS-based multi-criteria decision analysis for flood hazard assessment: A case study in Mazandaran, Iran. GeoJournal 2021, 86, 379–398. [Google Scholar] [CrossRef]
- Attri, R.; Grover, S. Application of preference selection index method for decision making over the design stage of production system life cycle. J. King Saud Univ.-Eng. Sci. 2015, 27, 207–216. [Google Scholar] [CrossRef]
- Petković, D.; Madić, M.; Radovanović, M.; Gečevska, V. Application of The Performance Selection Index Method For Solving Machining MCDM Problems. Facta Univ. Ser. Mech. Eng. 2017, 15, 97–106. [Google Scholar] [CrossRef]
- Vahdani, B.; Zandieh, M.; Tavakkoli-Moghaddam, R. Two novel FMCDM methods for alternative-fuel buses selection. Appl. Math. Model. 2011, 35, 1396–1412. [Google Scholar] [CrossRef]
- Jain, V. Application of combined MADM methods as MOORA and PSI for ranking of FMS performance factors. Benchmarking Int. J. 2018, 25, 1903–1920. [Google Scholar] [CrossRef]
- Ulutaş, A.; Balo, F.; Sua, L.; Demir, E.; Topal, A.; Jakovljević, V. A new integrated grey MCDM model: Case of warehouse location selection. Facta Univ. Ser. Mech. Eng. 2021, 19, 515. [Google Scholar] [CrossRef]
- Ulutaş, A.; Balo, F.; Sua, L.; Karabasevic, D.; Stanujkic, D.; Popovic, G. Selection of insulation materials with PSI-CRITIC based CoCoSo method. Rev. La Construcción 2021, 20, 382–392. [Google Scholar] [CrossRef]
- Stanujkic, M.; Stanujkic, D.; Karabasevic, D.; Sava, C.; Popovic, G. Comparison of Tourism Potentials Using Preference Selection Index Method. QUAESTUS Multidiscip. Res. J. 2020, 177–187. [Google Scholar]
- Madic, M.; Antucheviciene, J.; Radovanovic, M.; Petkovic, D. Determination of laser cutting process conditions using the preference selection index method. Opt. Laser Technol. 2017, 89, 214–220. [Google Scholar] [CrossRef]
- Sari, E.B. Measuring The performances of the machines via Preference Selection Index (PSI) method and comparing them with values of Overall Equipment Efficiency (OEE). Izmir J. Econ. 2019, 34, 573–581. [Google Scholar]
- Vahdani, B.; Mousavi, S.M.; Ebrahimnejad, S. Soft computing-based preference selection index method for human resource management. J. Intell. Fuzzy Syst. 2014, 26, 393–403. [Google Scholar] [CrossRef]
- Urošević, K.; Gligorić, Z.; Miljanović, I.; Beljić, Č.; Gligorić, M. Novel Methods in Multiple Criteria Decision-Making Process (MCRAT and RAPS)—Application in the Mining Industry. Mathematics 2021, 9, 1980. [Google Scholar] [CrossRef]
- Thanh, N.V. Designing a MCDM Model for Selection of an Optimal ERP Software in Organization. Systems 2022, 10, 95. [Google Scholar] [CrossRef]
- Stević, Ž.; Tanackov, I.; Puška, A.; Jovanov, G.; Vasiljević, J.; Lojaničić, D. Development of Modified SERVQUAL–MCDM Model for Quality Determination in Reverse Logistics. Sustainability 2021, 13, 5734. [Google Scholar] [CrossRef]
- Wang, C.N.; Tsai, H.T.; Ho, T.P.; Nguyen, V.T.; Huang, Y.F. Multi-criteria decision making (MCDM) model for supplier evaluation and selection for oil production projects in Vietnam. Processes 2020, 8, 134. [Google Scholar] [CrossRef]
- Ashraf, A.; Ullah, K.; Hussain, A.; Bari, M. Interval-Valued Picture Fuzzy Maclaurin Symmetric Mean Operator with application in Multiple Attribute Decision-Making. Rep. Mech. Eng. 2022, 3, 301–317. [Google Scholar] [CrossRef]
- Arora, H.; Naithani, A. Significance of TOPSIS approach to MADM in computing exponential divergence measures for pythagorean fuzzy sets. Decis. Mak. Appl. Manag. Eng. 2022, 5, 246–263. [Google Scholar] [CrossRef]
- Bairagi, B. A novel MCDM model for warehouse location selection in supply chain management. Decis. Mak. Appl. Manag. Eng. 2022, 5, 194–207. [Google Scholar] [CrossRef]
- Riaz, M.; Athar Farid, H.M. Picture fuzzy aggregation approach with application to third-party logistic provider selection process. Rep. Mech. Eng. 2022, 3, 318–327. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, C.; Deng, J.; Su, C.; Gao, Z. Analysis of factors influencing miners’ unsafe behaviors in intelligent mines using a novel hybrid MCDM model. Int. J. Environ. Res. Public Health 2022, 19, 7368. [Google Scholar] [CrossRef] [PubMed]
- Maniya, K.; Bhatt, M.G. A selection of material using a novel type decision-making method: Preference selection index method. Mater. Des. 2010, 31, 1785–1789. [Google Scholar] [CrossRef]
- Dehdasht, G.; Ferwati, M.S.; Zin, R.M.; Abidin, N.Z. A hybrid approach using entropy and TOPSIS to select key drivers for a successful and sustainable lean construction implementation. PLoS ONE 2020, 15, e0228746. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of objective weights using a new method based on the removal effects of criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Xu, Y.; Lai, K.K.; Leung, W.K.J. A consensus-based decision model for assessing the health systems. PLoS ONE 2020, 15, e0237892. [Google Scholar] [CrossRef]
- Vujičić, M.D.; Papić, M.Z.; Blagojević, M.D. Comparative analysis of objective techniques for criteria weighing in two MCDM methods on example of an air conditioner selection. Tehnika 2017, 72, 422–429. [Google Scholar] [CrossRef]
- Karim, R.; Karmaker, C.L. Machine selection by AHP and TOPSIS methods. Am. J. Ind. Eng. 2016, 4, 7–13. [Google Scholar]
- Balali, A.; Valipour, A.; Edwards, R.; Moehler, R. Ranking effective risks on human resources threats in natural gas supply projects using ANP-COPRAS method: Case study of Shiraz. Reliab. Eng. Syst. Saf. 2021, 208, 107442. [Google Scholar] [CrossRef]
- Ibrahim, A.; Surya, R.A. The Implementation of Simple Additive Weighting (SAW) Method in Decision Support System for the Best School Selection in Jambi. J. Phys. Conf. Ser. 2019, 1338, 012054. [Google Scholar] [CrossRef]
- Pamučar, D.; Ćirović, G. The selection of transport and handling resources in logistics centers using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).