Addressing Parameter Uncertainty in a Health Policy Simulation Model Using Monte Carlo Sensitivity Methods
Abstract
1. Introduction
1.1. Background and Approach
1.2. Prior Work in This Area
2. Materials and Methods
2.1. The Process: Initial Steps
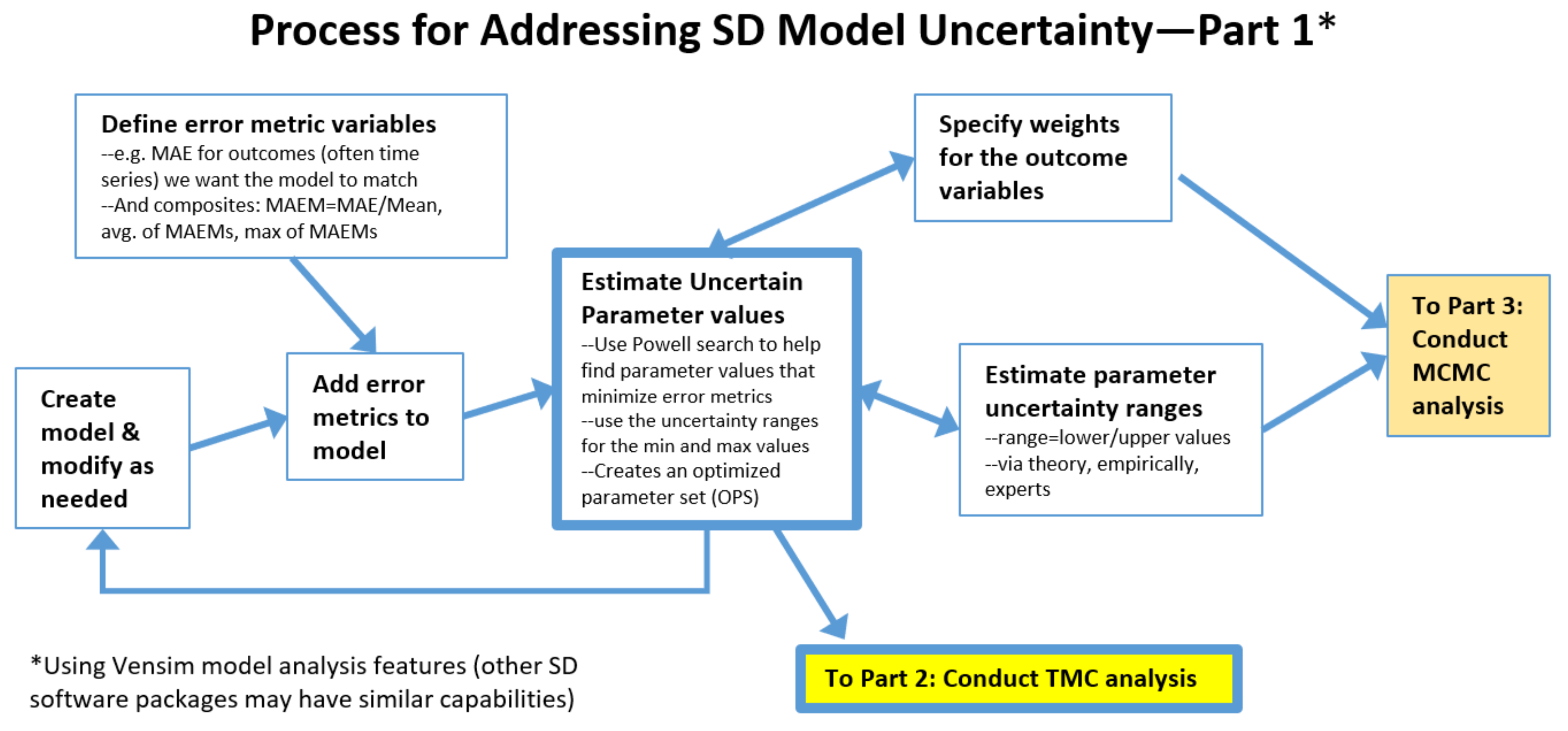
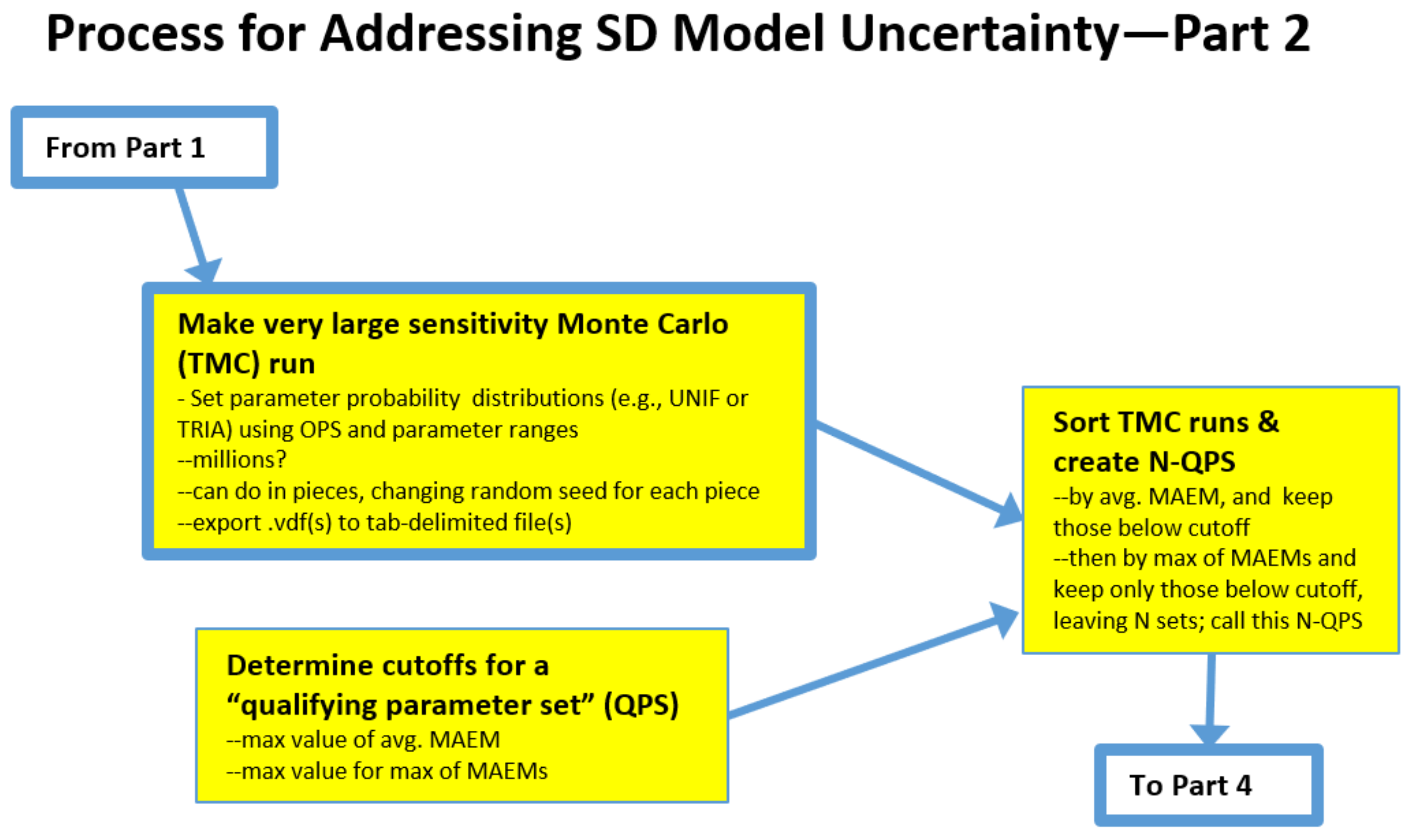
2.2. The Process: Intermediate Steps for the Traditional Monte Carlo (TMC) Approach
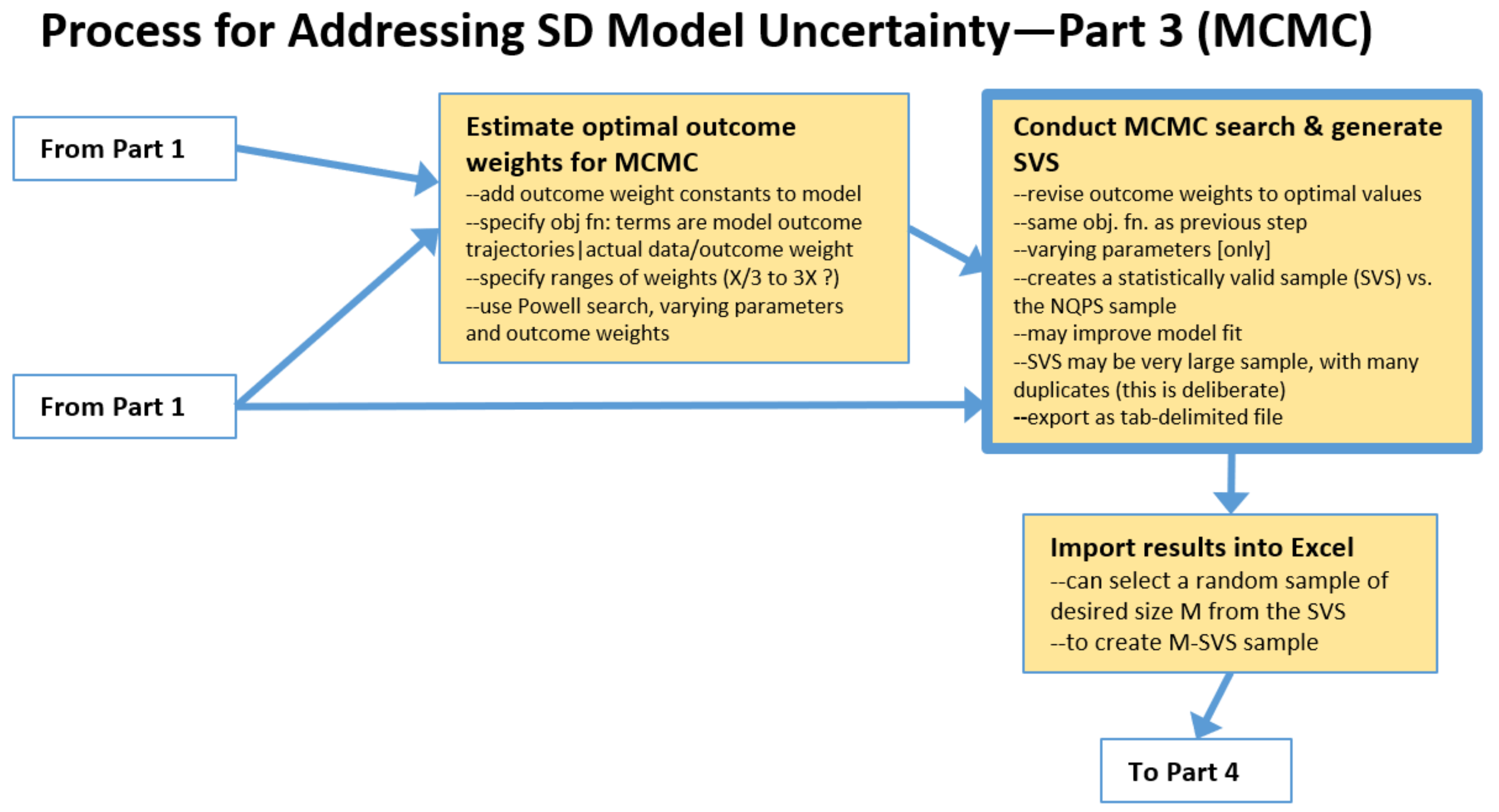
2.3. The Process: Intermediate Steps for Markov Chain Monte Carlo (MCMC) Approach
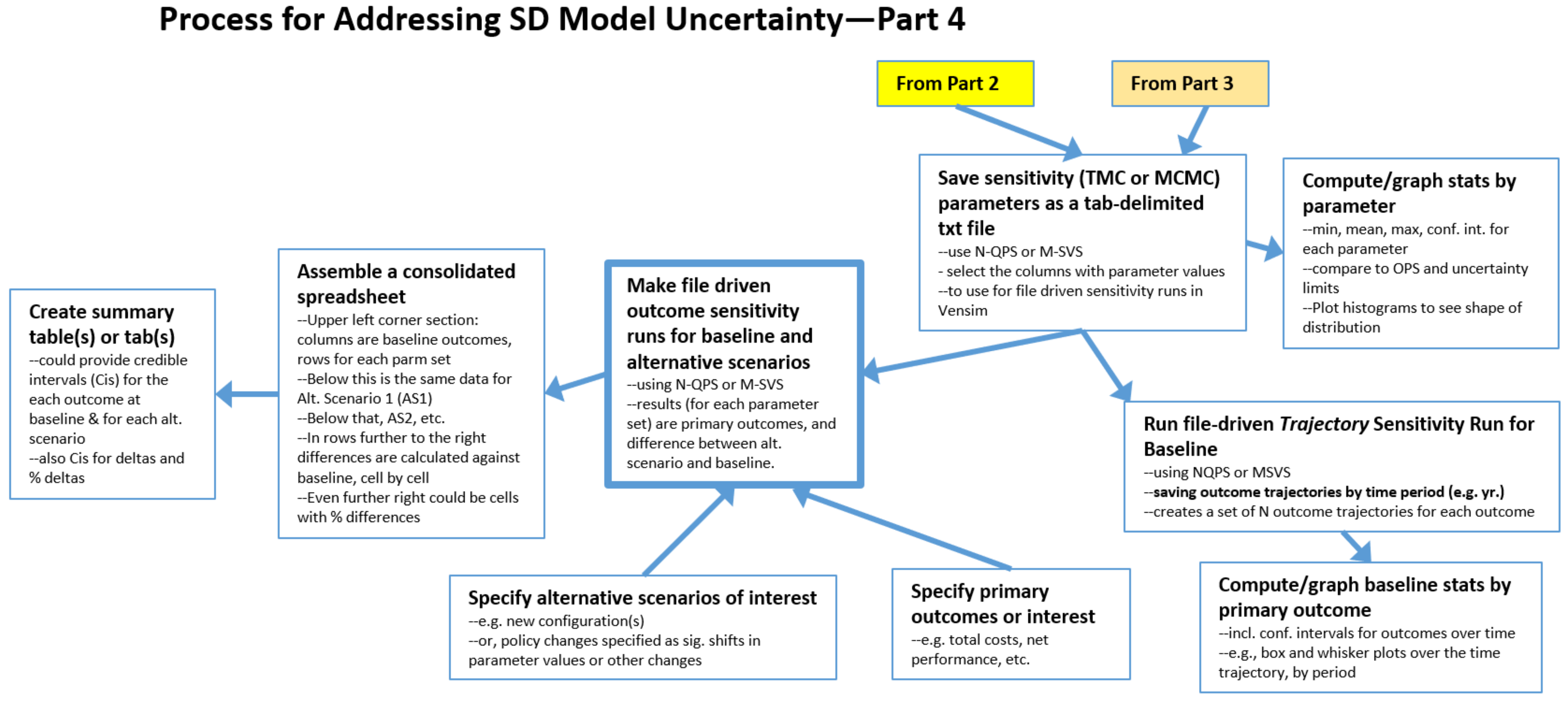
2.4. The Process: Final Steps for Both TMC and MCMC
2.5. About the Opioid Epidemic Model
3. Results
3.1. Error Metrics
3.2. Optimized Parameter Set (OPS)
3.3. Qualified Parameter Sets (N-QPS)
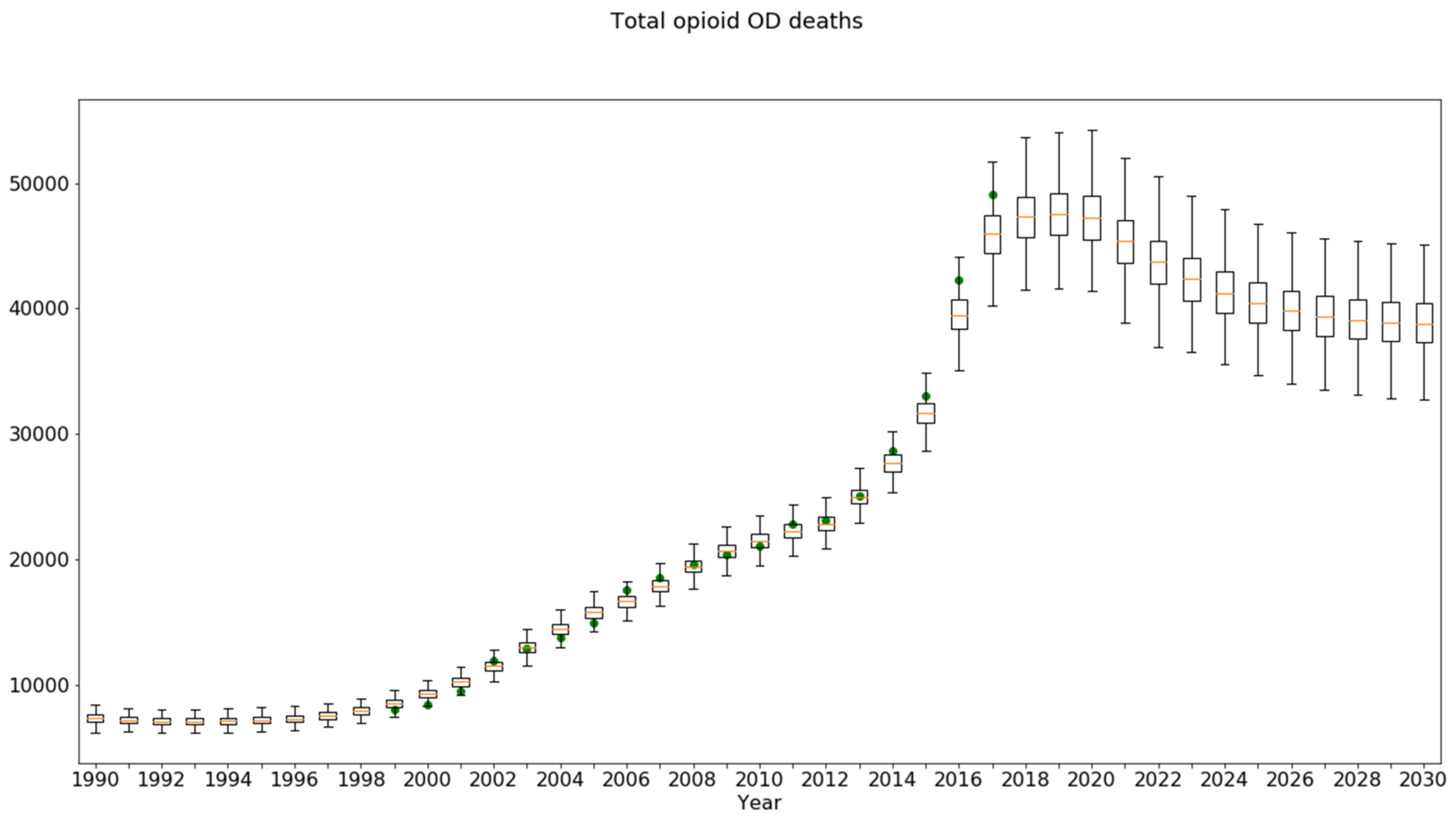
3.4. Sensitivity Runs for the Baseline Scenario
3.5. Sensitivity Runs for Alternative Scenarios (Policy Testing under Uncertainty)
- Treatment rate 65% (from 45%) policy and the outcome Persons with OUD: The model projected a modest unfavorable impact for the OPS and a modest favorable impact for the QPS. The QPS sample interval contained zero, so this policy should perhaps be considered not to impact Persons with OUD;
- All four policies combined and the outcome Overdoses Seen at ED: a mean beneficial outcome was predicted by both, but the credible interval again included zero, indicating that the net effect of all four policies on overdose events could be neutral;
- Diversion control policy and the outcome OD Deaths: The uncertainty interval again included zero, suggesting that for a significant number of the qualified parameter sets, the impact was unfavorable. This was likely due to persons switching to more dangerous drugs. This hypothesis could be examined directly by studying the uncertainty analysis results to find the specific parameter values which render the policy ineffective.
| Optimized Parameter Set | QPS 1119 MC Result | QPS 1119 MC, % Change vs. Baseline | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Outcome Measure | Test Condition | Result | % Change vs. Baseline | Mean | Credible Interval | Mean %Δ | Credible Interval | ||
| Min | Max | Min | Max | ||||||
| Persons with OUD (thou) | Baseline | 1694 | 1593 | 1111 | 2084 | ||||
| Avg MME dose down 20% | 1510 | −10.9% | 1416 | 1035 | 1823 | −11.1% | −25.7% | −3.4% | |
| Diversion Control 30% | 1428 | −15.7% | 1339 | 1007 | 1716 | −15.9% | −37.4% | −4.6% | |
| Treatment rate 65% (from 45%) | 1713 | 1.1% | 1585 | 1054 | 2130 | −0.5% | −9.0% | 5.0% | |
| Naloxone lay use 20% (from 4%) | 1728 | 2.0% | 1624 | 1150 | 2111 | 1.9% | 1.3% | 2.3% | |
| All four policies combined | 1285 | −24.1% | 1189 | 905 | 1560 | −25.4% | −60.2% | −6.5% | |
| Overdoses seen at ED (thou) | Baseline | 155 | 149 | 124 | 179 | ||||
| Avg MME dose down 20% | 153 | −1.3% | 145 | 118 | 176 | −2.7% | −8.2% | 3.8% | |
| Diversion Control 30% | 153 | −1.1% | 144 | 116 | 175 | −3.4% | −11.6% | 6.0% | |
| Treatment rate 65% (from 45%) | 150 | −3.0% | 144 | 118 | 171 | −3.7% | −11.3% | −0.3% | |
| Naloxone lay use 20% (from 4%) | 159 | 2.9% | 154 | 128 | 187 | 3.1% | 2.2% | 5.1% | |
| All four policies combined | 148 | −4.1% | 139 | 111 | 168 | −7.3% | −19.6% | 6.1% | |
| Overdose deaths (thou) | Baseline | 40.3 | 39.0 | 32.5 | 46.7 | ||||
| Avg MME dose down 20% | 39.8 | −1.3% | 37.9 | 30.9 | 46.0 | −2.7% | −8.2% | 0.6% | |
| Diversion Control 30% | 39.9 | −1.1% | 37.6 | 30.3 | 45.5 | −3.4% | −11.6% | 6.0% | |
| Treatment rate 65% (from 45%) | 39.2 | −3.0% | 37.5 | 30.8 | 44.6 | −3.7% | −11.3% | −0.3% | |
| Naloxone lay use 20% (from 4%) | 35.3 | −12.5% | 34.2 | 28.4 | 41.4 | −12.3% | −18.6% | −8.1% | |
| All four policies combined | 32.9 | −18.4% | 30.7 | 24.5 | 31.2 | −21.1% | −36.4% | −6.9% | |
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wakeland, W.; Hoarfrost, M. The case for thoroughly testing complex system dynamics models. In Proceedings of the 23rd International Conference of the System Dynamics Society, Boston, MA, USA, 17–21 July 2005. [Google Scholar]
- Homer, J.; Wakeland, W. A dynamic model of the opioid drug epidemic with implications for policy. Am. J. Drug Alcohol. Abuse. 2020, 47, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Ford, A. Estimating the impact of efficiency standards on the uncertainty of the northwest electric system. Oper. Res. 1990, 38, 580–597. [Google Scholar] [CrossRef]
- Sterman, J.D. Business Dynamics: Systems Thinking and Modeling for a Complex World; Irwin McGraw-Hill: Boston, MA, USA, 2000. [Google Scholar]
- Helton, J.C.; Johnson, J.D.; Sallaberry, C.J.; Storlie, C.B. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliab. Eng. Syst. Saf. 2006, 91, 1175–1209. [Google Scholar] [CrossRef]
- Dogan, G. Confidence interval estimation in system dynamics models: Bootstrapping vs. likelihood ratio method. In Proceedings of the 22nd International Conference of the System Dynamics Society, Oxford, UK, 25–29 July 2004. [Google Scholar]
- Dogan, G. Bootstrapping for confidence interval estimation and hypothesis testing for parameters of system dynamics models. Syst. Dyn. Rev. 2007, 23, 415–436. [Google Scholar] [CrossRef]
- Cheung, S.H.; Beck, J.L. Bayesian model updating using hybrid Monte Carlo simulation with application to structural dynamic models with many uncertain parameters. J. Eng. Mech. 2009, 135, 243–255. [Google Scholar] [CrossRef]
- Ter Braak, C.J.F. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Vrugt, J.A.; ter Braak, C.J.F.; Diks, C.G.H.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov Chain Monte Carlo Simulation by differential evolution with self-adaptive randomized subspace sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 271–288. [Google Scholar] [CrossRef]
- Fiddaman, T.; Yeager, L. Vensim calibration and Markov Chain Monte Carlo. In Proceedings of the 33rd International Conference of the System Dynamics Society, Cambridge, MA, USA, 19–23 July 2015. [Google Scholar]
- Osgood, N. Bayesian parameter estimation of system dynamics models using Markov Chain Monte Carlo methods: An informal introduction. In Proceedings of the 31st International Conference of the System Dynamics Society, Cambridge, MA, USA, 21–25 July 2013. [Google Scholar]
- Osgood, N.D.; Liu, J. Combining Markov Chain Monte Carlo approaches and dynamic modeling. In Analytical Methods for Dynamic Modelers; Rahmandad, H., Oliva, R., Osgood, N.D., Eds.; MIT Press: Cambridge MA, USA, 2015; Chapter 5; pp. 125–169. [Google Scholar]
- Andrade, J.; Duggan, J. A Bayesian approach to calibrate system dynamics models using Hamiltonian Monte Carlo. Syst. Dyn. Rev. 2021, 37, 283–309. [Google Scholar] [CrossRef]
- Jeon, C.; Shin, J. Long-term renewable energy technology valuation using system dynamics and Monte Carlo simulation: Photovoltaic technology case. Energy 2014, 66, 447–457. [Google Scholar] [CrossRef]
- Sterman, J.D.; Siegel, L.; Rooney-Varga, J.N. Does replacing coal with wood lower CO2 emissions? Dynamic lifecycle analysis of wood bioenergy. Environ. Res. Lett. 2018, 13, 015007. [Google Scholar] [CrossRef]
- Ghaffarzadegan, N.; Rahmandad, H. Simulation-based estimation of the early spread of COVID-19 in Iran: Actual versus confirmed cases. Syst. Dyn. Rev. 2020, 36, 101–129. [Google Scholar] [CrossRef]
- Lim, T.Y.; Stringfellow, E.J.; Stafford, C.A.; DiGennaro, C.; Homer, J.B.; Wakeland, W.; Jalali, M.S. Modeling the evolution of the US opioid crisis for national policy development. Proc. Natl. Acad. Sci. USA 2022, 119, e2115714119. [Google Scholar] [CrossRef]
- Rahmandad, H.; Lim, T.Y.; Sterman, J. Behavioral dynamics of COVID-19: Estimating underreporting, multiple waves, and adherence fatigue across 92 nations. Syst. Dyn. Rev. 2021, 37, 5–31. [Google Scholar] [CrossRef]
- Menzies, N.A.; Soeteman, D.I.; Pandya, A.; Kim, J.J. Bayesian methods for calibrating health policy models: A tutorial. Pharmacoeconomics 2017, 35, 613–624. [Google Scholar] [CrossRef]
- Homer, J. Reference Guide for the Opioid Epidemic Simulation Model (Version 2u); February 2020. Available online: https://pdxscholar.library.pdx.edu/cgi/viewcontent.cgi?filename=0&article=1154&context=sysc_fac&type=additional (accessed on 7 November 2022).
- Levin, G.; Roberts, E.B.; Hirsch, G.B. The Persistent Poppy: A Computer-Aided Search for Heroin Policy; Ballinger: Cambridge, MA, USA, 1975. [Google Scholar]
- Homer, J.B. A system dynamics model of national cocaine prevalence. Syst. Dyn. Rev. 1993, 9, 49–78. [Google Scholar] [CrossRef]
- Homer, J.; Hirsch, G. System dynamics modeling for public health: Background and opportunities. Am. J. Public Health 2006, 96, 452–458. [Google Scholar] [CrossRef]
- Wakeland, W.; Nielsen, A.; Schmidt, T.; McCarty, D.; Webster, L.; Fitzgerald, J.; Haddox, J.D. Modeling the impact of simulated educational interventions in the use and abuse of pharmaceutical opioids in the United States: A report on initial efforts. Health Educ. Behav. 2013, 40, 74S–86S. [Google Scholar] [CrossRef]
- Wakeland, W.; Nielsen, A.; Geissert, P. Dynamic model of nonmedical opioid use trajectories and potential policy interventions. Am. J. Drug Alcohol. Abuse 2015, 41, 508–518. [Google Scholar] [CrossRef]
- Bonnie, R.J.; Ford, M.A.; Phillips, J.K. (Eds.) Pain Management and the Opioid Epidemic: Balancing Societal and Individual Benefits and Risks of Prescription Opioid Use; National Academies Press: Washington, DC, USA, 2017. [Google Scholar]
- Homer, J.B. Why we iterate: Scientific modeling in theory and practice. Syst. Dyn. Rev. 1996, 12, 1–19. [Google Scholar] [CrossRef]
- Richardson, G.P. Reflections on the foundations of system dynamics. Syst. Dyn. Rev. 2011, 27, 219–243. [Google Scholar] [CrossRef]
- Rahmandad, H.; Sterman, J.D. Reporting guidelines for system dynamics modeling. Syst. Dyn. Rev. 2012, 8, 251–261. [Google Scholar]
- Ray, W.A.; Chung, C.P.; Murray, K.T.; Hall, K.; Stein, C.M. Prescription of long-acting opioids and mortality in patients with chronic noncancer pain. JAMA 2016, 315, 2415–2423. [Google Scholar] [CrossRef] [PubMed]
- Forrester, J.W. System dynamics—The next fifty years. Syst. Dyn. Rev. 2007, 23, 359–370. [Google Scholar] [CrossRef]
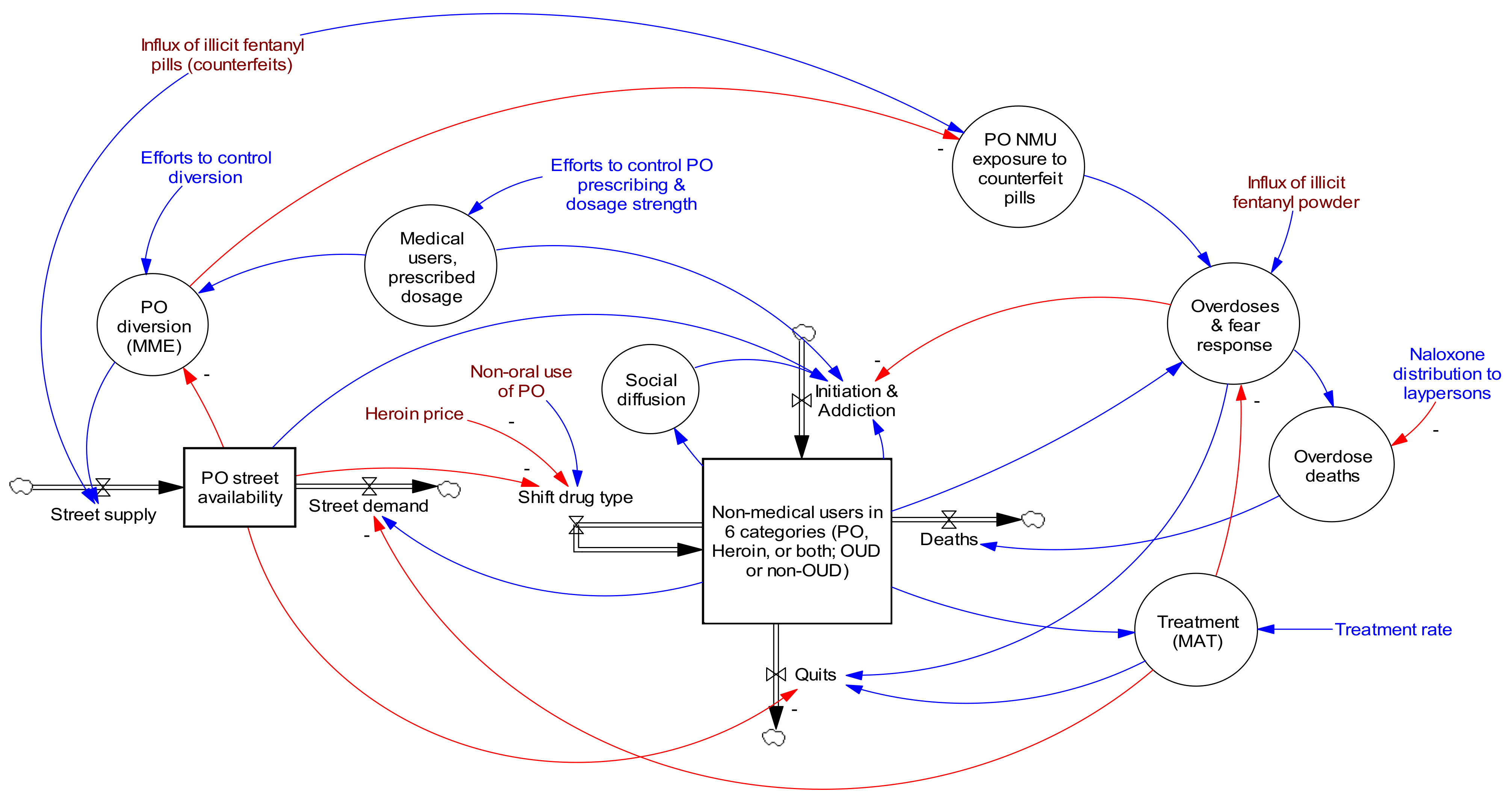
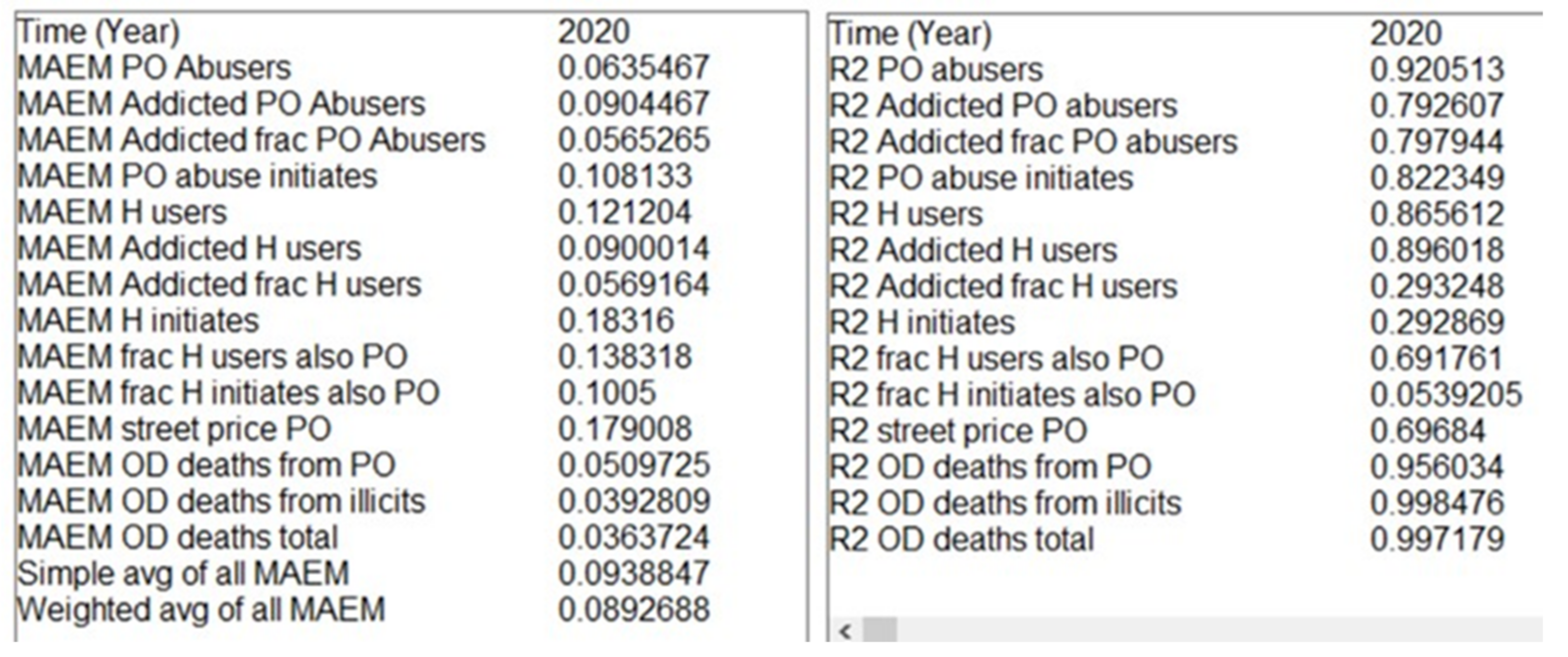


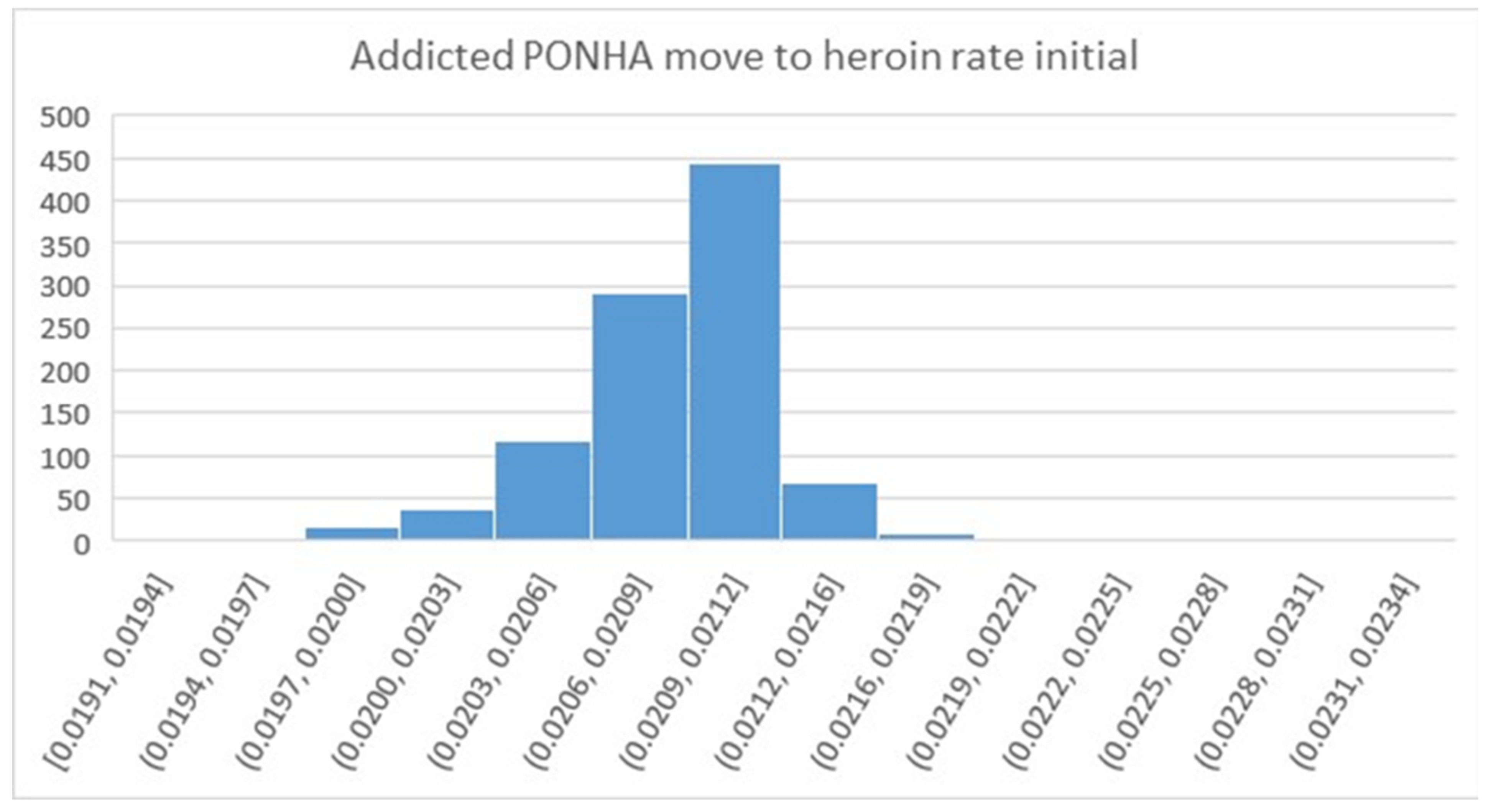
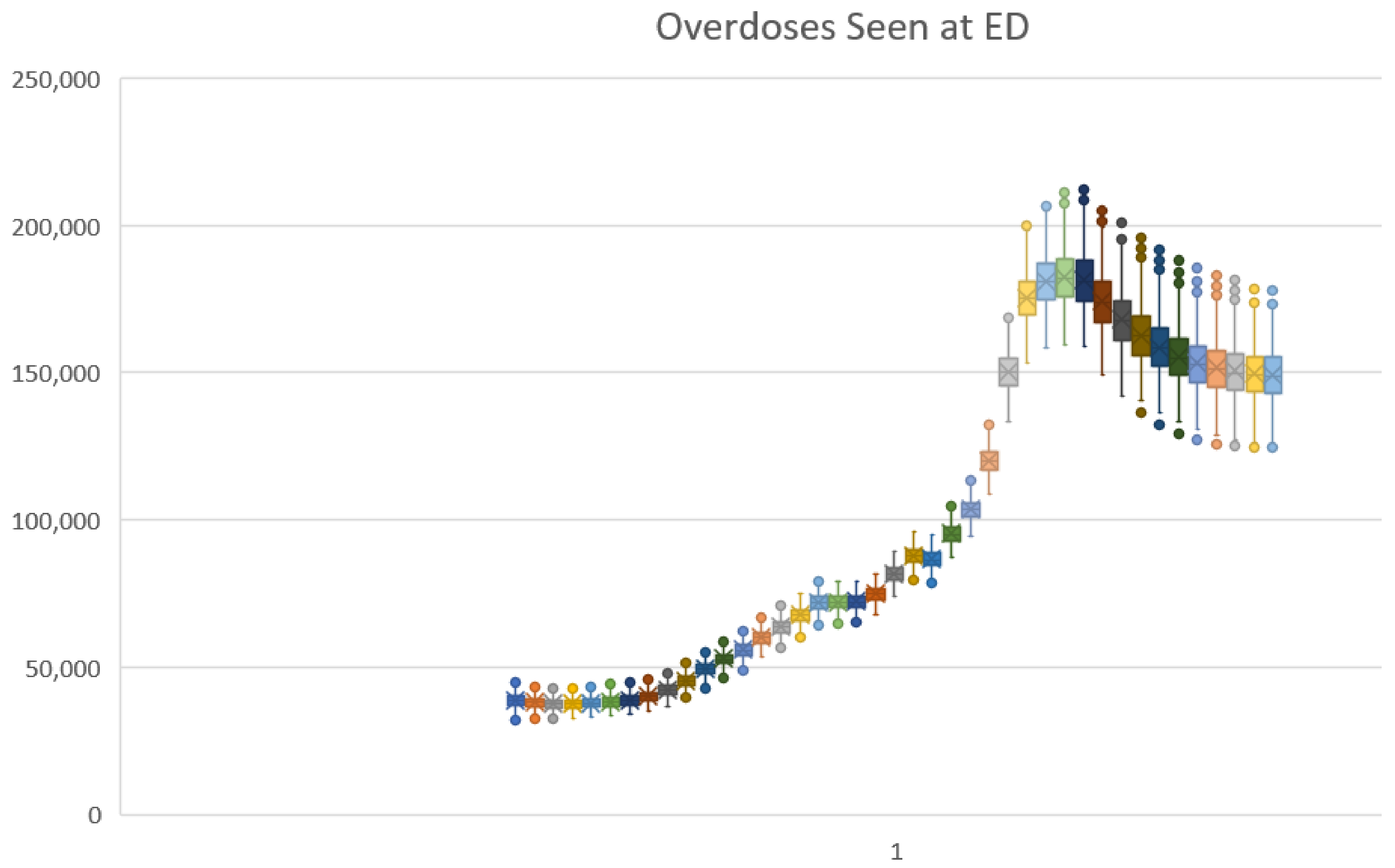
| Parameter | Units | Value | Sources | Min Value | Max Value |
|---|---|---|---|---|---|
| Addicted frac of H users initial | fraction | 0.65 | Optimized; our NSDUH analysis showed 60.8% 2000, 61.1% 2005. | 0.6 | 0.7 |
| Addicted frac of PONHA initial | fraction | 0.123 | Optimized; our NSDUH analysis showed 11.4% 2000, 14.2% 2005. | 0.1 | 0.15 |
| Addicted H user OD death rate initial | 1/year | 0.010 | Optimized | 0.005 | 0.015 |
| Addicted H user quit rate initial | 1/year | 0.138 | Optimized | 0.07 | 0.21 |
| Addicted opioid abuser misc death rate | 1/year | 0.0045 | Ray et al. 2016 [31] determined a mortality hazard ratio of 1.94 vs. general popn for high dose users (>60 mg ME). Multiplied by general popn: average of NVSR death rates for [age 25–34, 35–44, 45–54] = 0.0023 for 2000–2010 × 1.94 = 0.0045. | ||
| Addicted PONHA move to heroin rate initial | 1/year | 0.021 | Optimized | 0.01 | 0.03 |
| Addicted PONHA OD death rate initial | 1/year | 0.0059 | Optimized | 0.004 | 0.007 |
| Addicted PONHA quit rate initial | 1/year | 0.149 | Optimized | 0.08 | 0.22 |
| Uncertain Parameters | ||||||
|---|---|---|---|---|---|---|
| Addicted | Addicted | Addicted | ||||
| Frac | Frac | H User OD | MAEM Statistics | |||
| H Users | PONHA | Death Rate | Simple | Weighted | ||
| Simulation Number | Initial | Initial | Initial | Max | Average | Average |
| 681,526 | 0.6303 | 0.1269 | 0.0121 | 0.1994 | 0.1002 | 0.0958 |
| 376,905 | 0.6913 | 0.1186 | 0.0126 | 0.1975 | 0.1019 | 0.0969 |
| 131,761 | 0.6460 | 0.1180 | 0.0098 | 0.1967 | 0.1055 | 0.0980 |
| 67,350 | 0.6841 | 0.1172 | 0.0078 | 0.1713 | 0.1013 | 0.0982 |
| 726,864 | 0.6501 | 0.1246 | 0.0108 | 0.1838 | 0.1018 | 0.0983 |
| 736,791 | 0.6538 | 0.1236 | 0.0109 | 0.1904 | 0.1150 | 0.1100 |
| 358,518 | 0.6887 | 0.1224 | 0.0100 | 0.1849 | 0.1147 | 0.1100 |
| MIN all sims | 0.6012 | 0.1003 | 0.0059 | 0.1612 | 0.1002 | 0.0958 |
| MIN allowed | 0.6 | 0.1 | 0.005 | |||
| MAX all sims | 0.6998 | 0.1488 | 0.0145 | 0.2000 | 0.1191 | 0.1100 |
| MAX allowed | 0.7 | 0.15 | 0.015 | |||
| MEAN all sims | 0.6487 | 0.1247 | 0.0105 | |||
| OPS value | 0.650 | 0.123 | 0.010 | 0.1795 | 0.0994 | 0.0935 |
| STD DEV all sims | 0.0204 | 0.0100 | 0.0015 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wakeland, W.; Homer, J. Addressing Parameter Uncertainty in a Health Policy Simulation Model Using Monte Carlo Sensitivity Methods. Systems 2022, 10, 225. https://doi.org/10.3390/systems10060225
Wakeland W, Homer J. Addressing Parameter Uncertainty in a Health Policy Simulation Model Using Monte Carlo Sensitivity Methods. Systems. 2022; 10(6):225. https://doi.org/10.3390/systems10060225
Chicago/Turabian StyleWakeland, Wayne, and Jack Homer. 2022. "Addressing Parameter Uncertainty in a Health Policy Simulation Model Using Monte Carlo Sensitivity Methods" Systems 10, no. 6: 225. https://doi.org/10.3390/systems10060225
APA StyleWakeland, W., & Homer, J. (2022). Addressing Parameter Uncertainty in a Health Policy Simulation Model Using Monte Carlo Sensitivity Methods. Systems, 10(6), 225. https://doi.org/10.3390/systems10060225







