Abstract
Gas turbine cooling system is a typical multivariable, strongly coupled, nonlinear, and uncertain MIMO system. In order to solve the control problem of pressure, flow, and temperature of the system, an intelligent approach is necessary and more appropriate. The current system control mainly depends on the experience of the staff, which exists problems such as high labor intensity, low work efficiency and low control accuracy. Lack of accurate models make parameters tune difficultly, and ordinary control methods are difficult to control complex gas turbine cooling system. In this paper, the system transfer function model is built based on the field data obtained under different working conditions and system identification method. The diagonal matrix decoupling method is used to weaken the correlation between variables and achieve independent control among variables. When optimizing the parameters of the controller, Sine Cosine Egret Swarm Optimization Algorithm is proposed. Egret Swarm Optimization Algorithm is composed of Sit-And-Wait strategy, random walk, and encirclement strategy. The sit-and-wait strategy is prone to premature convergence, which makes the optimized parameters unsuitable for gas turbine cooling system. Sine Cosine Algorithm is introduced to randomly use the sine-cosine function for the pseudo-gradient of the weights of the observation equation, thus expanding the search range of the population. Friedman tests prove that the deviation of SE-ESOA is within the allowable range. The results show that the result of Sine Cosine Egret Swarm Optimization Algorithm is more stable and accurate, and it is more suitable for gas turbine cooling system, which solve the pressure, flow, and temperature control problems of complex systems.
1. Introduction
The gas turbine cooling system is a typical MIMO system. The complexity focuses on the multivariable, strongly coupled, nonlinear and uncertain characteristics. In order to solve the control problem for the strongly coupled multivariable of pressure, flow, and temperature, an intelligent approach is necessary and more appropriate. The swarm intelligence optimization algorithms have developed rapidly. Scholars propose new swarm intelligence optimization algorithms to solve the scientific problems of complex systems every year, which proves its important position in complex system models. The advantage of swarm intelligence is that it can solve nonlinear, time-varying, black box model problems in multi-dimensional space, and has the ability of global search. Of course, it also has some disadvantages. Every optimization search needs to traverse all agents before completing an iteration. For each agent, it can only move a small step in the process of completing an iteration. For an agent whose initial position is very far away from the point, it will take a long time. If the speed of the agent is set too fast, it will lead to the agent directly jumping out of the optimal solution in an iteration. These problems will lead to slow searching speed of multi-agent cooperation, or premature convergence and local optimal solution. Because of these shortcomings, many scholars have constantly proposed new intelligent optimization algorithms, or improved the original optimization algorithms. Reference [1] is inspired by the lifestyle, food search and food competition of various vultures on the African continent, proposes a new meta heuristic algorithm, which focuses more on exploration in the early stage of optimization operation. African vulture’s optimization algorithm (AOA) has significant advantages within 95% confidence interval. Its novelty lies in that it not only considers the best fitness individuals but also considers the suboptimal fitness individuals. Reference [2] is inspired by rabbits in nature. Artificial rabbit optimization (ARO) models the survival strategy of rabbits: detour foraging and random hiding. The novelty of the algorithm is that rabbits are willing to eat distant objects first because of their nature. This interesting phenomenon enables ARO to avoid local extremum and conduct a global search. ARO has significant competitiveness in dealing with engineering tasks of unknown and limited search space. Reference [3] simulates the foraging and burrowing activities of prairie dogs and the specific response to the unique alarm of prairie dogs performs well in finding the optimal global solution and having more stable convergence. The limitations in Prairie dog optimization algorithm (PDOA) are that only single objective continuous optimization problems are solved, and the performance of algorithms in solving complex industrial systems has not been studied. Beluga whale optimization (BWO) proposed in reference [4] is inspired by Beluga whale’s behavior, such as swimming, prey, and whale falling. It is composed of three stages: exploration stage, development stage, and whale falling stage, which have achieved very good results in benchmark function testing. The advantage and novelty of the algorithm is that Levy Flight is introduced to enhance the global convergence in the development phase. In addition, there are Harris Hawks Optimizer(HHO) [5], Red Fox Optimization (RFO) [6], Artificial Lizard Search Optimization (ALSO) [7], etc. These optimization algorithms have the same purpose, which is to improve the ability of local development and global exploration and obtain better convergence performance. Egret Swarm Optimization Algorithm (ESOA) is a heuristic algorithm combining the predatory behavior of snow egrets (sit-and-wait strategy) and big egrets (aggressive strategy) [8]. The advantage is that the performance and robustness of ESOA to typical optimization applications have been proved. The limitation is that other mathematical forms of predator-prey strategies have not been developed. Sine Cosine Algorithm [9] is an intelligent optimization algorithm proposed by Seyedali Mirjalili in 2016. In SCA, multiple initial random candidate solutions will be generated, and they will fluctuate outward or toward the optimal solution based on the mathematical model of sine and cosine. Multiple random variables and adaptive variables are used to calculate the current position of the solution. The advantage is that the principle of SCA is simple and easy to implement, it can be easily applied to optimization problems in different fields.
Many optimization algorithms will be integrated with SCA, so that different regions in the space can be searched, effectively avoiding local optimization, and converging to the global. References [10,11,12,13,14] are respectively the Barnacle Algorithm Optimizer, Arithmetic Optimization Algorithm, Dolphin Swarm Optimization, Crow Search Algorithm and Particle Swarm Optimization of mixed Sine Cosine Algorithm. These hybrid algorithms have verified the strong adaptability of SCA and can obtain good optimization results in different fields, which show their potential to solve many optimization problems in complex system. Algorithm review in the form of tables is shown in Table 1:

Table 1.
Algorithm Review.
One of the most widely used swarm intelligence optimization algorithms is to optimize the parameters of complex systems [15,16]. When the control system has multiple controlled variables, multiple control loops need to be added, which form a MIMO system. In the MIMO system, due to the actual process of industrial systems, there are often some coupling phenomena. The Once-through steam generator (OTSG) in reference [17] is a strong coupling system. In order to solve the problem of outlet pressure control, Proximal Policy Optimization (PPO) is used to optimize the PID parameters in real time. In addition, take the nozzle of the flame cutting machine as an example. There are dozens of variables, such as the length and diameter of the nozzle of the cutting machine, the pressure of the low-pressure chamber, intermediate pressure chamber and high-pressure chamber, and the length and diameter of the pressure chamber. Because of the serious coupling inside, it is difficult to obtain the relationship between variables through traditional modeling methods. Taking the cooling system of gas turbine as an example, the secondary circuit is designed to realize the cooling of gas turbine by using the secondary water cycle. The functions of target flow, target inlet water temperature and main pipe pressure are difficult to express accurately. In addition, they are also affected by the output temperature of heat exchanger, temperature loss of loop pipe, loop water volume and wastewater volume disturbance. For MIMO systems with large disturbance amplitude, it is difficult to achieve the desired control effect by using the usual control methods. However, if the above complex industrial systems can obtain the input and output conditions under different conditions, set some evaluation functions to obtain the impact of each dimension on the system. Then, set different weights through the swarm intelligence algorithm, the desired combination of parameters can be got to achieve system intelligent and automatic control. In order to solve the problem of real-time control of pressure, flow and temperature of gas turbine cooling system, the research in this paper is as follows:
- (1)
- A hybrid Sine Cosine Egret Swarm Optimization Algorithm (SC-ESOA) is proposed. The controller parameters are optimized by using ESOA’s sit-and-wait strategy and aggressive strategy. The hybrid Sine Cosine Egret Swarm Optimization Algorithm enlarges the search range, prevents trapping in local convergence, and achieves the optimization of target parameter combination.
- (2)
- Based on the input and output signals obtained from the field data under different operating conditions, the MIMO coupling system model of the gas turbine cooling system is built by system identification method.
- (3)
- The decoupler of the system is designed according to the multivariable coupling system model and the diagonal matrix decoupling method.
- (4)
- SC-ESOA, ESOA and typical Particle Swarm Optimization (PSO) are applied to the gas turbine cooling system. Discuss the deviation of controller parameters optimized by SC-ESOA according to Friedman tests. The optimized results are compared that prove the feasibility and superiority of SC-ESOA.
2. Sine Cosine Egret Swarm Optimization Algorithm
2.1. Egret Swarm Optimization Algorithm
Egret Swarm Optimization Algorithm was proposed by Zuyan Chen et al., in 2022. ESOA is inspired by the predatory behavior of snowy egrets and great egrets, which consists of three main parts: sit-and-wait strategy, aggressive strategy, and discriminant conditions. Egret population can be composed of groups of egret teams, and each egret team includes three egrets. Egret A adopts the sit-and-wait strategy, egret B and egret C respectively adopt the random walk and encirclement mechanism in the aggressive strategy.
2.1.1. Sit-and-Wait Strategy
The observation equation of the Egret A can be described as , function E represents the evaluation method of Egret A for possible targets at the current location, is the position of group . Calculate the current estimate value of prey by iteration, parameterize the evaluation method, and calculate the error .
is the weight of the evaluation method. means multiplication, the following is the same. means the practical gradient of . can be obtained by calculating the partial derivative of .
is a matrix randomly generated according to uniform distribution. is updated using a random algorithm:
where is set to 0.9, is set to 0.99, the initial value of and are set to 0. represents the direction of egret flight. Egrets will draw on the experience of two egrets’ predation directions. One is the direction revision of the best position of egret team (), and the other is the direction revision of the best position in the whole population ().
where means the flight direction of the best individual in the egret team, means the flight direction of the best individual in the egret population. If a team individual or a population individual finds a better solution, the real gradient will be assigned to them. and is the optimal value of egret team and egret population. and is the best fitness of egret team and egret population. Calculate the pseudo gradient of the weight in the observation equation according to Equations (1)–(9):
where , the updated position of Egret A is shown as:
where represents the current number of iterations, represents the maximum number of iterations, and represents D-value of the position boundary, which means that the value of is equal to the upper limit of solution minus the lower limit of solution. A priori knowledge is generally required for heuristic optimization of controller parameters. For PID controller, , and are tuned to a relatively appropriate value according to prior knowledge, which take the space range of the relatively feasible solution as the upper and lower limit of the solution.
2.1.2. Aggressive Strategy
The aggressive strategy adopted by Egret B is random walk. Although the energy consumption of random walk strategy is large, Egret B is likely to obtain higher benefits. The position update equation of Egret B is:
where is a random number in (−π/2, π/2).
Egret C adopts the encirclement strategy. Once it finds its prey, it will chase it until it is caught.
where represents the difference matrix between the current position and the optimal position of egret team, represents the difference matrix between the current position and the optimal position of egret population. and are random numbers in [0, 0.5].
2.1.3. Discriminant Condition
After each Egret in the egret team calculates the updated position, they will jointly determine the updated position of the egret team. The solution matrix is:
The Egret team compares the updated position and fitness of the three egrets with that of the previous iteration. If one Egret’s updated position is better than that of the previous iteration, it will adopt the update. If the update positions of all egrets are worse than that of the previous one, there is a 30% probability to adopt the scheme with the worse update position.
2.2. Sine Cosine Algorithm
SCA is a random optimization algorithm. Unlike ESOA, SCA has very few parameters, high flexibility, simple principle, easy implementation, and can be easily applied to optimization problems in different fields. SCA makes use of the mathematical properties of sine function and cosine function. By adaptively changing the global exploration and local development ability of the amplitude balance algorithm of sine function and cosine function in the search process, the optimization process can be divided into two stages. In the exploration stage, the optimization algorithm quickly finds the feasible region in the search space by combining a random solution in all random solutions. In development the stage, the random solution will gradually change, and the change speed of the random solution will be lower than that in the exploration stage. The position update equation is:
is the position of the dimension of the current individual in generation t, is a random number in [0, 2π], is a random number in [0, 2], is a random number in [0, 1], and parameter indicates that the location area of the next solution is within or outside the current optimal solution. As the number of iterations increases, the value of will gradually decrease, which helps to enhance the local development ability of the algorithm. defines how far the current solution is close to or away from the optimal solution. gives random weights for the optimal solution in order to enhance or weaken the effect of the optimal solution on defining the moving distance of the candidate solution and enhance the diversity of the population. is a random and balanced switching sine and cosine function of the conversion probability. In summary, these four parameters are easily available, even random numbers, and SCA can successfully balance the exploration and development based on the simple operation.
2.3. Sine Cosine Egret Swarm Optimization Algorithm
In this paper, Sine Cosine Egret Swarm Optimization Algorithm is proposed by combining ESOA with SCA. In an egret team, three egrets choose different strategies to cooperate to complete their predation. In fact, the concept of the predation strategy of egret A and egret B is opposite. The next position update of egret A with sit-and-wait strategy mainly depends on the change of the fitness function. In addition to the updated position calculated by themselves, it will be largely affected by the optimal value of egret team and egret population. Once and has a larger value (close to 0.5), we can assume that egrets currently have little to do with themselves, and that position updates are almost entirely dependent on the team and other egrets in the population, which can easily lead to local optimum solutions. For egret B which uses random walking, it symbolizes the aggressive predation behavior of the great egret in nature. Although it may get better benefit for the great egret, it consumes a lot of energy. For ESOA algorithm, the strategy of egret B has some blindness, but limits the scope of the optimization results in the algorithm.
2.3.1. Optimization Strategy
Based on the principle of sit-and-wait strategy, the position update of egret A is mainly determined by the pseudo gradient of the weight in the observation equation. The parameters affecting are composed of two random numbers: individual direction, the best direction of the egret team and the best direction of the egret population. When the values of and are not good, there are two extreme situations:
- The individual egret loses its own judgment and is almost entirely determined by the optimal direction of the egret team and egret population, leading to premature convergence.
- Ignoring the signals of other egrets, the direction of the egret itself determines the next location update. Due to the randomness of the parameters, the global search capability of ESOA is insufficient.
In order to enlarge the search solution range in the solution space, SC-ESOA is designed to allow egrets to traverse more locations, especially egret A. If the SCA is directly mixed, is a random number in [0, 2π], and may not be in the expected direction. In other words, for egret A, the optimal direction of the egret team and egret population may play a negative role. Therefore, is modified for sine function, should in [0, π], for cosine function, should in . The final range for is [0, π/2] shown in Figure 1; the horizontal axis of the orange area is the final range of .
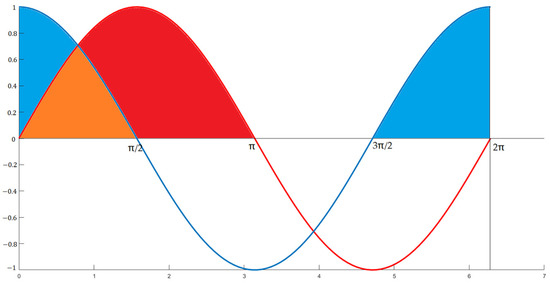
Figure 1.
s final range.
In Equation (17), , a is a constant, which is set as 4 in this paper. is a linear function, which multiply by sine function or cosine function randomly. Calculated results as coefficients decrease from 4 to 0 in a non-linear way, as shown in Figure 2.
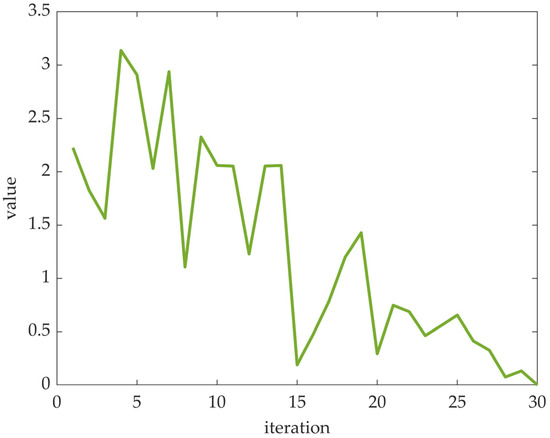
Figure 2.
Coefficient optimized by SCA.
Therefore, the SCA is mixed with ESOA, and improved by using strategies, such as sit-and-wait. Equation (10) is expressed as:
In the initial stage of optimization, SC-ESOA provides a large coefficient, which increases the displacement distance of egrets. Combined with Equation (11), function is a monotonically increasing function. The next iteration position of egret A will be in a broader range, which allows individual to access a larger exploration space, and thus allows the algorithm to explore a larger range. In the later stage of optimization, the coefficient will shorten the displacement of egret, which means that egrets will not change their positions on a large scale, but only search for the best solution or suboptimal solution.
2.3.2. SC-ESOA Flowchart
The pseudocode for SC-ESOA is explained in Algorithm 1, while the flowchart is shown in Figure 3.
| Algorithm 1 Sine Cosine Egret Swarm Optimization Algorithm. |
|
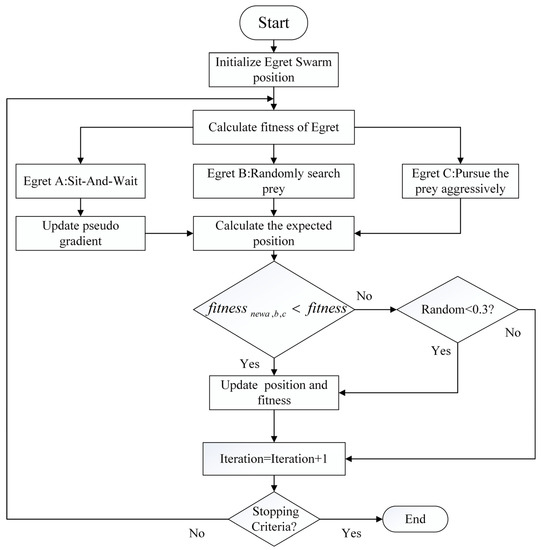
Figure 3.
SC-ESOA flowchart.
3. Gas Turbine Cooling System
In this paper, SC-ESOA is applied to the gas turbine cooling system to optimize the parameters of controllers, which can solve the temperature, flow, and pressure control problems under the constraints of controlled object delay, strong coupling, actuator nonlinearity, etc.
3.1. System Principle
The working principle of the gas turbine cooling system is based on heat conduction of the heat exchanger to design the secondary circuit to achieve cooling. The whole gas turbine cooling system is shown in Figure 4.
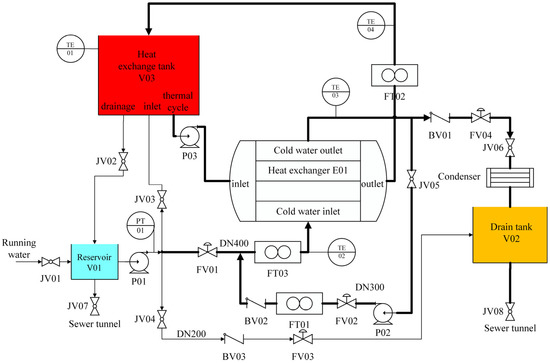
Figure 4.
Gas turbine cooling system.
The tap water enters the reservoir V01 through valve JV01 and enters the main pipeline through centrifugal pump P01. When the pressure sensor PT01 detects that the pressure of the main pipeline is too high, the opening of the electric diaphragm regulating valve FV03 increases, and more water delivered by the centrifugal pump flows into Drain tank V02 through check valve BV03 and is discharged into the sewer tunnel through JV08. The water enters the main pipeline of the system, flows through the electric control valve FV01 and the electromagnetic flowmeter FT03, and then enters the heat exchanger E01. Based on the principle of heat conduction, it transfers the heat of the gas turbine to the cold water in the heat exchanger. The heat exchange is carried out continuously. In the form of wastewater, the heat passes through check valve BV01 and electric control valve FV04, enters the condenser for cooling, and then enters Drain tank V02, which is discharged to the sewer tunnel through JV08. Centrifugal pump P02 pumps out a part of wastewater. After passing through electric control valve FV02, flowmeter FT01 and check valve BV02, it mixes with the cold water delivered by FV01 to realize the secondary circuit, ensuring the constant water temperature (TE02) delivered to the heat exchanger. Due to the large temperature difference between winter and summer in northern China, the water temperature in reservoir V01 is not constant. This cycle is conducive to the long-term stable operation of the entire gas turbine cooling system and prolongs the service life of the heat exchanger.
3.2. System Model Identification
The gas turbine cooling system is a multi-input and multi-output coupling system. The controlled target variables are FT03 (heat exchanger inlet flow), TE02 (heat exchanger inlet temperature) and PT01 (water inlet pressure). The control system block diagram is shown in Figure 5. More than 700 groups of input and output data collected from the field test can establish the mathematical model of each process control channel. The system transfer function model is obtained through the system identification method, as shown in Figure 6.
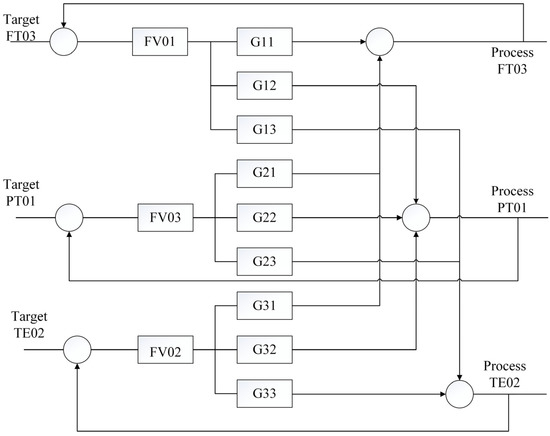
Figure 5.
Block diagram of MIMO coupling system.
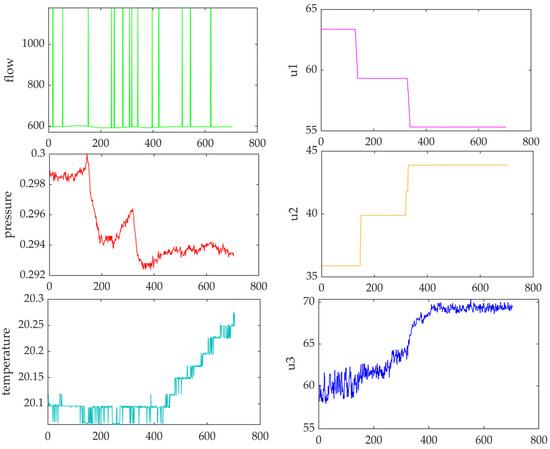
Figure 6.
Input and output signal curve.
is the transfer function that affects FT03-FT01, is the transfer function that affects (FT03-FT01) * TE06, is the transfer function that affects FT01, and is the transfer function that affects TE03 * FT01. and represent the relationship between pressure and other controlled variables. In a physical sense, there is no direct mathematical formula to describe pressure, flow, flow rate and temperature, which is related to pipe diameter, section length, whether there is a bend, and pipe wall roughness. This adds many harsh conditions and is unnecessary. As long as we know, if the opening of FV03 increases, regardless of pump power and gas turbine water supply and drainage, the water delivered by FV01 will inevitably decrease. Therefore, it will affect the flow and temperature of water flowing into the heat exchanger, so there is a correlation between variables, forming a coupling system.
3.3. Decoupling Control
The gas turbine cooling system is a multivariable, coupled nonlinear system. After obtaining the transfer function model of the system, decoupling control is required. In this paper, the pre-compensator is used to decouple, weaken the correlation between variables, and transform the MIMO system into an uncorrelated single loop system. The block diagram of decoupling control system is shown in Figure 7.
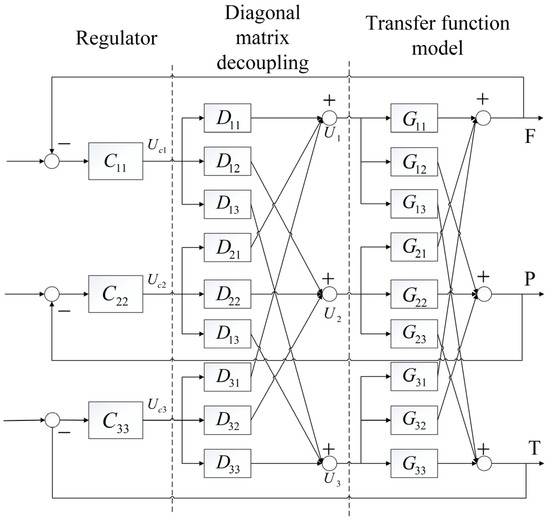
Figure 7.
Block diagram of decoupling control system.
For the controlled variable, the controlled target and the regulated target have the following relations:
If the control system is added, the regulation target comes from the decoupler, and the output of the regulator is the input of the decoupler.
Based on the above relationship, if the inverse of G matrix exists, a decoupler can be designed, which is equal to its inverse multiplied by a diagonal matrix, so that one regulated variable is only related to the output of one regulator, but independent of the other. Each loop realizes independent control through decoupling algorithm, the control algorithm adopts incremental PID, and the controller parameters are adjusted through system identification and SC-ESOA. Diagonal matrix decoupling method is adopted for decoupling, and the simulation block diagram of three inputs and three output decoupling control system is established as shown in Figure 8.
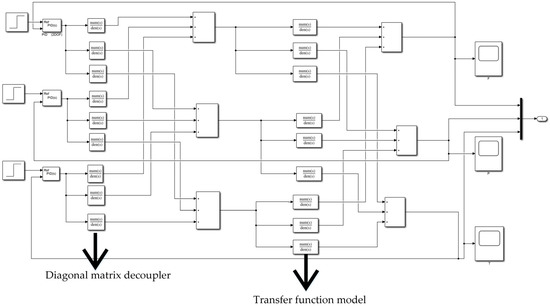
Figure 8.
Simulation block diagram of three input and three output system.
4. SC-ESOA Simulation
After designing the decoupler and controller, SC-ESOA and ESOA are respectively used to optimize the parameters of controllers. In addition, Particle Swarm Optimization has significant competitiveness for parameter tuning. References [18,19,20,21] is an application case of particle swarm optimization and an improved algorithm in different fields to optimize PID controller parameters. Reference [22] proposes a new control technology of fuzzy PID controller parameters based on Hybrid improved particle swarm optimization-cuckoo search, which improves the dynamic response performance of gas turbine. In this paper, there are three PID controllers of the gas turbine cooling system, which correspond to the flow control, pressure control and temperature control, respectively. After the simulink model is built, the simulation results are obtained by optimizing the PID controller parameters through sim function call and optimization algorithm, as shown in Figure 9, Figure 10 and Figure 11. The red represents SC-ESOA, the blue represents ESOA, and the black represents PSO.
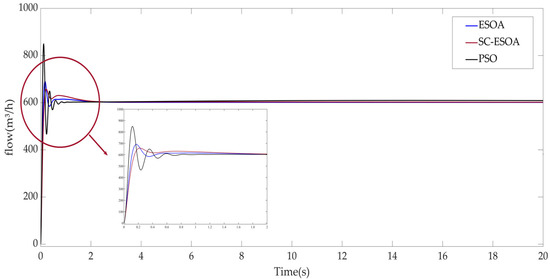
Figure 9.
Comparison of flow control effect.
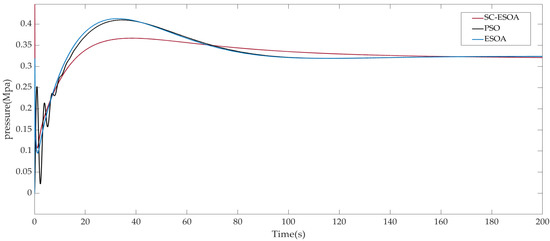
Figure 10.
Comparison of pressure control effect.
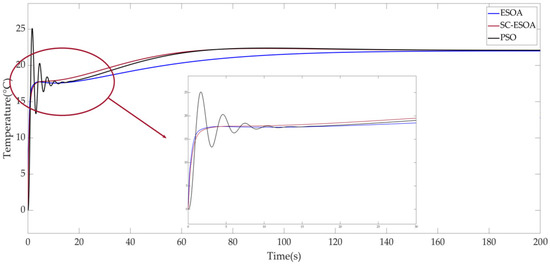
Figure 11.
Comparison of temperature control effect.
By comparing the simulation results, SC-ESOA optimized parameters perform better for the gas turbine cooling system. The overshoot of the particle swarm optimization algorithm is relatively large, because it is difficult to set the initial motion speed of particles. If the speed is set too small, the algorithm will run slowly, which will increase the iteration time. If the speed is set too large, the particle swarm will directly exceed the optimal solution in each iteration. Compared with ESOA, the improved SC-ESOA reduces overshoot, regulation time and peak time. For the gas turbine cooling system, the rapidity and stability of the system are conducive to extending the service life of the gas turbine. PID controller parameters obtained by applying the three optimization algorithms are shown in Table 2.

Table 2.
PID parameters.
Since SC-ESOA has random variables, the results of optimization do not necessarily converge to the optimal values. For experiments, Friedman tests are used. Nine sample sizes of three sets of samples are used to detect whether the optimized deviation is within the allowable range. Nine indexes are independently sorted, and rank is shown in Table 3.

Table 3.
Sample rank.
Calculating inspection value by Equation (21):
where is sample size, is sample number. Querying the Friedman Inspection Threshold Table, , this value is greater than the calculation statistics, so the original hypothesis can be tested at the 0.05 significance level. The test conclusion is no significant difference.
In order to compare experimental results, the system characteristics of the gas turbine cooling system are shown after optimizing the controller parameters in Table 4, Table 5 and Table 6.

Table 4.
Overshoot.

Table 5.
Steady-State errors.

Table 6.
Transient time.
For overshoot, SC-ESOA has been improved, which means that the system is more stable. The overshoot reflects the maximum deviation of the system, which is usually used to evaluate the damping degree of the system. For Steady-State errors, three controlled variables optimized by SC-ESOA are all less than 1%. Small steady-state error of control system means high control accuracy. Therefore, steady-state error is often used as an index to measure the performance of the control system. For transient time, SC-ESOA has some advantages in temperature control. Transient time is also an important index to evaluate the response speed of the system. According to the three important indexes, the controller parameters optimized by SC-ESOA are more suitable for the gas turbine cooling system.
SC-ESOA has shown some advantages and limitations when applied to gas turbine cooling system, which are shown as follow:
- (1)
- The controller parameters optimized by SC-ESOA make the system more stable and safe. After SCA is mixed, the search range of feasible solution is increased, effectively avoiding premature convergence.
- (2)
- The application of SC-ESOA in gas turbine cooling system can provide reference for other process control systems.
- (3)
- The transfer function model of gas turbine system is very complex. Although the decoupling device is designed in this paper, there is still weak coupling between the controlled variables. In fact, it is almost impossible to achieve absolute decoupling, especially for complex industrial systems. Just because of this complexity, the optimization results of SC-ESOA have inevitable overshoot and error.
In general, SC-ESOA integrates the advantages of ESOA and SCA, balancing the convergence speed and search capability.
5. Conclusions
In this paper, Sine Cosine Egret Swarm Optimization Algorithm is applied to the important industrial system of gas turbine cooling. Through mixing with SCA, the optimization strategies of other mathematical forms of ESOA are developed. In the simulation experiment, the controller parameters optimized by SC-ESOA have good performance in overshoot, steady-state error, and transition time. Although parameters in SC-ESOA have random states, Friedman tests prove that the deviation of SE-ESOA is within the allowable range. In addition, the mathematical model of the gas turbine cooling system is obtained through the testing experiment and system identification. the decoupler is designed by using diagonal matrix decoupling method to weaken the correlation between variables. Although the system still has weak coupling and disturbance, SC-ESOA has sufficient optimization capability, which can quickly and accurately adjust the controlled variable to the appropriate value. After the optimization of controller parameters is completed, the control of the target flow, target pressure and target temperature of the gas turbine cooling system is more stable and accurate with the help of the decoupler, which is more suitable for MIMO systems with multivariable, strong coupling and large disturbance amplitude. SC-ESOA is universal and can provide transplantation and reference for parameter optimization of other controllers and other complex systems.
Author Contributions
Conceptualization, Y.L., T.L. and Z.C.; methodology, T.L.; software, T.L. and Y.L.; validation, Y.L., T.L. and Z.C.; formal analysis, Y.L.; investigation, T.L.; data curation, Z.C. and Y.L.; writing—original draft preparation, T.L., Y.L. and Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Q.; Zhang, Z.; Mirjalili, S.; Zhao, W. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Agushaka, J.O.; Abualigah, L.; Mirjalili, S.; Gandomi, A.H. Prairie Dog Optimization Algorithm. Neural Comput. Appl. 2022, 34, 20017–20065. [Google Scholar] [CrossRef]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Połap, D.; Woźniak, M. Red fox optimization algorithm. Expert Syst. Appl. 2021, 166, 114107. [Google Scholar] [CrossRef]
- Kumar, N.; Singh, N.; Vidyarthi, D.P. Artificial lizard search optimization (ALSO): A novel nature-inspired meta-heuristic algorithm. Soft Comput. 2021, 25, 6179–6201. [Google Scholar] [CrossRef]
- Chen, Z.; Francis, A.; Li, S.; Liao, B.; Xiao, D.; Ha, T.T.; Li, J.; Ding, L.; Cao, X. Egret Swarm Optimization Algorithm: An Evolutionary Computation Approach for Model Free Optimization. Biomimetics 2022, 7, 144. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Ewees, A.A.; Al-qaness, M.A.A.; Abualigah, L.; Ibrahim, R.A. Sine–Cosine-Barnacles Algorithm Optimizer with disruption operator for global optimization and automatic data clustering. Expert Syst. Appl. 2022, 207, 117993. [Google Scholar] [CrossRef]
- Abdel-Mawgoud, H.; Fathy, A.; Kamel, S. An effective hybrid approach based on arithmetic optimization algorithm and sine cosine algorithm for integrating battery energy storage system into distribution networks. J. Energy Storage 2022, 49, 104154. [Google Scholar] [CrossRef]
- Ansari, S.A.; Zafar, A. A fusion of dolphin swarm optimization and improved sine cosine algorithm for automatic detection and classification of objects from surveillance videos. Measurement 2022, 192, 110921. [Google Scholar] [CrossRef]
- Surendar, P.; Ponni Bala, M. Diagnosis of lung cancer using hybrid deep neural network with adaptive sine cosine crow search algorithm. J. Comput. Sci. 2021, 53, 101374. [Google Scholar]
- Nenavath, H.; Jatoth, R.K.; Das, S. A synergy of the sine-cosine algorithm and particle swarm optimizer for improved global optimization and object tracking. Swarm Evol. Comput. 2018, 43, 1–30. [Google Scholar] [CrossRef]
- Xhelaj, A.; Burlando, M. Application of metaheuristic optimization algorithms to evaluate the geometric and kinematic parameters of downbursts. Adv. Eng. Softw. 2022, 173, 103203. [Google Scholar] [CrossRef]
- Nayak, J.R.; Shaw, B.; Sahu, B.K.; Naidu, K.A. Application of optimized adaptive crow search algorithm based two degree of freedom optimal fuzzy PID controller for AGC system. Eng. Sci. Technol. Int. J. 2022, 32, 101061. [Google Scholar] [CrossRef]
- Li, C.; Yu, R.; Yu, W.; Wang, T. Pressure control of Once-through steam generator using Proximal policy optimization algorithm. Ann. Nucl. Energy 2022, 175, 109232. [Google Scholar] [CrossRef]
- Kashyap, A.K.; Parhi, D.R. Particle Swarm Optimization aided PID gait controller design for a humanoid robot. ISA Trans. 2021, 114, 306–330. [Google Scholar]
- Copot, C.; Thi, T.M.; Ionescu, C. PID based Particle Swarm Optimization in Offices Light Control. IFAC-PapersOnLine 2018, 51, 382–387. [Google Scholar]
- Su, B.; Lin, Y.; Wang, J.; Quan, X.; Chang, Z.; Rui, C. Sewage treatment system for improving energy efficiency based on particle swarm optimization algorithm. Energy Rep. 2022, 8, 8701–8708. [Google Scholar] [CrossRef]
- Xiang, Z.; Ji, D.; Zhang, H.; Wu, H.; Li, Y. A simple PID-based strategy for particle swarm optimization algorithm. Inf. Sci. 2019, 502, 558–574. [Google Scholar] [CrossRef]
- Yang, R.; Liu, Y.; Yu, Y.; He, X.; Li, H. Hybrid improved particle swarm optimization-cuckoo search optimized fuzzy PID controller for micro gas turbine. Energy Rep. 2021, 7, 5446–5454. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).