Managing the Morning Commute Problem with Tradable Credit Schemes under a Fully Autonomous Vehicle Environment

Abstract

This study investigates the morning commute problem in a single corridor with a bottleneck under a fully automated vehicle environment. By extending Vickrey’s bottleneck model, we formulate the joint decisions on departure time and parking choices of morning commuters who make trade-offs among travel cost, the cost associated with parking, and the cost of tradable credits. To alleviate traffic congestion and improve social welfare, we propose a time-varying tradable credit scheme and integrate it with the morning commute problem. We explore the travel patterns and the optimal design of tradable credit schemes for the morning commute problem with homogeneous and heterogeneous commuters, respectively. For the homogeneous case, we derive the conditions on the tradable credit scheme to ensure the existence of equilibrium. The system-wide travel cost decreases with parking density after tradable credits are incorporated. Additionally, the efficiency of the tradable credits scheme can be improved by increasing the rate of credit charge rate. For the heterogeneous case, we propose an initial distribution strategy and combine it with the optimal tradable credit in order to guarantee social equity. The commuters with a low value of time (VOT) should be allocated more credits and the commuters with high VOT should be charged more credits. For both cases at system optimum, we find that the equilibrium price of tradable credits increases with parking density and decreases with the total amount of tradable credits.

1. Introduction

1.1. Background and Objectives

The rise of travel demand and parking demand in urban areas results in severe traffic congestion for the morning commute in many cities. In the meantime, the limitation of parking space may increase the time and cost of searching for parking slots. These phenomena are especially prominent during morning peak hours, which has negative effects on both individual welfare and social welfare. According to the TomTom Traffic Index in 2021 (https://www.tomtom.com/en_gb/traffic-index/hong-kong-traffic/ (accessed on 29 September 2022)), the average traffic congestion measured by travel time during morning peak hours is 34% higher compared with the case under non-congested conditions. The empirical study conducted by the authors of [1] reveals that 30% of traffic congestion results from cruising for on-street parking spaces. To alleviate traffic congestion and parking pressures in downtown areas, it is important to introduce efficient travel modes into existing urban transportation networks and propose effective traffic management policies as well.

The rapid advancement of information and autonomous vehicle technologies presents new directions and opportunities for the morning commute. Enabled by vehicle automation, the AV commuters can be dropped off at their workplace and the vehicles self-drive to respective parking locations, which facilitates the parking process in the morning commute. Different from the traditional morning commute problems with conventional vehicles, AV commuters can focus on productive work during morning rush hours, without bearing the cost of searching for parking slots and driving. Moreover, the AVs can self-drive with a relatively small headway under certain adaptive control strategies, so the use of AVs may contribute to road capacity improvement [2]. In consequence, the decision-making of commuters and the resulting dynamic evolution of traffic congestion may be affected after autonomous vehicles are utilized for morning commute [3]. Therefore, we aim to explore commuters’ decision-making and the design of management policies for morning commutes with autonomous vehicles, in order to extend the theoretical basis for the development of future urban mobility.

We are motivated to examine dynamic equilibrium travel patterns and the design of a tradable credit scheme for a single-corridor network under a fully automated environment. We will also explore the impacts of the tradable credit scheme on system performance and individual welfare. Specifically, this paper aims to investigate the following questions:

(1)

How does parking availability affect the departure time choice of travelers and the temporal distribution of traffic congestion?

(2)

How should we design the tradable credit scheme to facilitate congestion management in cases with homogeneous commuters and the case with heterogeneous commuters, respectively? What are the joint effects of parking availability and a tradable credit scheme on individual welfare and system performance?

1.2. Literature Review

The vast majority of studies on morning commute problems have been focused on commuters’ decision-making and its impacts on traffic congestion by formulating bottleneck models. The original bottleneck model proposed in [4] examines the dynamic evolution of traffic congestion during morning peak hours on a single highway connecting a residential area and a workplace. By extending Vickrey’s bottleneck model, researchers conduct further investigations of multi-modal travel patterns (e.g., [5]), simultaneous departure time and route choices (e.g., [6,7,8]), and user heterogeneity (e.g., [9]) in morning commute problems.

The relevant literature has been further extended to investigate travelers’ decision-making in morning commute problems with autonomous vehicles and the resulted effects on system performance. Van den Berg and Verhoef [3] investigated the welfare effects of autonomous cars using bottleneck model by incorporating the increase in bottleneck capacity, the value-of-time (VOT) reduction for autonomous vehicle commuters and the heterogeneity of VOT enabled by AV technologies. Zhang et al. [10] explored both the short-run and long-run effects of the changes in VOT for AV users on travel patterns. Lamotte et al. [11] integrated the morning commute problem with reservation-based car-sharing system using autonomous vehicles. In their work, the autonomous vehicle users can avoid travel delays by choosing an appropriate departure time slot. Additionally, the demand for conventional vehicles and autonomous vehicles is determined endogenously. Please refer to [12,13] for a comprehensive literature review on the development of bottleneck model.

Enabled by self-driving technologies, autonomous vehicles can self-drive and self-park without travelers in the vehicle. Thus, with autonomous vehicles, commuters can benefit from travel time reduction and convenience for parking, which may help increase travelers’ utility during peak hours. Liu [14] modeled the commuters’ simultaneous decisions on departure time and parking location under a fully automated environment. A location-based parking pricing scheme is developed in [14] to eliminate the queuing delay. Considering the travel process and decision-making for integrated morning-evening commute, Zhang et al. [15] built a bottleneck equilibrium model to investigate the departure time choices and parking choices of commuters. Zhang et al. [15] proposed an optimal parking supply strategy that aims to minimize the total system cost. In a mixed-traffic environment with conventional vehicles and autonomous vehicles, Nourinejad and Amirgholy [16] investigated the parking choices of morning commuters by characterizing the differences in parking behaviors and schedule delay preferences between AV users and CV users. To manage traffic congestion in the morning commute, they developed two parking pricing schemes in order to incentivize commuters to change departure time choices. Tian et al. [17] introduced the parking space constraint into the morning commute problem in mixed-traffic environments where autonomous vehicles are for shared use. Su and Wang [18] explored the parking prioritization of commuters and the equilibrium travel patterns in morning commute with three types of parking options: parking at home, parking at the workplace, and parking at shared parking slots owned privately.

Various travel demand management instruments are developed to manage congestion during peak hours in the presence of autonomous vehicles, such as congestion pricing (e.g., [19]) and parking pricing strategies (e.g., [16]). As alternatives to congestion pricing, tradable credit schemes are designed to manage traffic congestion and improve social welfare. In the meantime, the impacts of heterogeneity in the value of time are incorporated in modeling in many works. Assuming that commuters must arrive at the workplace by work start time, Xiao et al. [20] investigated how to optimally design tradable credit schemes for a morning commute with identical commuters in value of time and with non-identical commuters. Tian et al. [21] modeled the departure time choices and mode choices of commuters with a heterogeneous and continuous value of time. Liu et al. [22] proposed tradable parking permit schemes to facilitate parking reservation for the case with identical commuters and the case with non-identical commuters, respectively. By incorporating transaction cost and its asymmetric allocation between buyers and sellers, Fan et al. [23] developed an optimal tradable credit scheme for cases of homogeneous commuters and heterogeneous commuters, respectively. Miralinaghi et al. [24] studied how a tradable credit scheme affects traffic congestion when commuters are heterogeneous in value of time and schedule delay preferences. Additionally, they assumed commuters are loss-averse towards buying credits and investigated the effects of loss aversion behaviors on the credit price at equilibrium. Based on a rewarding mechanism, Nie and Yin [25] designed a tradable credit scheme under which commuters will be rewarded credits if they choose to travel on uncongested routes or travel during off-peak periods. Nie [26] developed tradable credit schemes combined with a single-step toll for morning commutes under different travel behaviors at the discontinuity points of the departure curves. Similar to [25], commuters will be rewarded with credits if they choose to travel during off-peak periods. Bao et al. [27] discussed the existence of uniqueness of equilibrium solution for morning commute under a tradable credit scheme. Xiao et al. [28] proposed differentiated parking permits and undifferentiated parking permits to manage parking and congestion in morning commutes where three travel options including transit, solo driving, and carpooling are provided.

1.3. Contributions

In this paper, we aim to investigate dynamic equilibrium travel patterns for a single-corridor network under a fully automated environment. By extending the classic bottleneck model, we formulate joint decisions on departure time and parking location of morning commuters. Furthermore, to manage traffic congestion and improve social welfare, we propose a tradable credit scheme and integrate it with the decision-making of AV commuters. The focus of our work is to examine the joint effects of parking availability and tradable credits on equilibrium patterns and welfare. Considering commuters’ preference towards the value of time, we consider the case with homogeneous commuters and the case with heterogeneous commuters. For the case with homogeneous commuters, we derive the conditions on the tradable credit scheme to ensure the existence of an equilibrium state. With the tradable credit scheme, we find that system performance measured by system-wide travel costs can be decreased. Additionally, it is possible to improve system performance by appropriately adjusting the rate of tradable credit charge rate by the government. We further explore the optimal design of the tradable credit scheme to eliminate queuing delay. For the case with heterogeneous commuters, we characterize commuters’ preferences using a continuous distribution of the value of time. In this case, we also derive the optimal tradable credit scheme to achieve system optimum. We analytically show that the individual welfare measured by both generalized travel time and generalized travel cost can be improved. To ensure social equity under the proposed tradable credit scheme, we develop an initial distribution strategy to determine how the credits should be allocated among different users such that the monetary cost reduction is identical to each individual commuter. Numerical analysis is conducted to show (1) the effects of tradable credits and parking density on individual welfare and system performance; (2) the influence of the total number of credits and parking density on the equilibrium price of credits; and (3) the change of the initial distribution scheme with respect to the parking density and commuters’ value of time.

The remainder of this paper is structured as follows. In Section 2, we review the bottleneck equilibrium without considering tradable credits. Here, we study the departure time choices and parking choices of commuters in morning commute where only autonomous vehicles are used. Section 3 introduces tradable credits into morning commute and further examines decision-making under the assumption of homogeneous commuters. The optimal tradable credit scheme is derived at equilibrium. Furthermore, we investigate the optimal design of tradable credits for morning commutes with heterogeneous commuters in Section 4. Section 5 concludes this study.

2. Review of the Bottleneck Model without Tradable Credits

In this section, we study the morning commute problem under a fully automated environment without introducing a tradable credit scheme. To make it consistent with the remaining sections that solve equilibrium models with tradable credits, we review the bottleneck model with autonomous vehicle users considering commuters’ parking choices without tradable credits. We examine the joint decision-making of commuters on departure time choices and parking location choices by extending the classic bottleneck model [4]. Our model is developed upon the assumption that autonomous vehicles are owned privately and late arrivals are not allowed.

Consider a corridor network containing a single bottleneck with a capacity of s, connecting a residential area and a workplace located at CBD. The network is illustrated in Figure 1. The notations in this work are listed in

Table 1. Notations.

Notation	Description
Parameters
t	Departure time;
N	Total demand;
n	The order of commuters when ranked in an increasing order of value of time $\alpha \left(n\right)$;
$t^{\ast }$	Desired arrival time at destination;
$\alpha$	Value of time;
$\beta$	Unit cost of early schedule delay;
$\lambda$	Unit cost of AV self-driving time after dropping off commuters at the workplace;
$\omega$	Travel time per distance unit after dropping off commuters at the workplace;
s	The capacity of bottleneck;
$t_e$	The end time of peak-hour congestion, i.e., the latest departure time from home during peak hours;
$\rho$	Market price of tradable credits;
b	The rate of tradable credit charge rate;
K	The total amount of tradable credits;
Functions
$x\left(t\right)$	The distance between the workplace and parking slot for commuters who depart from home at time t;
$m\left(x\right)$	The distribution density of parking slots (i.e., parking density) at location x;
$T\left(t\right)$	Travel time (i.e., queuing time) for commuters departing from home at time t;
$D\left(t\right)$	Queue length for commuters departing from home at time t;
$r\left(t\right)$	Departure rate for commuters departing from home at time t;
$c\left(t\right)$	Travel time cost for commuters departing from home at time t;
$k\left(t\right)$	The credit charge rate for commuters departing from home at time t.

. During morning peak hours, there are N commuters traveling from the residential area to the workplace along this corridor. The free flow travel time on the corridor is assumed to be 0. Thus, the commuters arrive at the bottleneck once they depart from home. A queue develops when the departure rate from home or the arrival rate at the bottleneck exceeds the bottleneck capacity s. We assume the commuters are required to arrive at the workplace no later than the desired arrival time, i.e., the work start time $t^{\ast }$. Let $T\left(t\right)$ denote the travel time experienced by commuters who depart from home at time t and their early schedule delay is given as $t^{\ast }-t-T\left(t\right)$.

After passing the bottleneck, the autonomous vehicles will drop off the commuters and self-drive to the nearest parking slots. Parking slots are distributed along this corridor as depicted in Figure 1. The cost associated with parking depends on the distance between the workplace and the parking location. Let $x\left(t\right)$ denote the nearest parking location for commuters who depart from home at time t and $\omega$ denote the driving time per travel distance during parking. After dropping off the commuters, the autonomous vehicles will experience a travel time of $\omega x\left(t\right)$ for self-driving from the workplace to the selected parking slot.

The commuters choose departure times from home t and the corresponding nearest parking spots at $x\left(t\right)$ to minimize their individual generalized travel costs that are composed of travel time cost, schedule delay cost, and the cost associated with parking. Under the fully automated vehicle environment, we define the generalized travel cost of commuters departing from home at time t as:

$$\begin{array}{c}\hfill c\left(t\right)=\alpha T\left(t\right)+\beta (t^{\ast }-t-T\left(t\right))+\lambda \omega x\left(t\right),\end{array}$$

(1)

where $\alpha$ is the value of traveling time, $\beta$ represents the unit early schedule delay cost, and $\lambda$ is unit cost of AV self-driving time after dropping off commuters at the workplace. We assume $\beta <\alpha$ to provide a necessary condition to ensure the existence of a bottleneck equilibrium [29]. The time per unit of driving distance $\omega$ can be interpreted as the inverse of travel speed. Please note that the model setting of linearly distributed parking slots is the same as in [14,30]. However, the focus of our work is to investigate the joint effects of tradable credits and parking density on the equilibrium in morning commutes.

It is assumed that the parking slots are uniformly distributed at workplace. Let m represent the density of parking slots. The distance between destination and parking slot for commuters who depart from home at time t is $x\left(t\right)=\frac{\left(T\right(t)+t)s}{m}$. By substituting it into Equation (1) and taking the first-order derivative of $c\left(t\right)$ with respect to t, we have:

$$\begin{array}{c}\hfill \dot{c}\left(t\right)=\alpha \dot{T}\left(t\right)+\beta (-1-\dot{T}\left(t\right))+\frac{\lambda \omega s}{m}(\dot{T}\left(t\right)+1).\end{array}$$

(2)

At equilibrium, no commuters can further reduce their individual generalized travel costs by changing departure time t, i.e., $\dot{c}\left(t\right)=0$. Therefore, we can obtain the changing rate of queuing time $\dot{T}\left(t\right)=\frac{\beta -\lambda \omega s/m}{\alpha -(\beta -\lambda \omega s/m)}$.

Let $D\left(t\right)$ denote the cumulative number of departures from home. The relationship between travel time $T\left(t\right)$ and cumulative number of departures is:

$$\begin{array}{c}\hfill T\left(t\right)=\frac{D\left(t\right)}{s}-t.\end{array}$$

Let $r\left(t\right)$ denote the departure rate from home for commuters who depart from home at t, thus,

$$\begin{array}{ccc}\hfill r\left(t\right)& =& \dot{D}\left(t\right),\hfill \\ \hfill & =& s(1+\dot{T}\left(t\right)),\hfill \\ \hfill & =& \frac{\alpha s}{\alpha -(\beta -\lambda \omega s/m)}.\hfill \end{array}$$

(3)

When the departure rate from home exceeds the bottleneck capacity, a queue will form at the bottleneck and commuters experience queuing time. Given $r\left(t\right)>s$, we have $\beta -\lambda \omega s/m>0$. Furthermore, the latest departure time from home during morning peak hours can be obtained:

$$\begin{array}{ccc}\hfill t_e& =& \frac{N}{r\left(t\right)},\hfill \\ \hfill & =& N\frac{\alpha -(\beta -\lambda \omega s/m)}{\alpha s}.\hfill \end{array}$$

(4)

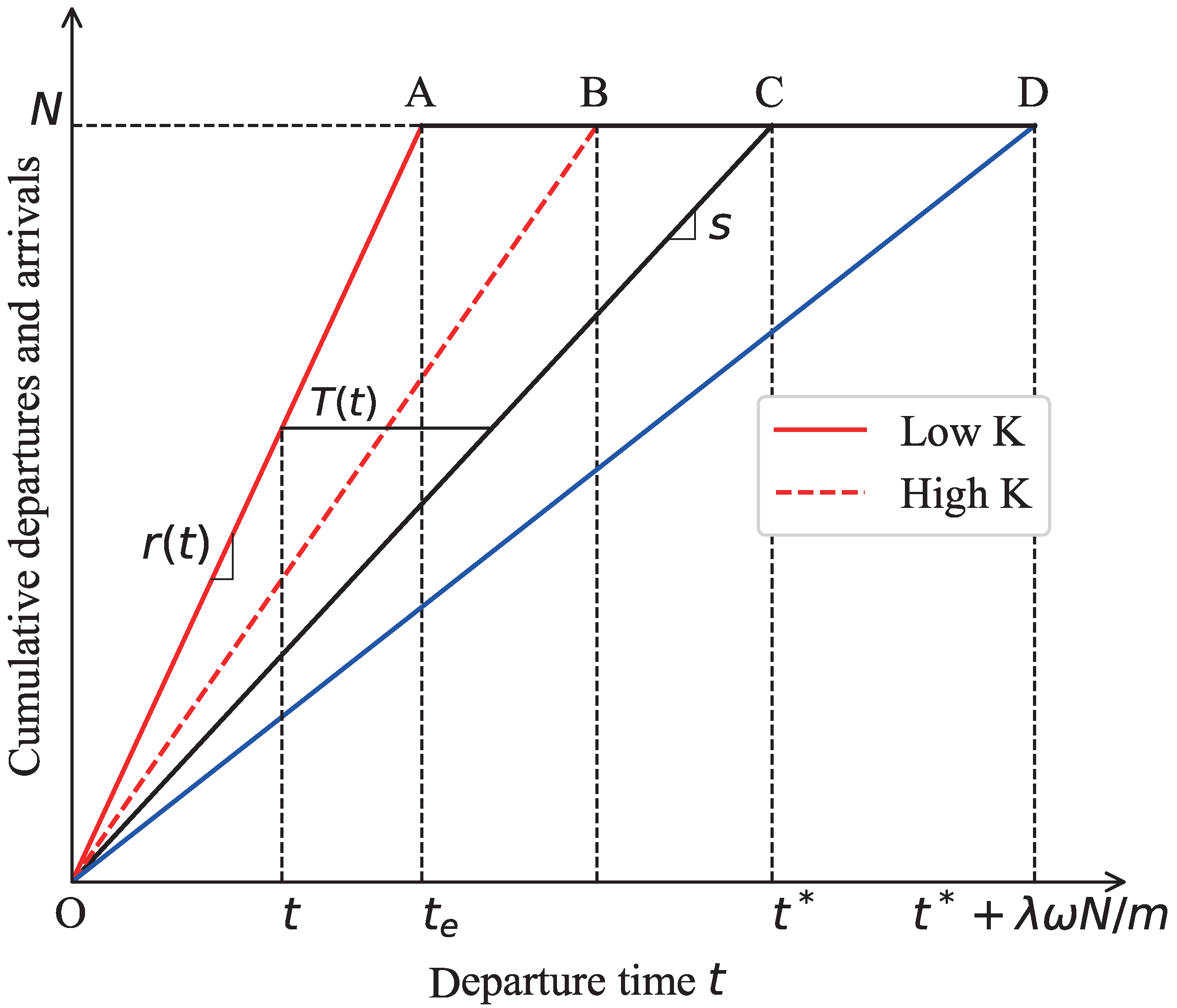
Equations (3) and (4) show that the equilibrium travel pattern is related to parking density m. Specifically, when the parking density m increases, the corresponding departure rate $r\left(t\right)$ grows up and the congestion period $[0,t_e]$ is shortened. The equilibrium travel pattern for a morning commute under a fully automated vehicle environment is shown in Figure 2. The solid red line represents the cumulative departures from home. The solid black line represents the cumulative arrivals at the workplace of AV users. The solid blue line is the cumulative arrival curve at parking slots.

At user equilibrium without tradable credits, the system-wide travel cost ($TC$) consists of three parts: total early schedule delay cost ($TS$), total cost of queuing time ($TQ$), and the cost associated with parking ($TP$), i.e., $TC=TS+TQ+TP$. According to the equilibrium pattern shown in Figure 2, we can further derive the above three cost components. Specifically,

$$\begin{array}{ccc}\hfill TS& =& \frac{\beta N^2}{2s},\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill TQ& =& \frac{N^2}{2s}(\beta -\frac{\lambda \omega s}{m}),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill TP& =& \frac{\lambda \omega N^2}{2m}.\hfill \end{array}$$

(7)

Combining Equations (5)–(7), we obtain the system wide-travel cost:

$$\begin{array}{c}\hfill TC=\frac{\beta N^2}{s}.\end{array}$$

(8)

Equations (5)–(7) show that the parking density affects both total cost of queuing time ($TQ$) and the cost associated with parking ($TP$). However, the system-wide travel cost (Equation (8)) will not be affected by m. When the parking density m increases, the total cost of queuing time $TQ$ increases and the cost associated with parking $TP$ decreases. The individual travel cost is $\beta N/s$, which is the same as the case with purely conventional vehicles.

3. Design of Tradable Credit Scheme Considering Homogeneous Commuters

To mitigate traffic congestion during the morning peak period, we further examine the design of a tradable credit scheme and study its impacts on commuters’ decision-making and congestion evolution. Following the same model setting in Section 2, we introduce a dynamic tradable credit scheme and integrate it with the morning commute problem in which all commuters are homogeneous with respect to the value of time. We will explore commuters’ decision-making under the proposed tradable credit scheme in Section 3.1 and analyze the design of tradable credits to maintain an equilibrium state in Section 3.2. Moreover, we evaluate system performance under the dynamic tradable credit scheme in Section 3.3. At last, we explore the optimal design of the tradable credit scheme to remove the queuing delay in Section 3.4.

3.1. Bottleneck Model under Dynamic Tradable Credit Scheme

We formulate commuters’ joint decisions on departure time and parking location choice under a dynamic tradable credit scheme. Suppose a dynamic tradable credit scheme has been implemented to manage the queuing delay on the corridor during morning peak hours. The dynamic tradable credit scheme can be described by $\left(k\right(t),K)$, where $k\left(t\right)$ is the time-varying credit charge rate and K is the total amount of tradable credits issued by the government. The government determines the tradable credit scheme $\left(k\right(t),K)$ and the distribution of the credits among commuters. As pointed out in [31], the decision-making of commuters does not rely on the initial distribution of tradable credits.

We assume the credit charge rate $k\left(t\right)$ is a linear function of departure time t and the amount of credits charged from the first departure is 0. Thus,

$$\begin{array}{c}\hfill k\left(t\right)=bt.\end{array}$$

(9)

As $k\left(t\right)$ increases linearly with departure time t, the required amount of tradable credits increases dynamically. The commuters bear costs in tradable credits with a rate of $\rho$ per credit. Therefore, under the proposed tradable credit scheme, the generalized travel cost of a commuter is composed of four parts: travel time cost, schedule delay cost, the cost associated with parking, and the cost of tradable credits. For commuters departing from home at time t, the generalized travel cost is defined as follows:

$$\begin{array}{c}\hfill c\left(t\right)=\alpha T\left(t\right)+\beta (t^{\ast }-t-T\left(t\right))+\lambda \omega x\left(t\right)+\rho k\left(t\right),\end{array}$$

(10)

where the first term on the right-hand side represents travel time cost, the second term is the schedule delay cost for early arrivals, the third term is the cost incurred during the self-parking process, and the last term is the cost of tradable credits. Different from [20], we model the joint decisions on commuters’ parking location choices in addition to departure time choices under a fully automated environment where the parking decisions affect the individual travel cost without changing schedule delay. Commuters make decisions on departure times to minimize individual generalized travel costs. When the equilibrium state arrives, all commuters have the same and lowest generalized travel cost. Namely, $\dot{c}\left(t\right)=0$. Combining Equation (10) and Equation (9), we can obtain:

$$\begin{array}{ccc}\hfill \dot{c}\left(t\right)& =& \alpha \dot{T}\left(t\right)+\beta (-1-\dot{T}\left(t\right))+\frac{\lambda \omega s}{m}(\dot{T}\left(t\right)+1)+b\rho ,\hfill \\ & =& 0,\hfill \end{array}$$

which gives the changing rate of queuing time $T\left(t\right)$:

$$\begin{array}{c}\hfill \dot{T}\left(t\right)=\frac{(\beta -b\rho )m-\lambda \omega s}{(\alpha -\beta )m+\lambda \omega s}.\end{array}$$

(11)

Let $D\left(t\right)$ denote the cumulative departures at time t, and $D\left(t\right)$ can be expressed as:

$$\begin{array}{c}\hfill D\left(t\right)=\left(T\right(t)+t)s.\end{array}$$

(12)

With Equation (11) and Equation (12), we obtain the expression of departure rate $r\left(t\right)$:

$$\begin{array}{ccc}\hfill r\left(t\right)& =& (\dot{T}\left(t\right)+1)s,\hfill \\ \hfill & =& \frac{(\alpha -b\rho )m}{(\alpha -\beta )m+\lambda \omega s}s,\hfill \end{array}$$

(13)

where the derived departure rate is a constant given the linear form of $k\left(t\right)$ (Equation (9)). The latest departure time $t_e$ can be derived based on the relation $t_e=\frac{N}{r\left(t\right)}$. Thus, given the departure rate $r\left(t\right)$ in Equation (13), we have:

$$\begin{array}{c}\hfill t_e=\frac{(\alpha -\beta )m+\lambda \omega s}{(\alpha -b\rho )m}\frac{N}{s}.\end{array}$$

(14)

The departure rate and the latest departure time describe the equilibrium travel pattern. After introducing tradable credit scheme, the departure rate decreases and the latest departure time is shifted later. It shows that the introduction of tradable credit scheme can help to alleviate traffic congestion. The impacts of tradable credits at equilibrium on traffic congestion are also verified based on the total queuing time in Equation (18).

The total amount of tradable credits issued and distributed by government K is fixed and constant. To manage the peak-hour congestion, the credits are charged from commuters and used for morning commute trips during the congestion period $[0,t_e]$. The total amount of tradable credits K can be expressed as below:

$$\begin{array}{c}\hfill K={\int }_0^{t_e}r\left(t\right)k\left(t\right)\mathrm{d}t=N\frac{b{t}_e}{2},\end{array}$$

so the latest departure time can be expressed in terms of the total amount of tradable credits:

$$\begin{array}{c}\hfill t_e=\frac{2K}{bN}.\end{array}$$

(15)

By substituting $r\left(t\right)=N/t_e$ into Equation (15), we can obtain the relationship between departure rate and total amount of tradable credits:

$$\begin{array}{c}\hfill r\left(t\right)=\frac{b{N}^2}{2K}.\end{array}$$

(16)

Compared with the case without tradable credit schemes, we find that the equilibrium travel pattern described in Equations (15) and (16) is independent of the parking density m. Furthermore, the equilibrium travel pattern is affected by the total amount of tradable credits K and the charging rate b. In particular, given a fixed b, the departure rate decreases and the latest departure time from home is shifted later when K takes a higher value. Therefore, distributing more tradable credits to commuters can help to alleviate traffic congestion from the perspective of policymakers. As depicted in Figure 3, we plot the departure curves for the cases with a high value of K and a low value of case, respectively.

3.2. Analysis of Tradable Credit Scheme at UE

Next, we proceed to analyze the setting of tradable credit scheme and the market price of tradable credits at equilibrium in order to provide policy sights for congestion management. By substituting Equation (16) into Equation (13), we can achieve the equilibrium price of tradable credits, i.e.,

$$\begin{array}{c}\hfill \rho =\frac{\alpha }{b}-\frac{N^2(\alpha -\beta )}{2Ks}-\frac{N^2\lambda \omega }{2Km}.\end{array}$$

(17)

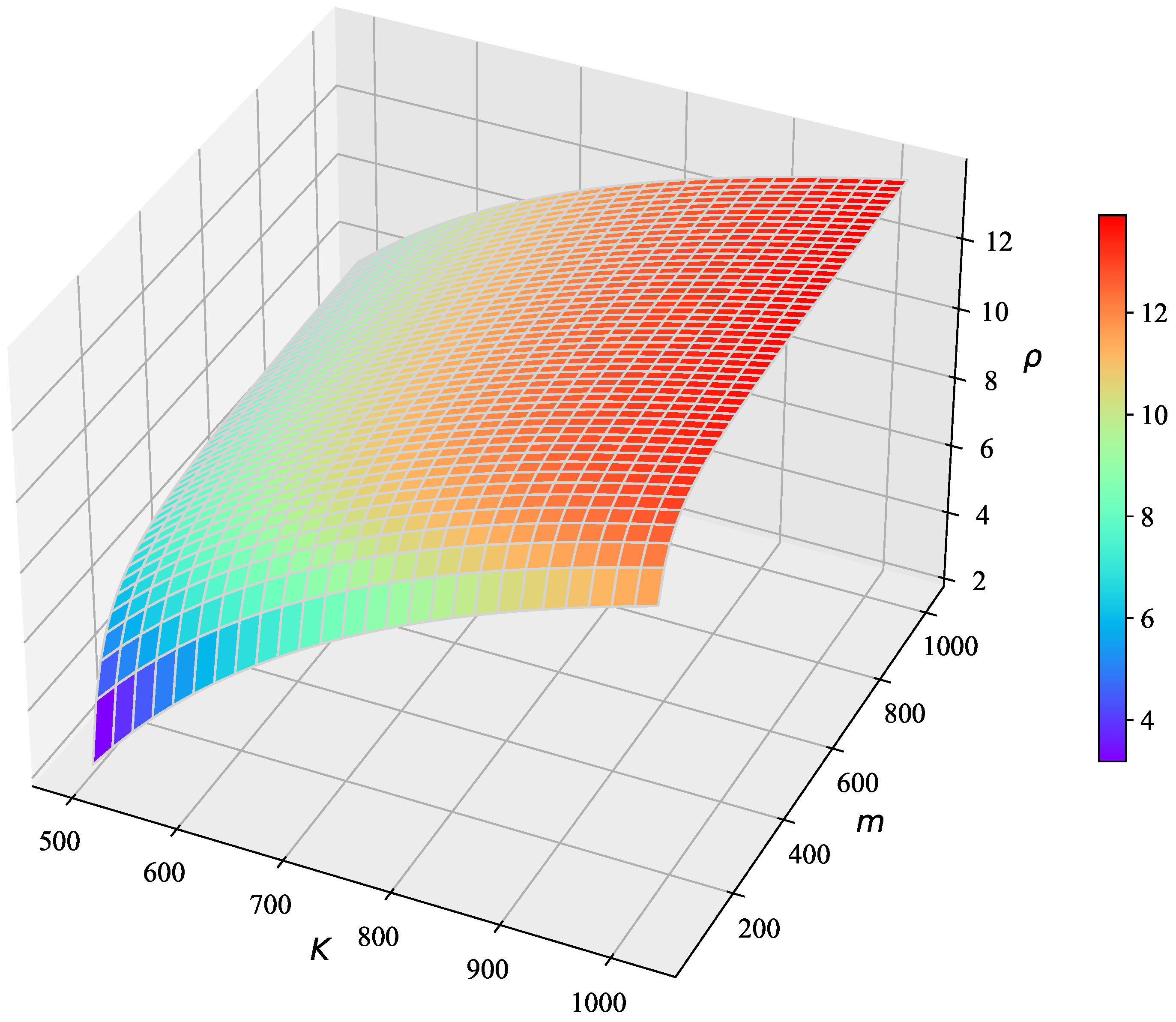
Equation (17) reflects that the market price of tradable credits is lower than that in the case with purely conventional vehicles at equilibrium. In addition, the price of tradable credits increases with both the total amount K and the parking density m. When the total amount of tradable credits issued and distributed by the government K is high, the departure rate $r\left(t\right)$ in Equation (16) is decreased. It shows that commuters tend to postpone their departure times to reduce schedule delay costs. The demand of commuters who choose departure times close to the desired arrival time is larger when K is higher, which results in a higher price $\rho$. The impacts of parking density m on the price of tradable credits can be interpreted in a similar way. When the parking density is high, the potential that commuters can secure parking slots close to the workplace at desired arrival time is large. In this case, the commuters are incentivized to depart from home at times close to $t^{\ast }$ in order to park their vehicles near the workplace. Thus, the market price of tradable credits rises when the parking density is high.

We further illustrate the joint effects of the total amount K and the parking density m on the equilibrium price of tradable credit numerically. The parameters are set as follows: the value of time $\alpha =10$ USD/hour, unit cost of early schedule delay $\beta =7$ USD/hour, the charging rate $b=5$ credits/hour, the self-driving time per parking distance unit $\omega =0.025$ hour/km, and the total travel demand $N=2000$ persons. We vary K in the range of $[500,1000]$ and m in the range of $[\lambda \omega s/\beta ,1000]$. The change of equilibrium price of tradable credit with respect to K and m is shown in Figure 4.

We further examine the conditions on the design of a tradable credit scheme in order to maintain the equilibrium in the morning commute problem. First, consider that the departure rate is higher than the bottleneck capacity during the morning peak, i.e., $r\left(t\right)>s$. We obtain the upper bound on $K/b$ by substituting $r\left(t\right)>s$ into Equation (15). Second, the equilibrium price of tradable credits in Equation (17) is required to be positive, which yields the lower bound on $K/b$. After combining the above two conditions, the range of $K/b$ at user equilibrium is presented in Proposition 1.

Proposition 1 

(The range of $K/b$ at UE). For the morning commute problem under a fully automated vehicle environment, the ratio of the total amount of tradable credits to the rate of credit charge rate $K/b$ varies in the following range: $\frac{K}{b}\in (\frac{N^2}{2s}\frac{\alpha -(\beta -\lambda \omega s/m)}{\alpha },\frac{N^2}{2s})$.

Proposition 1 describes the conditions to ensure the existence of an equilibrium state given a fixed parking density. $K/b$ measures the relative magnitude of the total amount of tradable credits to the rate of credit charge rate. When K is high or b is low, the ratio $K/b$ will exceed the upper bound. In this case, the departure rate from home $r\left(t\right)$ will be lower than the bottleneck capacity, which deviates from our assumption of peak-hour congestion for morning commute problems. When K is low or b is high, the ratio $K/b$ will be lower than the derived lower bound, i.e., $K/b<\frac{K}{b}\in \frac{N^2}{2s}\frac{\alpha -(\beta -\lambda \omega s/m)}{\alpha }$. In this case, the price of tradable credit is negative. It indicates that tradable credits are not required for morning commutes anymore, which is not realistic based on our model setting. Therefore, to obtain equilibrium, the tradable credit scheme determined by the government should satisfy the conditions included in Proposition 1.

3.3. Analysis of System Performance at UE

In this part, we aim to examine the impacts of the tradable credit scheme on system performance for morning commutes under a fully automated vehicle environment. We consider three system performance measures including total queuing time, system-wide travel cost, and efficiency of the tradable credit scheme. In the following, we will evaluate each of them to show the impacts of tradable credits at equilibrium.

Let $T{Q}^1$ denote the total queuing delay experienced by all commuters under the tradable credit scheme $\left(k\right(t),K)$. Based on Figure 3, $T{Q}^1$ corresponds to the area between the cumulative departure curve and the curve for cumulative arrivals at the workplace, i.e., the area of triangle $OAC$. Thus,

$$\begin{array}{c}\hfill T{Q}^1=\alpha {\int }_0^{t_e}T\left(t\right)\mathrm{d}\left(t\right)=\alpha (t^{\ast }-t_e)\frac{N}{2}.\end{array}$$

(18)

By substituting Equation (15), the expression of total queuing time can be derived as below.

$$\begin{array}{c}\hfill T{Q}^1=\frac{\alpha N^2}{2s}-\frac{\alpha K}{b},\end{array}$$

(19)

which reveals that the total queuing time decreases with both the total amount of tradable credit K and the rate of tradable credit charge rate b. In the meantime, the total schedule delay cost and the total cost associated with parking remain the same as the case without tradable credits in Section 2.

Let $T{C}^1$ denote the system-wide travel cost that is the sum of the total queuing cost, total schedule delay cost, and the total parking cost when a tradable credit scheme is implemented.

$$\begin{array}{c}\hfill T{C}^1=\frac{\alpha N^2}{2s}+\frac{\beta N^2}{2s}+\frac{\lambda \omega N^2}{2m}-\frac{\alpha K}{b},\end{array}$$

(20)

which is lower compared with the system-wide travel cost before introducing tradable credit schemes.

The system-wide travel cost for morning commute with autonomous vehicles relies on the parking density. Based on Equation (20), the system-wide travel cost can be reduced by providing more parking space for morning commute. Additionally, the tradable credit scheme also help to decrease the system-wide travel cost.

We further define the efficiency of the tradable credit scheme, denoted by $\theta$, as the proportion that the system-wide travel cost can be reduced compared with the case without tradable credits.

$$\begin{array}{c}\hfill \theta =\frac{1}{2}-\frac{\lambda \omega s}{2m\beta }-\frac{\alpha }{2\beta }+\frac{\alpha sK}{b\beta N^2}.\end{array}$$

(21)

The level of $\theta$ indicates the effects of the proposed tradable credit scheme on system performance measured by system-wide travel cost at equilibrium. It can be easily observed that $\theta$ decreases with the rate of tradable credit charge rate b. Given a fixed level of total amount of tradable credits K, it is possible to improve system performance through appropriately adjusting the rate of tradable credit charge rate b by the government or policymakers. In the next section, we will investigate the optimal design of the tradable credit scheme, which is described by optimal values of b, $\rho$, and K.

3.4. The Optimal Credit Charging Scheme

We solve the system optimum (SO) in this section to explore the optimal design of a tradable credit scheme for the morning commute problem with homogeneous commuters. The SO state is attained when the dynamic tradable credit scheme $(k^{\ast }\left(t\right),K^{\ast })$ completely eliminates queuing delay. In this situation, the following conditions should be satisfied: (1) the queueing time experienced by commuter departing from home at time t is 0, i.e., $T\left(t\right)=0$; (2) the departure rate from home equals to the bottleneck capacity, i.e., $r\left(t\right)=s$. At SO, the generalized cost function for commuters who depart from home at time t becomes $c\left(t\right)=\beta (t^{\ast }-t)+\lambda \omega x\left(t\right)+\rho k\left(t\right)$. We can thus derive the optimal charging rate $b^{\ast }$ by setting $\dot{c}\left(t\right)=0$:

$$\begin{array}{c}\hfill b^{\ast }=\frac{\beta m-\lambda \omega s}{{\rho }^{\ast }m}.\end{array}$$

(22)

The optimal amount of tradable credits $K^{\ast }$ is determined by $K^{\ast }={\int }_0^{t_e}{b}^{\ast }st\mathrm{d}t$ where the latest departure time $t_e=\frac{N}{s}$. That is,

$$\begin{array}{ccc}\hfill K^{\ast }& =& \frac{\beta m-\lambda \omega s}{{\rho }^{\ast }m}\frac{N^2}{2s}.\hfill \end{array}$$

(23)

The price of tradable credits at SO is obtained:

$$\begin{array}{c}\hfill {\rho }^{\ast }=\frac{\beta m-\lambda \omega s}{K^{\ast }m}\frac{N^2}{2s},\end{array}$$

(24)

which increases with parking density m and decreases with the total amount of credits $K^{\ast }$.

By substituting Equation (24) into Equation (22), we obtain the explicit form of optimal rate of credit charge rate $b^{\ast }$ here:

$$\begin{array}{c}\hfill b^{\ast }=\frac{2s{K}^{\ast }}{N^2},\end{array}$$

(25)

so the credit charge rate for commuters departing from home at time t is:

$$\begin{array}{c}\hfill k^{\ast }\left(t\right)=\frac{2s{K}^{\ast }}{N^2}t.\end{array}$$

(26)

Under the optimal tradable credit scheme, the system-wide travel cost can be derived:

$$\begin{array}{c}\hfill T{C}^{\ast }=\frac{\beta N^2}{2s}+\frac{\lambda \omega N^2}{2m},\end{array}$$

where the first term on the right-hand side is the total schedule delay cost and the second term is the total parking cost. At SO, the system-wide travel cost does not include the cost of queuing as the commuters depart from home at the rate of s.

We can measure efficiency of the optimal charging scheme using ${\theta }^{\ast }$:

$$\begin{array}{c}\hfill {\theta }^{\ast }=\frac{1}{2}-\frac{\lambda \omega s}{2m\beta },\end{array}$$

where ${\theta }^{\ast }$ does not vary with the total amount of tradable credits, which is different from the case at UE in Section 3.3. In the meantime, the parking density at the city center affects the efficiency of the optimal tradable credit scheme. When the parking density m approaches infinity, ${\theta }^{\ast }$ is close to 0.5. That is, with sufficient parking space, the introduction of the optimal tradable credit scheme $(k^{\ast }\left(t\right),K^{\ast })$ has the potential to reduce the system-wide travel cost by 50%. The change of ${\theta }^{\ast }$ with respect to parking density m is illustrated in Figure 5. Based on the efficiency of the optimal charging scheme, we can provide insights into managing morning commutes under a fully automated environment by regulating the parking provision.

4. Design of a Tradable Credit Scheme Considering Heterogeneous Commuters

In this section, we investigate the dynamic travel pattern and the optimal design of tradable credits for a morning commute with heterogeneous commuters. By adopting the assumption on heterogeneity presented in [20], we build our bottleneck equilibrium model for the morning commute problem with AV users and linearly distributed parking spaces in Section 4.1. Additionally, we further examine the optimal design of tradable credits in Section 4.2 to obtain the SO. Individual welfare analysis is conducted in Section 4.3 and the initial distribution of credits among commuters is provided in Section 4.4.

4.1. Bottleneck Equilibrium without Tradable Credits

We follow the model setting in [20] by adopting their assumption on heterogeneity in the value of time and early schedule delay preference. Specifically, we use a cumulative distribution function to describe $\alpha$: $F\left(\omega \right)=Pr(\alpha \le \omega )$. The commuters are ranked according to the decreasing order of their values of time. This model setting admits that commuters with a higher value of time prefer to depart from home at earlier time slots to save travel time costs. In this work, we consider the parking choices of AV commuters so we also incorporate the heterogeneity of the unit cost of AV self-driving time $\lambda$. Let nth denote the order of commuters’ value of time. For the nth commuter, the value of time, the unit cost of early schedule delay, and the unit cost of AV self-driving time after dropping off commuters at the workplace are denoted by $\alpha \left(n\right)$, $\beta \left(n\right)$, and $\lambda \left(n\right)$, respectively. Clearly, $n\in \{1,2,\cdots ,N\}$. Based on the aforementioned cumulative distribution, the value of time can be expressed by $\alpha \left(n\right)=F^{-1}(1-\frac{n}{N})$. For simplicity, we also assume a constant and fixed ratio of unit cost of early schedule delay to value of time for the nth commuter, i.e., $\eta =\frac{\beta \left(n\right)}{\alpha \left(n\right)}$ where $\eta \in (0,1)$. Additionally, the commuters with a high unit cost of early schedule delay prefer time slots close to $t^{\ast }$ to avoid high early schedule delay costs. Additionally, we impose the assumption that the ratio of unit cost of AV self-driving time to value of time is fixed and constant, i.e., $\phi =\frac{\lambda \left(n\right)}{\alpha \left(n\right)}$ with $\lambda \in (0,1)$.

Without tradable credits, the generalized travel cost for the nth commuter who departs from home at t is:

$$\begin{array}{c}\hfill c(n,t)=\alpha \left(n\right)T\left(t\right)+\beta \left(n\right)(t^{\ast }-t-T\left(t\right))+\lambda \left(n\right)\omega x\left(t\right),\end{array}$$

(27)

where the first term on the right-hand side represents the travel time cost of the nth commuter, the second term is her/his early schedule delay cost, and the last term is the cost associated with parking. $x\left(t\right)$ represents the travel distance from the destination of commuter to the parking slot and $x\left(t\right)=\left(T\right(t)+t)s/m$.

We further explore the equilibrium based on generalized travel cost in time units. In this paper, the generalized travel cost in time units is referred to as generalized travel time, which is the equivalent monetary travel cost measured in time units. Dividing Equation (27) by $\alpha \left(n\right)$, we can transfer the cost $c(n,t)$ into equivalent generalized travel time for the nth commuter.

$$\begin{array}{c}\hfill \widehat{c}(n,t)=T\left(t\right)+\eta (t^{\ast }-t-T\left(t\right))+\frac{\phi \omega s}{m}(T\left(t\right)+t),\end{array}$$

(28)

where we have converted the bottleneck cost and cost of travel time during parking to time units.

The definition of user equilibrium based on generalized travel cost in time units is similar to that based on monetary cost. Specifically, no one can reduce generalized travel time by unilaterally altering departure time at equilibrium with heterogeneous commuters. In this case, all commuters experience the same level of generalized travel time, i.e., $\dot{\widehat{c}}(n,t)=0$, which gives $\dot{T}\left(t\right)=\frac{\eta -\phi \omega s/m}{1-(\eta -\phi \omega s/m)}$. To sustain the peak-hour congestion during the morning peak, the rate of queuing time $\dot{T}\left(t\right)$ should be positive, which requires $0<\eta -\phi \omega s/m<1$. The relation $\eta -\phi \omega s/m<1$ holds all the time because $\eta <1$. Therefore, the condition $\eta -\phi \omega s/m>0$ should be imposed to ensure the existence of peak-hour congestion, which is a prerequisite in morning commutes. This condition is utilized in the analysis of the remaining sections.

Now we discuss the departure order of the heterogeneous commuters at UE. The departure order depends on the magnitude of $r\left(t\right)$ or $\dot{T}\left(t\right)$, which are identical to all commuters $n\in \{1,2,\cdots ,N\}$. It indicates the commuters are indifferent to departure times at equilibrium so they choose departure times randomly during the morning peak period.

Next, we proceed to investigate the equilibrium travel pattern and individual travel cost. Since the first commuter during morning peak does not experience queuing delay, i.e., $T\left(0\right)=0$, the queuing time function for commuters departing at time t can be expressed as below:

$$\begin{array}{c}\hfill T\left(t\right)=\frac{\eta -\phi \omega s/m}{1-(\eta -\phi \omega s/m)}t.\end{array}$$

(29)

Let ${\eta }^{\prime }=\eta -\phi \omega s/m$. Thus, the queuing time can be expressed by $T\left(t\right)=\frac{{\eta }^{\prime }}{1-{\eta }^{\prime }}t$ based on Equation (29). At UE, two conditions should be satisfied: (1) all commuters can arrive at the workplace by time $t^{\ast }$, i.e., $t^{\ast }=N/s$; and (2) the commuter departing at the end of congestion period experiences a travel time $t^{\ast }-t_e$, i.e., $T\left(t_e\right)=t^{\ast }-t_e=\frac{{\eta }^{\prime }}{1-{\eta }^{\prime }}{t}_e$. Combining these two conditions, we can obtain the latest departure time and departure rate:

$$\begin{array}{ccc}\hfill t_e& =& \frac{N}{s}(1-{\eta }^{\prime }),\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill r\left(t\right)& =& \frac{s}{1-{\eta }^{\prime }},\hfill \end{array}$$

(31)

which describe the equilibrium travel pattern for morning commute with heterogeneous commuters before introducing tradable credits. To ensure the existence of peak-hour congestion, it is required that the departure rate should be higher than the bottleneck capacity. Therefore, the imposed condition $\eta -\phi \omega s/m>0$ is actually consistent with Assumption 1 in [14].

At equilibrium, the commuters experience different levels of generalized travel cost at equilibrium, depending on their values of time. For the nth commuter, the generalized travel cost is given by:

$$\begin{array}{c}\hfill c\left(n\right)=\eta \alpha \left(n\right)\frac{N}{s},\end{array}$$

(32)

which can be transferred to equivalent generalized travel cost in time units by dividing $c\left(n\right)$ with $\alpha \left(n\right)$:

$$\begin{array}{c}\hfill \widehat{c}=\eta \frac{N}{s}.\end{array}$$

(33)

The generalized travel time is identical for each commuter at UE, whereas the generalized travel cost depends on value of time $\alpha \left(n\right)$. Similar to the case with homogeneous commuters, parking density only affects the equilibrium travel pattern. In the meantime, the generalized travel cost and the generalized travel time do not vary with parking density.

4.2. The Optimal Tradable Credit Scheme

After implementing a tradable credit scheme in morning commute problems with heterogeneous commuters, the generalized travel cost of commuters includes the cost in tradable credits in addition to queuing time cost, schedule delay cost, and cost for parking. In this part, we aim to study the optimal tradable credit scheme in order to achieve system optimum. At SO, no commuters will experience queuing time. Under these conditions, the generalized travel cost for the nth commuter becomes:

$$\begin{array}{c}\hfill c(n,t)=\eta \alpha \left(n\right)(t^{\ast }-t)+\frac{\phi \omega s}{m}\alpha \left(n\right)t+k^{\ast }\left(t\right)\rho .\end{array}$$

(34)

In addition to the elimination of queuing delay, the individual generalized travel cost should also be minimized at SO. Namely, $\frac{\partial c(n,t)}{\partial t}=0$, which gives:

$$\begin{array}{c}\hfill {\dot{k}}^{\ast }\left(t\right)=(\frac{\eta }{\rho }-\frac{\phi \omega s}{m\rho })\alpha \left(n\right).\end{array}$$

(35)

Because the condition $\eta -\phi \omega s/m>0$ holds, the credit charge rate ${\dot{k}}^{\ast }\left(t\right)$ should be an increasing function in terms of departure time.

Next, we discuss the departure order of heterogeneous commuters at SO by adopting similar procedures as in [20]. Given the condition $\eta -\phi \omega s/m>0$, we find that the commuters with higher values of time depart at times closer to the desired arrival time. Therefore, we can formulate the departure order as a linear function of departure time t as follows.

$$\begin{array}{c}\hfill n\left(t\right)=s(t^{\ast }-t),0\le t\le t^{\ast }.\end{array}$$

(36)

To achieve system optimum, the credit charge rate should be set as:

$$\begin{array}{c}\hfill k^{\ast }\left(t\right)={\int }_0^t{\dot{k}}^{\ast }\left(y\right)\mathrm{d}y=(\frac{\eta }{\rho }-\frac{\phi \omega s}{m\rho }){\int }_0^t\alpha \left(s(t^{\ast }-y)\right)\mathrm{d}y,0\le t\le t_e.\end{array}$$

(37)

Equation (37) depicts the number of credits charged if commuters depart from home at time t. The commuters choose their departure times by trading off different cost components, and the commuters with a high value of time tend to choose departure times close to $t^{\ast }$. Therefore, we can also express the credit charge rate in terms of the order of value of time n. Using Equation (36), we have:

$$\begin{array}{c}\hfill k^{\ast }\left(n\right)=\frac{1}{\rho }(\frac{\eta }{s}-\frac{\phi \omega }{m}){\int }_n^N\alpha \left(y\right)\mathrm{d}y,0\le n\le N.\end{array}$$

(38)

The total amount of tradable credits that should be issued given parking density m is derived:

$$\begin{array}{c}\hfill K^{\ast }=\frac{1}{\rho }(\frac{\eta }{s}-\frac{\phi \omega }{m}){\int }_0^N{\int }_n^N\alpha \left(y\right)\mathrm{d}y\mathrm{d}n.\end{array}$$

(39)

In the meantime, the optimal price of tradable credits for the heterogeneous case is determined:

$$\begin{array}{c}\hfill {\rho }^{\ast }=\frac{1}{K^{\ast }}(\frac{\eta }{s}-\frac{\phi \omega }{m}){\int }_0^{N}y\alpha \left(y\right)\mathrm{d}y.\end{array}$$

(40)

Equations (38)–(40) jointly describe the optimal design of a dynamic tradable credit scheme to achieve a system optimum state with the system-wide travel cost minimized. Under the circumstances of purely autonomous vehicles, it is significant to explore the impacts of parking density on the derived optimal tradable credit scheme. As observed in the above equations, the price of tradable credits increases with parking density but decreases with the total amount of tradable credits. The reason for this attribute of ${\rho }^{\ast }$ is the same as the explanation for Equation (17) in Section 3.2.

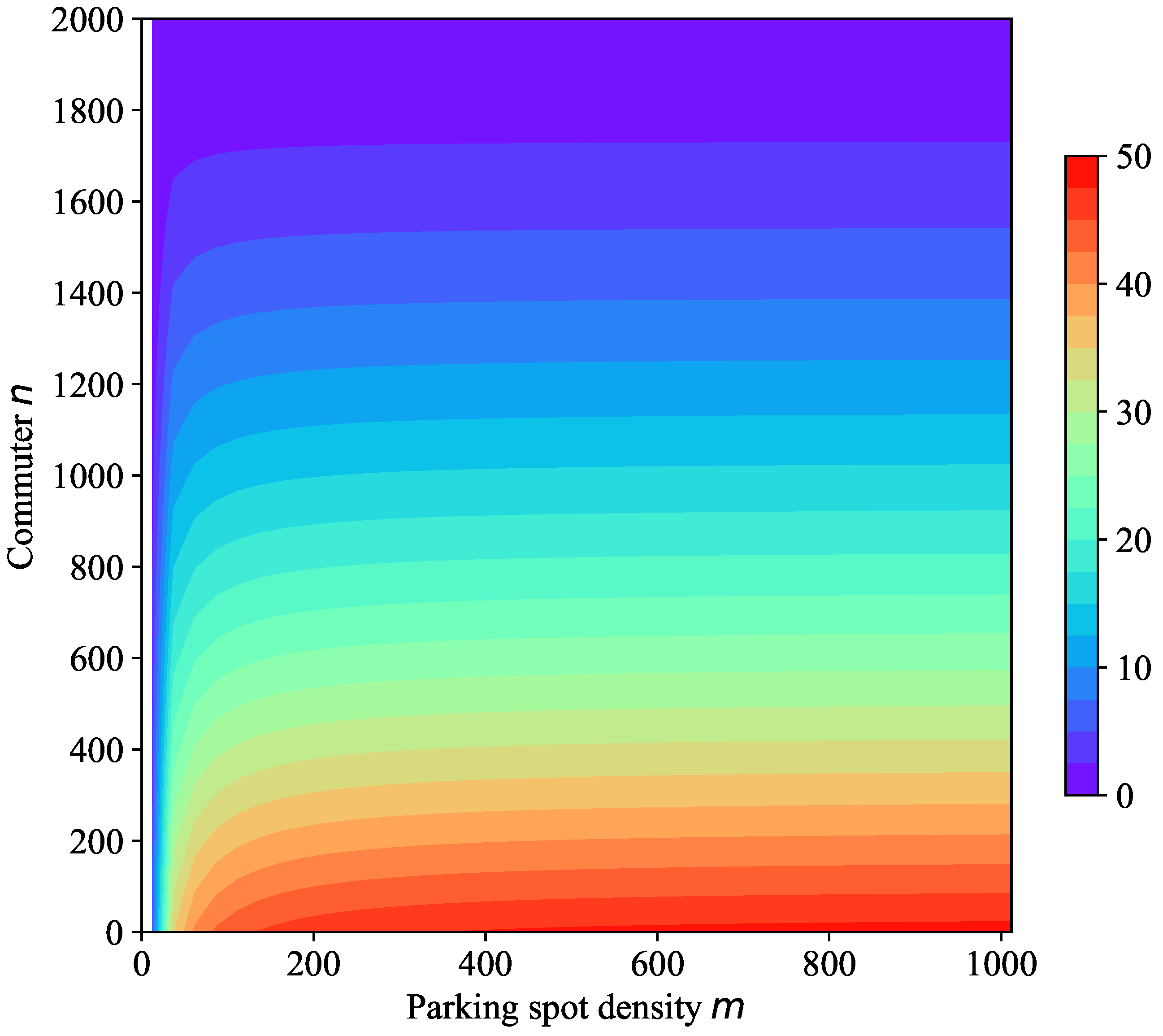
In addition to optimal price ${\rho }^{\ast }$, parking density affects the credit charge rate $k^{\ast }\left(n\right)$. The tendency of the number of tradable credits charged from commuters $k^{\ast }\left(n\right)$ is plotted against the departure order n and the parking density m in Figure 6. When the parking density m is low, the number of credits charged from commuters quickly increases with m. When the parking density is high, the change of $k^{\ast }\left(n\right)$ with respect to m is increasing but not significant. Thus, parking density should be considered for the design and implementation of a tradable credit scheme.

4.3. Analysis of Individual Welfare at SO

In this part, we evaluate individual welfare and system performance in morning commute problems with heterogeneous commuters and a tradable credit scheme. Here, individual welfare is measured using both generalized travel cost and generalized travel time. We adopt two performance measures to indicate the impacts of the proposed tradable credit scheme in Section 4.2, i.e., the system-wide travel cost and efficiency measure. The efficiency of the tradable credit scheme is also defined as the proportion of reduction in system-wide travel cost compared with the case without tradable credits at UE.

Firstly, we will focus on the individual welfare measured by generalized travel costs. When the optimal tradable credit scheme described in Equations (38)–(40) is implemented during morning peak period, we obtain the generalized travel cost for each commuter n at SO by substituting $n\left(t\right)$ (Equation (36)) into Equation (34). That is,

$$\begin{array}{c}\hfill c^{\ast }\left(n\right)=(\frac{\eta }{s}-\frac{\phi \omega }{m})(n\alpha \left(n\right)+{\int }_n^N\alpha \left(y\right)\mathrm{d}y)+\frac{\phi \omega }{m}\alpha \left(n\right)N.\end{array}$$

(41)

Compared with the case before introducing the tradable credit scheme in Section 4.1, we can show the effects of optimal tradable credit scheme on individual welfare improvement. Specifically, we calculate the difference between the individual generalized travel cost at UE without tradable credits and that at SO under optimal tradable credits:

$$\begin{array}{c}\hfill \Delta c\left(n\right)=(\frac{\eta }{s}-\frac{\phi \omega }{m})((N-n)\alpha \left(n\right)-{\int }_n^N\alpha \left(y\right)\mathrm{d}y).\end{array}$$

(42)

Because the value of time $\alpha \left(n\right)$ is a decreasing function of n, the integral ${\int }_n^N\alpha \left(y\right)\mathrm{d}y$ is strictly less than $(N-n)\alpha \left(n\right)$. Therefore, with the condition that $\frac{\eta }{\rho }-\frac{\phi \omega s}{m\rho }>0$, the derived $\Delta c\left(n\right)$ is always positive. In other words, each commuter will always benefit from the introduction of optimal tradable credits compared with the case without tradable credits. Additionally, the cost reduction under the optimal tradable credit scheme is larger for commuters with a higher value of time. The results show that the optimal tradable credit scheme $(k^{\ast }\left(t\right),K^{\ast })$ is Pareto optimal. However, the cost reduction may be not identical for all commuters, which may incur equity issues for the morning commute. To address this problem, we propose to implement a credit distribution strategy to reconcile user benefits under the tradable credit scheme in Section 4.4.

We can further explore the impacts of parking density m, which is given and fixed on the cost reduction $\Delta c\left(n\right)$ and individual generalized travel cost $c^{\ast }\left(n\right)$. We find that the individual generalized travel cost (Equation (41)) is affected by the parking density m, which is different from the case without tradable credits in Section 4.1. By taking the first-order derivative of $c^{\ast }\left(n\right)$ with respect to m, we obtain $\frac{\partial c^{\ast }\left(n\right)}{\partial m}=-\frac{\phi \omega }{m^2}\alpha \left(n\right)(N-n)$ which is negative for all n. It indicates that each commuter n can reduce the individual generalized travel cost when the parking density is promoted and the optimal tradable credit scheme is implemented. Additionally, the cost reduction $\Delta c\left(n\right)$ for each commuter n increases with the parking density m based on Equation (42).

Secondly, we proceed to explore the individual welfare measured by the generalized travel time. The individual generalized travel cost presented in Equation (41) can be easily transferred to time units, i.e.,

$$\begin{array}{c}\hfill {\widehat{c}}^{\ast }\left(n\right)=(\frac{\eta }{s}-\frac{\phi \omega }{m})(n+\frac{{\int }_n^N\alpha \left(y\right)\mathrm{d}y}{\alpha \left(n\right)})+\frac{\phi \omega }{m}N,\end{array}$$

(43)

and the cost reduction in time units is obtained taking the difference between the cost in Equation (33) and that in Equation (43):

$$\begin{array}{c}\hfill \Delta \widehat{c}\left(n\right)=(\frac{\eta }{s}-\frac{\phi \omega }{m})(N-n-\frac{{\int }_n^N\alpha \left(y\right)\mathrm{d}y}{\alpha \left(n\right)}).\end{array}$$

(44)

Similarly, as ${\int }_n^N\alpha \left(y\right)\mathrm{d}y<0$, $N-n-\frac{{\int }_n^N\alpha \left(y\right)\mathrm{d}y}{\alpha \left(n\right)}$ is positive, which gives $\Delta \widehat{c}\left(n\right)>0$. Thus, heterogeneous commuters experience lower generalized travel costs in time units in comparison with the case without tradable credits. Furthermore, we have that $\frac{\partial \Delta \widehat{c}\left(n\right)}{\partial m}$ is positive. With a higher parking density m, the cost reduction in time units is also larger, which is the same as using the monetary cost reduction in Equation (42).

The system-wide travel cost is composed of early schedule delay cost and cost of accessing to parking space.

$$\begin{array}{c}\hfill T{C}^{\ast }=(\frac{\eta }{s}-\frac{\phi \omega }{m}){\int }_0^{N}n\alpha \left(n\right)\mathrm{d}n+\frac{\phi \omega }{m}N{\int }_0^N\alpha \left(n\right)\mathrm{d}n.\end{array}$$

(45)

We further perform numerical analysis to illustrate the impacts of parking density m on the system-wide travel cost $T{C}^{\ast }$ and the efficiency measure ${\theta }^{\ast }$. Figure 7 depicts the tendency of the system-wide travel cost and efficiency measure against parking density. When the parking density is low, the system-wide travel cost decreases dramatically with the increase in parking density. In the meantime, the efficiency ${\theta }^{\ast }$ increases significantly with m. In contrast, the system-wide travel cost and efficiency measures do not vary with parking density significantly when the m becomes very high. In particular, when the parking density is larger than 100, the improvement in system performance is negligible. Thus, the increase in parking supply can help to improve system performance, and the improvement tends to a stable state when m is further increased.

4.4. Initial Distribution of Tradable Credits Considering Equity

From the perspective of social equity, the tradable credit schemes may be unacceptable to commuters considering the non-identical cost reduction among users. It is challenging to implement tradable credit schemes to improve system performance and in the meantime guarantee equitable individual welfare. Thus, we are motivated to investigate the initial distribution strategy of tradable credits among AV commuters. Moreover, we focus on the equity measured by generalized travel cost, i.e., the monetary travel cost of commuters. The research goal of this part is to generate the same level of individual cost reduction by implementing the optimal tradable credit scheme in Section 4.2 and the proposed initial distribution strategy proposed here.

Let $O\left(n\right)$ denote the number of credits distributed to the nth commuter. The total amount of tradable credits distributed during morning peak hours is restricted to K, so the conservation condition can be expressed as follows:

$$\begin{array}{c}\hfill {\int }_0^{N}O\left(n\right)\mathrm{d}n=K^{\ast }.\end{array}$$

(46)

Under the distribution scheme, the nth commuter receives an amount of $O\left(n\right)$ credits, which can be considered as a monetary incentive of ${\rho }^{\ast }O\left(n\right)$. Thus, the generalized travel cost for the nth commuter becomes:

$$\begin{array}{c}\hfill c_0^{\ast }\left(n\right)=(\frac{\eta }{s}-\frac{\phi \omega }{m})(n\alpha \left(n\right)+{\int }_n^N\alpha \left(y\right)\mathrm{d}y)+\frac{\phi \omega }{m}\alpha \left(n\right)N-{\rho }^{\ast }O\left(n\right).\end{array}$$

(47)

We further derive the change of individual generalized travel costs after the credit distribution scheme is introduced. To enforce the equity distribution based on monetary costs, we impose the condition that all commuters experience the same level of cost reduction under the proposed credit distribution scheme. Combining Equation (32) and Equation (47), we obtain the cost reduction for the nth commuter $\Delta c_0$ as follows,

$$\begin{array}{c}\hfill \Delta c_0=\eta \alpha \left(n\right)\frac{N}{s}-c_0^{\ast }\left(n\right).\end{array}$$

(48)

Under the credit distribution scheme based on monetary equity, the level of cost reduction is identical to all commuters, which requires $\frac{\mathrm{d}\Delta c_0\left(n\right)}{{\mathrm{d}}_n}=0$. Furthermore, we have the first-order derivative of $O\left(n\right)$ with respect to n is $\dot{O}\left(n\right)=\frac{K^{\ast }(n-N)\dot{\alpha }\left(n\right)}{{\int }_0^{N}y\alpha \left(y\right)\mathrm{d}y}$, which is non-negative since $n\le N$ and $\dot{\alpha \left(n\right)}<0$. The non-negativity of $\dot{O}\left(n\right)$ implies that the number of credits issued to commuters with low VOTs (large n) should not be lower than that for commuters with high VOTs.

Combining the cost reduction in Equation (48) and the individual generalized travel cost in Equation (47), we can derive the expression of $O\left(n\right)$.

$$\begin{array}{c}\hfill O\left(n\right)=K^{\ast }\frac{\alpha \left(n\right)(n-N)+{\int }_n^N\alpha \left(y\right)\mathrm{d}y+\frac{ms\Delta c_0}{m\eta -\phi \omega s}}{{\int }_0^{N}y\alpha \left(y\right)\mathrm{d}y}.\end{array}$$

(49)

Furthermore, the cost reduction is derived by substituting Equation (49) into Equation (46):

$$\begin{array}{c}\hfill \Delta c_0=(\frac{\eta }{s}-\frac{\phi \omega }{m})({\int }_0^N\alpha \left(n\right)\mathrm{d}n-\frac{{\int }_0^N{\int }_n^N\alpha \left(y\right)\mathrm{d}y\mathrm{d}n}{N}).\end{array}$$

(50)

Equation (50) reveals that the cost reduction depends on parking density. When the parking density is high, the cost reduction is large for all commuters. In contrast, the cost reduction becomes smaller for all commuters when the parking supply is lower at the city center. This result implies that the effects of tradable credit on individual welfare is weakened when the parking supply is insufficient.

With the derived cost reduction, we further derive the expression of credit distribution scheme $O\left(n\right)$:

$$\begin{array}{c}\hfill O\left(n\right)=K^{\ast }\frac{\alpha \left(n\right)(n-N)+{\int }_n^N\alpha \left(y\right)\mathrm{d}y+{\int }_0^N\alpha \left(n\right)\mathrm{d}n-{\int }_0^N{\int }_n^N\alpha \left(y\right)\mathrm{d}y/N}{{\int }_0^{N}y\alpha \left(y\right)\mathrm{d}y}.\end{array}$$

(51)

It is observed that the credit distribution scheme depends on the attributes of commuters (i.e., VOT $\alpha \left(n\right)$), the total travel demand N and the total amount of credits issued by the government $K^{\ast }$. The initial distribution of credits also varies parking density m as $K^{\ast }$ in Equation (51) depends on m, according to Equation (39).

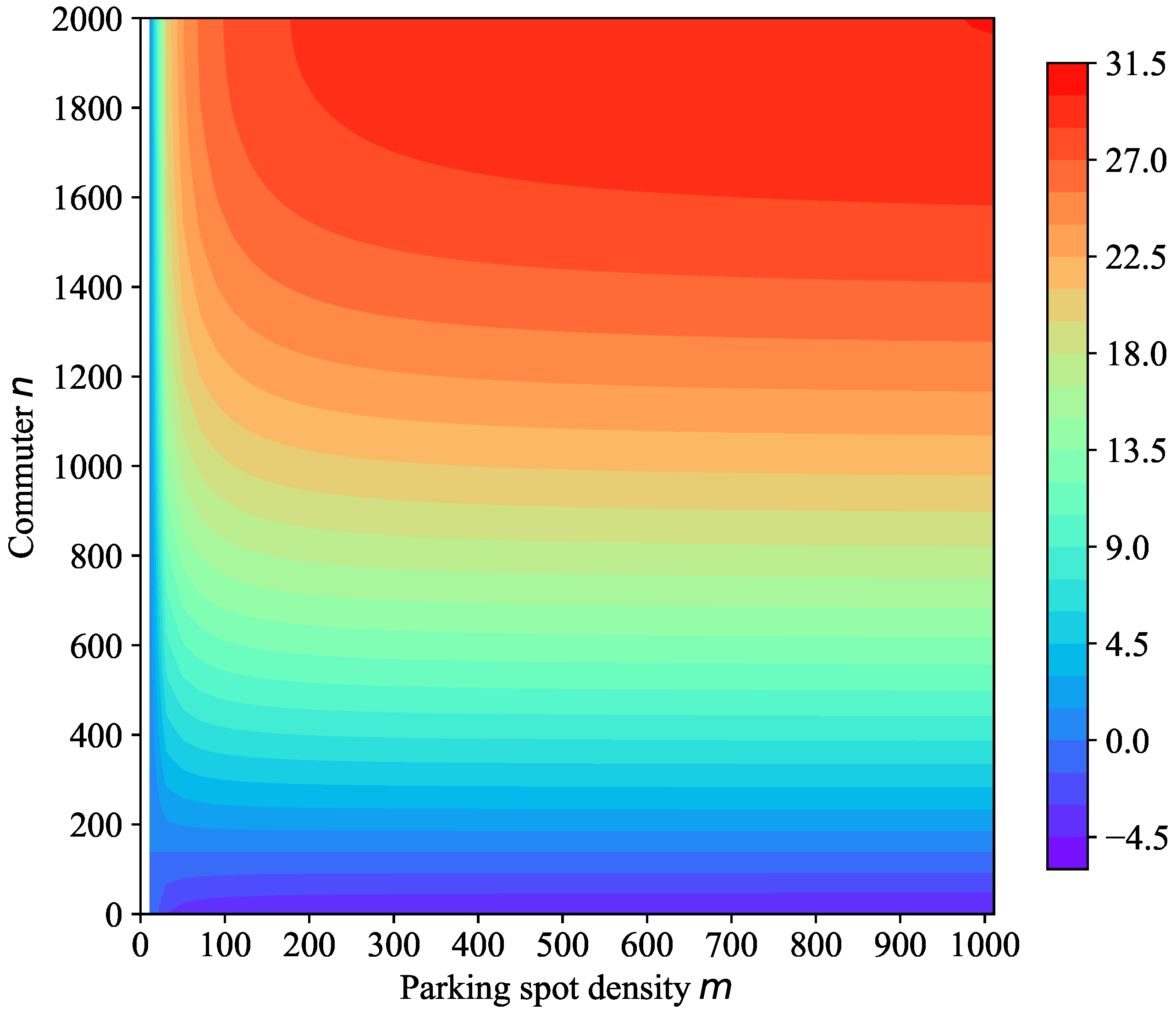
In the following, we numerically show the number of credits distributed to heterogeneous commuters $O\left(n\right)$ under the initial distribution scheme in Equation (51) and the resulted impacts on individual welfare. We plot the number of credits received by heterogeneous commuters against the order of VOT n and the parking density m in Figure 8. A low level of departure order n corresponds to a high level of value of time for commuter n. Figure 8 indicates that the number of credits distributed to commuters varies with the commuters’ values of time and the parking density. For commuters with a high value of time (i.e., small n), the number of initially distributed credits is negative. For commuters with low value of time (i.e., large n), the number of distributed credits is positive. Additionally, the number of credits distributed to heterogeneous commuters increases with parking density m. The results imply that commuters with low value of time should be distributed more credits and commuters with high value of time should be charged additional credits from the perspective of policymaking. Moreover, the distribution of credits should be based on the parking density.

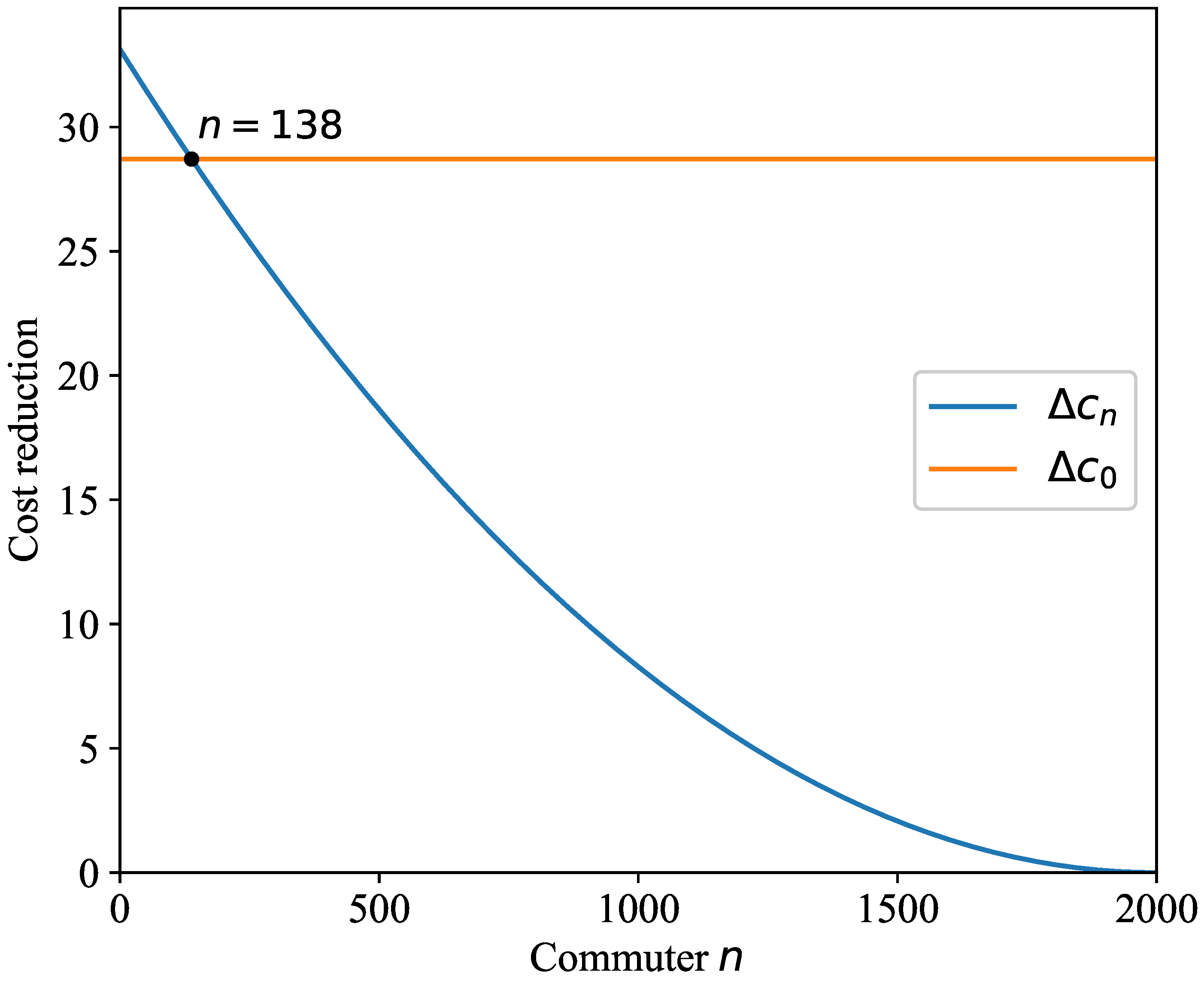
Figure 9 depicts the cost reduction for the cases without and with the initial distribution scheme. The cost reduction measures the change in individual travel costs of commuters compared with the case without tradable credits. Before introducing the proposed initial distribution strategy, the cost reduction for commuter n is described by the blue curve. The heterogeneous commuters enjoy different levels of cost reduction, which implies the existence of inequality. After that, we design the initial distribution scheme $O\left(n\right)$ in Section 4.4 to achieve the same cost reduction for heterogeneous commuters and thus ensure equity. In this case, the cost reduction is illustrated in the orange curve. The results in Figure 9 show that the commuters with low VOTs ($138<n\le 2000$) are better off after the initial distribution scheme is implemented. Additionally, the commuters with lower levels of value of time (n is larger) benefit more from the optimal tradable credits developed in Section 4.2. For the commuters with high VOTs ($n\le 138$), the cost reduction is decreased, which indicates that the commuters are worse off after the initial distribution scheme is introduced. In summary, the above results regarding cost reductions reflect the positive effects of the proposed optimal tradable credit scheme on individual welfare for commuters with low VOTs. Additionally, the implementation of the initial distribution strategy combined with the optimal tradable credit scheme can further improve their individual welfare.

5. Conclusions

This study examines the dynamic equilibrium of the morning commute where all commuters travel with autonomous vehicles and time-varying tradable credit schemes are utilized to regulate bottleneck congestion. Under the automated environment, the vehicles will self-drive to the corresponding parking slots after dropping off the commuters. The decision-making of commuters in a fully automated environment is different from morning commute problems with conventional vehicles. By extending Vickrey’s bottleneck model, we formulate the commuters’ simultaneous decisions on departure times and parking locations at equilibrium. To manage traffic congestion during morning rush hours, we propose time-varying tradable credit schemes and integrate these management instruments with commutes’ decision-making for the case with homogeneous commuters and that with heterogeneous commuters, respectively. Based on the modeling framework, we explore the joint effects of parking density and tradable credits on individual welfare and system performance.

For the case with homogeneous commuters, we investigate the equilibrium travel patterns before and after introducing tradable credits. We further explore the impacts of tradable credits and parking density on system performance and the optimal design of tradable credits. First, we analyze the equilibrium travel patterns at UE before introducing tradable credits. We find that the total cost of queuing time increases with parking density, whereas the system-wide travel cost and individual travel cost are independent of parking density. Second, we examine the equilibrium after tradable credits are incorporated. In this case, the equilibrium travel pattern does not rely on parking density, which is different from the case without tradable credits. We derive the equilibrium price of credits for morning commutes with homogeneous commuters under a fully automated environment. The equilibrium price increases with the total amount of credits issued by the government and the parking density, which is also demonstrated with numerical results. Moreover, we examine the conditions on the design of tradable credits to maintain an equilibrium state. We find that the ratio of the total amount of credits to the rate of credit charge rate should vary within a derived range. Finally, we investigate the optimal design of tradable credits to achieve system optimum. The optimal price of credits increases with parking density, whereas it decreases with the total amount of credits. We define an efficiency measure to indicate the influence of tradable credit on system performance. The efficiency measure is the ratio of reduction in system-wide travel cost under a tradable credit scheme compared with the case without tradable credits. The analysis result shows that we could improve system performance by adjusting the rate of tradable credits. Additionally, the system performance is optimal when the optimal tradable credit scheme is implemented.

For the case with heterogeneous commuters, we analytically investigate the equilibrium without tradable credits and the system optimum with tradable credits. To ensure social equity for heterogeneous commuters, we design an initial distribution strategy under which the commuters experience the same level of cost reduction. The main findings in this part are summarized as follows. First, similar to the homogeneous case, the equilibrium price of credits at SO also increases with parking density and decreases the total amount of credits. Second, at SO, the number of credits charged to commuters increases with parking density. With the proposed initial distribution strategy, the amount of credits distributed to commuters varies with both value of time and parking density. The number of credits received by commuters increases with parking density. Additionally, it is positive for commuters with a low value of time and negative for commuters with a high value of time. Finally, we analyze the impacts of optimal tradable credits and initial distribution strategy on individual welfare. Under the proposed tradable credit scheme, all commuters are better off as the cost reduction is positive for each commuter, which reveals its Pareto optimality for the heterogeneous case. Additionally, the individual cost reduction increases with parking density. After the initial distribution strategy is introduced, the commuters with low VOT are further better off since the cost reduction can be improved.

This work can be extended in the following directions. First, we aim to investigate the design of a tradable credit scheme when both AVs and conventional vehicles are utilized for morning commutes. Second, we may examine the equilibrium travel patterns by incorporating other travel modes, such as public transit and ridesharing. Last, the assumption can be relaxed to consider a limited parking supply.