Abstract
Video platforms allow users to interact with others. They enhance the user experience by providing interaction functions, such as “like”, “comment”, and “share”. In order to explore the value of the users’ behavior to the video platforms, we constructed a video platform operation model that considered interaction and then identified the logical relationships implied by the parameters. We adopted the mathematical model method and analyzed the entire video platform system using numerical optimization techniques. From the pricing decision, we obtained the equilibrium result for the video platform profits and analyzed the favorable market demands. We complemented this strategy by proposing a model that enables platforms to consider the promotion behavior of advertisers. Finally, we expanded the basic model by analyzing the competitive strategies of two video platforms in the market. Our research shows that interactivity, advertisement nuisance, and advertiser profitability are important factors that influence video platform pricing strategies. When interactivity is weak, the platforms need to adjust their pricing to obtain a share of the users in the market. However, they need to obtain all the users in the market to achieve optimal profit. In addition, it is profitable for platforms to adopt promotion strategies when the users are highly sensitive to promotions.
1. Introduction
Video platforms (e.g., YouTube, Netflix, etc.) satisfy the entertainment needs of users by providing video content. Some advertisers try to display product information on video platforms, to approach and acquire potential customers. In this way, video platforms make profits from advertisers and users [1]. For advertisers, the platforms offer different advertisement space services, depending on the amount of the sponsorship fees. For users, some platforms charge a membership fee and allow them to enjoy high-quality videos. Other platforms offer free services to users and attract advertisers by the increased number of customers [2]. For these platforms, the entire profit comes from advertisers. For video platforms to make profits, the pricing strategy is important. These observations create two challenges for video platforms: developing service strategies to increase user demand and adjusting pricing strategies to increase profits.
For video platforms, although charging higher fees can increase unit profits, it may also cause a loss of market demand. This holds true for both users and advertisers. In practice, a video platform is a kind of two-sided market [3]. However, in contrast to a normal two-sided market, the video platform users and advertisers are not in a relationship of mutual needs: users dislike excessive ads [4]. Video platforms need to control the number of advertisers: on the one hand, they need advertisers to generate profits, but on the other hand, they do not want advertisers to affect users. Some video platforms have devised complex strategies to deal with this situation, such as free content strategies, upgrade service strategies, etc. [5]. Therefore, when formulating strategies, video platforms need to consider both service and pricing issues.
Interactivity is one of the main features of video platforms [6]. With the development of online entertainment technology, video platforms have functions similar to electronic communities in that users can interact with each other. For example, when watching video content, users can perform activities such as “like”, “comment”, and “share” [7]. Such interactive behavior helps the video platform to attract more users [8]. Figure 1 illustrates the operation of the video platform with regard to interaction. It is true to say that interaction provides new opportunities for video platforms, but this raises two questions: how should prices be set, based on interactivity? How can the platform profit from interactivity?
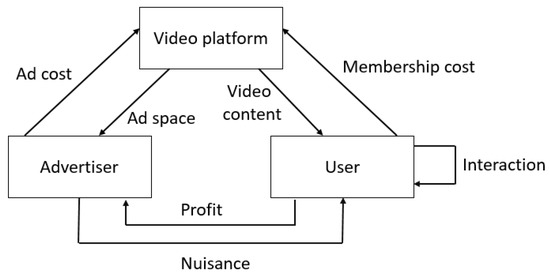
Figure 1.
Platform operating model, with regard to interaction.
In order to solve the research problem and achieve our objectives, the research process of this paper was as follows. Firstly, we constructed a video platform operation model that considers the interactions of users. In this model, the platforms can control the utility of users and advertisers through pricing strategies, thereby affecting demand. As a result of a pricing decision, the platforms can obtain profit-optimized equilibrium results and secure favorable market demand. Then, we considered the position regarding profit when the parameters were changed and analyzed how the pricing strategy would need to be adjusted. In addition, to take full advantage of interactivity, we propose a strategy for video platforms based on the promotions by advertisers. Because adopting a promotion pricing strategy is not necessarily beneficial, we compared the profits of the two strategies. Furthermore, considering the competition in the market, we adopted the hoteling model and extended the basic model by analyzing the competitive strategies for two video platforms. Finally, based on the research results, we provide some management implications for video platforms from different perspectives.
Our research has several interesting findings: (1) when interactivity is low or high, the video platform optimizes profit by absorbing some or all of the users in the market; (2) advertising nuisance, the advertisers’ profitability, and interactivity are the significant parameters for the adjusting decisions; (3) the advertisers’ promotions can make video platforms more profitable by modifying their strategies; and (4) the impact of various parameters on the platform strategy is different depending on whether the environment is competitive or noncompetitive.
This study makes several novel contributions. First, in contrast to the other research, we extend the impact of user interactivity with video platforms to include features such as “comment”, “like”, “share”, etc. Based on the strategy optimization and decision-making, the two-sided marketing theory is enriched. Second, we consider the scenario of advertisers adopting promotional strategies and provide a variety of strategies for the platform according to different situations, an approach which has been less considered in the existing literature. Third, we compare the pricing strategies of two platforms based on their differences in the competitive market. This can provide the platform with effective information for optimal decision-making in the competitive market.
The paper is structured as follows. Section 3 constructs the basic model of the video platform with regard to interaction and performs an equilibrium analysis of the pricing strategy. Section 4 proposes strategies for the video platforms based on the advertisers’ promotions and compares the profits from the basic strategy and the promotional strategy. Section 5 considers the competition of two video platforms in the market and formulates pricing strategies. Section 6 is the conclusion, which summarizes the research results and provides some management implications for video platforms.
2. Literature Review
This paper mainly concerns the research on the two-sided market. We reviewed three streams of two-sided market literature. The first stream of research focused on two-sided platform modeling. At the beginning of the 20th century, scholars put forward the two-sided market theory based on the case of intermediary services and devoted themselves to the construction of the two-sided market model. Caillaud et al. analyzed a model of incomplete price competition among intermediary service providers [9]. They considered the existence of indirect network externalities. The research found that intermediaries have an intention to provide nonexclusive services, as this can reduce competition. Rochet et al. defined the concept of a two-sided market as two or more groups interacting through an intermediary or platform [10] and noted that there are cross-group externalities in two-sided markets. Then, they proposed the early two-sided market research method and established the two-sided market platform model. Armstrong et al. classified the two-sided market according to a real-life situation [11]. Corresponding to the different situations of the two-sided market platform, they proposed three two-sided market models. In addition, they explained the issue of single/multiple homes. The research showed that the platform could observe the user’s reaction to adjustment of the charging model. Economides et al. established a framework to describe an optimal two-sided pricing strategy, based on the software development industry structure (such as Windows and Linux) [12]. They analyzed the competitive structure and industry impact in terms of pricing, sales, profitability, and social welfare.
After the perfection of the two-sided market theory, some researchers started working on the application and extension of the two-sided platform model, which is the second stream of the literature. Nocke et al. developed a theoretical framework for transacting on a platform where buyers and sellers interact [13]. They compared the impact of different platform ownership structures. Belleflamme et al. constructed a two-sided platform model based on negative intragroup externalities [14]. Based on Armstrong’s model, Bardey et al. focused on network platforms and proposed a concept of common network externalities [15]. Amelio and Jullien argued that tying could be deployed using the platforms as tools to introduce implicit subsidies [16]. They found that, in a duopoly, tying on one side made a platform more or less competitive on the other side, depending on the externalities. Moreover, tying increased the total welfare if the network effects were strong. Hagiu et al. focused on first-party content in a two-sided market [17]. They argued that in some operating contexts platforms provide content that is linked to the supply side, such as competing or complementary goods. They differentiated the platform environment (favorable/unfavorable) and analyzed the platform based on the substitution/complementary relationship between the first-party content and the seller’s product. Rasch et al. focused on software platforms [18]. They argued that reducing piracy helped developers to sell more software and increase their profits. However, this was bad for users, because software-protected platforms have high bargaining power, which makes users passive. Kaplow argued that the market power of a platform was directly proportional to its market share. As the market share increased, the platform’s market power became stronger, and higher profits were obtained [19]. Dou et al. explored value-added service strategies in the platform model [20,21]. They argued that platforms provided value-added strategies for sellers or users. Although the value-added strategy incurs additional costs for the platform, the number of sellers and buyers increases. Xue et al. focused on two-sided markets in the service industry [22]. They considered the impact of service quality on the two-sided market and studied platform pricing problems in cases of monopoly and duopoly competition. They also analyzed the effects of parameter changes on the system. Bakos et al. observed that participants on both sides of two-sided platforms were multi-home. Then, they developed a model for platform competition in a differentiated setting [23]. Nan et al. explored a platform’s promotional strategies for its first-party products when a third-party seller carries identical products. They classified users into high-price-sensitivity and low-price-sensitivity users based on heterogeneity and used this to provide optimal pricing decisions [24].
The third stream of research focuses on media platforms, which are directly related to our research. The development of internet technology has delivered a new space for the bilateral market economy, within which the media platform has attracted the attention of scholars. Wilbur conducted empirical research on media platforms. The research showed that advertising had a nuisance effect on consumers [4]. Conversely, Argentesi et al. found that advertisers tended to be closer to consumers [25]. Godes et al. discussed platform competition in terms of content and advertisers and then explored their impact on media company behavior and profit sources [26]. Reisinger argued that platform competition for users conformed to the hoteling model [27]. Advertisers, however, do not compete directly. This is because the platform is homogeneous to the advertisers. Chao and Derdenger referenced the practice of mixed bundling in the media industry, that is, the sale of two or more separate products together, at a discount [28]. They found that consumer heterogeneity was the primary reason for firms to adopt a bundling strategy. Hagiu et al. discussed the informational factors of platforms using game platforms as an example [29]. They focused on the difference in returns resulting from information asymmetry. They extended the model by assuming that a subset of users were informed. Roger studied duopoly, in which two-sided platforms compete in differentiated products, in a two-sided market [30]. His research mainly focused on media markets such as newsprint, operating systems, video game consoles, and even healthcare and education. Anderson et al. considered a multiplatform environment [31]. They distinguished between exclusive consumers and co-consumers and analyzed the platform merger problem. Zennyo studied competition between ad-sponsored platforms [2]. He believed that in this environment, every platform had a free normal service and a paid ad-free service. He described how platforms should divide users into those using free and those using paid services and analyzed business models based on different strategies. Cheng et al. researched the optimal price decisions of media platforms when users accessed video-on-demand (VOD) technology [32]. They found that as user advertisement boredom decreased, advertising fees decreased. Lin et al. discussed the advertising intensity and program content of pay-TV and free-to-air broadcasts [7]. Pay TV can charge both viewers and advertisers, whereas free-to-air broadcasts can only receive revenue from advertising. Carroni et al. focused on two strategies for media platforms: free basic services and paid upgrade services [3]. Amaldoss et al. discussed content delivery strategies for media platforms [1]. They identified three operational strategies based on the impact of advertisement space allocation on media platforms: free content, no ads, and paid content with ads. Li et al. focused on the quality of advertisements on short video platforms [33]. The researchers argued that the quality of advertisements is the main factor that attracts consumers on short video platforms.
Scholars have made substantial contributions to platform-related issues. The research of Hagiu et al. argued that the utility of sellers and buyers is mutually influenced within the platform [17]. In order to optimize profits, platforms need to adopt pricing or investment strategies to control market demand. Similar conclusions were reached by Dou et al. and Rasch et al. [18,20]. In addition, research by Amaldoss et al. improved the original platform model to reflect the characteristics of the video platform business [1]. They summarized three video platform operation strategies. Carroni et al. also distinguished the types of services on video platforms [3]. These studies demonstrate the particularity and complexity of the video platform issue and provide a reference for our research.
With the development of entertainment technology, video platforms function as an electronic community. Users can interact on the video platform by commenting and sharing, etc. However, there is a lack of literature that analyzes the video platform problem in combination with the interactions of the users. Our research is novel in that we analyzed the entire video platform system based on interactions. We adopted the mathematical model method and analyzed the video platform system using numerical optimization techniques. In addition, we used numerical simulation tools to verify the research results. Our research showed that as the number of users increases, the interaction behavior on the platform increases, which optimizes the users’ experience. Our findings may provide scholars and managers with a new perspective. Furthermore, when offering outreach strategies, most of the literature has only focused on the competition between platforms. Few scholars have suggested that platforms should observe the promotions of merchants as a reference. Therefore, the second novel feature of our research aims to take full advantage of the interaction behaviors by proposing an operational model for video platforms to take account of promotions so as to fill a gap in the field and provide a reference for other scholars.
3. Pricing Strategy
In this section, we construct a model for the two-sided video platform. In the process of using the video platform, the users obtain basic services and satisfy their entertainment needs. The advertisers place ads through the video platform to make money from the users [1]. The video platform provides advertisement slots for each advertiser, but users dislike an excess of ads [4]. Notably, the research on media platforms shows interactivity among users [7]. For example, user behaviors such as “comment”, “like”, and “share” can increase their utility [8]. As the number of users increases, the interaction becomes stronger, and the users’ utility also increases. Table 1 defines some of the notation.

Table 1.
Definition of the notation.
On the video platform, the utility of the users is mainly affected by four factors. Firstly, when watching videos, the users can obtain basic utility by satisfying their curiosity or entertainment needs; secondly, during interactions (such as: “like”, “comment”, and “share”), the users increase their perceived utility by increasing the content and entertainment and by showing their personalities; thirdly, the users become bored when they see lots of ads on video platforms, which reduces their utility; finally, if the users need to pay to use the platform, this also reduces their utility. In addition, the advertisers’ utility consists of three dimensions. On the one hand, advertisers can profit from users; on the other, advertisers must pay sponsorship fees to place ads on a video platform. In addition, advertisers incur fixed costs associated with the operation. Some scholars solve platform-related problems using utility models [1,20]. Based on their contribution, we suggest that the utility relationship between the users and the advertisers is as follows:
where is the utility of the users and advertisers in the video platform; represents the cross-market network externality of users and advertisers; is the degree of advertisement nuisance; is the profitability of the advertisers on the platform; is the strength of interaction or, in other words, its interactivity; is the demand of users and advertisers; indicates the negative effects on users of advertising nuisance; indicates the positive effect on users of interaction behavior; and represents the advertisers’ revenue from the users. We set , and to represent the price of the users and advertisers; is the basic utility of users, and is the fixed cost for advertisers. We assume that are distributed in the interval .
is the number of potential users and advertisers in the market; we normalize and to 1. When the users’ utility is , the users decide to join the video platform. According to and , it can be concluded that the demand of users in the video platform is:
Similarly, the demand of advertisers in the video platform is:
According to Equations (3) and (4), we can obtain , . As the video platform can control the demands of users and advertisers through pricing, the profit of the video platform is affected by both price and demand. Therefore, the optimization problem of the platform profit function can be expressed as:
By solving the optimization problem of Equation (5), using Equations (3) and (4), the following results can be obtained:
Lemma 1.
The pricing equilibrium results for users and advertisers are as follows:
When:
When:
Lemma 1 shows that the pricing strategy of the video platform is influenced by interactivity. There is a threshold for interactivity. According to the threshold, two pricing methods have been established for video platforms. When , there is an equilibrium pricing strategy that enables the video platform to obtain optimal profit. When , the video platform needs to absorb all the users in the market. The reason for this is that when interactivity is high, the increase in the quantity of users makes the platform more profitable. In addition, quantity is a positive factor for user utility which allows the platform to obtain secondary benefits, that is, to obtain an increment in the number of users. Therefore, in this case, the platform tends to make two efforts: on the one hand, it tends to reduce the charges for users because lower platform entry costs can attract more users to enter the platform, and on the other hand, it tends to control charges to advertisers because it is helpful to the platform to reduce the number of advertisers in order to ensure entertainment efficiency and attract more users. The proof of Lemma 1 is in Appendix A.
Figure 2 shows the relationship between interactivity and platform profit; the point means that interactivity reaches the threshold .
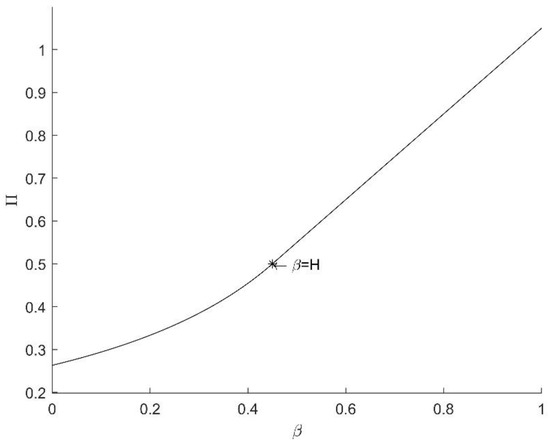
Figure 2.
The relationship between interactivity and profits. Note: .
Corollary 1.
,.
Corollary 1 shows that in the case of obtaining optimal profit, video platform pricing is positive for both the users and the advertisers. In addition, for the video platform, profitability is greater than the user advertisement nuisance degree, . If not, the video platform will refuse to offer advertisement slots to advertisers. The reason for this is that in the profit composition of the video platform, profits from users and advertisers are mutually affected by cross-market network externality. Although an increase in the number of advertisers can bring additional profits to the platform, it causes the platform to lose users. Once , the loss of users outweighs the profit provided by the advertiser. Therefore, the optimal strategy at this point is to deny advertisers the opportunity to join the video platform. The proof of Corollary 1 is in Appendix A.
Corollary 2.
Corollary 2 shows that the improvement of interactivity can increase the revenue of the video platform. This is because the users’ interactivity increases their perceived utility. With the increase in , more users are willing to join the platform. It is helpful for the platform, and for the advertisers and users, to achieve a win-win situation. In addition, advertising nuisance negatively affects video platform profit . For users, excessive advertising nuisance makes them reluctant to pay higher fees to the video platform, which reduces both the number of and the revenue from users. For advertisers, the number of users is an important factor in determining their profits. So, as user demand declines, they too are reluctant to pay more to use the video platform. These factors reduce video platform revenue. Furthermore, the profit coefficient positively affects the profit of the video platform . The reason for this is that advertisers feel that it makes sense to place ads on the video platform as the profits from users increase. Therefore, more advertisers are willing to join the video platform, and they are also willing to pay higher sponsorship fees, which can in turn increase the video platform’s profits. Finally, the market size of the users and advertisers positively affects platform profits. The proof of Corollary 2 is in Appendix A.
Corollary 3.
i. When
ii. When
Corollary 3 shows the user price adjustment strategy in different situations. In the case of , interactivity negatively affects the user price. The reason for this is that when the interactivity increases, the number of users boosts the platform profits significantly. Hence, the platform tends to reduce the price to attract more potential users. The advertisers’ profitability negatively affects the video platform’s charge to the users. This is because once the profitability increases, more advertisers are willing to join the platform. However, this may cause a loss of users, and therefore, the platform needs to reduce the user price to maintain the number of users. Both the user and the advertiser market sizes negatively affect user prices. When the market size increases, the most effective decision for the platform is to expand its market share, and reducing the price can bring more potential users to the platform. This in turn stimulates potential advertisers to join the platform. Advertising nuisance positively affects user prices. The reason for this is that when is too high, the advertisers cannot optimize income from the video platform. If the advertisers are reluctant to invest in the video platform, the managers can only maintain profits by increasing charges to the users.
In the case of , the difference is that interactivity positively affects platform pricing. When exceeds the threshold, the platform absorbs all of the potential users in the market. For this to happen, the user price cannot be excessive. As interactivity increases, so does user utility. This makes users tolerant of the price. Another difference between the two cases is where , . If the video platform has all of the users in the market and is sufficiently high, the advertisers can obtain optimal profits on the video platform. The problem of the optimal income in the previous case does not exist. Thus, the platform needs to reduce the user price to make up for the user’s utility loss caused by advertising nuisance, thereby retaining the number of users and increasing profit. The proof of Corollary 3 is in Appendix A.
Corollary 4.
i. When:
ii. When :
Corollary 4 shows the advertiser price adjustment strategy in different situations. In the case of , both and positively affect the price because they can increase the number of users, which makes advertisers willing to pay the platform. In addition, is the profitability of the advertisers in the platform. Because it can also increase the utility of advertisers, the feature of is similar to and . Both and positively affect the price because they may reduce the utility of the users. If or increases, the negative effect of the advertisers increases the users’ reluctance to join the platform. Hence, the platform should increase advertiser fees to reduce their number.
In the case of , and no longer affect the price for advertisers. The reason is that once the platform decides to absorb all of the users in the market, it does not need to adjust user market share by means of advertiser price. So, the relationship of and is independent. In addition, because the scale of advertisers does not change the number of users, cannot influence the willingness of advertisers to pay. The proof of Corollary 4 is in Appendix A.
In summary, interactivity has a significant impact on video platform profits. High interactivity makes the platform tend to absorb all of the users in the market. When interactivity is low, the platform can control the demand of users and advertisers by adjusting prices so as to obtain the optimal benefit. Both the market size and the features of the users and advertisers also affect the optimal profit of the platform. In this section, we discussed how the behavior of the users and advertisers changes when the relevant parameters in the market change. We also analyzed the price adjustment strategy to determine the optimal profit of the platform.
4. Pricing Strategy Based on Promotion
The analysis in the previous section shows that video platforms can profit via interaction. The benefits of interaction increase with the number of users. Platforms need to adopt business strategies to attract users, and an increase in users is also the main objective of advertisers, who generally make use of promotions to expand the market. Real-life examples on e-commerce platforms include coupons, gift cards, giveaways, memberships, etc. [34,35,36]. Through these promotions, advertisers gain more customers despite paying some costs. Increasing the number of customers also brings opportunities for video platforms. It can be said that advertisers’ promotions are also conducive to the development of the platforms. Therefore, the platforms need to consider both the interactions of users and the promotions of advertisers when adjusting their pricing strategies. By extending the basic model, we constructed a model for a platform which adopts a promotion pricing strategy:
where denotes the cost to the advertiser of providing promotions to the users, and represents the sensitivity to promotions of the users; in other words, the cost of makes the user increase the utility of . Therefore, the platform profit optimization of the promotion price strategy can be expressed as:
According to Equations (6)–(8), it can be seen that when the promotion cost to advertisers reaches a certain value the video platform achieves the optimal price strategy and profit. However, one condition must first be met: the promotions of the advertisers must be profitable, otherwise the advertisers will not conduct promotions on the platform. According to Equations (6) and (7), when , Lemma 2 can be obtained.
Lemma 2.
When, advertisers conduct promotions on the platform.
Lemma 2 shows that the more interactive the users, the more likely the advertisers are to use promotions to expand revenue. This also depends on the three variables of , , and . When the user market increases, the profitability of the advertisers increases, and when the user sensitivity to promotions is high, promotions make sense for the advertisers. This is another reason for the platforms to consider advertisers’ promotions in their pricing strategies. The proof of Lemma 2 is in Appendix A.
When , it is profitable for advertisers to adopt promotion strategies. However, if , video platforms also need advertisers to attract users even though the advertisers are reluctant to use promotions. In this scenario, platforms could help advertisers to offer promotions to users. Such a strategy can effectively improve user utility, thereby increasing the number of users, which is the fundamental purpose of the platform. In addition, from the perspective of the advertisers, promotions can increase the number of potential customers. Hence, the promotion pricing strategy is a win-win situation for the advertisers and the platform. The model can therefore be modified as:
As with Lemma 1, combined with the condition of and to solve the optimization issue, Lemma 3 can be obtained.
Lemma 3.
The optimal profit of the video platform adopting the promotion pricing strategy is:
When:
When:
Lemma 3 shows that in order to obtain the optimal profit, the platform needs to consider whether to adopt a promotion pricing strategy. If a promotion pricing strategy is adopted, the video platform helps the advertisers to offer promotions to the users. The proof of Lemma 3 is in Appendix A.
In addition, when adopting a promotion pricing strategy similar to that of Lemma 1, there is a threshold for interactivity. When exceeds the threshold, the video platform tends to absorb all the users in the market. Let .
Corollary 5.
,.
In contrast to Lemma 1, the interactivity threshold is affected by user promotion sensitivity and decreases as increases. The reason for this is that users are more likely to pay and to join the platform when the promotions provide them with a higher utility. In this case, even if the interactivity is not sufficiently strong, absorbing all the users is still the right choice. In addition, when adopting a promotion pricing strategy, the video platform’s profit increases as rises. This is because when the promotions generate a greater perceived utility for users, they are more willing to join the video platform and to pay more, which is beneficial for the video platform.
Promotion Pricing Strategy vs. Basic Pricing Strategy
A promotion pricing strategy is not always the best strategy for the platform. According to Lemma 3, by adopting the promotion pricing strategy there will be extra costs for the video platform. Therefore, once a promotion pricing strategy is adopted, the video platform must obtain sufficient profit from users. Hence, there are two potential problems with a promotion pricing strategy: on the one hand, if the increase in user quantity is not satisfactory, the promotion pricing strategy will not cover the loss; on the other hand, although the promotion improves the users’ utility, it may be difficult to induce them to pay more. Therefore, the video platform needs to compare the profits with and without the adoption of the promotion pricing strategy and then decide on the price.
By comparing the optimal profit of promotional and base strategies in the same interval, Lemma 4 can be obtained.
Lemma 4.
The results for the video platform, considering promotion, are as follows:
When:
i. If:
ii. Ifand:
iii. If:
When:
iv. If:
v. Ifand:
Lemma 4 shows that whether or not the video platform adopts a promotion pricing strategy is mainly influenced by the user sensitivity to the promotion, . It can be seen that there is a threshold for in the decision-making process. When the user sensitivity is higher (lower) than the threshold, the video platform adopts (does not adopt) the promotion pricing strategy. The reason for this is that the video platform’s profit comes from two sources: the users and the advertisers. Adopting a promotion pricing strategy means that the platform incurs some losses. If the user sensitivity to the promotion is strong, the user profit from the promotion pricing strategy can compensate for the loss. However, if the promotion sensitivity of the users is weak, the adoption of a promotion pricing strategy will not outweigh the cost. The proof of Lemma 4 is in Appendix A.
Although the video platform can adjust its pricing strategies according to the promotional behavior of the advertisers, it cannot intervene in the actual promotion activities of the advertisers. However, what the platform can do is observe the advertisers’ promotion to formulate price strategies.
According to Equations (6)–(8), considering and as exogenous variables and solving the optimization issue, Lemma 5 can be obtained.
Lemma 5.
The optimal profit of the video platform from observing promotions is:
The proof of Lemma 5 is in Appendix A. Figure 3 shows the optimized profits of the basic pricing strategy and the practical pricing strategy. It is shown that the practical pricing strategy generates higher profits than the basic pricing strategy.
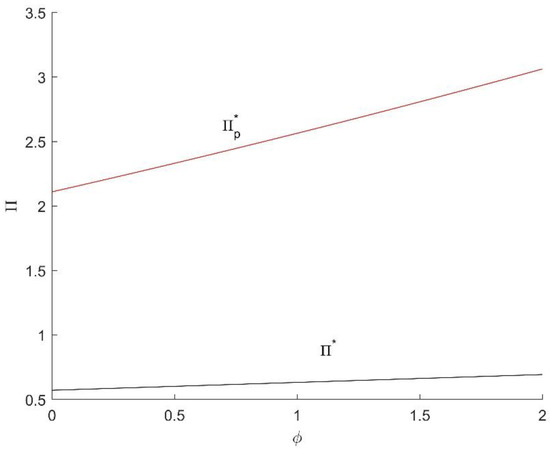
Figure 3.
The optimized profit of basic pricing strategy and promotion pricing strategy. Note: , is the profit of basic pricing strategy and is the profit of promotion pricing strategy.
In this section, we analyzed the strategies for video platforms to consider with regard to promotion activities. We summarized the pricing decisions and optimal profits of the video platform for a promotion pricing strategy when interaction was taken into account. In addition, to explore the optimal decisions of the video platform in different situations, we contrasted the promotion pricing strategy and the basic pricing strategy. Furthermore, we considered the scenario in which the platform cannot intervene in the advertiser’s promotion activity.
5. Competitive Strategy
Next, we discuss platforms in a competitive environment. When dealing with competition, some scholars use game theory to build equilibrium models [1,18], although none of them have discussed the video platform market. Based on their research, we are assuming that there are two horizontally differentiated video platforms. They are located at opposite ends of a hoteling line. Some researchers argue that in a two-sided market, platforms are homogeneous for advertisers but heterogeneous for users [27,29]. The basic utility of the users in platform 1 and platform 2 is and . We assume that the users are single-home; that is, each user can only join one platform at a time. They are uniformly distributed in the interval . The users’ locations are denoted by , and the transportation cost is . Therefore, the utility of the users in platform 1 and platform 2 is:
where and .
By solving Equations (12) and (13), we obtain:
Therefore, for the two platforms:
As :
By solving the profit optimization issue for the two platforms, Lemma 6 can be obtained:
Lemma 6.
The optimal pricing strategy of platform 1 and platform 2 is:
It can be seen that the difference between and is , and between and , it is . As the gap between the basic utility of the two platforms widens, the differences between the optimal price strategies increase, which is consistent with the Matthew effect. The proof of Lemma 6 is in Appendix A.
On the other hand, as the gap between the basic utility of the two platforms narrows, a special case should be considered in which the underlying utility of the two platforms is the same. Such a symmetrical equilibrium is helpful in explaining the condition of the video platforms. When , Lemma 7 can be obtained.
Lemma 7.
The optimal strategy for video platforms in a competitive environment is as follows:
Lemma 7 shows that in the case of competition, there are symmetrical equilibrium strategies between the two video platforms: each platform absorbs half the users in the market and determines the optimal price based on the number of users.
Figure 4 shows the relationship between and and and . At the point , interactivity reaches a threshold of . At this point, is equal to 0.
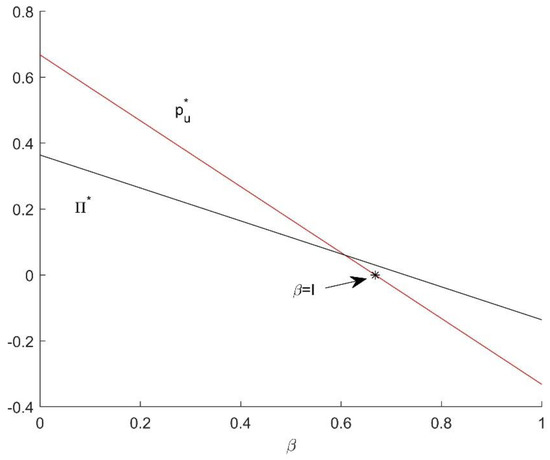
Figure 4.
The relationship between and and between and . Note: , * is the point when .
Corollary 6.
, ,;
; else;
if; else.
In contrast to the noncompetitive situations, it is impossible for each of the two platforms to absorb all the users in the competitive market. In addition, if the is or negative, it means that the platforms may adopt a free or a reward-based strategy. In the case where a portion of users in the market is acquired, the impact of the parameters on user prices differs in competitive and noncompetitive markets. The first difference is that positively affects user price. This is because in a competitive environment, it becomes difficult to obtain benefits from users by reducing user prices. Once the scale of advertising increases, platforms can make more profit from advertisers and thereby loosen the restrictions on user prices. The second difference is that the relationship of and is affected by the relationship of and . When the profitability of the advertisers is less than , the platforms tend to make profits from the users; so, they need to increase the price for the users. Conversely, when the profitability of the advertisers is greater than , the platforms tend to make profits from the advertisers; so, they reduce the to increase the number of users so as to ensure the participation of the advertisers. The third difference is that the relationship between and is affected by the relationship of and . When , the increase in allows the platforms to increase to obtain more profit. When , both high interactivity and the increase in lead to increased competition between the two platforms. Each of them want to lower to obtain a larger share of the user market.
Corollary 7.
,,.
The number of users on each platform in symmetric equilibrium represents half of the market. Therefore, in a competitive situation, only three factors affect advertiser prices. When the profitability and the market size of users increases, the advertisers’ utility increases. This is because as the platform becomes more valuable, it tends to increase the prices charged to advertisers to obtain more profit. In addition, as the advertising nuisance coefficient increases, the platforms need to reduce the number of advertisers to ensure the users’ utility. Hence, they tend to increase the prices for advertisers.
Corollary 8.
,;
if,, else;
if,, else;
if,, else.
Compared with the noncompetitive situation, the impact of the parameters on profit is different. Combined with the loss of competition and the fixed number of users, the increase in and the decrease in intensify competition, which causes a decrease in profit. The relationship of and is affected by the relationship of and . When , the benefits that creates for the platforms are greater than the losses for the platforms’ competition and vice versa. There is a threshold for . If , the loss of competition is less than the benefits and vice versa as increases.
In this section, we analyzed platform strategies in a competitive environment to refine our research. We considered a symmetric equilibrium and explored the impact of interactivity and other factors on platform pricing strategies and profits. It is worth noting that, in contrast with a noncompetitive situation, platforms can adopt free or reward strategies. We can identify such examples in our everyday lives. In the past, people could only watch videos on TV platforms, and all users had to pay for the service. However, there are many video platforms in the market today. As the competitive environment has developed, some of them provide users with free or reward services.
6. Discussion
6.1. Conclusions and Remarks
Based on interactivity, our research explored the operation mode of video platforms and obtained some results. First of all, this research constructed a video platform operation model, taking interaction into account, and then obtained the equilibrium strategy of profit via pricing decisions. Secondly, to efficiently exploit interaction, we proposed a strategy that could be used by video platforms when considering promotions and determined whether the promotion pricing strategy should be adopted to obtain the optimal profit. Finally, we used the hoteling model to analyze the scenario of competition between two platforms. We then discussed the optimal decision-making for the video platform in a competitive market under a symmetric equilibrium. The main conclusions are as follows:
- When the platform makes price decisions, there is a threshold for interactivity. If the interactivity is below the threshold, the video platforms tend to control the number of users and advertisers through pricing, and they obtain a state of equilibrium to optimize profits. If the interactivity is higher than the threshold, the optimal strategy of the video platform is to reduce the charges for users until they have obtained all the users in the market.
- The main parameters of platform decision-making have different effects on profits. Advertising nuisance negatively affects video platform profits, whereas advertiser profitability and interaction have positive effects. Therefore, platforms tend to formulate their optimal pricing strategy according to these three factors.
- Whether the platform adopts a promotion pricing strategy is mainly affected by the interactivity and promotion sensitivity: both of these factors facilitate the promotion pricing strategy. Once the promotion pricing strategy is adopted, the video platforms may help advertisers to provide users with promotions. The platform operation strategy will be different depending on whether the strategy is to acquire some or all of the users.
- When two video platforms in the market are in competition, as the difference in basic utility increases, the difference in their pricing strategies becomes larger. In contrast to a monopoly situation, intense competition may mean that the platforms provide users with free or reward services in order to retain their share of users.
6.2. Managerial Insights
Based on the conclusions and findings of this paper, we offer some management insights for video platforms.
First, interaction is an important factor for improving the profits of both the video platforms and the advertisers. Therefore, the video platforms need to give attention to improving user interactivity.
Second, both advertisement nuisance and advertiser profitability are closely related to the profitability of the video platforms. Therefore, the platforms need to strengthen their supervision of the advertisers. They should review the content of advertisements to ensure their entertainment value and effectiveness so as to reduce the nuisance to users as much as possible, and when providing advertising space, they should select advertisers that are highly profitable.
Third, video platforms need to keep abreast of user interactivity. When the user interaction is weak, the video platforms need to make profits based on user prices, but when the user interactivity is strong, the platforms need to focus more on the number of users.
Finally, video platforms need to identify user demand for promotions. They need to observe the advertisers’ promotions when making decisions and, when the users are sensitive to the promotions, can consider helping the advertisers to mount promotional activities, thus achieving a win-win situation with the advertisers.
6.3. Future Research
Some further research may be required. Although we identified that user interaction is an important factor for video platforms, we need to understand how user interaction is performed and how it can be improved. Hence, we need to analyze the internal mechanisms of the interactions in order to explore how video platforms can improve the users’ interaction utility.
In addition, when a platform adopts a promotion strategy, advertisers may be reluctant to mount promotions, even though their cost of entry is reduced. Meeting the needs of advertisers is a key factor in enabling their promotions on video platforms, and therefore, the features and mechanisms relevant to advertisers require further discussion.
Author Contributions
Conceptualization, W.L.; methodology, W.L. and W.Z.; software, W.L.; validation, W.L., M.J. and W.Z.; formal analysis, W.Z.; investigation, W.L. and W.Z.; resources, M.J.; writing—original draft preparation, W.L.; writing—review and editing, W.L., M.J. and W.Z.; visualization, W.L.; supervision, M.J.; project administration, M.J.; funding acquisition, M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the National Natural Science Foundation of China: No.71831005.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Lemma 1.
According to Equations (3) and (4): ,
Hence, can be solved in equilibrium
It can be seen that , whereas [0, 1]. Hence, when , . In this situation:
☐
Proof of Corollary 1.
According to Equations (3)–(5), it can be expressed as:
Hence, if , the platform’s optimal strategy is to prohibit advertisers. One-sided markets are not our research problem; so, in two-sided platforms, .
Analysis for price:
① When , both and are positive.
② When , . So both and are positive. ☐
Proof of Corollary 2, 3, and 4:
① When :
because , .
because and ,
It is obvious that
because
It is obvious that
② When :
It is obvious that:
if ; else .
☐
Proof of Lemma 2.
According to Equation (6),
hence,
so, when , . ☐
Proof of Lemma 3.
When
According to Equation (6)–(8):
so, the Hessian matrix of is:
A is neither positive nor negative. Therefore, there is no equilibrium solution for .
means that the platform does not adopt a promotion strategy. As is monotonic, if the platform adopts a promotion strategy, take the maximum value of . According to Equation (7), , . Therefore, once the platform adopts a promotion strategy, and .
where
According to Equations (9)–(11):
It can be seen that the second derivative of is 0. Similarly, where , we need to consider the maximum value of , which is .
Hence, the model can be changed as:
It can be seen that the second derivative of is 0. When takes the maximum value, which is , the condition is the same as in the case where the promotion strategy is not adopted. Hence, we only need to consider the condition of , that is, . So, the model of is same as the condition of .
By combining with Equation (8), the equilibrium solution can be obtained:
However, . If , .
Hence:
When :
☐
Proof of Lemma 4:
① When and
② When
When and
, . Hence
③ When
④ When
When and
, . Hence □.
Proof of Lemma 5:
According to Equations (6)–(8):
When video platforms cannot intervene in the promotion behavior of advertisers
When
We obtain the following result:
☐
Proof of Lemma 6:
For the two platforms:
As :
According to and :
Solving the four equations, we obtain:
According to the and equations, we obtain:
☐
References
- Amaldoss, W.; Du, J.Z.; Shin, W. Media platforms’ content provision strategies and sources of profits. Mark. Sci. 2021, 40, 527–547. [Google Scholar] [CrossRef]
- Zennyo, Y. Freemium competition among ad-sponsored platforms. Inf. Econ. Policy 2020, 50, 100848. [Google Scholar] [CrossRef]
- Carroni, E.; Paolini, D. Business models for streaming platforms: Content acquisition, advertising and users. Inf. Econ. Policy 2020, 52, 100877. [Google Scholar] [CrossRef]
- Wilbur, K.C. A two-sided, empirical model of television advertising and viewing markets. Mark. Sci. 2008, 27, 356–378. [Google Scholar] [CrossRef]
- Chi, X.; Fan, Z.P.; Wang, X.H. Pricing mode selection for the online short video platform. Soft Comput. 2021, 25, 5105–5120. [Google Scholar] [CrossRef]
- Hamilton, M.; Kaltcheva, V.D.; Rohm, A.J. Social Media and Value Creation: The Role of Interaction Satisfaction and Interaction Immersion. J. Interact. Mark. 2016, 36, 121–133. [Google Scholar] [CrossRef]
- Lin, X.G.; Hou, R.; Zhou, Y.W. Platform Competition for Advertisers and Viewers in Media Markets with Endogenous Content and Advertising. J. Syst. Sci. Syst. Eng. 2020, 29, 36–54. [Google Scholar] [CrossRef]
- Kim, C.; Yang, S.U. Like, comment, and share on Facebook: How each behavior differs from the other. Public Relat. Rev. 2017, 43, 441–449. [Google Scholar] [CrossRef]
- Caillaud, B.; Jullien, B. Chicken & egg: Competition among intermediation service providers. Rand J. Econ. 2003, 34, 309–328. [Google Scholar]
- Rochet, J.C.; Tirole, J. Platform competition in two-sided markets. J. Eur. Econ. Assoc. 2003, 1, 990–1029. [Google Scholar] [CrossRef]
- Armstrong, M. Competition in two-sided markets. Rand J. Econ. 2005, 37, 668–691. [Google Scholar] [CrossRef]
- Economides, N.; Katsamakas, E. Two-sided competition of proprietary vs. open source technology platforms and the implications for the software industry. Manag. Sci. 2006, 52, 1057–1071. [Google Scholar] [CrossRef]
- Nocke, V.; Stahl, K.; Peitz, M. Platform ownership. J. Eur. Econ. Assoc. 2007, 5, 1130–1160. [Google Scholar] [CrossRef]
- Belleflamme, P.; Toulemonde, E. Negative intra-group externalities in two-sided markets. Int. Econ. Rev. 2009, 50, 245–272. [Google Scholar] [CrossRef]
- Bardey, D.; Cremer, H.; Lozachmeur, J. Competition in two-sided markets with common network externalities. Rev. Ind. Organ. 2010, 44, 327–345. [Google Scholar] [CrossRef]
- Amelio, A.; Jullien, B. Tying and freebies in two-sided markets. Int. J. Ind. Organ. 2012, 30, 436–446. [Google Scholar] [CrossRef]
- Hagiu, A.; Spulber, D. First-Party content and coordination in two-sided markets. Manag. Sci. 2013, 59, 933–949. [Google Scholar] [CrossRef]
- Rasch, A.; Wenzel, T. Piracy in a two-sided software market. J. Econ. Behav. Organ. 2013, 88, 78–89. [Google Scholar] [CrossRef]
- Kaplow, L. Market definition, market power. Int. J. Ind. Organ. 2015, 43, 148–161. [Google Scholar] [CrossRef]
- Dou, G.W.; He, P.; Xu, X.Y. One-side value-added service investment and pricing strategies for a two-sided platform. Int. J. Prod. Res. 2016, 54, 3808–3821. [Google Scholar] [CrossRef]
- Dou, G.W.; Lin, X.D.; Xu, X.P. Value-added service investment strategy of a two-sided platform with the negative intra-group network externality. Kybernetes 2018, 47, 937–956. [Google Scholar] [CrossRef]
- Xue, Z.J.; Cheng, S.Q.; Yu, M.Z.; Zou, L. Pricing models of two-sided markets incorporating service quality. Kybernetes 2019, 48, 1827–1850. [Google Scholar] [CrossRef]
- Bakos, Y.; Halaburda, H. Platform Competition with Multihoming on Both Sides: Subsidize or Not? Manag. Sci. 2020, 66, 5599–5607. [Google Scholar] [CrossRef]
- Feng, N.; Chen, J.J.; Feng, H.Y.; Li, M.Q. Promotional pricing strategies for platform vendors: Competition between first- and third-party products. Decis. Support Syst. 2021, 151, 113627. [Google Scholar] [CrossRef]
- Argentesi, E.; Filistrucchl, L. Estimating market power in a two-sided market: The case of newspapers. J. Appl. Econom. 2007, 22, 1247–1266. [Google Scholar] [CrossRef]
- Godes, D.; Ofek, E.; Sarvary, M. Content vs. Advertising: The impact of competition on media firm strategy. Mark. Sci. 2009, 28, 20–35. [Google Scholar] [CrossRef]
- Reisinger, M. Platform competition for advertisers and users in media markets. Int. J. Ind. Organ. 2012, 30, 243–252. [Google Scholar] [CrossRef]
- Chao, Y.; Derdenger, T. Mixed Bundling in Two-Sided Markets in the Presence of Installed Base Effects. Manag. Sci. 2013, 59, 1904–1926. [Google Scholar] [CrossRef]
- Hagiu, A.; Halaburda, H. Information and two-sided platform profits. Int. J. Ind. Organ. 2014, 34, 25–35. [Google Scholar] [CrossRef]
- Roger, G. Two-sided competition with vertical differentiation. J. Econ. 2017, 120, 193–217. [Google Scholar] [CrossRef]
- Anderson, S.P.; Foros, O.; Kind, H.J. Competition for Advertisers and for Viewers in Media Markets. Econ. J. 2018, 128, 34–54. [Google Scholar] [CrossRef]
- Cheng, X.Y.; Mu, L.F.; Sun, Y.H.; Bian, Y.W. Optimal pricing decisions for the online video platform under customer choice. Asia Pac. J. Oper. Res. 2018, 35, 1850002. [Google Scholar] [CrossRef]
- Li, W.F.; Jiang, M.H.; Zhan, W.T. Why advertise on short video platforms? Optimizing online advertising using advertisement quality. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 54. [Google Scholar] [CrossRef]
- Liu, X.Q.; Zhou, Y.W.; Shen, Y.; Ge, C.M.; Jiang, J.H. Zooming in the impacts of merchants’ participation in transformation from online flash sale to mixed sale e-commerce platform. Inf. Manag. 2021, 58, 103409. [Google Scholar] [CrossRef]
- Shi, S.W.; Chen, M. Would you snap up the deal? A study of consumer behavior under flash sales. Int. J. Mark. Res. 2015, 57, 931–957. [Google Scholar] [CrossRef]
- Ando, T. Merchant selection and pricing strategy for a platform firm in the online group buying market. Ann. Oper. Res. 2018, 263, 209–230. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).