Initial Work on the Development of a Hardware-Based Gradient Descent Trained Expert System

Abstract

Prior work has introduced a form of explainable artificial intelligence that is able to precisely explain, in a human-understandable form, why it makes decisions. It is also able to learn to make better decisions without potentially learning illegal or invalid considerations. This defensible system is based on fractional value rule-fact expert systems and the use of gradient descent training to optimize rule weightings. This software system has demonstrated efficacy for many applications; however, it utilizes iterative processing and thus does not have a deterministic completion time. It also requires comparatively expensive general-purpose computing hardware to run on. This paper builds on prior work in the development of hardware-based expert systems and presents and assesses the efficacy of a hardware implementation of this system. It characterizes its performance and discusses its utility and trade-offs for several application domains.

1. Introduction

Artificial intelligence has been used for applications, including robotics [1], advertising [2], personal digital assistants [3], college admissions [4], operations management [5], gaming [6], determining borrowers credit worthiness [7,8], performing surgery [9,10], and scientific experimentation [11]. It has been identified as a source of future cyber threats [12] and a key mechanism to detect [13] and respond to them. Its use is pervasive in modern society.

One factor that inhibits the utility of artificial intelligence systems is humans’ trust in them. To this end, a key issue with some systems is that humans cannot readily understand techniques’ operations and how particular decisions are made. This is particularly vexing for individuals impacted by these decisions [14]. So-called “explainable” techniques [15,16] have been developed in response to these concerns.

This paper seeks to solve the problem of developing a time-definite, defensible, and low-power/low-cost artificial intelligence technique that is suitable for applications such as cyber-physical system command. Many existing state-of-the-art solutions, which are implemented as software running on general purpose computer systems, are limited by the power and hardware cost of their host hardware and the time variability introduced by algorithms’ iterative processing. Existing hardware implementations (see, e.g., [17]) are responsive to power [18] and cost limitations and some reduce time variability. However, no defensible hardware implementation has been previously produced.

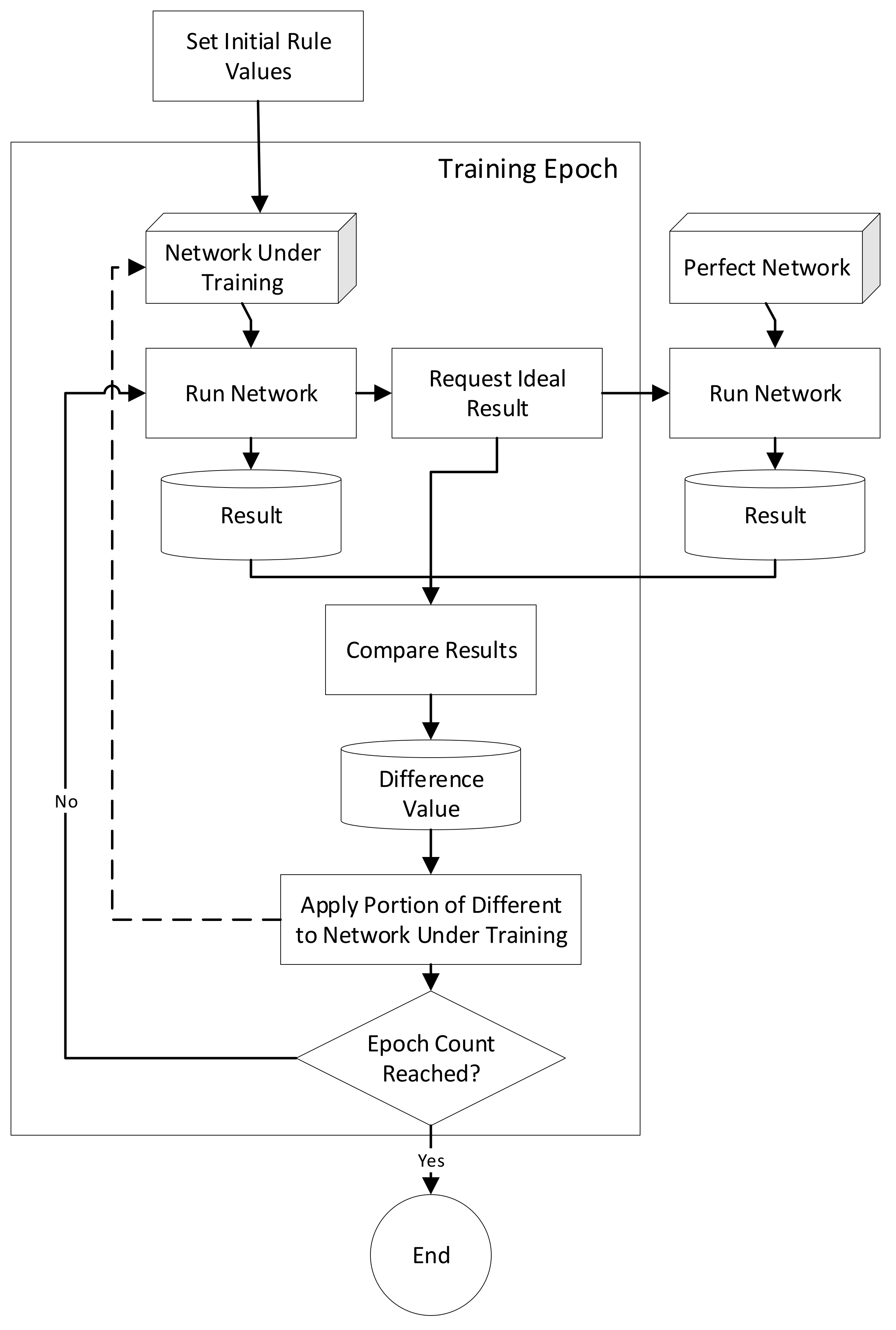
Defensible artificial intelligence, introduced in [19], goes beyond simply requiring the technique’s operations to be understood. It requires the technique to be demonstrably making the correct decision while still having the capability to learn from training and operations. Learning, however, is what creates the potential for artificial intelligence techniques to become “algorithms of oppression” [20] and associate outcomes with confounded characteristics, potentially illegally. Neural networks, in particular, are problematic as they have no specific meaning [21]; rather, they simply learn whatever associations may be present. Their decisions—also problematically—for a given set of inputs, could rapidly change with additional training.

The defensible artificial intelligence system, which was introduced in [19], demonstrated in [22], and refined in [23,24], utilizes expert systems as the basis of its design. Users begin by developing a logically valid network. Then, rule weights (which are floating point numbers between 0 and 1) are optimized using a gradient descent approach, similar to what is commonly used for neural networks.

Expert systems are an early form of artificial intelligence. They began with the Dendral and Mycin [25] systems in the 1960s and 1970s. Because of their design, they are inherently understandable. They utilize a rule-fact network with every fact, generally, having a specific meaning and every rule being logically valid. While they were initially designed to emulate the decisions an expert would make, they have grown and been used in other areas. Examples include control systems [26], facial expression analysis [27], and power system [28] analysis.

Versions of expert systems that use fuzzy logic have been proposed. They use fuzzy set concepts [29] and represent rules’ and facts’ value uncertainty. A taxonomy for these systems was defined by Mitra and Pal [30], who described a “knowledge-based connectionist expert system” that begins with “crude rules”, stores these as connection weights within a neural network, and uses training to produce refined rules. The floating point rule weighting values follow this conceptual model.

Both expert systems and neural networks have typically been implemented using an iterative algorithm. Expert systems use iteration for rule activation and neural networks utilize iteration for training. However, this is problematic for several reasons. First, the network’s output may differ based on the order that rules are selected for execution. The iteration of the expert system’s rule processing engine also means that the decision-making time can only be predicted, limiting the utility of expert systems for controlling robotics and other real-time applications.

The limitation of processing uncertainty can be removed by implementing the system in hardware, which allows rule execution to be performed in parallel. In [31,32], the use of a hardware-based (instead of a software-based) rule-fact network was proposed; however, these papers did not implement or test such a system. A basic hardware Boolean expert system was implemented previously [33] and its performance was characterized, showing that it had a relatively consistent operating speed and high accuracy. These factors, and its lower (as compared to a general-purpose computer) cost, made hardware implementation potentially beneficial for a number of different types of applications.

In this paper, the concept of hardware-based expert systems is further developed through the creation of a gradient descent trained version, which operates conceptually similarly to a neural network. While hardware AI systems have been developed previously, no defensible AI hardware system has been previously created. This paper describes the design of a hardware-implemented gradient descent trainable expert system and discusses its implementation. The efficacy and performance of hardware-based expert systems’ gradient descent-trainable networks are also explored and discussed.

In Section 2, this paper continues with a review of prior work, which provides a foundation for this paper. Section 3 presents the design of the system that was utilized for the experimentation presented herein. Section 4, then, presents the experimental design used for this experimentation. Next, Section 5 presents and analyzes the data collected using this system. Following this, in Section 6, several applications for the proposed system are discussed. Finally, the paper concludes with a discussion of key conclusions and future work in Section 7.

2. Background

This section reviews prior work in several areas, which provides a foundation for the work presented herein. First, prior work on machine learning techniques is reviewed. Next, work on expert systems is presented. Following this, the gradient descent expert system technique and its prior work are discussed. Finally, an overview of prior work on hardware-implemented artificial intelligence is provided.

2.1. Machine Learning

Machine learning is a popular area of artificial intelligence. It can be used to learn about and model complex phenomena from examples or intuit patterns within a dataset. With supervised learning [34], a system is provided a set of inputs and the desired answer. Reinforcement learning [35] is similar: a ‘prize’ is provided to the system to encourage it to learn a desired pattern. Finally, with unsupervised learning [36], the system is provided data and simply identifies patterns present in it (grouping like data, for example).

A number of techniques for training networks exist. One of the most well known is gradient descent [37]. With gradient descent, a partial correction is applied for multiple rounds for the error between the system’s current and target output. It is utilized as part of a supervised learning process and seeks to find the optimal (minimal) error level. The gradient descent technique is frequently used with neural networks.

Backpropagation [38] is a specific type of gradient descent that alters the weights throughout a neural network to correct the difference between the system’s current and target output values. It utilizes an iterative process. A gradient descent technique based on the backpropagation concept was introduced in [19] for use with GDES networks.

Gradient descent and backpropagation are not the only machine learning techniques that can be used. Other techniques have been proposed, which use spiking neural network concepts [39,40], memory use optimization [41], and speculative approaches [42]. Techniques for training neural networks without the use of backpropagation [43,44] have also been proposed.

2.2. Expert Systems

Expert systems began in the 1960s and 1970s with the Dendral [25,45] and Mycin systems [25]. Classical expert systems use rule-fact networks to perform inference [46]. Facts store binary values and rules identify output facts that can be asserted as true when two input facts are true. They utilize a processing engine, which scans through the knowledge base to identify rules that can be executed (based on having their input requirements satisfied). Rules that are identified are run, which results in setting their output facts to true.

In the intervening half-century since their introduction, numerous enhancements of expert systems have been introduced. Optimization techniques [47] and hybrid expert systems [48], which are neural networks, are examples of such enhancements. Fuzzy logic systems, which use fuzzy set concepts [29] and represent uncertainty, have also been proposed.

Mitra and Pal [30] defined a fuzzy logic expert system taxonomy, of which the most advanced level was “knowledge-based connectionist” systems. These start with “crude rules”, stored as neural network connection weights, and the network is trained for their refinement.

Expert systems have been used for application areas such as agriculture [49], autonomous vehicle control [50], education [51], geographic information systems [52], identification of facial features [27], medicine [53,54] (including diagnosing heart disease [55] and hypertension [56]), therapy [57], and software architecture [58].

2.3. Gradient Descent Expert Systems

A machine learning algorithm that trains an expert system was introduced in [19]. This technique, because of its rule-fact expert systems base, is inherently understandable. Moreover, because it is logically connected and cannot create new associations (it optimizes the weightings of existing ones), it is guaranteed to not learn invalid associations. This goes beyond Arrieta et al.’s [59] classifications of systems that are either inherently understandable or retrofit for understandability and was termed “defensible” artificial intelligence [19].

The system runs a gradient descent-style learning algorithm on an expert system rule-fact network to potentially change the weighting of its rule inputs. This is performed by iteratively allocating and correcting for a proportional fraction of the error, between the target and actual output of the system, to each node, which is identified as contributing to the target value. The algorithm is shown in Figure 1.

The gradient descent trained expert system (GDES) was introduced in [19] and techniques to enhance it by reducing error [24], using alternate training techniques [23] and automating network development [60], have been proposed. Its use has also been demonstrated for a limited number of applications (e.g., [22]).

2.4. Hardware AI

A significant amount of work has been performed in implementing artificial intelligence hardware. Batra et al. [17] proffer that AI hardware is creating “the best opportunities for semiconductor companies in decades”, referring both to developing AI-specific hardware and hardware that supports AI applications. Dally et al. [61] attribute the “current revolution in deep learning” as being “fueled by the availability of hardware fast enough to train deep networks in a reasonable amount of time”.

Many AI-related hardware implementations are accelerators. General hardware, such as field programable gate arrays (FPGAs), graphics processing units (GPUs), and application-specific integrated circuits (ASICs), have been utilized to enhance the performance of artificial intelligence systems [62] to meet speed and other needs. Specialized hardware includes ferroelectric memristors (which are suggested to be able to implement brain-inspired techniques) [63], hardware spiking neurons [64], and neuromorphic photonics [65], which can enable specific system types.

Using these and other hardware devices, a variety of hardware-based artificial intelligence systems have been developed. Examples include hardware-based Hopfield neural networks [66], expert systems [33], spiking neural networks [67], q-learning algorithm implementation [68], self-organizing maps [69], quantum neuromorphic systems [70], and hybrid oxide brain-inspired neuromorphic systems [71].

Hardware systems have been shown to provide benefits such as energy efficiency [72,73] and aid in delivering enhanced performance for various application areas, such as sustainable chemistry [74] and biomedical/healthcare [75]. As Berggren et al. [76] notes hardware capabilities set “the fundamental limit of the capability of machine learning” and thus the advancement of hardware capabilities—both generalized and bespoke—is critical to continued growth of machine learning capabilities and adoption.

Initiatives in this area have focused on delivering intelligence via edge computing [77], validating the capabilities, functionality, and reliability of hardware AI implementations [78] and incorporating knowledge of the hardware into system design decisions in hardware-aware [79], co-optimization [80], and co-design [81] processes. Research is also ongoing into hardware AI security [82], explainability [83], and dependability [83].

3. System Design and Implementation

The hardware-based GDES (HGDES) implementation utilizes a computer-based training mechanism (CBTM) and a hardware processing mechanism (HPM). The CBTM utilizes the GDES software that has been previously developed [84]. This software is utilized to determine weightings for the rules that are applied to the HPM. The HPM can serve as an advisor, such as how some traditional software expert systems were used, to another piece of command hardware or a software system (or even an in-the-loop human). The system, however, is designed so that its output can be used directly as a decision-making system via interfacing with and supplying its decisions (output) to other command and control hardware that communicates with sensors and actuators. It is, notably, in this last configuration that the time-determinism benefits of the system are most likely to be benefitted from.

3.1. Hardware Processing Mechanism

The HPM, shown in Figure 2, is comprised of an adder circuit and potentiometers. Each HGDES node takes in four direct current (DC) input voltages, in two pairs. For each component of the pair of input voltages, a potentiometer can be used to apply a weighting value to the source (note that, for experimental purpose, the power supplies’ were used to apply this weighting to the initial inputs). The HPM then adds the voltages from each component in the pair and passes the sum of each pair through another potentiometer, before adding these two results as well (as part of a second layer GDES node on each board). The output of this adder circuit is the output of the particular HGDES board (which can, potentially, serve as the input to another HGDES board). For experimental purposes, potentiometers were inserted between the boards, providing the scaling for the inputs to the next board.

As the potentiometers control the voltage, allowing a voltage ranging from 0 to the full input value to be sent onwards, the combination of the adder and potentiometer provides the fundamental capability of a GDES node. The basic design of the adder circuit that was used is shown in Figure 3. The adder circuits consist of operational amplifiers set up in the non-inverting summing amplifier mode. For this design, 8 pin MCP 602 dual operational amplifiers IC were utilized.

This circuit takes in four DC input voltages in two input pairs (V1, V2 and V3, V4) and adds the individual voltages in each pair, as shown in Figure 4.

The outputs from the operational amplifiers are then passed through two separate potentiometers, as shown in Figure 5. These potentiometers are used to vary the sum voltage between 0 and the full supplied value to apply a weighting to the inputs to the next node. The potentiometers that were utilized were MCP 4131 ICs. They were controlled using the serial peripheral interface (SPI) communications protocol.

Finally, the resulting voltages from the potentiometers are sent to another adder circuit, as shown in Figure 6. This is the last adder circuit in the schematic. The result of this adder is the output of the board, which can be supplied to another GDES node, if needed, for further processing. Note that this diagram includes a second OP AMP, which is shown without connections as the ICs have two packaged into a single chip and only one of the two is used in this instance.

3.2. Hardware Processing Mechanism Design

To provide the requisite functionality, a low-error adder circuit was needed. An operational amplifier (OP AMP)-based adder circuit was designed for this purpose. The values of resistance used for this were derived using the basic non-inverting op amp gain equation in (1), where V_out is the output voltage and V_in is the voltage at the non-inverting input of the amplifier (also labeled the summing junction). A_v is the voltage gain. The relationship between V_out, V_in, and A_v is defined by (1):

$$V_{OUT}=A_V{V}_{IN}$$

(1)

The relationship in (2) is derived by applying Kirchoff’s current law [85] at the summing junction while keeping R1 and R2 equal:

$$V_{IN}=\frac{V_C+V_D}{2}$$

(2)

Combining and simplifying (1) and (2) provides the relationship shown in (3):

$$V_{OUT}=A_V\frac{V_C+V_D}{2}$$

(3)

The voltage divider rule [85] provides that $V_c=0.18 V_1$ and $V_D=0.18 V_2$. By plugging in the values and simplifying further, (4) is derived:

$$V_{OUT}=A_V\times 0.09\left(V_1+V_2\right)$$

(4)

It is necessary to select a value of $A_V$ such that when $A_V$ is multiplied by 0.09, $V_{OUT}=V_A+V_B$. This value is calculated to be 11.1. Next, values of $R_A$ and $R_B$ are selected such that the target value of $A_V=11.1$ is satisfied, as shown in (5):

$$A_V=11.1=1+\frac{R_A}{R_B}$$

(5)

Given this, the value of R_A/R_B should ideally be equal to 10.1. In accordance with this ratio, values of 101 k and 10 k are chosen for R_A and R_B:

$$V_{OUT}=11.1\times \frac{0.18\left(V_1+V_2\right)}{2}$$

(6)

Simplifying this further provides the desired relationship, shown in (7), for the adder circuit:

$$V_{OUT}=0.999\left(V_1+V_2\right)\approx V_1+V_2$$

(7)

3.3. Hardware Processing Mechanism Implementation

The HGDES HPM modules were fabricated as 3.4 inch by 2.2-inch two-layer printed circuit boards (PCBs). This board design is shown in Figure 7. The inputs and outputs are located on the left and right sides of the board, respectively. A constant trace width of 35 mils was used to facilitate the use of a wide variety of fabrication options and to reduce voltage loss. In Figure 3, the blue traces represent the bottom copper layer, and the red traces represent the top copper layer.

The HGDES HPM board is powered by a standard 5 V power supply and the MCP 4131 potentiometer ICs are connected to an external Arduino UNO using header pins located at the top right of the HPM board. The Arduino communicates with the potentiometers, via 3 pins, using the serial peripheral interface (SPI) communications protocol. Figure 8 depicts the Arduino MCP 4131 connections. Multiple potentiometers are connected to the same Arduino microcontroller simultaneously using a chip select pin and two buses.

4. Experimental Design

The experimentation that provides the data analyzed herein was conducted in several parts. First, individual components and boards were analyzed using standard techniques, which are briefly described before the data collected from this is presented in Section 5. Following this, an experiment was conducted using basic GDES networks. These were created using two configurations of four HGDES boards (each of which has three GDES nodes on them). 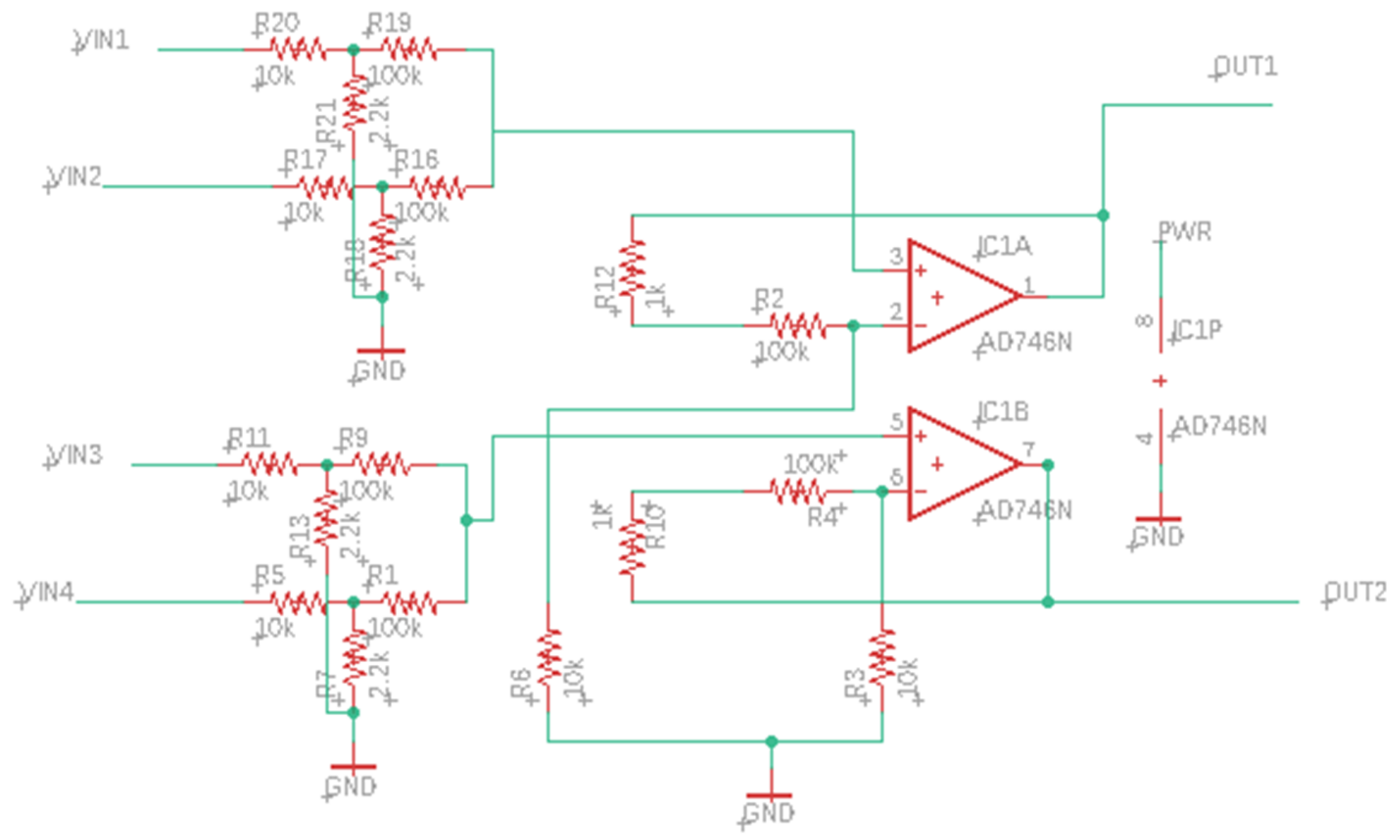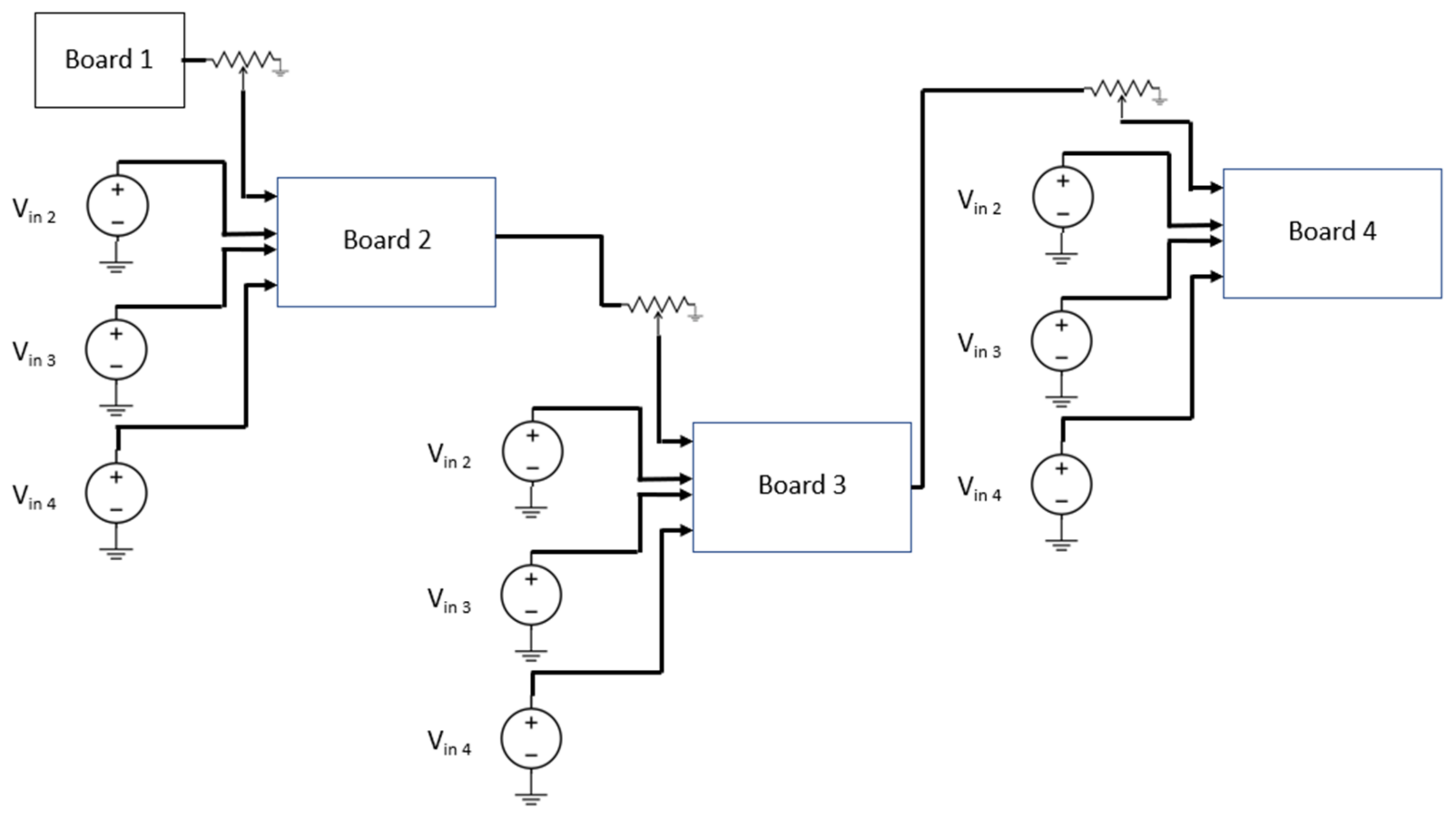Each of these boards has a set of four inputs labeled V₁(top) to V₄(bottom). In configuration 1, which is presented in Figure 9, the outputs of the three boards are used as input to the fourth board. Potentiometers are used to provide the weightings between the boards (controlling the input voltages of each of these four inputs to the first layer of adder circuits on the fourth board). The output of board 4 is the final system output. In this configuration, boards 1, 2, and 3 each have four individual inputs, which can be supplied with any voltage supply, which follows the previously described circuit constraints.

In the second configuration, shown in Figure 10, board 1 is connected to four independent inputs (not shown in the figure), as was the case in configuration 1. Boards 2, 3, and 4, receive their first input from the output of the previous board and the other inputs are connected to independent voltage sources.

As previously noted, the power supplies’ voltage regulation was used to provide the inputs’ weighting for the initial boards, under the first configuration, for experimental purposes. For the second configuration, the power supplies’ voltage regulation provided the weighting for all inputs for board 1 and the second through fourth inputs for boards 2, 3, and 4.

5. Data and Analysis

This section presents the data that was collected and analysis of it. First, basic analysis of the performance of potentiometer chips used for this implementation and the basic three-node board is provided. Next, analysis of the combined (multi-node) circuits is presented. Finally, a basic hardware gradient descent expert system, including its training and performance, is analyzed.

5.1. Basic Circuit Analysis

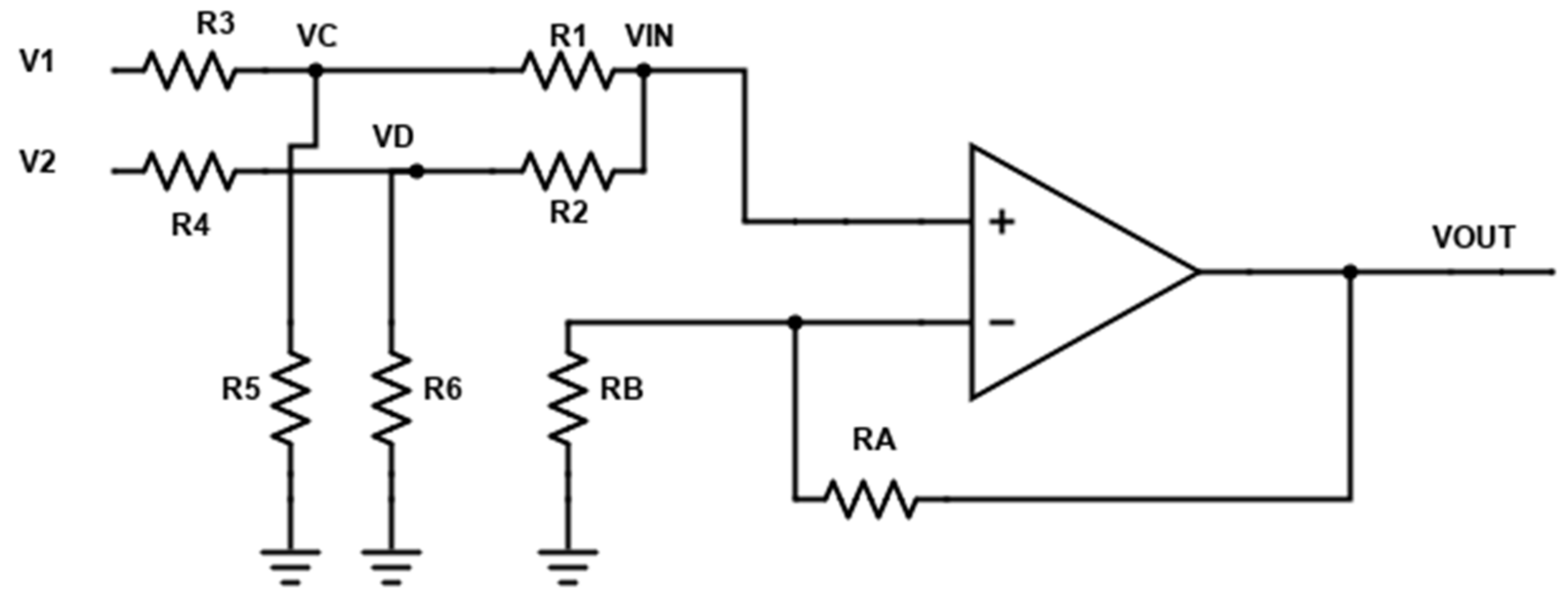
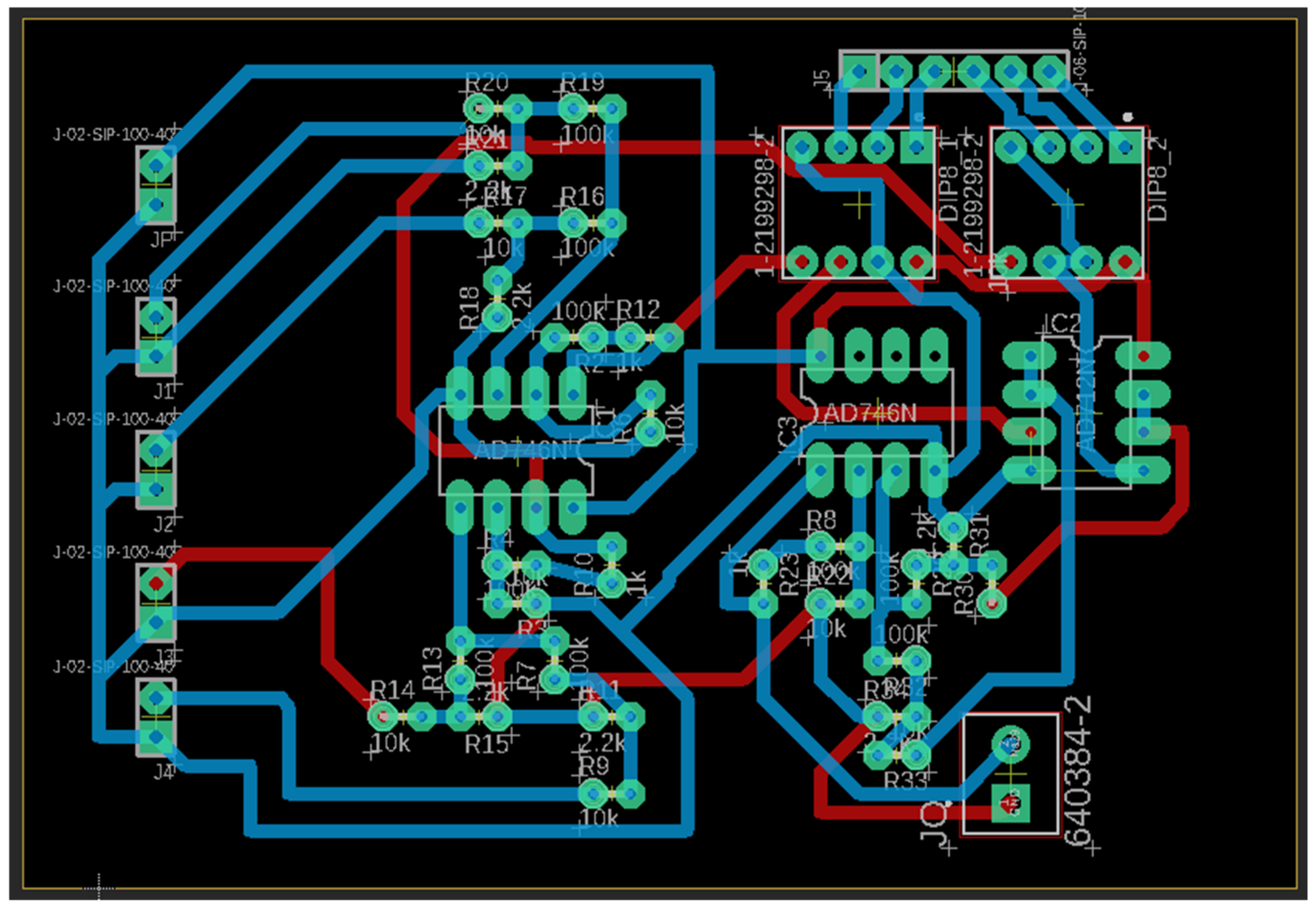
The first testing that was conducted was to validate the accuracy of the circuit design. This was conducted using the built-in SPICE simulation capability in the Eagle PCB Design software. The circuit was implemented using the OP AMP-based adders and potentiometer-based voltage divider circuits, as previously discussed.

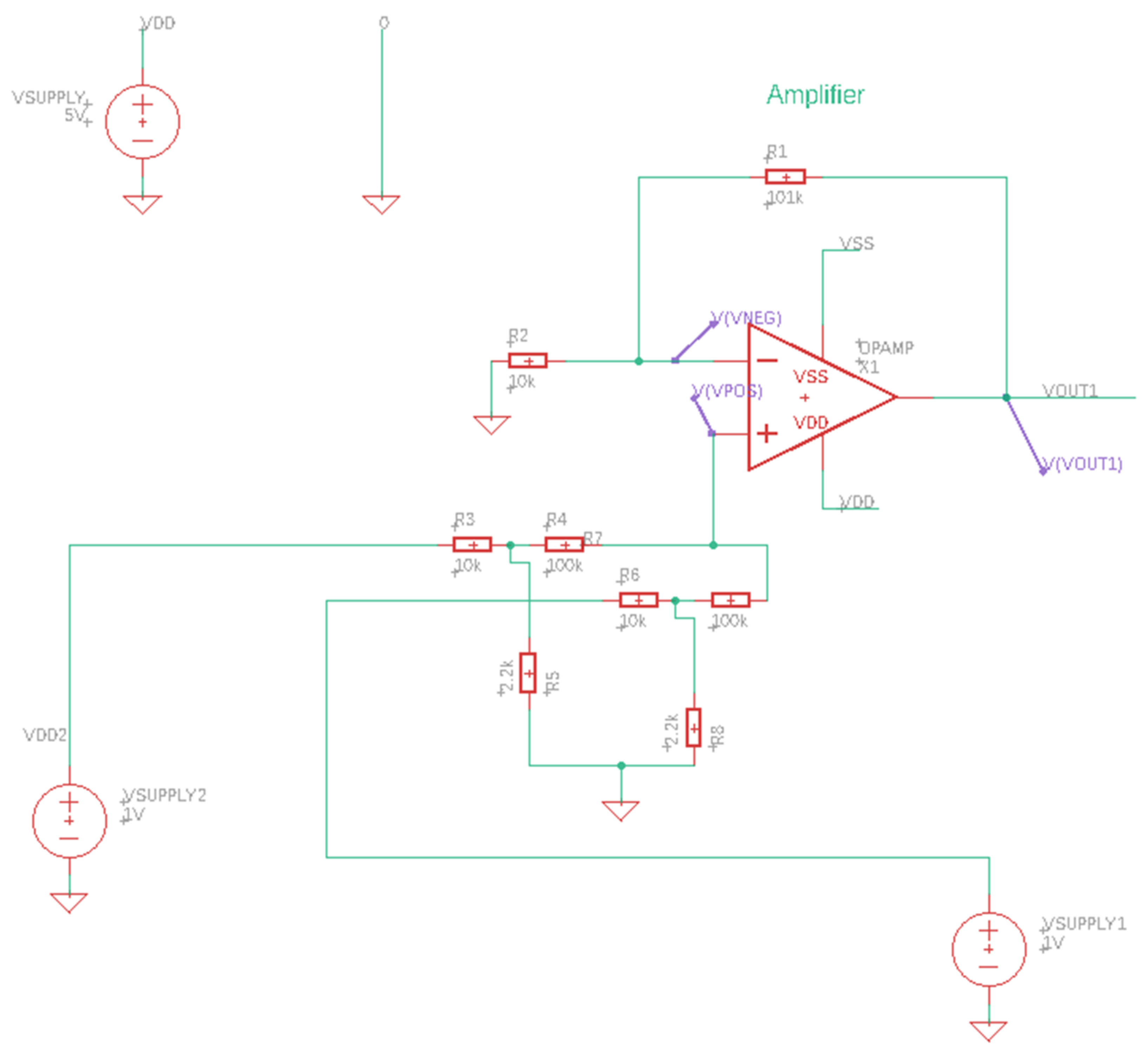
The first simulation, shown in Figure 11, tested the efficacy of a single OP AMP-based adder circuit using SPICE compatible components from the default ngspice library.

This simulation tested what level of error could occur, given different inputs to the adder circuit, which would introduce error into the result of the HGDES system. The results of this testing are recorded in

Table 1. Single OP amp circuit simulation.

Vin1	Vin2	Vout	Videal
1	1	1.803	2.0
1	2	2.999	3.0
2	2	3.999	4.0
3	2	4.999	5.0

.

In most cases, the level of error was minimal. The largest error was seen with the V_in1 = 1, V_in2 = 1 case, where a greater level of error was present. The results verify that the design of the adder circuit schematic is correct, acceptable for most uses, and operates as described in Section 3.2.

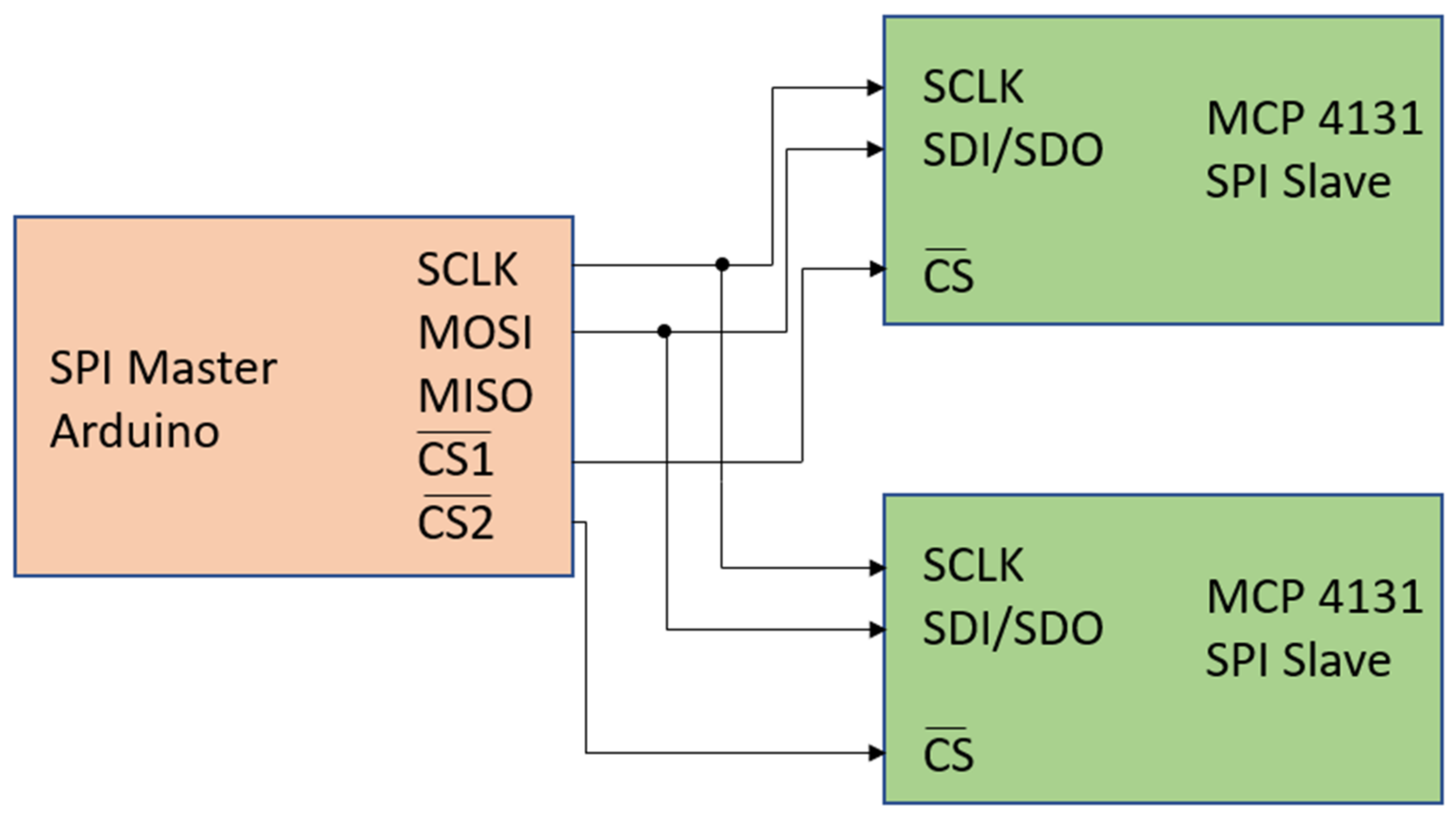
The potentiometer IC-based voltage divider circuit cannot be simulated using this simulation software, as it is operated using an Arduino microcontroller, which is not supported by the software. A hardware test of the MCP 4131 digital potentiometer IC was, thus, performed to characterize the values of resistance that it provides across the first two terminals of the potentiometer, given different input settings. These results are shown in

Table 2. Chip setting resistance values.

Settings	R (Ω)	Ratio
0	9.41 k	0.941
13	8.45 k	0.845
26	7.51 k	0.751
39	6.57 k	0.657
52	5.63 k	0.563
65	4.64 k	0.464
78	3.72 k	0.372
91	2.78 k	0.278
104	1.84 k	0.184
117	0.89 k	0.089
128	89.2	0.00892

. Note that the third column “Ratio” is the ratio of the resistance between terminals 1–2 and terminals 3–4 of the potentiometers and is also the number by which the input voltage of the potentiometers is multiplied.

Next, the individual boards were tested to demonstrate the efficacy of the HGDES nodes and to verify their functionality.

Table 3. First board’s HGDES nodes’ testing results.

Vin1	Vin2	Vin3	Vin4	P1	P2	Vout (Ideal)	Vout (Actual)	Error
1.113	1.062	2.509	0.97	64	64	2.827	2.763	0.064
1.113	1.062	2.509	0.97	32	96	3.153	3.028	0.125
1.113	1.062	2.509	0.97	96	32	2.501	2.394	0.107
1.113	1.062	2.509	0.97	16	112	3.316	3.131	0.185
1.113	1.062	2.509	0.97	112	16	2.338	2.191	0.147
1.113	2.5	2.5	0.97	112	16	3.595	3.475	0.120
1.113	2.5	2.5	0.97	16	112	3.488	3.359	0.129
1.113	2.5	2.5	0.97	96	32	3.577	3.457	0.120
1.113	2.4	2.4	0.97	32	96	3.406	3.377	0.029
1.113	2.5	2.5	0.97	64	64	3.542	3.399	0.143

,

Table 4. Second board’s HGDES nodes’ testing results.

Vin1	Vin2	Vin3	Vin4	P1	P2	Vout (Ideal)	Vout (Actual)	Error
1.113	1.062	2.509	0.97	64	64	2.827	2.833	0.006
1.113	1.062	2.509	0.97	32	96	3.153	2.165	0.988
1.113	1.062	2.509	0.97	96	32	2.501	2.521	0.020
1.113	1.062	2.509	0.97	16	112	3.316	3.322	0.006
1.113	1.062	2.509	0.97	112	16	2.338	2.392	0.054
1.113	1.513	2.509	0.97	112	16	2.733	2.747	0.014
1.113	1.513	2.509	0.97	16	112	3.372	3.378	0.006
1.113	1.513	2.509	0.97	96	32	2.839	2.841	0.002
1.113	1.513	2.509	0.97	32	96	3.266	3.286	0.020
1.113	1.513	2.509	0.97	64	64	3.053	3.050	0.003

,

Table 5. Third board’s HGDES nodes’ testing results.

Vin1	Vin2	Vin3	Vin4	P1	P2	Vout (Ideal)	Vout (Actual)	Error
1.113	1.04	2.509	0.97	64	64	2.816	2.828	0.012
1.113	1.04	2.509	0.97	32	96	3.148	3.164	0.017
1.113	1.04	2.509	0.97	96	32	2.485	2.497	0.012
1.113	1.04	2.509	0.97	16	112	3.313	3.328	0.015
1.113	1.04	2.509	0.97	112	16	2.319	2.33	0.011
1.113	1.513	2.509	0.97	112	16	2.733	2.735	0.002
1.113	1.513	2.509	0.97	16	112	3.372	3.389	0.017
1.113	1.513	2.509	0.97	96	32	2.839	2.848	0.009
1.113	1.513	2.509	0.97	32	96	3.266	3.287	0.021
1.113	1.513	2.509	0.97	64	64	3.053	3.066	0.013

and

Table 6. Fourth board’s HGDES nodes’ testing results.

Vin1	Vin2	Vin3	Vin4	P1	P2	Vout (Ideal)	Vout (Actual)	Error
1.113	1.04	2.509	0.97	64	64	2.816	2.828	0.012
1.113	1.04	2.509	0.97	32	96	3.148	3.171	0.023
1.113	1.04	2.509	0.97	96	32	2.485	2.497	0.012
1.113	1.04	2.509	0.97	16	112	3.313	3.341	0.028
1.113	1.04	2.509	0.97	112	16	2.319	2.327	0.008
1.113	1.519	2.509	0.97	112	16	2.738	2.758	0.020
1.113	1.519	2.509	0.97	16	112	3.373	3.403	0.030
1.113	1.519	2.509	0.97	96	32	2.844	2.864	0.020
1.113	1.519	2.509	0.97	32	96	3.267	3.293	0.026
1.113	1.519	2.509	0.97	64	64	3.056	3.075	0.020

present the results of the testing for boards 1 to 4, respectively.

The error levels present in the boards are quite limited (ranging from 0.002 to 0.185, with an apparent anomaly of almost a volt error in once instance). These are within acceptable levels of error for many, if not most, applications.

5.2. Combined Circuit Analysis

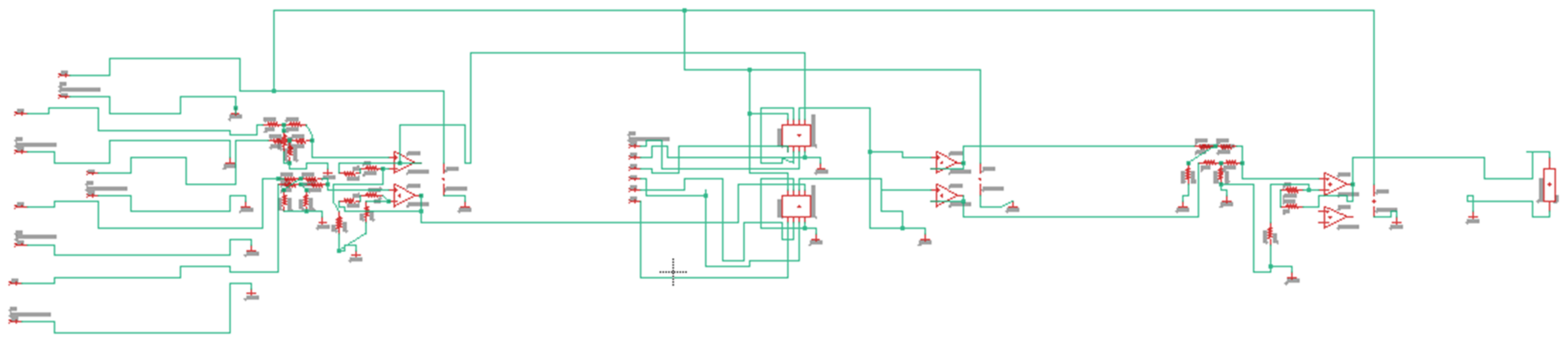
Next, testing was conducted using multiple boards in the configurations described in Section 4. The performance of these multi-board configurations was assessed. This testing was conducted using the experimental setup (with varying wiring between the two configurations) shown in Figure 12.

To test the multi-board configurations, pre-weighted inputs were supplied using voltage-regulated power supplies. The values of these supply voltages for the 11 tests are provided in

Table 7. Input voltages for network configuration 1 tests.

Vin1	Vin2	Vin3	Vin4
1	1	1	1
0.5	1.5	3	1
0.5	1.5	3	1
0.5	1.5	3	1
0.5	1.5	3	1
2	2	2.5	1
2	2	2.5	1
2	2	2.5	1
2	2	2.5	1
2	2	2.5	1
2	2	2.5	1

. Note that a limited amount of error, not considered in this table, was introduced by the voltage sources. This is anticipated to be less than ±0.1 V. The potentiometer settings used for the 11 tests are presented in

Table 8. Potentiometer settings for network configuration 1 tests.

B1P1	B1P2	B2P1	B2P2	B3P1	B3P2	B1OPot	B2OPot	B3OPot	B4P1	B4P2
64	64	64	64	64	64	0.5	0.5	0.5	64	64
64	64	64	64	64	64	0.5	0.5	0.5	64	64
64	64	64	64	64	64	0.5	0.5	0.5	16	112
64	64	64	64	64	64	0.355	0.666	0.345	112	16
64	64	64	64	64	64	0.355	0.666	0.67	112	16
64	64	64	64	64	64	0.499	0.493	0.499	64	64
64	64	64	64	64	64	0.499	0.493	0.499	28	100
64	64	64	64	64	64	0.499	0.493	0.499	100	28
64	64	64	64	64	64	0.3	0.7	0.499	100	28
28	100	64	64	64	64	0.3	0.7	0.499	100	28
28	100	96	32	64	64	0.3	0.7	0.499	100	28

.

Based on the input voltages and potentiometer settings presented in Table 7 and Table 8, the ideal output values were calculated. These are presented in

Table 9. Ideal and actual output voltages for network configuration 1 tests.

B4O (Ideal)	B4O (Actual)	% Error
2	2.044	2.20%
2.75	2.799	1.78%
2.5625	2.495	2.63%
2.9345	2.896	1.31%
3.056375	3.022	1.12%
3.295625	3.295	0.02%
3.056914	3.067	0.33%
3.534336	3.534	0.01%
3.557773	3.574	0.46%
3.524814	3.541	0.46%
3.593174	3.595	0.05%

. This table also includes the actual output values that were measured, using a digital multi-meter, from the hardware circuits. The percentage error was also calculated. These error values ranged from 0.02% to 2.63%. This level of error is tolerable for many, if not most, applications of this system.

Experimentation was also conducted using the second network configuration presented in Section 4. The input voltages used for the 10 tests for this configuration are presented in

Table 10. Input voltages for network configuration 2 tests.

Vin1	Vin2	Vin3	Vin4
2	1	2.5	1
2	1	2.5	1
2	1	2.5	1
2	1	2.5	1
2	1	2.5	1
2	1.5 *	2.5	1
2	2	2.5	1
2	2	2.5	1
2	2	2.5	1
2	2	2.5	1

* Measured at 1.583 V.

and the potentiometer settings used for these tests are presented in

Table 11. Potentiometer settings for network configuration 2 tests.

B1P1	B1P2	B1OPR	B1PPO	B2P1	B2P2	B2OPR	B2O	B3P1	B4P1	B4P2
64	64	0.502	1.6315	64	64	0.481	1.474626	64	16	112
64	64	0.502	1.6315	64	64	0.481	1.474626	64	64	64
64	64	0.502	1.6315	64	64	0.481	1.474626	64	112	16
64	64	0.502	1.6315	64	64	0.481	1.474626	32	112	16
64	64	0.502	1.6315	0	128	0.481	1.6835	32	112	16
64	64	0.502	1.777833	0	128	0.481	1.6835	32	112	16
64	64	0.502	1.8825	96	32	0.481	1.821487	32	112	16
64	64	0.502	1.8825	96	32	0.481	1.821487	32	112	16
64	64	0.502	1.8825	96	32	0.217	0.821752	32	112	16
64	64	0.3	1.125	96	32	0.145	0.466719	32	32	96

. Note that a limited amount of error, not considered in Table 10, was introduced by the voltage sources. This is anticipated to be less than ±0.1 V.

Based on the voltage inputs and potentiometer settings provided in Table 10 and Table 11, the ideal output values were again computed. These are presented in

Table 12. Ideal and actual output voltages for network configuration 2 tests.

B4O (Ideal)	B4O (Actual)	% Error
3.375327	3.397	0.64%
3.001309	3.031	0.99%
2.627291	2.677	1.89%
2.740114	2.787	1.71%
2.763097	2.805	1.52%
3.33737	3.354	0.50%
3.763311	3.81	1.24%
3.468826	3.5	0.90%
3.37938	3.401	0.64%
3.456462	3.467	0.30%

. The actual output values, collected using a digital multi-meter, are also presented in this table and the level of error was again calculated. The error level for this (longer) configuration ranged from 0.50% to 1.89%. Notably, the range of error closes somewhat. These error levels are, similarly, within the range acceptable for many, if not most, applications. Additionally, this testing demonstrates that error does not increase dramatically (average error increases from 0.94% to 1.03%) with more layers of nodes, which is critical to implementing more complex HGDES networks.

5.3. Training and Hardware Implementation

At present, the HGDES system relies upon the software implementation for its training operations, which generate the weighting values that are used as part of the HGDES networks. The digital implementation of the GDES system does not introduce error as part of the presentation function (which is the capability currently implemented via the HGDES system); however, its training mechanism is not perfect and introduces error. The error levels of the base system (without incorporating error reduction mechanisms) ranged from 5.2% to 8.3% [19], meaning that the training error will dominate the hardware implementation error. Even with error reduction, which showed potential to reduce the upper end of this range down to 5.5% [24], the training error would still be approximately 5 times greater than the hardware implementation presentation error.

Notably, the benefit of the hardware implementation, in terms of processing performance, is significant. It reduces the speed of processing from multiple iterations of network processing to the speed of the critical (longest time-wise) path of IC’s operating speeds. The ICs operate, inherently, in parallel while the software implementation must perform these same functions sequentially. Because of this, the level of benefit enjoyed will vary notably by network design. The assessment of this, with larger networks, is a planned area of future work.

In addition to the overall speed benefit, the hardware implementation will always process (for a given network) in the same amount of time. This is critical to time-sensitive applications, such as robotics, where decisions must be made within timeframes dictated by their real-world needs (e.g., the time between a robot sensing something up ahead and reaching its location). Thus, the hardware implementation will be suitable for some applications where a variable processing time software-based system would not be.

The hardware-based system also enjoys power consumption and cost-based benefits, as compared to operations on a general-purpose computer. For example, a laptop-based solution (such as what was used for testing) might cost hundreds of dollars and consume 20–50 watts of power [87]. The test boards cost less than $50 each (which would be further reduced significantly, on a per-GDES node basis, by the use of larger boards with more nodes on them and through mass production) and used only a small fraction (only about 3.475 micro amps) of the power [88,89]. Additional power savings are also enjoyed due to the fact that the HGDES system can be powered up, have its potentiometer values set, have needed tests run, and be powered-down, without requiring the boot-up and shut-down phases (introducing both a time and power cost) of conventional computers.

6. Application Areas

The HGDES system provides benefits that make it well suited for several types of application areas. Its key benefits are the lower cost and power requirements of the system, as compared to a conventional computer, solution defensibility, and processing time determinism. Applications that benefit from any (or several) of these are candidates for HGDES use. Each area of benefit is now discussed.

6.1. Cost and Power

Cost and power benefits can be enjoyed by most applications. Applications that may collect and process data in situ or in impoverished areas may benefit from the lower cost of purpose-developed computing hardware and the reduced power levels that it requires. The boards tested herein are estimated to require, on average, 10 milliwatts, as compared to many computers that may require hundreds of watts. Applications such as water sediment monitoring and prediction [90] and rainfall prediction [91] may benefit from performing processing using low-cost hardware at or near the points of data collection. In many cases, limited power may be available in these locations, which may be supplied using solar cells or batteries, allowing the application area to benefit from the hardware’s low power costs as well. Flore, Maximilien, and Sègbè [92] demonstrated the utility of using artificial intelligence to make public health decisions in under-resourced areas. These types of applications are also enabled by the low cost of the proposed HGDES. Robotic command applications may, similarly, benefit as robots typically have power limitations and operating cycles that are defined by their power consumption versus generation and storage capabilities.

6.2. Solution Defensibility

Defensibility is critical for numerous applications. Any application where liability may be associated with system performance failures can prospectively benefit from the concept of defensibility. This includes systems that make human-impacting decisions, such as for credit assessment and candidate screening purposes. Systems that operate in medical environments, such as those that aid in or perform diagnosis and surgery [93], may present a particular risk that defensibility can mitigate. Robots that interact with humans or other objects and could potentially injure or damage people or equipment nearby may need to explain and defend their decision making should an incident occur. Surgical robots [94,95], thus, may benefit particularly form this capability, which would allow them to prevent known issues from occurring and explain decisions made during surgery, both for continuous improvement and malpractice investigation purposes. Autonomous vehicles [96,97], similarly, make decisions that affect people and property and could, similarly, benefit from defensibility to attempt to avoid making problematic decisions and to justify the decisions that the system makes.

6.3. Processing Time Determinism

Processing time determinism can be critical for numerous applications, including those that must provide system responsiveness to users. It can also be useful for quantifying processing time needs for most applications. However, systems that operate in a real-world environment have a requirement for this determinism capability to allow them to make decisions fast enough to operate safely. A robot, for example, may need to make an avoidance decision or path planning change before colliding. An autonomous vehicle might face the difficult choice between colliding with a young or an elderly person, if no way to avoid them both is possible. In each of these cases, the decision must be made fast enough, after detection, to allow a maneuver to be performed before the obstacle is reached. Most robots, thus, have this type of a need, making the processing time determinism useful for surgical robots [94,95] and autonomous vehicles [96,97], as previously discussed. Supporting technologies for these types of systems, such as systems that evaluate data trust (e.g., [98]), may also require time determinism to support the time determinism of their dependent decision-making systems.

Some systems (e.g., [99]) will have needs that span two or more of these categories. Several examples of this have been discussed previously. These systems are the most logical candidates to make use of and benefit from HGDES.

7. Conclusions and Future Work

This paper has presented initial work on the implementation of a hardware-based implementation of a gradient-descent trained expert system. It has shown that the previously software-based GDES nodes can be readily implemented in hardware and an analog signal, voltage, can be sent between them as data. It has shown that the required circuits can be developed with a low level of data loss (an average of approximately 1%), making them suitable for many—if not most—applications. Further, it has discussed the speed, power reduction, and cost reduction benefits of this implementation approach.

Notably, the proposed approach also provides a time-determinism benefit as well, as the hardware-implemented GDES system operates within an a priori known amount of time (which does vary by GDES network). This makes the system suitable for applications that require real-time or near real-time processing, such as robotics. In many cases, unknown duration iterative-based processes (such as software-based GDES) cannot be used for real-time command or require compensation for potential processing delays via using hardware with capabilities that far exceed the typical needs (but are projected to be sufficient for worst case scenarios). Hardware-based GDES, thus, would be suitable for various real-world applications that software-based GDES would potentially either not be usable for or for which it would require additional hardware capabilities.

Based on this initial work, a number of areas of future work are planned. The implementation and testing of larger networks is one area of planned future work. With these larger networks, the potential for the training process to take the hardware implementation error into account when training will be assessed. A second area of potential future work is to develop a hardware-based training mechanism.

Overall, the work presented herein has demonstrated the potential efficacy of hardware implementation of the GDES system and its effectiveness and suitability for many applications. This initial work demonstrates the value of the system and serves as a potential justification for future work in the areas mentioned above, which will further advance the system to be ready for practical use.