A Robust Possibilistic Programming Approach for a Road-Rail Intermodal Routing Problem with Multiple Time Windows and Truck Operations Optimization under Carbon Cap-and-Trade Policy and Uncertainty
Abstract
1. Introduction
- (1)
- Establishing a road-rail intermodal hub-and-spoke network in which rail services are scheduled and road services are flexible to match a realistic transportation scenario.
- (2)
- Employing the carbon cap-and-trade policy to reduce carbon dioxide emissions to achieve sustainable transportation.
- (3)
- Setting multiple time windows and considering time window selection to enhance customer flexibility and realize on-time pickups and deliveries for the entire transportation process.
- (4)
- Formulating the routing problem in an uncertain environment where capacity and the carbon trading price rate are uncertain to reduce risks and improve the feasibility and optimality of the routing.
- (5)
- Integrating truck operations optimization, including departure time planning under traffic restrictions, and speed optimization into the routing to strengthen the comprehensive performance of the problem optimization on various objectives.
2. Literature Review
- (1)
- Although widely explored by current studies, the green intermodal routing neglects the carbon cap-and-trade policy that could be a better choice on emission reduction.
- (2)
- Current studies depend on distribution route design to realize emission reduction, which limits the performance of routing on reducing emissions. The diversity and integration of emission reduction approaches should thus be enhanced.
- (3)
- Pickup timeliness is not fully considered, and the use of a single time window for pickup or delivery of each transportation order does not match the realistic situation and limits the customer flexibility.
- (4)
- Combination of capacity fuzziness and the carbon trading price rate fuzziness is not well formulated, and the chance-constrained programming proposed by the existing literature has obvious weaknesses and cannot effectively handle the risks caused by the fuzzy environment.
- (5)
- Road service flexibility is not fully studied, and truck operations optimization combining truck departure time planning and speed optimization that could improve the performance of optimization is not paid enough attention by the current studies.
- (1)
- Multiple time windows for pickup and delivery services and road service flexible were comprehensively integrated into the green routing in a road-rail intermodal hub-and-spoke network to make the routing problem a combination of distribution route design, time window selection and truck operations optimization under traffic restrictions.
- (2)
- The carbon cap-and-trade policy was adopted by the proposed routing to reduce carbon dioxide emissions, in which its performance was compared with the carbon tax policy, and the effects of multiple time windows and truck operations optimization on the policy performance were evaluated.
- (3)
- A fuzzy environment containing both capacity and the carbon trading price rate fuzziness was associated with the proposed routing, and a robust possibilistic programming approach was developed to enhance the feasibility and optimality of the routing optimization.
3. Problem Description
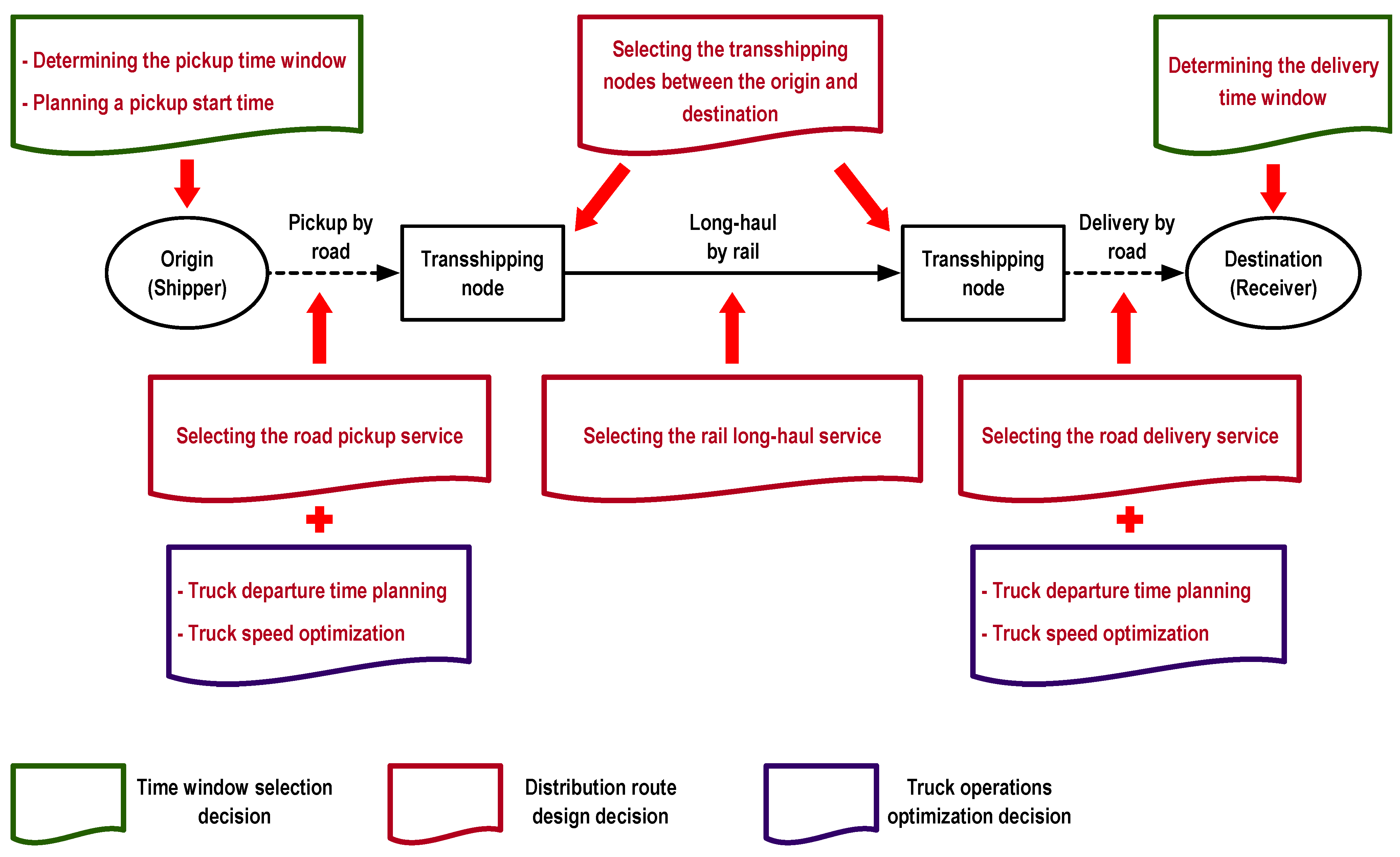
3.1. Decision Makings in the Proposed Routing Problem
3.2. Modeling of the Coordination between Road and Rail in the Transshipment
3.3. Modeling of the Speed-Dependent Carbon Dioxide Emissions for Road Services
3.4. Proposing of the Methodology
4. Proposed Green Road-Rail Intermodal Routing Model
4.1. Optimization Model
4.2. Model Linearization
5. Proposed Robust Possibilistic Programming Approach
5.1. Basic Possibilistic Chance-Constrained Programming Model
5.2. Robust Possibilistic Programming Model
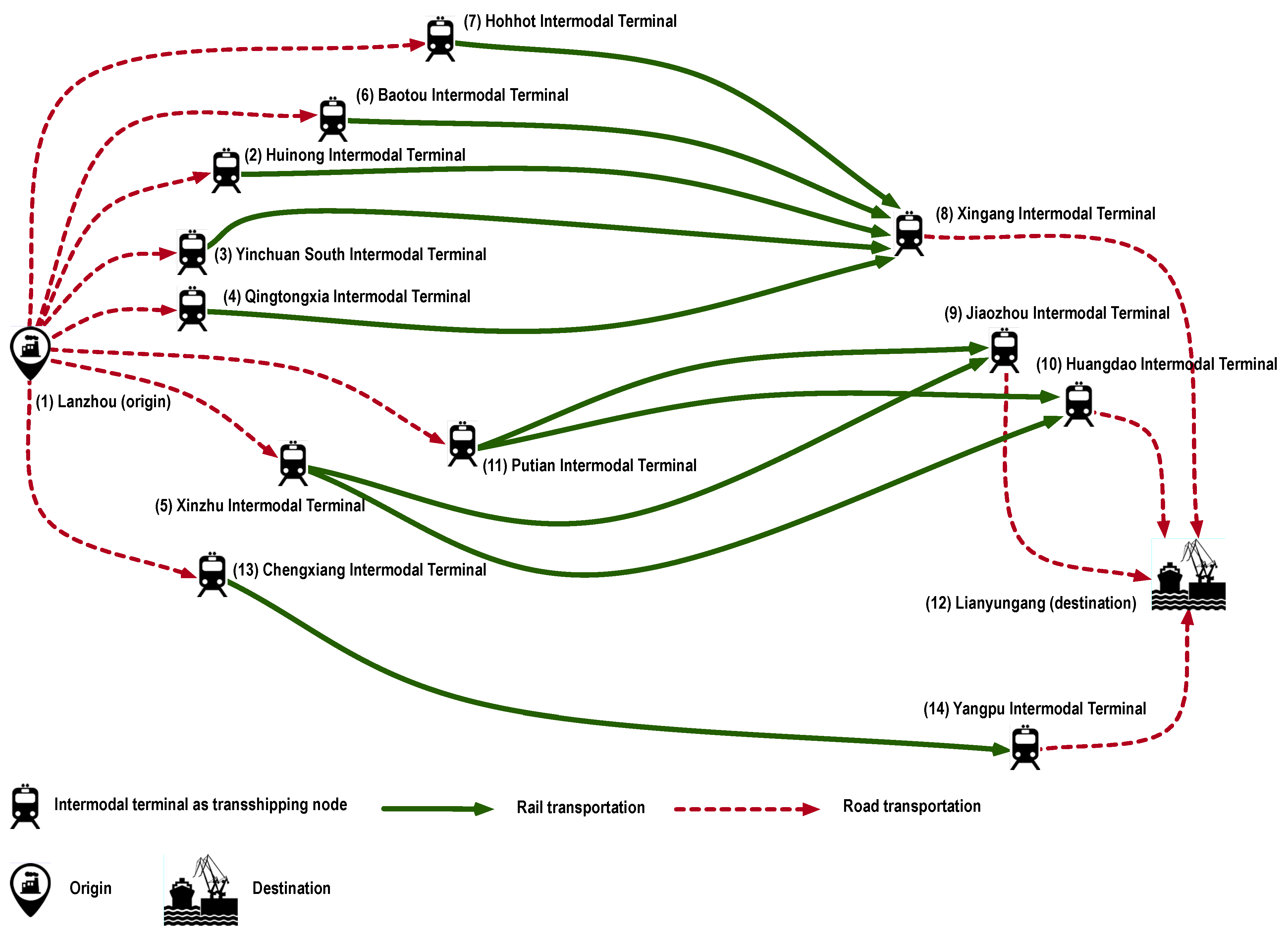
6. An Empirical Case Study
6.1. Optimization Results
6.2. Case Analysis
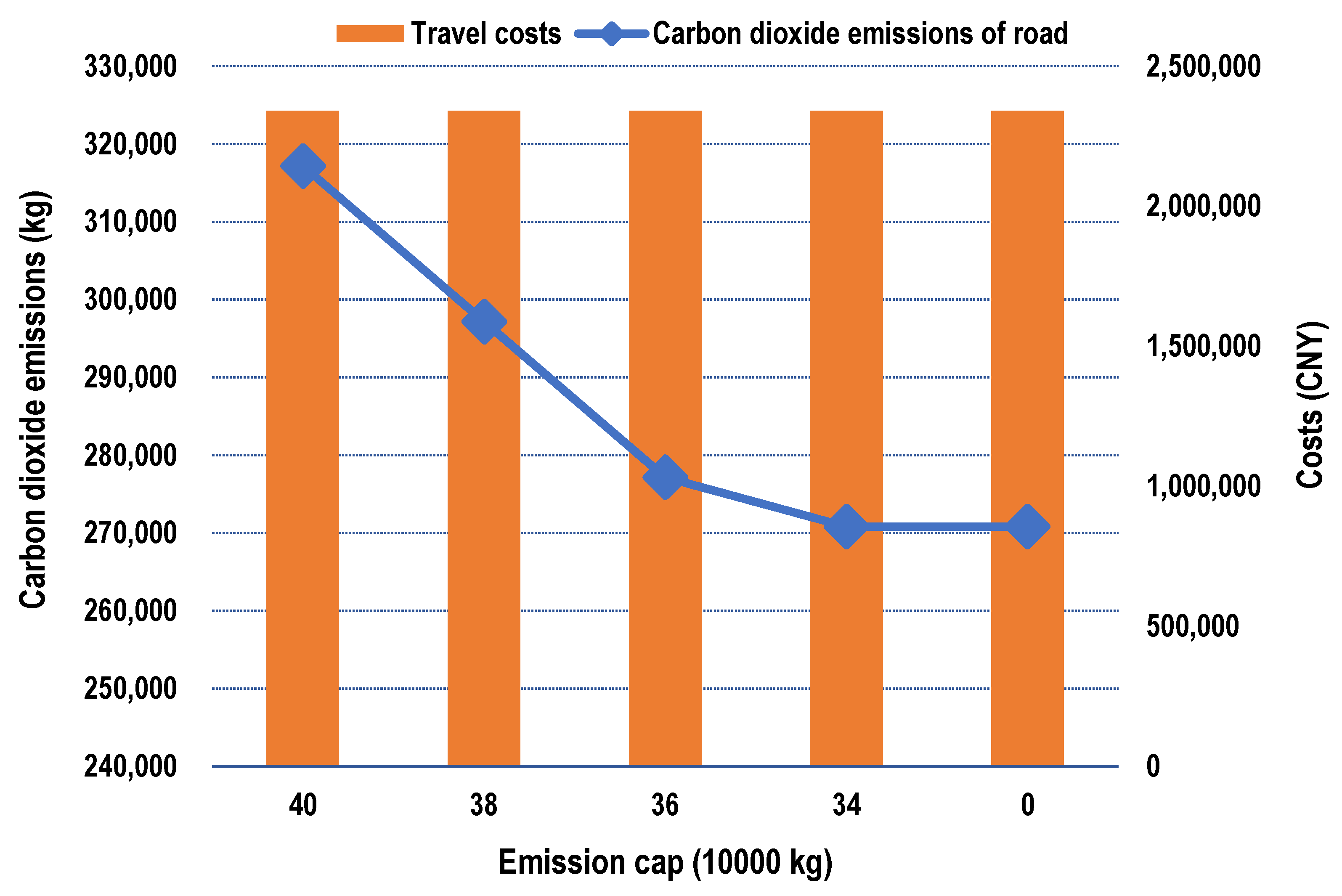
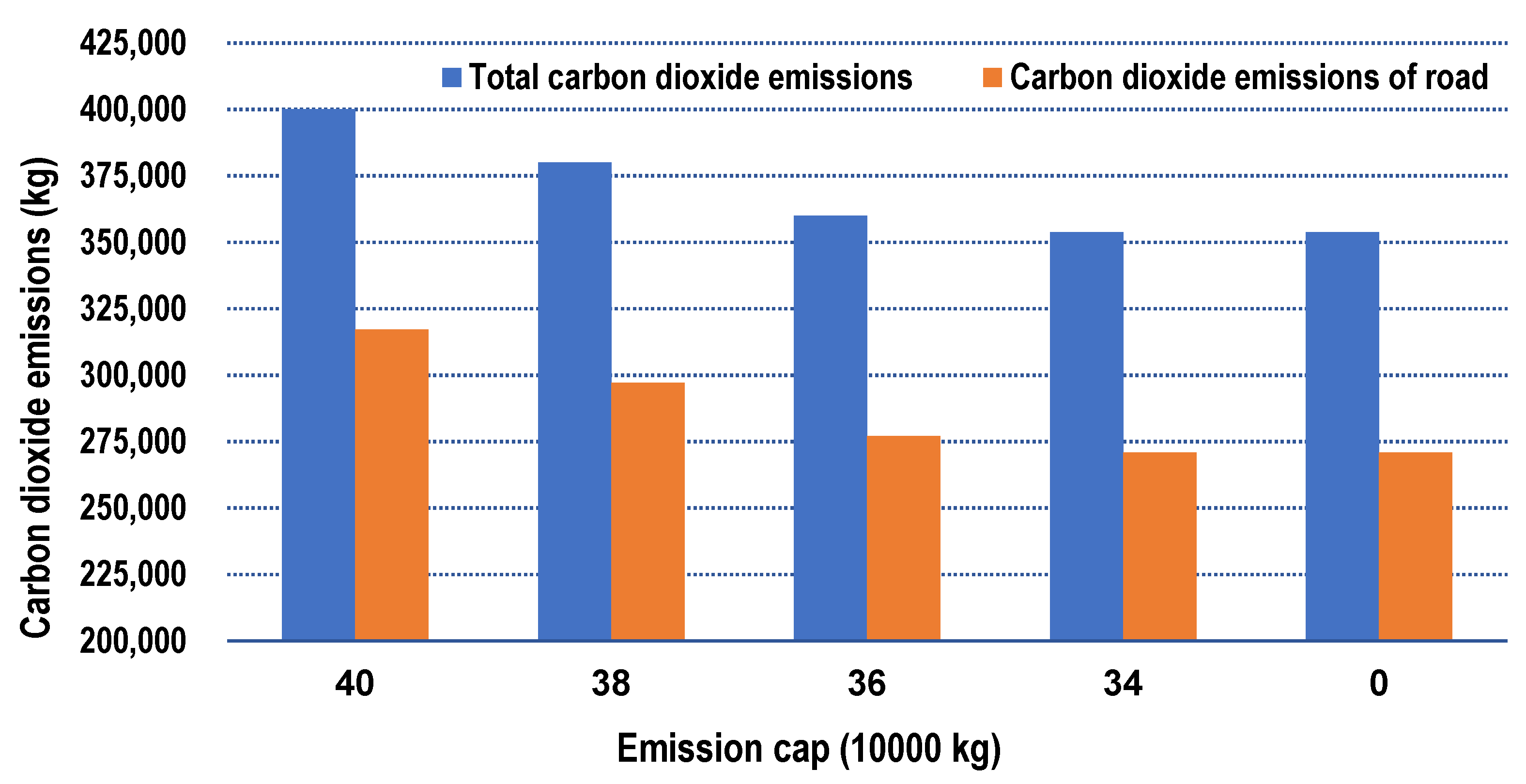
6.2.1. Analysis on the Effects of the Emission Cap on the Optimization Results
6.2.2. Analysis on the Effects of the Multiple Time Windows on the Optimization Results
6.2.3. Analysis on the Effects of the Truck Operations Optimization on the Optimization Results
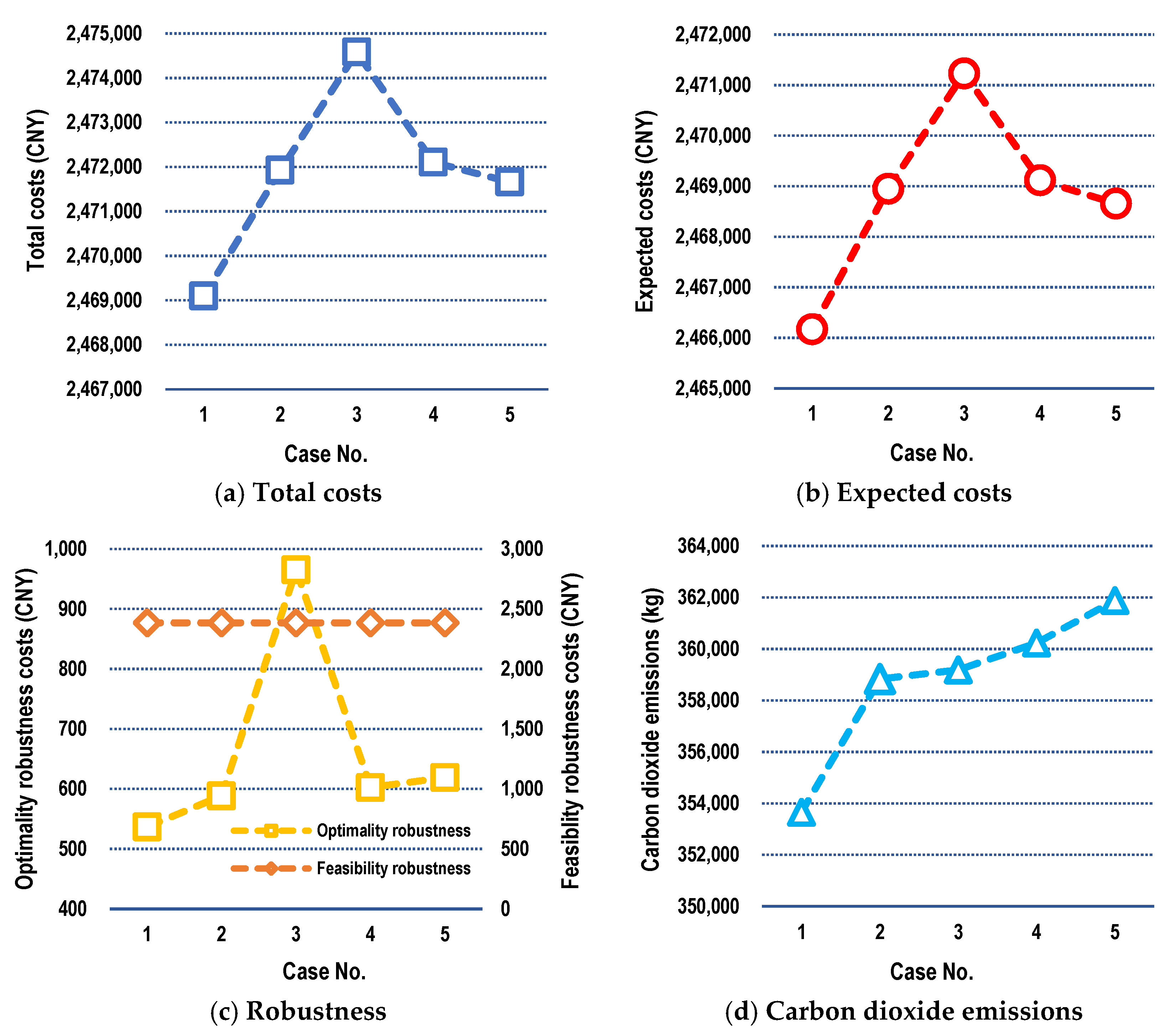
6.2.4. Sensitivity Analysis
6.3. Findings
- (1)
- The RPP model was more efficient than the BPCCP model in optimizing the routing problem by providing higher cost-efficient solutions and enhancing the robustness of the solutions.
- (2)
- The carbon cap-and-trade policy reduced the total costs and optimized the optimality robustness of the routing problem when compared with the carbon tax policy.
- (3)
- When reducing carbon dioxide emissions was the primary goal, the carbon cap-and-trade policy did not always work better than the carbon tax policy. However, when the two policies achieved the same performance on emission reduction, the carbon cap-and-trade policy was more suitable and motivating to be adopted due to its advantages in improving both the economy and robustness of the routing.
- (4)
- The carbon cap-and-trade policy in a fuzzy environment depended on the design of a suitable emission cap to improve its performance and should be attached with great importance by intermodal operators.
- (5)
- Multiple time windows and truck operations optimization significantly strengthened the comprehensive performance of the routing by reducing the costs, improving the optimality robustness, and lowering the carbon dioxide emissions.
- (6)
- In the truck operations optimization, the truck departure time planning ensured that a feasible routing decision can be made under road traffic restrictions.
- (7)
- Improving the confidence level provided a solution to enhance the robustness and reduce the carbon dioxide emissions of the routing. However, it caused an increase in the total costs. The intermodal operator thus needs to make tradeoffs in this conflicting situation.
7. Conclusions
- (1)
- A green road-rail intermodal routing that models both schedule-based and flexible services in a road-rail intermodal hub-and-spoke network and considers capacity uncertainty was explored to make the problem match the realistic transportation scenario.
- (2)
- The carbon cap-and-trade policy was introduced into the routing, in which the uncertainty of the carbon trading price was formulated. The performance of the carbon cap-and-trade policy was systematically discussed by comparison with the carbon tax policy.
- (3)
- Multiple time windows and truck operations optimization under road traffic restrictions were integrated into the routing to make the problem more realistic and was verified to be able to improve the comprehensive performance of the problem optimization.
- (4)
- A robust possibilistic programming approach was developed to deal with the problem and showed good feasibility on obtaining efficient solutions to the dynamic and uncertain decision-making environment.
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hosseini, S.; Al Khaled, A. Freight flow optimization to evaluate the criticality of intermodal surface transportation system infrastructures. Comput. Ind. Eng. 2021, 159, 107522. [Google Scholar] [CrossRef]
- Delbart, T.; Molenbruch, Y.; Braekers, K.; Caris, A. Uncertainty in intermodal and synchromodal transport: Review and future research directions. Sustainability 2021, 13, 3980. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Q.; Chen, D. Route selection of multimodal transport based on China railway transportation. J. Adv. Transp. 2021, 2021, 9984659. [Google Scholar] [CrossRef]
- Guo, W.; Atasoy, B.; Negenborn, R.R. Global synchromodal shipment matching problem with dynamic and stochastic travel times: A reinforcement learning approach. Ann. Oper. Res. 2022, 1–32. [Google Scholar] [CrossRef]
- Bierwirth, C.; Kirschstein, T.; Meisel, F. On transport service selection in intermodal rail/road distribution networks. Bus. Res. 2012, 5, 198–219. [Google Scholar] [CrossRef]
- Heggen, H.; Molenbruch, Y.; Caris, A.; Braekers, K. Intermodal container routing: Integrating long-haul routing and local drayage decisions. Sustainability 2019, 11, 1634. [Google Scholar] [CrossRef]
- Wang, Q.Z.; Chen, J.M.; Tseng, M.L.; Luan, H.M.; Ali, M.H. Modelling green multimodal transport route performance with witness simulation software. J. Clean. Prod. 2020, 248, 119245. [Google Scholar] [CrossRef]
- Caris, A.; Macharis, C.; Janssens, G.K. Decision support in intermodal transport: A new research agenda. Comput. Ind. 2013, 64, 105–112. [Google Scholar] [CrossRef]
- Sun, Y.; Yu, N.; Huang, B. Green road–rail intermodal routing problem with improved pickup and delivery services integrating truck departure time planning under uncertainty: An interactive fuzzy programming approach. Complex Intell. Syst. 2022, 8, 1459–1486. [Google Scholar] [CrossRef]
- Flodén, J.; Bärthel, F.; Sorkina, E. Transport buyers choice of transport service–A literature review of empirical results. Res. Transp. Bus. Manag. 2017, 100, 35–45. [Google Scholar] [CrossRef]
- Barnhart, C.; Ratliff, H.D. Modeling intermodal routing. J. Bus. Logist. 1993, 14, 205. [Google Scholar]
- Macharis, C.; Bontekoning, Y.M. Opportunities for OR in intermodal freight transport research: A review. Eur. J. Oper. Res. 2004, 153, 400–416. [Google Scholar] [CrossRef]
- Zweers, B.G.; van der Mei, R.D. Minimum costs paths in intermodal transportation networks with stochastic travel times and overbookings. Eur. J. Oper. Res. 2022, 300, 178–188. [Google Scholar] [CrossRef]
- Ahmady, M.; Eftekhari Yeghaneh, Y. Optimizing the cargo flows in multi-modal freight transportation network under disruptions. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 453–472. [Google Scholar] [CrossRef]
- Epicoco, N.; Falagario, M. Decision support tools for developing sustainable transportation systems in the EU: A review of research needs, barriers, and trends. Res. Transp. Bus. Manag. 2022, 43, 100819. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, W.; Negenborn, R.R.; Atasoy, B. Synchromodal transport planning with flexible services: Mathematical model and heuristic algorithm. Transp. Res. Part C Emerg. Technol. 2022, 140, 103711. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Q.; Wang, W. The impact of carbon abatement policies on port intermodal freight transportation routing and cost. In Proceedings of the International Conference on Electrical and Information Technologies for Rail Transportation, Changsha, China, 20–22 October 2017; Springer: Singapore; pp. 689–699. [Google Scholar]
- He, P.; Zhang, W.; Xu, X.; Bian, Y. Production lot-sizing and carbon emissions under cap-and-trade and carbon tax regulations. J. Clean. Prod. 2015, 103, 241–248. [Google Scholar] [CrossRef]
- Dua, A.; Sinha, D. Quality of multimodal freight transportation: A systematic literature review. World Rev. Intermodal Transp. Res. 2019, 8, 167–194. [Google Scholar] [CrossRef]
- Dragomir, A.G.; Doerner, K.F. Solution techniques for the inter-modal pickup and delivery problem in two regions. Comput. Oper. Res. 2020, 113, 104808. [Google Scholar] [CrossRef]
- Schaap, H.; Schiffer, M.; Schneider, M.; Walther, G. A large neighborhood search for the vehicle routing problem with multiple time windows. Transp. Sci. 2022. [Google Scholar] [CrossRef]
- Baltz, A.; El Ouali, M.; Jäger, G.; Sauerland, V.; Srivastav, A. Exact and heuristic algorithms for the travelling salesman problem with multiple time windows and hotel selection. J. Oper. Res. Soc. 2015, 66, 615–626. [Google Scholar] [CrossRef]
- Wang, R.; Yang, K.; Yang, L.; Gao, Z. Modeling and optimization of a road–rail intermodal transport system under uncertain information. Eng. Appl. Artif. Intel. 2018, 72, 423–436. [Google Scholar] [CrossRef]
- Hosseini, A.; Pishvaee, M.S. Capacity reliability under uncertainty in transportation networks: An optimization framework and stability assessment methodology. Fuzzy Optim. Decis. Mak. 2022, 21, 479–512. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, G.; Hong, Z.; Dong, K. How uncertain information on service capacity influences the intermodal routing decision: A fuzzy programming perspective. Information 2018, 9, 24. [Google Scholar] [CrossRef]
- Sun, Y. Fuzzy approaches and simulation-based reliability modeling to solve a Road–Rail intermodal routing problem with soft delivery time windows when demand and capacity are uncertain. Int. J. Fuzzy Syst. 2020, 22, 2119–2148. [Google Scholar] [CrossRef]
- Haddadsisakht, A.; Ryan, S.M. Closed-loop supply chain network design with multiple transportation modes under stochastic demand and uncertain carbon tax. Int. J. Prod. Econ. 2018, 195, 118–131. [Google Scholar] [CrossRef]
- Alizadeh, M.; Ma, J.; Marufuzzaman, M.; Yu, F. Sustainable olefin supply chain network design under seasonal feedstock supplies and uncertain carbon tax rate. J. Clean. Prod. 2019, 222, 280–299. [Google Scholar] [CrossRef]
- Hu, H.; Li, X.; Zhang, Y.; Shang, C.; Zhang, S. Multi-objective location-routing model for hazardous material logistics with traffic restriction constraint in inter-city roads. Comput. Ind. Eng. 2019, 128, 861–876. [Google Scholar] [CrossRef]
- Sung, I.; Nielsen, P. Speed optimization algorithm with routing to minimize fuel consumption under time-dependent travel conditions. Prod. Manuf. Res. 2020, 8, 1–19. [Google Scholar] [CrossRef]
- Sun, Y.; Lang, M. Modeling the multicommodity multimodal routing problem with schedule-based services and carbon dioxide emission costs. Math. Probl. Eng. 2015, 2015, 406218. [Google Scholar] [CrossRef]
- Duan, X.; Heragu, S. Carbon Emission Tax Policy in an Intermodal Transportation Network. In Proceedings of the IIE Annual Conference, Nashville, TN, USA, 30 May–2 June 2015; Institute of Industrial and Systems Engineers (IISE): Norcross, GA, USA; pp. 566–574. [Google Scholar]
- Zhang, D.; He, R.; Li, S.; Wang, Z. A multimodal logistics service network design with time windows and environmental concerns. PLoS ONE 2017, 12, e0185001. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.; Atasoy, B.; Beelaerts van Blokland, W.; Negenborn, R.R. A global intermodal shipment matching problem under travel time uncertainty. In International Conference on Computational Logistics; Springer: Cham, Switzerland, 2020; pp. 553–568. [Google Scholar]
- Hrušovský, M.; Demir, E.; Jammernegg, W.; Van Woensel, T. Hybrid simulation and optimization approach for green intermodal transportation problem with travel time uncertainty. Flex. Serv. Manuf. J. 2018, 30, 486–516. [Google Scholar] [CrossRef]
- Maiyar, L.M.; Thakkar, J.J. Modelling and analysis of intermodal food grain transportation under hub disruption towards sustainability. Int. J. Prod. Econ. 2019, 217, 281–297. [Google Scholar] [CrossRef]
- Qiu, Y.; Qiao, J.; Pardalos, P.M. A branch-and-price algorithm for production routing problems with carbon cap-and-trade. Omega 2017, 68, 49–61. [Google Scholar] [CrossRef]
- Cheng, X.Q.; Jin, C.; Wang, C.; Mamatok, Y. Impacts of different low-carbon policies on route decisions in intermodal freight transportation: The case of the west river region in China. In Proceedings of the International Forum on Shipping, Ports and Airports (IFSPA), Hong Kong, China, 20–24 May 2019; pp. 281–293. [Google Scholar]
- Xu, X.; Xu, X.; He, P. Joint production and pricing decisions for multiple products with cap-and-trade and carbon tax regulations. J. Clean. Prod. 2016, 112, 4093–4106. [Google Scholar] [CrossRef]
- Bai, Q.; Chen, M. The distributionally robust newsvendor problem with dual sourcing under carbon tax and cap-and-trade regulations. Comput. Ind. Eng. 2016, 98, 260–274. [Google Scholar] [CrossRef]
- Jharkharia, S.; Das, C. Vehicle routing analyses with integrated order picking and delivery problem under carbon cap and trade policy. Manag. Res. Rev. 2019, 43, 223–243. [Google Scholar] [CrossRef]
- Ji, H.; Wu, P. Sailing route and speed optimization for green intermodal transportation. In Proceedings of the 2020 IEEE 5th International Conference on Intelligent Transportation Engineering (ICITE), Beijing, China, 11–13 September 2020; IEEE: Piscataway, NJ, USA; pp. 18–22. [Google Scholar]
- Rosyida, E.E.; Santosa, B.; Pujawan, I.N. Freight route planning in intermodal transportation network to deal with combinational disruptions. Cogent Eng. 2020, 7, 1805156. [Google Scholar] [CrossRef]
- Fazayeli, S.; Eydi, A.; Kamalabadi, I.N. Location-routing problem in multimodal transportation network with time windows and fuzzy demands: Presenting a two-part genetic algorithm. Comput. Ind. Eng. 2018, 119, 233–246. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X. Fuzzy programming approaches for modeling a customer-centred freight routing problem in the road-rail intermodal hub-and-spoke network with fuzzy soft time windows and multiple sources of time uncertainty. Mathematics 2019, 7, 739. [Google Scholar] [CrossRef]
- Xie, L.; Cao, C. Multi-modal and multi-route transportation problem for hazardous materials under uncertainty. Eng. Optim. 2021, 53, 2180–2200. [Google Scholar] [CrossRef]
- Maity, G.; Yu, V.F.; Roy, S.K. Optimum intervention in transportation networks using multimodal system under fuzzy stochastic environment. J. Adv. Transp. 2022, 2022, 3997396. [Google Scholar] [CrossRef]
- Peng, Y.; Yong, P.; Luo, Y. The route problem of multimodal transportation with timetable under uncertainty: Multi-objective robust optimization model and heuristic approach. RAIRO-Oper. Res. 2021, 55, S3035–S3050. [Google Scholar] [CrossRef]
- Fattahi, Z.; Behnamian, J. Hazardous materials transportation with focusing on intermodal transportation: A state-of-the-art review. Int. J. Ind. Eng. 2021, 28, 390–411. [Google Scholar]
- Uddin, M.; Huynh, N. Reliable routing of road-rail intermodal freight under uncertainty. Netw. Spat. Econ. 2019, 19, 929–952. [Google Scholar] [CrossRef]
- Sun, Y.; Hrušovský, M.; Zhang, C.; Lang, M. A time-dependent fuzzy programming approach for the green multimodal routing problem with rail service capacity uncertainty and road traffic congestion. Complexity 2018, 2018, 8645793. [Google Scholar] [CrossRef]
- Lu, Y.; Lang, M.; Sun, Y.; Li, S. A fuzzy intercontinental road-rail multimodal routing model with time and train capacity uncertainty and fuzzy programming approaches. IEEE Access 2020, 8, 27532–27548. [Google Scholar] [CrossRef]
- Sun, Y. Green and reliable freight routing problem in the road-rail intermodal transportation network with uncertain parameters: A fuzzy goal programming approach. J. Adv. Transp. 2020, 2020, 7570686. [Google Scholar] [CrossRef]
- Pishvaee, M.S.; Razmi, J.; Torabi, S.A. Robust possibilistic programming for socially responsible supply chain network design: A new approach. Fuzzy Sets Syst. 2012, 206, 1–20. [Google Scholar] [CrossRef]
- Sun, Y. A Fuzzy Multi-objective routing model for managing hazardous materials door-to-door transportation in the road-rail multimodal network with uncertain demand and improved service level. IEEE Access 2020, 8, 172808–172828. [Google Scholar] [CrossRef]
- Hrušovský, M.; Demir, E.; Jammernegg, W.; Van Woensel, T. Real-time disruption management approach for intermodal freight transportation. J. Clean. Prod. 2021, 280, 124826. [Google Scholar] [CrossRef]
- Wang, W.; Xu, X.; Jiang, Y.; Xu, Y.; Cao, Z.; Liu, S. Integrated scheduling of intermodal transportation with seaborne arrival uncertainty and carbon emission. Transp. Res. Part D Transp. Environ. 2020, 88, 102571. [Google Scholar] [CrossRef]
- Shao, C.; Wang, H.; Yu, M. Multi-Objective Optimization of Customer-Centered Intermodal Freight Routing Problem Based on the Combination of DRSA and NSGA-III. Sustainability 2022, 14, 2985. [Google Scholar] [CrossRef]
- Guo, W.; Atasoy, B.; van Blokland, W.B.; Negenborn, R.R. A dynamic shipment matching problem in hinterland synchromodal transportation. Decis. Support Syst. 2020, 134, 113289. [Google Scholar] [CrossRef]
- Resat, H.G.; Turkay, M. A discrete-continuous optimization approach for the design and operation of synchromodal transportation networks. Comput. Ind. Eng. 2019, 130, 512–525. [Google Scholar] [CrossRef]
- Yu, V.F.; Redi AA, N.; Jewpanya, P.; Lathifah, A.; Maghfiroh, M.F.; Masruroh, N.A. A simulated annealing heuristic for the heterogeneous fleet pollution routing problem. In Environmental Sustainability in Asian Logistics and Supply Chains; Springer: Singapore, 2018; pp. 171–204. [Google Scholar]
- Demir, E.; Bektaş, T.; Laporte, G. The bi-objective pollution-routing problem. Eur. J. Oper. Res. 2014, 232, 464–478. [Google Scholar] [CrossRef]
- Franceschetti, A.; Honhon, D.; Van Woensel, T.; Bektaş, T.; Laporte, G. The time-dependent pollution-routing problem. Transp. Res. Part B Methodol. 2013, 56, 265–293. [Google Scholar] [CrossRef]
- Sun, Y.; Liang, X.; Li, X.; Zhang, C. A fuzzy programming method for modeling demand uncertainty in the capacitated road–rail multimodal routing problem with time windows. Symmetry 2019, 11, 91. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; van Hassel, E.; Negenborn, R.R.; Atasoy, B. Synchromodal transport planning considering heterogeneous and vague preferences of shippers. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102827. [Google Scholar] [CrossRef]
- Xiao, Y.; Konak, A. The heterogeneous green vehicle routing and scheduling problem with time-varying traffic congestion. Transp. Res. Part E Logist. Transp. Rev. 2016, 88, 146–166. [Google Scholar] [CrossRef]
- Hickman, J.; Hassel, D.; Joumard, R.; Samaras, Z.; Sorenson, S. Methodology for Calculating Transport Emissions and Energy Consumption. 1999. Available online: https://trimis.ec.europa.eu/sites/default/files/project/documents/meet.pdf (accessed on 7 July 2022).
- Mahlke, D.; Martin, A.; Moritz, S. A mixed integer approach for time-dependent gas network optimization. Optim. Methods Softw. 2010, 25, 625–644. [Google Scholar] [CrossRef]
- Xie, Y.; Lu, W.; Wang, W.; Quadrifoglio, L. A multimodal location and routing model for hazardous materials transportation. J. Hazard. Mater. 2012, 227, 135–141. [Google Scholar] [CrossRef] [PubMed]
- Zahiri, B.; Tavakkoli-Moghaddam, R.; Pishvaee, M.S. A robust possibilistic programming approach to multi-period location–allocation of organ transplant centers under uncertainty. Comput. Ind. Eng. 2014, 74, 139–148. [Google Scholar] [CrossRef]
- Habib, M.S.; Asghar, O.; Hussain, A.; Imran, M.; Mughal, M.P.; Sarkar, B. A robust possibilistic programming approach toward animal fat-based biodiesel supply chain network design under uncertain environment. J. Clean. Prod. 2021, 278, 122403. [Google Scholar] [CrossRef]
- Salimian, S.; Mousavi, S.M. A robust possibilistic optimization model for organ transplantation network design considering climate change and organ quality. J. Ambient. Intell. Humaniz. Comput. 2022, 1–24. [Google Scholar] [CrossRef]
- Kundu, P.; Kar, S.; Maiti, M. Multi-objective multi-item solid transportation problem in fuzzy environment. Appl. Math. Model. 2013, 37, 2028–2038. [Google Scholar] [CrossRef]
- Zahiri, B.; Pishvaee, M.S. Blood supply chain network design considering blood group compatibility under uncertainty. Int. J. Prod. Res. 2017, 55, 2013–2033. [Google Scholar] [CrossRef]
- Günay, E.E.; Kremer GE, O.; Zarindast, A. A multi-objective robust possibilistic programming approach to sustainable public transportation network design. Fuzzy Sets Syst. 2021, 422, 106–129. [Google Scholar] [CrossRef]
- Chiadamrong DH, T.N.; Doan, T.H. A robust possibilistic chance-constrained programming model for optimizing a multi-objective aggregate production planning problem under uncertainty. J. Ind. Eng. Int. 2022; in press. [Google Scholar]
- Delfani, F.; Kazemi, A.; SeyedHosseini, S.M.; Niaki, S.T.A. A novel robust possibilistic programming approach for the hazardous waste location-routing problem considering the risks of transportation and population. Int. J. Syst. Sci. Oper. Logist. 2021, 8, 383–395. [Google Scholar] [CrossRef]
- Beheshtinia, M.A.; Salmabadi, N.; Rahimi, S. A robust possibilistic programming model for production-routing problem in a three-echelon supply chain. J. Model. Manag. 2021, 16, 1328–1357. [Google Scholar] [CrossRef]
- Rabbani, M.; Hosseini-Mokhallesun, S.A.A.; Ordibazar, A.H.; Farrokhi-Asl, H. A hybrid robust possibilistic approach for a sustainable supply chain location-allocation network design. Int. J. Syst. Sci. Oper. Logist. 2020, 7, 60–75. [Google Scholar] [CrossRef]
- Resat, H.G.; Turkay, M. Design and operation of intermodal transportation network in the Marmara region of Turkey. Transp. Res. Part E Logist. Transp. Rev. 2015, 83, 16–33. [Google Scholar] [CrossRef]
- Zhang, X.; Yuan, X.; Jiang, Y. Optimization of multimodal transportation under uncertain demand and stochastic carbon trading price. Syst. Eng.—Theory Pract. 2021, 41, 2609–2620. [Google Scholar]
- Habib, M.S.; Omair, M.; Ramzan, M.B.; Chaudhary, T.N.; Farooq, M.; Sarkar, B. A robust possibilistic flexible programming approach toward a resilient and cost-efficient biodiesel supply chain network. J. Clean. Prod. 2022, 366, 132752. [Google Scholar] [CrossRef]
- J-Sharahi, S.; Khalili-Damghani, K.; Abtahi, A.R.; Rashidi-Komijan, A. Type-II fuzzy multi-product, multi-level, multi-period location–allocation, production–distribution problem in supply chains: Modelling and optimisation approach. Fuzzy Inf. Eng. 2018, 10, 260–283. [Google Scholar] [CrossRef]


| Symbols representing the transportation orders | |
| Transportation order set. | |
| Transportation order index, and . | |
| Demand of containers in TEU of transportation order k. | |
| Index of the origin of transportation order k. | |
| Index of the destination of transportation order k. | |
| Pickup time window set of transportation order k. | |
| Pickup time window index of transportation order k, and . | |
| Pickup time window p of transportation order k. | |
| Delivery time window set of transportation order k. | |
| Delivery time window index of transportation order k, and . | |
| Delivery time window g of transportation order k. | |
| Symbols representing the road-rail intermodal network | |
| Node set in the network. | |
| Node indices, and . | |
| Predecessor node set to node i, and . | |
| Successor node set to node i, and . | |
| Directed arc set in the network. | |
| Directed arc from node i to node j, and . | |
| Transportation service set in the network. | |
| Rail service set on arc (i, j) in the network. | |
| Road service set on arc (i, j) in the network. | |
| Transportation service set on arc (i, j) in the network, and . | |
| Transportation service indices in the network, and . | |
| Discrete travel speed option set of road service s on arc (i, j). | |
| Travel speed option index, and . | |
| Speed in km/h of option m of road service s on arc (i, j). | |
| Time interval set that the trucks of road service s on arc (i, j) are allowed to depart from node i. | |
| Time interval index, and . | |
| Allowable departure time interval f for road service s on arc (i, j) under road traffic restrictions. | |
| Travel distance in km of transportation service s on arc (i, j). | |
| Separate loading and unloading time in h/TEU of transportation service s at node i. | |
| Fixed loading and unloading service time window from service start time to service cutoff time of rail service s at node i. | |
| Fuzzy capacity in TEU of rail service s on arc (i, j), and . | |
| Symbols representing the costs and carbon dioxide emissions | |
| Rail travel cost rate in Chinese Yuan (CNY)/TEU. | |
| Rail travel cost rate in CNY/TEU/km. | |
| Inventory cost rate in CNY/TEU/h when containers need to be stored at intermodal terminals. | |
| Inventory period in h that is free of charge at intermodal terminals. | |
| Road travel cost rate in CNY/TEU/km. | |
| Separate loading and unloading cost rate in CNY/TEU of transportation service s. | |
| Fuzzy carbon trading price rate in CNY/kg under cap-and-trade policy, and | |
| Emission cap in kg for carbon dioxide under cap-and-trade policy. | |
| Rate of carbon dioxide emissions in kg/TEU/km of rail service s on arc (i, j). | |
| Rate of carbon dioxide emissions in kg/TEU/km of road service s on arc (i, j) when its truck speed is . | |
| Symbol representing the auxiliary parameter | |
| A predefined sufficient large number. | |
| Symbols representing the variables | |
| 0-1 binary decision variable. if transportation service s on arc (i, j) is used by the distribution route of transportation order k; otherwise. | |
| 0-1 binary decision variable. if the containers of transportation order k depart from node i within time interval f by road service s on arc (i, j); otherwise. | |
| 0-1 binary decision variable. if road service s on arc (i, j) uses travel speed option m to transport the containers of transportation order k; otherwise. | |
| 0-1 binary decision variable. if pickup time window p of transportation order k is selected; otherwise. | |
| 0-1 binary decision variable. if delivery time window g of transportation order k is selected; otherwise. | |
| Non-negative continuous decision variable denoting the planned time when the containers of transportation order k start to be loaded on trucks at node i before departure. | |
| Non-negative integer variable denoting the day in the planning horizon when the containers of transportation order k depart from node i by road service s on arc (i, j). | |
| Non-negative continuous variable denoting the time when the containers of transportation order k arrive at node i and get unloaded from rail or road. | |
| Non-negative continuous variable denoting the waiting period in h of the containers of transportation order k at node i before being transported by rail service s on arc (i, j). | |
| Non-negative continuous variable denoting the charged inventory period in h of the containers of transportation order k at node i before being transported by transportation service s on arc (i, j). | |
| Interactive Parameters | Models | Values |
|---|---|---|
| BPCCP and RPP | 300,000 kg | |
| BPCCP | 0.6, 0.8, 1.0 | |
| RPP | 0.5 | |
| RPP | 30 CNY/TEU | |
| RPP | 0.5 |
| RPP | ||||||
|---|---|---|---|---|---|---|
| Expected Costs (CNY) | Expected Costs (CNY) | Optimality Robustness Costs (CNY) | Feasibility Robustness Costs (CNY) | Total Costs (CNY) | ||
| 2,477,946 | 2,478,256 | 2,471,574 | 2,466,173 | 536.6 | 2385 | 2,469,095 |
| Running time (s) of LINGO optimizer | ||||||
| 22 | 21 | 27 | 56 | |||
| Emission Cap (kg) | Carbon Cap-and-Trade Policy | Carbon Tax Policy | |||||
|---|---|---|---|---|---|---|---|
| 400,000 | 380,000 | 360,000 | 340,000 | 320,000 | 300,000 | 0 | |
| Total Costs (CNY) | 2,469,345 | 2,467,950 | 2,466,949 | 2,467,495 | 2,468,295 | 2,469,095 | 2,481,095 |
| Expected Costs (CNY) | 2,466,960 | 2,465,565 | 2,464,564 | 2,464,973 | 2,465,573 | 2,466,173 | 2,475,173 |
| Optimality Robustness Costs (CNY) | 0.15 | 0.10 | 0.08 | 137 | 337 | 537 | 3538 |
| Feasibility Robustness Costs (CNY) | 2385 | 2385 | 2385 | 2385 | 2385 | 2385 | 2385 |
| Carbon Dioxide Emissions (kg) | 400,015 | 380,009 | 360,008 | 353,657 | 353,657 | 353,657 | 353,657 |
| Expected Costs (CNY) | Optimality Robustness Costs (CNY) | Feasibility Robustness Costs (CNY) | Total Costs (CNY) | Carbon Dioxide Emissions (kg) | ||
|---|---|---|---|---|---|---|
| 0.4 | 0.5 | 2,466,173 | 429 | 2385 | 2,468,988 | 353,657 |
| 0.6 | 2,471,574 | 423 | 1908 | 2,473,905 | 352,861 | |
| 0.7 | 2,477,946 | 401 | 0 | 2,478,347 | 350,065 | |
| 0.8 | 2,477,946 | 401 | 0 | 2,478,347 | 350,065 | |
| 0.9 | 2,477,946 | 401 | 0 | 2,478,347 | 350,065 | |
| 1.0 | 2,477,946 | 401 | 0 | 2,478,347 | 350,065 | |
| 0.6 | 0.5 | 2,466,173 | 644 | 2385 | 2,469,202 | 353,657 |
| 0.6 | 2,471,574 | 634 | 1908 | 2,474,117 | 352,861 | |
| 0.7 | 2,477,946 | 601 | 0 | 2,478,547 | 350,065 | |
| 0.8 | 2,477,946 | 601 | 0 | 2,478,547 | 350,065 | |
| 0.9 | 2,477,946 | 601 | 0 | 2,478,547 | 350,065 | |
| 1.0 | 2,477,946 | 601 | 0 | 2,478,547 | 350,065 | |
| 0.8 | 0.5 | 2,466,173 | 859 | 2385 | 2,469,417 | 353,657 |
| 0.6 | 2,471,574 | 846 | 1908 | 2,474,328 | 352,861 | |
| 0.7 | 2,477,946 | 801 | 0 | 2,478,747 | 350,065 | |
| 0.8 | 2,477,946 | 801 | 0 | 2,478,747 | 350,065 | |
| 0.9 | 2,477,946 | 801 | 0 | 2,478,747 | 350,065 | |
| 1.0 | 2,477,946 | 801 | 0 | 2,478,747 | 350,065 | |
| 1.0 | 0.5 | 2,466,173 | 1073 | 2385 | 2,469,632 | 353,657 |
| 0.6 | 2,471,574 | 1057 | 1908 | 2,474,539 | 352,861 | |
| 0.7 | 2,477,946 | 1001 | 0 | 2,478,948 | 350,065 | |
| 0.8 | 2,477,946 | 1001 | 0 | 2,478,948 | 350,065 | |
| 0.9 | 2,477,946 | 1001 | 0 | 2,478,948 | 350,065 | |
| 1.0 | 2,477,946 | 1001 | 0 | 2,478,948 | 350,065 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y. A Robust Possibilistic Programming Approach for a Road-Rail Intermodal Routing Problem with Multiple Time Windows and Truck Operations Optimization under Carbon Cap-and-Trade Policy and Uncertainty. Systems 2022, 10, 156. https://doi.org/10.3390/systems10050156
Sun Y. A Robust Possibilistic Programming Approach for a Road-Rail Intermodal Routing Problem with Multiple Time Windows and Truck Operations Optimization under Carbon Cap-and-Trade Policy and Uncertainty. Systems. 2022; 10(5):156. https://doi.org/10.3390/systems10050156
Chicago/Turabian StyleSun, Yan. 2022. "A Robust Possibilistic Programming Approach for a Road-Rail Intermodal Routing Problem with Multiple Time Windows and Truck Operations Optimization under Carbon Cap-and-Trade Policy and Uncertainty" Systems 10, no. 5: 156. https://doi.org/10.3390/systems10050156
APA StyleSun, Y. (2022). A Robust Possibilistic Programming Approach for a Road-Rail Intermodal Routing Problem with Multiple Time Windows and Truck Operations Optimization under Carbon Cap-and-Trade Policy and Uncertainty. Systems, 10(5), 156. https://doi.org/10.3390/systems10050156





