Abstract
With the continuous expansion of the industrial production scale and the rapid promotion of urbanization, more and more serious air pollution threatens people’s lives and social development. To reduce the losses caused by polluted weather, it is popular to predict the concentration of pollutants timely and accurately, which is also a research hotspot and challenging issue in the field of systems engineering. However, most studies only pursue the improvement of prediction accuracy, ignoring the function of robustness. To make up for this defect, a novel air pollutant concentration prediction (APCP) system is proposed for environmental system management, which is constructed by four modules, including time series reconstruction, submodel simulation, weight search, and integration. It not only realizes the filtering and reconstruction of redundant series based on the decomposition-ensemble mode, but also the weight search mechanism is designed to trade off precision and stability. Taking the hourly concentration of PM2.5 in Guangzhou, Shanghai, and Chengdu, China as an example, the simulation results show that the APCP system has perfect prediction capacity and superior stability performance, which can be used as an effective tool to guide early warning decision-making in the management of environmental engineering.
1. Introduction
With the continuous promotion of global industrialization and urbanization, the environmental problems accumulated by rapid development, especially the problem of air pollution, have become increasingly prominent. The harm caused by air pollution not only seriously affects human health [1,2] but also causes substantial economic losses to all countries [3]. The specific numerical results show that the rise of PM2.5 concentration by 10 g/m3 can increase mortality by 2% [4] and in 2016, bring a total loss of 101.39 billion dollars to 338 cities in China [5]. Therefore, it is imperative to establish an accurate, reliable, and effective air pollutant concentration prediction (APCP) system to announce the expected pollutant concentration to the public in the successive few periods, which is also a research hotspot and challenging issue in the field of systems engineering.
The state-of-the-art work for the prediction of air pollutants (APs) mainly includes deterministic models [6] and data-driven models [7]. The deterministic model relies on the emission source data and various historical meteorological data to simulate the formation of pollutants through the physical and chemical processes of the generation, conversion, and diffusion of APs [8]. For example, CMaq [9,10,11], Wrf-Chem [12,13,14], and LOtos-EUros [15] are all popular deterministic models. W. Wei et al. [16] adopted the Wrf-Chem model to effectively simulate the concentration of APs in Beijing. Based on this model, the impact of pollution emissions on air quality is quantified. However, the complexity of climate, land use, and emission sources is difficult to capture, which limits the development of such models to a certain extent [17].
Relying on the continuous in-depth study of algorithm models and the continuous improvement of computer hardware performance, data-driven models [18] have become the preferred method of prediction, including linear models [19] and nonlinear models [20]. Classical linear models, such as autoregressive integrated moving average (ARima) models [21] and seasonal autoregressive integrated moving average (SARima) [22], are based on the assumption that the studied sequence is linear. In addition, quantile regression (Qr) [23] and other models are also widely used in the field of AP concentration prediction. T. Liu et al. [24] integrated ARima model with three deterministic models (ARimaX) to predict APs, respectively. Taking the results of CMaq-ARima model as an example, the mean of daily root mean squared error (RMSE) at the three stations decreased by . S. Abdullah et al. [25] fitted the multiple linear regression (MLR) model to study the cross-border impact of APs on Malaysia. Based on the MLR model, the values of the next one, two, and three time points in the input sequence of PM10 concentration were predicted, that is, the 1–3 step prediction was performed in the experiment. It is verified that the result of 1-step prediction is the best, in which and . Due to the prevalence of multicollinearity, N. Mohd Napi et al. [26] applied principal component analysis (PCA) to reduce the high correlation between the data and then used MLR to predict the ozone concentration. It was shown that the value of R2 was improved by compared with MLR model.
Although the application of the linear model is relatively simple, in practice, the characteristics of the AP series appear nonlinear and time-varying complexity. Thus, nonlinear models are widely utilized. Y. Bai et al. [27] combined wavelet transform technology with the back propagation (BP) model, named the W-BPnn model, to improve the nonlinear mapping performance of the prediction model. Compared with the BP model, the value of RMSE was reduced by . Because the sequence of APs concentration has long-term correlation characteristics, scientifically determining the lag order can avoid the gradient disappearance of artificial neural networks (ANNs). Considering the relationship between space and time, X. Li et al. [28] extended the Lstm model (LstmE) to predict multi-scale APs, which successfully realized the scientific identification of lag order. The comparison results showed that with the extension of prediction time, the required lag order gradually increased. Although the error also increased, it was still within the acceptable interval of long-term prediction results. In order to reduce the noise of input data, X. Jiang et al. [29] split the original sequence with the complete ensemble empirical mode decomposition with adaptive noise (CEemdan) strategy and entropy method, and then input the subsequences into the bidirectional Lstm (Bilstm) model for prediction respectively. This method greatly improved the efficiency of the prediction model.
The individual ANN model is lack flexibility for the adjustment of parameters, which limits the improvement of prediction accuracy [30]. The optimization algorithm provides a new solution for improving the prediction performance [31,32]. J. Murillo-Escobar et al. [33] designed the Svr-Pso model to estimate the concentration of APs in five regions. Compared with the feedforward artificial neural network (FAnn) model used in the San Buenaventura University in Bello (BEL-USBV) (), Pso optimized the prediction performance of the hybrid model (). Q. Wu et al. [34] constructed the Ba-LSsvm model to predict the decomposed low-frequency data, while the high-frequency data were simulated after secondary decomposition. Ba-LSsvm model not only produced better prediction results than Pso optimization, for example, the value of mean absolute percentage error (MAPE) is reduced by but also included the function of external variables. Similarly, G. Li et al. [35] proposed the CEemdan-Dse-BVmd-Csa-KElm model to disintegrate the data with high complexity to simplify the input sequence. Csa mechanism searched the optimal adjustable parameters of the KElm model, which was conducive to configuring the model on demand and realizing effective prediction in multiple fields. However, the optimization mechanism only focuses on the improvement of the precision of model prediction, and the importance of model robustness is ignored. To balance various performances, a series of multi-objective optimization mechanisms [36,37] represented by the multi-objective dragonfly algorithm (Moda) [38], multi-objective chameleon swarm algorithm (MOcsa) [39], and multi-objective salp swarm algorithm (MSsa) [40] have achieved good results in energy prediction. It can be considered to develop a multi-objective optimization mechanism to weigh the prediction performance of APs. In addition, some of the latest research models are evaluated in Table 1.

Table 1.
Evaluation of data-driven prediction models for AP concentration.
According to the analysis of existing literature, the shortcomings of different prediction models can be summarized as follows: (i) Deterministic models are highly professional and expensive, which limits the extendability of the model. (ii) The data-driven linear model is limited by linear assumptions, while the actual data is a mixture of linear and nonlinear characteristics. Only a single feature is extracted, which causes the loss of input information. (iii) Although the optimization mechanism avoids the randomness of parameter setting, in most cases, the accuracy of the model is only set as the unique objective function, which lacks the measurement of the stability of the prediction model. Therefore, to solve these drawbacks, a novel air pollutant concentration prediction (APCP) system is proposed for environmental system management in this paper. It is mainly established by four modules, namely time series reconstruction, submodel simulation, weight search, and integration. Specifically, in the time series reconstruction module, the decomposition-ensemble (DE) mode is constructed to filter the redundancy of the original sequence and then merge similar features. The obtained reconstruction sequence is trained by four prediction submodels (convolutional neural network (Cnn), long short-term memory (Lstm), extreme learning machine (Elm), and Elman neural network (Enn)) as input in the submodel simulation module. The outputs of four independent prediction sequences are assigned appropriate weights applying the weight search (Ws) mechanism. Based on this optimal weight, the final prediction results of the APCP system are integrated.
The main contributions of this paper are introduced as follows:
(1) DE mode is designed in the APCP systemto filter out the interference of high-frequency noise signals. The sequence of APs contains more information and has strong volatility. The DE mode is applied to reconstruct the original sequence, which not only eliminates the interference of high-frequency noise signals but also integrates the key information.
(2) A novel weight search mechanism, Ws, is developed in the weight search module. This mechanism makes up for the limitations of the previous optimization mechanism, such as the single objective function, ease of falling into the dilemma of local optimization, and long running time. By the comparative experiment, it can be proved that the weight search mechanism used in this paper is superior to previous optimization mechanisms both in searchability and stability.
(3) The construction of the four prediction submodels in the APCP system covers the inherent modes of sequence as much as possible, including three ANN models (Cnn, Elm, and Enn) and a deep learning model called Lstm. The four models make use of each other’s advantages to fill in the deficiencies and comprehensively capture sequence modes. Based on the extracted sequence modes, the prediction performance of the APCP system is improved.
(4) The proposed APCP system achieves the trade-off between double objectives, prediction precision, and robustness, in the paper. It comprises four modules: time series reconstruction, submodel simulation, weight search, and integration. Based on hourly PM2.5 concentration data in Guangzhou, Shanghai, and Chengdu, China, the superiority of the APCP system is testified by three experiments and discussions. It can also provide scientific data support for air pollution control and policy-making.
The remainder of the paper is arranged as follows. The next section introduces the design of the APCP system, including the construction principles of decomposition-ensemble mode and weight search mechanism, and the structure of the APCP system. Section 3 describes three experiments to verify the superiority of the proposed APCP system. Three discussions, which are significance analysis, correlation analysis, and sensitivity analysis, are carried out in Section 4. Section 5 summarizes the conclusions and prospects for the further development of the APCP system.
2. Design of the APCP System
The APCP system is established by four modules, which are time series reconstruction, submodel simulation, weight search, and integration. As depicted visually in Figure 1, firstly, the original sequence is split into subsequences of different frequencies by DE mode, and noise is filtered out. After recombining the subsequences according to the similarity, the multi-step prediction is realized in four individual prediction submodels, respectively. Next, under the constraint of the multi-objective function, the weight search mechanism is constructed to determine the appropriate weights of the four submodels. Finally, the multi-step prediction results are output based on the obtained weights.
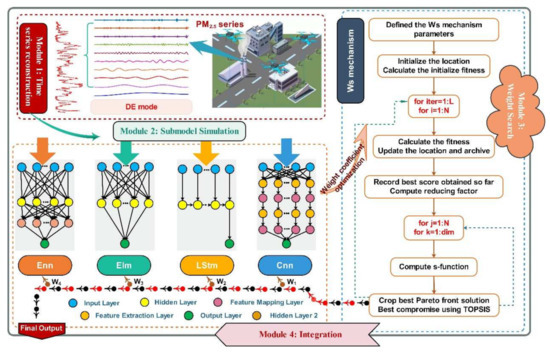
Figure 1.
The flowchart of the APCP system.
In this section, before the structure of the APCP system is elaborated in detail, the DE mode and weight search mechanism applied to the system are designed as follows.
2.1. Decomposition-Ensemble Mode
The concentration series of AP has a complex structure and frequent fluctuations, which will cause a computational burden if directly input into the prediction model. Therefore, the paper designs the DE mode to divide the sequence structure and clarify the modal characteristics.
First, is added to the original concentration sequence to form a new fluctuation sequence , where means standard normal distribution and is a random number. Then, the upper and lower boundaries of are calculated, where is the cubic spline difference function, and and represent local maximum and minimum value sequences of , respectively. The first component is obtained. If satisfies Equation (1), then the first mode component can be expressed as , otherwise, let and repeat the above process.
where stands for counting function, represents the set of points with zero value in the sequence of , , and indicate the upper and lower boundaries of at time point c, and C is the total number of time points in the .
Based on this, the first intrinsic mode function (IMF) and residual sequence are listed in Equations (2) and (3).
Similarly, let and all the above steps are executed again. The results of and are expressed in Equations (4) and (5).
And so on, until is a monotonic function and DE mode is completed. All output results ( and ) meet Equation (6).
2.2. Weight Search Mechanism
To improve the comprehensive ability of the APCP system, the weight allocation of four individual submodels is the key to the successful application under the constraints of multi-objective functions. As an effective weight search mechanism, the multi-objective grasshopper optimization algorithm (Mogoa) is developed in the APCP system, and its structure is constructed as follows. Initially, the grasshopper population with individuals and dimensions is listed in Equation (7).
According to [52], the location of is not only affected by the other individuals , but also related to gravity and wind direction , as shown in Equation (8).
where , and are two attractive parameters, and , .
Due to insufficient convergence, Equation (8) cannot realize the search for optimal weight. An improved convergence function is developed in the APCP system, as described in Equation (9). It is assumed that the change of is not affected by , and remains towards the food source .
where and are inequality constraint range of , , , and satisfy Equation (10).
where , , indicates the current times, and ITer expresses the total number of cycles.
If the location of moves beyond the boundaries ( and ), is reset by Equation (11).
When , the output results are the suitable weights of the APCP system. The pseudo-code of the weight search mechanism is listed in Algorithm 1.
| Algorithm 1. Weight search mechanism |
| Input: Outputs: F—the best fitness results —the suitable weights Parameters: ITer—the iteration number —the current iteration number —the location of -th grasshopper —the number of —the dimension of ARchIvemax—the archive size ARchIvenum—the number of repositories 1: /* Initialize . */ 2: /*Set , , and ITer.*/ 3. /*Calculate F of each search agent.*/ 4. /*.*/ 5. WHILE () DO 6. /*Update coefficient .*/ 7. 8. FOR (each search agent) DO 9. /*Normalize .*/ 10. /*Update .*/ 11. 12. /*Reset if it moves beyond the boundaries.*/ 13. 14. /*Update if a better solution is produced.*/ 15. /*Calculate F of each search agent.*/ 16. /*Identify the non-dominated solutions.*/ 17. /*Extended repository based on the non-dominated solutions.*/ 18. IF DO 19. /* Start the repository maintainer to remove one repository resident.*/ 20. /*Put the new non-dominated solution into it.*/ 21. END IF 22. END FOR 23. 24. END WHILE 25. RETURN |
2.3. Framework of the APCP System
The APCP system is designed into four modules, as described in Figure 1, which are independent and coordinated. In this subsection, the structural design of each module is carefully explained to prove the scientific nature and rationality of the proposed system.
2.3.1. Time Series Reconstruction
Since only the influence of the historical AP series is considered, extracting as much information as possible from the original series is the premise to enhance the APCP system performance. The frequent fluctuation and disordered noise bring a burden to the prediction model. Therefore, the DE mode is designed to split the concentration series of AP to clarify the structure by increasing quantity. Based on the principle of similarity, the AP series is reconstructed. It not only reduces redundant interference but also ensures the integrity of series information.
2.3.2. Submodel Simulation
Using the PM2.5 data of Guangzhou, Shanghai, and Chengdu in January 2015, the pre-experiment, including Cnn, Bilstm, least square support vector machine (Lssvm), gaussian process (Gp), Lstm, gate recurrent unit (Gru), Elm, and Enn models, is carried out to select the appropriate prediction submodels. From the results of the four evaluation indicators in Table 2, the prediction ability of the Cnn, Lstm, Elm, and Enn models is similar and superior to other models. Thus, Cnn, Lstm, Elm, and Enn as effective prediction tools are applied in the submodel simulation module.

Table 2.
Comparison results of pre-experiment.
2.3.3. Weight Search
The prediction ability of the individual submodel is limited, and it fails to fit all the characteristics of the AP series. The weight search mechanism can provide a new solution for identifying information from multiple perspectives by integrating all submodels. The APCP system aims to balance the prediction precision and robustness, so the objective functions of the weight search mechanism are shown in Equation (12). After the iteration, the optimal weights of the four submodels are output.
where means the original series, is the fitting results, and represents the AP series used for testing.
2.3.4. Integration
According to Equation (13), the fitting values of the four submodels are integrated with the corresponding optimal weights to obtain the final prediction results .
where .
Furthermore, to ensure the best performance of the APCP system, the parameters of all models included in the system are default as listed in Table 3, which is set by trial-and-error results.

Table 3.
The explanation and the corresponding value of the APCP system.
3. Establishment and Evaluation of Experiment
Taking the hourly PM2.5 concentration data of Guangzhou, Shanghai, and Chengdu as an example, this section makes a comparative analysis of three experiments on the APCP system, which aims to explain the performance of the proposed system from multiple perspectives.
3.1. Description of Datasets
This paper adopts hourly PM2.5 concentration data from three cities in China, namely Guangzhou (Gz), Shanghai (Sh), and Chengdu (Cd), in January 2015, which are from http://archive.ics.uci.edu/ (accessed on 8 July 2022). The division of datasets and basic information such as maximum (Max.), minimum (Min.), mean (Mean), standard deviation (Std.), and maximum Lyapunov exponent (Mlye) are shown in Table 4.

Table 4.
The statistical assessments of the dataset.
According to the results of statistical evaluation, this month, the average PM2.5 concentration in Chengdu is the highest and has a large fluctuation range . Besides, the Mlye values of the three cities are greater than zero, suggesting that the experimental data are chaotic. It proves the necessity of the time series reconstruction module in the APCP system.
3.2. Evaluation Indexes
For convenience to compare the experimental results, four evaluation criteria are utilized, including MAPE, MRE, MSE, and R2. The expressions are given in Table 5.

Table 5.
The mathematical formula of four evaluation metrics.
3.3. Experiment I: Comparison with the Individual Models
Experiment I analyzes the multi-step prediction results of the APCP system compared with well-known models, which are Bilstm, Gru, Gp, and Lssvm models, and individual submodels, including Cnn, Lstm, Elm, and Enn models, as revealed in Table 6 and Figure 2. In order to ensure fairness, the data of the first four hours are used as input to predict the value of the fifth time point in all models. Moreover, the parameter settings of all models are shown in Table 3.

Table 6.
Comparison results with the individual models.
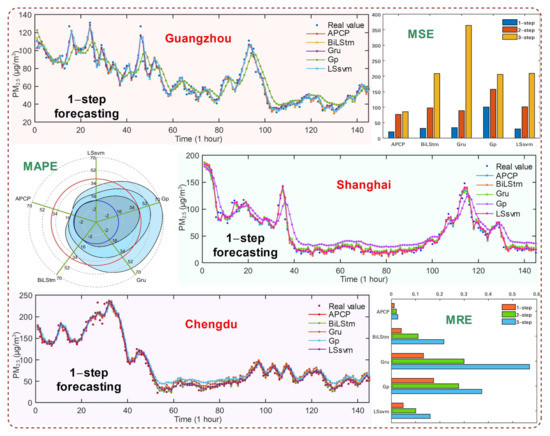
Figure 2.
The prediction results of the APCP system and four well-known models in Experiment I. The three-line charts represent the fitting results of the 1-step prediction in the three regions. The bar chart shows the difference in MSE values for the dataset in Gz. The radar chart describes the changes in MAPE values in well-known models and the APCP system for the dataset in Sh. The horizontal bar chart depicts the comparison results of MRE values in different models for the dataset in Cd.
(a) For the dataset in Gz, the APCP system produces the best results in all measurement indicators. For the 1-step prediction, the MSE value of the APCP system is only , while the minimum value of the other individual models is . Similar results are also found in MRE and MAPE values. Based on the positive indicator, the R2 value of the APCP system is , which is higher than the average result of the four well-known individual models . From the evaluation index of the 2-step prediction, the MRE value of the APCP system is even better than that of the Gru and GP models in the 1-step prediction ( and ). Besides, the performance of the 3-step prediction in the APCP system has little difference from that of the 2-step prediction , which indicates that the proposed system has better stability.
(b) For the dataset in Sh, although the overall performance of the APCP system is not as good as that of the dataset in Gz, it is still superior to the other individual models. For the 1-step prediction, the advantage of the APCP system is not outstanding . Because the individual submodels show good prediction capacity, the improvement space of the APCP system is limited. However, with the increase in prediction steps, the superiority of the APCP system becomes more and more obvious. Based on the evaluation results of MSE, the APCP system is lower than the Elm model, which has the optimal result among all individual models, in the 2-step prediction. In the 3-step prediction, the APCP system is less than the Cnn model with the best results. It is worth noting that the MAPE of the APCP system in the 3-step is less than that in the 2-step .
(c) For the dataset in Cd, the R2 value is the largest, which indicates that historical data has the strongest ability to interpret the predicted value at the next time point. For example, in the 3-step prediction of the APCP system, R2 in Cd is much higher than that in Gz and Sh . Due to the frequent fluctuations of the dataset in Cd, the APCP system still achieves exact prediction in the case that the measurement errors of the models are large. Compared with the average value of MSE in four well-known models , the MSE of the APCP system is only . For the 3-step prediction results, though the Cnn model performs the best of all individual models, it is inferior to the APCP system .
Remark 1.
Compared with all individual models, including Bilstm, Gru, Gp, Lssvm, Cnn, Lstm, Elm, and Enn models, the APCP system has perfect prediction performance. Even in multi-step prediction, the proposed system represents strong robustness as usual.
3.4. Experiment II: Test the Superiority of the APCP System
Based on the results of Experiment I, Experiment II mainly analyzes the percentage improvement of the APCP system compared with four well-known models, which are listed in Table 7. The influence of the magnitude is eliminated, and the superiority of the APCP system can be objectively evaluated. In addition, the average percentage improvement of the three regions is also calculated to illustrate the generality of the APCP system performance.

Table 7.
The improvement percentage of the APCP system.
(a) For the dataset in Gz, the performance of the APCP system is greatly improved in the 1-step and 3-step prediction, while it is relatively small in the 2-step prediction. For example, the MRE value of the APCP system increases by at least in one-step prediction. In contrast, in the two-step prediction, it improves by at most. The APCP system also has a significant advantage in the 3-step prediction, with MSE ranging from to , which is also better than the 2-step prediction .
(b) For the dataset in Sh, the improvement of the APCP system for some models is even higher than that of the dataset in Gz. From the results of Experiment I, the fitting result of the dataset in Gz is significantly better than that of the dataset in Sh. It may be because the dataset in Sh is noisier. However, from the perspective of improvement effect, the APCP system can also exactly predict redundant data. Taking 2-step and 3-step predictions as examples, the values of MSE and MRE in the APCP system increase by at least and , respectively, while for the dataset in Gz, the minimum values of and are only and respectively.
(c) For the dataset in Cd, with the increase of prediction steps, the performance advantage of the APCP system becomes more and more significant. From the comparison of MSE results, the percentage of improvement of the APCP system gradually increases . More prediction steps increase the complexity so that the well-known individual model is difficult to maintain a stable prediction, which may cause the percentage change in the APCP system. Similarly, the same conclusion can be drawn in and .
Remark 2.
In the comparative analysis with the above individual model, the superiority of the APCP system is scientifically and systematically verified. Even though there are slight differences between different regions, the average effect is still outstanding.
3.5. Experiment III: Comparison of Different Module Strategies
Experiment III mainly compares the combined models using different module strategies. Specifically, by changing the strategies of the time series reconstruction module and weight search module, the effectiveness of the DE mode and weight search mechanism in the APCP system is proved. The experimental results of the combined model are depicted in Table 8 and Figure 3. To ensure the comparability of the experiment, the settings of all model parameters remain the same as before, as listed in Table 3.

Table 8.
Error evaluation based on different module strategies.
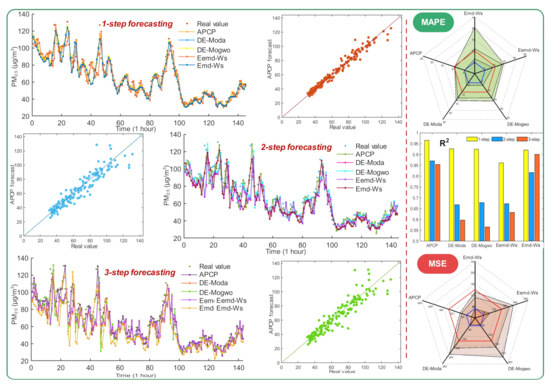
Figure 3.
Performance comparison of different combined models for the dataset in Gz. The six subfigures on the left side of the dotted line indicate how close the predicted results of all models in Experiment III are to the real values. The three subfigures on the right compare the differences in MAPE, R2, and MSE values between the APCP system and the other combined models.
(a) For the dataset in Gz, the time series reconstruction module strategy applied by the APCP system achieves the best prediction effect. The above experiment shows that when the number of prediction steps increases, the prediction result of the individual model is poor. In order to reduce the difficulty of the prediction model, different time series reconstruction strategies are applied to the experiment, which is the empirical mode decomposition (Emd) and ensemble Emd (Eemd). It can be seen that the Eemd strategy does not produce the expected effect , while the Emd strategy helps to improve the prediction accuracy . Although the R2 value at the 3-step prediction is higher than that of the APCP system , it is not as perfect as the APCP system at all other times .
(b) For the dataset in Sh, based on the same DE mode, the weight search mechanism of the APCP system can contain the advantages of all individual models as much as possible. Considering the function of the multi-objective optimization mechanism, Moda and Mogwo optimization mechanism is utilized to evaluate the weight search capacity. The effects of these two optimization mechanisms are basically the same , except that they are better than the APCP system in individual indicators, and the prediction performance is far inferior to the APCP system .
(c) For the dataset in Cd, no matter how the module strategies change, the APCP system still maintains an absolute advantage. Taking the result of the 1-step prediction as an example, the MSE value of the APCP system is reduced by to that of the DE-Moda model. Compared with the MRE value of the DE-Mogwo model , the APCP system is only . Similarly, the MAPE value of the APCP system is lower than that of the Emd-Ws model. The R2 value reaches the maximum .
Remark 3.
The DE mode and weight search mechanism adopted by the APCP system can minimize the complexity of input data and integrate the advantages of the individual models, which is the key to improving the prediction performance of the APCP system.
4. Discussions
In this section, three discussions, which are significance analysis, correlation analysis, and sensitivity analysis, are implemented to more comprehensively and scientifically demonstrate the perfect performance of the APCP system.
4.1. Significance Analysis
Significance analysis aims to explain whether the difference between the APCP system and the model involved in Experiment I~III is significant. Diebold-Mariano (DM) statistic is a general indicator to measure the consistency of two sequences [53]. Based on this , this subsection compares the results between the APCP system and eight models, and the results are represented in Table 9.

Table 9.
Significance comparison results of the APCP model.
Compared with the four well-known individual models, the prediction results of the APCP system have significant advantages at the significance level of , except that there is no significant difference between the Gru and Lssvm models and the APCP system in the 2-step prediction results. For the combined models with different module strategies, although the Emd-Ws model accepts in the 2-step and 3-step prediction results of the Sh dataset , in other cases (DE-Moda, DE-Mogwo, and Eemd-Ws models), is rejected at the significance level of , such as . In other words, it is significantly different from the APCP system. In summary, the APCP system has significant advantages in improving prediction performance.
4.2. Correlation Analysis
This subsection mainly adopts the method of grey relational degree analysis [54] to calculate the correlation between the prediction results of all models and the real values . The comparison results are revealed in Table 10.

Table 10.
Discussion results of correlation analysis.
In the correlation analysis of all models, the APCP system has the strongest correlation with the real value . The predicted value of the APCP system not only does not decrease with the increase of prediction steps but also improves , which also confirms the stability of APCP system performance. For example, for the dataset in Cd, the value of the 1-step prediction is , while the value of the 3-step prediction is .
4.3. Sensitivity Analysis
In order to verify the generality of the APCP system, this section discusses the stability of the weight search mechanism. Three important parameters, including iteration number , population number , and archive size , are selected to evaluate changes in APCP system performance. The results of the discussion are depicted in Table 11 and Figure 4.

Table 11.
Sensitivity analysis results of the APCP system.
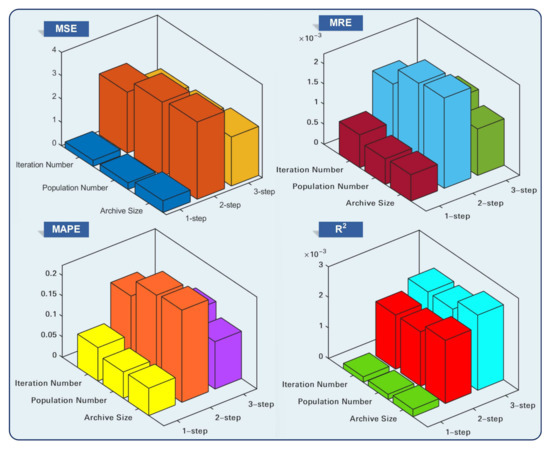
Figure 4.
Sensitivity assessment of average results in three cities.
(a) The performance of the APCP system can not fluctuate greatly with the change in ITer. The sensitivity indicators and show the volatility of MRE and R2 values in the APCP system when ITer changes. From the results of the three cities, the and values remain unchanged, which are close to 0.
(b) The change inhas no obvious influence on the evaluation index of the APCP system. Although fluctuate significantly in the 2-step prediction, this is only an individual case. It may be caused by insufficient times of experiments. In most cases, the four evaluation indicators of the APCP system reflect good stability .
(c) From the adjustment of ARchIvemax, the stability of the APCP system can also be verified. Except for in the two-step prediction of the dataset in Cd, the error evaluation index of the APCP system has no significant fluctuation. Even the results in the 3-step prediction emerge with superior stability .
Remark 4.
The parameter adjustment of the weight search mechanism has no significant impact on the APCP system, which demonstrates that the system has excellent stability.
5. Conclusions and Prospect
With the comprehensive popularization of urbanization and the rapid increase in energy consumption, many air pollution problems have been brought to cities. To formulate protective measures timely and effectively, a novel APCP system is proposed for environmental system management in this paper. First, based on DE mode, the AP sequence is reconstructed to reduce redundant interference. Then, four individual models with superior performance are selected to realize AP prediction. Next, the weight search mechanism is designed to balance the precision and robustness of the proposed system. Finally, appropriate weights are adopted to integrate the advantages of all models, which can obtain a perfect prediction value.
From Experiment I~III, this conclusion can be drawn that the multi-step prediction performance of the APCP system is superior. Taking the dataset in Gz as an example, in the 1-step prediction, the MSE of the APCP system has a minimum value . Compared with the Lssvm model, the value of MRE is reduced by . For the results of the 2-step prediction, the value of MAPE is less than that of the Emd-Ws model. It is worth noting that the R2 value predicted by the APCP system in 3-step is even better than that predicted by the DE-Moda model in 2-step . To sum up, the comprehensive capacity of the APCP system is outstanding, which can be used as an effective tool in actual AP prediction.
Although this paper assumes that the AP concentration sequence is only related to historical values, many external factors, such as wind speed, affect the concentration changes of AP in real life. Based on this consideration, the APCP system can be further expanded in future research to improve its prediction performance.
Author Contributions
Y.H.: Conceptualization, software, writing—original draft preparation. Y.Z.: methodology, visualization, writing—reviewing and editing. J.G.: writing—original draft preparation, software validation. J.W.: formal analysis, software validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Major Program of National Social Science Foundation of China (Grant No. 17ZDA093).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the contribution of the anonymous reviewers and the editors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, H.Y.; Dunea, D.; Iordache, S.; Pohoata, A. A Review of Airborne Particulate Matter Effects on Young Children’s Respiratory Symptoms and Diseases. Atmosphere 2018, 9, 150. [Google Scholar] [CrossRef]
- Yang, S.; Fang, D.; Chen, B. Human Health Impact and Economic Effect for PM2.5 Exposure in Typical Cities. Appl. Energy 2019, 249, 316–325. [Google Scholar] [CrossRef]
- Hao, Y.; Niu, X.; Wang, J. Impacts of Haze Pollution on China’s Tourism Industry: A System of Economic Loss Analysis. J. Environ. Manag. 2021, 295, 113051. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.H.; Kabir, E.; Kabir, S. A Review on the Human Health Impact of Airborne Particulate Matter. Environ. Int. 2015, 74, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Maji, K.J.; Ye, W.F.; Arora, M.; Shiva Nagendra, S.M. PM2.5-Related Health and Economic Loss Assessment for 338 Chinese Cities. Environ. Int. 2018, 121, 392–403. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Bocquet, M.; Mallet, V.; Seigneur, C.; Baklanov, A. Real-Time Air Quality Forecasting, Part I: History, Techniques, and Current Status. Atmos. Environ. 2012, 60, 632–655. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Li, Z. A Combined Forecasting System Based on Multi-Objective Optimization and Feature Extraction Strategy for Hourly PM2.5 Concentration. Appl. Soft Comput. 2022, 114, 108034. [Google Scholar] [CrossRef]
- Djalalova, I.; Delle Monache, L.; Wilczak, J. PM2.5 Analog Forecast and Kalman Filter Post-Processing for the Community Multiscale Air Quality (CMAQ) Model. Atmos. Environ. 2015, 108, 76–87. [Google Scholar] [CrossRef]
- Baker, K.R.; Woody, M.C.; Valin, L.; Szykman, J.; Yates, E.L.; Iraci, L.T.; Choi, H.D.; Soja, A.J.; Koplitz, S.N.; Zhou, L.; et al. Photochemical Model Evaluation of 2013 California Wild Fire Air Quality Impacts Using Surface, Aircraft, and Satellite Data. Sci. Total Environ. 2018, 637–638, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Xue, D.; Liu, X.; Gong, X.; Gao, H. Process Analysis of PM2.5 Pollution Events in a Coastal City of China Using CMAQ. J. Environ. Sci. 2019, 79, 225–238. [Google Scholar] [CrossRef]
- Lee, K.; Yu, J.; Lee, S.; Park, M.; Hong, H.; Park, S.Y.; Choi, M.; Kim, J.; Kim, Y.; Woo, J.H.; et al. Development of Korean Air Quality Prediction System Version 1 (KAQPS v1) with Focuses on Practical Issues. Geosci. Model Dev. 2020, 13, 1055–1073. [Google Scholar] [CrossRef]
- Ryu, Y.H.; Hodzic, A.; Barre, J.; Descombes, G.; Minnis, P. Quantifying Errors in Surface Ozone Predictions Associated with Clouds over the CONUS: A WRF-Chem Modeling Study Using Satellite Cloud Retrievals. Atmos. Chem. Phys. 2018, 18, 7509–7525. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, Y.; Xu, X.; You, W.; Zang, Z.; Gao, L.; Chen, Y.; Su, D.; Yan, P. Lidar Data Assimilation Method Based on CRTM and WRF-Chem Models and Its Application in PM2.5 Forecasts in Beijing. Sci. Total Environ. 2019, 682, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Abdi-Oskouei, M.; Carmichael, G.; Christiansen, M.; Ferrada, G.; Roozitalab, B.; Sobhani, N.; Wade, K.; Czarnetzki, A.; Pierce, R.B.; Wagner, T.; et al. Sensitivity of Meteorological Skill to Selection of WRF-Chem Physical Parameterizations and Impact on Ozone Prediction During the Lake Michigan Ozone Study (LMOS). J. Geophys. Res. Atmos. 2020, 125, e2019JD031971. [Google Scholar] [CrossRef]
- Lopez-Restrepo, S.; Yarce, A.; Pinel, N.; Quintero, O.L.; Segers, A.; Heemink, A.W. Forecasting PM10 and PM2.5 in the Aburrá Valley (Medellín, Colombia) via EnKF Based Data Assimilation. Atmos. Environ. 2020, 232, 117507. [Google Scholar] [CrossRef]
- Wei, W.; Lv, Z.F.; Li, Y.; Wang, L.T.; Cheng, S.; Liu, H. A WRF-Chem Model Study of the Impact of VOCs Emission of a Huge Petro-Chemical Industrial Zone on the Summertime Ozone in Beijing, China. Atmos. Environ. 2018, 175, 44–53. [Google Scholar] [CrossRef]
- Chen, Q.; Taylor, D. Transboundary Atmospheric Pollution in Southeast Asia: Current Methods, Limitations and Future Developments. Crit. Rev. Environ. Sci. Technol. 2018, 48, 997–1029. [Google Scholar] [CrossRef]
- De Mattos Neto, P.S.G.; Madeiro, F.; Ferreira, T.A.E.; Cavalcanti, G.D.C. Hybrid Intelligent System for Air Quality Forecasting Using Phase Adjustment. Eng. Appl. Artif. Intell. 2014, 32, 185–191. [Google Scholar] [CrossRef]
- Baptista, M.; Sankararaman, S.; de Medeiros, I.P.; Nascimento, C.; Prendinger, H.; Henriques, E.M.P. Forecasting Fault Events for Predictive Maintenance Using Data-Driven Techniques and ARMA Modeling. Comput. Ind. Eng. 2018, 115, 41–53. [Google Scholar] [CrossRef]
- Wang, J.; Lei, C.; Guo, M. Daily Natural Gas Price Forecasting by a Weighted Hybrid Data-Driven Model. J. Pet. Sci. Eng. 2020, 192, 107240. [Google Scholar] [CrossRef]
- Aladağ, E. Forecasting of Particulate Matter with a Hybrid ARIMA Model Based on Wavelet Transformation and Seasonal Adjustment. Urban Clim. 2021, 39, 100930. [Google Scholar] [CrossRef]
- Bhatti, U.A.; Yan, Y.; Zhou, M.; Ali, S.; Hussain, A.; Qingsong, H.; Yu, Z.; Yuan, L. Time Series Analysis and Forecasting of Air Pollution Particulate Matter (PM2.5): An SARIMA and Factor Analysis Approach. IEEE Access 2021, 9, 41019–41031. [Google Scholar] [CrossRef]
- Shaziayani, W.N.; Ul-Saufie, A.Z.; Ahmat, H.; Al-Jumeily, D. Coupling of Quantile Regression into Boosted Regression Trees (BRT) Technique in Forecasting Emission Model of PM10 Concentration. Air Qual. Atmos. Health 2021, 14, 1647–1663. [Google Scholar] [CrossRef]
- Liu, T.; Lau, A.K.H.; Sandbrink, K.; Fung, J.C.H. Time Series Forecasting of Air Quality Based On Regional Numerical Modeling in Hong Kong. J. Geophys. Res. Atmos. 2018, 123, 4175–4196. [Google Scholar] [CrossRef]
- Abdullah, S.; Napi, N.N.L.M.; Ahmed, A.N.; Mansor, W.N.W.; Mansor, A.A.; Ismail, M.; Abdullah, A.M.; Ramly, Z.T.A. Development of Multiple Linear Regression for Particulate Matter (PM10) Forecasting during Episodic Transboundary Haze Event in Malaysia. Atmosphere 2020, 11, 289. [Google Scholar] [CrossRef]
- Mohd Napi, N.N.L.; Noor Mohamed, M.S.; Abdullah, S.; Mansor, A.A.; Ahmed, A.N.; Ismail, M. Multiple Linear Regression (MLR) and Principal Component Regression (PCR) for Ozone (O3) Concentrations Prediction. IOP Conf. Ser. Earth Environ. Sci. 2020, 616, 012004. [Google Scholar] [CrossRef]
- Bai, Y.; Li, Y.; Wang, X.; Xie, J.; Li, C. Air Pollutants Concentrations Forecasting Using Back Propagation Neural Network Based on Wavelet Decomposition with Meteorological Conditions. Atmos. Pollut. Res. 2016, 7, 557–566. [Google Scholar] [CrossRef]
- Li, X.; Peng, L.; Yao, X.; Cui, S.; Hu, Y.; You, C.; Chi, T. Long Short-Term Memory Neural Network for Air Pollutant Concentration Predictions: Method Development and Evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef]
- Jiang, X.; Wei, P.; Luo, Y.; Li, Y. Air Pollutant Concentration Prediction Based on a CEEMDAN-FE-BiLSTM Model. Atmosphere 2021, 12, 1452. [Google Scholar] [CrossRef]
- Weihong, W.; Shuangshuang, N. The Performance of Several Combining Forecasts for Stock Index. In Proceedings of the 2008 International Seminar on Future Information Technology and Management Engineering, Leicestershire, UK, 20 November 2008; pp. 450–455. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Li, Z. Prediction of Air Pollution Interval Based on Data Preprocessing and Multi-Objective Dragonfly Optimization Algorithm. Front. Ecol. Evol. 2022, 10, 855606. [Google Scholar] [CrossRef]
- Yang, W.; Sun, S.; Hao, Y.; Wang, S. A Novel Machine Learning-Based Electricity Price Forecasting Model Based on Optimal Model Selection Strategy. Energy 2022, 238, 121989. [Google Scholar] [CrossRef]
- Murillo-Escobar, J.; Sepulveda-Suescun, J.P.; Correa, M.A.; Orrego-Metaute, D. Forecasting Concentrations of Air Pollutants Using Support Vector Regression Improved with Particle Swarm Optimization: Case Study in Aburrá Valley, Colombia. Urban Clim. 2019, 29, 100473. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, H. A Novel Optimal-Hybrid Model for Daily Air Quality Index Prediction Considering Air Pollutant Factors. Sci. Total Environ. 2019, 683, 808–821. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Chen, L.; Yang, H. Prediction of PM2.5 Concentration Based on Improved Secondary Decomposition and CSA-KELM. Atmos. Pollut. Res. 2022, 13, 101455. [Google Scholar] [CrossRef]
- Gan, R.; Guo, Q.; Chang, H.; Yi, Y. Improved Ant Colony Optimization Algorithm for the Traveling Salesman Problems. J. Syst. Eng. Electron. 2010, 21, 329–333. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull Optimization Algorithm: Theory and Its Applications for Large-Scale Industrial Engineering Problems. Knowledge-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- Zhou, Q.; Lv, Q.; Zhang, G. A Combined Forecasting System Based on Modified Multi-Objective Optimization for Short-Term Wind Speed and Wind Power Forecasting. Appl. Sci. 2021, 11, 9383. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Li, Z.; Lu, H. Short-Term Photovoltaic Power Forecasting Based on Signal Decomposition and Machine Learning Optimization. Energy Convers. Manag. 2022, 267, 115944. [Google Scholar] [CrossRef]
- Wang, J.; Gao, J.; Wei, D. Electric Load Prediction Based on a Novel Combined Interval Forecasting System. Appl. Energy 2022, 322, 119420. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, S. Study on the Spatial–Temporal Change Characteristics and Influence Factors of Fog and Haze Pollution Based on GAM. Neural Comput. Appl. 2019, 31, 1619–1631. [Google Scholar] [CrossRef]
- Zakaria, N.N.; Othman, M.; Sokkalingam, R.; Daud, H.; Abdullah, L.; Kadir, E.A. Markov Chain Model Development for Forecasting Air Pollution Index of Miri, Sarawak. Sustainability 2019, 11, 5190. [Google Scholar] [CrossRef]
- Zhou, W.; Wu, X.; Ding, S.; Cheng, Y. Predictive Analysis of the Air Quality Indicators in the Yangtze River Delta in China: An Application of a Novel Seasonal Grey Model. Sci. Total Environ. 2020, 748, 141428. [Google Scholar] [CrossRef]
- Kim, J.; Wang, X.; Kang, C.; Yu, J.; Li, P. Forecasting Air Pollutant Concentration Using a Novel Spatiotemporal Deep Learning Model Based on Clustering, Feature Selection and Empirical Wavelet Transform. Sci. Total Environ. 2021, 801, 149654. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Huang, G.; Zeng, H.; Zhou, F. PM2.5 Volatility Prediction by XGBoost-MLP Based on GARCH Models. J. Clean. Prod. 2022, 356, 131898. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Chen, J.; Wang, Q. Air Pollution Concentration Forecasting Based on Wavelet Transform and Combined Weighting Forecasting Model. Atmos. Pollut. Res. 2021, 12, 101144. [Google Scholar] [CrossRef]
- Sayeed, A.; Choi, Y.; Eslami, E.; Lops, Y. Using a Deep Convolutional Neural Network to Predict 2017 Ozone Concentrations, 24 Hours in Advance. Neural Netw. 2019, 121, 396–408. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Li, Q.; Karimian, H.; Fang, S.; Tang, B.; Chen, G. A Novel Framework for Daily Forecasting of Ozone Mass Concentrations Based on Cycle Reservoir with Regular Jumps Neural Networks. Atmos. Environ. 2020, 220, 117072. [Google Scholar] [CrossRef]
- Chen, S.; Wang, J.; Zhang, H. A Hybrid PSO-SVM Model Based on Clustering Algorithm for Short-Term Atmospheric Pollutant Concentration Forecasting. Technol. Forecast. Soc. Chang. 2019, 146, 41–54. [Google Scholar] [CrossRef]
- Huang, G.; Li, X.; Zhang, B.; Ren, J. PM2.5 Concentration Forecasting at Surface Monitoring Sites Using GRU Neural Network Based on Empirical Mode Decomposition. Sci. Total Environ. 2021, 768, 144516. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Jiang, Q.; Jiang, P. A Combined Forecasting Structure Based on the L 1 Norm: Application to The. J. Environ. Manag. 2019, 246, 299–313. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and Application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Y. Introduction to Grey Systems Theory. In Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2010; Volume 68, pp. 1–399. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).