Research on the Coupling Coordination Relationship between Urban Rail Transit System and Sustainable Urban Development
Abstract
:1. Introduction
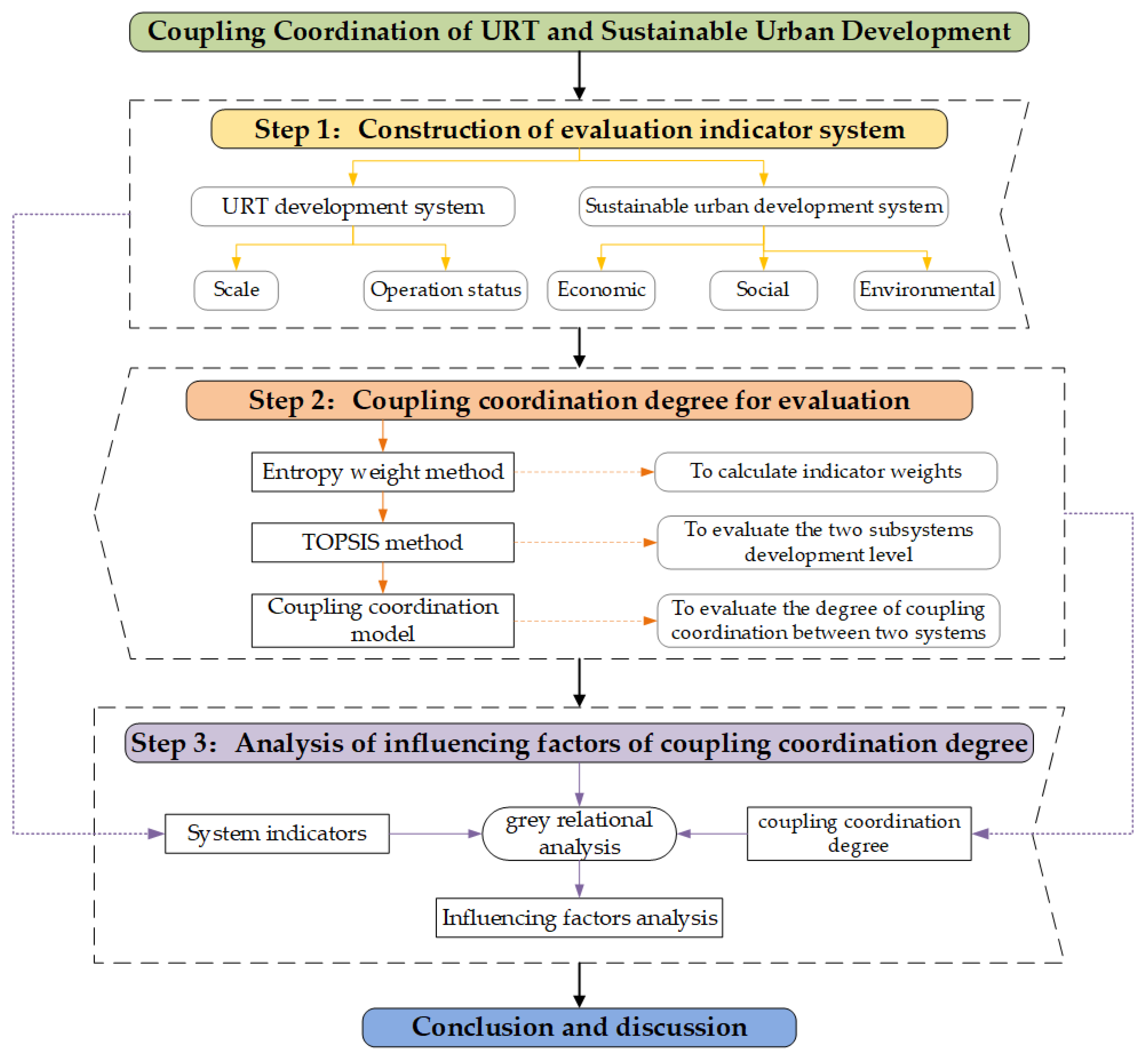
2. Methods
2.1. Entropy Weight Method
- (1)
- Establishment of an evaluation matrix
- (2)
- Normalization of all indicators
- (3)
- Calculation of the entropy
- (4)
- Calculation of the weight
2.2. TOPSIS Method
- (1)
- Construction of a weighted decision matrix
- (2)
- Calculation of the positive ideal distance and the negative ideal distance
- (3)
- Calculation of relative closeness
2.3. Coupling Coordination Degree Model
- (1)
- Calculation of coupling degree
- (2)
- Calculation of coordination degree
- (3)
- Calculation of coupling coordination degree
2.4. Grey Relational Analysis
- (1)
- Determine the reference sequence and comparative sequences
- (2)
- Normalize the values of the original sequences
- (3)
- Calculate the grey correlation coefficient
- (4)
- Calculate the grey relational degree (GRD)
3. Selection of the Evaluation Indicators
3.1. Construction of the Evaluation Indicator System
3.2. Data Sources
4. Analysis Results
4.1. Calculation Results of the Indicator Weights
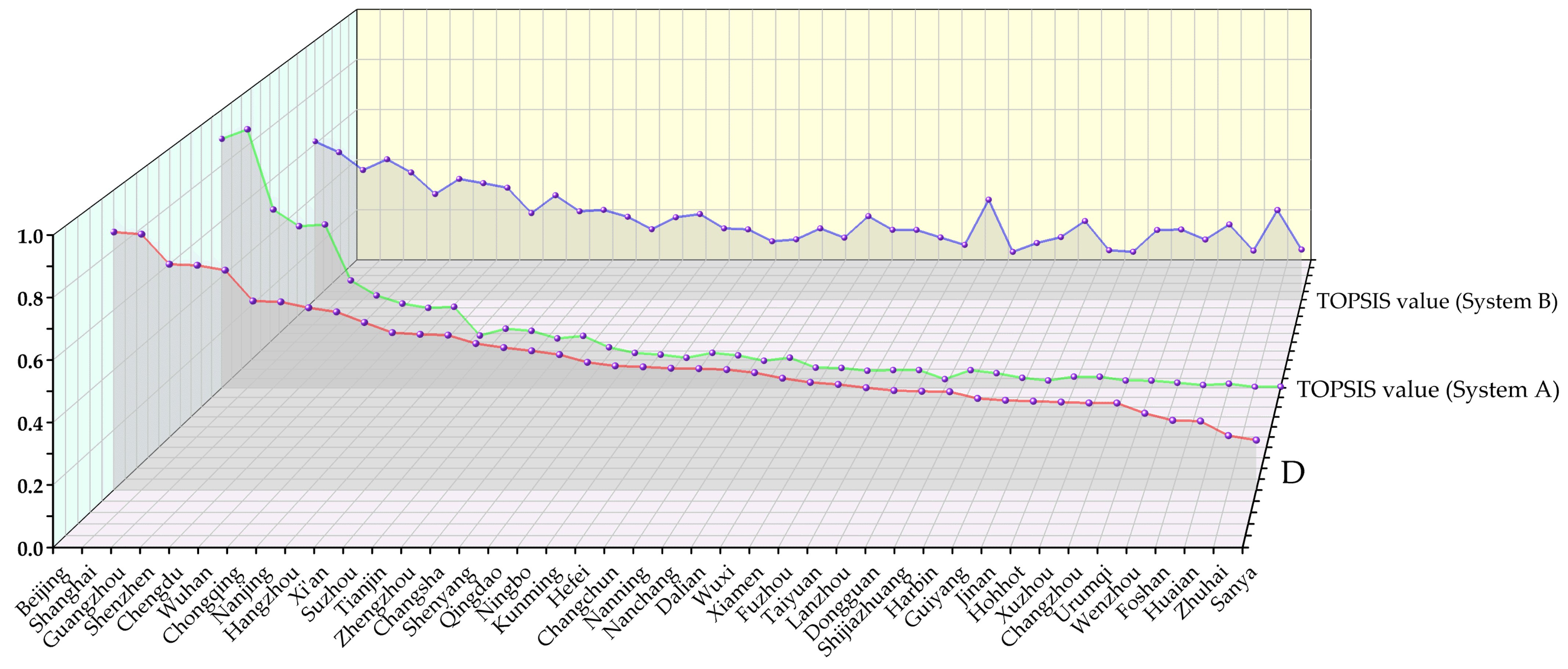
4.2. Calculation Results of the URT and SUD
4.3. Calculation Results of Coupling Coordination Degree Values
4.4. Calculation Results of Influencing Factors of Coupling Coordination Degree
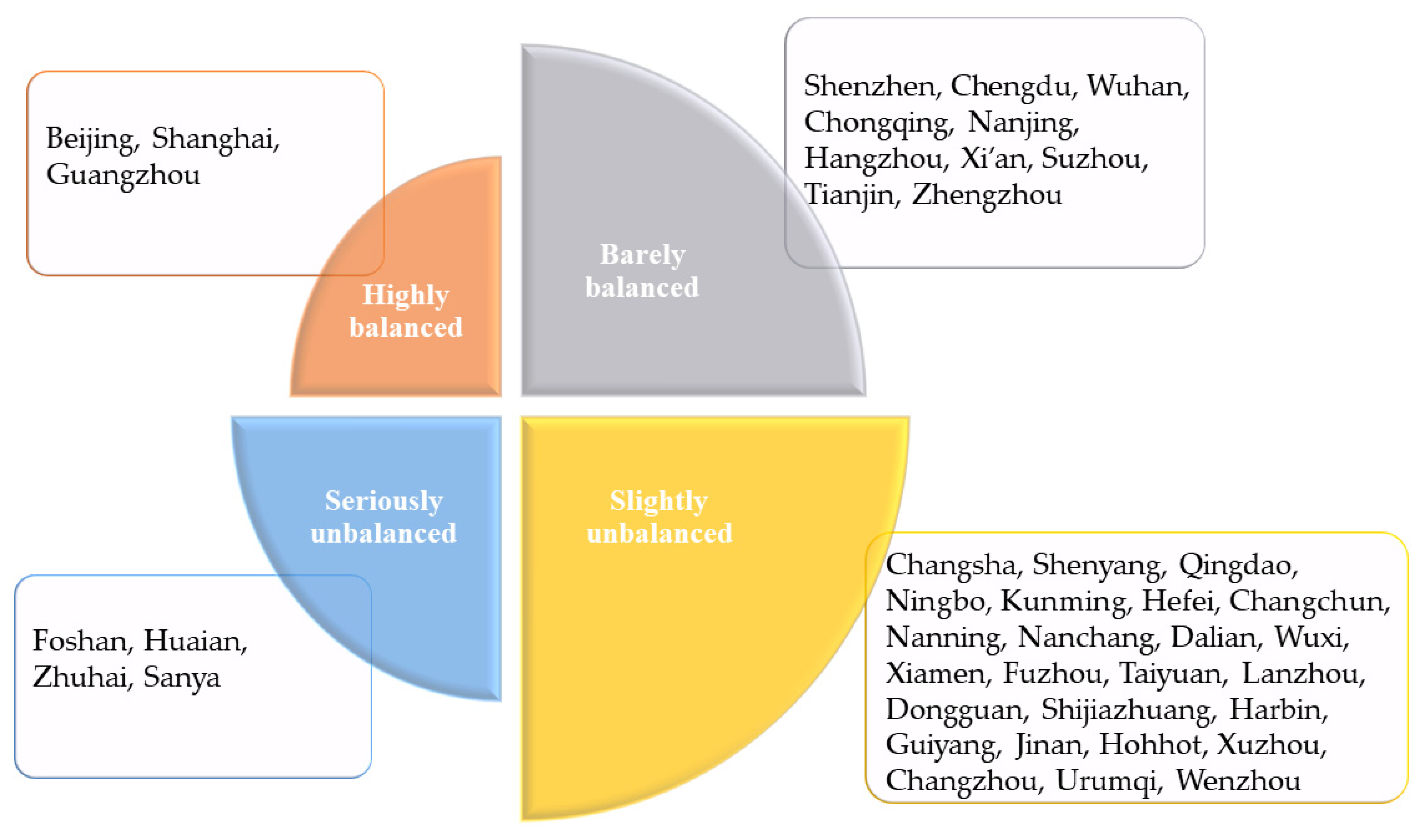
5. Discussion
- (1)
- Cities with highly balanced development in two systems: Beijing, Shanghai and Guangzhou. They opened their first URT in 1971, 1993 and 1997, respectively, ranking high among the cities in mainland China that have opened URT. Due to the early start for metro development, strong industrial and economic strength and the URT system after years of construction and development, these first-tier cities have been scaled up and networked with a high degree of SUD [63]. The raw data show that the scale of rail transit passenger volume, line length and the number of operating vehicles is more significant in this category compared to other cities. The URT system formed a complete road network structure. At the same time, the overall urban sustainability value is also ranked high, indicating that this category of cities has a higher level of URT development, SUD and coupled and coordinated development between the two, which is worthy of reference for other cities.
- (2)
- Cities with barely balanced development in two systems: This includes eight cities, such as Shenzhen, Chengdu, Wuhan and Chongqing. From Figure 2, it can be seen that although the coupling and coordination between URT development and SUD in Chongqing are high, the gap between the comprehensive evaluation value of the two is significant. It indicates that the URT development in Chongqing still needs to be improved. It should scientifically plan and reasonably design the URT system, further develop the rail transit network structure and improve the rail transit operation mode and service quality, so that the level of coupling and coordination between URT development and SUD can be improved. Some scholars have related findings and recommendations [64]. However, the passenger volume in Suzhou and Tianjin is not supported enough. The original data show that the average daily passenger volume of URT in Suzhou and Tianjin in 2020 is only 84.5 and 92.6 10,000 persons, which is low compared to other cities. Some scholars found that URT is not the most preferred mode of transportation for Tianjin residents due to high fares, general walkable neighborhoods and inconvenient old subway stations [65]. For Suzhou and Tianjin, the attractiveness of rail transit to passengers can be increased by adjusting URT fares and other means. In addition, non-green transportation, such as private cars or cabs, can be appropriately restricted, thus, promoting green transportation development. Other cities in this category, such as Shenzhen, Chengdu and Nanjing, have a relatively good scale of URT development, which is compatible with the city’s sustainable development and positively impacts the city’s sustainable development.
- (3)
- Cities with slightly unbalanced development in two systems: This includes 25 cities, including Changsha, Shenyang and Qingdao; the total number of cities in this category accounts for more than 50% of the total cities studied. These cities are at a low level of coordinated development on a national scale. They need to improve their lagging items to improve the coupling and coordination between URT and SUD at a higher level. Most cities are slightly unbalanced with lagging uA type, indicating that the current process of rail transit construction in most Chinese cities is still slow and unable to provide public solid transportation support for rapid socio-economic development [15]. For example, Dongguan and Jinan, two cities, are similar to Chongqing in category 2 and have a higher overall urban sustainability system rating value than their counterparts. This indicates that the level of URT development has not kept up with the development of the cities and there is still a lot of room and potential for development. Cities, such as Lanzhou and Shijiazhuang, have low SUD levels compared to their counterparts. They should develop a public transportation strategy compatible with urban social and environmental development and transportation construction, focus on improving the technical equipment and technical performance of the existing URT, as well as the operation mode and service quality, to further reduce exhaust emissions and noise pollution and improve the level of SUD.
- (4)
- Cities with seriously unbalanced development in two systems: Foshan, Huaian, Zhuhai and Sanya. Cities in this category are at a low level for urban rail development and sustainable urban development systems. Both have much room for improvement. As can be seen from Table 7, the resident population is the most crucial factor affecting the level of coordination between URT development and SUD coupling. Cities should formulate their development strategies according to the size of their population, that is, the public transport demand, for example, Foshan with a high resident population in this category. The managers should insist on developing urban public transportation with rail transit as the core, increase rail transit investment and policy preferences and cooperate with the introduction of corresponding local policies to improve the efficiency of local URT development to improve the level of coordination between URT and SUD coupling [20,66]. However, as China’s urbanization process has been accelerating in recent years, the original approval standards are increasingly not applicable to the current level of urban socio-economic development. In the future, with the continuous development of the economy and society, the approval system of URT construction planning also needs to be improved continuously to improve and enrich the corresponding approval standard and approval content to ensure the healthy and stable dynamic coordination between URT construction and SUD [11,67]. Huai’an, Zhuhai and Sanya ranked at the bottom among all cities regarding Gross Regional Product. That is, the economy of the cities cannot create a good economic environment for the development of URT. In the future, such cities should pay more attention to the development of the economy.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| City | Scale (A1) | Operation Status (A2) | ||||||
|---|---|---|---|---|---|---|---|---|
| A11 | A12 | A13 | A14 | A21 | A22 | A23 | A24 | |
| Beijing | 799.1 | 382 | 62 | 1108 | 10,367 | 626.9 | 0.78 | 67,257.0 |
| Shanghai | 834.2 | 432 | 65 | 1038 | 8337 | 779.0 | 1.07 | 64,317.1 |
| Tianjin | 238.8 | 157 | 15 | 224 | 1817 | 92.6 | 0.39 | 13,669.0 |
| Chongqing | 343.3 | 178 | 20 | 328 | 3427 | 229.4 | 0.67 | 23,469.9 |
| Guangzhou | 531.6 | 277 | 35 | 558 | 7073 | 660.2 | 1.19 | 41,422.4 |
| Shenzhen | 422.6 | 263 | 48 | 532 | 4677 | 479.4 | 1.13 | 34,584.8 |
| Wuhan | 387.5 | 254 | 29 | 493 | 3751 | 207.8 | 0.56 | 18,687.5 |
| Nanjing | 394.3 | 187 | 13 | 291 | 3140 | 218.0 | 0.58 | 21,207.0 |
| Shenyang | 211.5 | 157 | 13 | 180 | 1700 | 90.9 | 0.43 | 8125.0 |
| Changchun | 117.7 | 119 | 8 | 134 | 1425 | 43.3 | 0.43 | 3621.7 |
| Dalian | 181.3 | 106 | 3 | 114 | 1162 | 34.1 | 0.22 | 5379.1 |
| Chengdu | 652.0 | 327 | 46 | 672 | 5062 | 399.2 | 0.72 | 29,226.5 |
| Xi’an | 239.0 | 154 | 13 | 321 | 3437 | 247.6 | 1.04 | 15,631.6 |
| Harbin | 30.3 | 26 | 1 | 31 | 485 | 14.0 | 0.46 | 1603.0 |
| Suzhou | 210.1 | 151 | 9 | 221 | 2198 | 84.5 | 0.40 | 12,100.5 |
| Zhengzhou | 244.0 | 133 | 17 | 175 | 1547 | 111.9 | 0.56 | 8217.6 |
| Kunming | 139.4 | 83 | 9 | 122 | 1166 | 51.2 | 0.37 | 5523.4 |
| Hangzhou | 300.6 | 169 | 20 | 325 | 2862 | 179.4 | 0.60 | 15,506.3 |
| Foshan | 28.1 | 25 | 0 | 5 | 75 | 0.1 | 0.01 | 37.6 |
| Changsha | 157.9 | 95 | 12 | 152 | 1736 | 122.0 | 0.77 | 8305.7 |
| Ningbo | 154.3 | 97 | 6 | 150 | 1523 | 59.9 | 0.39 | 6183.1 |
| Wuxi | 87.1 | 66 | 3 | 75 | 780 | 29.7 | 0.34 | 3318.5 |
| Nanchang | 88.9 | 70 | 4 | 105 | 920 | 50.8 | 0.57 | 3883.7 |
| Lanzhou | 86.9 | 26 | 0 | 26 | 270 | 14.3 | 0.55 | 1320.2 |
| Qingdao | 255.0 | 119 | 4 | 191 | 1728 | 44.6 | 0.18 | 7340.3 |
| Huaian | 20.1 | 23 | 0 | 26 | 203 | 1.9 | 0.10 | 565.4 |
| Fuzhou | 58.5 | 45 | 1 | 59 | 482 | 25.9 | 0.44 | 2937.8 |
| Dongguan | 37.8 | 15 | 0 | 20 | 259 | 9.6 | 0.25 | 2040.7 |
| Nanning | 108.0 | 80 | 7 | 103 | 1181 | 61.2 | 0.57 | 5595.3 |
| Hefei | 112.5 | 80 | 3 | 122 | 1255 | 56.1 | 0.50 | 6739.1 |
| Shijiazhuang | 59.0 | 48 | 3 | 68 | 696 | 23.0 | 0.39 | 2394.5 |
| Guiyang | 34.8 | 25 | 0 | 34 | 276 | 10.1 | 0.29 | 1888.4 |
| Xiamen | 71.9 | 55 | 1 | 86 | 687 | 21.1 | 0.43 | 4691.1 |
| Zhuhai | 8.8 | 14 | 0 | 12 | 93 | 0.3 | 0.03 | 24.2 |
| Urumqi | 26.8 | 21 | 0 | 27 | 244 | 7.3 | 0.22 | 869.8 |
| Wenzhou | 53.5 | 18 | 0 | 18 | 189 | 2.1 | 0.04 | 1219.3 |
| Jinan | 47.7 | 24 | 0 | 42 | 486 | 2.4 | 0.05 | 2001.2 |
| Changzhou | 34.2 | 29 | 0 | 28 | 228 | 6.2 | 0.18 | 1694.6 |
| Xuzhou | 46.0 | 37 | 1 | 47 | 491 | 12.1 | 0.26 | 1126.4 |
| Hohhot | 49.0 | 43 | 1 | 52 | 435 | 11.3 | 0.23 | 1348.9 |
| Sanya | 8.4 | 15 | 0 | 11 | 157 | 0.3 | 0.03 | 11.0 |
| Taiyuan | 23.6 | 22 | 0 | 16 | 258 | 14.8 | 0.62 | 22.8 |
| City | Economic (B1) | |||||||
|---|---|---|---|---|---|---|---|---|
| B11 | B12 | B13 | B14 | B15 | B16 | B17 | B18 | |
| Beijing | 164,889 | 827,343.8 | 3028 | 62,660.6 | 7,399,399 | 185,026 | 0.44 | 0.34 |
| Shanghai | 155,800 | 584,114.4 | 8804 | 64,037.4 | 6,455,623 | 174,678 | 0.72 | 0.58 |
| Tianjin | 101,614 | 238,194.9 | 5120 | 25,832.1 | 2,553,324 | 118,918 | 0.94 | 0.88 |
| Chongqing | 78,173 | 128,607.7 | 6938 | 36,731.7 | 3,708,338 | 98,380 | 1.91 | 1.50 |
| Guangzhou | 135,047 | 350,135.9 | 6208 | 49,192.4 | 4,193,638 | 135,138 | 0.82 | 0.65 |
| Shenzhen | 159,309 | 539,404.1 | 11,255 | 49,148.2 | 5,052,706 | 139,436 | 0.53 | 0.44 |
| Wuhan | 131,441 | 245,978.5 | 2958 | 49,877.1 | 1,763,564 | 107,567 | 2.15 | 1.83 |
| Nanjing | 159,322 | 419,056.5 | 3231 | 77,285.8 | 2,161,081 | 138,005 | 1.42 | 1.30 |
| Shenyang | 75,570 | 212,487.6 | 1592 | 40,106.1 | 1,184,237 | 95,908 | 1.52 | 1.42 |
| Changchun | 77,634 | 156,071.7 | 1214 | 22,085.0 | 1,102,433 | 92,905 | 1.16 | 1.03 |
| Dalian | 94,685 | 208,221.5 | 1898 | 24,536.9 | 1,047,641 | 98,812 | 0.96 | 0.84 |
| Chengdu | 85,679 | 201,745.0 | 3664 | 38,752.0 | 11,433,200 | 104,463 | 1.76 | 1.35 |
| Xi’an | 79,181 | 198,537.9 | 1667 | 38,497.9 | 2,135,688 | 104,363 | 1.98 | 1.61 |
| Harbin | 54,570 | 137,356.2 | 1196 | 22,213.8 | 1,070,519 | 84,796 | 0.77 | 0.68 |
| Suzhou | 158,466 | 275,809.3 | 11,900 | 60,407.7 | 2,974,094 | 113,744 | 1.72 | 1.56 |
| Zhengzhou | 96,134 | 198,053.3 | 2295 | 40,224.3 | 2,139,900 | 89,464 | 2.71 | 2.40 |
| Kunming | 80,584 | 192,962.8 | 997 | 36,293.6 | 1,126,367 | 102,304 | 2.22 | 1.80 |
| Hangzhou | 136,617 | 433,525.8 | 5992 | 50,588.7 | 2,923,541 | 132,188 | 1.42 | 1.23 |
| Foshan | 114,157 | 197,293.4 | 8020 | 34,549.3 | 1,513,137 | 94,536 | 2.27 | 1.78 |
| Changsha | 123,297 | 228,695.5 | 2912 | 44,431.0 | 1,425,867 | 105,603 | 2.37 | 2.04 |
| Ningbo | 132,614 | 245,930.8 | 8571 | 44,992.2 | 1,647,943 | 111,286 | 1.97 | 1.67 |
| Wuxi | 165,851 | 252,918.4 | 7006 | 40,138.8 | 1,254,021 | 115,748 | 2.08 | 1.83 |
| Nanchang | 92,697 | 216,082.5 | 1553 | 39,181.1 | 1,239,463 | 93,774 | 2.83 | 2.18 |
| Lanzhou | 66,680 | 206,974.1 | 371 | 37,557.0 | 785,040 | 93,847 | 1.94 | 1.83 |
| Qingdao | 123,828 | 196,061.3 | 3856 | 51,468.8 | 1,477,012 | 116,115 | 1.64 | 1.41 |
| Huaian | 87,507 | 106,403.6 | 1486 | 36,751.2 | 449,447 | 83,216 | 2.03 | 1.85 |
| Fuzhou | 121,015 | 208,930.1 | 2662 | 50,788.5 | 1,561,135 | 96,478 | 2.27 | 1.83 |
| Dongguan | 92,176 | 166,416.8 | 11,525 | 35,688.4 | 2,863,056 | 79,601 | 0.84 | 0.73 |
| Nanning | 54,669 | 131,408.6 | 1155 | 24,918.4 | 1,097,670 | 97,079 | 2.10 | 1.70 |
| Hefei | 108,427 | 195,269.3 | 2150 | 48,172.5 | 1,729,908 | 104,818 | 1.59 | 1.38 |
| Shijiazhuang | 52,961 | 146,692.9 | 2183 | 21,198.0 | 1,050,390 | 84,870 | 0.58 | 0.55 |
| Guiyang | 72,246 | 208,433.6 | 764 | 36,531.9 | 1,132,677 | 101,829 | 2.07 | 1.85 |
| Xiamen | 123,962 | 242,343.2 | 2420 | 44,283.2 | 1,267,026 | 108,554 | 1.20 | 0.73 |
| Zhuhai | 145,645 | 382,989.0 | 1492 | 37,602.5 | 843,819 | 107,284 | 1.97 | 1.71 |
| Urumqi | 82,314 | 237,147.1 | 445 | 25,765.7 | 819,995 | 98,907 | 1.80 | 1.60 |
| Wenzhou | 71,766 | 156,746.2 | 6724 | 36,473.3 | 330,442 | 96,775 | 1.26 | 1.09 |
| Jinan | 110,199 | 224,188.0 | 2215 | 48,367.2 | 1,549,779 | 108,391 | 1.45 | 1.24 |
| Changzhou | 147,939 | 231,317.3 | 5065 | 45,859.1 | 671,577 | 113,273 | 1.97 | 1.66 |
| Xuzhou | 80,673 | 100,682.7 | 2024 | 36,190.4 | 747,702 | 86,138 | 1.83 | 1.74 |
| Hohhot | 81,656 | 177,279.5 | 252 | 29,940.1 | 437,896 | 89,549 | 1.20 | 1.11 |
| Sanya | 68,656 | 156,830.0 | 33 | 36,639.2 | 151,084 | 93,152 | 0.74 | 0.63 |
| Taiyuan | 78,734 | 267,151.7 | 622 | 31,111.1 | 1,013,630 | 88,650 | 1.48 | 1.32 |
| City | Social (B2) | |||||||
|---|---|---|---|---|---|---|---|---|
| B21 | B22 | B23 | B24 | B25 | B26 | B27 | B28 | |
| Beijing | 2189 | 7.67 | 10.94 | 1469.00 | 15,018,987 | 54.50 | 590,335 | 17,778,150 |
| Shanghai | 2488 | 4.76 | 7.10 | 1237.85 | 4,737,785 | 57.73 | 540,693 | 16,166,700 |
| Tianjin | 1387 | 14.91 | 8.94 | 1170.24 | 4,472,897 | 44.36 | 572,152 | 7,308,300 |
| Chongqing | 3209 | 14.65 | 2.97 | 1565.61 | 9,735,406 | 54.52 | 915,556 | 12,033,548 |
| Guangzhou | 1874 | 13.82 | 8.32 | 1350.40 | 3,571,356 | 49.66 | 1,307,144 | 8,204,077 |
| Shenzhen | 1763 | 9.11 | 21.76 | 955.68 | 5,053,281 | 32.70 | 109,986 | 12,685,530 |
| Wuhan | 1233 | 15.62 | 7.78 | 885.11 | 7,052,843 | 65.88 | 1,067,206 | 5,310,300 |
| Nanjing | 932 | 25.00 | 9.39 | 868.28 | 5,940,046 | 61.65 | 918,141 | 3,376,045 |
| Shenyang | 907 | 15.02 | 6.63 | 567.00 | 1,554,961 | 74.98 | 440,146 | 4,417,422 |
| Changchun | 907 | 16.80 | 5.55 | 550.96 | 1,662,945 | 64.98 | 483,034 | 2,761,830 |
| Dalian | 745 | 15.93 | 7.67 | 444.04 | 1,035,177 | 60.96 | 325,738 | 2,198,977 |
| Chengdu | 2095 | 18.70 | 7.01 | 977.12 | 9,857,289 | 61.05 | 927,111 | 9,607,500 |
| Xi’an | 1296 | 18.23 | 7.22 | 700.69 | 8,417,443 | 51.32 | 783,893 | 5,383,600 |
| Harbin | 1001 | 16.01 | 7.21 | 473.00 | 2,030,700 | 76.82 | 591,940 | 2,754,830 |
| Suzhou | 1275 | 26.92 | 4.98 | 481.33 | 3,094,452 | 49.89 | 263,246 | 5,978,357 |
| Zhengzhou | 1262 | 9.61 | 5.00 | 640.80 | 4,958,199 | 72.69 | 1,160,303 | 5,682,800 |
| Kunming | 846 | 12.58 | 7.79 | 482.80 | 1,635,613 | 68.90 | 697,961 | 2,058,113 |
| Hangzhou | 1197 | 12.42 | 8.48 | 666.18 | 8,801,127 | 70.39 | 465,963 | 7,515,404 |
| Foshan | 952 | 17.43 | 7.30 | 162.35 | 1,368,576 | 37.66 | 146,297 | 3,413,009 |
| Changsha | 1006 | 22.29 | 11.79 | 409.51 | 4,016,368 | 66.81 | 697,407 | 4,160,672 |
| Ningbo | 942 | 18.58 | 6.49 | 377.87 | 3,229,396 | 40.79 | 168,310 | 4,873,849 |
| Wuxi | 746 | 27.15 | 4.07 | 349.55 | 1,483,873 | 57.48 | 133,163 | 4,141,800 |
| Nanchang | 626 | 11.34 | 7.00 | 366.02 | 1,844,746 | 61.98 | 687,852 | 2,224,822 |
| Lanzhou | 437 | 21.95 | 7.30 | 329.10 | 740,340.7 | 65.11 | 390,906 | 1,075,717 |
| Qingdao | 1011 | 19.10 | 8.46 | 758.16 | 2,805,832 | 61.77 | 430,671 | 4,772,874 |
| Huaian | 456 | 23.38 | 4.16 | 208.00 | 172,150.5 | 43.30 | 49,222 | 944,369 |
| Fuzhou | 832 | 13.44 | 5.91 | 305.30 | 2,804,912 | 41.46 | 363,738 | 2,215,488 |
| Dongguan | 1048 | 11.13 | 5.61 | 1194.31 | 1,131,446 | 31.39 | 134,546 | 5,809,506 |
| Nanning | 875 | 20.44 | 4.19 | 326.70 | 2,035,307 | 48.77 | 568,756 | 1,880,246 |
| Hefei | 937 | 18.76 | 6.68 | 502.50 | 2,967,805 | 63.26 | 586,170 | 2,877,855 |
| Shijiazhuang | 1124 | 18.83 | 3.71 | 311.83 | 1,041,077 | 49.53 | 583,472 | 2,804,498 |
| Guiyang | 599 | 16.73 | 4.90 | 369.00 | 1,614,016 | 61.23 | 440,212 | 2,542,439 |
| Xiamen | 518 | 17.67 | 8.33 | 401.94 | 2,077,884 | 35.21 | 169,288 | 3,180,800 |
| Zhuhai | 245 | 12.93 | 10.07 | 152.85 | 1,023,091 | 41.09 | 143,778 | 1,468,847 |
| Urumqi | 405 | 19.68 | 11.01 | 521.60 | 618,179 | 74.98 | 237,556 | 1,596,259 |
| Wenzhou | 959 | 16.72 | 2.84 | 275.87 | 1,455,280 | 40.33 | 120,734 | 3,403,512 |
| Jinan | 924 | 19.67 | 8.63 | 793.65 | 3,349,288 | 63.63 | 687,878 | 4,373,163 |
| Changzhou | 528 | 25.74 | 4.59 | 277.29 | 1,012,432 | 45.19 | 145,032 | 1,716,587 |
| Xuzhou | 908 | 23.43 | 3.07 | 289.64 | 1,402,594 | 45.85 | 145,857 | 2,138,916 |
| Hohhot | 345 | 14.30 | 8.29 | 272.16 | 1,062,088 | 54.26 | 248,552 | 924,255 |
| Sanya | 104 | 17.48 | 10.74 | 51.63 | 194,063.6 | 45.20 | 60,798 | 364,160 |
| Taiyuan | 532 | 17.70 | 7.00 | 340.00 | 1,283,156 | 78.61 | 482,167 | 1,741,964 |
| City | Environmental (B3) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| B31 | B32 | B33 | B34 | B35 | B36 | B37 | B38 | B39 | |
| Beijing | 38 | 4 | 29 | 276 | 154.19 | 42.34 | 847.02 | 96.56% | 16,775.08 |
| Shanghai | 32 | 6 | 37 | 319 | 203.92 | 66.16 | 361.34 | 96.68% | 18,699.42 |
| Tianjin | 48 | 8 | 39 | 245 | 115.69 | 31.51 | 433.72 | 96.42% | 13,287.01 |
| Chongqing | 53 | 8 | 39 | 135 | 179.80 | 22.03 | 163.97 | 98.17% | 22,754.62 |
| Guangzhou | 23 | 7 | 36 | 331 | 316.25 | 78.87 | 144.14 | 97.90% | 24,458.15 |
| Shenzhen | 19 | 6 | 23 | 355 | 230.02 | 55.12 | 193.52 | 98.11% | 26,706.00 |
| Wuhan | 37 | 8 | 36 | 309 | 234.23 | 26.60 | 202.31 | 97.00% | 21,171.79 |
| Nanjing | 31 | 7 | 36 | 304 | 296.54 | 100.33 | 150.95 | 97.90% | 8628.71 |
| Shenyang | 42 | 18 | 35 | 287 | 196.68 | 26.50 | 73.20 | 98.94% | 15,741.33 |
| Changchun | 42 | 10 | 32 | 305 | 150.13 | 48.82 | 95.50 | 95.69% | 6975.00 |
| Dalian | 30 | 10 | 25 | 332 | 153.63 | 51.41 | 68.88 | 98.78% | 7309.40 |
| Chengdu | 41 | 6 | 37 | 280 | 280.44 | 17.34 | 165.75 | 97.62% | 16,623.68 |
| Xi’an | 51 | 8 | 41 | 250 | 177.70 | 27.34 | 249.02 | 96.66% | 12,268.13 |
| Harbin | 47 | 17 | 32 | 303 | 141.07 | 15.34 | 71.27 | 95.23% | 9742.00 |
| Suzhou | 31 | 8 | 34 | 307 | 261.04 | 18.51 | 101.62 | 96.84% | 11,332.25 |
| Zhengzhou | 51 | 9 | 39 | 230 | 128.95 | 20.34 | 122.05 | 98.51% | 7578.32 |
| Kunming | 24 | 9 | 25 | 366 | 157.99 | 22.33 | 38.71 | 98.89% | 8059.64 |
| Hangzhou | 30 | 6 | 38 | 334 | 244.82 | 41.41 | 161.16 | 97.11% | 11,171.93 |
| Foshan | 22 | 7 | 31 | 333 | 335.81 | 7.68 | 115.16 | 100.34% | 4381.10 |
| Changsha | 41 | 6 | 28 | 309 | 277.33 | 14.39 | 79.11 | 98.40% | 5187.20 |
| Ningbo | 23 | 8 | 32 | 340 | 250.14 | 17.52 | 120.06 | 99.73% | 5153.57 |
| Wuxi | 33 | 7 | 35 | 299 | 196.22 | 26.66 | 150.28 | 98.92% | 4645.00 |
| Nanchang | 33 | 9 | 29 | 335 | 219.78 | 23.66 | 78.49 | 98.84% | 5242.04 |
| Lanzhou | 34 | 15 | 47 | 312 | 174.12 | 22.24 | 396.43 | 96.35% | 5065.99 |
| Qingdao | 31 | 7 | 31 | 315 | 142.91 | 41.37 | 129.32 | 98.20% | 7489.70 |
| Huaian | 42 | 7 | 25 | 294 | 155.62 | 20.50 | 62.98 | 95.76% | 3396.38 |
| Fuzhou | 21 | 5 | 21 | 364 | 224.16 | 15.63 | 34.39 | 96.88% | 4535.36 |
| Dongguan | 24 | 8 | 27 | 334 | 168.75 | 70.65 | 115.56 | 96.21% | 20,855.68 |
| Nanning | 31 | 8 | 24 | 357 | 314.12 | 16.25 | 35.52 | 100.00% | 8175.72 |
| Hefei | 36 | 7 | 39 | 310 | 243.82 | 21.63 | 122.49 | 97.75% | 8149.00 |
| Shijiazhuang | 58 | 12 | 41 | 205 | 122.22 | 13.10 | 128.35 | 99.30% | 7551.20 |
| Guiyang | 41 | 10 | 18 | 362 | 216.50 | 33.21 | 72.13 | 98.09% | 5709.00 |
| Xiamen | 18 | 6 | 19 | 365 | 197.95 | 45.69 | 63.11 | 100.00% | 4965.46 |
| Zhuhai | 19 | 5 | 24 | 342 | 292.69 | 127.58 | 69.24 | 96.81% | 6256.92 |
| Urumqi | 47 | 9 | 42 | 279 | 134.92 | 81.90 | 700.23 | 99.20% | 5034.00 |
| Wenzhou | 23 | 6 | 30 | 355 | 235.00 | 10.05 | 32.56 | 98.12% | 3716.18 |
| Jinan | 47 | 12 | 35 | 227 | 126.00 | 31.61 | 164.84 | 99.23% | 8934.00 |
| Changzhou | 39 | 9 | 35 | 295 | 234.95 | 23.81 | 287.03 | 98.06% | 3528.00 |
| Xuzhou | 50 | 10 | 35 | 261 | 167.87 | 19.12 | 73.53 | 94.95% | 3586.98 |
| Hohhot | 40 | 18 | 39 | 294 | 89.24 | 45.46 | 174.01 | 98.94% | 5189.82 |
| Sanya | 11 | 4 | 9 | 365 | 399.16 | 20.90 | 82.91 | 96.44% | 1825.00 |
| Taiyuan | 54 | 23 | 48 | 224 | 150.50 | 26.32 | 174.89 | 103.24% | 6568.80 |
References
- Zhang, X.; Han, L.; Wei, H.; Tan, X.; Zhou, W.; Li, W.; Qian, Y. Linking urbanization and air quality together: A review and a perspective on the future sustainable urban development. J. Clean. Prod. 2022, 346, 130988. [Google Scholar] [CrossRef]
- Gu, D.; Andreev, K.; Dupre, M.E. Major Trends in Population Growth Around the World. China CDC Wkly. 2021, 3, 604–613. [Google Scholar] [CrossRef] [PubMed]
- Cengiz, S.; Görmüş, S.; Oğuz, D. Analysis of the urban growth pattern through spatial metrics; Ankara City. Land Use Policy 2022, 112, 105812. [Google Scholar] [CrossRef]
- Fan, Y.; Fang, C. Evolution process analysis of urban metabolic patterns and sustainability assessment in western China, a case study of Xining city. Ecol. Indic. 2019, 109, 105784. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, L. Exploring the relation between the industrial structure and the eco-environment based on an integrated approach: A case study of Beijing, China. Ecol. Indic. 2019, 103, 83–93. [Google Scholar] [CrossRef]
- Buzási, A.; Jäger, B.S. District-scale assessment of urban sustainability. Sustain. Cities Soc. 2020, 62, 102388. [Google Scholar] [CrossRef]
- Kaur, H.; Garg, P. Urban sustainability assessment tools: A review. J. Clean. Prod. 2019, 210, 146–158. [Google Scholar] [CrossRef]
- Taecharungroj, V. An analysis of tripadvisor reviews of 127 urban rail transit networks worldwide. Travel Behav. Soc. 2021, 26, 193–205. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015, pp. 1–41. Available online: https://sdgs.un.org/2030agenda (accessed on 25 July 2022).
- International Energy Agency. Data, Data Browser, Explore Energy Data by Category, Indicator, Country or Region; Countries & Regions—IEA; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Lin, D.; Nelson, J.D.; Beecroft, M.; Cui, J. An overview of recent developments in China’s metro systems. Tunn. Undergr. Space Technol. 2021, 111, 103783. [Google Scholar] [CrossRef]
- Yin, D.; Huang, W.; Shuai, B.; Liu, H.; Zhang, Y. Structural characteristics analysis and cascading failure impact analysis of urban rail transit network: From the perspective of multi-layer network. Reliab. Eng. Syst. Saf. 2021, 218, 108161. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Zhou, J.; Zheng, H. Sudden passenger flow characteristics and congestion control based on intelligent urban rail transit network. Neural Comput. Appl. 2021, 34, 6615–6624. [Google Scholar] [CrossRef]
- Li, X.; Love, P.E. Procuring urban rail transit infrastructure by integrating land value capture and public-private partnerships: Learning from the cities of Delhi and Hong Kong. Cities 2021, 122, 103545. [Google Scholar] [CrossRef]
- Wen, S.; Shi, J.; Zhang, W. Impact of Urban Rail Transit Network on Residential and Commercial Land Values in China: A Complex Network Perspective. Complexity 2021, 2021, 8849066. [Google Scholar] [CrossRef]
- Meng, R.; Mao, B.; Xu, Q.; Yang, Y. Evaluation of Public Welfare Level of Urban Rail Transit considering Operation Management. J. Adv. Transp. 2022, 2022, 1245639. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Wang, S.; Shao, W.; Zhao, X.; Liu, W. Vulnerability assessments of weighted urban rail transit networks with integrated coupled map lattices. Reliab. Eng. Syst. Saf. 2021, 214, 107707. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Xu, N.; Zhao, R.; Chau, K.; Hong, S. Place-varying impacts of urban rail transit on property prices in Shenzhen, China: Insights for value capture. Sustain. Cities Soc. 2020, 58, 102140. [Google Scholar] [CrossRef]
- Sun, Y.; Cui, Y. Analyzing the Coupling Coordination among Economic, Social, and Environmental Benefits of Urban Infrastructure: Case Study of Four Chinese Autonomous Municipalities. Math. Probl. Eng. 2018, 2018, 8280328. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Bobylev, N.; Li, S.; Liu, J. Coupling Coordination of “Urban Rail Transit—Social Economy” Composite System. Infrastructures 2022, 7, 56. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, M.; Aditjandra, P.T. The impact of urban rail transit on commercial property value: New evidence from Wuhan, China. Transp. Res. Part A Policy Pract. 2016, 91, 223–235. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Zhang, Y.; Alsulaiman, H. Spatial structure system of land use along urban rail transit based on GIS spatial clustering. Eur. J. Remote Sens. 2020, 54, 438–445. [Google Scholar] [CrossRef]
- Ko, K.; Cao, X. The Impact of Hiawatha Light Rail on Commercial and Industrial Property Values in Minneapolis. J. Public Transp. 2013, 16, 47–66. [Google Scholar] [CrossRef] [Green Version]
- Pacheco-Raguz, I.F. Assessing the impacts of Light Rail Transit an urban land in Manila. J. Transp. Land Use 2010, 3, 113–138. [Google Scholar] [CrossRef] [Green Version]
- Wu, J. Study on the Model of Integrated Urban Rail Transit Hub Transfer Site Layout. Appl. Mech. Mater. 2013, 401–403, 2133–2138. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J. Evaluation of coupling coordination degree between urban rail transit and land use. Int. J. Commun. Syst. 2019, 34, e4015. [Google Scholar] [CrossRef]
- Xia, X.; Li, H.; Kuang, X.; Strauss, J. Spatial–Temporal Features of Coordination Relationship between Regional Urbanization and Rail Transit—A Case Study of Beijing. Int. J. Environ. Res. Public Health 2021, 19, 212. [Google Scholar] [CrossRef] [PubMed]
- Hou, Q.; Xing, Y.; Wang, D.; Liu, J.; Fan, X.; Duan, Y. Study on coupling degree of rail transit capacity and land use based on multivariate data from cloud platform. J. Cloud Comput. Adv. Syst. Appl. 2020, 9, 4. [Google Scholar] [CrossRef]
- Jingjing, C.; Changjiang, Z.; Ming, Y. Research on Rail Transit Network System and its Connection Model in the Metropolitan Area. Procedia Soc. Behav. Sci. 2013, 96, 1286–1292. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez, D.A.; Kang, C.-D. A typology of the built environment around rail stops in the global transit-oriented city of Seoul, Korea. Cities 2020, 100, 102663. [Google Scholar] [CrossRef]
- Ferbrache, F.; Knowles, R.D. City boosterism and place-making with light rail transit: A critical review of light rail impacts on city image and quality. Geoforum 2017, 80, 103–113. [Google Scholar] [CrossRef]
- Li, Z.; Luo, Z.; Wang, Y.; Fan, G.; Zhang, J. Suitability evaluation system for the shallow geothermal energy implementation in region by Entropy Weight Method and TOPSIS method. Renew. Energy 2021, 184, 564–576. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Wang, L.; Liang, L. Regional environmental efficiency in China: An empirical analysis based on entropy weight method and non-parametric models. J. Clean. Prod. 2020, 276, 124147. [Google Scholar] [CrossRef]
- Wu, H.-W.; Li, E.-Q.; Sun, Y.-Y.; Dong, B.-T. Research on the operation safety evaluation of urban rail stations based on the improved TOPSIS method and entropy weight method. J. Rail Transp. Plan. Manag. 2021, 20, 100262. [Google Scholar] [CrossRef]
- Cunha-Zeri, G.; Guidolini, J.F.; Branco, E.A.; Ometto, J.P. How sustainable is the nitrogen management in Brazil? A sustainability assessment using the Entropy Weight Method. J. Environ. Manag. 2022, 316, 115330. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yuan, W.; Qin, X.; Qi, X.; Meng, L. Coupling coordination degree for urban green growth between public demand and government supply in urban agglomeration: A case study from China. J. Environ. Manag. 2021, 304, 114209. [Google Scholar] [CrossRef] [PubMed]
- Gan, L.; Shi, H.; Hu, Y.; Lev, B.; Lan, H. Coupling coordination degree for urbanization city-industry integration level: Sichuan case. Sustain. Cities Soc. 2020, 58, 102136. [Google Scholar] [CrossRef]
- Toumi, O.; Le Gallo, J.; Ben Rejeb, J. Assessment of Latin American sustainability. Renew. Sustain. Energy Rev. 2017, 78, 878–885. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Z.; Long, T.; Sun, S.; Gao, J. Mega-city region sustainability assessment and obstacles identification with GIS–entropy–TOPSIS model: A case in Yangtze River Delta urban agglomeration, China. J. Clean. Prod. 2021, 294, 126147. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, L.; Suo, J. Comprehensive Assessment on Sustainable Development of Highway Transportation Capacity Based on Entropy Weight and TOPSIS. Sustainability 2014, 6, 4685–4693. [Google Scholar] [CrossRef] [Green Version]
- Dolatabadi, A.M.; Masoumi, S.; Lakzian, E. Optimization variables of the injection of hot-steam into the non-equilibrium condensing flow using TOPSIS method. Int. Commun. Heat Mass Transf. 2021, 129, 105674. [Google Scholar] [CrossRef]
- Wątróbski, J.; Bączkiewicz, A.; Ziemba, E.; Sałabun, W. Sustainable cities and communities assessment using the DARIA-TOPSIS method. Sustain. Cities Soc. 2022, 83, 103926. [Google Scholar] [CrossRef]
- Yang, S.; Pan, Y.; Zeng, S. Decision making framework based Fermatean fuzzy integrated weighted distance and TOPSIS for green low-carbon port evaluation. Eng. Appl. Artif. Intell. 2022, 114, 105048. [Google Scholar] [CrossRef]
- Xing, L.; Xue, M.; Hu, M. Dynamic simulation and assessment of the coupling coordination degree of the economy–resource–environment system: Case of Wuhan City in China. J. Environ. Manag. 2018, 230, 474–487. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Fan, Z.; Feng, W.; Yuxin, C.; Keyu, Q. Coupling coordination degree spatial analysis and driving factor between socio-economic and eco-environment in northern China. Ecol. Indic. 2022, 135, 108555. [Google Scholar] [CrossRef]
- Li, X.; Lu, Z.; Hou, Y.; Zhao, G.; Zhang, L. The coupling coordination degree between urbanization and air environment in the Beijing(Jing)-Tianjin(Jin)-Hebei(Ji) urban agglomeration. Ecol. Indic. 2022, 137, 108787. [Google Scholar] [CrossRef]
- Liu, T.-L.; Song, Q.-J.; Lu, J.; Qi, Y. An integrated approach to evaluating the coupling coordination degree between low-carbon development and air quality in Chinese cities. Adv. Clim. Chang. Res. 2021, 12, 710–722. [Google Scholar] [CrossRef]
- Fei, J.; Lin, Y.; Jiang, Q.; Jiang, K.; Li, P.; Ye, G. Spatiotemporal coupling coordination measurement on islands’ economy-environment-tourism system. Ocean Coast. Manag. 2021, 212, 105793. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiao, L.; Zhang, Y.; Wu, Y.; Huo, X. Sustainable Development of Urban Metro System: Perspective of Coordination between Supply and Demand. Int. J. Environ. Res. Public Health 2021, 18, 10349. [Google Scholar] [CrossRef]
- Li, W.; Ren, X.; Ding, S.; Dong, L. A multi-criterion decision making for sustainability assessment of hydrogen production technologies based on objective grey relational analysis. Int. J. Hydrogen Energy 2020, 45, 34385–34395. [Google Scholar] [CrossRef]
- Long, X.; Wu, S.; Wang, J.; Wu, P.; Wang, Z. Urban water environment carrying capacity based on VPOSR-coefficient of variation-grey correlation model: A case of Beijing, China. Ecol. Indic. 2022, 138, 108863. [Google Scholar] [CrossRef]
- Yuan, G.; Yang, Y.; Tian, G.; Zhuang, Q. Comprehensive evaluation of disassembly performance based on the ultimate cross-efficiency and extension-gray correlation degree. J. Clean. Prod. 2020, 245, 118800. [Google Scholar] [CrossRef]
- Liu, G.; Yu, J. Gray correlation analysis and prediction models of living refuse generation in Shanghai city. Waste Manag. 2007, 27, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Verma, P.; Raghubanshi, A. Urban sustainability indicators: Challenges and opportunities. Ecol. Indic. 2018, 93, 282–291. [Google Scholar] [CrossRef]
- Shen, L.; Jiao, L.; He, B.; Li, L. Evaluation on the utility efficiency of metro infrastructure projects in China from sustainable development perspective. Int. J. Proj. Manag. 2015, 33, 528–536. [Google Scholar] [CrossRef]
- Huang, W.; Shuai, B.; Sun, Y.; Wang, Y.; Antwi, E. Using entropy-TOPSIS method to evaluate urban rail transit system operation performance: The China case. Transp. Res. Part A Policy Prcat. 2018, 111, 292–303. [Google Scholar] [CrossRef]
- Merino-Saum, A.; Halla, P.; Superti, V.; Boesch, A.; Binder, C. Indicators for urban sustainability: Key lessons from a systematic analysis of 67 measurement initiatives. Ecol. Indic. 2020, 119, 106879. [Google Scholar] [CrossRef]
- Piña, W.H.A.; Martínez, C.I.P. Development and Urban Sustainability: An Analysis of Efficiency Using Data Envelopment Analysis. Sustainability 2016, 8, 148. [Google Scholar] [CrossRef] [Green Version]
- Phillis, Y.A.; Kouikoglou, V.S.; Verdugo, C. Urban sustainability assessment and ranking of cities. Comput. Environ. Urban Syst. 2017, 64, 254–265. [Google Scholar] [CrossRef]
- Patias, N.; Rowe, F.; Cavazzi, S.; Arribas-Bel, D. Sustainable urban development indicators in Great Britain from 2001 to 2016. Landsc. Urban Plan. 2021, 214, 104148. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, Z.; Shang, M. Risk Evaluation Study of Urban Rail Transit Network Based on Entropy-TOPSIS-Coupling Coordination Model. Discret. Dyn. Nat. Soc. 2021, 2021, 5124951. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, X.; Gong, Q.; Ji, Z. Measurement of Regional Green Economy Sustainable Development Ability Based on Entropy Weight-Topsis-Coupling Coordination Degree—A Case Study in Shandong Province, China. Sustainability 2019, 11, 280. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Jiao, J. How Does Urban Rail Transit Influence Residential Property Values? Evidence from An Emerging Chinese Megacity. Sustainability 2019, 11, 534. [Google Scholar] [CrossRef] [Green Version]
- Jiao, L.; Luo, F.; Wu, F.; Zhang, Y.; Huo, X.; Wu, Y. Exploring the Interactive Coercing Relationship between Urban Rail Transit and the Ecological Environment. Land 2022, 11, 836. [Google Scholar] [CrossRef]
- Lan, A. Transport Orientated Development and Commercialization of Underground Space in China: Trends in Shanghai, Tianjin and Shenzhen. Procedia Eng. 2016, 165, 555–563. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Li, Z.; Wu, Z.; Yan, Z.; Chen, Y.; Gao, F. Spatial and Temporal Dynamics of Urban Expansion along the Guangzhou–Foshan Inter-City Rail Transit Corridor, China. Sustainability 2018, 10, 593. [Google Scholar] [CrossRef] [Green Version]
- Bao, X. Urban Rail Transit Present Situation and Future Development Trends in China: Overall Analysis Based on National Policies and Strategic Plans in 2016–2020. Urban Rail Transit 2018, 4, 1–12. [Google Scholar] [CrossRef] [Green Version]
| Value of D | Comprehensive Type | Comparison of u | Subtype |
|---|---|---|---|
| 0.75 ≤ D ≤ 1 | Highly balanced | uA < uB | Highly balanced with lagging uA |
| uA ≈ uB | Highly balanced | ||
| uA > uB | Highly balanced with lagging uB | ||
| 0.5 ≤ D < 0.75 | Barely balanced | uA < uB | Barely balanced with lagging uA |
| uA ≈ uB | Barely balanced | ||
| uA > uB | Barely balanced with lagging uB | ||
| 0.25 ≤ D < 0.5 | Slightly unbalanced | uA < uB | Slightly unbalanced with lagging uA |
| uA ≈ uB | Slightly unbalanced | ||
| uA > uB | Slightly unbalanced with lagging uB | ||
| 0 ≤ D < 0.25 | Seriously unbalanced | uA < uB | Seriously unbalanced with lagging uA |
| uA ≈ uB | Seriously unbalanced | ||
| uA > uB | Seriously unbalanced with lagging uB |
| System Layer | Factor Layer | Indicator Layer | Indicator Direction (+/−) | Unit | Supporting Literature References |
|---|---|---|---|---|---|
| URT development system (A) | Scale (A1) | Length of Lines (A11) | + | km | [20] |
| Number of Stations (A12) | + | unit | [20,26] | ||
| Number of Transfer Stations (A13) | + | unit | [55] | ||
| Number of Vehicles in Service (A14) | + | unit | [20] | ||
| Operation status (A2) | Daily Average Times of the Train Operations (A21) | + | unit | [55] | |
| Average Daily Passenger Volume (A22) | + | 10,000 persons | [26,49,56] | ||
| Passenger Transport Intensity (A23) | + | 10,000 person/km day | [20,49,56] | ||
| Operation Mileage (A24) | + | 10,000 vehicle km | [26] | ||
| Sustainable urban development system (B) | Economic (B1) | Per Capita Gross Regional Product (B11) | + | yuan | [57] |
| Per Capita Deposits of Financial Institutions at Year-end (B12) | + | yuan | [45] | ||
| Number of Industrial Enterprises (B13) | + | unit | [6] | ||
| Per Capita Retail Sales of Consumer Goods (B14) | + | yuan | [26,27] | ||
| Persons Employed in Urban Non-Private Units at Year-end (B15) | + | 10,000 person | [27] | ||
| Average Wage of Employed Staff and Workers in Urban Non-Private Units (B16) | + | yuan | [57] | ||
| Per Sales Area of Commercial Residential Building (B17) | + | 10,000 sq.m | [27,58] | ||
| Per Sales Area of Residential Buildings (B18) | + | 10,000 sq.m | [27,58] | ||
| Social (B2) | Resident Population (B21) | + | 10,000 person | [41] | |
| Per Capita Road Area (B22) | + | sq.m | [41] | ||
| Buses under Operation (B23) | + | unit | [6,59] | ||
| Area of Built District (B24) | + | sq.km | [60] | ||
| Fixed Assets Investment in Urban Service Facilities (B25) | + | 10,000 yuan | [27,58] | ||
| Per Capita Number of Beds of Hospitals (B26) | + | unit | [59,61] | ||
| Undergraduate in Regular HEIs (B27) | + | 10,000 person | [39] | ||
| Number of Employees Joining Urban Basic Pension Insurance (B28) | + | 10,000 person | [54] | ||
| Environmental (B3) | Annual Mean Concentration of PM2.5 (B31) | − | ug/m3 | [6,7] | |
| Annual Mean Concentration of SO2 (B32) | − | ug/m3 | [6,7,59] | ||
| Annual Mean Concentration of NO2 (B33) | − | ug/m3 | [6,7,59] | ||
| Days with good air quality (B34) | + | unit | [7] | ||
| Daily Water Consumption Per Capita (B35) | − | litre | [7,57,62] | ||
| Per Capita Area of Parks and Green Space (B36) | + | 10,000 sq.m | [6,57,60,59] | ||
| Per Capita Natural Gas Supplied (B37) | − | 10,000 cu.m | [6,7,59,62] | ||
| Wastewater Treatment Rate (B38) | + | % | [59] | ||
| Surface Area of Roads Cleaned and Maintained (B39) | + | 10,000 sq.m | [7] |
| System Layer | Factor Layer | Indicator Layer | ||
|---|---|---|---|---|
| Code | Weight | Code | Weight | |
| URT development system (A) | A1 | 0.5102 | A11 | 0.1064 |
| A12 | 0.1037 | |||
| A13 | 0.1725 | |||
| A14 | 0.1276 | |||
| A2 | 0.4898 | A21 | 0.1239 | |
| A22 | 0.1718 | |||
| A23 | 0.0471 | |||
| A24 | 0.1470 | |||
| Sustainable urban development system (B) | B1 | 0.3946 | B11 | 0.0416 |
| B12 | 0.0610 | |||
| B13 | 0.0665 | |||
| B14 | 0.0379 | |||
| B15 | 0.0779 | |||
| B16 | 0.0503 | |||
| B17 | 0.0310 | |||
| B18 | 0.0283 | |||
| B2 | 0.3624 | B21 | 0.0361 | |
| B22 | 0.0180 | |||
| B23 | 0.0434 | |||
| B24 | 0.0423 | |||
| B25 | 0.0758 | |||
| B26 | 0.0298 | |||
| B27 | 0.0532 | |||
| B28 | 0.0638 | |||
| B3 | 0.2430 | B31 | 0.0268 | |
| B32 | 0.0103 | |||
| B33 | 0.0253 | |||
| B34 | 0.0105 | |||
| B35 | 0.0143 | |||
| B36 | 0.0641 | |||
| B37 | 0.0083 | |||
| B38 | 0.0278 | |||
| B39 | 0.0556 | |||
| City | Relative Closeness Value (uA) | Rank | City | Relative Closeness Value (uA) | Rank |
|---|---|---|---|---|---|
| Shanghai | 0.9297 | 1 | Hefei | 0.1082 | 22 |
| Beijing | 0.8952 | 2 | Nanchang | 0.0975 | 23 |
| Guangzhou | 0.6413 | 3 | Wuxi | 0.0727 | 24 |
| Chengdu | 0.5874 | 4 | Xiamen | 0.0716 | 25 |
| Shenzhen | 0.5812 | 5 | Lanzhou | 0.0640 | 26 |
| Wuhan | 0.3864 | 6 | Taiyuan | 0.0640 | 27 |
| Chongqing | 0.3321 | 7 | Shijiazhuang | 0.0637 | 28 |
| Nanjing | 0.3029 | 8 | Fuzhou | 0.0616 | 29 |
| Xi’an | 0.2915 | 9 | Harbin | 0.0528 | 30 |
| Hangzhou | 0.2875 | 10 | Hohhot | 0.0403 | 31 |
| Tianjin | 0.2128 | 11 | Xuzhou | 0.0401 | 32 |
| Zhengzhou | 0.2050 | 12 | Guiyang | 0.0360 | 33 |
| Suzhou | 0.1880 | 13 | Dongguan | 0.0313 | 34 |
| Shenyang | 0.1869 | 14 | Jinan | 0.0264 | 35 |
| Changsha | 0.1777 | 15 | Changzhou | 0.0264 | 36 |
| Qingdao | 0.1459 | 16 | Urumqi | 0.0261 | 37 |
| Changchun | 0.1259 | 17 | Wenzhou | 0.0185 | 38 |
| Ningbo | 0.1256 | 18 | Huaian | 0.0148 | 39 |
| Kunming | 0.1194 | 19 | Foshan | 0.0100 | 40 |
| Nanning | 0.1167 | 20 | Sanya | 0.0040 | 41 |
| Dalian | 0.1086 | 21 | Zhuhai | 0.0031 | 42 |
| Mean | 0.1876 |
| City | Relative Closeness Value (uB) | Rank | City | Relative Closeness Value (uB) | Rank |
|---|---|---|---|---|---|
| Beijing | 0.6106 | 1 | Nanchang | 0.2749 | 22 |
| Shanghai | 0.5687 | 2 | Kunming | 0.2749 | 23 |
| Shenzhen | 0.5416 | 3 | Shenyang | 0.2716 | 24 |
| Guangzhou | 0.5000 | 4 | Hefei | 0.2711 | 25 |
| Chengdu | 0.4907 | 5 | Urumqi | 0.2706 | 26 |
| Chongqing | 0.4658 | 6 | Xiamen | 0.2693 | 27 |
| Nanjing | 0.4495 | 7 | Fuzhou | 0.2691 | 28 |
| Hangzhou | 0.4318 | 8 | Changzhou | 0.2688 | 29 |
| Wuhan | 0.4074 | 9 | Guiyang | 0.2413 | 30 |
| Suzhou | 0.4027 | 10 | Taiyuan | 0.2399 | 31 |
| Dongguan | 0.3858 | 11 | Dalian | 0.2390 | 32 |
| Zhengzhou | 0.3463 | 12 | Nanning | 0.2325 | 33 |
| Zhuhai | 0.3459 | 13 | Wenzhou | 0.2318 | 34 |
| Tianjin | 0.3408 | 14 | Changchun | 0.2250 | 35 |
| Xi’an | 0.3338 | 15 | Harbin | 0.2185 | 36 |
| Ningbo | 0.3303 | 16 | Lanzhou | 0.2113 | 37 |
| Wuxi | 0.3222 | 17 | Sanya | 0.1932 | 38 |
| Changsha | 0.3197 | 18 | Hohhot | 0.1906 | 39 |
| Qingdao | 0.3178 | 19 | Huaian | 0.1889 | 40 |
| Jinan | 0.3034 | 20 | Xuzhou | 0.1846 | 41 |
| Foshan | 0.2901 | 21 | Shijiazhuang | 0.1843 | 42 |
| Mean | 0.3204 |
| City | C | T | D | D Rank | City | C | T | D | D Rank |
|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.9820 | 0.7529 | 0.8598 | 1 | Nanchang | 0.8792 | 0.1862 | 0.4046 | 22 |
| Shanghai | 0.9705 | 0.7492 | 0.8527 | 2 | Dalian | 0.9269 | 0.1738 | 0.4013 | 23 |
| Guangzhou | 0.9923 | 0.5707 | 0.7525 | 3 | Wuxi | 0.7752 | 0.1974 | 0.3912 | 24 |
| Shenzhen | 0.9994 | 0.5614 | 0.7490 | 4 | Xiamen | 0.8146 | 0.1704 | 0.3726 | 25 |
| Chengdu | 0.9960 | 0.5391 | 0.7327 | 5 | Fuzhou | 0.7786 | 0.1654 | 0.3588 | 26 |
| Wuhan | 0.9997 | 0.3969 | 0.6299 | 6 | Taiyuan | 0.8155 | 0.1519 | 0.3520 | 27 |
| Chongqing | 0.9859 | 0.3990 | 0.6271 | 7 | Lanzhou | 0.8450 | 0.1376 | 0.3410 | 28 |
| Nanjing | 0.9809 | 0.3762 | 0.6074 | 8 | Dongguan | 0.5272 | 0.2086 | 0.3316 | 29 |
| Hangzhou | 0.9797 | 0.3597 | 0.5936 | 9 | Shijiazhuang | 0.8737 | 0.1240 | 0.3291 | 30 |
| Xi’an | 0.9977 | 0.3127 | 0.5585 | 10 | Harbin | 0.7919 | 0.1356 | 0.3277 | 31 |
| Suzhou | 0.9316 | 0.2954 | 0.5246 | 11 | Guiyang | 0.6721 | 0.1387 | 0.3053 | 32 |
| Tianjin | 0.9729 | 0.2768 | 0.5189 | 12 | Jinan | 0.5425 | 0.1649 | 0.2991 | 33 |
| Zhengzhou | 0.9666 | 0.2756 | 0.5162 | 13 | Hohhot | 0.7591 | 0.1154 | 0.2960 | 34 |
| Changsha | 0.9584 | 0.2487 | 0.4882 | 14 | Xuzhou | 0.7656 | 0.1123 | 0.2932 | 35 |
| Shenyang | 0.9828 | 0.2293 | 0.4747 | 15 | Changzhou | 0.5704 | 0.1476 | 0.2901 | 36 |
| Qingdao | 0.9287 | 0.2318 | 0.4640 | 16 | Urumqi | 0.5667 | 0.1484 | 0.2900 | 37 |
| Ningbo | 0.8936 | 0.2279 | 0.4513 | 17 | Wenzhou | 0.5234 | 0.1251 | 0.2559 | 38 |
| Kunming | 0.9189 | 0.1972 | 0.4256 | 18 | Foshan | 0.3593 | 0.1500 | 0.2322 | 39 |
| Hefei | 0.9030 | 0.1896 | 0.4138 | 19 | Huaian | 0.5184 | 0.1018 | 0.2298 | 40 |
| Changchun | 0.9593 | 0.1755 | 0.4103 | 20 | Zhuhai | 0.1886 | 0.1745 | 0.1814 | 41 |
| Nanning | 0.9434 | 0.1746 | 0.4059 | 21 | Sanya | 0.2807 | 0.0986 | 0.1664 | 42 |
| Mean | 0.8099 | 0.2540 | 0.4406 |
| Indicators | GRD | Rank | Indicators | GRD | Rank |
|---|---|---|---|---|---|
| B21 | 0.9628 | 1 | A22 | 0.9077 | 18 |
| B16 | 0.9608 | 2 | A13 | 0.9074 | 19 |
| B24 | 0.9542 | 3 | A24 | 0.9051 | 20 |
| B39 | 0.9485 | 4 | B36 | 0.9022 | 21 |
| B11 | 0.9410 | 5 | B27 | 0.8977 | 22 |
| B14 | 0.9408 | 6 | B31 | 0.8859 | 23 |
| A23 | 0.9390 | 7 | B38 | 0.8719 | 24 |
| B12 | 0.9379 | 8 | B26 | 0.8701 | 25 |
| B23 | 0.9367 | 9 | B33 | 0.8512 | 26 |
| A12 | 0.9328 | 10 | B34 | 0.8489 | 27 |
| B28 | 0.9310 | 11 | B13 | 0.8399 | 28 |
| B15 | 0.9249 | 12 | B35 | 0.8084 | 29 |
| A11 | 0.9207 | 13 | B32 | 0.6834 | 30 |
| B25 | 0.9189 | 14 | B22 | 0.6723 | 31 |
| A14 | 0.9097 | 15 | B17 | 0.5509 | 32 |
| A21 | 0.9097 | 16 | B18 | 0.5173 | 33 |
| B37 | 0.9091 | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, L.; Wu, F.; Zhu, Y.; Luo, Q.; Luo, F.; Zhang, Y. Research on the Coupling Coordination Relationship between Urban Rail Transit System and Sustainable Urban Development. Systems 2022, 10, 110. https://doi.org/10.3390/systems10040110
Jiao L, Wu F, Zhu Y, Luo Q, Luo F, Zhang Y. Research on the Coupling Coordination Relationship between Urban Rail Transit System and Sustainable Urban Development. Systems. 2022; 10(4):110. https://doi.org/10.3390/systems10040110
Chicago/Turabian StyleJiao, Liudan, Fengyan Wu, Yinghan Zhu, Qiudie Luo, Fenglian Luo, and Yu Zhang. 2022. "Research on the Coupling Coordination Relationship between Urban Rail Transit System and Sustainable Urban Development" Systems 10, no. 4: 110. https://doi.org/10.3390/systems10040110
APA StyleJiao, L., Wu, F., Zhu, Y., Luo, Q., Luo, F., & Zhang, Y. (2022). Research on the Coupling Coordination Relationship between Urban Rail Transit System and Sustainable Urban Development. Systems, 10(4), 110. https://doi.org/10.3390/systems10040110








