Abstract
Social welfare and profit are two main factors to be included in the operational goal of bus services. It is assumed that conventional bus services are “welfare pro” with more consideration of social welfare, while customized bus services are “profit pro” with more consideration of profit, and the goal of each bus service is to maximize the overall payoffs, namely, the weighted sum of social welfare and profit. A bi-level pricing game is proposed to shed light on the impact of two bus services’ pricing competition on the payoffs when the operational objectives with different weights of social welfare are adopted. A case study shows that the pricing strategies of conventional bus services have a significant impact on the customized bus services. The customized bus operator should consider more “social welfare” to attract customers and to achieve the overall payoffs when the conventional bus service takes a high price strategy, and the customized bus operator can take a strategy of a high price to maintain its overall payoffs when the conventional bus operator maximizes the social welfare. It is found that there exists a trade-off by which both sides obtain the balanced overall payoffs.
1. Introduction
Customized bus service is an innovative mode of demand-responsive transportation that serve people with common travel routes and certain requirements for travel time and service quality, mainly including customized business shuttles, customized commuter buses, customized community buses, customized tour buses, and other types [1,2]. It can be used to perform any part of the trip, ranging from a first/last mile service to an exclusive direct door-to-door connection [3]. However, as a complementary service to the traditional public transport, customized bus services have to compete with existing conventional bus service in the urban city, so the operators have to keep their strategies and services at a competitive level. In fact, competitions are common and popular in the transportation market [4], including not only a single transport service, but also the combinations of different transport modes, e.g., the combination of flexible bus and e-bike-sharing, and the combination of bicycle and rail systems [5,6]. From this perspective, it is of great practical significance to analyze the diversified transport competition in the context of the ever-increasing and diversified mobility needs of large population in urban transport systems.
As an emerging operational transport mode, customized buses serve as a good alternative to meet the diversification of user demand and to fill the demand that is not adequately being addressed by conventional buses. The comparative advantages of customized buses against conventional buses are based on the high quality of the services. Therefore, the operating costs of customized buses are usually higher than those for conventional buses. Generally, as an important component in urban public transportation systems, the operation of a conventional bus is supervised by the government and provided certain financial subsidies, and its fares are often set for the purpose of social welfare, to ensure that the daily travel demands of residents are met as far as possible [7]. However, the customized bus is a market-oriented operational product whose operators always have the incentive to keep the corporate profits at the maximum level by virtue of its own advantages. Therefore, formulating reasonable fares is necessary for operators to maintain their development. While the customized bus and the conventional bus are collaboratively participating in the market environment, the fare formulation strategies of both parties not only affect their respective corporate benefits, but also affect the urban traffic structure by adjusting the demands for public transportation through fare competitions. It has certain practical significance to study the reasonable strategy for fare formulation from the perspective of pricing game.
From the perspective of transportation operators, corresponding price strategies are adopted for different transportation modes to meet market demand [4]. Under the market environment of free competition among transportation operators, the formulation of one party′s price strategy not only affects its own ticket revenue but also influences the other party′s price strategy by affecting the distribution of passengers, thereby forming a dynamic competition process of pricing game [8]. Combined with the utility theory, the travel demands of different transport modes are mainly described on the theoretical basis of the logit discrete choice model to represent consumer preferences in travel choices [9,10]. In recent years, with the increase of product differentiation in the transportation market, some scholars have studied the pricing game of transportation products from the perspective of heterogeneous product competition. The Hotelling model has been widely applied to capture the transportation demand of product differentiation in oligopolistic markets [11,12,13]. By introducing product differentiation, quantity competitions in the Cournot model and price competition in the Bertrand model caused by homogeneous products are avoided. In line with the standard Hotelling model, consumers’ personal preferences were represented by their locations, which was widely employed to analyze the competition between high-speed railway and air transport [14,15].
The current research on pricing games for public transportation are mostly based on the pursuit of profit goals, although it should be noted that ideally the objective of public transport is not to generate operating profits, but to optimize the level of transport demand, which is consistent with the goal of social welfare [16,17]. Especially in the case of China, with regulation and subsidization from the government, the objectives of the customized bus and the conventional bus are not necessarily pure profit maximization or welfare maximization. This paper focused on the fact that each transport carrier can maximize its own respective objectives in the pricing game. We proposed two different operational functions based on the operator types between the customized bus and the conventional bus, which individually consist of a weighted sum of social welfare and profit. In order to construct a game matrix model for combining the different operational objectives of conventional bus services and customized bus services, the Hotelling model is applied to describe the demand functions of the two modes of transportation services. The combined strategy provides a basis for transportation operators to formulate pricing strategies and the government to supervise the transportation product market by discussing the pricing and competitive strategies in the game between the conventional bus and customized bus.
The structure of the paper is as follows. In Section 2, a bi-level game model has been set up in order to better explain the best payoffs on fares and the weight of social welfare in a competitive market. As will be discussed in detail, the different transport operators compete for demand, described in Section 2.1, using the Hotelling model to capture the travel mode choices between conventional bus and customized bus. The objective functions of the two transport operator types are developed in Section 2.2. In Section 2.3 and Section 2.4, we assume a bi-level game model in which the operators set the weight of social welfare to formulate the combined operational objectives in the upper level, and the two operators simultaneously determine their prices considering the riders’ preferred demand to maximize their payoffs in the lower level. In Section 3, a numerical study on market is conducted in which both price and weight of welfare in operating goal are considered as decision variables. We discussed the subsequent analysis of the equilibrium outcomes, including computations of payoffs, social welfare, and corporate profits under the combined operational objectives. Finally, Section 4 provides concluding remarks.
2. Model
Considering the competition between the customized bus and conventional bus services, the public interests is one of the main factors that must be considered by the operators and the profit is another one, so the operator of each bus service wishes to achieve the balanced objective between the social welfare and the profit. Given that the conditions of two bus services are almost fixed, the prices of two services become the main variable factor to affect the realization of the goals. The process of the two operators constantly adjusting the price to achieve their goals in the changing market is a dynamic non-cooperative game [17]. In this section, a pricing game is proposed to describe the competition between the customized bus and conventional bus, while the Nash equilibrium solutions of the game at different weight of social welfare placed on the operational goals are used to find the best pricing strategy for each side.
The key concern here is how the weight of social welfare on both operational objectives would affect the market equilibrium and most importantly the implications on the payoffs. This motivates a bi-level model, in which the operators set the weight of social welfare to formulate the combined operational objectives in the upper level, and the two operators simultaneously determine their prices considering the riders’ preferred demand to maximize their payoffs in the lower level.
2.1. Travel Mode Choice
Traditionally, mode choice models include objective attributes, such as travel time and travel costs. Over the last few decades, numerous improvements have been made that aim to better unravel the underlying process leading up to observed choice outcomes, while also better predicting the outcomes of choice behavior. In addition to the prices and travel time, service quality and consumer preference are found to affect the decision process of the travel mode choice [18,19,20]. Based on the characteristic difference of the transport services in competition, the Hotelling model has been widely applied to capture the transportation demand of product differentiation in oligopolistic markets [11,12,13]. Following the standard Hotelling model, consumers’ personal preferences were represented by their locations, which were widely employed to analyze the competition in the transportation market.
We consider a model that involves competition between the customized bus and the conventional bus over a single origin-destination link. The choice of mode between customized bus and conventional bus is also a complex decision process that is influenced by various factors. Previous studies have shown that price and travel time are two especially important factors in the competitive transport market while considering public travel choice [17]. Apart from the two factors, we also focused on the fact that customized bus services and conventional bus services have different product positioning, which can be captured by the service difference between the two modes of transport. Unlike the conventional bus, the customized bus provides point-to-point transportation service without frequent stops at each bus station, and provides reserved seats for each passenger and ensures comfort during the journey, which is perceived to be more pleasurable compared to conventional bus services with fixed timetables and routes [2]. The impact of these service differences for the two modes of transport on consumers’ choice are noted and treated as the product differentiation in the Hotelling model. In line with the previous studies [14,15], we develop a Hoteling-type model with two firms offering two transport products, so as to analyze the competition between the two bus services.
The Hotelling model that involves competition between customized bus and conventional bus is shown in Figure 1.
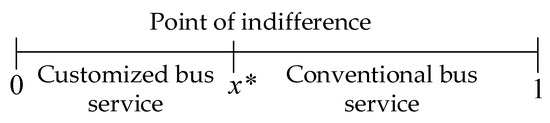
Figure 1.
Demand distribution of customized bus and conventional bus.
It is assumed that the riders are evenly distributed in the interval ; the two ends of the interval represent two modes of transportation with different travel services. More specifically, the customized bus service is located at 0 and conventional bus service at 1. A rider will make travel choices based on the utility preferences for the two travel services. Following the Hotelling model developed in the previous studies, we consider ticket price, travel time, and traveler′s choice of service preference [14,15] in the travel disutility of our model. The disutility of choosing customized bus and conventional bus for a rider at a given point is given by:
where is the location of the rider in the interval; is the disutility of choosing travel mode ( (customized bus) or (conventional bus)); represents the price of transport mode ; is the travel time of transport mode ; is the value of traveler’s time; and represents the value of the disutility generated by the traveler′s preference for the two transportation services, that is, the difference other than the price and travel time (for example, comfort and speed) for the two modes of transport.
By setting , one gets the point where a rider is indifferent between the two bus services:
The point divides the riders into two parts, the riders located in the interval will choose the customized bus and the riders located in the interval will choose conventional bus. It is clear that the value of is exactly the share ratio of the customized bus riders and is the share ratio of the conventional bus riders. Let be the total travel demand; the demand functions for the customized bus and conventional bus are given by Equations (4) and (5).
2.2. Combined Operational Objectives
It is reasonable, as discussed in the introduction, to assume that the customized bus operator usually aims to maximize corporate profits, with less consideration on the social welfare [16,17], while the operators of the conventional bus usually try to maximize the social welfare [21,22]. In this study, the operational goal of each bus operator is assumed to be a weighted sum of social welfare and the profit. The operator of the customized bus is “profit pro” so that its weight for the social welfare is smaller than that of profit; on the other hand, the conventional bus emphasizes “social welfare pro” so that its weight of social welfare is higher than that of profit. Each operator wishes to maximize its combined operational objectives.
- (1)
- Calculation of social welfare
Urban public transportation usually has the characteristics of economies of scale [23,24], the average costs of both conventional bus and customized bus will decrease due to the increasing amount of long-term passengers [22,25]. In this study, the total social surplus is taken as the measure of the social welfare. It is reasonable to assume that the marginal costs of these two modes of transportation are negligible, and the social welfares of mode is calculated as:
where
is the social welfare of mode (customized bus) or (conventional bus));
represents the travel demand at the corresponding price level of mode ;
is the inverse demand function of mode which can be calculated by Equations (4) and (5);
is the fixed cost of mode .
- (2)
- Calculation of profits
The passenger ticket revenue is usually taken as the benefit function for calculation [26,27]; considering that customized bus and conventional bus have different operating costs [21,28], the profit for the operator of mode is:
where
is the profit of mode ;
is the variable operating costs.
- (3)
- Combined operational objectives
Assuming that the operational objectives of both conventional bus and customized bus are the weighted sum of social welfare and profit, the combined operational objective of mode given by:
where is the weight of social welfare for mode . Since the operator of customized bus service is “profit pro”, its weight of social welfare should be less than 0.5, i.e., ; on the other hand, the weight of social welfare for conventional bus should be greater than 0.5 due to the characteristic of “social welfare pro”, i.e., . It is worth noting that the “social welfare pro” does not mean the maximization of the consumer surplus, as it includes both the producer surplus and consumer surplus.
2.3. Lower-Level Pricing Game
Once the weights of social welfare of the two operators are given, the operators must choose their price strategies to maximize the combined operational objectives, the competition process forms a typical two-person non-cooperative game. Since the fares of public transportation tend to be discrete, a limited set of discrete pricing strategies of conventional bus and customized bus is adopted in this study. The games with discrete strategies consisting of two players are usually described by bimatrix games [29,30], and the previous studies have explored the solution of bimatrix problems and shown that Nash equilibrium points exist for any bimatrix games [30,31,32,33]. Assuming that the numbers of pricing strategies for given mode are and , respectively, the competition between the customized bus and conventional bus services can be described by the two-person non-cooperative game as follows:
where
is the kth price strategy of mode ;
is the price strategy sets of mode ;
is the pay-off matrix for the operator of mode .
is the payoff of mode when the price strategy combination is , which can be calculated by Equation (8).
If the pricing game has a pure-strategy , it is well known that Equations (10) and (11) is an equivalent condition for the pure-strategy to be a Nash equilibrium, in which the corresponding payoffs to the equilibrium solution are and , respectively:
when there is no pure strategy equilibrium solution, the mixed strategy of the game players can be defined [34]. A mixed strategy is a sequence and a probability distribution when the operator of mode selects the price strategy with probability , which should satisfy the following equation:
If the customized bus and the conventional bus select a pure strategy randomly, according to the probability distributions given by the two players, the expected payoff of mode (C or B) is:
A mixed strategy that satisfies Equations (14) and (15) at the same time is defined as the mixed strategy Nash equilibrium solution of the game.
2.4. Upper-Level Weighting Game
Because of the difficulties experienced with the equilibrium solution of an infinite number of possible weight of social welfare on operational goals, the weight of social welfare for mode is assumed to be discrete in this study, so the process of the operators choosing the weights turn out to be a game between the two operators. As discussed previously, the weights imply the preferences of the bus operators to the social welfare and are set as for customized bus and for conventional bus, respectively. The process by which the customized bus and conventional bus services choose their weights of social welfare forms the upper level game as follows:
where
is the kth weight strategy of mode ;
is the weight strategy sets of mode ;
is the pay-off matrix of the operator of mode .
is the payoff of mode when the social weight pair is , which can be obtained by solving the lower-level game as described by Equations (9)–(15).
By setting up the weighting game model, we focus on the consequences for the operators and society of different competitive situations in the transport market by analyzing how the differences between the equilibrium prices, payoffs, and profit depend on the weights the operators place on different goals. Since the conventional bus service is often regulated by the government, the weight of social welfare for the conventional bus service might be a given one. The upper-level game is explored to find the optimal weighting strategies for both operators.
3. Case Study
The customized bus routes between the Guangzhou Higher Education Mega Center (GZHEMC) North, Panyu District, Guangzhou (started from North Comprehensive Commercial District Bus Station), and the Sports Center Station Road, located in the CBD of Guangzhou, is selected as the study case. The existing conventional bus line B25 has eleven stops, and it takes 1 h to complete the entire route. B25 buses are overcrowded during the morning and evening peak hours, so that there is a high potential demand for the customized bus service.
According to the Guangzhou Statistics Bureau, the average annual income of Guangzhou residents in 2020 was CNY 130,110 [35], and the average wage rate is 65 CNY/h (calculated based on 249 working days and eight working hours per day). Considering that the commuting time value of residents is generally 20–50% of the labor time value [36], the value of travel time is set to 24 CNY/h. The preference coefficient , which represents the value of disutility generated by different travelers′ preferences for transport services, is set to 8.0 [22]. The minimum fare for transit in Guangzhou is CNY 2 and increases by 1; therefore, the optional fares for conventional bus are set to CNY 2, 3, 4, 5, and 6. The optional fares for customized bus are CNY 4, 5, 6, 7, 8, 9, 10, 11, and 12 for one-way trip. The point is that the relative profits realized by typical pricing schemes are not related to infrastructure fixed cost, so we only calculate the variable costs in the case [9,37]. Due to the presence of economies of scale in public transportation, we combined the calculation of operating costs in existing research, the unit variable cost of the conventional bus is ignored [9,21], and the unit variable cost of the customized bus is set to CNY 3. The travel time of the customized bus can be set to 45 min, and 60 min for the B25 bus line, respectively. Assuming that the weight of social welfare takes discrete values within the corresponding range, , . The parameter values used in the case study are summarized in Table 1.

Table 1.
Parameter values for numerical analysis.
3.1. Two Dominant Scenarios
Based on the analysis in Section 2, we extend the model to treat the weight of social welfare on operational goals as a decision variable in addition to prices. By considering all the possible weight placed on social welfare in operational goals, a total of 36 combinations on pricing game competition could be formed with different scenarios. At each pricing game, the Nash equilibrium conditions for all the possible scenarios will be explored. The equilibrium strategy for both bus services is a two-dimensional space for the weight of welfare combinations. The equilibrium pay offs under the welfare combinations for the customized bus and conventional bus are shown in Figure 2 and Figure 3, respectively.
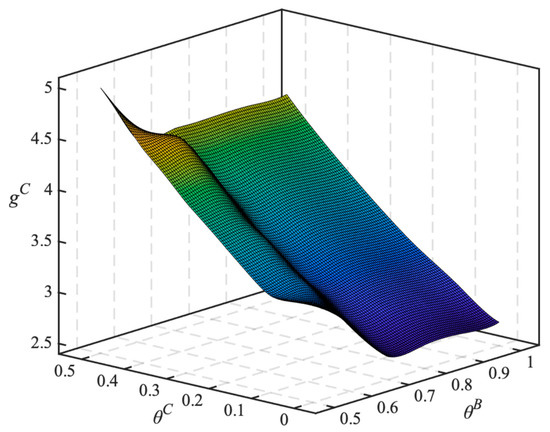
Figure 2.
The equilibrium payoffs under the combinations of welfare for the customized bus.
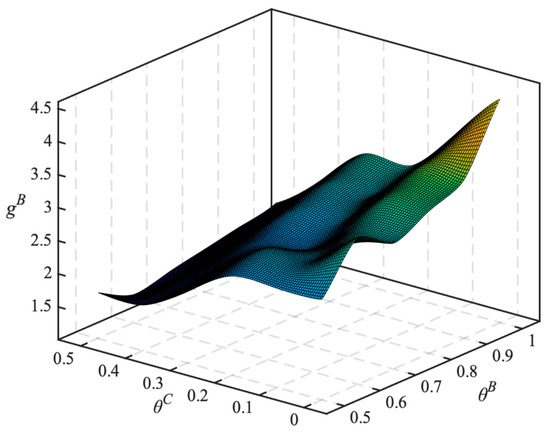
Figure 3.
The equilibrium payoffs under the combinations of welfare for the conventional bus.
To examine the effect of weight of welfare on the equilibrium prices and payoffs, two dominant scenarios that bring the highest payoffs for both operators can be determined. As shown in Figure 2 and Figure 3, the combination with the maximum payoffs (combined operating benefits) of customized bus and conventional bus, respectively, appear in ( and (. Table 2 and Table 3 show the pay-off matrix under the combined operating objectives of the two modes of transport. The first column of the table represents the payoffs for customized bus and the second column represents the conventional bus; Table 4 lists the two combined strategy scenarios in which the payoffs of the customized bus and the conventional bus reach the maximum value, and the equilibrium solution of the fares are presented.

Table 2.
The pay-off matrix for the two modes under the scenario (.

Table 3.
The pay-off matrix for the two modes under the scenario (.

Table 4.
Equilibrium results of the maximum payoffs with combined operational objectives.
As summarized in Table 4, Scenario 1 is the case where the payoff of customized bus is maximized, and Scenario 2 is the case where the payoff of conventional bus is maximized. The results are in accordance with the operational goals of the two bus services. In the proposed game, the “social welfare pro” conventional bus operator is in a dominant position to take its own price strategy, as the conventional bus services are often regulated by the government, and the “profit pro” customized bus operator simply reacts to the actions of the conventional bus. The results indicate that the customized bus operator can take a relatively low-price strategy when the conventional side places less emphasis on social welfare since it can reach the optimal goal by setting a low fare to attract more riders as shown in Scenario 1, while it has to take a high price strategy to maintain its payoff when the conventional bus operator tries to maximize the social welfare by a low fare as shown in Scenario 2.
The results are interesting: the low price of conventional bus service does not lead a low price of customized bus service, and a high price of conventional bus service may result in a low price for the customized bus. It also should be noticed that the Nash equilibrium on both scenarios could not lead to the optimal global payoffs for the two players, which may reflect the fact that the rational choices can lead to the outcomes that are ”Pareto inefficient” in the non-cooperative game [38]. Thus, the important motivation we analyzed with the Nash equilibrium is the idea that no individuals can do strictly better deviating by holding everyone else’s actions, which can be considered as the self-enforcing agreement that guarantees the stability of the conditions where no one regrets his choices given the choices of the other players.
3.2. The Effects of Weight of Social Welfare on Equilibrium Conditions
With the possibility of considering the weight of social welfare on the objective functions, it is interesting to further study how they interact with equilibrium conditions. Considering all the equilibrium strategies under different market scenarios, the equilibrium conditions for the two modes of transport can be determined.
First, we examine the effect of weight of social welfare on equilibrium price for the two bus services. By setting the other player’s weight of social welfare to be a fixed value (for customized bus, ; for conventional bus, ), it is straightforward to derive the effects of weight of welfare on the equilibrium price, which are shown in Figure 4.
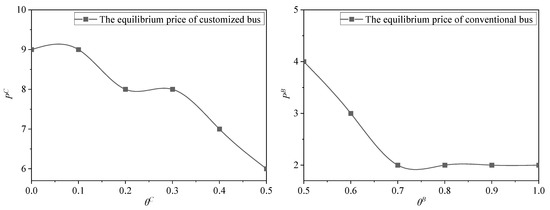
Figure 4.
The effects of weight of social welfare on equilibrium price.
As shown in Figure 4, as the operators puts more weights on welfare relative to profit in its decision making, both equilibrium price for the customized bus and conventional decrease. For a given equilibrium price and weight of social welfare, the payoffs, profits, and social welfare under the game equilibrium of two modes of transport with combined operational goals are illustrated in Table 5 and Table 6, respectively.

Table 5.
The profit, social welfare, and payoffs of customized bus when the game is balanced.

Table 6.
The profit, social welfare, and payoffs of conventional bus when the game is balanced.
According to Table 5, the profits of customized bus services can be divided into two stages, which are in accordance with the impact on the weight of social welfare of conventional bus. When , the profit of customized bus reaches the maximum at . This means that customized bus operators will be able to achieve the goal with maximum profit by choosing the lowest weight of social welfare at this stage. When , the effect of the social welfare of conventional bus on the customized bus tends to be flat at this stage. That is to say, the customized bus operators have reached the maximum profit at and also obtained higher payoffs than when . Therefore, customized bus operators will select to ensure the maximum profit and overall payoffs in the pricing game. The conclusion is that, when conventional bus formulates an operation strategy considering a higher degree of social welfare, there is a certain constraint on the formulation of the customized bus, which participates as the other player in the pricing game. Namely, the customized bus operator has to consider a certain degree of public welfare to achieve the overall payoffs according to the conventional bus. This is probably a consequence of the fact that the “social welfare pro” conventional bus services, which serve as public companies, usually take maximization of social welfare as a goal in their objective functions.
The analysis in Table 6 shows that the social welfare objectives of the customized bus services will cause conventional bus services to lose their competitive edge in the pricing game. As the weight of social welfare for the customized bus ( increases from 0 to 0.5, the payoffs, corporate profits, and fares of the equilibrium solution after the game competition of the conventional bus all decrease. This shows that, when customized bus services join the competition for passengers with the conventional bus as new participants in the market, conventional bus services will be significantly impacted if they formulate a fare strategy that considers “social welfare” to a greater extent. In this case, the conventional bus will lose its own price advantage in the game competition with the customized bus; due to the inability to obtain sufficient passengers, conventional bus operators will not be able to create more corporate profits and payoffs.
According to the discussion above, a number of conclusions from the analysis can be stated:
- (1)
- The customized bus operators have to consider more about social welfare () to attract riders and to achieve the optimal equilibrium payoffs when the conventional bus operators place the lowest weight on social welfare () and take a high price strategy, while the optimal payoff of the conventional bus appears in the combination of the two sides with the largest difference in “social welfare”; that is, the highest weight placed on social welfare and lower price of conventional bus services () will be expected to obtain the optimal equilibrium payoffs in the case when the goal of customized bus operators is pure profit maximization (.
- (2)
- When a higher weight of social welfare is considered into the operational objectives for conventional bus, the customized bus can possibly obtain higher payoffs by reducing the weight of social welfare and increasing ticket price. However, simply increasing fares does not result in the optimal solution. The results show that when the social welfare of the conventional bus takes a high degree (), customized bus operators can obtain the best relative profit by ensuring a certain degree of social welfare (. That is to say, an operational goal of a certain degree of “social welfare” is properly considered, which will help it obtain an advantage in the game competition with the conventional bus.
- (3)
- Overall, for the conventional bus, the operational objectives of considering social welfare protect the interests of itself and travelers, so it can obtain better payoffs compared with other situational objectives in the competition game with the customized bus. For the customized bus, the company′s fare formulation should fully consider the best countermeasures under the existing pricing strategies of the conventional bus and develop a reasonable price strategy based on their own product positioning and consumers′ preferences for travel service products.
4. Conclusions
This paper analyses competition between conventional bus services and customized bus services that have goals that extend beyond traditional profit maximization and social welfare maximization. Specifically, operators maximize a weighted sum of profits and social welfare. A bi-level pricing game is applied to model the strategic interactions between the two operators in a competitive market, taking into consideration price as well as the weight of social welfare being placed on the operational goals. The analysis shows the unusual result that the corporate profits of the customized bus, as a new competitor in the areas already covered by conventional bus lines, do not always increase along with a higher weight being placed on profit while formulating pricing strategies. In fact, the nature of higher social welfare operational objective of the conventional bus, which is provided as a public transportation service, could help to determine the weight of social welfare operational objective in customized bus pricing formulation. A numerical study based on the Chinese market is applied to elaborate thoroughly on the relationships between the weight put on welfare and profits producing equilibrium prices for each possible competitive situation between the conventional bus and customized bus. Namely, for each of the operators, simply pursuing the maximization of ticket revenue could not achieve the expected target under the market mechanism of free competition. In order to formulate the optimum pricing strategies, operators should take the fare policies of other local transportation into consideration and make appropriate operational plans with their own product advantages.
In this paper we have shown that a transport competition model with two different types of operators (conventional bus and customized bus) can be formulated, yielding results that may be interesting when the weights of social welfare on operational goals are considered as the decision variable in addition to price strategies. Such results depend on the parameterization of the model, but the contribution of this paper is the methodology to analyze different policy options in a transportation system setting, taking into account the reactions of relevant competitors. The model presented above can be easily adapted to any context of price competition with respect to consumer preferences and product differentiation, where the corresponding pricing strategies and operational goals are adopted in the competitive market. As a more general setting, however, there is a competitive market in which two or more transport modes exist. This type of analysis, based on game theory, attempts to explore the effects of transportation provision and charging on the best response function of all competitors in the competitive market. Our results should provide useful information to policymakers and transportation planners developing sustainable transportation systems.
The game-theoretic model was constructed to capture the competition aspect between conventional bus and customized bus based on the non-cooperative game theory. In fact, the conventional bus and customized bus may cooperate with each other to achieve the “win-win” situation. It would be an interesting direction to study both the competition and cooperation issues involved in the model. Additionally, the influences of user classification and other interfering factors on the equilibrium solution can be considered to make the pricing game model more suitable for the development of urban public transportation.
Author Contributions
Conceptualization, J.L.; funding acquisition, J.L.; investigation, X.F. and B.J.; methodology, J.L.; software, X.F.; supervision, J.L.; validation, J.L.; writing—original draft, X.F. and B.J; writing—review and editing, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Research and Development Project in Key Areas of Guangdong Province (No. 2019B090913001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy protection of respondents.
Acknowledgments
We are very grateful to the editors and reviewers for their hard work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, T.; Ceder, A.A. Analysis of a new public-transport-service concept: Customized bus in China. Transp. Policy 2015, 39, 63–76. [Google Scholar] [CrossRef]
- Tao, L.; Ceder, A.A.; Bologna, R.; Cabantous, B. Commuting by Customized Bus: A Comparative Analysis with Private Car and Conventional Public Transport in Two Cities. J. Public Transp. 2016, 19, 55–74. [Google Scholar]
- Narayan, J.; Cats, O.; Oort, N.V.; Hoogendoorn, S. Integrated route choice and assignment model for fixed and flexible public transport systems. Transp. Res. Part C Emerg. Technol. 2020, 115, 102631. [Google Scholar] [CrossRef]
- Wang, J.; Hai, Y. A game-theoretic analysis of competition in a deregulated bus market. Transp. Res. Part E 2005, 41, 329–355. [Google Scholar] [CrossRef]
- Bruzzone, F.; Scorrano, M.; Nocera, S. The combination of e-bike-sharing and demand-responsive transport systems in rural areas: A case study of Velenje. Res. Transp. Bus. Manag. 2020, 40, 100570. [Google Scholar] [CrossRef]
- Capodici, A.E.; D’Orso, G.; Migliore, M. A GIS-Based Methodology for Evaluating the Increase in Multimodal Transport between Bicycle and Rail Transport Systems. A Case Study in Palermo. Int. J. Geo-Inf. 2021, 10, 321. [Google Scholar] [CrossRef]
- Van Reeven, P. Subsidisation of Urban Public Transport and the Mohring Effect. J. Transp. Econ. Policy 2008, 42, 349–359. [Google Scholar]
- Nash, P.C. High-speed rail and air transport competition: Game engineering as tool for cost-benefit analysis. Transportation Res. Part B Methodol. 2010, 44, 812–833. [Google Scholar]
- Bian, C.Z.; Hua-Pu, L.U.; Xin-Xin, Y.U. Price Game between Intercity Railway and Bus. J. Transp. Syst. Eng. Inf. Technol. 2010, 10, 184–189. [Google Scholar]
- Chen, K.M.; Luo, X.Q. Game-theory of reasonable ticket price for urban railway transport. J. Chang. Univ. (Nat. Sci. Ed.) 2005, 25, 52–55. [Google Scholar]
- Kats, A. More on Hotelling’s stability in competition. Int. J. Ind. Organ. 1995, 13, 89–93. [Google Scholar] [CrossRef]
- Hernandez, M.A. Nonlinear pricing and competition intensity in a Hotelling-type model with discrete product and consumer types. Econ. Lett. 2011, 110, 174–177. [Google Scholar] [CrossRef]
- Weijde, A.; Verhoef, E.T.; Berg, V. Hotelling Models with Price-Sensitive Demand and Asymmetric Transport Costs: An Application to Public Transport Scheduling. J. Transp. Econ. Policy 2014, 48, 261–277. [Google Scholar]
- Yang, H.; Zhang, A. Effects of high-speed rail and air transport competition on prices, profits and welfare. Transp. Res. Part B Methodol. 2012, 46, 1322–1333. [Google Scholar] [CrossRef]
- Yushi, T. Transportation policy for high-speed rail competing with airlines. Transp. Res. Part A Policy Pract. 2018, 116, 350–360. [Google Scholar]
- Guan, Y.; Wang, Y.; Yan, X.; Guo, H.; Zhao, Y. The One E-Ticket Customized Bus Service Mode for Passengers with Multiple Trips and the Routing Problem. Sustainability 2022, 14, 2124. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Zhang, S. Optimal pricing of customized bus services and ride-sharing based on a competitive game model. Omega 2021, 103, 102413. [Google Scholar] [CrossRef]
- Nocera, S. An operational approach for the quality evaluation in public transport services. Ing. Ferrov. 2010, 65, 363–383. [Google Scholar]
- Lai, W.-T.; Chen, C.-F. Behavioral intentions of public transit passengers—The roles of service quality, perceived value, satisfaction and involvement. Transp. Policy 2011, 18, 318–325. [Google Scholar] [CrossRef]
- Nocera, S. The key role of quality assessment in public transport policy. Traffic Eng. Control. 2011, 52, 394–398. [Google Scholar]
- Borndörfer, R.; Hoang, N.-D. Fair ticket pricing in public transport as a constrained cost allocation game. Ann. Oper. Res. 2015, 226, 51–68. [Google Scholar] [CrossRef]
- Mathisen, T.A.; Solvoll, G. Competitive tendering and structural changes: An example from the bus industry. Transp. Policy 2008, 15, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Farsi, M.; Filippini, F.M. Economies of Scale and Scope in Local Public Transportation. J. Transp. Econ. Policy 2007, 41, 345–361. [Google Scholar]
- Singh, S.K. Costs, economies of scale and factor demand in municipal transport undertakings in india. In Proceedings of the SCRA 2004-FIM XI, Lucknow, India, 27–29 December 2004; pp. 7–24. [Google Scholar]
- Gómez-Lobo, A. Why Competition Does Not Work in Urban Bus Markets: Some New Wheels for Some Old Ideas. J. Transp. Econ. Policy 2007, 41, 283–308. [Google Scholar]
- Wang, J. Theories and Methods of Pricing and Subsidizing in Urban Public Traffic Based on Game Analysis. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2008. [Google Scholar]
- Gong, H.W.; Jin, W.Z.; Hao, X.N.; Luo, Q. Investigation into Pricing Game of Customized City Bus Service. J. South China Univ. Technol. (Nat. Sci. Ed.) 2017, 45, 70–76. [Google Scholar]
- Grange, L.; Troncoso, R.; Briones, I. Cost, production and efficiency in local bus industry: An empirical analysis for the bus system of Santiago. Transp. Res. Part A Policy Pract. 2018, 108, 1–11. [Google Scholar] [CrossRef]
- Nash, J.F. Equilibrium Points in N-Person Games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lemke, C.E. Bimatrix Equilibrium Points and Mathematical Programming. Manag. Sci. 1965, 11, 681–689. [Google Scholar] [CrossRef] [Green Version]
- Howson, C., Jr. Equilibrium Points of Bimatrix Games. J. Soc. Ind. Appl. Math. 1964, 12, 413–423. [Google Scholar]
- Orlov, A.V.; Strekalovski, A.S. Numerical search for equilibria in bimatrix games. Inst. Syst. Dyn. Control. Theory 2005, 45, 983–997. [Google Scholar]
- Quintas, L.G. Constructing bimatrix games with unique equilibrium points. Math. Soc. Sci. 2006, 15, 61–72. [Google Scholar] [CrossRef]
- Facchinei, F.; Kanzow, C. Generalized Nash equilibrium problems. Ann. Oper. Res. 2007, 175, 173–210. [Google Scholar] [CrossRef]
- Bureau, G.S. The Average Annual Salary of Employees in Urban Non-Private and Private Units in Guangzhou in 2020. Available online: http://tjj.gz.gov.cn/tjgb/qtgb/content/post_7319136.html (accessed on 7 June 2021).
- Ozbay, K.; Yanmaz-Tuzel, O. Valuation of travel time and departure time choice in the presence of time-of-day pricing. Transp. Res. Part A Policy Pract. 2008, 42, 577–590. [Google Scholar] [CrossRef]
- D’Alfonso, T.; Jiang, C.; Bracaglia, V. Would competition between air transport and high-speed rail benefit environment and social welfare? Transp. Res. Part B Methodol. 2015, 74, 118–137. [Google Scholar] [CrossRef]
- Hurwicz, L.; Schmeidler, D. Construction of outcome functions guaranteeing existence and Pareto optimality of Nash equilibria. Econom. J. Econom. Soc. 1978, 46, 1447–1474. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).