Stability Assessment of Rock Mass System under Multiple Adjacent Structures

Abstract

Numerical modeling is important for exploring the fundamental processes occurring in rock and for evaluating the real performance of structures built on and in rock mass system, and thus for supporting the design of rock engineering problems. Estimating the stability of rock mass foundation systems entirely based on a theoretical approach is a complicated task if there exists overlapping of their potential collapse modes. This paper applies finite element limit analysis to evaluate the bearing capacity of equally spaced multiple strip footings resting on rock mass obeying the modified non-linear Hoek–Brown failure criterion. Numerical solutions are expressed in terms of the efficiency factor that is dependent on the spacing between footings, as well as the rock mass properties. In addition, the effects of surface surcharge and footing roughness are quantified. The maximum spacing at which the interfering effect of adjacent footings becomes disappeared is evaluated and an algebraic expression for approximating the maximum spacing is proposed. Failure mechanisms for a few cases of rock mass under multiple strip footings are examined.

1. Introduction

Rock differs from most other engineering materials in that it contains fractures of one type or another which render its structure discontinuous. Hence, a clear distinction must be made between the intact rock and the rock mass [1]. The intact rock refers to the unfractured blocks between discontinuities comprised of rock-forming minerals. The rock mass is the in situ medium consisting of intact rock blocks separated by discontinuities, such as bedding plane, faults, joints, and folds, and often has in inhomogeneous and anisotropic properties. Numerous classification systems of intact rock and rock mass have been developed and the overview of the classification systems is given in [2].

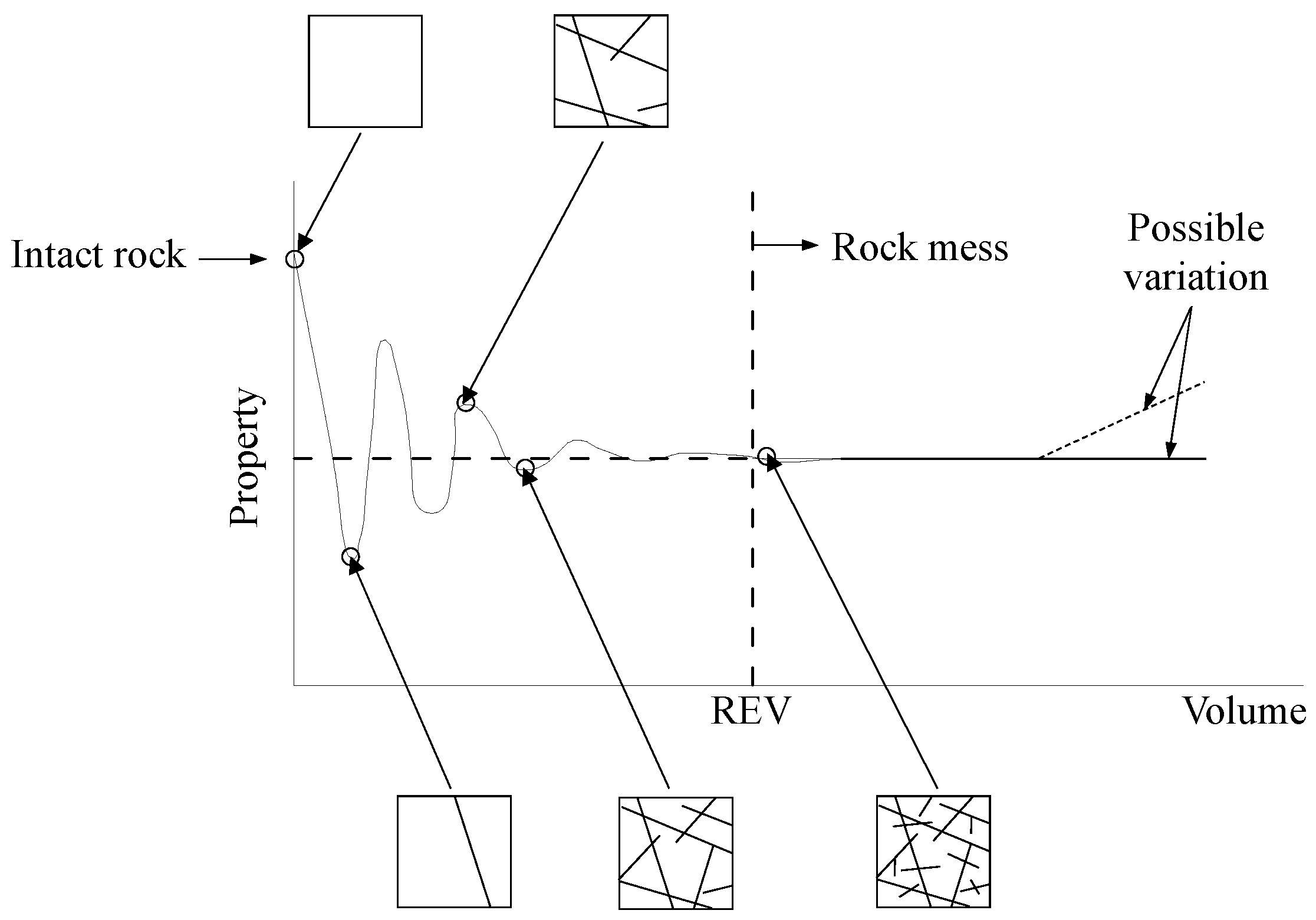
As shown in Figure 1, the properties of the rock mass are significantly dependent on the problem domain, When the domain enlarges to a certain volume, called representative elementary volume (REV), the rock properties will reach a steady magnitude [3]. In other words, the rock properties become constant at some REV if the discontinuity existence is statistically homogeneous in the domain considered. The rock properties may further oscillations in the trace if the discontinuity existence is heterogeneous. Thus, numerical stress analysis consists of discontinuous method for sub-REV scale and continuum method for large volume of rock mass.

In engineering practice, it is necessary to place footings so close to each other or to build them adjacent to another structures. Especially, multiple equally spaced footings are encountered in the form of railway sleepers and grillage foundations [4,5,6]. From the available literature for a group of multiple footings, it is revealed that the ultimate bearing capacity of interfering footings is always greater than that of single isolated footings due to the overlapping of their failure surface. The different investigations were based on small scale model test [7,8], field plate load test [9], stress characteristic method [7], finite element method [10,11], lower bound limit analysis [12], and upper bound limit analysis [13,14].

All existing studies mentioned above are concerned with multiple strip footings on soils following Mohr–Coulomb failure criterion. However, these solutions have some limitations in determining the bearing capacity of rock masses with joints and fractures. Additionally, the linear Mohr–Coulomb failure criterion may not capture the nonlinear failure behavior of rock mass [15,16]. Alternatively, a non-linear failure criterion proposed by Hoek and Brown [17] is considered for the ultimate bearing capacity of footings over rock mass, although only limited studies on the interfering effect of rock footings were reported. Javid et al. [18] estimated the bearing capacity of two closely spaced strip footings using the distinct element method. More recently, Shamloo and Imani [19] evaluated the bearing capacity of two neighboring strip footings based on the upper bound limit analysis.

In this study, the vertical bearing capacity of a group of multiple strip footings, identically spaced and equally loaded to failure simultaneously, is computed with the finite element limit analysis. The modified Hoek–Brown non-linear failure criterion is used for intact rock or heavily jointed rock mass. The obtained results are compared with the existing solutions and the bearing capacity calculations are presented as a function of spacing between the footings, rock mass properties, footing roughness, and surface surcharge. Collapse mechanisms of rock mass under multiple closely spaced footings are broadly discussed.

2. Background

The numerical methods commonly used for predicting the response of rock mass are presented in Figure 2. The method selection depends on system geometry and problem domain. The numerical analysis consists of discontinuous method for sub-REV scale and continuum method for large volume of rock mass.

To estimate the non-linear strength envelope of intact rock and jointed rock masses, the original Hoek–Brown (HB) failure criterion was proposed in 1980 and has been subsequently updated. The last version, used here, is expressed as [20]

$${\sigma }_1^{\prime }={\sigma }_3^{\prime }+{\sigma }_{ci}^{\prime }{\left(m_b\frac{{\sigma }_3^{\prime }}{{\sigma }_{ci}^{\prime }}+s\right)}^a$$

(1)

where σ_ci is the uniaxial compressive strength of the intact rock. σ₁ and σ₃ are the major and minor principal stresses, respectively, which are considered as positive when tensile in nature. m_b, s, and a are the dimensionless material parameters, defined as

$$m_b=m_i\exp \left(\frac{GSI-100}{28-14D}\right)$$

(2)

$$s= \exp \left(\frac{GSI-100}{9-3D}\right)$$

(3)

$$a=\frac{1}{2}+\frac{1}{6}\left(e^{-GSI/15}-e^{-20/3}\right)$$

(4)

where m_i is the value of m_b for intact rock. The value of m_i is related to the minerology and texture of the intact rock, varying from 4 for very fine weak rock (e.g., claystone) to 33 for coarse igneous light-colored rocks (e.g., granite). The value of m_i can be obtained from experiments. GSI is the geological strength index which features the quality of the rock mass [21]. The value of GSI ranges from about 10 for extremely poor rock masses to 100 for intact rock. D is the disturbance factor which depends on the extent of weathering and blast damage of the rock mass. The value of D varies from 0 for the undisturbed in situ rock masses to 1 form extremely disturbed rock masses. The modified HB criterion is applicable to intact rock or heavy jointed rock mass that can be considered is isotropic and homogeneous and therefore is proper to estimate the bearing capacity of surface footings on rock.

The ultimate bearing capacity of a strip footing subjected to vertical loading is expressed as

$$q_u={\sigma }_{ci}{N}_{\sigma }$$

(5)

where N_σ is the bearing capacity factor, which is related to the HB material parameters, namely, m_i, GSI, and D. However, the value of σ_ci is very little effect on the footing capacity [16,18].

3. Problem Statement

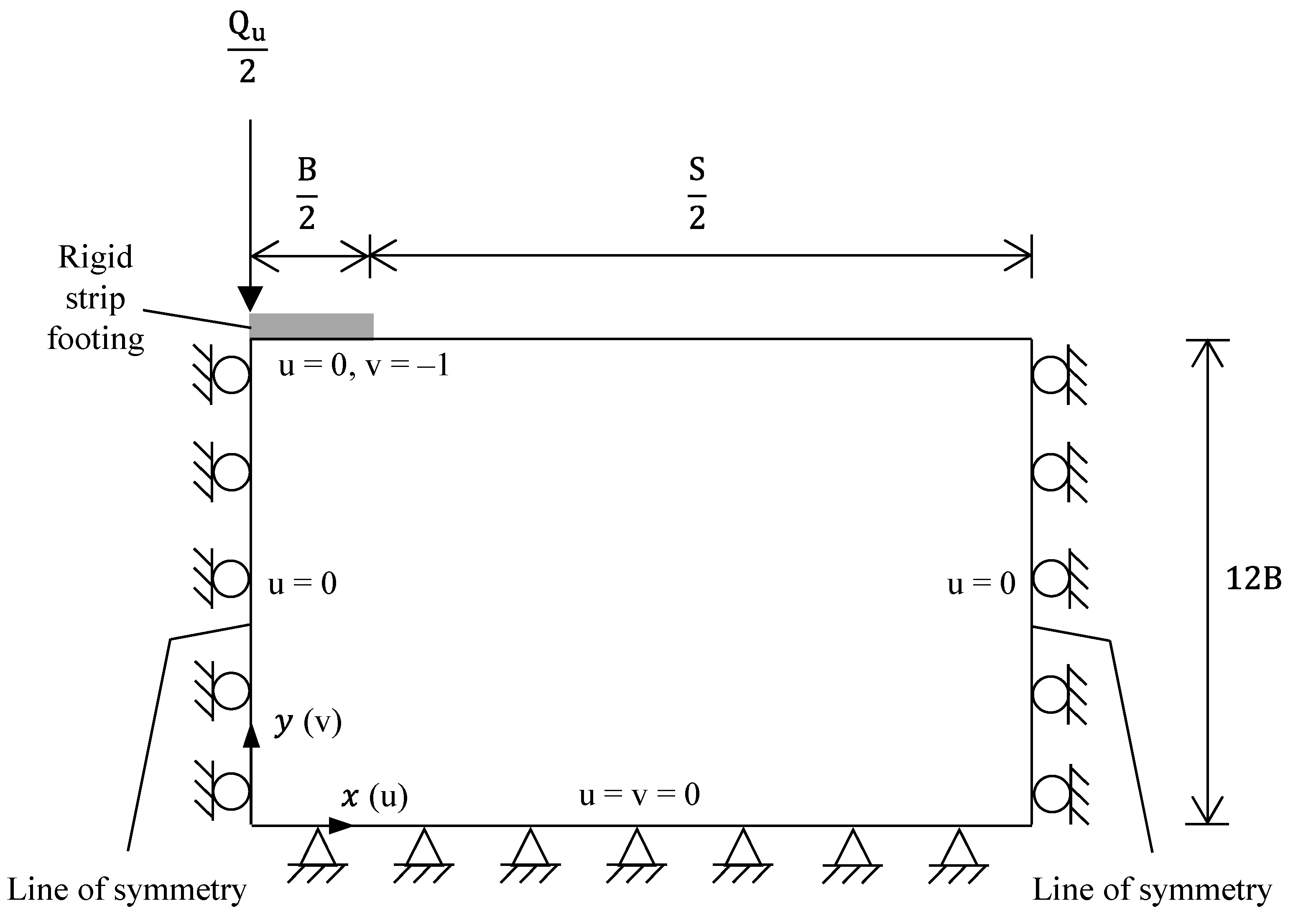
Figure 3 illustrates the geometry and parameters of the rock-footing system considered. A number of multiple strip rigid footings rest upon a rock medium with horizontal ground surface. The footings are having width B and are placed at equal clear spacing S. The interfering effect of multiple footings is quantified by the adjacent spacing ratio S/B, which ranges from 0.1 to 6. The base of the footing is considered as the perfectly smooth and perfectly rough providing upper and lower limits of capacity for multiple footings with given material properties. The rock mass obeys the Hoek–Brown failure criterion as a function of σ_ci, m_i, GSI, and D. The σ_ci value is kept equal to 20 MPa [22] and the m_i values are taken as 7, 10, 15, 17, and 25 for five types of rocks [23]. The values of GSI and D are within the range of 10 to 90 and 0 to 1, respectively. The rock mass has unit weight γ, which is quantified by σ_ci/γB. The value of σ_ci/γB varies from 125 to ∞ that indicates the weightless rock mass [24]. The ground is loaded with a uniform surcharge pressure q and its effect is represented by q/σ_ci. The value of q/σ_ci ranges between 0 to 1, which cover most problems of practical interest [25]. The vertical downward load is simultaneously applied to the center of each footing and all footings are collapsed exactly at the identical bearing load Q_u.

To compare the bearing capacity of an interfering strip footing with that of a single isolated footing, the efficiency factor ξ is introduced:

$$\xi =\frac{N_{\sigma \left(mul\right)}}{N_{\sigma \left(iso\right)}}$$

(6)

where N_σ(mul) is the bearing capacity factor for an interfering footing in a group of multiple footings and N_σ(iso) is the bearing capacity factor for single isolated footing with the same width of the interfering footing. From this, the ultimate bearing capacity of an intervening footing is determined using the following expression:

$$q_u={\sigma }_{ci}{N}_{\sigma \left(iso\right)}\xi$$

(7)

4. Finite Element Limit Analysis

In finite element limit analysis (FELA), the following assumptions are made: the material is rigid perfectly plastic, obeys an associated flow rule and calculations based on this theory only apply for small deformations. Furthermore, rigorous lower bound (LB) and upper bounds (UB) which bracket the true solution can only be obtained in FELA with the correct element types. The LB solution aims for the lower bound of the ultimate load in the static admissible stress field, while the UB solution considers that there exists an upper bound of the true bearing capacity based on the kinematically allowable velocity field [26]. In the presents study, FELA were carried out by using the commercially available software Optum G2 [27]. All numerical results from presents study are described by using an average (AVG) solution:

$$\mathrm{AVG}=\left(UB+LB\right)/2$$

(8)

Figure 4 shows that the problem domain and the stress boundary conditions. The footing is adopted as a weightless and perfectly rigid element and only vertical displacement applies. To achieve a perfectly smooth and perfectly rough interface between the rock mass and footing, the interface factors is set as 0 and 1. Owing to a symmetrical nature of the problem about a vertical line passing through the center of the multiple footing, only quarter of the problem is considered in the computations. The horizontal boundary was placed S/2 away from the center of multiple footings and the vertical boundary was placed at a depth of 12B from the surface to avoid boundary effects. The vertical boundaries were modeled fixed horizontally, and the bottom boundary was modeled as fully fixed horizontally and vertically. The footing and rock mass were discretized into either 6-noded triangular elements in UB analysis or 3-noded triangular elements in LB analysis. An automatically adaptive mesh refinement was used for all analyses, and a total of 10,000 upper bound and lower bound elements were used in three adaptive steps. In addition, 5000 elements were used in the initial mesh stage.

5. Results and Comparison

To validate the results of the present study on strip footings for weightless rock mass with different GSI and m_i, a comparison of bearing capacity N_σ0 obtained in this study with the analyses of Serrano et al. [28] using the slip line method, Merifield et al. [24] using the finite element limit analysis, Chakraborty and Kumar [29] using lower bound finite element limit analysis, and Keshavarz and Kumar [25] using the stress characteristics method. A comparative representation of all these values is given in

Table 1. Comparisons of N_σ0 values obtained from this study and literature for single isolated strip footings on rock mass.

GSI	mi	SE	ME	CK	KK	This Study
10	10	0.072	0.077	0.075	0.077	0.075
	20	0.159	0.156	0.151	0.153	0.151
	30	0.259	0.238	0.230	0.237	0.226
30	10	0.393	0.397	0.388	0.393	0.390
	20	0.716	0.713	0.701	0.702	0.685
	30	1.038	0.988	1.015	1.007	0.960
50	10	1.031	1.037	1.028	1.025	1.024
	20	1.760	1.765	1.739	1.742	1.722
	30	2.458	2.367	2.406	2.426	2.366
70	10	2.434	2.444	2.415	2.415	2.437
	20	3.998	4.012	3.978	3.961	3.904
	30	5.470	5.491	5.437	5.417	5.389
90	10	5.741	5.758	5.724	5.689	5.683
	20	9.100	9.125	9.086	9.015	9.015
	30	12.237	12.270	12.198	12.114	12.085

Note: SE = Serrano et al. (2000)—stress characteristics method; ME = Merifield et al. (2006)—finite element limit analysis; CK = Chakraborty and Kumar (2015)—lower bound finite element limit analysis; KK = Keshavarz and Kumar (2017)—stress characteristics method.

. The present results remain very close to the existing solutions. Additionally, the values of N_σ0 for isolated foundation with rough and smooth roughness for GSI = 50, m_i = 20 are determined to be 1.722 and 1.709, respectively, which are 1.2% and 3.0% in error compared with those from Keshavarz and Kumar [25].

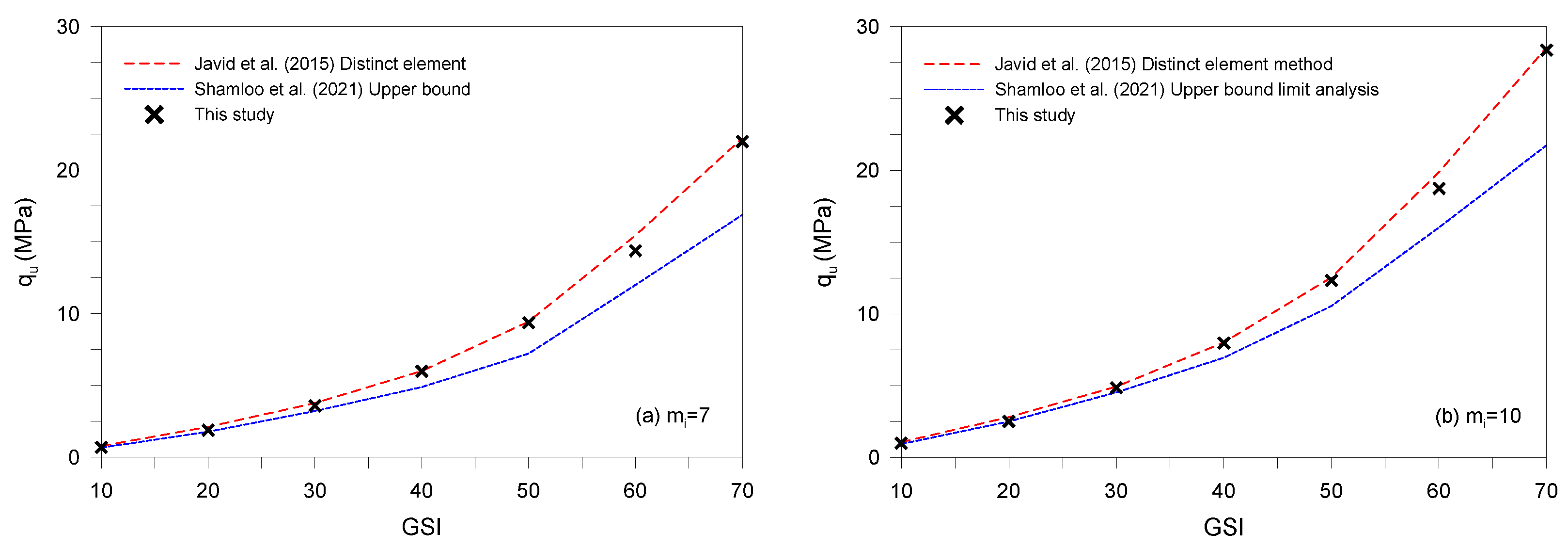
Figure 5 provides the obtained q_u value of two interfering footings (S/B = 1) on rock mass, together with other numerical analysis for same footing and soil conditions. The Figure 5 shows the variation of q_u values with GSI for the case of m_i = 7 and 10. As shown in the Figure 5, the results of the numerical analysis are very close to those obtained with distinct element method of Javid et al. [18]. However, the value of q_u in upper bound solutions by Shamloo et al. [19] was under-predicted, and the difference increases with increasing GSI. Given that the result of present study is included in the result of Javid et al. [15] and Shamloo et al. [19], it can be seen that agree well with previous study.

The variation of the efficiency factors ξ for different combinations of S/B and GSI is shown in Figure 6 for the case of D = 0, σ_ci/γB = infinite, q/σ_ci = 0 and m_i = 7, 15, and 25. Figure 6 shows that the ξ value decreases as S/B increases. It is important to note that the lower GSI, the greater ξ value, however the greater rate at which ξ values decreases as adjacent space increases. Furthermore, as m_i increases, the ξ values according to each GSI increases in the same adjacent space. All ξ values decrease as S/B increases, reached value of 1. In the case of ξ = 1, the bearing capacity of multiple footing has no adjacent distance influence, meaning that the behavior of isolated footing is performed. In the present study, the space ratio corresponding to ξ = 1 is defined as S_max/B. 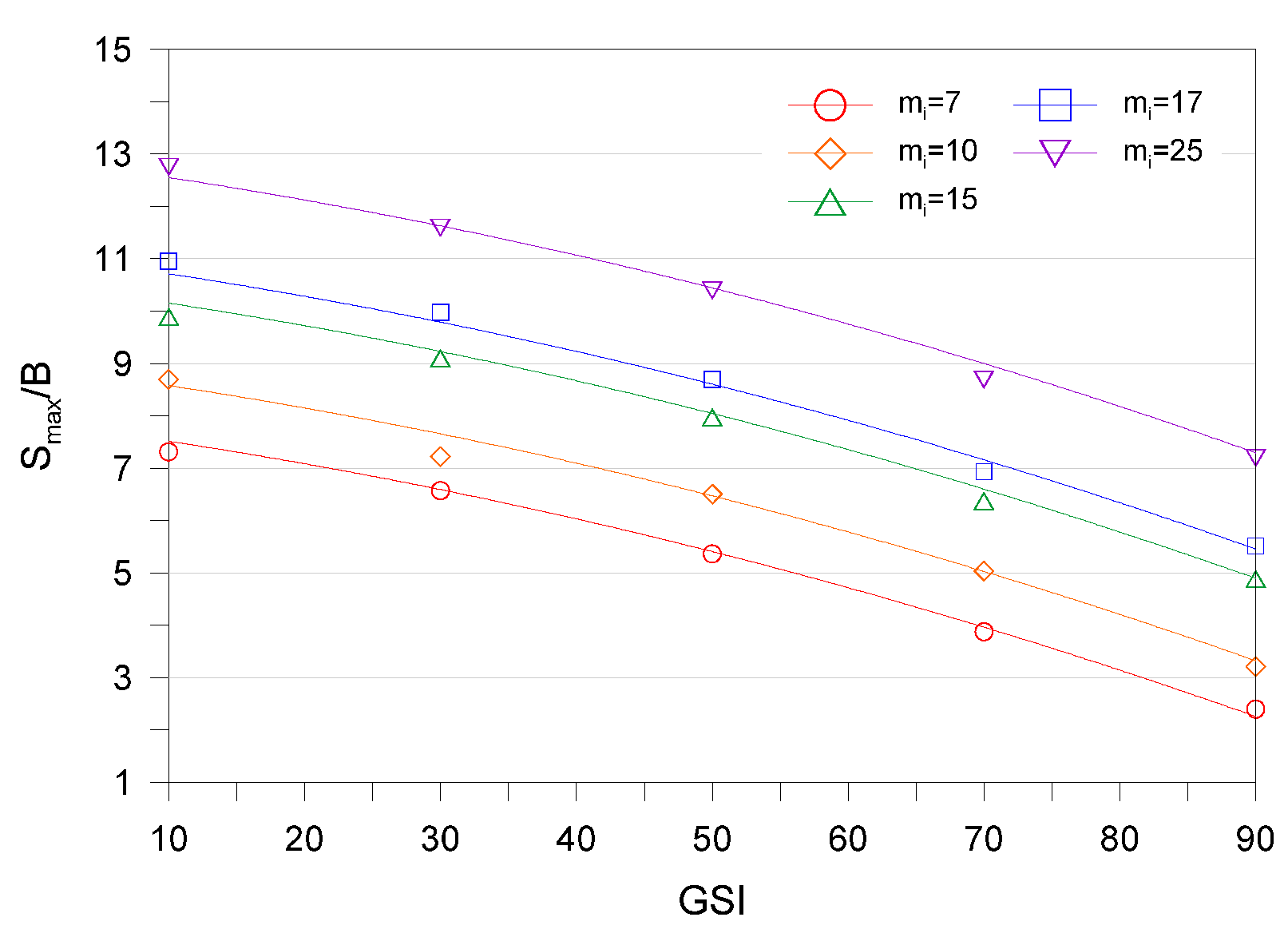S_max/B varies depending on GSI and m_i, respectively, and details of this are illustrated in Figure 7.

The variation of S_max/B for different combinations GSI and m_i is shown in Figure 7 for the case of D = 0, σ_ci/γB = infinite, q/σ_ci = 0. Figure 7 shows that S_max/B decreases with increasing GSI, but for a given GSI, S_max/B increases with increasing m_i. It should be noted that the maximum value of S_max/B is 12.76 for GSI = 10, m_i = 25 and the minimum value of S_max/B is 2.41 for GSI = 90, m_i = 7. In addition, the S_max/B can be described as exponential function of GSI. Expressed in terms of the S_max/B:

$$S_{max}/B=a-3.9\exp \left(0.01\mathrm{GSI}\right)$$

(9)

where a is the coefficients for the parameters of m_i. As stated in Equation (9), it is obvious that the value of S_max/B for multiple footings on rock mass drops towards decreases with increasing of GSI. It is worth noting that these coefficients are accurate for interpolation only, and should not be used for extrapolation beyond 10 < GSI < 90. The relations of a with m_i have the form of (R² = 0.991 and R² = 0.997, respectively)

$$a=9+0.441m_i-0.005m_i{}^2$$

(10)

The proposed expressions of Equations (9) and (10) provide a satisfactory fit and good prediction.

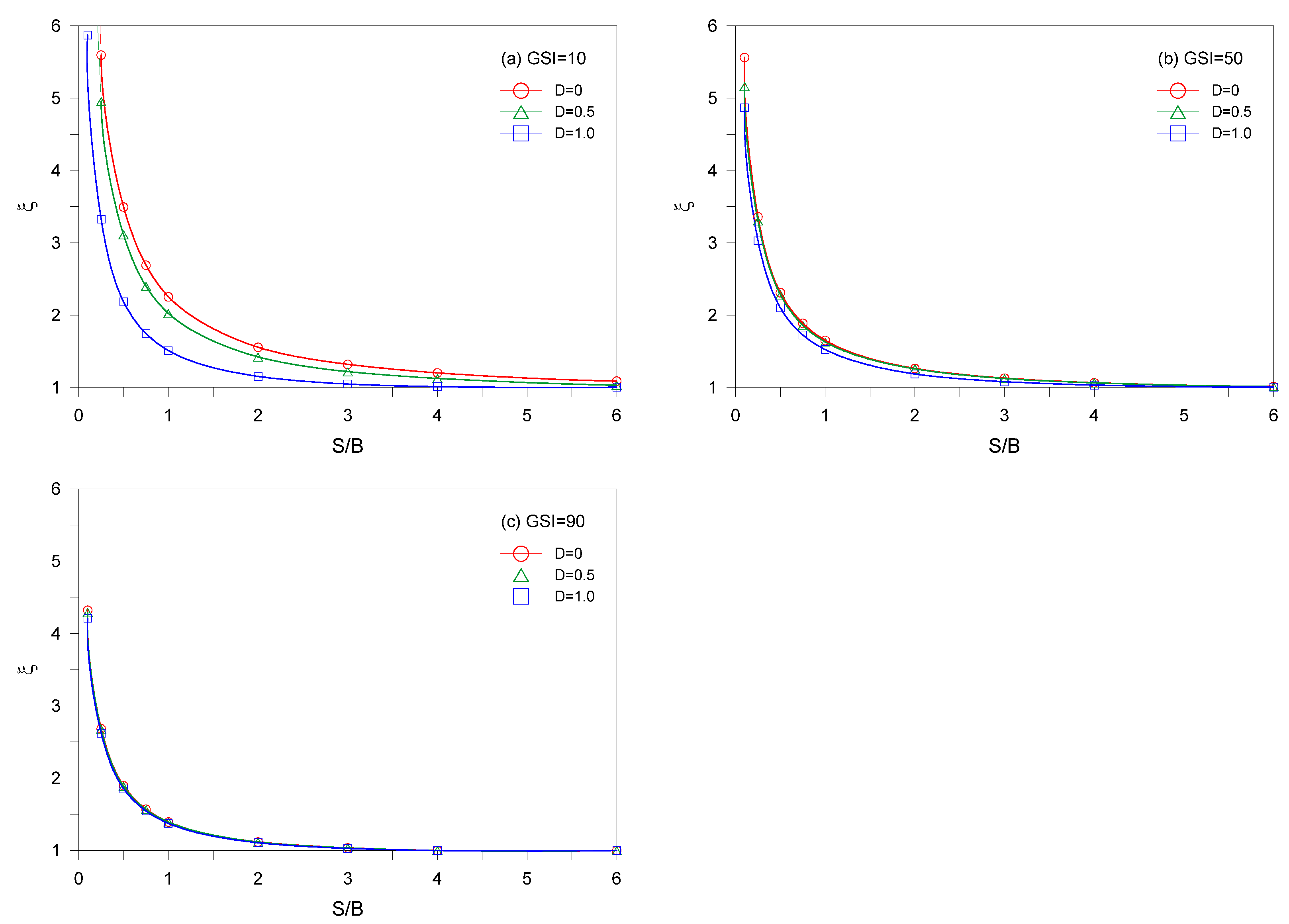
The variation of the efficiency factor ξ for different combinations of S/B and D is shown in Figure 8 for the case of m_i = 10, σ_ci/γB = infinite, q/σ_ci = 0 and GSI = 10, 50, and 90. Figure 8 shows that the value of ξ decreases as D increases. It can also be seen that as GSI increases, the value of ξ decreases and this trend increases as D decreases.

The variation of the efficiency factors ξ for different combinations of S/B and σ_ci/γB is shown in Figure 9 for the case of m_i = 10, D = 0, q/σ_ci = 0 and GSI = 10, 50, and 90. Figure 9 shows that the greater σ_ci/γB for a given value of σ_ci/γB, the greater the value of ξ. However, it should be noted that the smaller GSI, the significant the difference in the value of ξ according to σ_ci/γB, but the greater GSI, the smaller the difference in the value of ξ. This indicated that for the case of GSI = 90, the unit weight of rock mass has little effect on the value of ξ of multiple footings. In addition, as GSI decreases, the efficiency factor of σ_ci/γB except 125 decreases. For the case of σ_ci/γB = 125, the value of ξ increases slightly when GSI increases from 10 to 50, but when it is greater than 50, the value of ξ decreases.

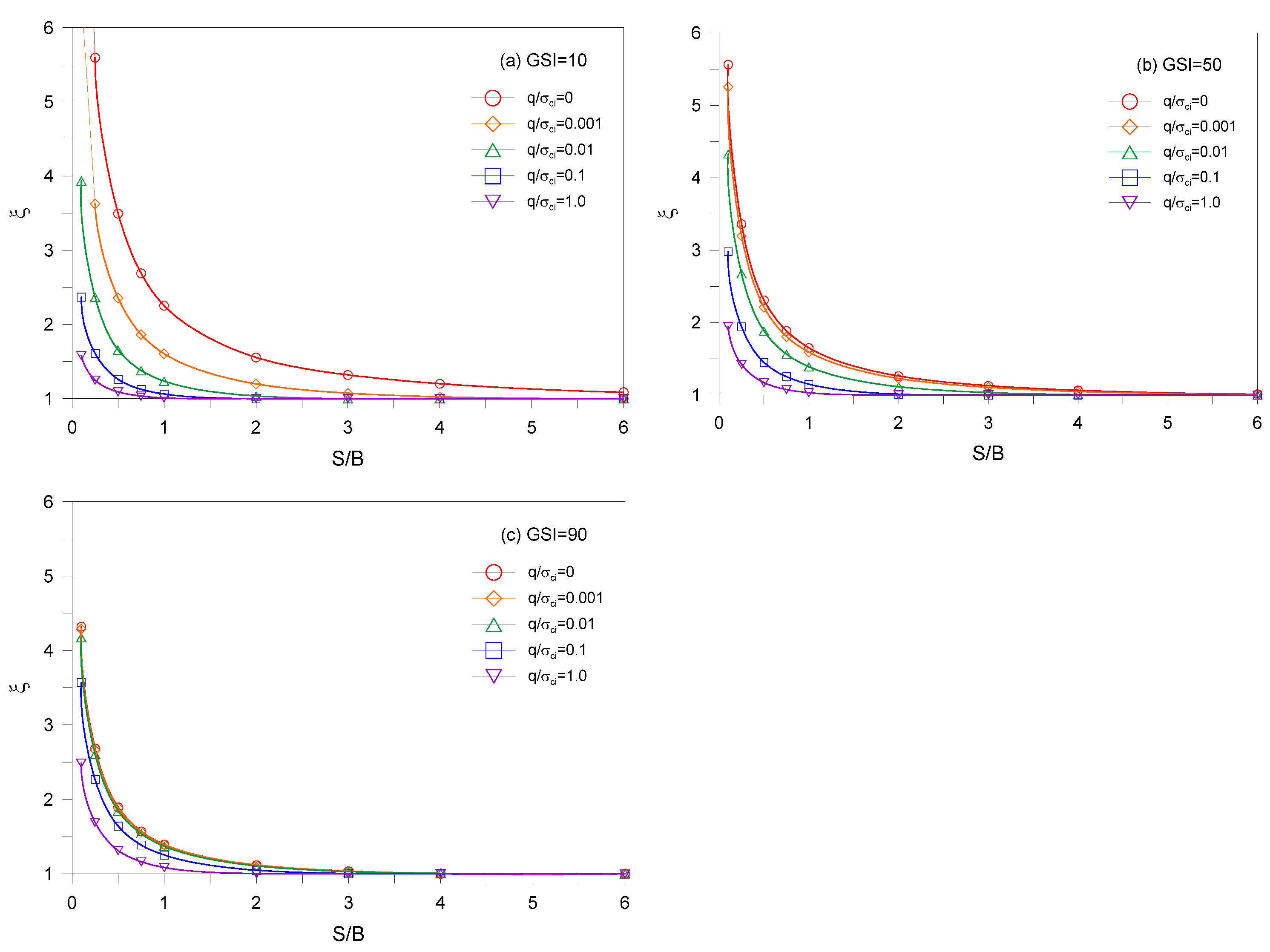
The variation of the efficiency factor ξ for different combinations of S/B and q/σ_ci is shown in Figure 10 for the case of m_i = 10, D = 0, σ_ci/γB = infinite and GSI = 10, 50, and 90. Figure 10 shows that decrease in the value of ξ when surcharges are applied. Given that the value of ξ resulting from the applied of surcharge is smaller than the value of ξ in the without of surcharge, this implies that surcharge reduces the value of ξ. As the GSI increases, the ξ values continues to decrease for q/σ_ci = 0 and 0.001, while for q/σ_ci = 0.1 and 1.0, the ξ values increases. For the case of q/σ_ci = 0.01, the ξ values varies slightly with the change in GSI. It should also be noted that increasing GSI from 10 to 50 increases ξ values, however decreasing ξ value from 50 to 90.

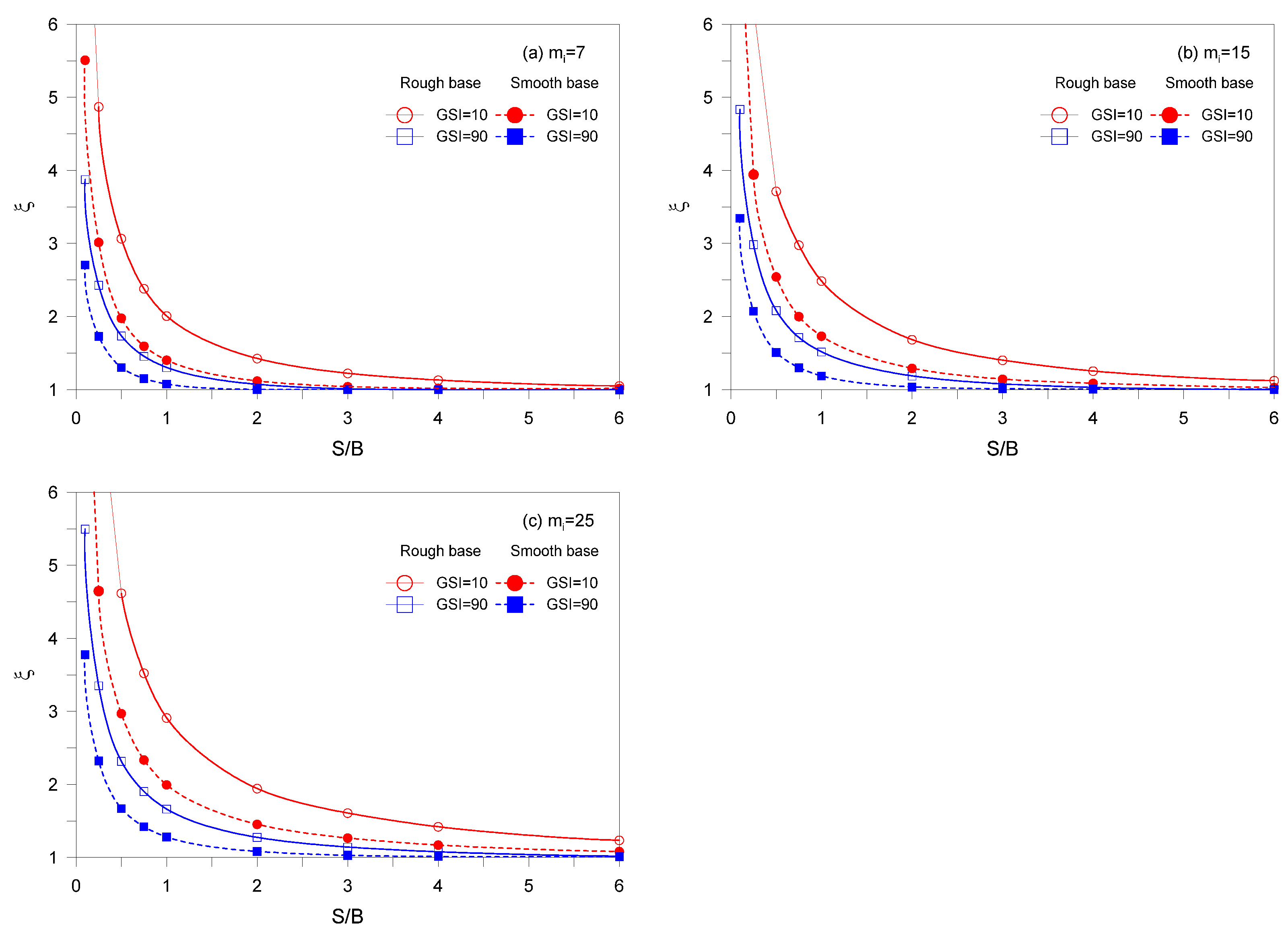
The variation of the efficiency factor ξ for different combinations of S/B and GSI = 10, 90 for smooth and rough bases footings are shown in Figure 11 for the case of D = 0, σ_ci/γB = infinite, q/σ_ci = 0 and m_i = 7, 15, and 25. Figure 11 shows that rough bases always maintain ξ value greater than smooth bases. It can be seen that the varies in ξ values due to roughness becomes smaller as GSI increases and vice versa increases as m_i increases. However, it should be noted that m_i has a small effect on the ξ value and that GSI is significant.

Figure 12 shows the failure mechanism of the smooth and rough base multiple footings on the rock masses for different adjacent spacing ratios S/B with GSI = 30, m_i = 10, D = 0, σ_ci/γB = infinite and q/σ_ci = 0. Figure 12 shows that unlike isolated footings, the failure mechanism of multiple footings does not lead to surface and is formed below the surface. As the S/B of multiple footing increases, the failure mechanism of multiple footings changes close to failure mechanism of independent foundations. In the case of S/B = 2, adjacent effects are expressed between the spacing of multiple footing and failure mechanisms are formed at relatively low depths. These effects can be seen to become decreases as S/B increases. For rough bases, failure mechanism of multiple footing is formed in the external rather than center of the footing. On the other hand, for smooth bases, it should be noted that failure mechanism of multiple footings is formed simultaneously at center of footing and at the external.

6. Conclusions

Advances in the use of numerical methods in rock engineering have been achieved, especially for continuum approaches for comprehensive constitutive models for rock fracture system. By means of the finite element limit analysis, the vertical bearing capacity of equally spaced multiple strip footings resting on rock mass is investigated. The rock mass is modeled by the modified Hoek–Brown failure criterion. Consideration is given to the effects of footing interference, Hoek–Brown parameters, surface surcharge, and footing roughness. The results are presented as efficiency factor ξ in graphical form and failure mechanisms of multiple strip footings are discussed. The following conclusions can be drawn from the present study.

As the spacing between the multiple footings decreases, the value of ξ increases continuously and reach infinity at zero spacing. This indicates that the bearing capacity of an interfering footing with a given width is always greater than that of a single isolated footing with the same width. The effect of footings interference is found to be more significant for the lower values of GSI and D and the higher value of m_i and σ_ci/γB. An increase in surface surcharge leads to a decrease in ξ and its trend is predominant for smaller GSI. The value of ξ for rough footings is higher than smooth footings and the effect of the interference on the bearing capacity for rough base is greater than that for smooth base. The maximum spacing for which the nearby footings influence each other is determined and the closed-form expression is proposed. The zone of failure mechanism decreases dramatically for the interfering footings, implying a significant interaction between the adjacent footing and hence an increase in the bearing capacity of individual footings.