Mechanisms to Avoid and Correct Erroneous Kinetochore-Microtubule Attachments
Abstract
:1. Introduction
2. Literature Review Sections
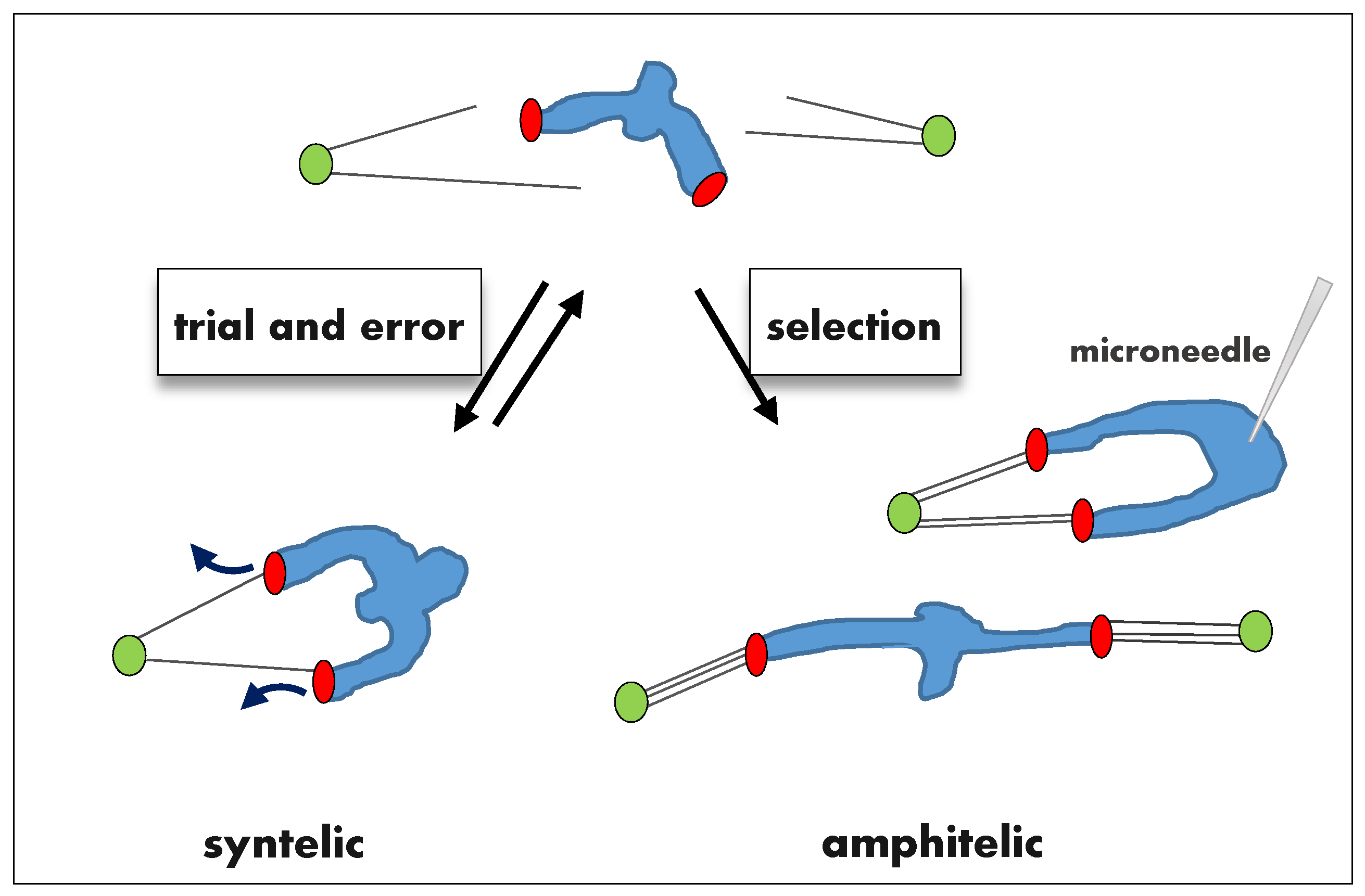
2.1. Error Correction of Syntelic Attachments
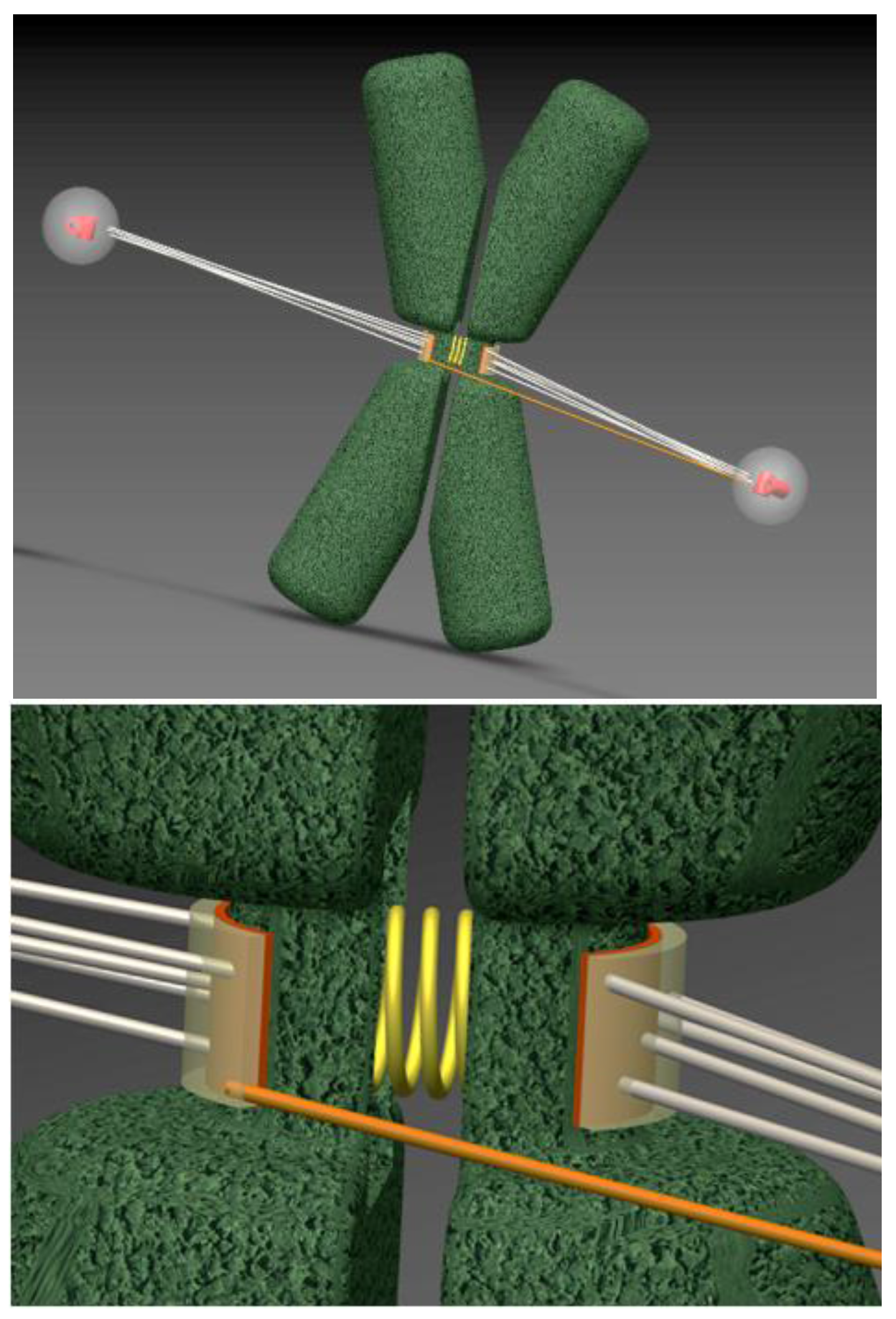
2.2. Error Correction of Merotelic Attachments
2.3. Tension-Independent Error-Correction Mechanism
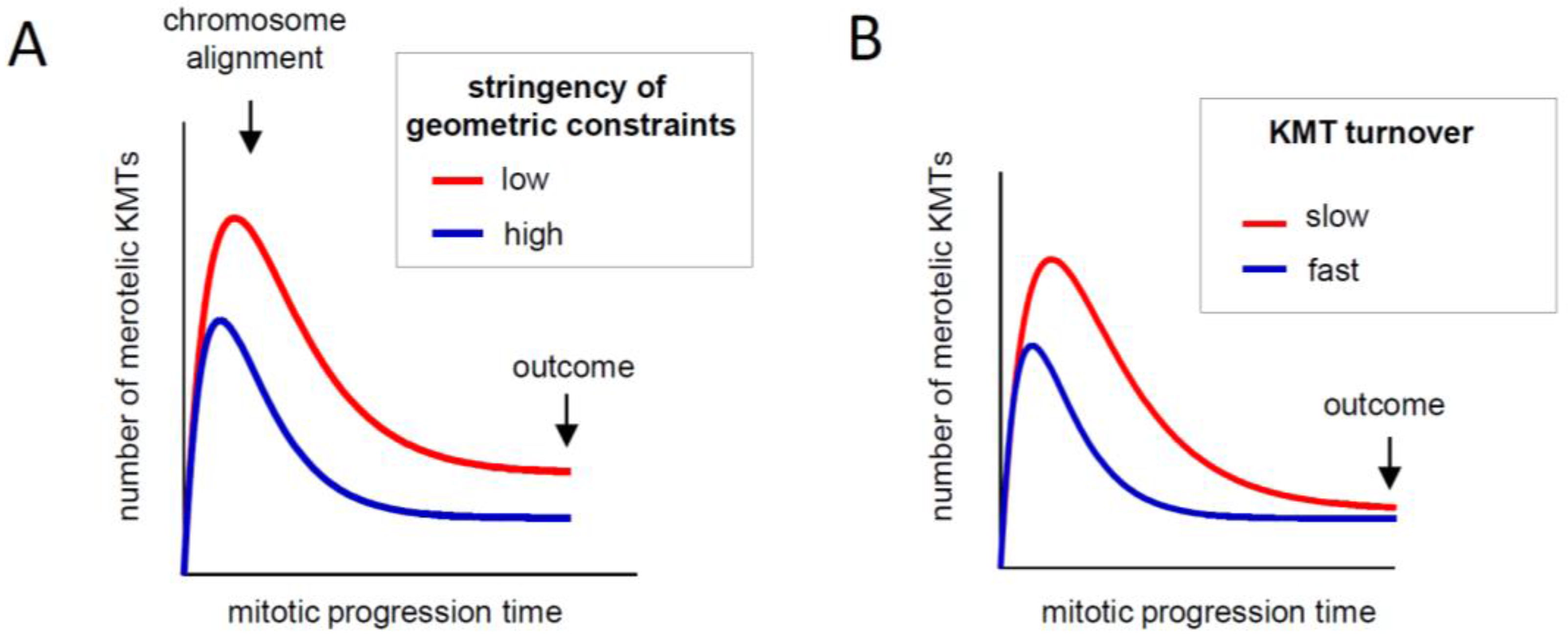
2.3.1. How Strongly Should Kinetochores Shield Themselves from Wrong MTs?
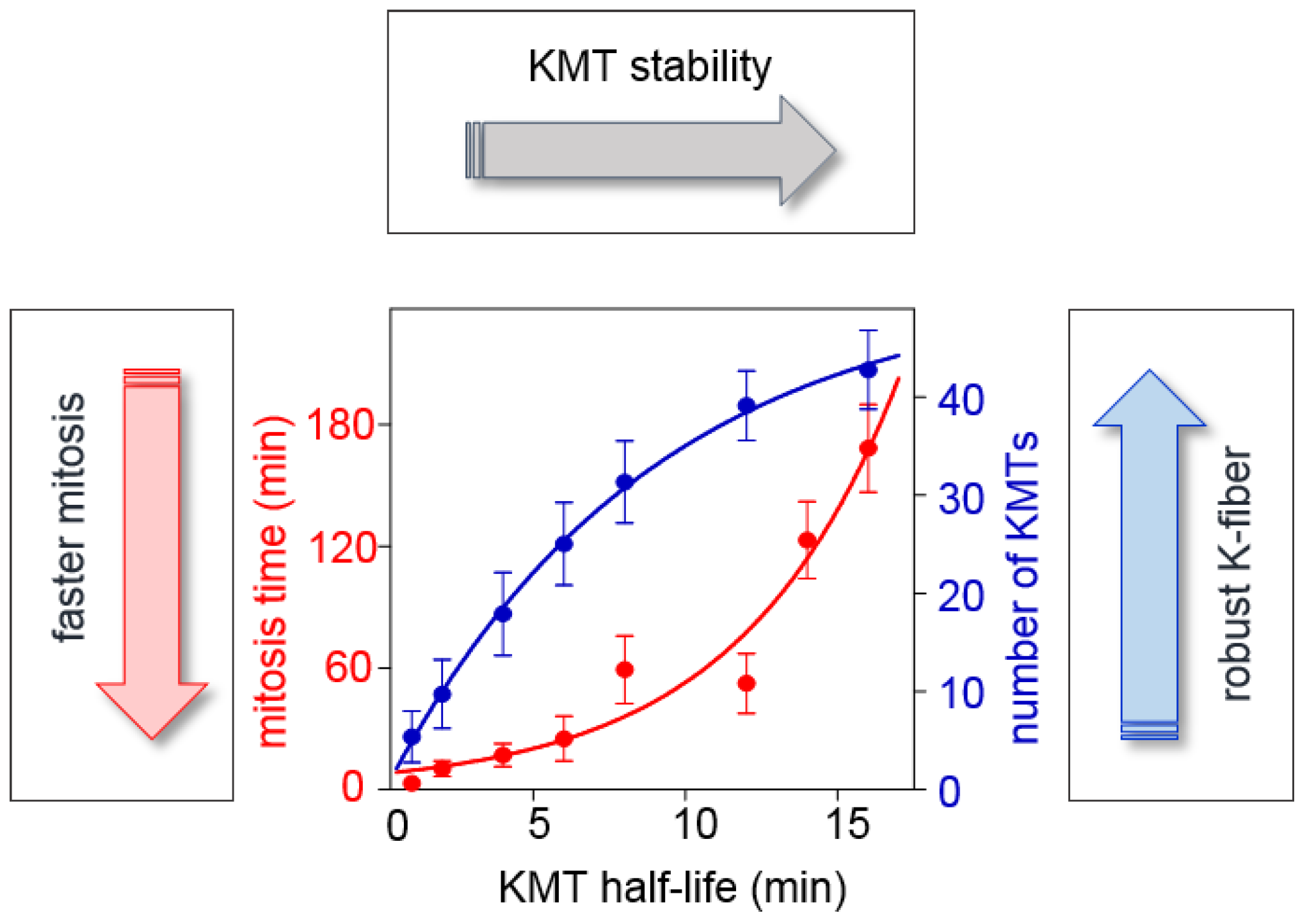
2.3.2. What Determines the Rate of KMT Turnover during Mitosis?
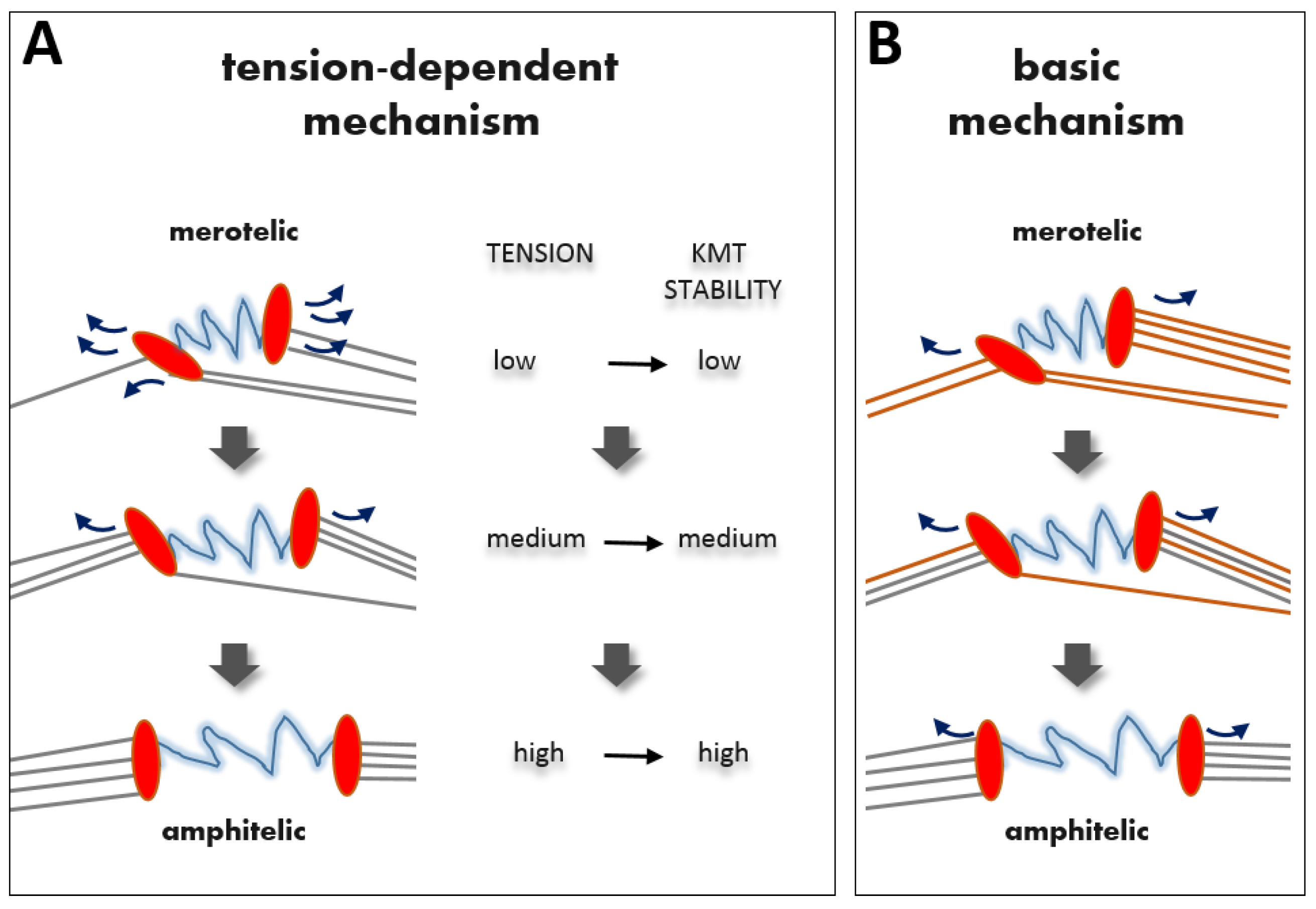
2.4. Molecular Mechanisms of Tension-Dependent Feedback for KMT Stabilization
2.4.1. Direct Regulation of MT Dynamics
2.4.2. Aurora B-Dependent Mechanisms
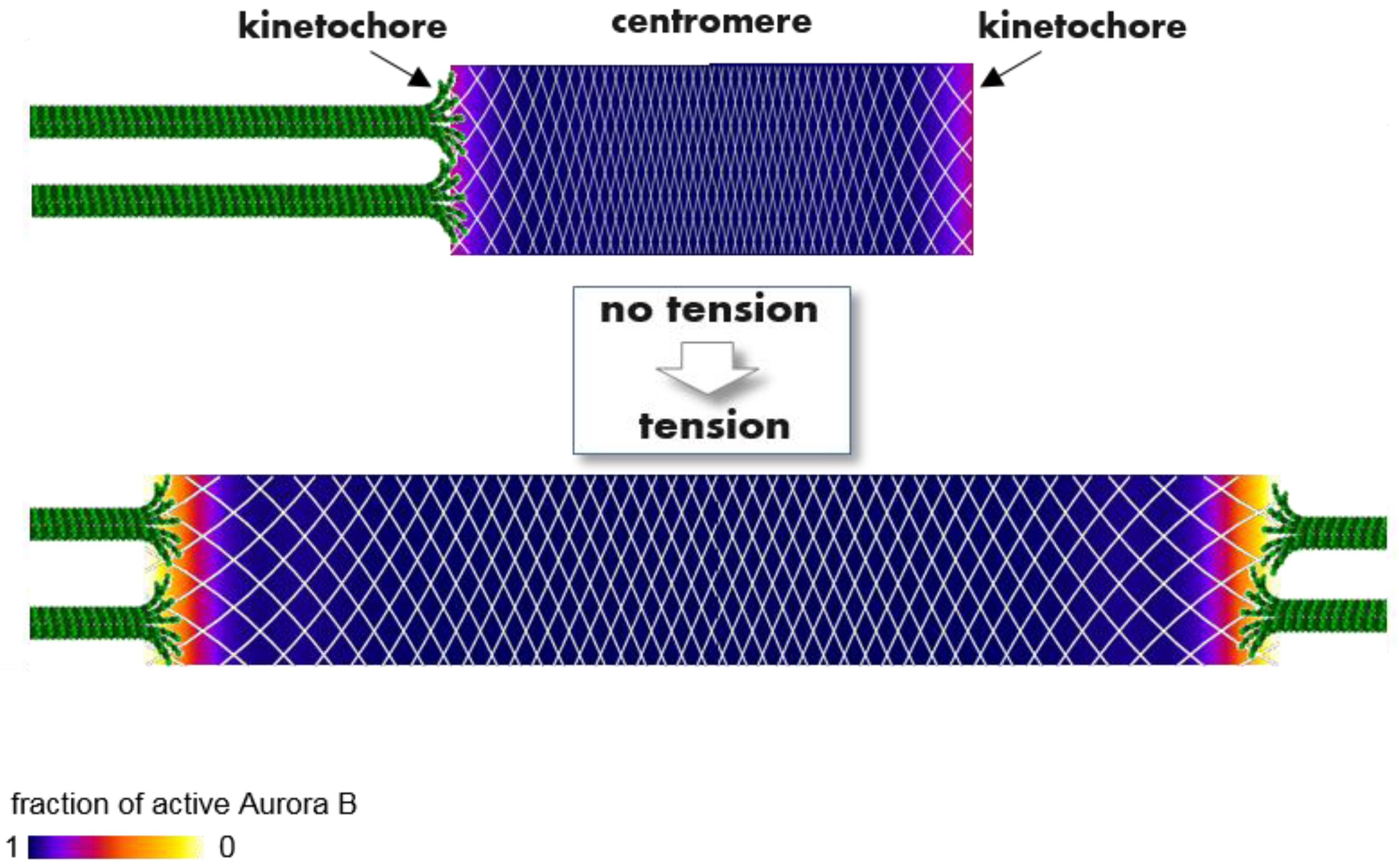
2.4.3. Spatial Separation Model
2.4.4. Alternative Models
2.4.5. Selectivity of Aurora B-Dependent Error-Correction Mechanisms
3. Conclusions
Acknowledgments
Conflicts of Interest
References
- Rieder, C.L.; Salmon, E.D. The vertebrate cell kinetochore and its roles during mitosis. Trends Cell Biol. 1998, 8, 310–318. [Google Scholar] [CrossRef]
- Walczak, C.E.; Cai, S.; Khodjakov, A. Mechanisms of chromosome behaviour during mitosis. Nat. Rev. Mol. Cell Biol. 2010, 11, 91–102. [Google Scholar] [CrossRef] [PubMed]
- Weaver, B.A.; Cleveland, D.W. Does aneuploidy cause cancer? Curr. Opin. Cell. Biol. 2006, 18, 658–667. [Google Scholar] [CrossRef] [PubMed]
- Bakhoum, S.F.; Compton, D.A. Chromosomal instability and cancer: A complex relationship with therapeutic potential. J. Clin. Investig. 2012, 122, 1138–1143. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, J.M.; Cimini, D. Link between aneuploidy and chromosome instability. Int. Rev. Cell Mol. Biol. 2015, 315, 299–317. [Google Scholar] [PubMed]
- Silk, A.D.; Zasadil, L.M.; Holland, A.J.; Vitre, B.; Cleveland, D.W.; Weaver, B.A. Chromosome missegregation rate predicts whether aneuploidy will promote or suppress tumors. Proc. Natl. Acad. Sci. USA 2013, 110, E4134–E4141. [Google Scholar] [CrossRef] [PubMed]
- Nicklas, R.B. How cells get the right chromosomes. Science 1997, 275, 632–637. [Google Scholar] [CrossRef] [PubMed]
- Wendell, K.L.; Wilson, L.; Jordan, M.A. Mitotic block in HeLa cells by vinblastine: Ultrastructural changes in kinetochore-microtubule attachment and in centrosomes. J. Cell Sci. 1993, 104, 261–274. [Google Scholar] [PubMed]
- McEwen, B.F.; Chan, G.K.; Zubrowski, B.; Savoian, M.S.; Sauer, M.T.; Yen, T.J. CENP-E is essential for reliable bioriented spindle attachment, but chromosome alignment can be achieved via redundant mechanisms in mammalian cells. Mol. Biol. Cell 2001, 12, 2776–2789. [Google Scholar] [CrossRef] [PubMed]
- Knouse, K.A.; Wu, J.; Whittaker, C.A.; Amon, A. Single cell sequencing reveals low levels of aneuploidy across mammalian tissues. Proc. Natl. Acad. Sci. USA 2014, 111, 13409–13414. [Google Scholar] [CrossRef] [PubMed]
- Van den Bos, H.; Spierings, D.C.J.; Taudt, A.S.; Bakker, B.; Porubský, D.; Falconer, E.; Novoa, C.; Halsema, N.; Kazemier, H.G.; Hoekstra-Wakker, K.; et al. Single-cell whole genome sequencing reveals no evidence for common aneuploidy in normal and Alzheimer’s disease neurons. Genome Biol. 2016. [Google Scholar] [CrossRef]
- Santaguida, S.; Amon, A. Short- and long-term effects of chromosome mis-segregation and aneuploidy. Nat. Rev. Mol. Cell Biol. 2015, 16, 473–485. [Google Scholar] [CrossRef] [PubMed]
- Thompson, S.L.; Compton, D.A. Examining the link between chromosomal instability and aneuploidy in human cells. J. Cell Biol. 2008, 180, 665–672. [Google Scholar] [CrossRef] [PubMed]
- Nicklas, R.B.; Koch, C.A. Chromosome micromanipulation. 3. Spindle fiber tension and the reorientation of mal-oriented chromosomes. J. Cell Biol. 1969, 43, 40–50. [Google Scholar] [CrossRef] [PubMed]
- Skibbens, R.V.; Salmon, E.D. Micromanipulation of chromosomes in mitotic vertebrate tissue cells: Tension controls the state of kinetochore movement. Exp. Cell Res. 1997, 235, 314–324. [Google Scholar] [CrossRef] [PubMed]
- Cane, S.; Ye, A.A.; Luks-Morgan, S.J.; Maresca, T.J. Elevated polar ejection forces stabilize kinetochore-microtubule attachments. J. Cell Biol. 2013, 200, 203–218. [Google Scholar] [CrossRef] [PubMed]
- Cimini, D. Merotelic kinetochore orientation, aneuploidy, and cancer. Biochim. Biophys. Acta 2008, 1786, 32–40. [Google Scholar] [CrossRef] [PubMed]
- Cimini, D.; Fioravanti, D.; Salmon, E.D.; Degrassi, F. Merotelic kinetochore orientation versus chromosome mono-orientation in the origin of lagging chromosomes in human primary cells. J. Cell Sci. 2002, 115, 507–515. [Google Scholar] [PubMed]
- Bakhoum, S.F.; Compton, D.A. Kinetochores and disease: Keeping microtubule dynamics in check! Curr. Opin. Cell Biol. 2012, 24, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Cimini, D.; Howell, B.; Maddox, P.; Khodjakov, A.; Degrassi, F.; Salmon, E.D. Merotelic kinetochore orientation is a major mechanism of aneuploidy in mitotic mammalian tissue cells. J. Cell Biol. 2001, 153, 517–527. [Google Scholar] [CrossRef] [PubMed]
- Bakhoum, S.F.; Genovese, G.; Compton, D.A. Deviant kinetochore microtubule dynamics underlie chromosomal instability. Curr. Biol. 2009, 19, 1937–1942. [Google Scholar] [CrossRef] [PubMed]
- Bakhoum, S.F.; Silkworth, W.T.; Nardi, I.K.; Nicholson, J.M.; Compton, D.A.; Cimini, D. The mitotic origin of chromosomal instability. Curr. Biol. 2014, 24, R148–R149. [Google Scholar] [CrossRef] [PubMed]
- Zaytsev, A.V.; Grishchuk, E.L. Basic mechanism for biorientation of mitotic chromosomes is provided by the kinetochore geometry and indiscriminate turnover of kinetochore microtubules. Mol. Biol. Cell 2015. [Google Scholar] [CrossRef] [PubMed]
- Cimini, D.; Moree, B.; Canman, J.C.; Salmon, E.D. Merotelic kinetochore orientation occurs frequently during early mitosis in mammalian tissue cells and error correction is achieved by two different mechanisms. J. Cell Sci. 2003, 116, 4213–4225. [Google Scholar] [CrossRef] [PubMed]
- Pereira, A.J.; Maiato, H. Maturation of the kinetochore-microtubule interface and the meaning of metaphase. Chromosome Res. 2012, 20, 563–577. [Google Scholar] [CrossRef] [PubMed]
- Civelekoglu-Scholey, G.; Scholey, J.M. Mitotic force generators and chromosome segregation. Cell. Mol. Life Sci. 2010, 67, 2231–2250. [Google Scholar] [CrossRef] [PubMed]
- Stumpff, J.; Wagenbach, M.; Franck, A.; Asbury, C.L.; Wordeman, L. Kif18A and chromokinesins confine centromere movements via microtubule growth suppression and spatial control of kinetochore tension. Dev. Cell 2012, 22, 1017–1029. [Google Scholar] [CrossRef] [PubMed]
- Cimini, D.; Cameron, L.A.; Salmon, E.D. Anaphase spindle mechanics prevent mis-segregation of merotelically oriented chromosomes. Curr. Biol. 2004, 14, 2149–2155. [Google Scholar] [CrossRef] [PubMed]
- Thompson, S.L.; Compton, D.A. Chromosome missegregation in human cells arises through specific types of kinetochore-microtubule attachment errors. Proc. Natl. Acad. Sci. USA 2011, 108, 17974–17978. [Google Scholar] [CrossRef] [PubMed]
- Leibowitz, M.L.; Zhang, C.-Z.; Pellman, D. Chromothripsis: A New Mechanism for Rapid Karyotype Evolution. Annu. Rev. Genet. 2015, 49, 183–211. [Google Scholar] [CrossRef] [PubMed]
- Hinchcliffe, E.H.; Day, C.A.; Karanjeet, K.B.; Fadness, S.; Langfald, A.; Vaughan, K.T.; Dong, Z. Chromosome missegregation during anaphase triggers p53 cell cycle arrest through histone H3.3 Ser31 phosphorylation. Nat. Cell Biol. 2016, 18, 668–675. [Google Scholar] [CrossRef] [PubMed]
- Journey, L.; Whaley, A. Kinetochore Ultrastructure in Vincristine-Treated Mammalian Cells. J. Cell Sci. 1970, 7, 49–54. [Google Scholar]
- Östergren, G. The mechanism of co-orientation in bivalents and multivalents. Hereditas 1951, 37, 85–156. [Google Scholar] [CrossRef]
- Nicklas, R.B.; Ward, S.C. Elements of error correction in mitosis: Microtubule capture, release, and tension. J. Cell Biol. 1994, 126, 1241–1253. [Google Scholar] [CrossRef] [PubMed]
- Cimini, D.; Wan, X.; Hirel, C.B.; Salmon, E.D. Aurora kinase promotes turnover of kinetochore microtubules to reduce chromosome segregation errors. Curr. Biol. 2006, 16, 1711–1718. [Google Scholar] [CrossRef] [PubMed]
- Kabeche, L.; Compton, D.A. Cyclin A regulates kinetochore microtubules to promote faithful chromosome segregation. Nature 2013, 502, 110–113. [Google Scholar] [CrossRef] [PubMed]
- Zhai, Y.; Kronebusch, P.J.; Borisy, G.G. Kinetochore microtubule dynamics and the metaphase-anaphase transition. J. Cell Biol. 1995, 131, 721–734. [Google Scholar] [CrossRef] [PubMed]
- Kapoor, T.M.; Lampson, M.A.; Hergert, P.; Cameron, L.; Cimini, D.; Salmon, E.D.; McEwen, B.F.; Khodjakov, A. Chromosomes can congress to the metaphase plate before biorientation. Science 2006, 311, 388–391. [Google Scholar] [CrossRef] [PubMed]
- Bakhoum, S.F.; Thompson, S.L.; Manning, A.L.; Compton, D.A. Genome stability is ensured by temporal control of kinetochore-microtubule dynamics. Nat. Cell Biol. 2009, 11, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Loncarek, J.; Kisurina-Evgenieva, O.; Vinogradova, T.; Hergert, P.; La Terra, S.; Kapoor, T.M.; Khodjakov, A. The centromere geometry essential for keeping mitosis error free is controlled by spindle forces. Nature 2007, 450, 745–749. [Google Scholar] [CrossRef] [PubMed]
- Holy, T.E.; Leibler, S. Dynamic instability of microtubules as an efficient way to search in space. Proc. Natl. Acad. Sci. USA 1994, 91, 5682–5685. [Google Scholar] [CrossRef] [PubMed]
- Wollman, R.; Cytrynbaum, E.N.; Jones, J.T.; Meyer, T.; Scholey, J.M.; Mogilner, A. Efficient chromosome capture requires a bias in the “search-and-capture” process during mitotic-spindle assembly. Curr. Biol. 2005, 15, 828–832. [Google Scholar] [CrossRef] [PubMed]
- Paul, R.; Wollman, R.; Silkworth, W.T.; Nardi, I.K.; Cimini, D.; Mogilner, A. Computer simulations predict that chromosome movements and rotations accelerate mitotic spindle assembly without compromising accuracy. Proc. Natl. Acad. Sci. USA 2009, 106, 15708–15713. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, D.B.; Pearson, C.G.; Yen, T.J.; Howell, B.J.; Salmon, E.D. Microtubule-dependent changes in assembly of microtubule motor proteins and mitotic spindle checkpoint proteins at PtK1 kinetochores. Mol. Biol. Cell 2001, 12, 1995–2009. [Google Scholar] [CrossRef] [PubMed]
- Magidson, V.; Paul, R.; Yang, N.; Ault, J.G.; O’Connell, C.B.; Tikhonenko, I.; McEwen, B.F.; Mogilner, A.; Khodjakov, A. Adaptive changes in the kinetochore architecture facilitate proper spindle assembly. Nat. Cell Biol. 2015, 17, 1134–1144. [Google Scholar] [CrossRef] [PubMed]
- Wynne, D.J.; Funabiki, H. Kinetochore function is controlled by a phospho-dependent coexpansion of inner and outer components. J. Cell Biol. 2015, 210, 899–916. [Google Scholar] [CrossRef] [PubMed]
- Godek, K.M.; Kabeche, L.; Compton, D.A. Regulation of kinetochore-microtubule attachments through homeostatic control during mitosis. Nat. Rev. Mol. Cell Biol. 2014, 16, 57–64. [Google Scholar] [CrossRef] [PubMed]
- Grishchuk, E.L.; Molodtsov, M.I.; Ataullakhanov, F.I.; McIntosh, J.R. Force production by disassembling microtubules. Nature 2005, 438, 384–388. [Google Scholar] [CrossRef] [PubMed]
- Franck, A.D.; Powers, A.F.; Gestaut, D.R.; Gonen, T.; Davis, T.N.; Asbury, C.L. Tension applied through the Dam1 complex promotes microtubule elongation providing a direct mechanism for length control in mitosis. Nat. Cell Biol. 2007, 9, 832–837. [Google Scholar] [CrossRef] [PubMed]
- Akiyoshi, B.; Sarangapani, K.K.; Powers, A.F.; Nelson, C.R.; Reichow, S.L.; Arellano-Santoyo, H.; Gonen, T.; Ranish, J.A.; Asbury, C.L.; Biggins, S. Tension directly stabilizes reconstituted kinetochore-microtubule attachments. Nature 2010, 468, 576–579. [Google Scholar] [CrossRef] [PubMed]
- Armond, J.W.; Vladimirou, E.; Erent, M.; McAinsh, A.D.; Burroughs, N.J. Probing microtubule polymerisation state at single kinetochores during metaphase chromosome motion. J. Cell Sci. 2015, 3, 1991–2001. [Google Scholar] [CrossRef] [PubMed]
- Tirnauer, J.S.; Canman, J.C.; Salmon, E.D.; Mitchison, T.J. EB1 targets to kinetochores with attached, polymerizing microtubules. Mol. Biol. Cell 2002, 13, 4308–4316. [Google Scholar] [CrossRef] [PubMed]
- Biggins, S.; Severin, F.F.; Bhalla, N.; Sassoon, I.; Hyman, A.A.; Murray, A.W. The conserved protein kinase Ipl1 regulates microtubule binding to kinetochores in budding yeast. Genes Dev. 1999, 13, 532–544. [Google Scholar] [CrossRef] [PubMed]
- Cheeseman, I.M.; Anderson, S.; Jwa, M.; Green, E.M.; Kang, J.; Yates, J.R., 3rd; Chan, C.S.; Drubin, D.G.; Barnes, G. Phospho-regulation of kinetochore-microtubule attachments by the Aurora kinase Ipl1p. Cell 2002, 111, 163–172. [Google Scholar] [CrossRef]
- Francisco, L.; Wang, W.; Chan, C.S. Type 1 protein phosphatase acts in opposition to IpL1 protein kinase in regulating yeast chromosome segregation. Mol. Cell. Biol. 1994, 14, 4731–4740. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.U.; Rachidi, N.; Janke, C.; Pereira, G.; Galova, M.; Schiebel, E.; Stark, M.J.; Nasmyth, K. Evidence that the Ipl1-Sli15 (Aurora kinase-INCENP) complex promotes chromosome bi-orientation by altering kinetochore-spindle pole connections. Cell 2002, 108, 317–329. [Google Scholar] [CrossRef]
- Hauf, S.; Cole, R.W.; LaTerra, S.; Zimmer, C.; Schnapp, G.; Walter, R.; Heckel, A.; van Meel, J.; Rieder, C.L.; Peters, J.M. The small molecule Hesperadin reveals a role for Aurora B in correcting kinetochore-microtubule attachment and in maintaining the spindle assembly checkpoint. J. Cell Biol. 2003, 161, 281–294. [Google Scholar] [CrossRef] [PubMed]
- Ditchfield, C.; Johnson, V.L.; Tighe, A.; Ellston, R.; Haworth, C.; Johnson, T.; Mortlock, A.; Keen, N.; Taylor, S.S. Aurora B couples chromosome alignment with anaphase by targeting BubR1, Mad2, and Cenp-E to kinetochores. J. Cell Biol. 2003, 161, 267–280. [Google Scholar] [CrossRef] [PubMed]
- Lampson, M.A.; Renduchitala, K.; Khodjakov, A.; Kapoor, T.M. Correcting improper chromosome-spindle attachments during cell division. Nat. Cell Biol. 2004, 6, 232–237. [Google Scholar] [CrossRef] [PubMed]
- Kallio, M.J.; McCleland, M.L.; Stukenberg, P.T.; Gorbsky, G.J. Inhibition of aurora B kinase blocks chromosome segregation, overrides the spindle checkpoint, and perturbs microtubule dynamics in mitosis. Curr. Biol. 2002, 12, 900–905. [Google Scholar] [CrossRef]
- Chan, C.S.; Botstein, D. Isolation and characterization of chromosome-gain and increase-in-ploidy mutants in yeast. Genetics 1993, 135, 677–691. [Google Scholar] [PubMed]
- Liu, D.; Vader, G.; Vromans, M.J.M.; Lampson, M.A.; Lens, S.M.A. Sensing chromosome bi-orientation by spatial separation of aurora B kinase from kinetochore substrates. Science 2009, 323, 1350–1353. [Google Scholar] [CrossRef] [PubMed]
- Welburn, J.P.; Vleugel, M.; Liu, D.; Yates, J.R., 3rd; Lampson, M.A.; Fukagawa, T.; Cheeseman, I.M. Aurora B phosphorylates spatially distinct targets to differentially regulate the kinetochore-microtubule interface. Mol. Cell 2010, 38, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Keating, P.; Rachidi, N.; Tanaka, T.U.; Stark, M.J. Ipl1-dependent phosphorylation of Dam1 is reduced by tension applied on kinetochores. J. Cell Sci. 2009, 122, 4375–4382. [Google Scholar] [CrossRef] [PubMed]
- DeLuca, K.F.; Lens, S.M.; DeLuca, J.G. Temporal changes in Hec1 phosphorylation control kinetochore-microtubule attachment stability during mitosis. J. Cell Sci. 2011, 124, 622–634. [Google Scholar] [CrossRef] [PubMed]
- Salimian, K.J.; Ballister, E.R.; Smoak, E.M.; Wood, S.; Panchenko, T.; Lampson, M.A.; Black, B.E. Feedback control in sensing chromosome biorientation by the Aurora B kinase. Curr. Biol. 2011, 21, 1158–1165. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; Badger, B.L.; Wan, X.; DeLuca, J.G.; Salmon, E.D. The Architecture of CCAN Proteins Creates a Structural Integrity to Resist Spindle Forces and Achieve Proper Intrakinetochore Stretch. Dev. Cell 2014, 30, 717–730. [Google Scholar] [CrossRef] [PubMed]
- Krenn, V.; Musacchio, A. The Aurora B Kinase in Chromosome Bi-Orientation and Spindle Checkpoint Signaling. Front. Oncol. 2015, 5, 225. [Google Scholar] [CrossRef] [PubMed]
- Sarangapani, K.K.; Asbury, C.L. Catch and release: How do kinetochores hook the right microtubules during mitosis? Trends Genet. 2014, 30, 150–159. [Google Scholar] [CrossRef] [PubMed]
- Cheeseman, I.M.; Chappie, J.S.; Wilson-Kubalek, E.M.; Desai, A. The conserved KMN network constitutes the core microtubule-binding site of the kinetochore. Cell 2006, 127, 983–997. [Google Scholar] [CrossRef] [PubMed]
- Gestaut, D.R.; Graczyk, B.; Cooper, J.; Widlund, P.O.; Zelter, A.; Wordeman, L.; Asbury, C.L.; Davis, T.N. Phosphoregulation and depolymerization-driven movement of the Dam1 complex do not require ring formation. Nat. Cell Biol. 2008, 10, 407–414. [Google Scholar] [CrossRef] [PubMed]
- Sarangapani, K.K.; Akiyoshi, B.; Duggan, N.M.; Biggins, S.; Asbury, C.L. Phosphoregulation promotes release of kinetochores from dynamic microtubules via multiple mechanisms. Proc. Natl. Acad. Sci. USA 2013, 110, 7282–7287. [Google Scholar] [CrossRef] [PubMed]
- Umbreit, N.T.; Gestaut, D.R.; Tien, J.F.; Vollmar, B.S.; Gonen, T.; Asbury, C.L.; Davis, T.N. The Ndc80 kinetochore complex directly modulates microtubule dynamics. Proc. Natl. Acad. Sci. USA 2012, 109, 16113–16118. [Google Scholar] [CrossRef] [PubMed]
- Zaytsev, A.V.; Sundin, L.J.R.; DeLuca, K.F.; Grishchuk, E.L.; DeLuca, J.G. Accurate phosphoregulation of kinetochore-microtubule affinity requires unconstrained molecular interactions. J. Cell Biol. 2014, 206, 45–59. [Google Scholar] [CrossRef] [PubMed]
- Ye, A.A.; Deretic, J.; Hoel, C.M.; Hinman, A.W.; Cimini, D.; Welburn, J.P.; Maresca, T.J. Aurora A Kinase Contributes to a Pole-Based Error Correction Pathway. Curr. Biol. 2015, 25, 1842–1851. [Google Scholar] [CrossRef] [PubMed]
- Chmátal, L.; Yang, K.; Schultz, R.M.; Lampson, M.A. Spatial Regulation of Kinetochore Microtubule Attachments by Destabilization at Spindle Poles in Meiosis I. Curr. Biol. 2015, 25, 1835–1841. [Google Scholar] [CrossRef] [PubMed]
- Kawashima, S.A.; Yamagishi, Y.; Honda, T.; Ishiguro, K.; Watanabe, Y. Phosphorylation of H2A by Bub1 prevents chromosomal instability through localizing shugoshin. Science 2010, 327, 172–177. [Google Scholar] [CrossRef] [PubMed]
- Kelly, A.E.; Ghenoiu, C.; Xue, J.Z.; Zierhut, C.; Kimura, H.; Funabiki, H. Survivin Reads Phosphorylated Histone H3 Threonine 3 to Activate the Mitotic Kinase Aurora B. Science 2010. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Dai, J.; Daum, J.R.; Niedzialkowska, E.; Banerjee, B.; Stukenberg, P.T.; Gorbsky, G.J.; Higgins, J.M. Histone H3 Thr-3 phosphorylation by Haspin positions Aurora B at centromeres in mitosis. Science 2010, 330, 231–235. [Google Scholar] [CrossRef] [PubMed]
- Yamagishi, Y.; Honda, T.; Tanno, Y.; Watanabe, Y. Two histone marks establish the inner centromere and chromosome bi-orientation. Science 2010, 330, 239–243. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Ulyanova, N.P.; Daum, J.R.; Patnaik, D.; Kateneva, A.V.; Gorbsky, G.J.; Higgins, J.M. Haspin inhibitors reveal centromeric functions of Aurora B in chromosome segregation. J. Cell Biol. 2012, 199, 251–268. [Google Scholar] [CrossRef] [PubMed]
- Yue, Z.; Carvalho, A.; Xu, Z.; Yuan, X.; Cardinale, S.; Ribeiro, S.; Lai, F.; Ogawa, H.; Gudmundsdottir, E.; Gassmann, R.; et al. Deconstructing Survivin: Comprehensive genetic analysis of Survivin function by conditional knockout in a vertebrate cell line. J. Cell Biol. 2008, 183, 279–296. [Google Scholar] [CrossRef] [PubMed]
- Tsukahara, T.; Tanno, Y.; Watanabe, Y. Phosphorylation of the CPC by Cdk1 promotes chromosome bi-orientation. Nature 2010. [Google Scholar] [CrossRef] [PubMed]
- Bishop, J.D.; Schumacher, J.M. Phosphorylation of the carboxyl terminus of inner centromere protein (INCENP) by the Aurora B Kinase stimulates Aurora B kinase activity. J. Biol. Chem. 2002, 277, 27577–27580. [Google Scholar] [CrossRef] [PubMed]
- Honda, R.; Korner, R.; Nigg, E.A. Exploring the functional interactions between Aurora B, INCENP, and survivin in mitosis. Mol. Biol. Cell 2003, 14, 3325–3341. [Google Scholar] [CrossRef] [PubMed]
- Yasui, Y.; Urano, T.; Kawajiri, A.; Nagata, K.; Tatsuka, M.; Saya, H.; Furukawa, K.; Takahashi, T.; Izawa, I.; Inagaki, M. Autophosphorylation of a newly identified site of Aurora-B is indispensable for cytokinesis. J. Biol. Chem. 2004, 279, 12997–13003. [Google Scholar] [CrossRef] [PubMed]
- Sessa, F.; Mapelli, M.; Ciferri, C.; Tarricone, C.; Areces, L.B.; Schneider, T.R.; Stukenberg, P.T.; Musacchio, A. Mechanism of Aurora B activation by INCENP and inhibition by hesperadin. Mol. Cell 2005, 18, 379–391. [Google Scholar] [CrossRef] [PubMed]
- Kelly, A.E.; Sampath, S.C.; Maniar, T.A.; Woo, E.M.; Chait, B.T.; Funabiki, H. Chromosomal enrichment and activation of the aurora B pathway are coupled to spatially regulate spindle assembly. Dev. Cell 2007, 12, 31–43. [Google Scholar] [CrossRef] [PubMed]
- Zaytsev, A.V.; Segura-Pena, D.; Godzi, M.; Calderon, A.; Ballister, E.R.; Stamatov, R.; Mayo, A.M.; Peterson, L.; Black, B.E.; Ataullakhanov, F.I.; et al. Bistability of a coupled aurora B kinase-phosphatase system in cell division. eLife 2016, 5, e10644. [Google Scholar] [CrossRef] [PubMed]
- Campbell, C.S.; Desai, A. Tension sensing by Aurora B kinase is independent of survivin-based centromere localization. Nature 2013, 497, 118–121. [Google Scholar] [CrossRef] [PubMed]
- Samejima, K.; Platani, M.; Wolny, M.; Ogawa, H.; Vargiu, G.; Knight, P.J.; Peckham, M.; Earnshaw, W.C. The inner centromere protein (INCENP) coil is a single α-helix (SAH) domain that binds directly to microtubules and is important for chromosome passenger complex (CPC) localization and function in mitosis. J. Biol. Chem. 2015, 290, 21460–21472. [Google Scholar] [CrossRef] [PubMed]
- Uchida, K.S.K.; Takagaki, K.; Kumada, K.; Hirayama, Y.; Noda, T.; Hirota, T. Kinetochore stretching inactivates the spindle assembly checkpoint. J. Cell Biol. 2009, 184, 383–390. [Google Scholar] [CrossRef] [PubMed]
- Dumont, S.; Salmon, E.D.; Mitchison, T.J. Deformations within moving kinetochores reveal different sites of active and passive force generation. Science 2012, 337, 355–358. [Google Scholar] [CrossRef] [PubMed]
- Khodjakov, A.; Pines, J. Centromere tension: A divisive issue. Nat. Cell Biol. 2010, 12, 919–923. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Vleugel, M.; Backer, C.B.; Hori, T.; Fukagawa, T.; Cheeseman, I.M.; Lampson, M.A. Regulated targeting of protein phosphatase 1 to the outer kinetochore by KNL1 opposes Aurora B kinase. J. Cell Biol. 2010, 188, 809–820. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, J.S.; Cross, F.R.; Funabiki, H. KNL1/Spc105 recruits PP1 to silence the spindle assembly checkpoint. Curr. Biol. 2011, 21, 942–947. [Google Scholar] [CrossRef] [PubMed]
- Gregan, J.; Polakova, S.; Zhang, L.; Tolić-Nørrelykke, I.M.; Cimini, D. Merotelic kinetochore attachment: Causes and effects. Trends Cell Biol. 2011, 21, 374–381. [Google Scholar] [CrossRef] [PubMed]
- Kalantzaki, M.; Kitamura, E.; Zhang, T.; Mino, A.; Novák, B.; Tanaka, T.U. Kinetochore-microtubule error correction is driven by differentially regulated interaction modes. Nat. Cell Biol. 2015. [Google Scholar] [CrossRef]
- Pearson, C.G.; Yeh, E.; Gardner, M.; Odde, D.; Salmon, E.D.; Bloom, K. Stable kinetochore-microtubule attachment constrains centromere positioning in metaphase. Curr. Biol. 2004, 14, 1962–1967. [Google Scholar] [CrossRef] [PubMed]
- McIntosh, J.R.; Hering, G.E. Spindle fiber action and chromosome movement. Annu. Rev. Cell Biol. 1991, 7, 403–426. [Google Scholar] [CrossRef] [PubMed]
- Kline-Smith, S.L.; Khodjakov, A.; Hergert, P.; Walczak, C.E. Depletion of centromeric MCAK leads to chromosome congression and segregation defects due to improper kinetochore attachments. Mol. Biol. Cell 2004, 15, 1146–1159. [Google Scholar] [CrossRef] [PubMed]
- Tanno, Y.; Susumu, H.; Kawamura, M.; Sugimura, H.; Honda, T.; Watanabe, Y. The inner centromere-shugoshin network prevents chromosomal instability. Science 2015, 349, 1237–1240. [Google Scholar] [CrossRef] [PubMed]
- Knowlton, A.L.; Lan, W.; Stukenberg, P.T. Aurora B is enriched at merotelic attachment sites, where it regulates MCAK. Curr. Biol. 2006, 16, 1705–1710. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lampson, M.A.; Grishchuk, E.L. Mechanisms to Avoid and Correct Erroneous Kinetochore-Microtubule Attachments. Biology 2017, 6, 1. https://doi.org/10.3390/biology6010001
Lampson MA, Grishchuk EL. Mechanisms to Avoid and Correct Erroneous Kinetochore-Microtubule Attachments. Biology. 2017; 6(1):1. https://doi.org/10.3390/biology6010001
Chicago/Turabian StyleLampson, Michael A., and Ekaterina L. Grishchuk. 2017. "Mechanisms to Avoid and Correct Erroneous Kinetochore-Microtubule Attachments" Biology 6, no. 1: 1. https://doi.org/10.3390/biology6010001
APA StyleLampson, M. A., & Grishchuk, E. L. (2017). Mechanisms to Avoid and Correct Erroneous Kinetochore-Microtubule Attachments. Biology, 6(1), 1. https://doi.org/10.3390/biology6010001





