Algorithmic Perspectives of Network Transitive Reduction Problems and their Applications to Synthesis and Analysis of Biological Networks
Abstract
:1. Introduction
- Problem name: Minimum equivalent digraph (Min-Ed)
- Input: a directed graph (digraph) G = (V, E).
- Definition: for a digraph (V, E) the transitive closure of E is the relation
on V × V defined as
- Valid solution: A ⊆ E such that
is equal to
.
- Objective: minimize |A|.

1.1. Three Extensions of the Basic Version

1.1.1. Min-Ed and Max-Ed with Critical Edges
1.1.2. Weighted Version of Min-Ed or Max-Ed
1.1.3. Binary Transitive Reduction (Btr)
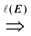 = {(ui, uj, q):∃ path P using edges in E from ui to uj and ℓ(P) = q}. Then, A is a binary transitive reduction of E with a required subset D if D ⊆ A ⊆ E and
= {(ui, uj, q):∃ path P using edges in E from ui to uj and ℓ(P) = q}. Then, A is a binary transitive reduction of E with a required subset D if D ⊆ A ⊆ E and 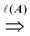 =
= 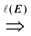 . Obviously, the basic version with critical edges is a special case of Btr when every edge label is 1. There are two (maximization and minimization) objective functions corresponding to the two generalizations of the basic version Min-Ed and Max-Ed; they will be denoted by Min-Btr and Max-Btr, respectively. We will use the notation ui
. Obviously, the basic version with critical edges is a special case of Btr when every edge label is 1. There are two (maximization and minimization) objective functions corresponding to the two generalizations of the basic version Min-Ed and Max-Ed; they will be denoted by Min-Btr and Max-Btr, respectively. We will use the notation ui 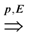 uj to indicate a path from node ui to node uj of parity p ∈ {−1, 1}.
uj to indicate a path from node ui to node uj of parity p ∈ {−1, 1}.2. Summary of Known Algorithmic and Inapproximability Results
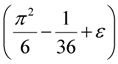 ≈ 1.617 + ε (for any constant ε > 0), which was improved to an approximation algorithm with an approximation ratio of
≈ 1.617 + ε (for any constant ε > 0), which was improved to an approximation algorithm with an approximation ratio of 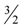 independently by Vetta [12] and by Berman, DasGupta and Karpinski [13]. Except [13], none of these approximation algorithms will generalize directly to critical-Min-Ed with the same approximation ratio. The only non-trivial approximation algorithm known for either MAX-Ed or critical-MAX-Ed is a 2-approximation algorithm described in [13].
independently by Vetta [12] and by Berman, DasGupta and Karpinski [13]. Except [13], none of these approximation algorithms will generalize directly to critical-Min-Ed with the same approximation ratio. The only non-trivial approximation algorithm known for either MAX-Ed or critical-MAX-Ed is a 2-approximation algorithm described in [13].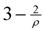 . They also provided a 2-approximation for Min-Btr, but in fact, minor modification of their method and analysis as outlined in [13] yields a
. They also provided a 2-approximation for Min-Btr, but in fact, minor modification of their method and analysis as outlined in [13] yields a 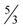 -approximation. Other heuristics for these problems were investigated in [5,6] but none of these heuristics guarantees a better approximation ratio. Table 1 shows a theoretical comparison of running times and approximation ratios of some of the known algorithms for the transitive reduction problems. Unfortunately, a systematic comparative empirical evaluation of these algorithmic approaches is not available in the published literature. However, implementations of several algorithmic approaches on an individual level are available. For example, Kachalo et al. [6] provided a software called NET-SYNTHESIS which used some of the algorithmic approaches described in Section 3.2 and Section 3.4, and Milanovíc et al. [17] discussed two meta-heuristic approaches to solve a more general version of the Min-Btr problem.
-approximation. Other heuristics for these problems were investigated in [5,6] but none of these heuristics guarantees a better approximation ratio. Table 1 shows a theoretical comparison of running times and approximation ratios of some of the known algorithms for the transitive reduction problems. Unfortunately, a systematic comparative empirical evaluation of these algorithmic approaches is not available in the published literature. However, implementations of several algorithmic approaches on an individual level are available. For example, Kachalo et al. [6] provided a software called NET-SYNTHESIS which used some of the algorithmic approaches described in Section 3.2 and Section 3.4, and Milanovíc et al. [17] discussed two meta-heuristic approaches to solve a more general version of the Min-Btr problem.| Problem name | Algorithmic approach | Worst-case running time using straightforward implementation | Approximation ratio |
|---|---|---|---|
| Min-Ed | Khuller, Raghavachari and Young [11] | O(n1/ε) | 1.617 + ε2 |
| Min-Ed | Vetta [12] Berman, DasGupta and Karpinski [13] | O(n log n) | 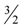 |
| Max-Ed | Berman, DasGupta and Karpinski [13] | O(n log n) | 2 |
| critical-Min-Ed | Khuller, Raghavachari and Young [11] | O(n1/ε) | 2.617 + ε2 |
| critical-Min-Ed | Berman, DasGupta and Karpinski [13] | O(n log n) | 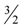 |
| critical-Min-Ed | Frederickson and JàJà [14] | O(n) | 2 |
| critical-Min-Ed | Albert et al. [4] | O(n3) | 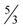 |
| critical-Max-Ed | Berman, DasGupta and Karpinski [13] | O(n log n) | 2 |
| weighted-Min-Ed | Frederickson and JàJà [14] | O(n) | 2 |
| Min-Btr | Albert et al. [4] | O(n3) | 2 |
| Min-Btr | Berman, DasGupta and Karpinski [13] | O(n log n) | 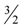 |
| Max-Btr | Berman, DasGupta and Karpinski [13] | O(n log n) | 2 |
3. Review of a Few Algorithmic Techniques Used for Transitive Reduction Problems
3.1. From General Graphs to Strongly Connected Graphs
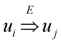 and
and 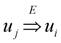 exist. A reduction that was originally suggested in [1] and have been implicit in all subsequent works is the assumption that an ε-approximation algorithm for critical-Min-Ed and critical-Max-Ed when the given graph is strongly connected also implies an ε-approximation algorithm for the same problem on arbitrary digraphs. To understand why this is true, we first note that all these four problems can be solved easily in polynomial time using the following greedy approach if the input graph G = (V, E) is a directed acyclic graph (Dag) with D ⊆ E as the set of required edges (ϕ is the standard mathematical symbol of an empty set):
exist. A reduction that was originally suggested in [1] and have been implicit in all subsequent works is the assumption that an ε-approximation algorithm for critical-Min-Ed and critical-Max-Ed when the given graph is strongly connected also implies an ε-approximation algorithm for the same problem on arbitrary digraphs. To understand why this is true, we first note that all these four problems can be solved easily in polynomial time using the following greedy approach if the input graph G = (V, E) is a directed acyclic graph (Dag) with D ⊆ E as the set of required edges (ϕ is the standard mathematical symbol of an empty set):
- E’ = E ; A = ϕ
- for i = n, n − 1, n − 2, …, 1 do
- for j = n, n − 1, n − 2, …, i + 1 do
- if (ui, uj) ∈ E then
- if (ui, uj) ∈ D then add the edge (ui, uj) to A
- else if the path ui
uj does not exist then add the edge (ui, uj) to A
- Return (V, A) as the solution
3.2. The Cycle Contraction Method [11]
- for i = c, c − 1, … ,4 do
- while (the graph contains a cycle of at least i edges) do
- Find a cycle C of at least i edges
- Select the edges in C and contract C
- endwhile
- endfor
- (* now the graph contains no cycle of more than 3 edges *)

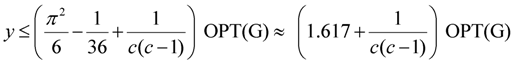 edges.
edges.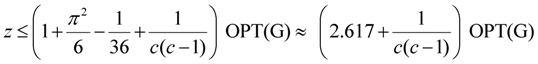 since obviously |D| ≤ OPT. Another possibility outlined in [4] is to replace every required edge (ui, uj) ∈ D by introducing a new node uij and adding two new edges (ui, uij) and (uij, uj), running the approximation algorithm for Min-Ed on this new graph, and then replacing the edges (ui, uij) and (uij, uj) in the solution by the original edge (ui, uj). If an optimal solution of critical-Min-Ed on G uses β edges from E\D then this approach returns a solution (V,A) with
since obviously |D| ≤ OPT. Another possibility outlined in [4] is to replace every required edge (ui, uj) ∈ D by introducing a new node uij and adding two new edges (ui, uij) and (uij, uj), running the approximation algorithm for Min-Ed on this new graph, and then replacing the edges (ui, uij) and (uij, uj) in the solution by the original edge (ui, uj). If an optimal solution of critical-Min-Ed on G uses β edges from E\D then this approach returns a solution (V,A) with 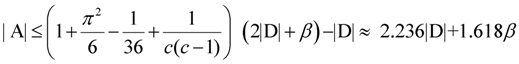 .
.3.3. The Arborescence Approach [14]
- Select an arbitrary node v of G
- Find a minimum weight spanning in-arborescence (V, A1) of G rooted at v
- Find a minimum weight spanning out-arborescence (V, A2) of G rooted at v
- Return (V, A1
A2) as the solution

- Define the weight w(e) of an edge e ∈ E as
- Select an arbitrary node vr of G
- Find a minimum weight spanning in-arborescence T = (V, A1) of G rooted at node vr
- Redefine the weight w(e) of an edge e ∈ E as
- Find a minimum weight spanning out-arborescence T = (V, A2) of G rooted at node vr
- Return (V, A1
A2
D) as the solution
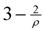 . Currently, the best possible value of ρ is 1.5 which leads to a
. Currently, the best possible value of ρ is 1.5 which leads to a 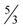 -approximation for critical-Min-Ed using this approach.
-approximation for critical-Min-Ed using this approach.3.4. From Critical-Min-Ed And Critical-Max-Ed To Min-Ed And Max-Ed [4,13]
- If G is a single parity graph then for every pair of nodes ui, uj ∈ V, exactly one of the two the paths ui
uj and ui
uj exists. Then, we can simply ignore the edge labels and compute a solution (V, A) of critical-Min-Ed (respectively, critical-Max-Ed) on G. It can be seen that (V, A) also provides a valid solution for Min-Ed (respectively, Max-Ed).
- Otherwise, G is a double parity graph. We again first ignore the edge labels and compute a solution (V, A) of critical-Min-Ed (respectively, critical-Max-Ed) on G. Note that (V, A) contains a rooted arborescence, say (V, A1) with A1 ⊆ A, rooted at some node ur. We label each node ui ∈ V with ℓ(ui) = ℓ(Pi) where Pi is the unique path in (V, A1) from ur to ui. Since G is a double parity graph, there must exist an edge (ui, uj) ∈ E such that ℓ(ui) ℓ(uj) ≠ ℓ(ui, uj), and adding this edge (if not already present) to A produces a valid solution of critical-Min-Ed or critical-Max-Ed for G.
3.5. Linear Programming Based Approach [13]
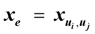 for every edge e = (ui, uj) ∈ E which describes whether we select e (xe = 1) or do not select e (xe = 0) in our solution. For U ⊂ V, define ι(U) = {(ui, uj) ∈ E:ui ∉ U and uj ∈ U}. Then, the Lp formulation is:
for every edge e = (ui, uj) ∈ E which describes whether we select e (xe = 1) or do not select e (xe = 0) in our solution. For U ⊂ V, define ι(U) = {(ui, uj) ∈ E:ui ∉ U and uj ∈ U}. Then, the Lp formulation is:

| (primal Lp P1) | (dual Lp D1) |
 |  |
3.5.1. Applying Lp-Based Approach to Critical-Min-Ed
- We start with an initial assignment of values to variables in IP1 in the following manner. We keep only a subset of constraints of IP1 such that the resulting Ilp can be solved exactly in polynomial time, giving an optimal solution A1 ⊆ E. Then, it follows that OPT(G) ≥ |A1|.
- However, (V, A1) may not be a valid solution for critical-Min-Ed on G (i.e., IP1). Then, we try to make A1 a valid solution by adding and/or removing edges so that we use a total of at most
edges where OPT(G) ≥ η ≥ |A1|, giving a
- approximation for critical-Min-Ed. The edge alteration procedure was carried out in [13] using the DFS (depth-first-search) algorithm as originally outlined in a seminal paper by Tarjan (e.g., see the textbook [22]).

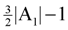 edges. Then, we look at the “non-tractable” constraints of the primal P1 or dual D1 to get an improved lower-bound η for OPT(G) (i.e., OPT(G) ≥ η > A1) to ensure that we use at most
edges. Then, we look at the “non-tractable” constraints of the primal P1 or dual D1 to get an improved lower-bound η for OPT(G) (i.e., OPT(G) ≥ η > A1) to ensure that we use at most 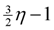 edges. In the proof we need to crucially use the weak-duality theorem of linear programming which states that if OPT(P1) and OPT(D1) are the objective values of an optimal solution of P1 and D1, respectively, then OPT(P1) ≥ OPT(D1).
edges. In the proof we need to crucially use the weak-duality theorem of linear programming which states that if OPT(P1) and OPT(D1) are the objective values of an optimal solution of P1 and D1, respectively, then OPT(P1) ≥ OPT(D1).3.5.2. Applying Lp-Based Approach to Critical-Max-Ed

 . Now, suppose that we set
. Now, suppose that we set  . This assignment of variables is a valid solution of the above Lp.
. This assignment of variables is a valid solution of the above Lp. , is still a valid solution of the Lp, and thus the total value of the objective function of this fractional solution is at most
, is still a valid solution of the Lp, and thus the total value of the objective function of this fractional solution is at most 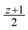 , which together with the result of Edmonds [15] that showed that “the Lp always has an integral optimal solution” implies that OPTin-arb(G) ≤
, which together with the result of Edmonds [15] that showed that “the Lp always has an integral optimal solution” implies that OPTin-arb(G) ≤ 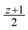 , which implies that we delete at least z + 1 −
, which implies that we delete at least z + 1 − 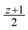 =
= 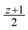 edges from the in-arborescence and take the remaining edges of the in-arborescence together with all the edges in Aout to get a valid solution of critical-Max-Ed on G. The total number of edges we have deleted in at least
edges from the in-arborescence and take the remaining edges of the in-arborescence together with all the edges in Aout to get a valid solution of critical-Max-Ed on G. The total number of edges we have deleted in at least 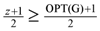 . A slight modification in the argument shows that in fact we can delete at least
. A slight modification in the argument shows that in fact we can delete at least 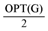 edges.
edges.3.5.3. Limitations of Lp-Based Approaches
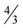 by giving an explicit construction of an input graph for which this ratio is achieved. The same input graph also shows that the integrality gap for the modification of P1 corresponding to Max-Ed is at least
by giving an explicit construction of an input graph for which this ratio is achieved. The same input graph also shows that the integrality gap for the modification of P1 corresponding to Max-Ed is at least 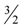 .
.4. Biological Applications
- Mammalian network of signaling pathways and cellular machines in the hippocampal CA1 neuron having 512 nodes and 1,047 edges [24].
- S. cerevisiae transcriptional regulatory network of interactions between transcription factor proteins and genes having 690 nodes and 1,082 edges [25].
- C. elegans metabolic network having 651 nodes and 2,040 edges [26].
- Oriented version of an unweighted PPI network constructed from S. cerevisiae interactions in the BioGRID database having 786 nodes and 2,453 edges [27].
4.1. Network Construction and Simplification from Direct and Double-Causal Data
- (i)
- “Direct” interactions corresponding to biochemical evidences that provide information on enzymatic activity or protein-protein interactions and represent direct physical interactions. An interaction of this type is of the form “A promotes B” or “A inhibits B”, and is represented in the usual manner by a directed edge A → B and A —| B, respectively. Edges corresponding to known (documented) direct interactions are marked as “critical” and belong to the set D of required edges.
- (ii)
- “Putative” interaction patterns that arise, for example, during differential responses to a stimulus, which in a wild-type organism versus a mutant organism implicates the product of the mutated gene in the signal transduction process. This type of interaction pattern is not a direct interaction but rather corresponds to an indirect (double-causal) relationship most likely resulting from a chain of direct interactions and reactions, and is a 3-component inference represented by a small-size sub-graph among three or four nodes.
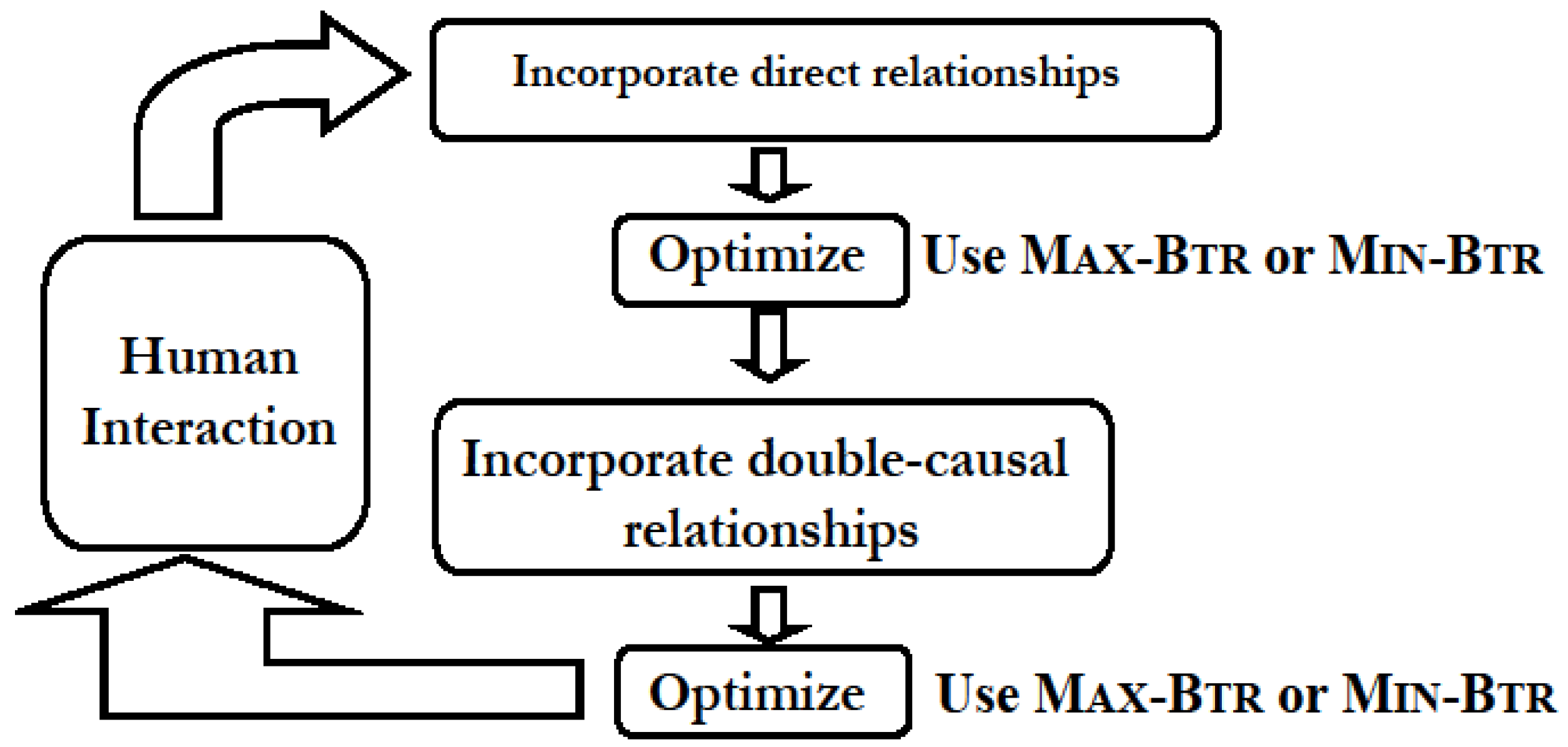
4.1.1. Applications in Agronomic Research
4.2. Analyzing Disease Networks (Biomedical Application)
4.3. Measuring Topological Redundancy of Biological Networks
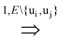 uj or ui
uj or ui 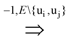 uj respectively, exists, thus truly removing redundant connections. Thus, if (V, E1) is an optimal solution of Min-Btr and Max-Btr on the input graph G = (V, E) then
uj respectively, exists, thus truly removing redundant connections. Thus, if (V, E1) is an optimal solution of Min-Btr and Max-Btr on the input graph G = (V, E) then 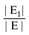 provides a measure of global compressibility of the network. Based on this intuition, Albert et al. in [47] proposed a new redundancy measure
provides a measure of global compressibility of the network. Based on this intuition, Albert et al. in [47] proposed a new redundancy measure  , where the |E| term in the denominator is simply a “min-max normalization” of the measure to ensure that 0 < R < 1. Note that the higher the value of R is, the more redundant the network is. Since Min-Btr or Max-Btr can be computed efficiently, Albert et al. were able to evaluate R on a variety of large biological and directed social networks to derive interesting conclusions such as transcriptional networks are less redundant than signaling networks, directed social networks are more redundant than biological networks, the topological redundancy of the C. elegans metabolic network is largely due to its inclusion of currency metabolites and the redundancy of signaling networks is highly (negatively) correlated with the monotonicity of their dynamics.
, where the |E| term in the denominator is simply a “min-max normalization” of the measure to ensure that 0 < R < 1. Note that the higher the value of R is, the more redundant the network is. Since Min-Btr or Max-Btr can be computed efficiently, Albert et al. were able to evaluate R on a variety of large biological and directed social networks to derive interesting conclusions such as transcriptional networks are less redundant than signaling networks, directed social networks are more redundant than biological networks, the topological redundancy of the C. elegans metabolic network is largely due to its inclusion of currency metabolites and the redundancy of signaling networks is highly (negatively) correlated with the monotonicity of their dynamics.5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Moyles, D.M.; Thompson, G.L. Finding a minimum equivalent of a digraph. J. ACM 1969, 16, 455–460. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability—A Guide to the Theory of NP-Completeness; W. H. Freeman & Co.: New York, NY, USA, 1979. [Google Scholar]
- Aho, A.; Garey, M.R.; Ullman, J.D. The transitive reduction of a directed graph. SIAM J. Comput. 1972, 1, 131–137. [Google Scholar] [CrossRef]
- Albert, R.; DasGupta, B.; Dondi, R.; Sontag, E.D. Inferring (Biological) signal transduction networks via transitive reductions of directed graphs. Algorithmica 2008, 51, 129–159. [Google Scholar] [CrossRef]
- Albert, R.; DasGupta, B.; Dondi, R.; Kachalo, S.; Sontag, E.D.; Zelikovsky, A.; Westbrooks, K. A novel method for signal transduction network inference from indirect experimental evidence. J. Comput. Biol. 2007, 14, 927–949. [Google Scholar] [CrossRef]
- Kachalo, S.; Zhang, R.; Sontag, E.D.; Albert, R.; DasGupta, B. NET-SYNTHESIS: A software for synthesis, inference and simplification of signal transduction networks. Bioinformatics 2008, 24, 293–295. [Google Scholar] [CrossRef]
- Albert, R.; DasGupta, B.; Sontag, E.D. Inference of Signal Transduction Networks from Double Causal Evidence. In Methods in Molecular Biology: Topics in Computational Biology; Fenyo, D., Ed.; Springer Science + Business Media, LLC: New York, NY, USA, 2010; Volume 673. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Gusfield, D. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Pevzner, P.A. Computational Molecular Biology: An Algorithmic Approach; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Khuller, S.; Raghavachari, B.; Young, N. Approximating the minimum equivalent digraph. SIAM J. Comput. 1995, 24, 859–872. [Google Scholar] [CrossRef]
- Vetta, A. Approximating the minimum strongly connected subgraph via a matching lower bound. In Proceedings of the 12th ACM-SIAM Symposium on Discrete Algorithms, Washington, DC, USA, 7–9 January 2001; pp. 417–426.
- Berman, P.; DasGupta, B.; Karpinski, M. Approximating transitive reduction problems for directed networks. In Proceedings of the 11th Algorithms and Data Structures Symposium, Banff, AB, Canada, 21–23 August 2009; pp. 74–85.
- Frederickson, G.N.; JàJà, J. Approximation algorithms for several graph augmentation problems. SIAM J. Comput. 1981, 10, 270–283. [Google Scholar] [CrossRef]
- Edmonds, J. Optimum branchings. In Mathematics and the Decision Sciences, Part 1; Dantzig, G.B., Veinott, A.F., Jr., Eds.; American Mathematical Society Lectures on Applied Mathematics: Providence, RI, USA, 1968; pp. 335–345. [Google Scholar]
- Karp, R.M. A simple derivation of Edmonds’ algorithm for optimum branching. Networks 1972, 1, 265–272. [Google Scholar] [CrossRef]
- Milanovíc, M.; Matíc, D.; Savíc, A.; Kratica, J. Two metaheuristic approaches to solving the p-ary transitive reduction problem. Appl. Comput. Math. 2011, 10, 294–308. [Google Scholar]
- Papadimitriou, C. Computational Complexity; Addison-Wesley: New York, NY, USA, 1994; p. 212. [Google Scholar]
- Khuller, S.; Raghavachari, B.; Young, N. On strongly connected digraphs with bounded cycle length. Discret. Appl. Math. 1996, 69, 281–289. [Google Scholar] [CrossRef]
- Chu, Y.; Liu, T. On the shortest arborescence of a directed graph. Sci. Sin. 1965, 4, 1396–1400. [Google Scholar]
- Vazirani, V. Approximation Algorithms; Springer: New York, NY, USA, 2001. [Google Scholar]
- Aho, A.; Hopcroft, J.E.; Ullman, J.D. The Design and Analysis of Computer Algorithms; Addison-Wesley: Reading, MA, USA, 1974. [Google Scholar]
- Dubois, V.; Bothorel, C. Transitive reduction for social network analysis and visualization. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence, Compiègne, France, 19–22 September 2005; pp. 128–131.
- Ma’ayan, A.; Jenkins, S.L.; Neves, S.; Hasseldine, A.; Grace, E.; Dubin-Thaler, B.; Eungdamrong, N.J.; Weng, G.; Ram, P.T.; Rice, J.J.; et al. Formation of regulatory patterns during signal propagation in a mammalian cellular network. Science 2005, 309, 1078–1083. [Google Scholar] [CrossRef]
- Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Alon, D.U. Network motifs: Simple building blocks of complex networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvai, Z.N.; Barabasi, A.L. The large-scale organization of metabolic networks. Nature 2000, 407, 651–654. [Google Scholar] [CrossRef]
- Gitter, A.; Klein-Seetharaman, J.; Gupta, A.; Bar-Joseph, Z. Discovering pathways by orienting edges in protein interaction networks. Nucleic Acids Res. 2011, 39, e22. [Google Scholar] [CrossRef]
- Lee, T.I.; Rinaldi, N.J.; Robert, F.; Odom, D.T.; Bar-Joseph, Z.; Gerber, G.K.; Hannett, N.M.; Harbison, C.T.; Thompson, C.M.; Simon, I.; et al. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science 2002, 298, 799–804. [Google Scholar] [CrossRef]
- Giot, L.; Bader, J.S.; Brouwer, C.; Chaudhuri, A.; Kuang, B.; Li, Y.; Hao, Y.L.; Ooi, C.E.; Godwin, B.; Vitols, E.; et al. A protein interaction map of Drosophila melanogaster. Science 2003, 302, 1727–1736. [Google Scholar] [CrossRef]
- Han, J.-D.J.; Bertin, N.; Hao, T.; Goldberg, D.S.; Berriz, G.F.; Zhang, L.V.; Dupuy, D.; Walhout, A.J.M.; Cusick, M.E.; Roth, F.P.; et al. Evidence for dynamically organized modularity in the yeast protein-protein interaction network. Nature 2004, 430, 88–93. [Google Scholar] [CrossRef]
- Li, S.; Armstrong, C.M.; Bertin, N.; Ge, H.; Milstein, S.; Boxem, M.; Vidalain, P.-O.; Han, J.-D.J.; Chesneau, A.; Hao, T.; et al. A map of the interactome network of the metazoan C. elegans. elegans. Science 2004, 303, 540–543. [Google Scholar]
- Friedman, C.; Kra, P.; Yu, H.; Krauthammer, M.; Rzhetsky, A. GENIES: A natural-language processing system for the extraction of molecular pathways from journal articles. Bioinformatics 2001, 17, S74–S82. [Google Scholar] [CrossRef]
- Alberts, B. Molecular Biology of the Cell; Garland Publishing: New York, NY, USA, 1994. [Google Scholar]
- Hetherington, A.M.; Woodward, F.I. The role of stomata in sensing and driving environmental change. Nature 2003, 424, 901–908. [Google Scholar] [CrossRef]
- Fan, L.M.; Zhao, Z.; Assmann, S.H. Guard cells: A dynamic signaling model. Curr. Opin. Plant Biol. 2004, 7, 537–546. [Google Scholar] [CrossRef]
- Blatt, M.R.; Grabov, A. Signal redundancy, gates and integration in the control of ion channels for stomatal movement. J. Exp. Bot. 1997, 48, 529–537. [Google Scholar] [CrossRef]
- MacRobbie, E.A. Signal transduction and ion channels in guard cells. Philos. Trans. R. Soc. Lond. BBiol. Sci. 1998, 353, 1475–1488. [Google Scholar] [CrossRef]
- Li, S.; Assmann, S.M.; Albert, A. Predicting essential components of signal transduction networks: A dynamic model of guard cell abscisic acid signaling. PLoS Biol. 2006. [Google Scholar] [CrossRef]
- Zhang, R.; Shah, M.V.; Yang, J.; Nyland, S.B.; Liu, X.; Yun, J.K.; Albert, R.; Loughran, T.P. Network model of survival signaling in LGL leukemia. Proc. Natl. Acad. Sci. USA 2008, 105, 16308–16313. [Google Scholar] [CrossRef]
- Albert, R.; DasGupta, B.; Mobasheri, N. Some perspectives on network modeling in therapeutic target prediction. Biomed. Eng. Computat. Biol. 2013, 5, 17–24. [Google Scholar]
- Kafri, R.; Bar-Even, A.; Pilpel, Y. Transcription control reprogramming in genetic backup circuits. Nat. Genet. 2005, 37, 295–299. [Google Scholar] [CrossRef]
- Kolb, B.; Whishaw, I.Q. Fundamentals of Human Neuropsychology; Freeman: New York, NY, USA, 1996. [Google Scholar]
- Tononi, G.; Sporns, O.; Edelman, G.M. Measures of degeneracy and redundancy in biological networks. Proc. Natl. Acad. Sci. USA 1999, 96, 3257–3262. [Google Scholar] [CrossRef]
- Papin, A.; Palsson, B.O. Topological analysis of mass-balanced signaling networks: A framework to obtain network properties including crosstalk. J. Theor. Biol. 2004, 227, 283–297. [Google Scholar] [CrossRef]
- Beckage, N.; Smith, L.; Hills, T. Semantic network connectivity is related to vocabulary growth rate in children. In Proceedings of the 32nd Annual Conference of the Cognitive Science Society, Portland, OR, USA, 11–14 August 2010; pp. 2769–2774.
- Dall’Astaa, L.; Alvarez-Hamelina, I.; Barrata, A.; Vázquezb, A.; Vespignania, A. Exploring networks with traceroute-like probes: Theory and simulations. Theor. Comput. Sci. 2006, 355, 6–24. [Google Scholar] [CrossRef]
- Albert, R.; DasGupta, B.; Gitter, A.; Gürsoy, G.; Hegde, R.; Pal, P.; Sivanathan, G.S.; Sontag, E.D. A new computationally efficient measure of topological redundancy of biological and social networks. Phys. Rev. E 2011, 84, 036117. [Google Scholar] [CrossRef]
- Wagner, A. Estimating coarse gene network structure from large-scale gene perturbation data. Genome Res. 2002, 12, 309–315. [Google Scholar] [CrossRef]
- Chen, T.; Filkov, V.; Skiena, S. Identifying gene regulatory networks from experimental data. In Proceedings of the 3rd Annual International Conference on Computational Molecular Biology, Lyon, France, 11–14 April 1999; pp. 94–103.
- Klamt, S.; Flassig, R.J.; Sundmacher, K. Transwesd: Inferring cellular networks with transitive reduction. Bioinformatics 2010, 26, 2160–2168. [Google Scholar] [CrossRef]
- Bosnacki, D.; Odenbrett, M.R.; Wijs, A.; Ligtenberg, W.; Hilbers, P. Efficient reconstruction of biological networks via transitive reduction on general purpose graphics processors. BMC Bioinform. 2012, 13, 281. [Google Scholar] [CrossRef]
- Feizi, S.; Marbach, D.; Médard, M.; Kellis, M. Network deconvolution as a general method to distinguish direct dependencies in networks. Nat. Biotechnol. 2011, 31, 726–733. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Aditya, S.; DasGupta, B.; Karpinski, M. Algorithmic Perspectives of Network Transitive Reduction Problems and their Applications to Synthesis and Analysis of Biological Networks. Biology 2014, 3, 1-21. https://doi.org/10.3390/biology3010001
Aditya S, DasGupta B, Karpinski M. Algorithmic Perspectives of Network Transitive Reduction Problems and their Applications to Synthesis and Analysis of Biological Networks. Biology. 2014; 3(1):1-21. https://doi.org/10.3390/biology3010001
Chicago/Turabian StyleAditya, Satabdi, Bhaskar DasGupta, and Marek Karpinski. 2014. "Algorithmic Perspectives of Network Transitive Reduction Problems and their Applications to Synthesis and Analysis of Biological Networks" Biology 3, no. 1: 1-21. https://doi.org/10.3390/biology3010001
APA StyleAditya, S., DasGupta, B., & Karpinski, M. (2014). Algorithmic Perspectives of Network Transitive Reduction Problems and their Applications to Synthesis and Analysis of Biological Networks. Biology, 3(1), 1-21. https://doi.org/10.3390/biology3010001













