Algorithms for Hidden Markov Models Restricted to Occurrences of Regular Expressions
Abstract
:1. Introduction
2. Methods
2.1. Hidden Markov Models
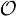 * and a hidden sequence x1:T = x1x2 … xT ∈
* and a hidden sequence x1:T = x1x2 … xT ∈
 *, where
*, where
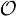 and
and
 are finite alphabets of observables and hidden states, respectively. The hidden sequence is a realization of a Markov process that explains the hidden properties of the observed data. We can formally define an HMM as consisting of a finite alphabet of hidden states
are finite alphabets of observables and hidden states, respectively. The hidden sequence is a realization of a Markov process that explains the hidden properties of the observed data. We can formally define an HMM as consisting of a finite alphabet of hidden states
 = {h1, h2, …, hN}, a finite alphabet of observables
= {h1, h2, …, hN}, a finite alphabet of observables
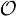 = {o1,o2, …, oM}, a vector Π = (πhi)1≤i≤N, where πhi = ℙ(X1 = hi) is the probability of the hidden sequence starting in state hi, a matrix A = {ahi,hj}1≤i,j≤N, where ahi,hj = ℙ(Xt = hj | Xt−1 = hi) is the probability of a transition from state hi to state hj, and a matrix
, where bhi,oj = ℙ(Yt = oj | Xt = hi) is the probability of state hi emitting oj.
= {o1,o2, …, oM}, a vector Π = (πhi)1≤i≤N, where πhi = ℙ(X1 = hi) is the probability of the hidden sequence starting in state hi, a matrix A = {ahi,hj}1≤i,j≤N, where ahi,hj = ℙ(Xt = hj | Xt−1 = hi) is the probability of a transition from state hi to state hj, and a matrix
, where bhi,oj = ℙ(Yt = oj | Xt = hi) is the probability of state hi emitting oj.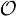 = {A, C, G, T}, while the hidden states encode if a position is in a non-coding area (N) or is part of a gene on the positive strand (C) or on the negative strand (R). The model incorporates the fact that nucleotides come in multiples of three within genes, where each nucleotide triplet codes for an amino acid. The set of hidden states is
= {A, C, G, T}, while the hidden states encode if a position is in a non-coding area (N) or is part of a gene on the positive strand (C) or on the negative strand (R). The model incorporates the fact that nucleotides come in multiples of three within genes, where each nucleotide triplet codes for an amino acid. The set of hidden states is
 = {N} ∪ {Ci, Ri|1 ≤ i ≤ 3}. In practice, models used for gene finding are much more complex, but this model captures the essential aspects of a gene finder.
= {N} ∪ {Ci, Ri|1 ≤ i ≤ 3}. In practice, models used for gene finding are much more complex, but this model captures the essential aspects of a gene finder.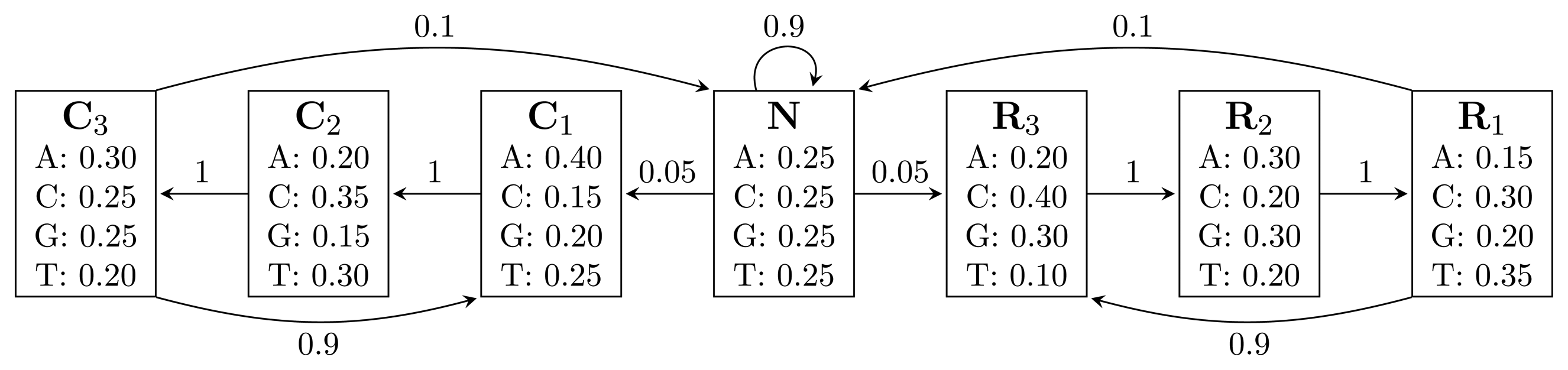
 (TN2) time, using
(TN2) time, using
 (TN) space.
(TN) space.2.1.1. The Forward Algorithm
2.1.2. The Viterbi Algorithm
2.1.3. The Posterior Decoding Algorithm
2.1.4. The Posterior-Viterbi Algorithm
2.2. Automata
 = {h1, h2, …, hN} of an HMM. Let r be a regular expression over
= {h1, h2, …, hN} of an HMM. Let r be a regular expression over
 , and let FA
, and let FA  (r) = (Q,
(r) = (Q,
 , q0, A, δ) [23] be the deterministic finite automaton (DFA) that recognizes the language described by (h1 ∣ h2 ∣ … ∣ hN)*(r), where Q is the finite set of states, q0 ∈ Q is the initial state, A ⊆ Q is the set of accepting states and δ : Q ×
, q0, A, δ) [23] be the deterministic finite automaton (DFA) that recognizes the language described by (h1 ∣ h2 ∣ … ∣ hN)*(r), where Q is the finite set of states, q0 ∈ Q is the initial state, A ⊆ Q is the set of accepting states and δ : Q ×
 → Q is the transition function. FA
→ Q is the transition function. FA  (r) accepts any string that has r as a suffix. We construct the DFA EA
(r) accepts any string that has r as a suffix. We construct the DFA EA  (r) = (Q,
(r) = (Q,
 , q0, A, δE) as an extension of FA
, q0, A, δE) as an extension of FA  (r), where δE is defined by:
(r), where δE is defined by:
 (r) restarts every time it reaches an accepting state. Figure 2 shows FA
(r) restarts every time it reaches an accepting state. Figure 2 shows FA  (r) and EA
(r) and EA  (r) for r = (NC1) ∣ (R1N) with the hidden alphabet
(r) for r = (NC1) ∣ (R1N) with the hidden alphabet
 = {N} ∪ {Ci, Ri ∣ 1 ≤ i ≤ 3} of the HMM from Figure 2. Both automata have Q = {0, 1, 2, 3, 4}, q0 = 0, and A = {2, 4}. State 1 marks the beginning of NC1, while state 3 corresponds to the beginning of R1N. State 2 accepts NC1, and state 4 accepts R1N. As C2, C3, R2 and R3 are not part of r, using them, the automaton restarts by transitioning to state 0 from all states. We left these transitions out of the figure for clarity. The main difference between FA
= {N} ∪ {Ci, Ri ∣ 1 ≤ i ≤ 3} of the HMM from Figure 2. Both automata have Q = {0, 1, 2, 3, 4}, q0 = 0, and A = {2, 4}. State 1 marks the beginning of NC1, while state 3 corresponds to the beginning of R1N. State 2 accepts NC1, and state 4 accepts R1N. As C2, C3, R2 and R3 are not part of r, using them, the automaton restarts by transitioning to state 0 from all states. We left these transitions out of the figure for clarity. The main difference between FA  (r) and EA
(r) and EA  (r) is that they correspond to overlapping and non-overlapping occurrences, respectively. For example, for the input string, R1NC1, FA
(r) is that they correspond to overlapping and non-overlapping occurrences, respectively. For example, for the input string, R1NC1, FA  (r) first finds R1N using state 4, from which it transitions to state 2 and matches NC1. However, after EA
(r) first finds R1N using state 4, from which it transitions to state 2 and matches NC1. However, after EA  (r) recognizes R1N, it transitions back to state 0, not matching NC1. The algorithms we provide are independent of which of the two automata is used, and therefore, all that remains is to switch between them when needed. In our implementation, we used an automata library for Java [24] to obtain FA
(r) recognizes R1N, it transitions back to state 0, not matching NC1. The algorithms we provide are independent of which of the two automata is used, and therefore, all that remains is to switch between them when needed. In our implementation, we used an automata library for Java [24] to obtain FA  (r), which we then converted to EA
(r), which we then converted to EA  (r).
(r). (r) and EA
(r) and EA  (r), for the pattern r = (NC1) ∣ (R1N),
(r), for the pattern r = (NC1) ∣ (R1N),
 = {N} ∪ {Ci, Ri ∣ 1 ≤ i ≤ 3}, Q = {0, 1, 2, 3, 4}, q0 = 0, and A = {2, 4}. States 1, 2 and 3, 4 are used for matching sequences ending with NC1 and R1N, respectively, as marked with gray boxes. The two automata differ only with respect to transitions from accepting states: the dotted transition belongs to FA
= {N} ∪ {Ci, Ri ∣ 1 ≤ i ≤ 3}, Q = {0, 1, 2, 3, 4}, q0 = 0, and A = {2, 4}. States 1, 2 and 3, 4 are used for matching sequences ending with NC1 and R1N, respectively, as marked with gray boxes. The two automata differ only with respect to transitions from accepting states: the dotted transition belongs to FA  (r) and the dashed one to EA
(r) and the dashed one to EA  (r). For clarity, the figure lacks transitions going from all states to state 0 using C2, C3, R2 and R3.
(r). For clarity, the figure lacks transitions going from all states to state 0 using C2, C3, R2 and R3.
 (r) and EA
(r) and EA  (r), for the pattern r = (NC1) ∣ (R1N),
(r), for the pattern r = (NC1) ∣ (R1N),
 = {N} ∪ {Ci, Ri ∣ 1 ≤ i ≤ 3}, Q = {0, 1, 2, 3, 4}, q0 = 0, and A = {2, 4}. States 1, 2 and 3, 4 are used for matching sequences ending with NC1 and R1N, respectively, as marked with gray boxes. The two automata differ only with respect to transitions from accepting states: the dotted transition belongs to FA
= {N} ∪ {Ci, Ri ∣ 1 ≤ i ≤ 3}, Q = {0, 1, 2, 3, 4}, q0 = 0, and A = {2, 4}. States 1, 2 and 3, 4 are used for matching sequences ending with NC1 and R1N, respectively, as marked with gray boxes. The two automata differ only with respect to transitions from accepting states: the dotted transition belongs to FA  (r) and the dashed one to EA
(r) and the dashed one to EA  (r). For clarity, the figure lacks transitions going from all states to state 0 using C2, C3, R2 and R3.
(r). For clarity, the figure lacks transitions going from all states to state 0 using C2, C3, R2 and R3.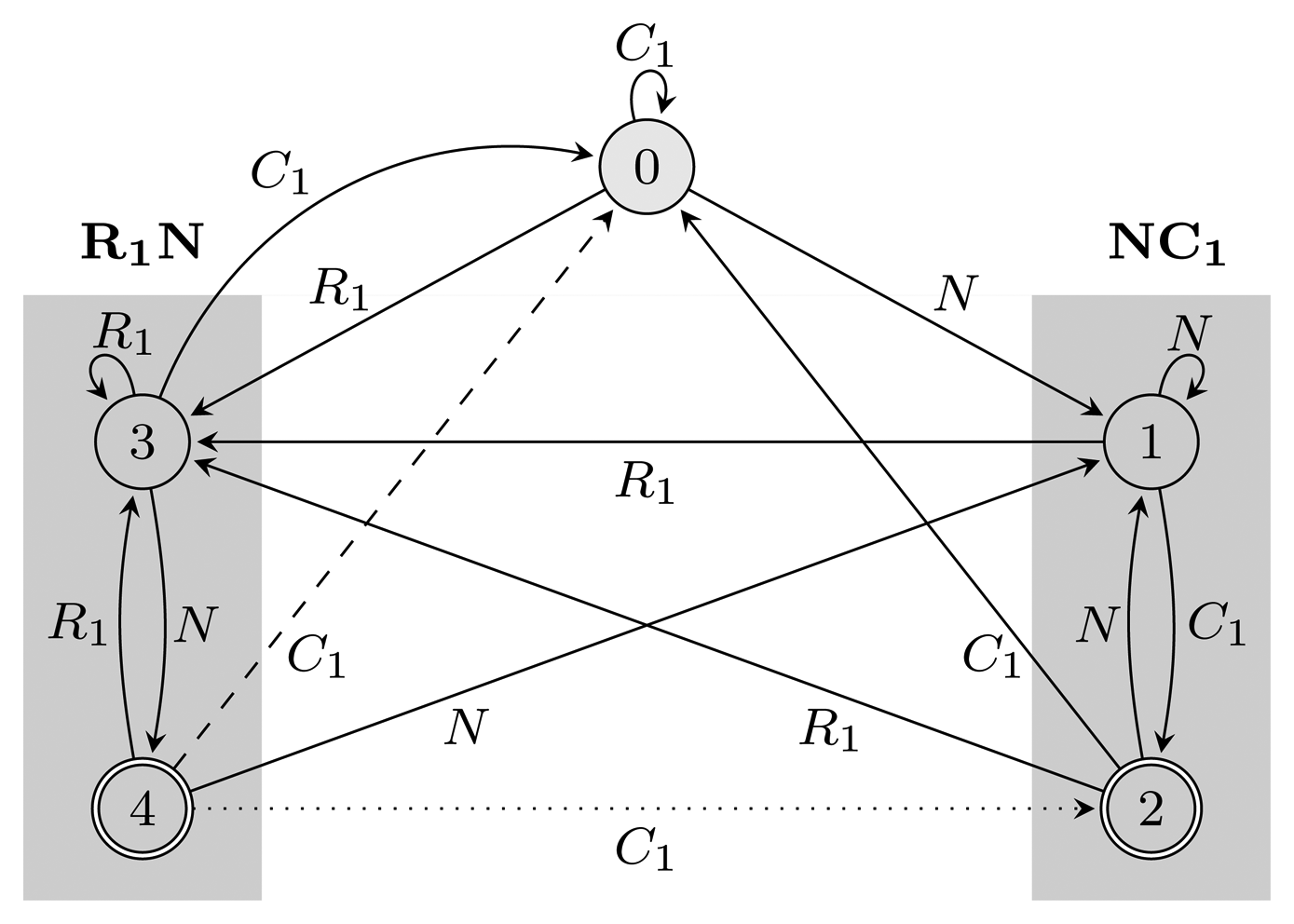
3. Results and Discussion
 . We present a modified version of the forward algorithm to compute the distribution of the number of occurrences of r, which we then use in an adaptation of the Viterbi algorithm and the posterior-Viterbi algorithm to obtain an improved prediction.
. We present a modified version of the forward algorithm to compute the distribution of the number of occurrences of r, which we then use in an adaptation of the Viterbi algorithm and the posterior-Viterbi algorithm to obtain an improved prediction.3.1. The Restricted Forward Algorithm
 (r) in parallel. Let FA
(r) in parallel. Let FA  (r)t be the state in which the automaton is after t transitions, and define α̂t(xt, k, q) = Σ{x1:t−1:Or(x1:t) =k} ℙ(y1:t, x1:t, FA
(r)t be the state in which the automaton is after t transitions, and define α̂t(xt, k, q) = Σ{x1:t−1:Or(x1:t) =k} ℙ(y1:t, x1:t, FA  (r)t = q) to be the entries of a new table, α̂, where k = 0, …, m and m ≤ T is the maximum number of pattern occurrences in a hidden sequence of length T. The table entries are the probabilities of having observed y1:t, being in hidden state xt and automaton state q at time t and having seen k occurrences of the pattern, corresponding to having visited accepting states k times. Letting δ−1(q, hi) = {q′ ∣ δ(q′, hi) = q} be the automaton states from which a transition to q exists, using hidden state hi and
(r)t = q) to be the entries of a new table, α̂, where k = 0, …, m and m ≤ T is the maximum number of pattern occurrences in a hidden sequence of length T. The table entries are the probabilities of having observed y1:t, being in hidden state xt and automaton state q at time t and having seen k occurrences of the pattern, corresponding to having visited accepting states k times. Letting δ−1(q, hi) = {q′ ∣ δ(q′, hi) = q} be the automaton states from which a transition to q exists, using hidden state hi and
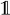 being the indicator function, mapping a Boolean expression to one if it is satisfied and to zero otherwise, we have that:
being the indicator function, mapping a Boolean expression to one if it is satisfied and to zero otherwise, we have that:
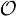 (N|Q|), leading to a
(N|Q|), leading to a
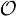 (TN2m|Q|2) running time and a space consumption of
(TN2m|Q|2) running time and a space consumption of
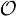 (TNm|Q|). In practice, both time and space consumption can be reduced. The restricted forward algorithm can be run for values of k that are gradually increasing up to kmax for which ℙ(at most kmax occurrences of r ∣ y1:T) is greater than, e.g., 99.99%. This kmax is generally significantly less than m, while the expectation of the number of matches of r can be reliably calculated from this truncated distribution. The space consumption can be reduced to
(TNm|Q|). In practice, both time and space consumption can be reduced. The restricted forward algorithm can be run for values of k that are gradually increasing up to kmax for which ℙ(at most kmax occurrences of r ∣ y1:T) is greater than, e.g., 99.99%. This kmax is generally significantly less than m, while the expectation of the number of matches of r can be reliably calculated from this truncated distribution. The space consumption can be reduced to
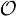 (N|Q|), because the calculation at time t for a specific value, k, depends only on the results at time t − 1 for k and k − 1.
(N|Q|), because the calculation at time t for a specific value, k, depends only on the results at time t − 1 for k and k − 1.3.2. Restricted Decoding Algorithms
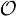 (TNu|Q|) space and
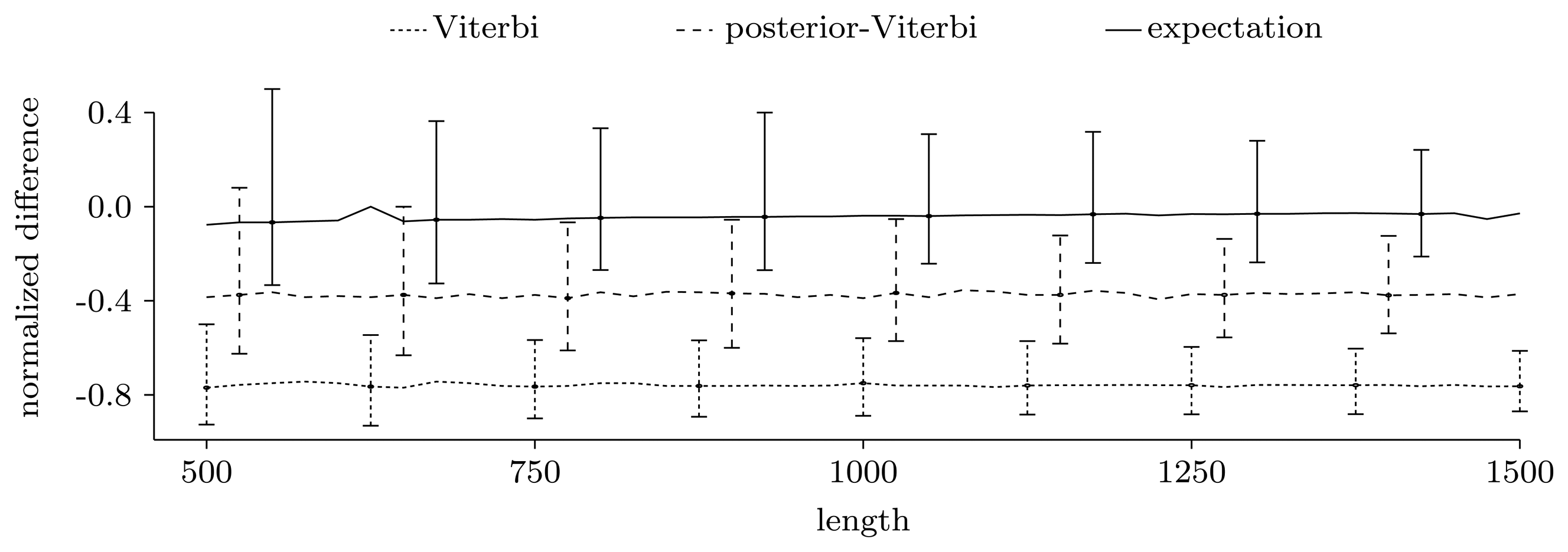
(TNu|Q|) space and
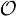 (TN2u|Q|2) time.
(TN2u|Q|2) time. (r)t = q)} with k = 0, …, u. The corresponding recursion is:
(r)t = q)} with k = 0, …, u. The corresponding recursion is:
 (r)t = q ∣ y1:T)}. We have:
(r)t = q ∣ y1:T)}. We have:
3.3. Experimental Results on Simulated Data
3.3.1. Counting Pattern Occurrences
3.3.2. Quality of Predictions
Nucleotide level
Gene level

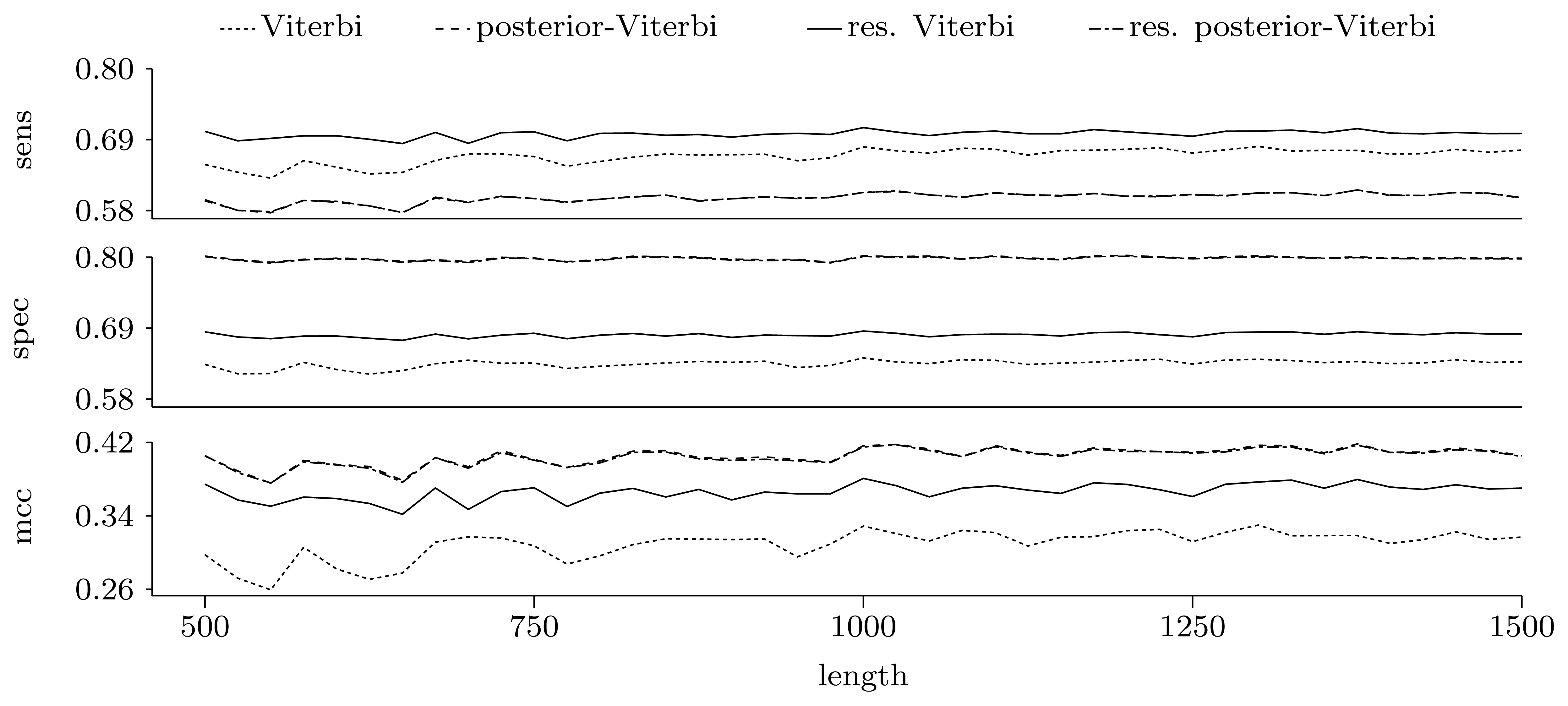
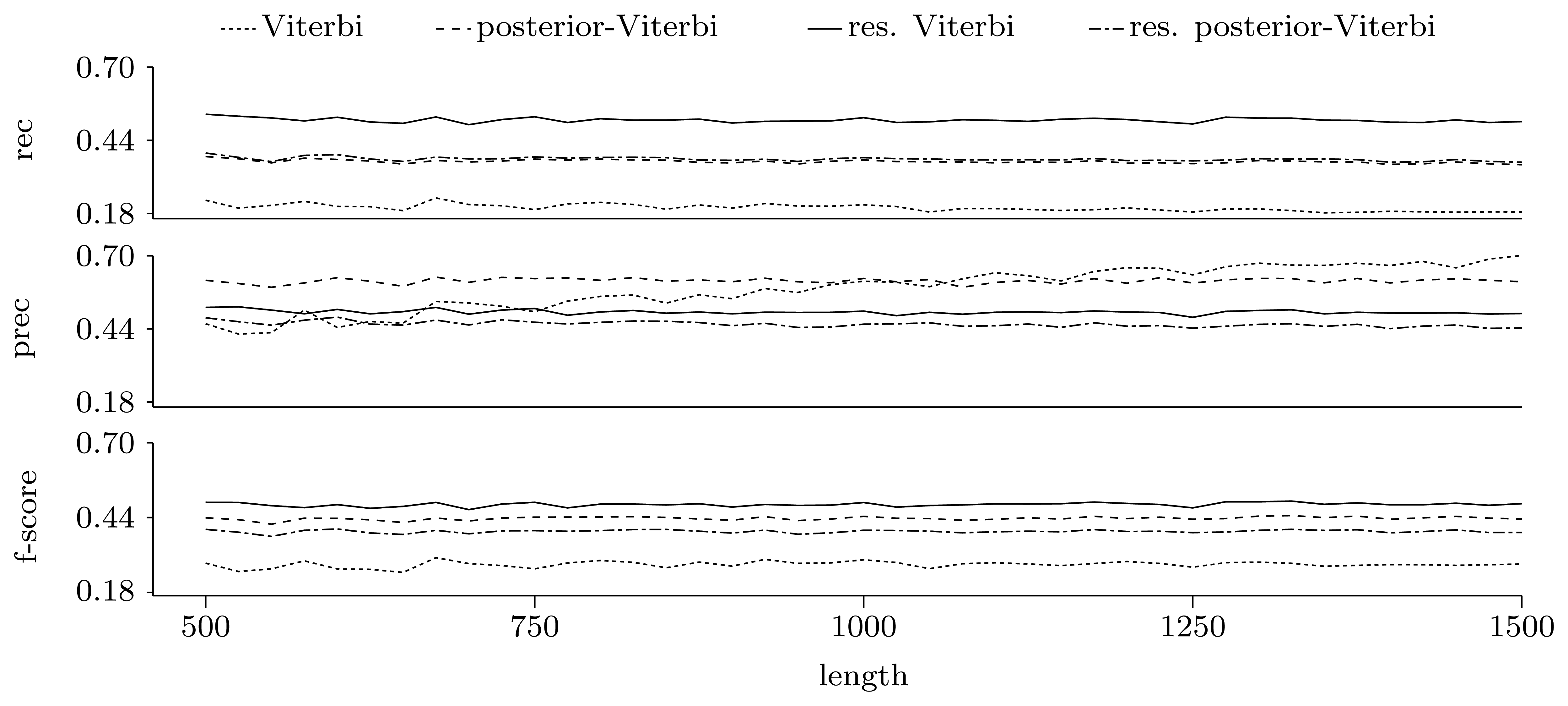
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Chong, J.; Yi, Y.; Faria, A.; Satish, N.; Keutzer, K. Data-parallel Large Vocabulary Continuous Speech Recognition on Graphics Processors. Proceedings of the 1st Annual Workshop on Emerging Applications and Many Core Architecture, Beijing, China, June 2008; pp. 23–35.
- Gales, M.; Young, S. The application of hidden Markov models in speech recognition. Found. Trends Signal Process. 2007, 1, 195–304. [Google Scholar]
- Rabiner, L. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar]
- Li, J.; Gray, R. Image Segmentation and Compression Using Hidden Markov Models; Springer: Berlin/Heidelberg, Germany, 2000; Volume 571. [Google Scholar]
- Karplus, K.; Barrett, C.; Cline, M.; Diekhans, M.; Grate, L.; Hughey, R. Predicting protein structure using only sequence information. Proteins Struct. Funct. Bioinformatics 1999, 37, 121–125. [Google Scholar]
- Krogh, A.; Brown, M.; Mian, I.; Sjolander, K.; Haussler, D. Hidden Markov models in computational biology: Applications to protein modeling. J. Mol. Biol. 1994, 235, 1501–1531. [Google Scholar]
- Krogh, A.; Larsson, B.; von Heijne, G.; Sonnhammer, E. Predicting transmembrane protein topology with a hidden Markov model: Application to complete genomes. J. Mol. Biol. 2001, 305, 567–580. [Google Scholar]
- Eddy, S. Multiple Alignment Using Hidden Markov Models. Proceedings of the Third International Conference on Intelligent Systems for Molecular Biology, Cambridge, UK, 16–19 July 1995; Volume 3, pp. 114–120.
- Eddy, S. Profile hidden Markov models. Bioinformatics 1998, 14, 755–763. [Google Scholar]
- Lunter, G. Probabilistic whole-genome alignments reveal high indel rates in the human and mouse genomes. Bioinformatics 2007, 23, i289–i296. [Google Scholar]
- Mailund, T.; Dutheil, J.Y.; Hobolth, A.; Lunter, G.; Schierup, M.H. Estimating divergence time and ancestral effective population size of bornean and sumatran orangutan subspecies using a coalescent hidden Markov model. PLoS Genet. 2011, 7, e1001319. [Google Scholar]
- Siepel, A.; Haussler, D. Phylogenetic Hidden Markov Models. In Statistical Methods in Molecular Evolution; Nielsen, R., Ed.; Springer: New York, NY, USA, 2005; pp. 325–351. [Google Scholar]
- Antonov, I.; Borodovsky, M. GeneTack: Frameshift identification in protein-coding sequences by the Viterbi algorithm. J. Bioinforma. Comput. Biol. 2010, 8, 535–551. [Google Scholar]
- Lukashin, A.; Borodovsky, M. GeneMark.hmm: New solutions for gene finding. Nucleic Acids Res. 1998, 26, 1107–1115. [Google Scholar]
- Krogh, A.; Mian, I.S.; Haussler, D. A hidden Markov model that finds genes in E.coli DNA. Nucleic Acids Res. 1994, 22, 4768–4778. [Google Scholar]
- Aston, J.A.D.; Martin, D.E.K. Distributions associated with general runs and patterns in hidden Markov models. Ann. Appl. Stat. 2007, 1, 585–611. [Google Scholar]
- Fu, J.; Koutras, M. Distribution theory of runs: A Markov chain approach. J. Am. Stat. Appl. 1994, 89, 1050–1058. [Google Scholar]
- Nuel, G. Pattern Markov chains: Optimal Markov chain embedding through deterministic finite automata. J. Appl. Probab. 2008, 45, 226–243. [Google Scholar]
- Wu, T.L. On finite Markov chain imbedding and its applications. Methodol. Comput. Appl. Probab. 2011, 15, 453–465. [Google Scholar]
- Lladser, M.; Betterton, M.; Knight, R. Multiple pattern matching: A Markov chain approach. J. Math. Biol. 2008, 56, 51–92. [Google Scholar]
- Nicodeme, P.; Salvy, B.; Flajolet, P. Motif statistics. Theor. Comput. Sci. 2002, 287, 593–617. [Google Scholar]
- Fariselli, P.; Martelli, P.L.; Casadio, R. A new decoding algorithm for hidden Markov models improves the prediction of the topology of all-beta membrane proteins. BMC Bioinformatics 2005, 6. [Google Scholar] [CrossRef]
- Thompson, K. Programming techniques: Regular expression search algorithm. Commun. ACM 1968, 11, 419–422. [Google Scholar]
- Møller, A. dk.brics.automaton—Finite-State Automata and Regular Expressions for Java. 2010. Available online: http://www.brics.dk/automaton/ (accessed on 16 January 2012).
- Burset, M.; Guigo, R. Evaluation of gene structure prediction programs. Genomics 1996, 34, 353–367. [Google Scholar]
- Mohri, M. Weighted Automata Algorithms. In Handbook of Weighted Automata; Springer: Berlin/Heidelberg, Germany, 2009; pp. 213–254. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Tataru, P.; Sand, A.; Hobolth, A.; Mailund, T.; Pedersen, C.N.S. Algorithms for Hidden Markov Models Restricted to Occurrences of Regular Expressions. Biology 2013, 2, 1282-1295. https://doi.org/10.3390/biology2041282
Tataru P, Sand A, Hobolth A, Mailund T, Pedersen CNS. Algorithms for Hidden Markov Models Restricted to Occurrences of Regular Expressions. Biology. 2013; 2(4):1282-1295. https://doi.org/10.3390/biology2041282
Chicago/Turabian StyleTataru, Paula, Andreas Sand, Asger Hobolth, Thomas Mailund, and Christian N. S. Pedersen. 2013. "Algorithms for Hidden Markov Models Restricted to Occurrences of Regular Expressions" Biology 2, no. 4: 1282-1295. https://doi.org/10.3390/biology2041282
APA StyleTataru, P., Sand, A., Hobolth, A., Mailund, T., & Pedersen, C. N. S. (2013). Algorithms for Hidden Markov Models Restricted to Occurrences of Regular Expressions. Biology, 2(4), 1282-1295. https://doi.org/10.3390/biology2041282



