Use of Multivariate Adaptive Regression Splines (MARS) and Classification and Regression Tree (CART) Data Mining Algorithms to Predict Live Body Weight of Tswana Sheep
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
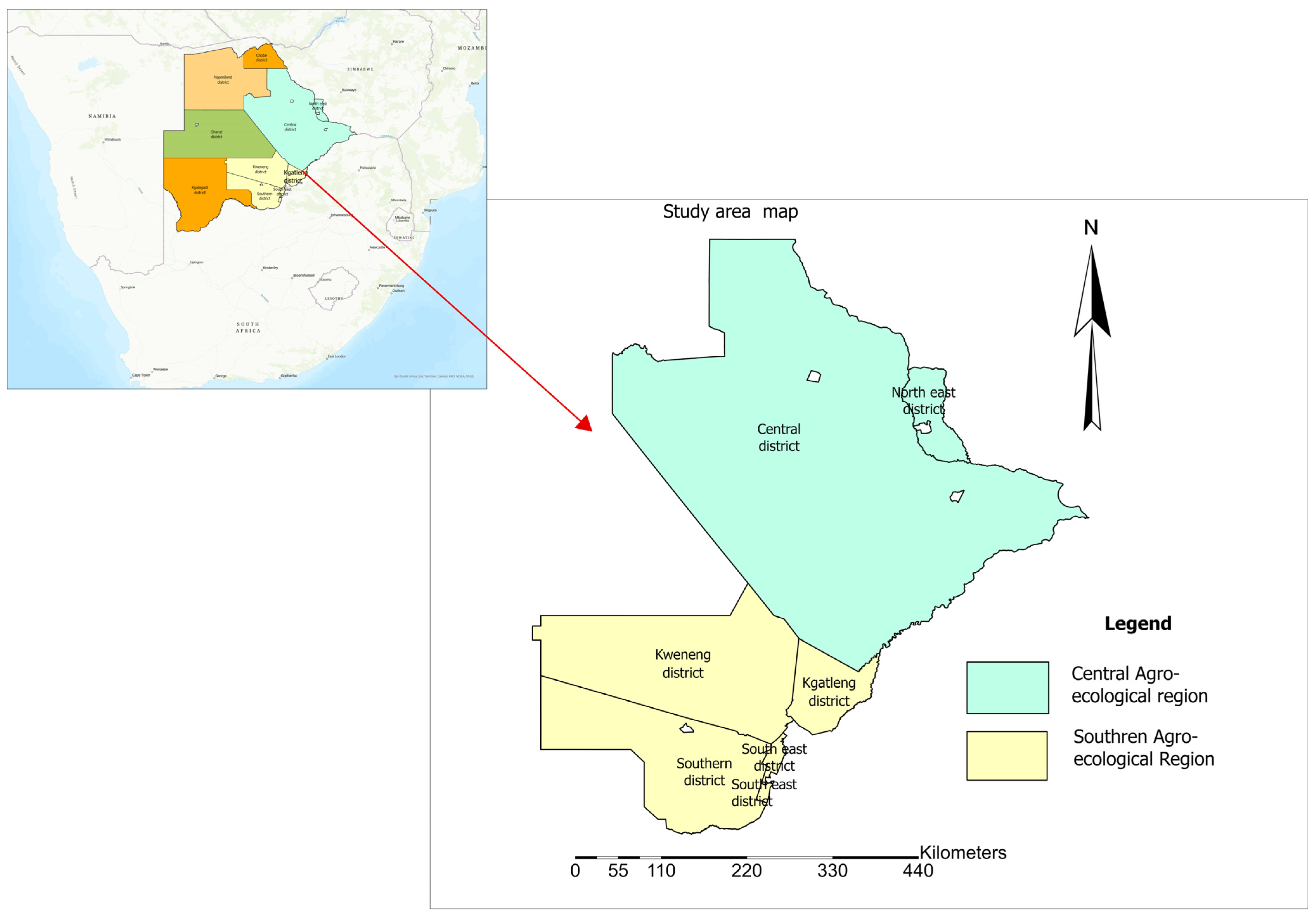
2.1. Study Site
2.2. Source of Animal and Management
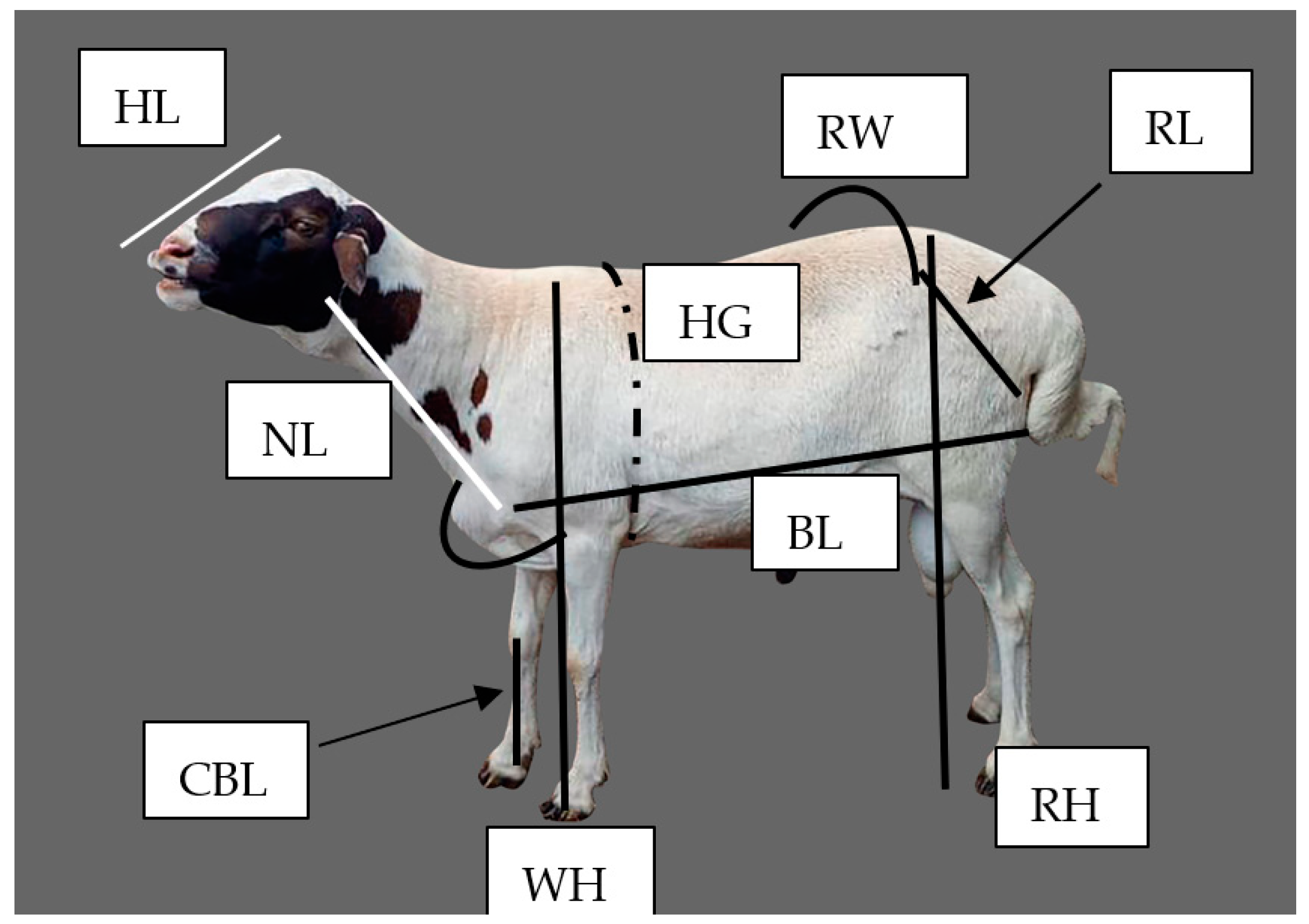
2.3. Sampling Methods
- n = the required sample size,
- N = the population size,
- e = the acceptable error of estimation (0.05).
2.4. Data Collection Procedures
2.5. Statistical Analysis
2.5.1. Descriptive Statistical Analysis
- Yij = Body weight or linear body measurement,
- µ = overall mean,
- Si = the fixed effect of the ith sex (i = male, female),
- eij = random residual error.
2.5.2. Multivariate Adaptive Regression Spline (MARS) Algorithm
2.5.3. Classification and Regression Tree (CART) Algorithm
2.5.4. Goodness of Fit Test
3. Results
3.1. Descriptive Statistics
3.2. Pearson’s Correlation Coefficients Between BW and Linear Body Measurements
3.3. MARS Model Outcome
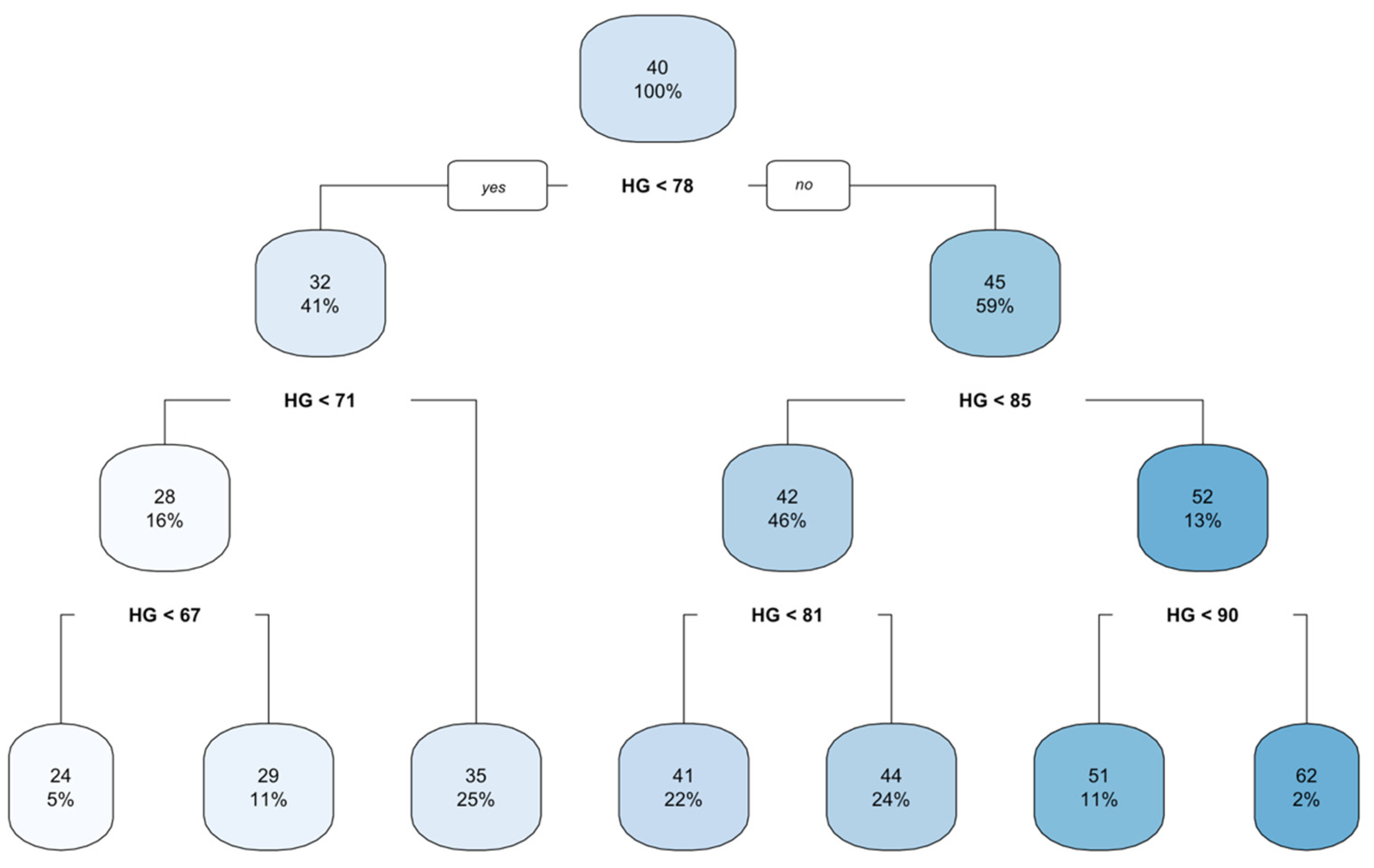
3.4. CART Model
3.5. Comparison of MARS and CART Data Mining Algorithms
4. Discussion
4.1. Pearson’s Correlation Coefficients
4.2. MARS Model
4.3. MARS and CART Data Mining Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bolowe, M.A.; Thutwa, K.; Monau, P.I.; Malejane, C.; Kgwatalala, P.M. Production Characteristics and Management Practices of Indigenous Tswana Sheep in Southern Districts of Botswana. Animals 2022, 12, 830. [Google Scholar] [CrossRef] [PubMed]
- Fatih, A.; Celik, S.; Eyduran, E.; Tirink, C.; Tariq, M.M.; Sheikh, I.S.; Faraz, A.; Waheed, A. Use of MARS algorithm for predicting mature weight of different camel (Camelus dromedarius) breeds reared in Pakistan and morphological characterization via cluster analysis. Trop. Anim. Health Prod. 2021, 53, 191. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Dahiya, S.P.; Malik, Z.S.; Patil, C.S. Prediction of body weight from linear body measurements in sheep. Indian J. Anim. Res. 2017, 52, 1263–1266. [Google Scholar] [CrossRef]
- Abera, B.; Kebede, K.; Gizaw, S. Indigenous Breeding Practices and Selection Criteria of Sheep Breed in Selale Area, Central Ethiopia. Int. J. Livest. Res. 2014, 4, 49–56. [Google Scholar] [CrossRef]
- Bila, L.; Malatji, D.P.; Tyasi, T.L. Predicting body weight of South African Sussex cattle at weaning using multivariate adaptive regression splines and classification and regression tree data mining algorithms. J. Appl. Anim. Res. 2023, 51, 608–615. [Google Scholar] [CrossRef]
- Phaladi, A.M.; Tyasi, T.L.; Tada, O.; Mogashoa, S. Use of data mining algorithms to predict body weight of Dorper sheep Breed in two selected villages of Lepelle-Nkumpi local municipality in Limpopo province, South Africa. Smart Agric. Technol. 2024, 8, 100479. [Google Scholar] [CrossRef]
- Tirink, C.; Tosun, R.; Saftan, M.; Kaya, E.; Atalay, A.I. Prediction of Birth Weight from Body Measurements with the CART Algorithm in Morkaraman Lambs. Large Anim. Rev. 2022, 28, 187–192. [Google Scholar]
- Tyasi, T.L.; Mathye, N.D.; Danguru, L.W.; Rashijane, L.T.; Mokoena, K.; Makgowo, K.M.; Mathapo, M.C.; Molabe, K.M.; Bopape, P.M.; Maluleke, D. Correlation and path analysis of body weight and biometric traits of Nguni cattle breed. J. Adv. Vet. Anim. Res. 2020, 7, 148–155. [Google Scholar] [CrossRef]
- Mathapo, M.C.; Mugwabana, T.J.; Tyasi, T.L. Prediction of body weight from morphological traits of South African non-descript indigenous goats of Lepelle-Nkumbi Local Municipality using different data mining algorithm. Trop. Anim. Health Prod. 2022, 54, 101–109. [Google Scholar] [CrossRef]
- Norris, D.; Brown, D.; Moela, A.K.; Selolo, T.C.; Mabelebele, M.; Ngambi, J.W.; Tyasi, T.L. Path coefficient and path analysis of body weight and biometrie traits in indigenous goats. Indian J. Anim. Res. 2015, 49, 573–578. [Google Scholar]
- Faraz, A.; Tirink, C.; Eyduran, E.; Waheed, A.; Tauqir, N.A.; Nabeel, M.S.; Tariq, M.M. Prediction of live body weight based on body measurements in Thalli sheep under tropical conditions of Pakistan using cart and mars. Trop. Anim. Health Prod. 2021, 53, 301. [Google Scholar] [CrossRef] [PubMed]
- Atta, M.; Ali, A.; Baker, S.; Mohamed, M.B.; Al-Dosari, H.M.; Al-Shamari, H.S. Prediction of body weight using body measurements in some sheep and goats in Qatar. J. Appl. Anim. Res. 2023, 52, 2288917. [Google Scholar] [CrossRef]
- Eyduran, E.; Zaborski, D.; Waheed, A.; Celik, S.; Karadas, K.; Grzesiak, W. Comparison of the predictive capabilities of several data mining algorithms and multiple linear regression in the prediction of body weight by means of body measurements in the indigenous Beetal goat of Pakistan. Pak. J. Zool. 2017, 49, 257–265. [Google Scholar] [CrossRef]
- Celik, S. Comparing predictive performances of tree-based data mining algorithms and Mars algorithm in the prediction of live body weight from body traits in Pakistan goats. Pak. J. Zool. 2019, 51, 1447–1456. [Google Scholar] [CrossRef]
- Aytekin, I.; Eyduran, E.; Karadas, K.; Akşahan, R.; Keskin, I. Prediction of fattening final live weight from some body measurements and fattening period in young bulls of crossbred and exotic breeds using MARS data mining algorithm. Pak. J. Zool. 2018, 50, 189–195. [Google Scholar] [CrossRef]
- Altay, Y.; Boztepe, S.; Eyduran, E.; Keskin, I.; Tariq, M.M.; Bukhari, F.A.; Ali, I. Description of factors affecting wool finness in Karacabey merino sheep using chaid and Mars Algorithms. Pak. J. Zool. 2021, 53, 691–697. [Google Scholar]
- Huma, Z.E.; Iqbal, F. Predicting the body weight of Balochi sheep using a machine learning approach. Turk. J. Vet. Anim. Sci. 2019, 43, 500–506. [Google Scholar] [CrossRef]
- Celik, S.; Yilmaz, O. comparison of different data mining algorithms for prediction of body weight from several morphological measurements in dogs. J. Anim. Plant Sci. 2017, 27, 57. [Google Scholar]
- Friedman, F. Multivariate Adaptive Regression Plines. Ann. Stat. 1991, 19, 1–144. [Google Scholar]
- Sengül, T.; Çelik, S.; Sengül, Ö. Use of multivariate adaptive regression splines (MARS) for predicting parameters of breast meat in quails. J. Anim. Plant Sci. 2020, 30, 786–793. [Google Scholar]
- Hlokoe, V.R.; Mokoena, K.; Tyasi, T.L. Using multivariate adaptive regression splines and classification and regression tree data mining algorithms to predict body weight of Nguni cows. J. Appl. Anim. Res. 2022, 50, 534–539. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2020; pp. 173–220. [Google Scholar]
- Sam, I.M.; Usoro, O.O.; Udo, A.F. Relationship of linear body measurements with live body weight in West African Dwarf sheep raised in Tropical Rainforest of Nigeria. JASVM 2023, 8, 46–51. [Google Scholar] [CrossRef]
- Abera, M.; Kebede, K.; Mengesha, Y. Phenotypic Characterization of Indigenous Sheep Types in Northern Ethiopia. J. Nat. Sci. Res. 2016, 6, 16–27. [Google Scholar]
- Demeke, T.; Getachew, T.; Bayou, E. On farm Phenotypic Characterization of Indigenous Sheep Breeds within Their Production Systems in Meket and Gidan District, North Wollo Zone, Ethiopia. Int. J. Sci. Res. 2020, 6, 29–39. [Google Scholar]
- Rashijane, L.T.; Mokoena, K.; Tyasi, T.L. Using Multivariate Adaptive Regression Splines to Estimate the Body Weight of Savanna Goats. Animals 2023, 13, 1146. [Google Scholar] [CrossRef]
- Çanga, D. Use of MARS Data Mining Algorithm Based on Training and Test Sets in Determining Carcass Weight of Cattle in Different Breeds. Tarim Bilim. Derg. 2022, 28, 259–268. [Google Scholar] [CrossRef]
- Komadja, G.C.; Rana, A.; Glodji, L.A.; Anye, V.C.; Jadaun, G.; Onwualu, P.A.; Sawmliana, C. Assessing Ground Vibration Caused by Rock Blasting in Surface Mines Using Machine-Learning Approaches: A Comparison of CART, SVR and MARS. Sustainability 2022, 14, 11060. [Google Scholar] [CrossRef]
- Mathapo, M.C.; Tyasi, T.L.; Mugwabana, J.T. Prediction of body weight from linear body measurement traits of Nguni goats in the Limpopo province. J. Appl. Anim. Res. 2025, 53, 1. [Google Scholar] [CrossRef]
- Matvieiev, M.; Bila, L.; Ugnivenko, A.; Nosevych, D.; Getya, A.; Tyasi, T.L. Application of data mining algorithms for estimating live body weight from linear body measurements of Ukrainian beef cattle breed. Appl. Ecol. Environ. Res. 2025, 23, 1853–1864. [Google Scholar]
- Celik, S.; Eyduran, E.; Karadas, K.; Tariq, M.M. Comparison of predictive performance of data mining algorithms in predicting body weight in Mengali rams of Pakistan. Rev. Bras. De Zootec. 2017, 46, 863–872. [Google Scholar] [CrossRef]
- Tırınk, C.; Önder, H.; Francois, D.; Marcon, D.; Şen, U.; Shaikenova, K.; Omarova, K.; Tyasi, T.L. Comparison of the data mining and machine learning algorithms for predicting the final body weight for Romane sheep breed. PLoS ONE 2023, 18, e0289348. [Google Scholar] [CrossRef] [PubMed]
- Assan, N.; Mpofu, M.M.; Musasira, M.; Mokoena, K.; Tyasi, T.L.; Mwareya, N. predicting body weight of three chicken genotypes from linear body measurements using mars and cart data mining algorithms. Appl. Ecol. Environ. Res. 2024, 22, 2531–2540. [Google Scholar] [CrossRef]
- Mathapo, M.C.; Mthembu, R.B.; Tsenane, A.J.; Sako, T.; Tyasi, T.L. Comparison of Multivariate Adaptive Regression Splines and Classification Regression Tree for Prediction of Body Weight of Bapedi Sheep. Am. J. Anim. Vet. Sci. 2024, 19, 226–232. [Google Scholar] [CrossRef]
- Marco, R.; Ahmad, S.S.S.; Ahmad, S. Bayesian Hyperparameter Optimization and Ensemble Learning for Machine Learning Models on Software Effort Estimation. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 419–429. [Google Scholar] [CrossRef]
| Trait | Rams | Ewes | ||||
|---|---|---|---|---|---|---|
| Mean ± SD | Min | Max | Mean ± SD | Min | Max | |
| BW (kg) | 43.20 ± 0.55 | 26.00 | 73.00 | 36.95 ± 0.35 | 20.00 | 59.00 |
| HG (cm) | 80.56 ± 0.44 | 65.00 | 99.00 | 75.41 ± 0.28 | 60.00 | 91.00 |
| BL (cm) | 62.67 ± 0.46 | 52.00 | 80.00 | 61.28 ± 0.29 | 32.00 | 75.00 |
| SW (cm) | 22.51 ± 0.20 | 17.00 | 31.00 | 20.59 ± 0.13 | 14.00 | 28.00 |
| NL (cm) | 31.65 ± 0.28 | 22.00 | 40.00 | 29.90 ± 0.18 | 18.00 | 38.00 |
| WH (cm) | 67.50 ± 0.34 | 52.00 | 79.00 | 63.23 ± 0.21 | 46.00 | 73.00 |
| RH (cm) | 66.64 ± 0.33 | 54.00 | 80.00 | 63.47 ± 0.21 | 42.00 | 73.00 |
| HW (cm) | 12.33 ± 0.11 | 8.00 | 17.00 | 10.45 ± 0.07 | 7.00 | 16.00 |
| HL (cm) | 16.92 ± 0.18 | 10.00 | 26.00 | 15.31 ± 0.11 | 9.00 | 27.00 |
| EW (cm) | 6.12 ± 0.07 | 4.00 | 8.00 | 5.83 ± 0.04 | 3.00 | 8.00 |
| EL (cm) | 11.87 ± 0.12 | 9.00 | 16.00 | 11.97 ± 0.07 | 8.00 | 16.00 |
| CBC (cm) | 7.79 ± 0.23 | 6.00 | 9.00 | 7.19 ± 0.14 | 5.00 | 10.00 |
| CBL (cm) | 15.98 ± 0.12 | 13.00 | 20.00 | 15.20 ± 0.08 | 11.00 | 18.00 |
| RL (cm) | 25.23 ± 0.32 | 14.00 | 33.00 | 23.44 ± 0.20 | 14.00 | 30.00 |
| RW (cm) | 17.33 ± 0.16 | 13.00 | 24.00 | 16.76 ± 0.10 | 12.00 | 22.00 |
| TL (cm) | 37.09 ± 0.41 | 26.00 | 49.00 | 34.56 ± 0.26 | 21.00 | 51.00 |
| TC (cm) | 21.75 ± 0.42 | 11.00 | 35.00 | 17.27 ± 0.27 | 8.50 | 37.00 |
| SC (cm) | 26.75 ± 0.23 | 16.00 | 32.00 | N/A | N/A | N/A |
| Trait | Rams | Ewes | Castrates |
|---|---|---|---|
| BW (kg) | 43.20 ± 0.55 a | 36.95 ± 0.35 b | 42.34 ± 0.63 a |
| HG (cm) | 80.56 ± 0.44 a | 75.41 ± 0.28 b | 80.62 ± 0.41 a |
| BL (cm) | 62.67 ± 0.46 | 61.28 ± 0.29 | 63.04 ± 0.40 |
| SW (cm) | 22.51 ± 0.20 a | 20.59 ± 0.13 b | 22.66 ± 0.23 a |
| NL (cm) | 31.65 ± 0.28 | 29.90 ± 0.18 | 32.00 ± 0.25 |
| WH (cm) | 67.50 ± 0.34 a | 63.23 ± 0.21 b | 66.79 ± 0.32 a |
| RH (cm) | 66.64 ± 0.33 a | 63.47 ± 0.21 b | 66.43 ± 0.27 a |
| HW (cm) | 12.33 ± 0.11 a | 10.45 ± 0.07 b | 12.43 ± 0.14 a |
| HL (cm) | 16.92 ± 0.18 a | 15.31 ± 0.11 b | 16.01 ± 0.22 a |
| EW (cm) | 6.12 ± 0.07 | 5.83 ± 0.04 | 5.98 ± 0.05 |
| EL (cm) | 11.87 ± 0.12 | 11.97 ± 0.07 | 11.91 ± 0.15 |
| CBC (cm) | 7.79 ± 0.23 a | 6.88 ± 0.14 b | 7.89 ± 0.21 a |
| CBL (cm) | 15.98 ± 0.12 | 15.20 ± 0.08 | 15.78 ± 0.15 |
| RL (cm) | 25.23 ± 0.32 a | 23.44 ± 0.20 b | 24.67 ± 0.41 a |
| RW (cm) | 17.33 ± 0.16 a | 16.76 ± 0.10 b | 17.67 ± 0.21 a |
| TL (cm) | 37.09 ± 0.41 a | 34.56 ± 0.26 b | 39.13 ± 0.36 a |
| TC (cm) | 21.75 ± 0.42 a | 17.27 ± 0.27 b | 23.61 ± 0.39 a |
| SC (cm) | 26.75 ± 0.23 | N/A | N/A |
| BW | HG | BL | SW | NL | WH | RH | HW | HL | EW | EL | CBC | CBL | RL | RW | TL | TC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BW | 0.99 ** | 0.83 ** | 0.72 ** | 0.53 ** | 0.80 ** | 0.85 ** | 0.38 | 0.49 * | 0.12 | 0.095 | 0.09 | 0.46 * | 0.66 ** | 0.52 ** | 0.21 | 0.20 | |
| HG | 0.99 ** | 0.82 ** | 0.76 ** | 0.55 ** | 0.81 ** | 0.85 ** | 0.36 | 0.50 * | 0.10 | 0.089 | 0.030 | 0.50 * | 0.66 ** | 0.53 ** | 0.21 | 0.17 | |
| BL | 0.79 ** | 0.64 ** | 0.52 ** | 0.33 | 0.57 ** | 0.70 ** | 0.22 | 0.30 | 0.14 | 0.028 | 0.020 | 0.41 * | 0.45 * | 0.35 | 0.01 | 0.01 | |
| SW | 0.66 ** | 0.49 * | 0.81 ** | 0.57 ** | 0.66 ** | 0.53 ** | 0.51 * | 0.51 * | −0.16 | −0.11 | −0.019 | 0.60 ** | 0.53 ** | 0.60 ** | 0.20 | −0.01 | |
| NL | 0.58 ** | 0.38 | 0.60 * | 0.45 * | 0.48 * | 0.44 * | 0.71 ** | 0.41 * | 0.042 | −0.014 | −0.33 | 0.30 | 0.48 * | 0.30 | 0.50 * | 0.09 | |
| WH | 0.80 ** | 0.73 * | 0.44 * | 0.27 | 0.31 | 0.90 ** | 0.34 | 0.48 * | 0.22 | 0.16 | 0.002 | 0.52 ** | 0.78 ** | 0.61 ** | 0.42 * | 0.12 | |
| RH | 0.77 ** | 0.67 ** | 0.50 | 0.37 | 0.27 | 0.66 ** | 0.22 | 0.36 | 0.36 | 0.13 | −0.030 | 0.46 * | 0.81 ** | 0.58 ** | 0.34 | 0.23 | |
| HW | 0.23 | 0.44 * | 0.38 | 0.34 | 0.22 | −0.29 | 0.34 | 0.52 ** | −0.08 | 0.13 | −0.22 | 0.26 | 0.21 | 0.20 | 0.40 | −0.32 | |
| HL | 0.38 | 0.45 * | 0.46 * | 0.22 | 0.72 ** | 0.32 | 0.37 | 0.19 | −0.04 | 0.12 | −0.04 | 0.26 | 0.15 | 0.016 | −0.01 | −0.11 | |
| EW | 0.091 | 0.38 | 0.22 | 0.45 * | 0.34 | 0.22 | −0.12 | −0.019 | −0.22 | 0.75 ** | 0.044 | 0.23 | 0.25 | −0.024 | 0.30 | 0.16 | |
| EL | 0.19 | −0.20 | 0.17 | 0.38 | −0.28 | −0.023 | −0.28 | 0.12 | 0.23 | 0.76 ** | 0.21 | 0.17 | −0.13 | −0.27 | 0.13 | −0.17 | |
| CBC | 0.10 | 0.11 | −0.21 | −0.13 | 0.23 | 0.44 * | 0.27 | 0.14 | −0.38 | −0.20 | −0.012 | −0.004 | −0.14 | −0.033 | −0.16 | −0.07 | |
| CBL | 0.38 * | 0.27 | 0.10 | 0.23 | 0.37 | 0.29 | 0.31 | 0.19 | −0.41 | 0.34 | 0.23 | 0.20 | 0.51 * | 0.48 * | 0.25 | −0.04 | |
| RL | 0.57 ** | 0.33 | 0.22 | 0.27 | 0.19 | 0.092 | 0.24 | 0.34 | 0.29 | −0.23 | −0.14 | 0.23 | −0.29 | 0.80 ** | 0.50 * | 0.43 * | |
| RW | 0.61 ** | 0.56 * | 0.39 | 0.22 | 0.42 | 0.51 * | 0.70 * | 0.26 | 0.19 | −0.27 | −0.22 | 0.30 | 0.27 | 0.41 * | 0.40 | 0.17 | |
| TL | 0.18 | 0.31 | 0.22 | 0.32 | 0.28 | 0.19 | 0.32 | −0.098 | 0.21 | 0.29 | 0.15 | 0.21 | −0.67 | −0.33 | −0.56 | 0.40 | |
| TC | 0.11 | 0.19 | 0.19 | 0.16 | 0.22 | 0.34 | 0.24 | 0.33 | 0.36 | 0.21 | −0.021 | 0.32 | −0.09 | 0.06 | 0.15 | 0.42 * |
| BW | HG | BL | SW | NL | WH | RH | HW | HL | EW | EL | CBC | CBL | RL | RW | TL | TC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BW | 0.99 ** | 0.77 ** | 0.58 ** | 0.12 | 0.32 | 0.41 | 0.01 | 0.20 | 0.35 | 0.25 | 0.41 | 0.56 * | 0.57 ** | 0.63 ** | 0.20 | 0.44 * | |
| HG | 0.78 ** | 0.58 ** | 0.08 | 0.32 | 0.42 * | −0.02 | 0.18 | 0.34 | 0.22 ns | 0.42 * | 0.55 ** | 0.59 ** | 0.62 ** | 0.20 | 0.43 * | ||
| BL | 0.55 ** | 0.31 | 0.29 | 0.42 * | 0.27 | 0.15 | 0.10 | 0.11 | 0.39 | 0.42 * | 0.46 * | 0.54 ** | −0.01 | 0.38 | |||
| SW | 0.42 * | 0.31 | 0.40 | 0.04 | 0.54 ** | 0.16 | 0.06 | 0.41 ns | 0.52 * | 0.48 * | 0.61 ** | 0.23 | 0.34 | ||||
| NL | 0.52 * | 0.40 | 0.34 | 0.62 ** | 0.08 | 0.42 * | 0.42 * | 0.56 ** | 0.16 | 0.45 * | 0.30 | 0.38 | |||||
| WH | 0.89 ** | 0.05 | 0.49 | 0.25 | 0.45 * | 0.20 | 0.77 ** | 0.44 * | 0.63 ** | 0.59 ** | 0.22 | ||||||
| RH | −0.11 | 0.40 | 0.19 | 0.18 | 0.18 | 0.65 ** | 0.57 ** | 0.67 ** | 0.42 * | 0.33 | |||||||
| HW | 0.14 | −0.11 | 0.41 | 0.23 | 0.05 | −0.25 | 0.10 | 0.15 | 0.02 | ||||||||
| HL | 0.11 | 0.44 * | 0.50 * | 0.72 ** | 0.16 | 0.41 | 0.33 | 0.39 | |||||||||
| EW | 0.48 * | −0.01 | 0.40 | 0.61 ** | 0.50 * | 0.45 * | 0.20 | ||||||||||
| EL | 0.33 | 0.54 ** | 0.05 | 0.23 | 0.46 * | 0.11 | |||||||||||
| CBC | 0.55 ** | 0.12 | 0.24 | −0.09 | 0.41 | ||||||||||||
| CBL | 0.45 * | 0.71 ** | 0.54 ** | 0.43 * | |||||||||||||
| RL | 0.80 ** | 0.46 * | 0.39 | ||||||||||||||
| RW | 0.42 * | 0.61 ** | |||||||||||||||
| TL | 0.08 | ||||||||||||||||
| TC |
| Variables | Coefficients |
|---|---|
| Intercept | 46.32 |
| h (84-HG) | −1.11 |
| h (HG84) | 1.81 |
| Estimator | Model | RMSE | Rsq | CV | F-Value |
|---|---|---|---|---|---|
| Rams | |||||
| HG | BW = −60.14 + 1.29HG | 1.43 | 0.976 | 3.37 | 5581.33 ** |
| HG + BL | BW = −68.43 + 0.65HG + 0.94BL | 1.04 | 0.987 | 2.46 | 5288.24 ** |
| HG + BL + SW | BW = −58.89 + 0.53HG + 0.73BL + 0.61SW | 0.98 | 0.989 | 2.31 | 4031.80 ** |
| HG + BL + SW + WH | BW = −58.5 + 0.53HG + 0.73BL + 0.62SW − 0.02WH | 0.978 | 0.989 | 2.31 | 3002.07 ** |
| Ewes | |||||
| HG | BW = −49.86 + 1.15HG | 0.744 | 0.989 | 1.93 | 33041.2 ** |
| HG + BL | BW = −49.71 + 1.10HG + 0.06BL | 0.741 | 0.989 | 1.92 | 16668.1 ** |
| HG + BL + WH | BW = −50.79 + 1.09HG = 0.03BL + 0.06WH | 0.741 | 0.989 | 1.92 | 11105.3 ** |
| Castrates | |||||
| HG | BW = −60.10 + 1.28HG | 1.78 | 0.962 | 4.22 | 3517.47 ** |
| HG + BL | BW = −66.55 + 0.70HG + 086BL | 1.40 | 0.977 | 3.31 | 2889.75 ** |
| HG + BL + RW | BW = −55.87 + 053HG + 0.61BL + 1.04RW | 1.22 | 0.983 | 2.88 | 2561.89 ** |
| Complexity | Parameter | Number of Splits | Relative Error | Mean of the Error |
|---|---|---|---|---|
| 1 | 0.61 | 0 | 1.00 | 1.00 |
| 2 | 0.17 | 1 | 0.38 | 0.39 |
| 3 | 0.09 | 2 | 0.21 | 0.22 |
| 4 | 0.03 | 3 | 0.12 | 0.12 |
| 5 | 0.03 | 4 | 0.09 | 0.12 |
| 6 | 0.02 | 5 | 0.06 | 0.08 |
| 7 | 0.01 | 6 | 0.04 | 0.05 |
| MARS | CART | |||
|---|---|---|---|---|
| Criterion | Training | Test | Training | Test |
| RMSE | 0.476 | 0.442 | 1.611 | 1.917 |
| RRMSE | 1.200 | 1.095 | 4.059 | 4.475 |
| SDR | 0.060 | 0.049 | 0.209 | 0.212 |
| CV | 1.200 | 1.100 | 4.060 | 4.750 |
| R | 0.998 | 0.999 | 0.978 | 0.977 |
| PI | 0.601 | 0.548 | 2.052 | 2.400 |
| ME | 0.000 | 0.021 | 0.000 | −0.009 |
| RAE | 0.000 | 0.000 | 0.002 | 0.002 |
| MAPE | 0.975 | 0.860 | 3.465 | 3.690 |
| MAD | 0.371 | 0.329 | 1.302 | 1.454 |
| Rsq | 0.996 | 0.998 | 0.956 | 0.995 |
| ARSq | 0.996 | 0.998 | 0.956 | 0.995 |
| AIC | −669.26 | −307.34 | 433.89 | 249.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolowe, M.A.; Bila, L.; Thutwa, K.; Kgwatalala, P.M. Use of Multivariate Adaptive Regression Splines (MARS) and Classification and Regression Tree (CART) Data Mining Algorithms to Predict Live Body Weight of Tswana Sheep. Biology 2025, 14, 1516. https://doi.org/10.3390/biology14111516
Bolowe MA, Bila L, Thutwa K, Kgwatalala PM. Use of Multivariate Adaptive Regression Splines (MARS) and Classification and Regression Tree (CART) Data Mining Algorithms to Predict Live Body Weight of Tswana Sheep. Biology. 2025; 14(11):1516. https://doi.org/10.3390/biology14111516
Chicago/Turabian StyleBolowe, Monosi Andries, Lubabalo Bila, Ketshephaone Thutwa, and Patrick Monametsi Kgwatalala. 2025. "Use of Multivariate Adaptive Regression Splines (MARS) and Classification and Regression Tree (CART) Data Mining Algorithms to Predict Live Body Weight of Tswana Sheep" Biology 14, no. 11: 1516. https://doi.org/10.3390/biology14111516
APA StyleBolowe, M. A., Bila, L., Thutwa, K., & Kgwatalala, P. M. (2025). Use of Multivariate Adaptive Regression Splines (MARS) and Classification and Regression Tree (CART) Data Mining Algorithms to Predict Live Body Weight of Tswana Sheep. Biology, 14(11), 1516. https://doi.org/10.3390/biology14111516





