Novel Model for Stomatal Conductance: Enhanced Accuracy Under Variable Irradiance and CO2 in C3 Plant Species
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Stomatal Conductance Models Description
2.1.1. Stomatal Conductance of Ball–Woodrow–Berry Model
2.1.2. Stomatal Conductance Model of Medlyn et al. [26]
2.1.3. Stomatal Conductance Model by Ye et al. [2]
2.2. Study Site and Plants
2.3. Gas Exchange and Chl Fluorescence Measurement
2.4. Statistical Analysis
3. Results
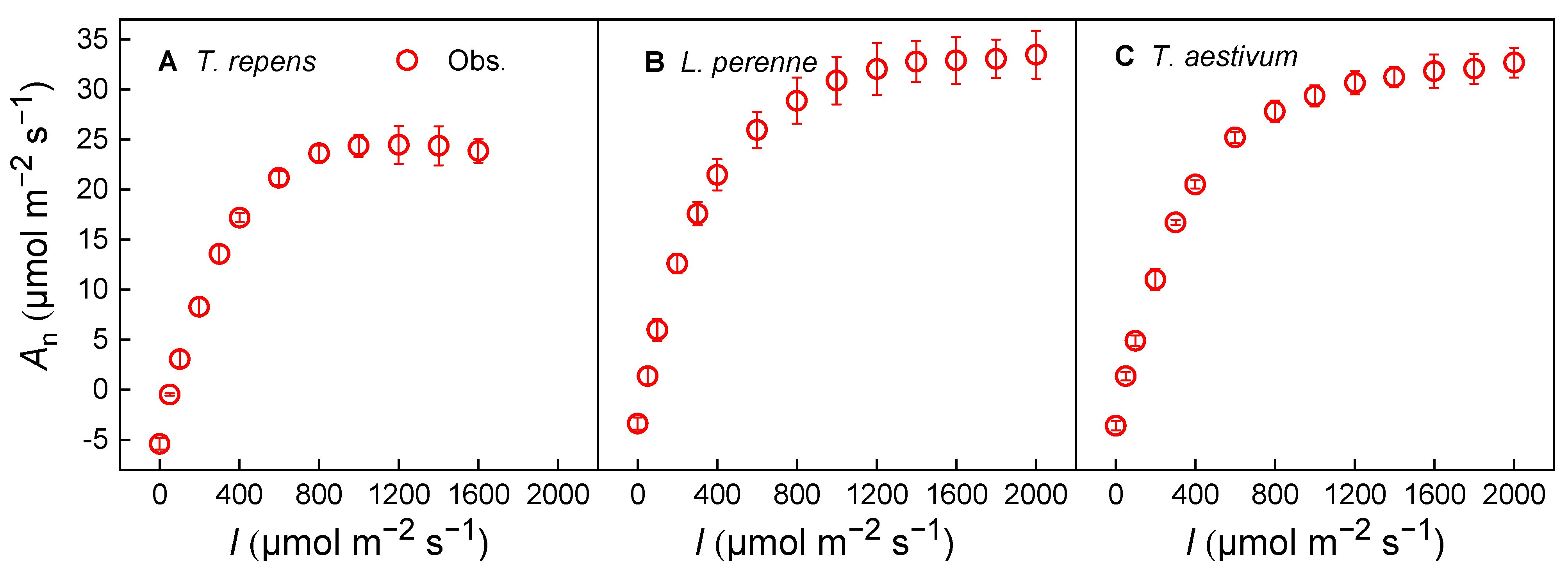
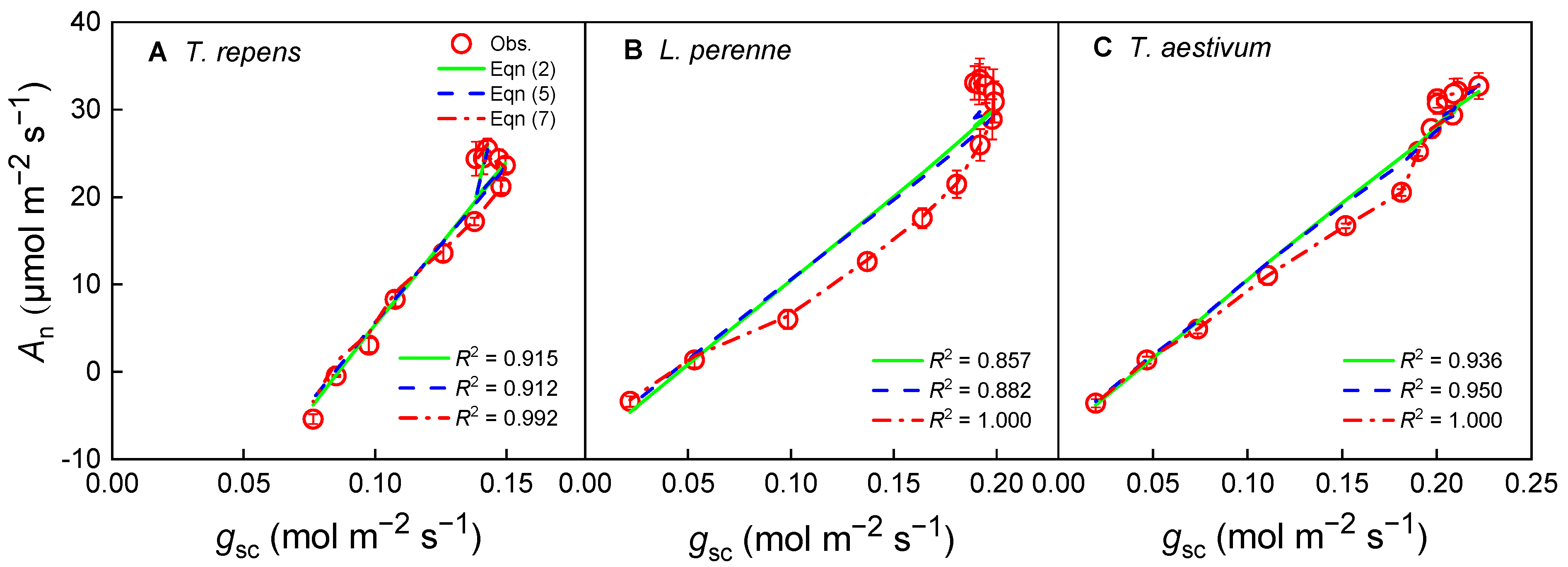
3.1. Photosynthesis and Stomatal Conductance Response Under Variable Irradiance
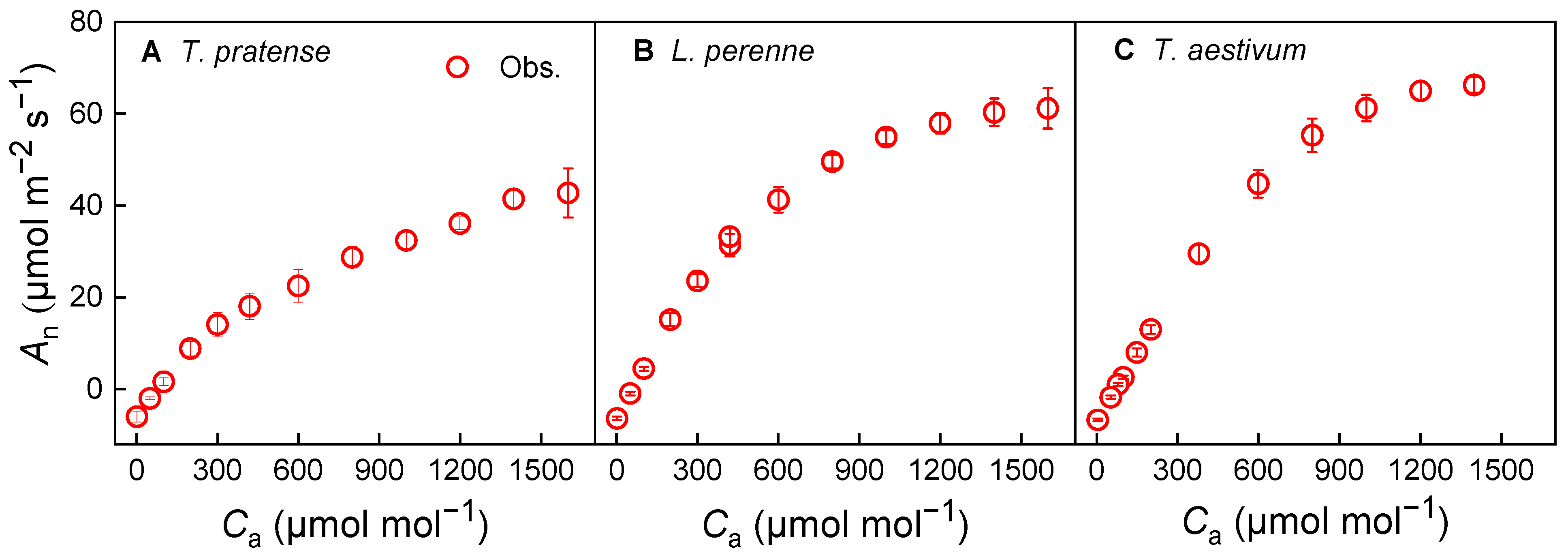
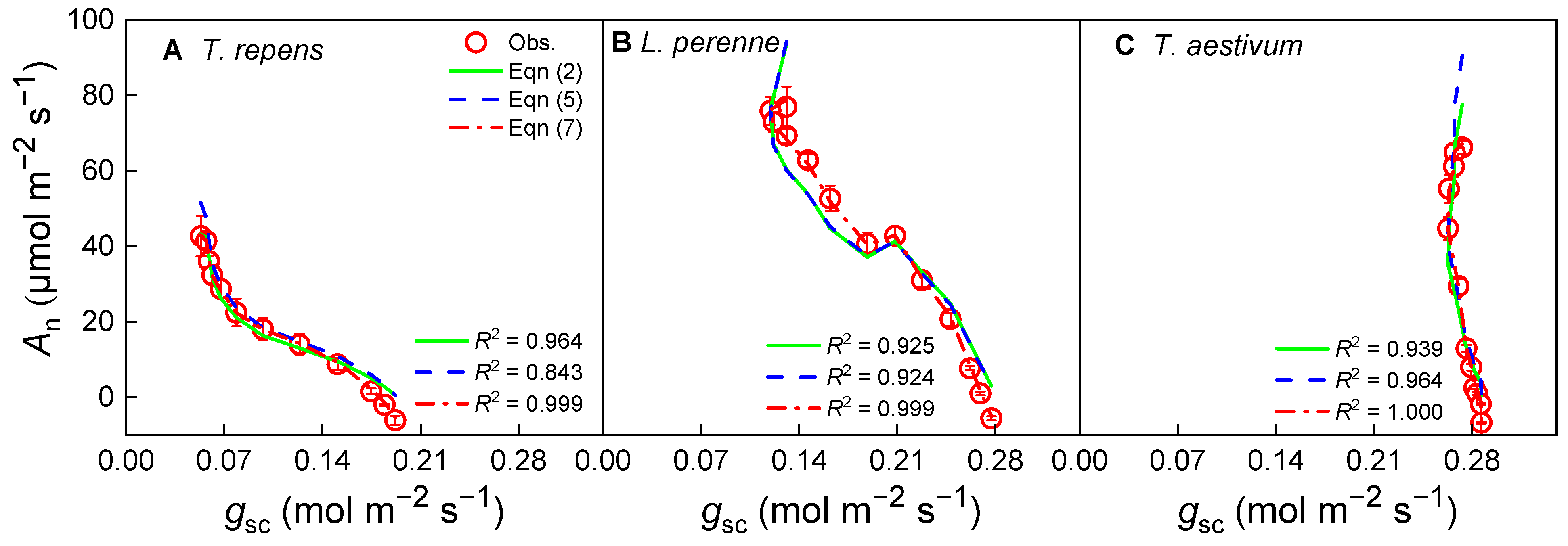
3.2. Photosynthesis and Stomatal Conductance Response Under Variable CO2 Concentration at Isat
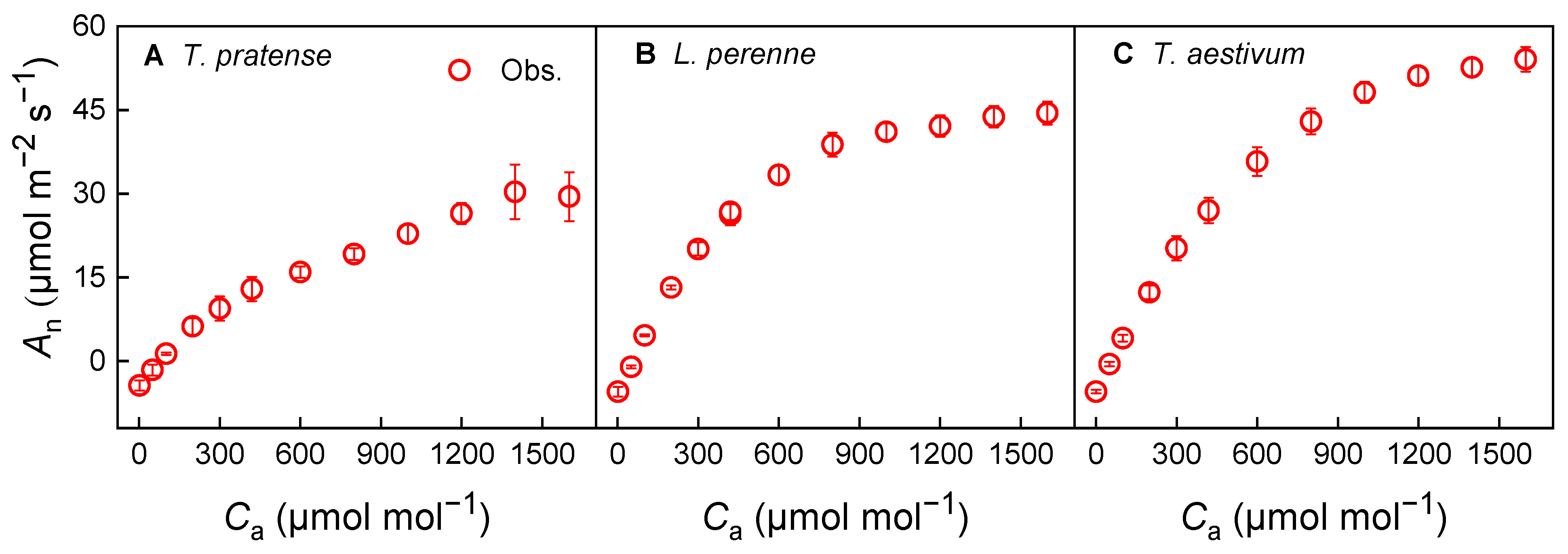
3.3. Photosynthesis and Stomatal Conductance Response Under Variable CO2 Concentration at Half of Isat
4. Discussions
4.1. Theoretical Framework and Innovation of the New Model by Ye et al. [2]
4.2. Model Comparison and Fit
4.3. Photosynthetic Response and Stomatal Conductance
4.4. Limitations and Future Perspectives
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, S.H.; Leith, H.J. A coupled model of photosynthesis, stomatal conductance and transpiration for a rose leaf (Rosa hybrida L.). Ann. Bot. 2003, 91, 771–781. [Google Scholar] [CrossRef]
- Ye, Z.P.; He, J.Q.; An, T.; Duan, S.H.; Kang, H.J.; Wang, F.B. Infuences of residual stomatal conductance on the intrinsic water use effciency of two C3 and two C4 species. Agric. Water Manag. 2024, 306, 109136. [Google Scholar] [CrossRef]
- Ozeki, K.; Miyazawa, Y.; Sugiura, D. Rapid stomatal closure contributes to higher water use efficiency in major C4 compared to C3 Poaceae crops. Plant Physiol. 2022, 189, 188–203. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Wang, Z.; Zhang, Y.; Li, J.; Jia, L.; Chen, Q.; Ding, Y.; Wang, S.H. A mechanistic model for estimating rice photosynthetic capacity and stomatal conductance from sun-induced chlorophyll fluorescence. Plant Phenomics 2023, 5, 47. [Google Scholar] [CrossRef]
- Liang, X.; Wang, D.; Ye, Q.; Zhang, J.; Liu, M.; Liu, H.; Yu, K.L.; Wang, Y.J.; Hou, E.Q.; Zhong, B.Q.; et al. Stomatal responses of terrestrial plants to global change. Nat. Commun. 2023, 14, 2188. [Google Scholar] [CrossRef]
- Ru, C.; Liu, Y.X.; Wang, W.; Hu, X.T. Moderate intermittent water deficit enhances dry matter remobilization, nitrogen uptake, and water and nitrogen use efficiency in winter wheat. Agric. Commun. 2025, 3, 100098. [Google Scholar] [CrossRef]
- Tao, L.; Johannes, K.; Ep, H.; Van, N.F.R.; Elias, K.; Marcelis, L.F.M. Effects of diffuse light on radiation use efficiency of two Anthurium cultivars depend on the response of stomatal conductance to dynamic light intensity. Front. Plant Sci. 2016, 7, 56. [Google Scholar] [CrossRef]
- Zhang, N.Y.; Li, G.; Yu, S.X.; An, D.S.; Sun, Q.; Luo, W.H.; Yin, X. Can the responses of photosynthesis and stomatal conductance to water and nitrogen stress combinations be modeled using a single set of parameters? Front. Plant Sci. 2017, 8, 328. [Google Scholar] [CrossRef] [PubMed]
- Zait, Y.; Ferrero-Serrano, A.; Assmann, S.M. The alpha subunit of the heterotrimeric G protein regulates mesophyll CO2 conductance and drought tolerance in rice. New Phytol. 2021, 232, 2324–2338. [Google Scholar] [CrossRef]
- Wei, Z.; Abdelhakim, L.O.A.; Fang, L.; Peng, X.; Liu, J.; Liu, F. Elevated CO2 effect on the response of stomatal control and water use efficiency in amaranth and maize plants to progressive drought stress. Agric. Water Manag. 2022, 266, 107609. [Google Scholar] [CrossRef]
- Dow, G.J.; Bergmann, D.C.; Berry, J.A. An integrated model of stomatal development and leaf physiology. New Phytol. 2014, 201, 1218–1226. [Google Scholar] [CrossRef]
- Silva-Pérez, V.; Furbank, R.T.; Condon, A.G.; Evans, J. Biochemical model of C3 photosynthesis applied to wheat at different temperatures. Plant. Cell Environ. 2017, 40, 1552–1564. [Google Scholar] [CrossRef] [PubMed]
- Fila, G.; Badeck, F.W.; Meyer, S.; Cerovic, Z.; Ghashghaie, A.J. Relationships between leaf conductance to CO2 diffusion and photosynthesis in micropropagated grapevine plants, before and after ex vitro acclimatization. J. Exp. Bot. 2006, 57, 2687–2695. [Google Scholar] [CrossRef]
- Buckley, T.N.; Turnbull, T.L.; Adams, M.A. Simple models for stomatal conductance derived from a process model: Cross-validation against sap flux data. Plant. Cell Environ. 2012, 35, 1647–1662. [Google Scholar] [CrossRef]
- Lv, Y.; Xu, J.; Liu, X. A process-based coupled model of stomatal conductance–photosynthesis–transpiration during leaf ontogeny for water-saving irrigated rice. Photosynth. Res. 2021, 147, 145–160. [Google Scholar] [CrossRef] [PubMed]
- Sakurai, G.; Miklavcic, S.J. A whole leaf comparative study of stomatal conductance models. Front. Plant Sci. 2022, 13, 766975. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, X.; Lv, S.Y.; Lin, X.H.; Ma, J.F.; Liu, J.M.; Fang, Q.Z.; Tang, L.; Liu, L.L.; Cao, W.X.; et al. Improving the predictions of leaf photosynthesis during and after short-term heat stress with current rice models. Plant. Cell Environ. 2023, 46, 3353–3370. [Google Scholar] [CrossRef] [PubMed]
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A model predicting stomatal conductance and its contribution to photosynthesis. In Physiological Plant Ecology; Houghton, G.H.F., Ed.; Springer: Cham, Switzerland, 1987; Volume 4, pp. 221–224. [Google Scholar]
- Collatz, G.J.; Ball, J.T.; Grivet, C.; Berry, J.A. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorol. 1991, 54, 107–136. [Google Scholar] [CrossRef]
- Leuning, R. A critical appraisal of a combined stomatal photosynthesis model for C3 plants. Plant. Cell Environ. 1995, 18, 339–355. [Google Scholar] [CrossRef]
- Leuning, R. Modelling stomatal behaviour and photosynthesis of Eucalyptus grandis. Aust. J. Plant Physiol. 1990, 17, 159–175. [Google Scholar] [CrossRef]
- Tuzet, A.; Perrier, A.; Leuning, R. A coupled model of stomatal conductance, photosynthesis and transpiration. Plant. Cell Environ. 2003, 26, 1097–1116. [Google Scholar] [CrossRef]
- Ainsworth, E.A.; Rogers, A. The response of photosynthesis and stomatal conductance to rising [CO2]: Mechanisms and environmental interactions. Plant. Cell Environ. 2010, 30, 258–270. [Google Scholar] [CrossRef]
- Bellasio, C.; Quirk, J.; Buckley, T.N.; Beerling, D.J. A dynamic hydro-mechanical and biochemical model of stomatal conductance for C4 photosynthesis. Plant Physiol. 2017, 175, 104–119. [Google Scholar] [CrossRef]
- Deans, R.M.; Farquhar, G.D.; Busch, F.A. Estimating stomatal and biochemical limitations during photosynthetic induction. Plant. Cell Environ. 2019, 42, 3227–3240. [Google Scholar] [CrossRef]
- Medlyn, B.E.; Duursma, R.A.; Eamus, D.; Ellsworth, D.S.; Prentice, C.; Barton, C.V.M.; Crous, K.Y.; de Angelis, P.; Freeman, M.; Wingate, L. Reconciling the optimal and empirical approaches to modelling stomatal conductance. Glob. Change Biol. 2011, 17, 2225–2235. [Google Scholar] [CrossRef]
- Buckley, T.N. Modeling stomatal conductance. Plant Physiol. 2017, 174, 572–582. [Google Scholar] [CrossRef] [PubMed]
- De Kauwe, M.G.; Medlyn, B.E.; Zaehle, S.; Walker, A.P.; Dietze, M.C.; Hickler, T. Forest water use and water use efficiency at elevated CO2: A model-data intercomparison at two contrasting temperate forest FACE sites. Glob. Change Biol. 2013, 19, 1759–1779. [Google Scholar] [CrossRef]
- Medlyn, B.E.; De Kauwe, M.G.; Lin, Y.S.; Knauer, J.; Duursma, R.A.; William, C.A.; Arneth, A.; Clement, R.; Isaac, P.; Limousin, J.M. How do leaf and ecosystem measures of water-use efficiency compare? New Phytol. 2017, 216, 758–770. [Google Scholar] [CrossRef]
- Ye, Z.P.; Suggett, J.; Robakowski, P.; Kang, H.J. A mechanistic model for the photosynthesis-light response based on the photosynthetic electron transport of PSII in C3 and C4 species. New Phytol. 2013, 152, 1251–1262. [Google Scholar]
- Knauer, J.; Zaehle, S.; Medlyn, B.E.; Reichstein, M.; Williams, C.A.; Migliavacca, M.; De Kauwe, M.G.; Werner, C.; Keitel, C.; Kolari, P.; et al. Towards physiologically meaningful water-use efficiency estimates from eddy covariance data. Glob. Change Biol. 2018, 24, 694–710. [Google Scholar] [CrossRef] [PubMed]
- Miner, G.L.; Bauerle, W.L.; Baldocchi, D.D. Estimating the sensitivity of stomatal conductance to photosynthesis: A review. Plant. Cell Environ. 2017, 40, 1214–1238. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Sharkey, T.D. Stomatal conductance and photosynthesis. Annu. Rev. Plant Physiol. 1982, 33, 317–345. [Google Scholar] [CrossRef]
- Long, S.P.; Bernacchi, C.J. Gas exchange measurements, what can they tell us about the underlying limitations to photosynthesis? Procedures and sources of error. J. Exp. Bot. 2003, 54, 2393–2401. [Google Scholar] [CrossRef] [PubMed]
- Damour, G.; Simonneau, T.; Cochard, H.; Urban, L. An overview of models of stomatal conductance at the leaf level. Plant. Cell Environ. 2010, 33, 1419–1438. [Google Scholar] [CrossRef]
- Ye, Z.P.; Yang, X.L.; Ye, Z.W.Y.; An, T.; Duan, S.H.; Kang, H.J.; Wang, F.B. Evaluating photosynthetic models and their potency in assessing plant responses to changing oxygen concentrations: A comparative analysis of An–Ca and An–Ci curves in Lolium perenne and Triticum aestivum. Front. Plant Sci. 2025, 16, 1575217. [Google Scholar] [CrossRef] [PubMed]
- Marchin, R.M.; Medlyn, B.E.; Tjoelker, M.G.; Ellsworth, D.S. Decoupling between stomatal conductance and photosynthesis occurs under extreme heat in broadleaf tree species regardless of water access. Glob. Change Biol. 2023, 29, 6319–6335. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.S.; Medlyn, B.E.; Duursma, R.; Prentice, I.C.; Wingate, L. Optimal stomatal behaviour around the world. Nat. Clim. Change 2015, 5, 459–464. [Google Scholar] [CrossRef]
- Murchie, E.H.; Niyogi, K.K. Manipulation of photoprotection to improve plant photosynthesis. Plant Physiol. 2011, 155, 86–92. [Google Scholar] [CrossRef]
- Yin, X.; Busch, F.; Struik, P.; Sharkey, T. Evolution of a biochemical model of steady-state photosynthesis. Plant. Cell Environ. 2021, 44, 2811–2837. [Google Scholar] [CrossRef]

| T. repens | L. perenne | T. aestivum | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Equation (2) | Equation (5) | Equation (7) | Equation (2) | Equation (5) | Equation (7) | Equation (2) | Equation (5) | Equation (7) | |
| g0 | 0.087 ± 0.008 a | 0.085 ± 0.008 a | −0.002 ± 0.005 b | 0.045 ± 0.009 a | 0.042 ± 0.009 a | −0.002 ± 0.000 b | 0.040 ± 0.012 a | 0.037 ± 0.010 a | −0.002 ± 0.000 b |
| g1 | 3.446 ± 0.294 | 0.209 ± 0.209 | 0.756 ± 0.039 | 4.515 ± 0.065 | 1.499 ± 0.089 | 0.727 ± 0.004 | 4.574 ± 0.455 | 1.513 ± 0.223 | 0.724 ± 0.006 |
| R2 | 0.914 | 0.912 | 0.992 | 0.857 | 0.882 | 1.000 | 0.936 | 0.950 | 1.000 |
| AIC | 12.08 | 12.07 | 10.18 | 21.01 | 18.57 | 4.32 | 26.75 | 25.53 | 3.91 |
| T. repens | L. perenne | T. aestivum | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Equation (2) | Equation (5) | Equation (7) | Equation (2) | Equation (5) | Equation (7) | Equation (2) | Equation (5) | Equation (7) | |
| g0 | −0.162 ± 0.051 a | −0.105 ± 0.005 a | −0.002 ± 0.000 b | 0.000 ± 0.039 a | 0.018 ± 0.028 a | −0.001 ± 0.003 a | −0.280 ± 0.220 a | 0.035 ± 0.079 a | −0.264 ± 0.157 a |
| g1 | 34.391 ± 8.301 | 6.701 ± 1.599 | 0.742 ± 0.015 | 8.633 ± 1.613 | 2.214 ± 0.564 | 0.740 ± 0.018 | 17.406 ± 7.652 | 4.572 ± 2.820 | 1.952 ± 0.695 |
| R2 | 0.964 | 0.843 | 0.999 | 0.925 | 0.924 | 0.999 | 0.939 | 0.964 | 1.000 |
| AIC | 22.39 | 19.21 | 6.06 | 26.27 | 22.87 | 9.36 | 23.68 | 23.42 | 8.69 |
| T. repens | L. perenne | T. aestivum | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Equation (2) | Equation (5) | Equation (7) | Equation (2) | Equation (5) | Equation (7) | Equation (2) | Equation (5) | Equation (7) | |
| g0 | −0.082 ± 0.038 a | −0.033 ± 0.015 a | −0.002 ± 0.000 a | −0.324 ± 0.176 a | −0.312 ± 0.175 a | −0.005 ± 0.003 a | −0.269 ± 0.150 a | −0.586 ± 0.309 a | −0.013 ± 0.008 a |
| g1 | 25.502 ± 5.474 | 4.853 ± 1.891 | 0.760 ± 0.046 | 41.855 ± 15.809 | 18.901 ± 8.429 | 0.782 ± 0.025 | 22.981 ± 10.228 | 21.427 ± 10.123 | 0.811 ± 0.067 |
| R2 | 0.882 | 0.777 | 0.989 | 0.741 | 0.720 | 0.996 | 0.744 | 0.849 | 0.999 |
| AIC | 21.98 | 19.61 | 12.18 | 25.74 | 24.79 | 12.02 | 27.94 | 27.81 | 10.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Z.; An, T.; Yang, X.; Kang, H.; Wang, F. Novel Model for Stomatal Conductance: Enhanced Accuracy Under Variable Irradiance and CO2 in C3 Plant Species. Biology 2025, 14, 1501. https://doi.org/10.3390/biology14111501
Ye Z, An T, Yang X, Kang H, Wang F. Novel Model for Stomatal Conductance: Enhanced Accuracy Under Variable Irradiance and CO2 in C3 Plant Species. Biology. 2025; 14(11):1501. https://doi.org/10.3390/biology14111501
Chicago/Turabian StyleYe, Zipiao, Ting An, Xiaolong Yang, Huajing Kang, and Fubiao Wang. 2025. "Novel Model for Stomatal Conductance: Enhanced Accuracy Under Variable Irradiance and CO2 in C3 Plant Species" Biology 14, no. 11: 1501. https://doi.org/10.3390/biology14111501
APA StyleYe, Z., An, T., Yang, X., Kang, H., & Wang, F. (2025). Novel Model for Stomatal Conductance: Enhanced Accuracy Under Variable Irradiance and CO2 in C3 Plant Species. Biology, 14(11), 1501. https://doi.org/10.3390/biology14111501







