Study of the Synchronization and Transmission of Intracellular Signaling Oscillations in Cells Using Bispectral Analysis
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Animals
2.2. Cell Isolation
2.3. Fluorescence Microscopy
2.4. Data Analysis
2.5. Bispectral Analysis Method
2.6. Statistical Processing
3. Results
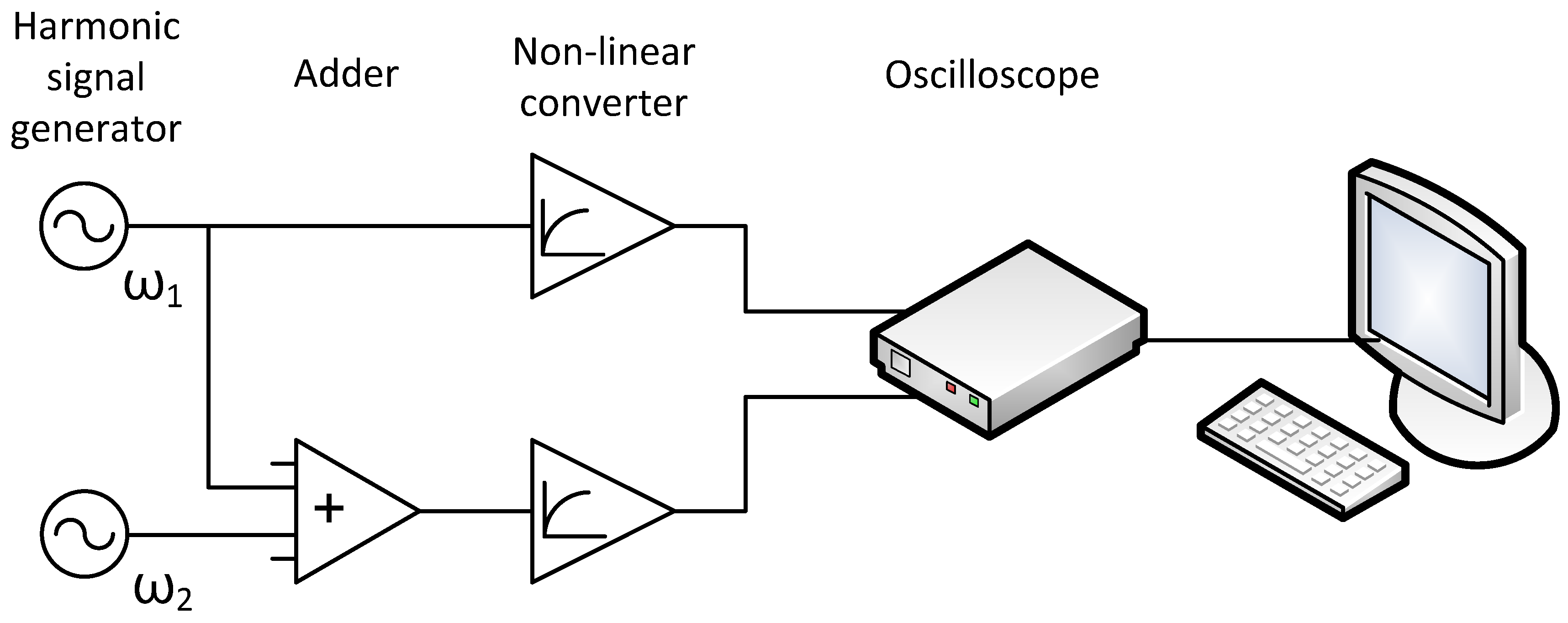
3.1. Application of Bispectral Method for Non-Lineal System Analisys
- Synchronous registration of signals occurs both from node “1” and from node “2”,
- Each node has its own generator of harmonic oscillations with characteristic frequencies ω1 and ω2, respectively,
- There is a channel for transmitting oscillations from node “1” to node “2”, and in node “2”, the linear summation of oscillations “1” and “2” occurs,
- Analog nonlinear signal conversion occurs at the registration stage in each node.
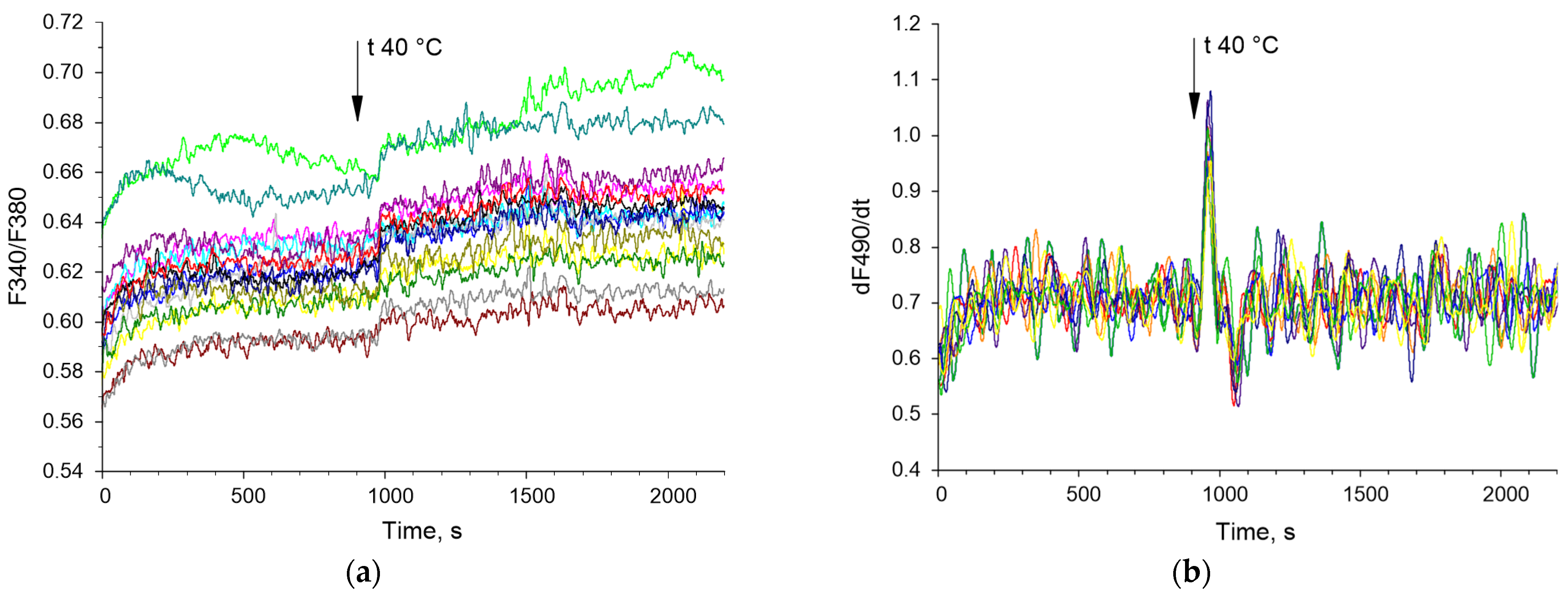
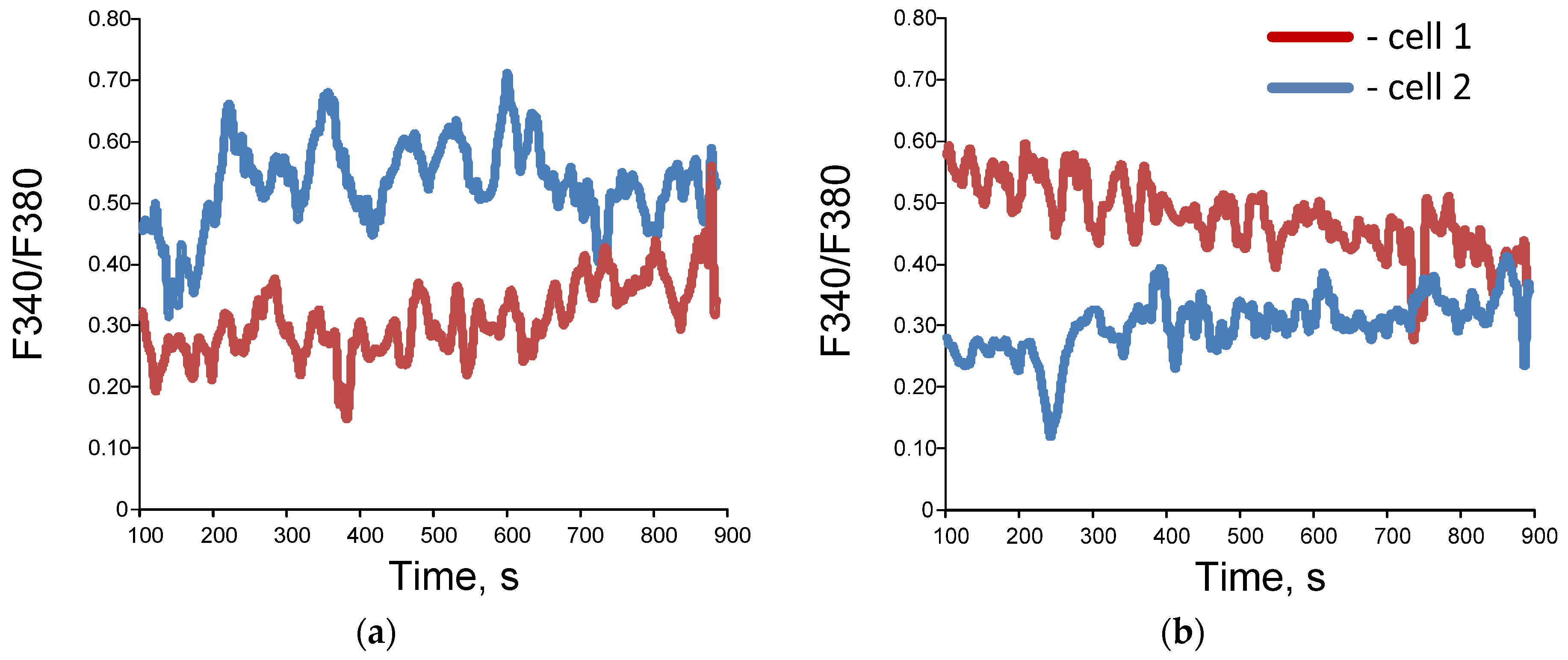
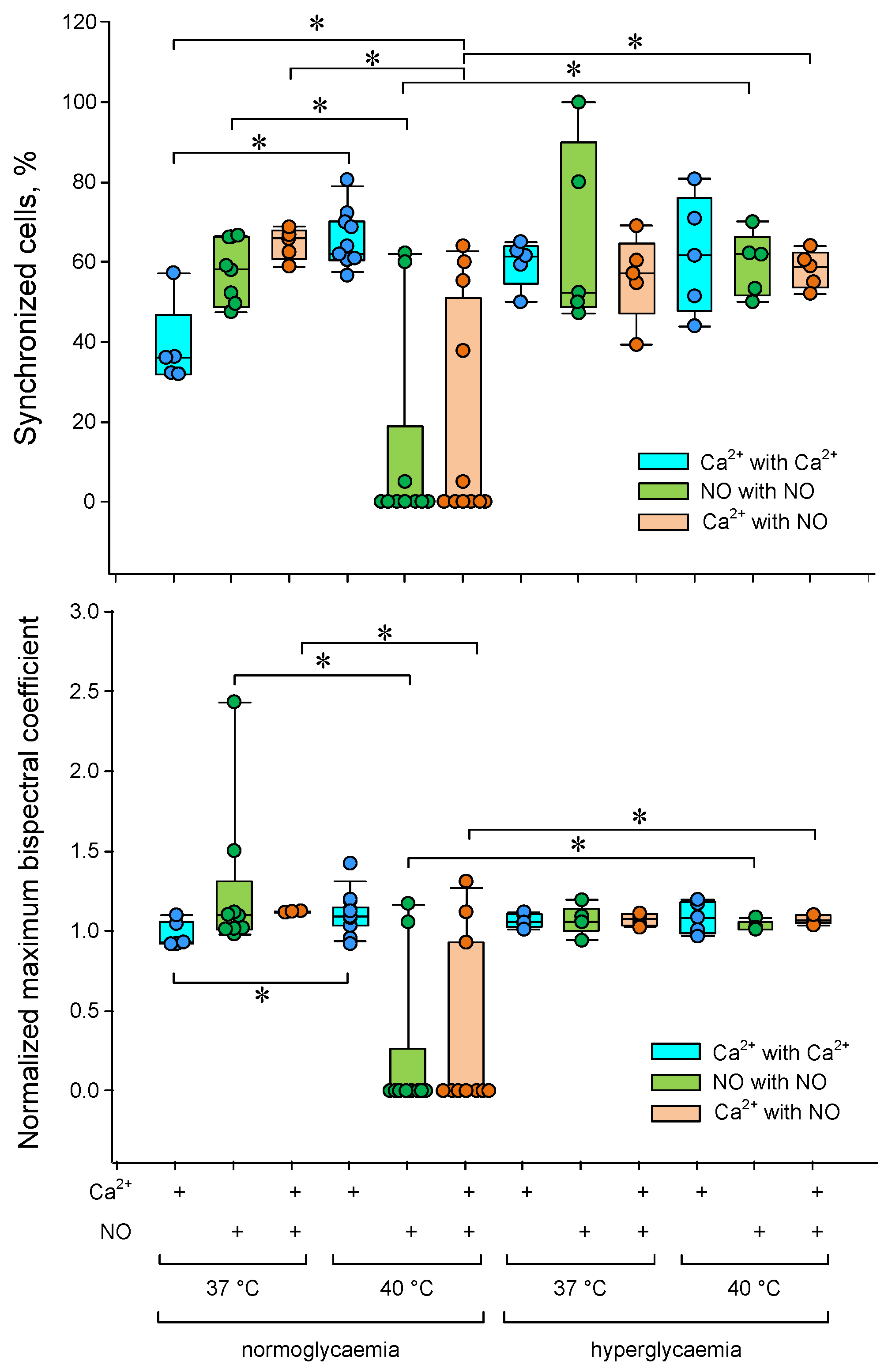
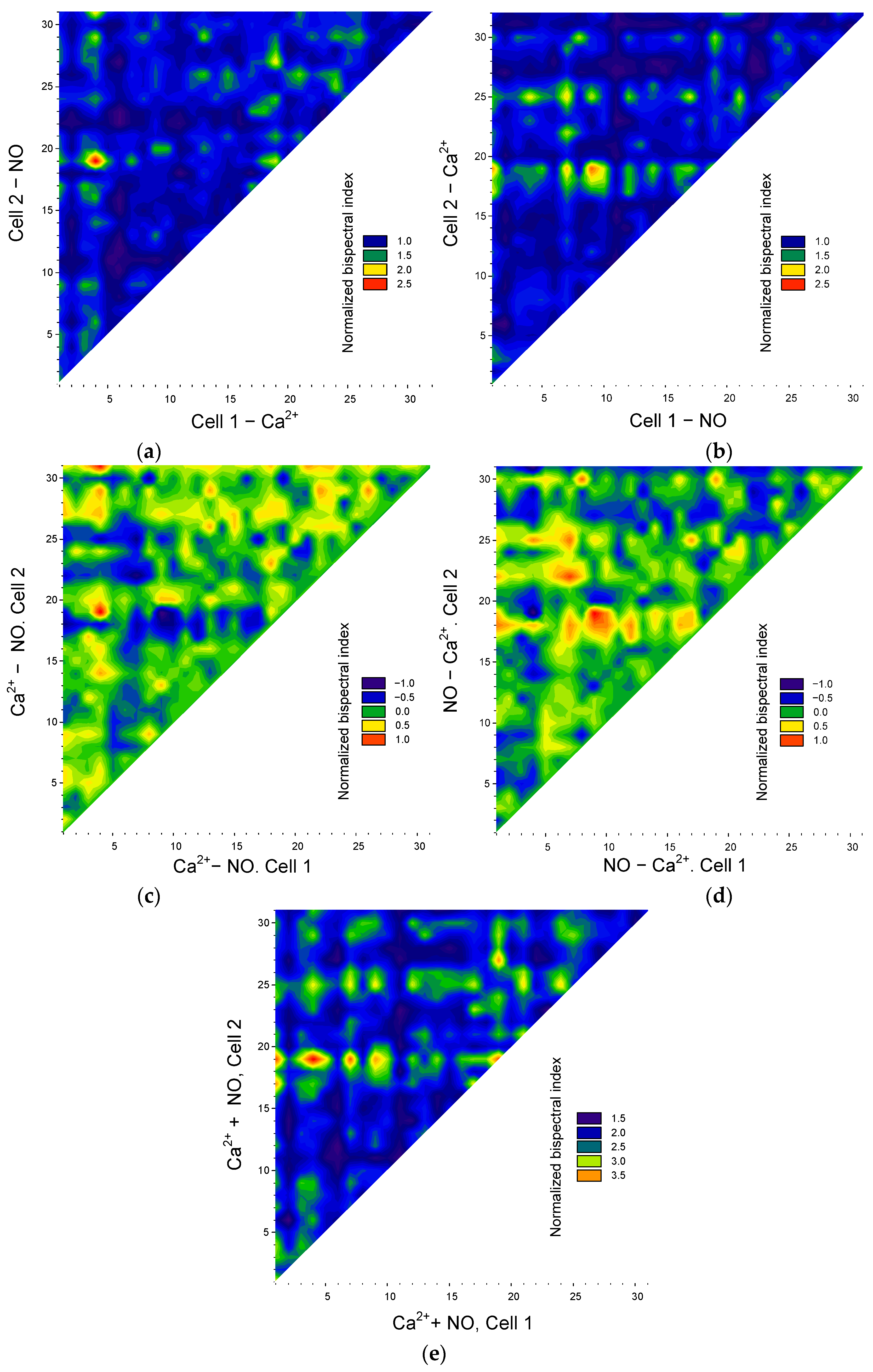
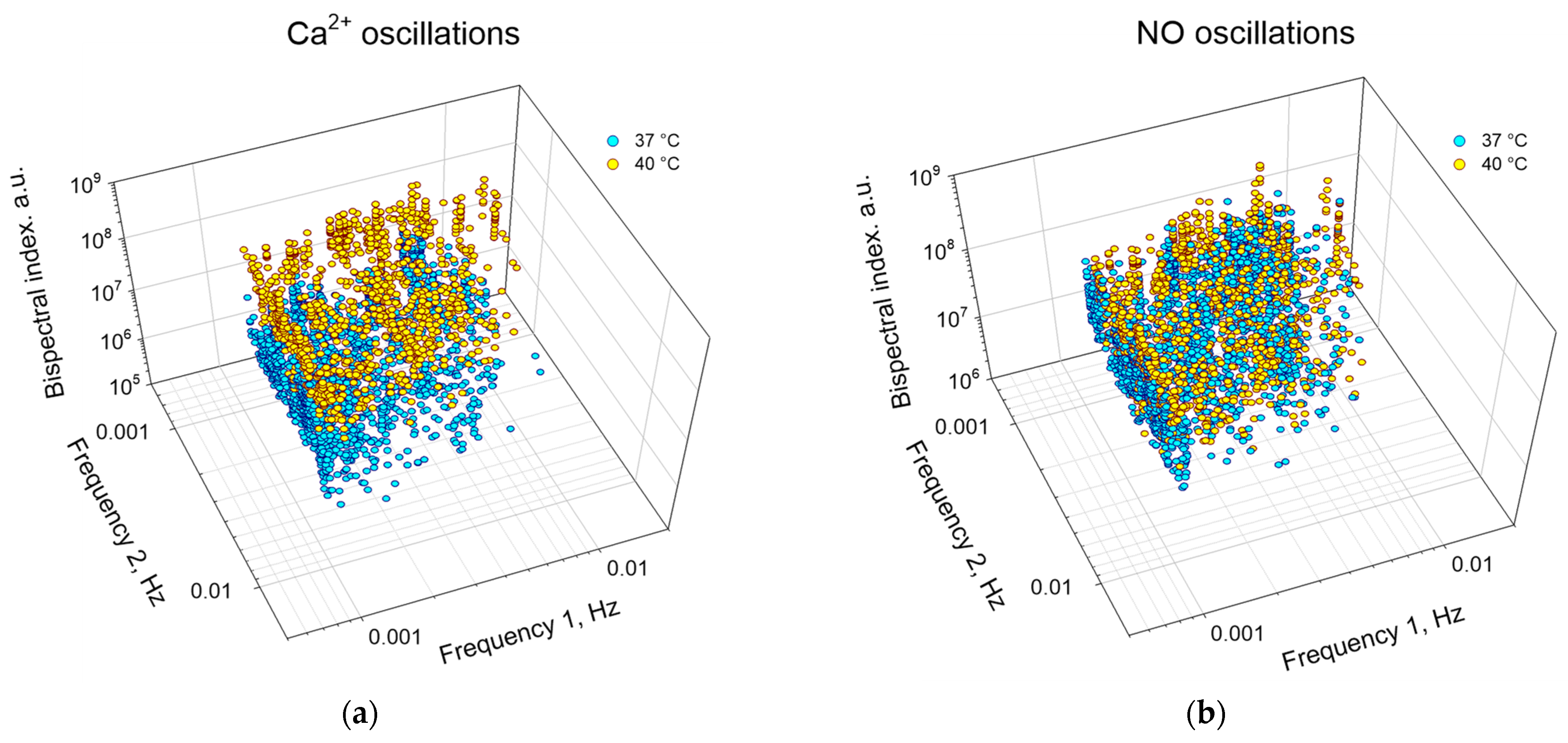
3.2. Application of the Bispectral Analysis Method to Assess the Synchronization of Vibrations of Intracellular Signaling Molecules
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kruse, K.; Jülicher, F. Oscillations in cell biology. Curr. Opin. Cell Biol. 2005, 17, 20–26. [Google Scholar] [CrossRef] [PubMed]
- Tonnelier, A.; Meignen, S.; Bosch, H.; Demongeot, J. Synchronization and desynchronization of neural oscillators. Neural Netw. 1999, 12, 1213–1228. [Google Scholar] [CrossRef] [PubMed]
- Vidal-Puig, A.J.; Walker, J.J.; Spiga, F.; Waite, E.; Zhao, Z.; Kershaw, Y.; Terry, J.R.; Lightman, S.L. The Origin of Glucocorticoid Hormone Oscillations. PLoS Biol. 2012, 10, e1001341. [Google Scholar] [CrossRef]
- Kishi, A.; Yasuda, H.; Matsumoto, T.; Inami, Y.; Horiguchi, J.; Tamaki, M.; Struzik, Z.R.; Yamamoto, Y. NREM Sleep Stage Transitions Control Ultradian REM Sleep Rhythm. Sleep 2011, 34, 1423–1432. [Google Scholar] [CrossRef]
- Kononov, A.V.; Bal’, N.V.; Zinchenko, V.P. Control of spontaneous synchronous Ca2+ oscillations in hippocampal neurons by GABAergic neurons containing kainate receptors without desensitization. Biochem. Suppl. Ser. A Membr. Cell Biol. 2012, 6, 215–220. [Google Scholar] [CrossRef]
- Zambrano, S.; De Toma, I.; Piffer, A.; Bianchi, M.E.; Agresti, A. NF-κB oscillations translate into functionally related patterns of gene expression. eLife 2016, 5, e09100. [Google Scholar] [CrossRef]
- Wang, B.; Ke, W.; Guang, J.; Chen, G.; Yin, L.; Deng, S.; He, Q.; Liu, Y.; He, T.; Zheng, R.; et al. Firing Frequency Maxima of Fast-Spiking Neurons in Human, Monkey, and Mouse Neocortex. Front. Cell. Neurosci. 2016, 10, 239. [Google Scholar] [CrossRef]
- Hu, H.; Jonas, P. A supercritical density of Na+ channels ensures fast signaling in GABAergic interneuron axons. Nat. Neurosci. 2014, 17, 686–693. [Google Scholar] [CrossRef] [PubMed]
- Smirni, S.; McNeilly, A.D.; MacDonald, M.P.; McCrimmon, R.J.; Khan, F. In-vivo correlations between skin metabolic oscillations and vasomotion in wild-type mice and in a model of oxidative stress. Sci. Rep. 2019, 9, 186. [Google Scholar] [CrossRef]
- Luciani, D.S.; Misler, S.; Polonsky, K.S. Ca2+controls slow NAD(P)H oscillations in glucose-stimulated mouse pancreatic islets. J. Physiol. 2006, 572, 379–392. [Google Scholar] [CrossRef]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef]
- Zharkikh, E.V.; Loktionova, Y.I.; Fedorovich, A.A.; Gorshkov, A.Y.; Dunaev, A.V. Assessment of Blood Microcirculation Changes after COVID-19 Using Wearable Laser Doppler Flowmetry. Diagnostics 2023, 13, 920. [Google Scholar] [CrossRef] [PubMed]
- Stefanovska, A.; Bracic, M.; Kvernmo, H.D. Wavelet analysis of oscillations in the peripheral blood circulation measured by laser Doppler technique. IEEE Trans. Biomed. Eng. 1999, 46, 1230–1239. [Google Scholar] [CrossRef]
- Kember, G.C.; Fenton, G.A.; Collier, K.; Armour, J.A. Aperiodic stochastic resonance in a hysteretic population of cardiac neurons. Phys. Rev. E 2000, 61, 1816–1824. [Google Scholar] [CrossRef] [PubMed]
- Bigger, J.T.; Fleiss, J.L.; Steinman, R.C.; Rolnitzky, L.M.; Kleiger, R.E.; Rottman, J.N. Frequency domain measures of heart period variability and mortality after myocardial infarction. Circulation 1992, 85, 164–171. [Google Scholar] [CrossRef] [PubMed]
- Carney, R.M.; Freedland, K.E.; Stein, P.K.; Miller, G.E.; Steinmeyer, B.; Rich, M.W.; Duntley, S.P. Heart rate variability and markers of inflammation and coagulation in depressed patients with coronary heart disease. J. Psychosom. Res. 2007, 62, 463–467. [Google Scholar] [CrossRef]
- Lampert, R.; Bremner, J.D.; Su, S.; Miller, A.; Lee, F.; Cheema, F.; Goldberg, J.; Vaccarino, V. Decreased heart rate variability is associated with higher levels of inflammation in middle-aged men. Am. Heart J. 2008, 156, 759.e1–759.e7. [Google Scholar] [CrossRef]
- Rosenberg, R.; Citrome, L.; Drake, C.L. Advances in the Treatment of Chronic Insomnia: A Narrative Review of New Nonpharmacologic and Pharmacologic Therapies. Neuropsychiatr. Dis. Treat. 2021, 17, 2549–2566. [Google Scholar] [CrossRef]
- Gudkov, S.V.; Burmistrov, D.E.; Kondakova, E.V.; Sarimov, R.M.; Yarkov, R.S.; Franceschi, C.; Vedunova, M.V. An emerging role of astrocytes in aging/neuroinflammation and gut-brain axis with consequences on sleep and sleep disorders. Ageing Res. Rev. 2023, 83, 101775. [Google Scholar] [CrossRef]
- Zharkikh, E.; Loktionova, Y.; Zherebtsova, A.; Tsyganova, M.; Zherebtsov, E.; Tiselko, A. Skin Blood Perfusion and Fluorescence Parameters in Pregnant Women with Type 1 Diabetes Mellitus. In Proceedings of the 2021 International Conference on Electrical Engineering and Photonics (EExPolytech), Saint Petersburg, Russia, 14–15 October 2021; pp. 238–240. [Google Scholar]
- Tikhonova, I.V.; Tankanag, A.V.; Guseva, I.E.; Grinevich, A.A. Analysis of interactions between cardiovascular oscillations for discrimination of early vascular disorders in arterial hypertension and type 2 diabetes. Biomed. Signal Process. Control. 2023, 79, 104222. [Google Scholar] [CrossRef]
- Romero, E.; Augulis, R.; Novoderezhkin, V.I.; Ferretti, M.; Thieme, J.; Zigmantas, D.; van Grondelle, R. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 2014, 10, 676–682. [Google Scholar] [CrossRef]
- Jeon, B.W.; Acharya, B.R.; Assmann, S.M. The Arabidopsis heterotrimeric G-protein β subunit, AGB1, is required for guard cell calcium sensing and calcium-induced calcium release. Plant J. 2019, 99, 231–244. [Google Scholar] [CrossRef]
- Shabala, S.; Shabala, L.; Gradmann, D.; Chen, Z.; Newman, I.; Mancuso, S. Oscillations in plant membrane transport: Model predictions, experimental validation, and physiological implications. J. Exp. Bot. 2006, 57, 171–184. [Google Scholar] [CrossRef] [PubMed]
- van den Berg, T.; Yalamanchili, K.; de Gernier, H.; Santos Teixeira, J.; Beeckman, T.; Scheres, B.; Willemsen, V.; ten Tusscher, K. A reflux-and-growth mechanism explains oscillatory patterning of lateral root branching sites. Dev. Cell 2021, 56, 2176–2191.e10. [Google Scholar] [CrossRef] [PubMed]
- Tsai, T.Y.; Choi, Y.S.; Ma, W.; Pomerening, J.R.; Tang, C.; Ferrell, J.E., Jr. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science 2008, 321, 126–129. [Google Scholar] [CrossRef]
- Arsenault, E.A.; Yoneda, Y.; Iwai, M.; Niyogi, K.K.; Fleming, G.R. Vibronic mixing enables ultrafast energy flow in light-harvesting complex II. Nat. Commun. 2020, 11, 1460. [Google Scholar] [CrossRef]
- Grinberg, M.; Mudrilov, M.; Kozlova, E.; Sukhov, V.; Sarafanov, F.; Evtushenko, A.; Ilin, N.; Vodeneev, V.; Price, C.; Mareev, E. Effect of extremely low-frequency magnetic fields on light-induced electric reactions in wheat. Plant Signal. Behav. 2022, 17, 2021664. [Google Scholar] [CrossRef]
- Antonova, E.V.; Pozolotina, V.N. Investigation of biological-rhythm patterns: Physiological and biochemical effects in herbaceous plants exposed to low-level chronic radiation—Part 1: Nonirradiated seeds. Int. J. Radiat. Biol. 2024, 100, 1051–1071. [Google Scholar] [CrossRef] [PubMed]
- Weiss, S.; Rappelsberger, P. Long-range EEG synchronization during word encoding correlates with successful memory performance. Cogn. Brain Res. 2000, 9, 299–312. [Google Scholar] [CrossRef]
- Vecchio, F.; Miraglia, F.; Curcio, G.; Della Marca, G.; Vollono, C.; Mazzucchi, E.; Bramanti, P.; Rossini, P.M. Cortical connectivity in fronto-temporal focal epilepsy from EEG analysis: A study via graph theory. Clin. Neurophysiol. 2015, 126, 1108–1116. [Google Scholar] [CrossRef]
- Pedersen, M.; Omidvarnia, A.H.; Walz, J.M.; Jackson, G.D. Increased segregation of brain networks in focal epilepsy: An fMRI graph theory finding. NeuroImage Clin. 2015, 8, 536–542. [Google Scholar] [CrossRef]
- Betzel, R.F.; Byrge, L.; He, Y.; Goñi, J.; Zuo, X.-N.; Sporns, O. Changes in structural and functional connectivity among resting-state networks across the human lifespan. NeuroImage 2014, 102, 345–357. [Google Scholar] [CrossRef]
- Frost, J.D., Jr.; Carrie, J.R.; Borda, R.P.; Kellaway, P. The effects of dalmane (flurazepam hydrochloride) on human EEG characteristics. Electroencephalogr. Clin. Neurophysiol. 1973, 34, 171–175. [Google Scholar] [CrossRef]
- Nayak, C.S.; Anilkumar, A.C. EEG Normal Waveforms. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2022. [Google Scholar]
- Barone, J.; Rossiter, H.E. Understanding the Role of Sensorimotor Beta Oscillations. Front. Syst. Neurosci. 2021, 15, 655886. [Google Scholar] [CrossRef]
- Ogawa, Y.; Shimada, S. Inter-Subject EEG Synchronization during a Cooperative Motor Task in a Shared Mixed-Reality Environment. Virtual Worlds 2023, 2, 129–143. [Google Scholar] [CrossRef]
- Fedotchev, A.I.; Parin, S.B.; Polevaya, S.A.; Velikova, S.D. Brain–Computer Interface and Neurofeedback Technologies: Current State, Problems and Clinical Prospects (Review). Sovrem. Tehnol. V Med. 2017, 9, 175. [Google Scholar] [CrossRef]
- Fedotchev, A.I. On efficiency of biomanagement with negative feedback from patient’s EEG in correction of functional disorders, caused by stress (in russ). Fiziol Cheloveka 2010, 36, 100–105. [Google Scholar]
- Altoum, A.E.A.; Babker, A.M.; Osman, A.L.; Ismail, M.; Lyashenko, V. New Approach for Analysis the Correlation of Some Oxidative Markers in Type 2 Diabetes Mellitus by Data Wavelet Analysis. Indian J. Public Health Res. Dev. 2019, 10, 2449–2455. [Google Scholar] [CrossRef]
- Achermann, P.; Rusterholz, T.; Dürr, R.; König, T.; Tarokh, L. Global field synchronization reveals rapid eye movement sleep as most synchronized brain state in the human EEG. R. Soc. Open Sci. 2016, 3, 160201. [Google Scholar] [CrossRef]
- Wen, D.; Zhou, Y.; Li, X. A Critical Review: Coupling and Synchronization Analysis Methods of EEG Signal with Mild Cognitive Impairment. Front. Aging Neurosci. 2015, 7, 54. [Google Scholar] [CrossRef]
- Legendre, P.; Sourioux, M.; Bertrand, S.S.; Cazalets, J.-R. Cholinergic-mediated coordination of rhythmic sympathetic and motor activities in the newborn rat spinal cord. PLOS Biol. 2018, 16, e2005460. [Google Scholar] [CrossRef]
- Mizeva, I.; Di Maria, C.; Frick, P.; Podtaev, S.; Allen, J. Quantifying the correlation between photoplethysmography and laser Doppler flowmetry microvascular low-frequency oscillations. J. Biomed. Opt. 2015, 20, 037007. [Google Scholar] [CrossRef] [PubMed]
- Tankanag, A.; Krasnikov, G.; Mizeva, I. A pilot study: Wavelet cross-correlation of cardiovascular oscillations under controlled respiration in humans. Microvasc. Res. 2020, 130, 103993. [Google Scholar] [CrossRef] [PubMed]
- Martín-Montero, A.; Gutiérrez-Tobal, G.C.; Gozal, D.; Barroso-García, V.; Álvarez, D.; del Campo, F.; Kheirandish-Gozal, L.; Hornero, R. Bispectral Analysis of Heart Rate Variability to Characterize and Help Diagnose Pediatric Sleep Apnea. Entropy 2021, 23, 1016. [Google Scholar] [CrossRef]
- Dauwels, J.; Vialatte, F.; Musha, T.; Cichocki, A. A comparative study of synchrony measures for the early diagnosis of Alzheimer’s disease based on EEG. NeuroImage 2010, 49, 668–693. [Google Scholar] [CrossRef] [PubMed]
- Dauwels, J.; Vialatte, F.; Weber, T.; Musha, T.; Cichocki, A. Quantifying Statistical Interdependence by Message Passing on Graphs—Part II: Multidimensional Point Processes. Neural Comput. 2009, 21, 2203–2268. [Google Scholar] [CrossRef]
- Bandrivskyy, A.; Bernjak, A.; McClintock, P.; Stefanovska, A. Wavelet Phase Coherence Analysis: Application to Skin Temperature and Blood Flow. Cardiovasc. Eng. 2004, 4, 89–93. [Google Scholar] [CrossRef]
- Newman, J.; Pidde, A.; Stefanovska, A. Defining the wavelet bispectrum. Appl. Comput. Harmon. Anal. 2021, 51, 171–224. [Google Scholar] [CrossRef]
- Sheeba, J.H.; Chandrasekar, V.K.; Stefanovska, A.; McClintock, P.V.E. Asymmetry-induced effects in coupled phase-oscillator ensembles: Routes to synchronization. Phys. Rev. E 2009, 79, 046210. [Google Scholar] [CrossRef] [PubMed]
- Astashev, M.E.; Serov, D.A.; Gudkov, S.V. Application of Spectral Methods of Analysis for Description of Ultradian Biorhythms at the Levels of Physiological Systems, Cells and Molecules (Review). Mathematics 2023, 11, 3307. [Google Scholar] [CrossRef]
- Turovsky, E.A.; Turovskaya, M.V.; Dolgacheva, L.P.; Zinchenko, V.P.; Dynnik, V.V. Acetylcholine Promotes Ca2+ and NO− Oscillations in Adipocytes Implicating Ca2+→NO→cGMP→cADP-ribose→Ca2+ Positive Feedback Loop—Modulatory Effects of Norepinephrine and Atrial Natriuretic Peptide. PLoS ONE 2013, 8, e63483. [Google Scholar] [CrossRef] [PubMed]
- Serov, D.; Tankanag, A.; Astashev, M. Low-frequency oscillations of murine skin microcirculations and periodic changes of [Ca2+]i and [NO]i levels in murine endotheliocytes: An effect of provocative tests. Cell Biol. Int. 2021, 46, 427–442. [Google Scholar] [CrossRef] [PubMed]
- Turovsky, E.A.; Kaimachnikov, N.P.; Turovskaya, M.V.; Berezhnov, A.V.; Dynnik, V.V.; Zinchenko, V.P. Two mechanisms of calcium oscillations in adipocytes. Biochem. Suppl. Ser. A Membr. Cell Biol. 2012, 6, 26–34. [Google Scholar] [CrossRef]
- Volotovski, I.D.; Sokolovsky, S.G.; Nikiforov, E.L.; Zinchenko, V.P. Calcium oscillations in plant cell cytoplasm induced by red and far-red light irradiation. J. Photochem. Photobiol. B Biol. 1993, 20, 95–100. [Google Scholar] [CrossRef]
- Maltsev, A.V.; Kokoz, Y.M. Cardiomyocytes generating spontaneous Ca2+-transients as tools for precise estimation of sarcoplasmic reticulum Ca2+ transport. Arch. Biochem. Biophys. 2020, 693, 108542. [Google Scholar] [CrossRef]
- Kuijlaars, J.; Oyelami, T.; Diels, A.; Rohrbacher, J.; Versweyveld, S.; Meneghello, G.; Tuefferd, M.; Verstraelen, P.; Detrez, J.R.; Verschuuren, M.; et al. Sustained synchronized neuronal network activity in a human astrocyte co-culture system. Sci. Rep. 2016, 6, 36529. [Google Scholar] [CrossRef]
- Zhang, M.; Fendler, B.; Peercy, B.; Goel, P.; Bertram, R.; Sherman, A.; Satin, L. Long Lasting Synchronization of Calcium Oscillations by Cholinergic Stimulation in Isolated Pancreatic Islets. Biophys. J. 2008, 95, 4676–4688. [Google Scholar] [CrossRef]
- Lee, M.T.; Sakaguchi, R.; Nakamura, S.; Iha, H.; Tanaka, M. Phenotypic screening using waveform analysis of synchronized calcium oscillations in primary cortical cultures. PLoS ONE 2023, 18, e0271782. [Google Scholar] [CrossRef]
- Laryushkin, D.P.; Maiorov, S.A.; Zinchenko, V.P.; Gaidin, S.G.; Kosenkov, A.M. Role of L-Type Voltage-Gated Calcium Channels in Epileptiform Activity of Neurons. Int. J. Mol. Sci. 2021, 22, 10342. [Google Scholar] [CrossRef]
- Ji-Qian, Z.; Han-Shuang, C.; Mao-Sheng, W. Enhanced Synchronization of Intercellular Calcium Oscillations by Noise Contaminated Signals. Commun. Theor. Phys. 2008, 50, 903–906. [Google Scholar] [CrossRef]
- Šterk, M.; Barać, U.; Stožer, A.; Gosak, M. Both electrical and metabolic coupling shape the collective multimodal activity and functional connectivity patterns in beta cell collectives: A computational model perspective. Phys. Rev. E 2023, 108, 054409. [Google Scholar] [CrossRef] [PubMed]
- Debir, B.; Meaney, C.; Kohandel, M.; Unlu, M.B. The role of calcium oscillations in the phenotype selection in endothelial cells. Scientific Reports 2021, 11, 23781. [Google Scholar] [CrossRef] [PubMed]
- Korobkin, J.; Balabin, F.A.; Yakovenko, S.A.; Simonenko, E.Y.; Sveshnikova, A.N. Occurrence of Calcium Oscillations in Human Spermatozoa Is Based on Spatial Signaling Enzymes Distribution. Int. J. Mol. Sci. 2021, 22, 8018. [Google Scholar] [CrossRef] [PubMed]
- Compte, A.; Reig, R.; Descalzo, V.F.; Harvey, M.A.; Puccini, G.D.; Sanchez-Vives, M.V. Spontaneous high-frequency (10–80 Hz) oscillations during up states in the cerebral cortex in vitro. J. Neurosci. 2008, 28, 13828–13844. [Google Scholar] [CrossRef]
- Perc, M.; Ruffinatti, F.A.; Gilardino, A.; Lovisolo, D.; Ferraro, M. Spatial Wavelet Analysis of Calcium Oscillations in Developing Neurons. PLoS ONE 2013, 8, e75986. [Google Scholar] [CrossRef]
- Fedotova, A.; Brazhe, A.; Doronin, M.; Toptunov, D.; Pryazhnikov, E.; Khiroug, L.; Verkhratsky, A.; Semyanov, A. Dissociation Between Neuronal and Astrocytic Calcium Activity in Response to Locomotion in Mice. Function 2023, 4, zqad019. [Google Scholar] [CrossRef] [PubMed]
- Soteropoulos, D.S.; Baker, S. Cortico-Cerebellar Coherence During a Precision Grip Task in the Monkey. J. Neurophysiol. 2006, 95, 1194–1206. [Google Scholar] [CrossRef]
- Ross, W. Translating from Na+ to Ca2+: Na/Ca-exchanger exerts Na+-dependent control over astrocytic Ca2+ oscillations. Eur. Phys. J. Plus 2021, 136, 718. [Google Scholar] [CrossRef]
- Zinchenko, V.P.; Teplov, I.Y.; Kosenkov, A.M.; Gaidin, S.G.; Kairat, B.K.; Tuleukhanov, S.T. Participation of calcium-permeable AMPA receptors in the regulation of epileptiform activity of hippocampal neurons. Front. Synaptic Neurosci. 2024, 16, 1349984. [Google Scholar] [CrossRef]
- Slaby, O.; Lebiedz, D. Oscillatory NAD(P)H Waves and Calcium Oscillations in Neutrophils? A Modeling Study of Feasibility. Biophys. J. 2009, 96, 417–428. [Google Scholar] [CrossRef]
- Khazen, R.; Corre, B.; Garcia, Z.; Lemaître, F.; Bachellier-Bassi, S.; d’Enfert, C.; Bousso, P. Spatiotemporal dynamics of calcium signals during neutrophil cluster formation. Proc. Natl. Acad. Sci. 2022, 119, e2203855119. [Google Scholar] [CrossRef]
- Yokota, Y.; Nakajima, H.; Wakayama, Y.; Muto, A.; Kawakami, K.; Fukuhara, S.; Mochizuki, N. Endothelial Ca2+ oscillations reflect VEGFR signaling-regulated angiogenic capacity in vivo. eLife 2015, 4, e08817. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, H.; Chen, Y.; He, J.; Zhu, L.; Yang, B.; Zhao, W. High glucose-induced injury in human umbilical vein endothelial cells is alleviated by vitamin D supplementation through downregulation of TIPE1. Diabetol. Metab. Syndr. 2024, 16, 18. [Google Scholar] [CrossRef] [PubMed]
- Pieper, G.M.; Dondlinger, L. Glucose elevations alter bradykinin-stimulated intracellular calcium accumulation in cultured endothelial cells. Cardiovasc. Res. 1997, 34, 169–178. [Google Scholar] [CrossRef][Green Version]
- Chen, Y.; Chen, Y.; Tang, C.; Zhao, Q.; Xu, T.; Kang, Q.; Jiang, B.; Zhang, L. RPS4Y1 Promotes High Glucose-Induced Endothelial Cell Apoptosis and Inflammation by Activation of the p38 MAPK Signaling. Diabetes Metab. Syndr. Obes. Targets Ther. 2021, 14, 4523–4534. [Google Scholar] [CrossRef]
- Wong, B.J.; Fieger, S.M. Transient receptor potential vanilloid type-1 (TRPV-1) channels contribute to cutaneous thermal hyperaemia in humans. J. Physiol. 2010, 588, 4317–4326. [Google Scholar] [CrossRef] [PubMed]
- Beddek, K.; Raffin, F.; Borgel, D.; Saller, F.; Riccobono, D.; Bobe, R.; Boittin, F.X. TRPV4 channel activation induces the transition of venous and arterial endothelial cells toward a pro-inflammatory phenotype. Physiol. Rep. 2021, 9, e14613. [Google Scholar] [CrossRef]
- Watanabe, H.; Vriens, J.; Suh, S.H.; Benham, C.D.; Droogmans, G.; Nilius, B. Heat-evoked Activation of TRPV4 Channels in a HEK293 Cell Expression System and in Native Mouse Aorta Endothelial Cells. J. Biol. Chem. 2002, 277, 47044–47051. [Google Scholar] [CrossRef]
- Sobczak, M.; Dargatz, J.; Chrzanowska-Wodnicka, M. Isolation and Culture of Pulmonary Endothelial Cells from Neonatal Mice. J. Vis. Exp. 2010, 46, e2316. [Google Scholar] [CrossRef]
- Serov, D.; Tikhonova, I.; Safronova, V.; Astashev, M. Calcium activity in response to nAChR ligands in murine bone marrow granulocytes with different Gr-1 expression. Cell Biol. Int. 2021, 45, 1533–1545. [Google Scholar] [CrossRef]
- Astasheva, E.V.; Astashev, M.E.; Kichigina, V.F. Oscillatory Activity and Cross-Frequency Interactions in the Hippocampus and Connected Brain Structures during Sensory Information Processing. Neurosci. Behav. Physiol. 2018, 48, 758–763. [Google Scholar] [CrossRef]
- Astashev, M.E.; Serov, D.A.; Tankanag, A.V. Anesthesia effects on the low frequency blood flow oscillations in mouse skin. Ski. Res. Technol. 2018, 25, 40–46. [Google Scholar] [CrossRef]
- Tsetlin, V.; Haufe, Y.; Safronova, V.; Serov, D.; Shadamarshan, P.; Son, L.; Shelukhina, I.; Kudryavtsev, D.; Kryukova, E.; Kasheverov, I.; et al. Interaction of α9α10 Nicotinic Receptors With Peptides and Proteins From Animal Venoms. Front. Cell. Neurosci. 2021, 15, 765541. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.-X.; Li, T.-T.; Jiang, H.-Y.; He, J. Calcium oscillation on homogeneous and heterogeneous networks of ryanodine receptor. Phys. Rev. E 2023, 107, 024402. [Google Scholar] [CrossRef]
- Ji, Q.; Zuo, H.; Meng, P. Burst synchronization transition of intracellular Ca2+ oscillations in coupled cell systems. AIP Adv. 2017, 7, 115212. [Google Scholar] [CrossRef]
- Zinchenko, V.P.; Kosenkov, A.M.; Gaidin, S.G.; Sergeev, A.I.; Dolgacheva, L.P.; Tuleukhanov, S.T. Properties of GABAergic Neurons Containing Calcium-Permeable Kainate and AMPA-Receptors. Life 2021, 11, 1309. [Google Scholar] [CrossRef] [PubMed]
- Kapela, A.; Parikh, J.; Tsoukias, N.M. Multiple Factors Influence Calcium Synchronization in Arterial Vasomotion. Biophys. J. 2012, 102, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Balaji, R.; Bielmeier, C.; Harz, H.; Bates, J.; Stadler, C.; Hildebrand, A.; Classen, A.-K. Calcium spikes, waves and oscillations in a large, patterned epithelial tissue. Sci. Rep. 2017, 7, srep42786. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef]
- Li, X.; Cui, D.; Jiruska, P.; Fox, J.E.; Yao, X.; Jefferys, J.G.R. Synchronization Measurement of Multiple Neuronal Populations. J. Neurophysiol. 2007, 98, 3341–3348. [Google Scholar] [CrossRef]
- Patel, T.P.; Ventre, S.C.; Meaney, D.F. Dynamic Changes in Neural Circuit Topology Following Mild Mechanical Injury In Vitro. Ann. Biomed. Eng. 2011, 40, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Chiarion, G.; Sparacino, L.; Antonacci, Y.; Faes, L.; Mesin, L. Connectivity Analysis in EEG Data: A Tutorial Review of the State of the Art and Emerging Trends. Bioengineering 2023, 10, 372. [Google Scholar] [CrossRef] [PubMed]
- Du, X.L.; Edelstein, D.; Dimmeler, S.; Ju, Q.; Sui, C.; Brownlee, M. Hyperglycemia inhibits endothelial nitric oxide synthase activity by posttranslational modification at the Akt site. J. Clin. Investig. 2001, 108, 1341–1348. [Google Scholar] [CrossRef]
- Pandey, S.; Li, L.; Tan, H.; Gu, Z.; Liu, Z.; Geng, Y.; Liu, Y.; Tong, H.; Tang, Y.; Qiu, J.; et al. Heat Stress Induces Apoptosis through a Ca2+-Mediated Mitochondrial Apoptotic Pathway in Human Umbilical Vein Endothelial Cells. PLoS ONE 2014, 9, e111083. [Google Scholar] [CrossRef]
- Paltauf-Doburzynska, J.; Malli, R.; Graier, W.F. Hyperglycemic Conditions Affect Shape and Ca2+ Homeostasis of Mitochondria in Endothelial Cells. J. Cardiovasc. Pharmacol. 2004, 44, 423–436. [Google Scholar] [CrossRef]
- Kimura, C.; Oike, M.; Ito, Y. Acute Glucose Overload Abolishes Ca2+ Oscillation in Cultured Endothelial Cells From Bovine Aorta. Circ. Res. 1998, 82, 677–685. [Google Scholar] [CrossRef]
- Boulay, G.; Guillemette, G.t.; Klarskov, K.; Chartrand, V.r.; Francoeur, N.; Nguyen, N. Insulin Promotes the Association of Heat Shock Protein 90 with the Inositol 1,4,5-Trisphosphate Receptor to Dampen Its Ca2+ Release Activity. Endocrinology 2009, 150, 2190–2196. [Google Scholar] [CrossRef]
- García-Morales, V.; Luaces-Regueira, M.; Campos-Toimil, M. The cAMP effectors PKA and Epac activate endothelial NO synthase through PI3K/Akt pathway in human endothelial cells. Biochem. Pharmacol. 2017, 145, 94–101. [Google Scholar] [CrossRef]
- Bootman, M.D.; Bultynck, G. Fundamentals of Cellular Calcium Signaling: A Primer. Cold Spring Harb. Perspect. Biol. 2020, 12, a038802. [Google Scholar] [CrossRef]
- Aird, W.C. Endothelial Cell Heterogeneity. Cold Spring Harb. Perspect. Med. 2011, 2, a006429. [Google Scholar] [CrossRef]
- Kiuchi, S.; Usami, A.; Shimoyama, T.; Otsuka, F.; Yamaguchi, S.; Nakamura, T.; Suzuki, S.; Ono, K. Cardiac Pacemaker Cells Generate Cardiomyocytes from Fibroblasts in Long-Term Cultures. Sci. Rep. 2019, 9, 15174. [Google Scholar] [CrossRef]
- Berra-Romani, R.; Faris, P.; Pellavio, G.; Orgiu, M.; Negri, S.; Forcaia, G.; Var---gaz-Guadarrama, V.; Garcia-Carrasco, M.; Botta, L.; Sancini, G.; et al. Histamine induces intracellular Ca2+ oscillations and nitric oxide release in endothelial cells from brain microvascular circulation. J. Cell. Physiol. 2019, 235, 1515–1530. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-H.; Wang, X.-J. Spike-Frequency Adaptation of a Generalized Leaky Integrate-and-Fire Model Neuron. J. Comput. Neurosci. 2001, 10, 25–45. [Google Scholar] [CrossRef]
- Cooke, J.P.; Ghebremariam, Y.T. Endothelial Nicotinic Acetylcholine Receptors and Angiogenesis. Trends Cardiovasc. Med. 2008, 18, 247–253. [Google Scholar] [CrossRef]
- Davenport, A.P.; Hyndman, K.A.; Dhaun, N.; Southan, C.; Kohan, D.E.; Pollock, J.S.; Pollock, D.M.; Webb, D.J.; Maguire, J.J.; Barker, E.L. Endothelin. Pharmacol. Rev. 2016, 68, 357–418. [Google Scholar] [CrossRef] [PubMed]
- Wilson, C.; Zhang, X.; Buckley, C.; Heathcote, H.R.; Lee, M.D.; McCarron, J.G. Increased Vascular Contractility in Hypertension Results From Impaired Endothelial Calcium Signaling. Hypertension 2019, 74, 1200–1214. [Google Scholar] [CrossRef]
- Sakurada, R.; Odagiri, K.; Hakamata, A.; Kamiya, C.; Wei, J.; Watanabe, H. Calcium Release from Endoplasmic Reticulum Involves Calmodulin-Mediated NADPH Oxidase-Derived Reactive Oxygen Species Production in Endothelial Cells. Int. J. Mol. Sci. 2019, 20, 1644. [Google Scholar] [CrossRef] [PubMed]
- Suresh, K.; Servinsky, L.; Reyes, J.; Baksh, S.; Undem, C.; Caterina, M.; Pearse, D.B.; Shimoda, L.A. Hydrogen peroxide-induced calcium influx in lung microvascular endothelial cells involves TRPV4. Am. J. Physiol. Lung Cell. Mol. Physiol. 2015, 309, L1467–L1477. [Google Scholar] [CrossRef]
- Berkels, R.; Suerhoff, S.; Roesen, R.; Klaus, W. Nitric Oxide Causes a cGMP-Independent Intracellular Calcium Rise in Porcine Endothelial Cells—A Paradox? Microvasc. Res. 2000, 59, 38–44. [Google Scholar] [CrossRef]
- Marziano, C.; Hong, K.; Cope, E.L.; Kotlikoff, M.I.; Isakson, B.E.; Sonkusare, S.K. Nitric Oxide–Dependent Feedback Loop Regulates Transient Receptor Potential Vanilloid 4 (TRPV4) Channel Cooperativity and Endothelial Function in Small Pulmonary Arteries. J. Am. Heart Assoc. 2017, 6, e007157. [Google Scholar] [CrossRef]
- Bahadoran, Z.; Mirmiran, P.; Kashfi, K.; Ghasemi, A. Vascular nitric oxide resistance in type 2 diabetes. Cell Death Dis. 2023, 14, 410. [Google Scholar] [CrossRef]
- Nikolova, M.P.; Chavali, M.S. Metal Oxide Nanoparticles as Biomedical Materials. Biomimetics 2020, 5, 27. [Google Scholar] [CrossRef] [PubMed]
- Gudkov, S.V.; Sarimov, R.M.; Astashev, M.E.; Pishchalnikov, R.Y.; Yanykin, D.V.; Simakin, A.V.; Shkirin, A.V.; Serov, D.A.; Konchekov, E.M.; Gusein-zade Namik Guseynaga, O.; et al. Modern physical methods and technologies in agriculture. Phys. Uspekhi 2023, 194, 208–226. [Google Scholar] [CrossRef]
- Lee, D.; Hong, J.H. Physiological Application of Nanoparticles in calcium-related Proteins and Channels. Nanomedicine 2019, 14, 2479–2486. [Google Scholar] [CrossRef] [PubMed]
- Quinn, J.F.; Whittaker, M.R.; Davis, T.P. Delivering nitric oxide with nanoparticles. J. Control. Release 2015, 205, 190–205. [Google Scholar] [CrossRef]
- Gudkov, S.V.; Burmistrov, D.E.; Smirnova, V.V.; Semenova, A.A.; Lisitsyn, A.B. A Mini Review of Antibacterial Properties of Al2O3 Nanoparticles. Nanomaterials 2022, 12, 2635. [Google Scholar] [CrossRef]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. Synchronization Approach to Analysis of Biological Systems. Fluct. Noise Lett. 2012, 4, L53–L62. [Google Scholar] [CrossRef]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J.; Schäfer, C.; Tass, P.A. Phase synchronization: From theory to data analysis, in neuro-informatics and neural modeling. In Handbook of Biological Physics; Moss, F., Gielen, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 4, pp. 279–321. [Google Scholar]
- Tikhonova, I.V.; Grinevich, A.A.; Guseva, I.E.; Tankanag, A.V. Effect of local heating on couplings between cardio-respiratory and peripheral oscillations in type 2 diabetes mellitus. Res. Biomed. Eng. 2024, 40, 397–407. [Google Scholar] [CrossRef]
- Pikovsky, A.; Smirnov, L.A. Dynamics of large oscillator populations with random interactions. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 073120. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Arnhold, J.; Grassberger, P. Learning driver-response relationships from synchronization patterns. Phys. Rev. E 2000, 61, 5142–5148. [Google Scholar] [CrossRef]
- Fraker, M.E.; Sinclair, J.S.; Frank, K.T.; Hood, J.M.; Ludsin, S.A. Temporal scope influences ecosystem driver-response relationships: A case study of Lake Erie with implications for ecosystem-based management. Sci. Total Environ. 2022, 813, 152473. [Google Scholar] [CrossRef] [PubMed]
- Hunsicker, M.E.; Kappel, C.V.; Selkoe, K.A.; Halpern, B.S.; Scarborough, C.; Mease, L.; Amrhein, A. Characterizing driver—Response relationships in marine pelagic ecosystems for improved ocean management. Ecol. Appl. 2016, 26, 651–663. [Google Scholar] [CrossRef] [PubMed]
- Steinbach, P.; Werner, M. gearshifft—The FFT Benchmark Suite for Heterogeneous Platforms. In High Performance Computing; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; pp. 199–216. [Google Scholar]
- Gambron, P.; Thorne, S. Comparison of several FFT libraries in C/C++. Sci. Technol. Facil. Counc. 2020, 45434573. [Google Scholar] [CrossRef]
- Cullinan, C.R.; Frattesi, T.R.; Wyant, C.M. Computing Performance Benchmarks among CPU, GPU, and FPGA; Worcester Polytechnic Institute: Worcester, MA, USA, 2012; p. 124. [Google Scholar]
- Yasuhito, O.; Toshio, E.; Naoya, M.; Satoshi, M. An efficient, model-based CPU-GPU heterogeneous FFT library. In Proceedings of the 2008 IEEE International Symposium on Parallel and Distributed Processing, Miami, FL, USA, 14–18 April 2008; pp. 1–10. [Google Scholar]
- Jiruska, P.; de Curtis, M.; Jefferys, J.G.R.; Schevon, C.A.; Schiff, S.J.; Schindler, K. Synchronization and desynchronization in epilepsy: Controversies and hypotheses. J. Physiol. 2013, 591, 787–797. [Google Scholar] [CrossRef]
- Levy, R.; Hutchison, W.D.; Lozano, A.M.; Dostrovsky, J.O. High-frequency Synchronization of Neuronal Activity in the Subthalamic Nucleus of Parkinsonian Patients with Limb Tremor. J. Neurosci. 2000, 20, 7766–7775. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Ávila, G.M.; Kurths, J.; Gonze, D.; Dupont, G. Exploring chronomodulated radiotherapy strategies in a chaotic population model. Chaos Solitons Fractals 2023, 173, 113743. [Google Scholar] [CrossRef]
- Pavlov, A.N.; Khorovodov, A.P.; Mamedova, A.T.; Koronovskii, A.A.; Pavlova, O.N.; Semyachkina-Glushkovskaya, O.V.; Kurths, J. Changes in blood–brain barrier permeability characterized from electroencephalograms with a combined wavelet and fluctuation analysis. Eur. Phys. J. Plus 2021, 136, 577. [Google Scholar] [CrossRef]
- Dunaev, A.V.; Sidorov, V.V.; Krupatkin, A.I.; Rafailov, I.E.; Palmer, S.G.; Stewart, N.A.; Sokolovski, S.G.; Rafailov, E.U. Investigating tissue respiration and skin microhaemocirculation under adaptive changes and the synchronization of blood flow and oxygen saturation rhythms. Physiol. Meas. 2014, 35, 607–621. [Google Scholar] [CrossRef]
- Song, W.-Y.; Zhang, Z.-B.; Shao, H.-B.; Guo, X.-L.; Cao, H.-X.; Zhao, H.-B.; Fu, Z.-Y.; Hu, X.-J. Relationship between calcium decoding elements and plant abiotic-stress resistance. Int. J. Biol. Sci. 2008, 4, 116–125. [Google Scholar] [CrossRef]
- Tonnang, H.E.Z.; Hervé, B.D.B.; Biber-Freudenberger, L.; Salifu, D.; Subramanian, S.; Ngowi, V.B.; Guimapi, R.Y.A.; Anani, B.; Kakmeni, F.M.M.; Affognon, H.; et al. Advances in crop insect modelling methods—Towards a whole system approach. Ecol. Model. 2017, 354, 88–103. [Google Scholar] [CrossRef]



| Frequency | Φ1(t,ω) | Φ2(t,ω) |
|---|---|---|
| ω1 | A1exp(jω1t) | kA1exp(jω1t) |
| 2ω1 | A12B1exp(j(2ω1t + π/2))/2 | k2A12B2exp(j(2ω1t + π/2))/2 |
| ω2 | 0 | A2exp(jω2t) |
| 2ω2 | 0 | A22B2exp(j(2ω2t + π/2))/2 |
| ω1 + ω2 | 0 | kA1 A2B2exp(j((ω1 + ω2)t − π/2)) |
| No. | Intracellular Messenger | Ca2+ Oscillations | NO Oscillations | ||
|---|---|---|---|---|---|
| Temperature, °C Characteristics | 37 | 40 | 37 | 40 | |
| 1 | Frequency 1, Hz × 10−3 | 2.2 (1.2; 4.2) | 2.4 (1.1; 3.9) | 1.9 (1.1; 3.9) | 3.0 (1.6; 4.6) * |
| 2 | Frequency 2, Hz × 10−3 | 1.7 (1.2; 3.6) | 2.8 (1.4; 3.9) * | 2.5 (1.3; 4.2) | 2.5 (1.6; 4.6) |
| 3 | Peak Value, a. u. × 106 | 8 (5; 13) | 116 (69; 170) * | 51 (29; 84) | 93 (60; 146) * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Astashev, M.E.; Serov, D.A.; Tankanag, A.V.; Knyazeva, I.V.; Dorokhov, A.A.; Simakin, A.V.; Gudkov, S.V. Study of the Synchronization and Transmission of Intracellular Signaling Oscillations in Cells Using Bispectral Analysis. Biology 2024, 13, 685. https://doi.org/10.3390/biology13090685
Astashev ME, Serov DA, Tankanag AV, Knyazeva IV, Dorokhov AA, Simakin AV, Gudkov SV. Study of the Synchronization and Transmission of Intracellular Signaling Oscillations in Cells Using Bispectral Analysis. Biology. 2024; 13(9):685. https://doi.org/10.3390/biology13090685
Chicago/Turabian StyleAstashev, Maxim E., Dmitriy A. Serov, Arina V. Tankanag, Inna V. Knyazeva, Artem A. Dorokhov, Alexander V. Simakin, and Sergey V. Gudkov. 2024. "Study of the Synchronization and Transmission of Intracellular Signaling Oscillations in Cells Using Bispectral Analysis" Biology 13, no. 9: 685. https://doi.org/10.3390/biology13090685
APA StyleAstashev, M. E., Serov, D. A., Tankanag, A. V., Knyazeva, I. V., Dorokhov, A. A., Simakin, A. V., & Gudkov, S. V. (2024). Study of the Synchronization and Transmission of Intracellular Signaling Oscillations in Cells Using Bispectral Analysis. Biology, 13(9), 685. https://doi.org/10.3390/biology13090685








