Profound Non-Randomness in Dinucleotide Arrangements within Ultra-Conserved Non-Coding Elements and the Human Genome
Abstract
Simple Summary
Abstract
1. Introduction
1.1. Ultra-Conserved Non-Coding Elements (UCNEs)
1.2. Levels of Genomic Sequence Non-Randomness
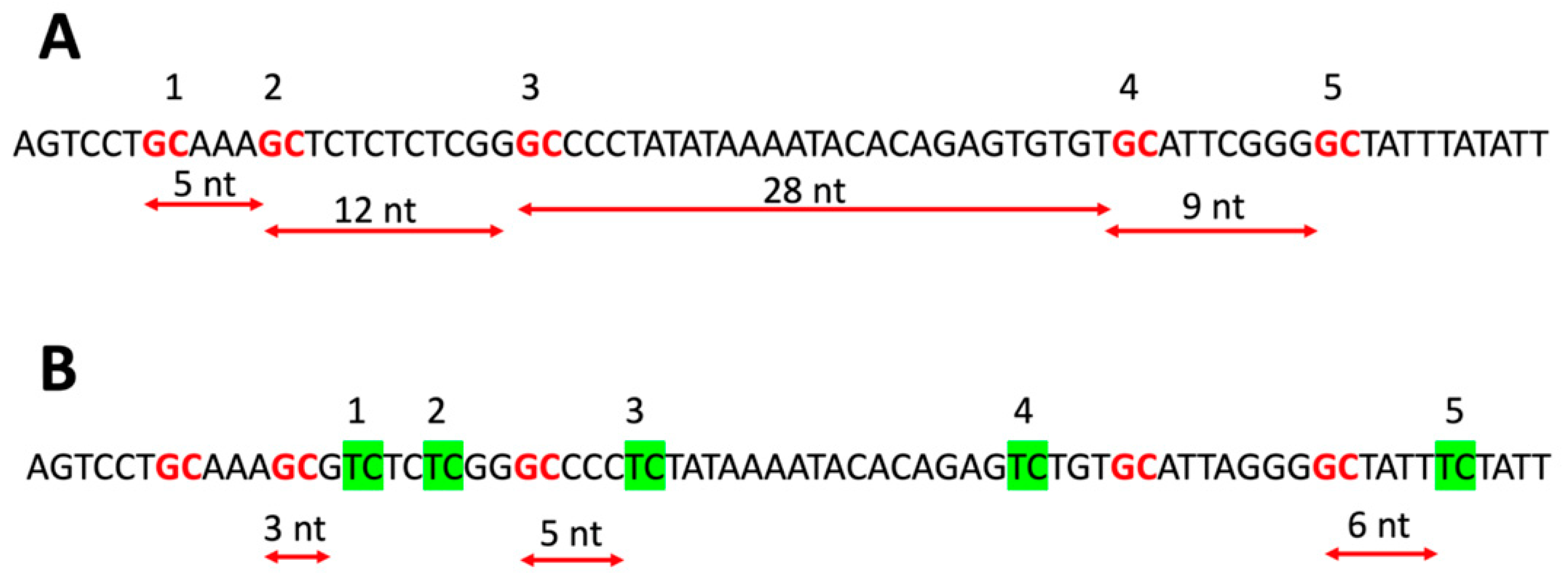
2. Materials and Methods
2.1. Databases
2.2. Programs for SNP Computational Processing
2.3. Statistics
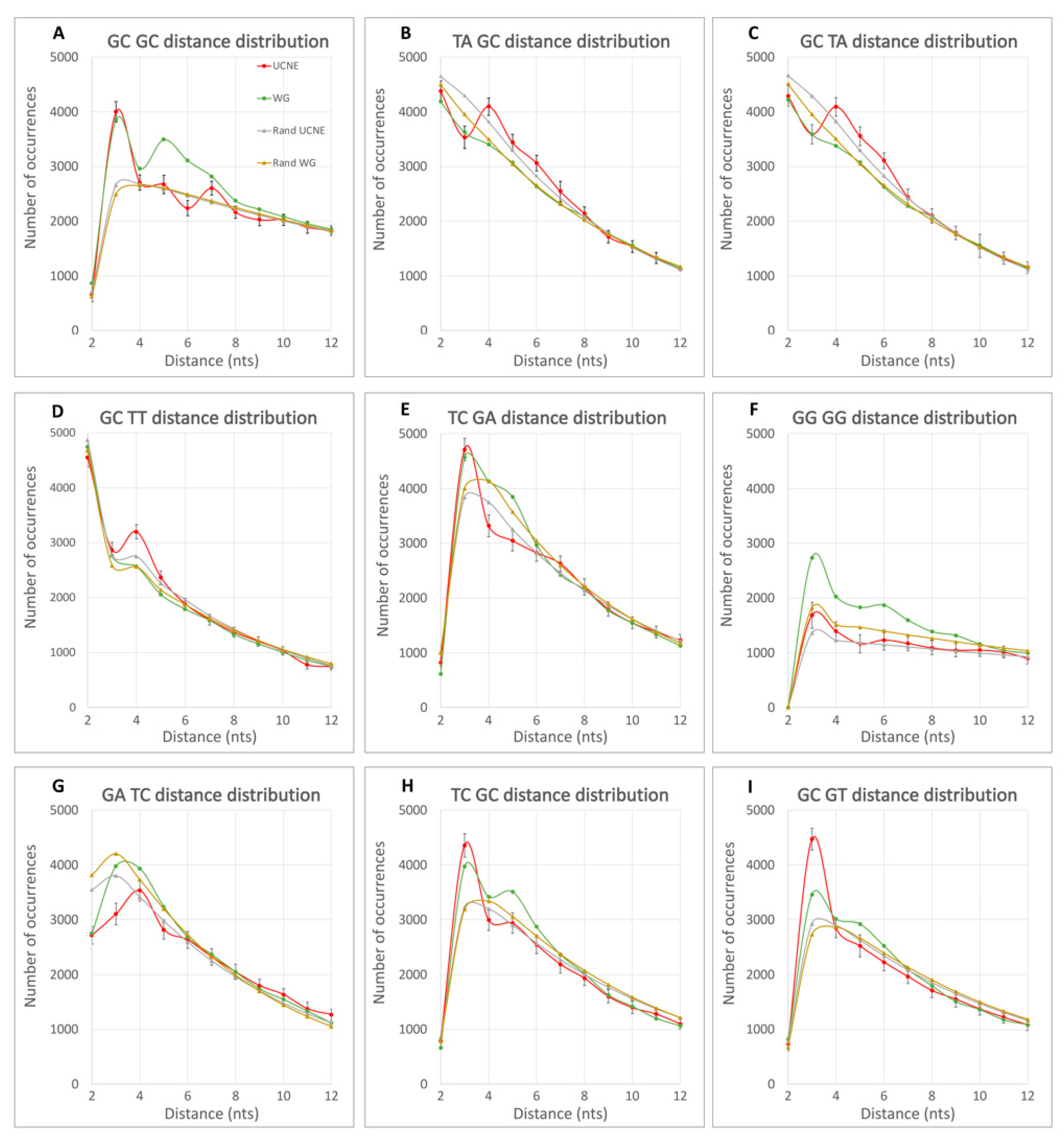
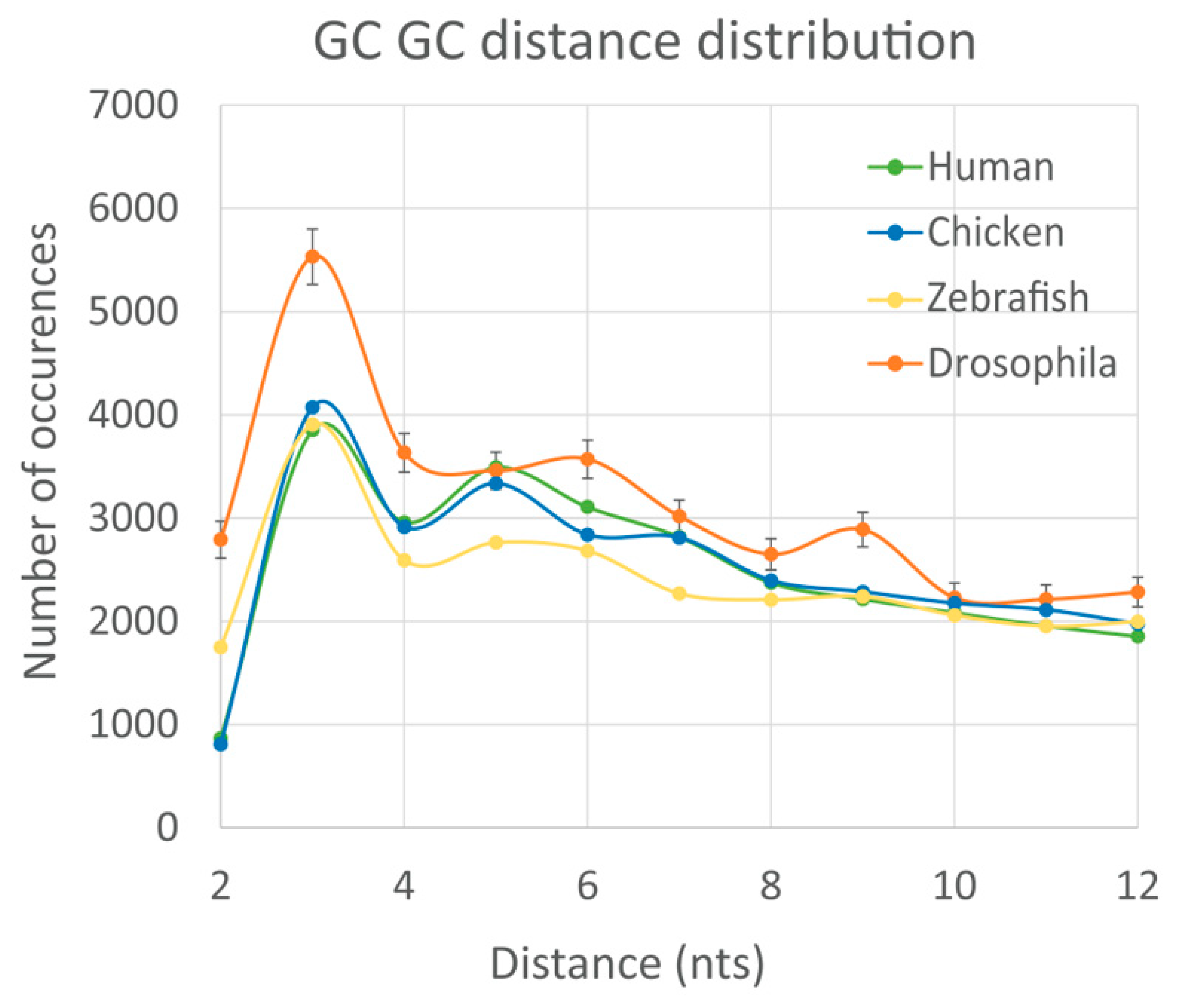
3. Results
4. Discussion
4.1. DN Stacking Energy
4.2. Non-Randomness in DN Spacing Arrangements
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bejerano, G.; Pheasant, M.; Makunin, I.; Stephen, S.; Kent, W.J.; Mattick, J.S.; Haussler, D. Ultraconserved elements in the human genome. Science 2004, 304, 1321–1325. [Google Scholar] [CrossRef]
- Habic, A.; Mattick, J.S.; Calin, G.A.; Krese, R.; Konc, J.; Kunej, T. Genetic Variations of Ultraconserved Elements in the Human Genome. OMICS 2019, 23, 549–559. [Google Scholar] [CrossRef] [PubMed]
- Snetkova, V.; Pennacchio, L.A.; Visel, A.; Dickel, D.E. Perfect and imperfect views of ultraconserved sequences. Nat. Rev. Genet 2022, 23, 182–194. [Google Scholar] [CrossRef]
- Fedorova, L.; Mulyar, O.A.; Lim, J.; Fedorov, A. Nucleotide Composition of Ultra-Conserved Elements Shows Excess of GpC and Depletion of GG and CC Dinucleotides. Genes 2022, 13, 2053. [Google Scholar] [CrossRef] [PubMed]
- Trifonov, E.N. The Codes of Life; Barbieri, M., Ed.; Springer: Dordrecht, The Netherlands, 2007; pp. 4–17. [Google Scholar]
- Karlin, S.; Burge, C. Dinucleotide relative abundance extremes: A genomic signature. Trends Genet 1995, 11, 283–290. [Google Scholar]
- Karlin, S.; Mrazek, J. Compositional differences within and between eukaryotic genomes. Proc. Natl. Acad. Sci. USA 1997, 94, 10227–10232. [Google Scholar] [CrossRef] [PubMed]
- Fedorova, L.; Fedorov, A. Mid-range inhomogeneity of eukaryotic genomes. Sci. World J. 2011, 11, 842–854. [Google Scholar] [CrossRef]
- Bettecken, T.; Trifonov, E.N. Repertoires of the nucleosome-positioning dinucleotides. PLoS ONE 2009, 4, e7654. [Google Scholar] [CrossRef]
- Bastos, C.A.; Afreixo, V.; Pinho, A.J.; Garcia, S.P.; Rodrigues, J.M.; Ferreira, P.J. Inter-dinucleotide distances in the human genome: An analysis of the whole-genome and protein-coding distributions. J. Integr. Bioinform. 2011, 8, 172. [Google Scholar] [CrossRef]
- Cohen, D. General Designs Reveal Distinct Codes in Protein-Coding and Non-Coding Human DNA. Genes 2022, 13, 1970. [Google Scholar] [CrossRef]
- Basu, A.; Bobrovnikov, D.G.; Cieza, B.; Arcon, J.P.; Qureshi, Z.; Orozco, M.; Ha, T. Deciphering the mechanical code of the genome and epigenome. Nat. Struct. Mol. Biol. 2022, 29, 1178–1187. [Google Scholar] [CrossRef] [PubMed]
- Valenzuela, C.Y. Selective intra-dinucleotide interactions and periodicities of bases separated by K sites: A new vision and tool for phylogeny analyses. Biol. Res. 2017, 50, 3. [Google Scholar] [CrossRef][Green Version]
- Mrazek, J. Comparative analysis of sequence periodicity among prokaryotic genomes points to differences in nucleoid structure and a relationship to gene expression. J. Bacteriol. 2010, 192, 3763–3772. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kravatskaya, G.I.; Kravatsky, Y.V.; Chechetkin, V.R.; Tumanyan, V.G. Coexistence of different base periodicities in prokaryotic genomes as related to DNA curvature, supercoiling, and transcription. Genomics 2011, 98, 223–231. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, F.E.; Korotkova, M.A.; Korotkov, E.V. Database of Periodic DNA Regions in Major Genomes. Biomed. Res. Int. 2017, 2017, 7949287. [Google Scholar] [CrossRef] [PubMed]
- Atzinger, A.; Lawrence, J.G. Selection for ancient periodic motifs that do not impart DNA bending. PLoS Genet. 2020, 16, e1009042. [Google Scholar] [CrossRef] [PubMed]
- Trifonov, E.N.; Sussman, J.L. The pitch of chromatin DNA is reflected in its nucleotide sequence. Proc. Natl. Acad. Sci. USA 1980, 77, 3816–3820. [Google Scholar] [CrossRef]
- Kumar, L.; Futschik, M.; Herzel, H. DNA motifs and sequence periodicities. Silico Biol. 2006, 6, 71–78. [Google Scholar]
- Serizay, J.; Ahringer, J. periodicDNA: An R/Bioconductor package to investigate k-mer periodicity in DNA. F1000Research 2021, 10, 141. [Google Scholar] [CrossRef]
- Travers, A.; Hiriart, E.; Churcher, M.; Caserta, M.; Di Mauro, E. The DNA sequence-dependence of nucleosome positioning in vivo and in vitro. J. Biomol. Struct. Dyn. 2010, 27, 713–724. [Google Scholar] [CrossRef]
- Moqtaderi, Z.; Brown, S.; Bender, W. Genome-wide oscillations in G + C density and sequence conservation. Genome Res. 2021, 31, 2050–2057. [Google Scholar] [CrossRef] [PubMed]
- Dimitrieva, S.; Bucher, P. UCNEbase—A database of ultraconserved non-coding elements and genomic regulatory blocks. Nucleic Acids Res. 2013, 41, D101–D109. [Google Scholar] [CrossRef] [PubMed]
- Bechtel, J.M.; Wittenschlaeger, T.; Dwyer, T.; Song, J.; Arunachalam, S.; Ramakrishnan, S.K.; Shepard, S.; Fedorov, A. Genomic mid-range inhomogeneity correlates with an abundance of RNA secondary structures. BMC Genom. 2008, 9, 284. [Google Scholar] [CrossRef]
- Prakash, A.; Bechtel, J.; Fedorov, A. Genomic MRI—A public resource for studying sequence patterns within genomic DNA. J. Vis. Exp. 2011, 51, e2663. [Google Scholar]
- Vologodskii, A.; Frank-Kamenetskii, M.D. DNA melting and energetics of the double helix. Phys. Life Rev. 2018, 25, 1–21. [Google Scholar] [CrossRef]
- SantaLucia, J., Jr.; Allawi, H.T.; Seneviratne, P.A. Improved nearest-neighbor parameters for predicting DNA duplex stability. Biochemistry 1996, 35, 3555–3562. [Google Scholar] [CrossRef] [PubMed]
- Sugimoto, N.; Nakano, S.; Yoneyama, M.; Honda, K. Improved thermodynamic parameters and helix initiation factor to predict stability of DNA duplexes. Nucleic Acids Res. 1996, 24, 4501–4505. [Google Scholar] [CrossRef]
- Huguet, J.M.; Bizarro, C.V.; Forns, N.; Smith, S.B.; Bustamante, C.; Ritort, F. Single-molecule derivation of salt dependent base-pair free energies in DNA. Proc. Natl. Acad. Sci. USA 2010, 107, 15431–15436. [Google Scholar] [CrossRef]
- Kilchherr, F.; Wachauf, C.; Pelz, B.; Rief, M.; Zacharias, M.; Dietz, H. Single-molecule dissection of stacking forces in DNA. Science 2016, 353, aaf5508. [Google Scholar] [CrossRef]
- Sponer, J.; Jurecka, P.; Marchan, I.; Luque, F.J.; Orozco, M.; Hobza, P. Nature of base stacking: Reference quantum-chemical stacking energies in ten unique B-DNA base-pair steps. Chemistry 2006, 12, 2854–2865. [Google Scholar] [CrossRef]
- Alexandrov, B.S.; Gelev, V.; Monisova, Y.; Alexandrov, L.B.; Bishop, A.R.; Rasmussen, K.O.; Usheva, A. A nonlinear dynamic model of DNA with a sequence-dependent stacking term. Nucleic Acids Res. 2009, 37, 2405–2410. [Google Scholar] [CrossRef]
- Svozil, D.; Hobza, P.; Sponer, J. Comparison of intrinsic stacking energies of ten unique dinucleotide steps in A-RNA and B-DNA duplexes. Can we determine correct order of stability by quantum-chemical calculations? J. Phys. Chem. B 2010, 114, 1191–1203. [Google Scholar] [CrossRef]
- Ussery, D.W. DNA Structure: A-, B-and Z-DNA Helix Families. Encycl. Life Sci. 2002, 1, e003122. [Google Scholar] [CrossRef]
- Ravichandran, S.; Subramani, V.K.; Kim, K.K. Z-DNA in the genome: From structure to disease. Biophys. Rev. 2019, 11, 383–387. [Google Scholar] [CrossRef]
- Travers, A.; Muskhelishvili, G. DNA structure and function. FEBS J. 2015, 282, 2279–2295. [Google Scholar] [CrossRef]
- Jain, A.; Wang, G.; Vasquez, K.M. DNA triple helices: Biological consequences and therapeutic potential. Biochimie 2008, 90, 1117–1130. [Google Scholar] [CrossRef]
- Jin, H.; Rube, H.T.; Song, J.S. Categorical spectral analysis of periodicity in nucleosomal DNA. Nucleic Acids Res. 2016, 44, 2047–2057. [Google Scholar] [CrossRef] [PubMed]
- Fedorova, L.V.; Dizadex, I.; Fedorov, A.N.; Ryskov, A.P. In silico analysis of the restriction fragments length distribution in the human genome. Genetika 2001, 37, 456–466. [Google Scholar] [PubMed]
- Quante, T.; Bird, A. Do short, frequent DNA sequence motifs mould the epigenome? Nat. Rev. Mol. Cell Biol. 2016, 17, 257–262. [Google Scholar] [CrossRef] [PubMed]
- van Mierlo, G.; Pushkarev, O.; Kribelbauer, J.F.; Deplancke, B. Chromatin modules and their implication in genomic organization and gene regulation. Trends Genet. 2023, 39, 140–153. [Google Scholar] [CrossRef]
- Chilinski, M.; Sengupta, K.; Plewczynski, D. From DNA human sequence to the chromatin higher order organisation and its biological meaning: Using biomolecular interaction networks to understand the influence of structural variation on spatial genome organisation and its functional effect. Semin. Cell Dev. Biol. 2022, 121, 171–185. [Google Scholar] [CrossRef] [PubMed]
- Herbert, A. The Simple Biology of Flipons and Condensates Enhances the Evolution of Complexity. Molecules 2021, 26, 4881. [Google Scholar] [CrossRef] [PubMed]

| Distance | UCNE | WG, Average | randUCNE, Average | randWG, Average | WG | randUCNE | randWG |
|---|---|---|---|---|---|---|---|
| (nts) | #Observations | #Observations | #Observations | #Observations | SD | SD | SD |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 4380 | 4186 | 4650 | 4499 | 62.3 | 62 | 62.9 |
| 3 | 3531 | 3625 | 4292 | 3952 | 62.7 | 60.9 | 61.1 |
| 4 | 4096 | 3401 | 3818 | 3499 | 68.4 | 59.6 | 55.6 |
| 5 | 3440 | 3066 | 3295 | 3044 | 53.3 | 55.7 | 55.3 |
| 6 | 3064 | 2634 | 2826 | 2656 | 49.2 | 52.2 | 49.7 |
| 7 | 2545 | 2305 | 2422 | 2319 | 47.9 | 44.9 | 46.8 |
| 8 | 2138 | 2082 | 2074 | 2021 | 61.7 | 44.3 | 43.9 |
| 9 | 1716 | 1779 | 1778 | 1760 | 41.9 | 40.3 | 41.2 |
| 10 | 1537 | 1555 | 1522 | 1537 | 37.9 | 37.9 | 37.1 |
| 11 | 1325 | 1333 | 1304 | 1341 | 36.2 | 37.5 | 35.2 |
| 12 | 1115 | 1138 | 1117 | 1171 | 33.5 | 34.5 | 33.9 |
| … | |||||||
| 50 | 6 | 12 | 3 | 7 | 3.4 | 1.8 | 2.6 |
| abs(RPD) Threshold | MAX (Peaks) | MIN (Dips) | TOTAL (Peaks + Dips) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| UCNE-Rand | WG-Rand | WG-UCNE | UCNE-Rand | WG-Rand | WG-UCNE | UCNE-Rand | WG-Rand | WG-UCNE | |
| 10% | 69% | 62% | 56% | 73% | 54% | 68% | 90% | 83% | 84% |
| 20% | 27 | 34 | 7 | 16 | 14 | 19 | 40 | 44 | 25 |
| 30% | 9 | 13 | 0 | 2 | 3 | 8 | 11 | 17 | 8 |
| 40% | 4 | 7 | 0 | 0.4 | 0.4 | 0.8 | 4 | 7 | 1 |
| DN | UCNE vs. randUCNE | WG vs. randWG | WG vs. UCNE |
|---|---|---|---|
| AA | 3 | 2 | 4 |
| AG | 4 | 3 | 0 |
| AC | 6 | 3 | 1 |
| AT | 2 | 7 | 6 |
| GA | 0 | 3 | 0 |
| GG | 3 | 8 | 3 |
| GC | 10 | 9 | 2 |
| GT | 6 | 3 | 1 |
| CA | 3 | 4 | 1 |
| CG | 5 | 11 | 7 |
| CC | 1 | 8 | 4 |
| CT | 4 | 3 | 0 |
| TA | 2 | 5 | 5 |
| TG | 3 | 4 | 0 |
| TC | 0 | 3 | 0 |
| TT | 4 | 3 | 3 |
| TOTAL | 29 | 43 | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedorova, L.; Crossley, E.R.; Mulyar, O.A.; Qiu, S.; Freeman, R.; Fedorov, A. Profound Non-Randomness in Dinucleotide Arrangements within Ultra-Conserved Non-Coding Elements and the Human Genome. Biology 2023, 12, 1125. https://doi.org/10.3390/biology12081125
Fedorova L, Crossley ER, Mulyar OA, Qiu S, Freeman R, Fedorov A. Profound Non-Randomness in Dinucleotide Arrangements within Ultra-Conserved Non-Coding Elements and the Human Genome. Biology. 2023; 12(8):1125. https://doi.org/10.3390/biology12081125
Chicago/Turabian StyleFedorova, Larisa, Emily R. Crossley, Oleh A. Mulyar, Shuhao Qiu, Ryan Freeman, and Alexei Fedorov. 2023. "Profound Non-Randomness in Dinucleotide Arrangements within Ultra-Conserved Non-Coding Elements and the Human Genome" Biology 12, no. 8: 1125. https://doi.org/10.3390/biology12081125
APA StyleFedorova, L., Crossley, E. R., Mulyar, O. A., Qiu, S., Freeman, R., & Fedorov, A. (2023). Profound Non-Randomness in Dinucleotide Arrangements within Ultra-Conserved Non-Coding Elements and the Human Genome. Biology, 12(8), 1125. https://doi.org/10.3390/biology12081125






