Single-Step Genomic Prediction of Superovulatory Response Traits in Japanese Black Donor Cows
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics Statement
2.2. Phenotypic, SNP Genotype, and Pedigree Data
2.3. A and G Matrices
2.4. Variance Component Estimation
2.5. Breeding Value Prediction
2.6. Selection Simulation
3. Results and Discussion
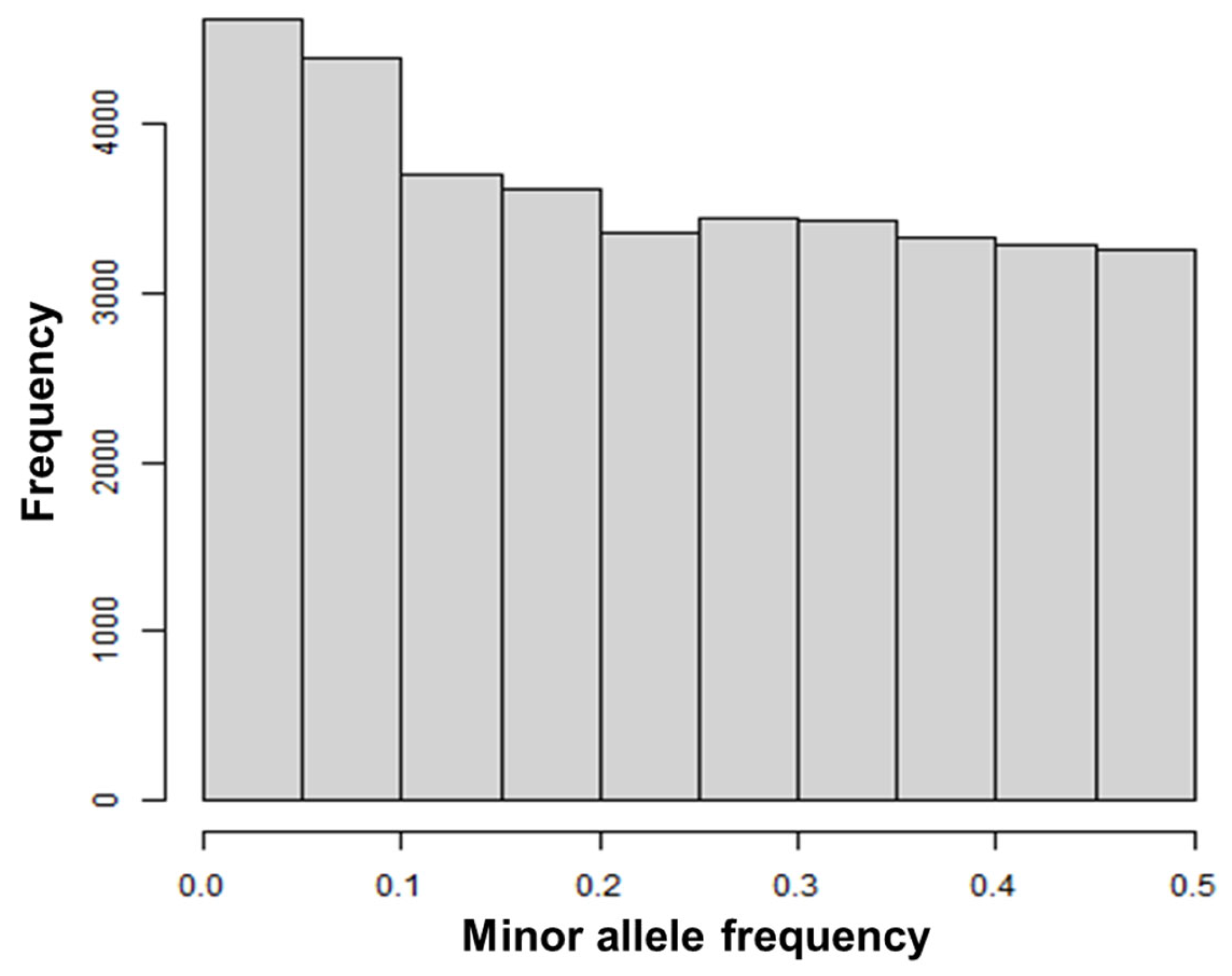
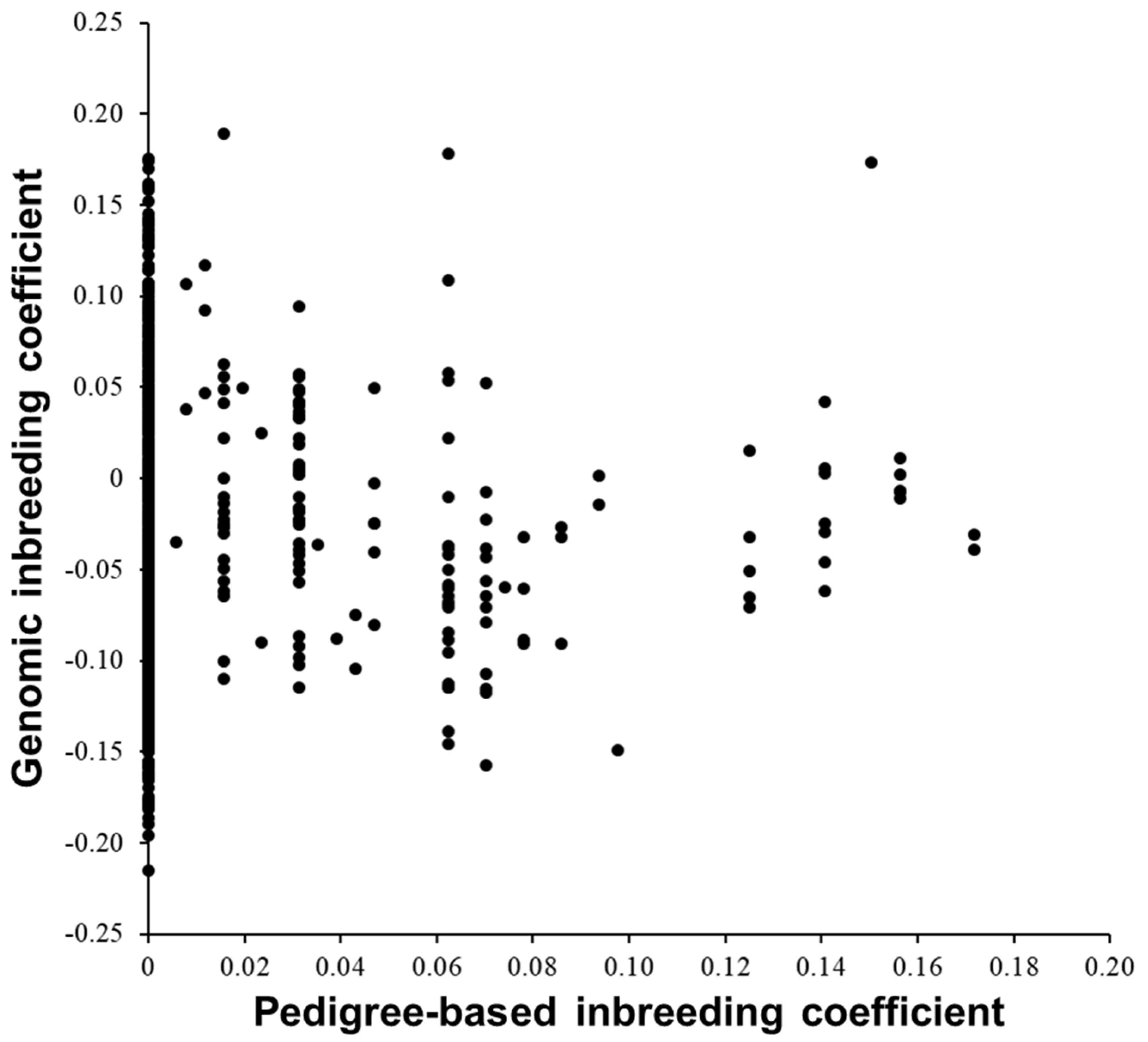
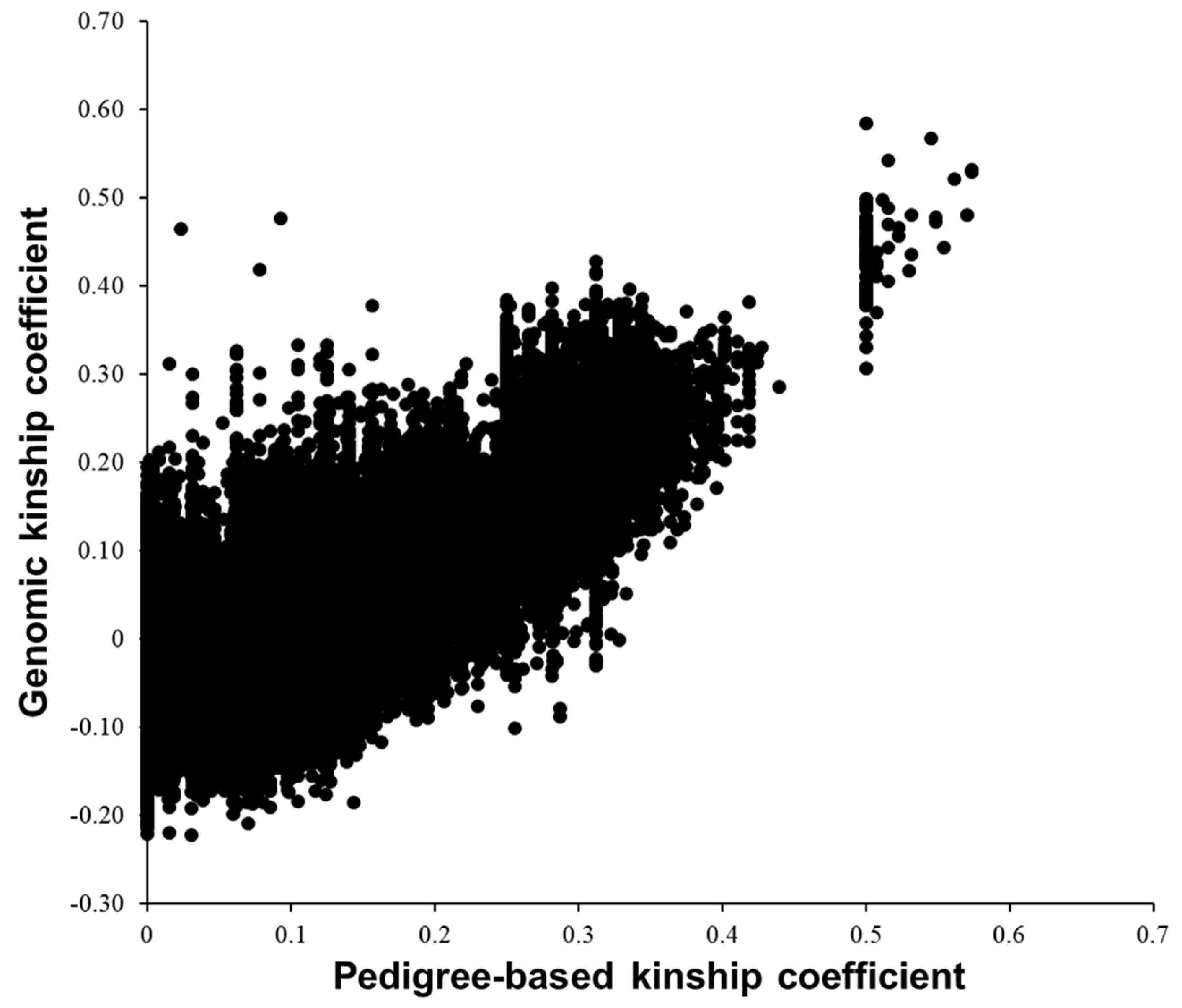
3.1. Comparing A and G Matrices for the 575 Cows
3.2. Variance Component Estimation
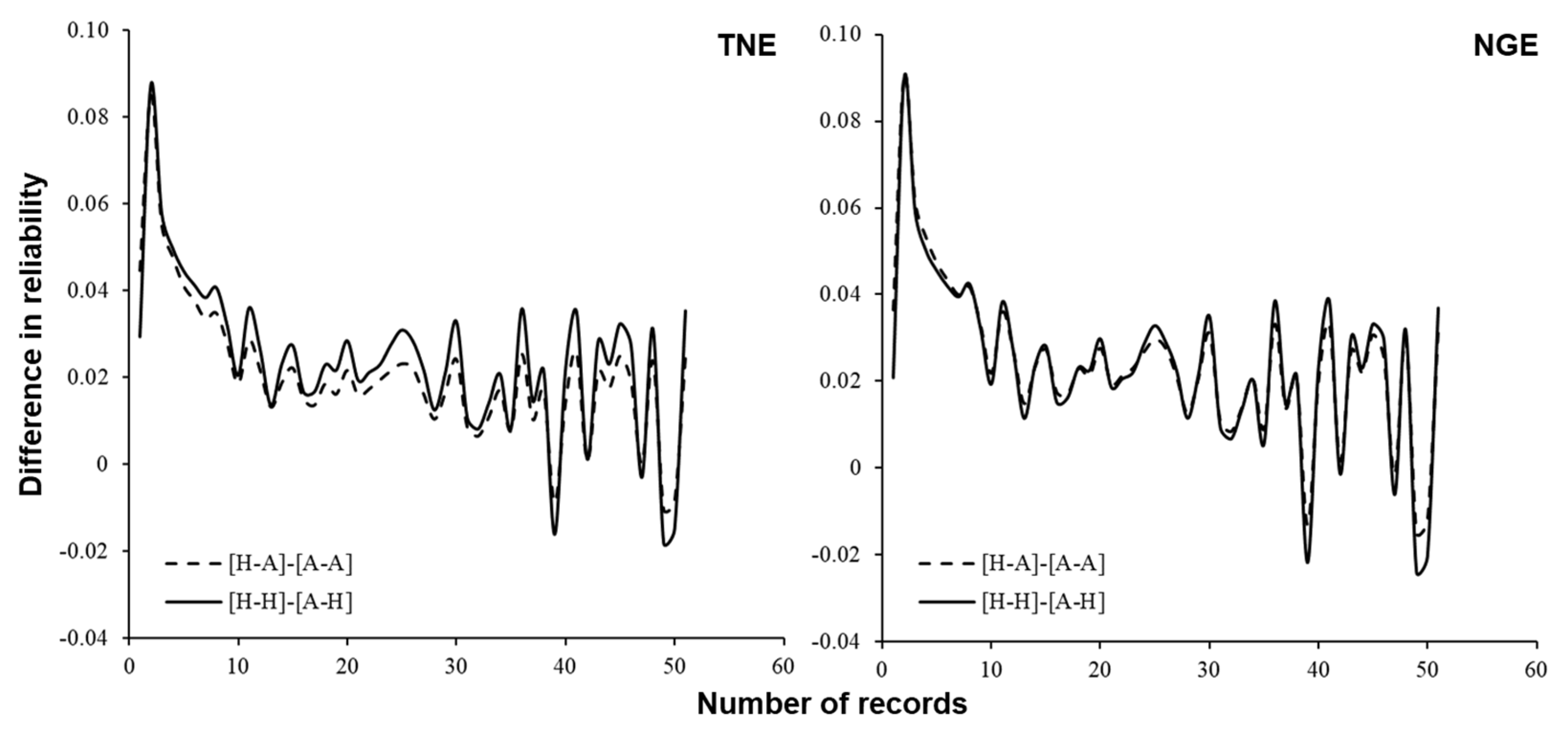
3.3. Reliability of Predicted Breeding Values
3.4. Selection Simulation
3.5. General Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Namikawa, K. Wagyu: Japanese Beef Cattle—Historical Breeding Processes of Japanese Beef Cattle and Preservation of Genetic Resources as Economic Farm Animal; Wagyu Registry Association: Kyoto, Japan, 1992. [Google Scholar]
- Gotoh, T.; Takahashi, H.; Nishimura, T.; Kuchida, K.; Mannen, H. Meat produced by Japanese Black cattle and Wagyu. Anim. Front. 2014, 4, 46–54. [Google Scholar] [CrossRef]
- Motoyama, M.; Sasaki, K.; Watanabe, A. Wagyu and the factors contributing to its beef quality: A Japanese industry overview. Meat Sci. 2016, 120, 10–18. [Google Scholar] [CrossRef] [PubMed]
- Gilmour, A.R.; Thompson, R.; Cullis, B.R. Average information REML: An efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 1995, 51, 1440–1450. [Google Scholar] [CrossRef]
- Johnson, D.L.; Thompson, R. Restricted maximum likelihood estimation of variance components for univariate animal models using sparse matrix techniques and average information. J. Dairy Sci. 1995, 78, 449–456. [Google Scholar] [CrossRef]
- Henderson, C.R. Best linear unbiased estimation and prediction under a selection model. Biometrics 1975, 31, 423–447. [Google Scholar] [CrossRef]
- Ashida, I.; Iwaisaki, H. A numerical technique for REML estimation of variance components using average information algorithm and its computing property. Anim. Sci. Technol. 1998, 69, 631–636. [Google Scholar]
- Ashida, I.; Iwaisaki, H. An expression for average information matrix for a mixed linear multi-component of variance model and REML iteration equations. Anim. Sci. J. 1999, 70, 282–289. [Google Scholar] [CrossRef]
- Wagyu Registry Association. Breeding and Improvement of Wagyu; Wagyu Registry Association: Kyoto, Japan, 2007. (In Japanese) [Google Scholar]
- Misztal, I.; Legarra, A.; Aguilar, I. Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J. Dairy Sci. 2009, 92, 4648–4655. [Google Scholar] [CrossRef]
- Legarra, A.; Aguilar, I.; Misztal, I. A relationship matrix including full pedigree and genomic information. J. Dairy Sci. 2009, 92, 4656–4663. [Google Scholar] [CrossRef]
- Lourenco, D.; Legarra, A.; Tsuruta, S.; Masuda, Y.; Aguilar, I.; Misztal, I. Single-step genomic evaluations from theory to practice: Using SNP chips and sequence data in BLUPF90. Genes 2020, 11, 790. [Google Scholar] [CrossRef]
- Watanabe, T.; Matsuda, H.; Arakawa, A.; Yamada, T.; Iwaisaki, H.; Nishimura, S.; Sugimoto, Y. Estimation of variance components for carcass traits in Japanese Black cattle using 50K SNP genotype data. Anim. Sci. J. 2014, 85, 1–7. [Google Scholar] [CrossRef]
- Onogi, A.; Ogino, A.; Komatsu, T.; Shoji, N.; Simizu, K.; Kurogi, K.; Yasumori, T.; Togashi, K.; Iwata, H. Genomic prediction in Japanese Black cattle: Application of a single-step approach to beef cattle. J. Anim. Sci. 2014, 92, 1931–1938. [Google Scholar] [CrossRef]
- Ogawa, S.; Taniguchi, Y.; Watanabe, T.; Iwaisaki, H. Fitting genomic prediction models with different marker effects among prefectures to carcass traits in Japanese Black cattle. Genes 2023, 14, 24. [Google Scholar] [CrossRef]
- Ogawa, S.; Kitajima, S.; Saito, H.; Satoh, M. Deriving economic values for female reproductive traits in lifetime carcass production of Japanese Black cows using deterministic profit function. Agriculture 2021, 11, 1055. [Google Scholar] [CrossRef]
- Agriculture and Livestock Industry Promotion Organization. Chikusan no Joho; Agriculture and Livestock Industry Promotion Organization: Tokyo, Japan, 2019; Volume 10, pp. 53–71. (In Japanese) [Google Scholar]
- Oyama, K.; Katsuta, T.; Anada, K.; Mukai, F. Heritability and repeatability estimates for reproductive traits of Japanese Black cows. Asian Australas. J. Anim. Sci. 2002, 15, 1680–1685. [Google Scholar] [CrossRef]
- Setiaji, A.; Oikawa, T. Genetic parameters of reproductive traits from artificial insemination records of Japanese Black cows. Livest. Sci. 2019, 229, 85–89. [Google Scholar] [CrossRef]
- Ogawa, S.; Satoh, M. Random regression analysis of calving interval of Japanese Black cows. Animals 2021, 11, 202. [Google Scholar] [CrossRef]
- Zoda, A.; Urakawa, M.; Oono, Y.; Ogawa, S.; Satoh, M. Estimation of genetic parameters for superovulatory response traits in Japanese Black cows. J. Anim. Sci. 2021, 99, skab265. [Google Scholar] [CrossRef]
- Ogawa, S.; Zoda, A.; Kagawa, R.; Obinata, R.; Urakawa, M.; Oono, Y. Bayesian estimation of genetic parameters for superovulatory response traits in Japanese Black donor cows using count data models. Theriogenology 2022, 190, 38–45. [Google Scholar] [CrossRef]
- Zoda, A.; Kagawa, R.; Obinata, R.; Urakawa, M.; Oono, Y.; Ogawa, S.; Uemoto, Y.; Satoh, M. Genetic relationship between superovulatory response traits and carcass traits in Japanese Black cattle. Anim. Sci. J. 2022, 93, e13731. [Google Scholar] [CrossRef]
- Mehrabani-Yegane, H.; Gibson, J.P.; Schaeffer, L.R. Using recent versus complete pedigree data in genetic evaluation of a closed nucleus broiler line. Poult. Sci. 1999, 78, 937–941. [Google Scholar] [CrossRef] [PubMed]
- Cantet, R.J.C.; Birchmeier, A.N.; Santos-Cristal, M.G.; de Avila, V.S. Comparison of restricted maximum likelihood and Method R for estimating heritability and predicting breeding value under selection. J. Anim. Sci. 2000, 78, 2554–2560. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Su, G. Impact of phenotypic information of previous generations and depth of pedigree on estimates of genetic parameters and breeding values. Livest. Sci. 2016, 187, 61–67. [Google Scholar] [CrossRef]
- Wang, H.; Misztal, I.; Legarra, A. Differences between genomic-based and pedigree-based relationships in a chicken population, as a function of quality control and pedigree links among individuals. J. Anim. Breed. Genet. 2014, 131, 445–451. [Google Scholar] [CrossRef] [PubMed]
- Porto-Neto, L.R.; Barendse, W.; Henshall, J.M.; McWilliam, S.M.; Lehnert, S.A.; Reverter, A. Genomic correlation: Harnessing the benefit of combining two unrelated populations for genomic selection. Genet. Sel. Evol. 2015, 47, 84. [Google Scholar] [CrossRef]
- Zhang, J.; Song, H.; Zhang, Q.; Ding, X. Assessment of relationships between pigs based on pedigree and genomic information. Animal 2020, 14, 697–705. [Google Scholar] [CrossRef]
- Ogawa, S.; Zoda, A.; Kagawa, R.; Obinata, R. Comparing methods to select candidates for re-genotyping to impute higher-density genotype data in a Japanese Black cattle population: A case study. Animals 2023, 13, 638. [Google Scholar] [CrossRef]
- Browning, B.L.; Zhou, Y.; Browning, S.R. A one-penny imputed genome from next generation reference panels. Am. J. Hum. Genet. 2018, 103, 338–348. [Google Scholar] [CrossRef]
- Misztal, I.; Tsuruta, S.; Strabel, T.; Auvray, B.; Druet, T.; Lee, D.H. BLUPF90 and related programs (BGF90). In Proceedings of the 7th World Congress on Genetics Applied to Livestock Production, Montpellier, France, 19−23 August 2002. [Google Scholar]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Fernando, R.L.; Cheng, H.; Sun, X.; Garrick, D.J. A comparison of identity-by-descent and identity-by-state matrices that are used for genetic evaluation and estimation of variance components. J. Anim. Breed. Genet. 2017, 134, 213–223. [Google Scholar] [CrossRef]
- Christensen, O.F.; Lund, M.S. Genomic prediction when some animals are not genotyped. Genet. Sel. Evol. 2010, 42, 2. [Google Scholar] [CrossRef]
- Aguilar, I.; Misztal, I.; Johnson, D.L.; Legarra, A.; Tsuruta, S.; Lawlor, T.J. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 2010, 93, 743–752. [Google Scholar] [CrossRef]
- Ogawa, S.; Matsuda, H.; Taniguchi, Y.; Watanabe, T.; Nishimura, S.; Sugimoto, Y.; Iwaisaki, H. Effects of single nucleotide polymorphism marker density on degree of genetic variance explained and genomic evaluation for carcass traits in Japanese Black beef cattle. BMC Genet. 2014, 15, 15. [Google Scholar] [CrossRef]
- Komiya, R.; Ogawa, S.; Aonuma, T.; Satoh, M. Performance of using opposing homozygotes for paternity testing in Japanese Black cattle. J. Anim. Breed. Genet. 2022, 139, 113–124. [Google Scholar] [CrossRef]
- Zoda, A.; Ogawa, S.; Matsuda, H.; Taniguchi, Y.; Watanabe, T.; Sugimoto, Y.; Iwaisaki, H. Inferring genetic characteristics of Japanese Black cattle populations using genome-wide single nucleotide polymorphism markers. J. Anim. Genet. 2022, 50, 3–9. [Google Scholar] [CrossRef]
- Ogawa, S.; Matsuda, H.; Taniguchi, Y.; Watanabe, T.; Kitamura, Y.; Tabuchi, I.; Sugimoto, Y.; Iwaisaki, H. Genomic prediction for carcass traits in Japanese Black cattle using single nucleotide polymorphism markers of different densities. Anim. Prod. Sci. 2016, 57, 1631–1636. [Google Scholar] [CrossRef]
- Takeda, M.; Uemoto, Y.; Inoue, K.; Ogino, A.; Nozaki, T.; Kurogi, K.; Yasumori, T.; Satoh, M. Evaluation of feed efficiency traits for genetic improvement in Japanese Black cattle. J. Anim. Sci. 2018, 96, 797–805. [Google Scholar] [CrossRef]
- Nagai, R.; Kinukawa, M.; Watanabe, T.; Ogino, A.; Kurogi, K.; Adachi, K.; Satoh, M.; Uemoto, Y. Genomic dissection of repeatability considering additive and nonadditive genetic effects for semen production traits in beef and dairy bulls. J. Anim. Sci. 2022, 100, skac241. [Google Scholar] [CrossRef]
- Onogi, A.; Ogino, A.; Komatsu, T.; Shoji, N.; Shimizu, K.; Kurogi, K.; Yasumori, T.; Togashi, K.; Iwata, H. Whole-genome prediction of fatty acid composition in meat of Japanese Black cattle. Anim. Genet. 2015, 46, 557–559. [Google Scholar] [CrossRef]
- Atagi, Y.; Onogi, A.; Kinukawa, M.; Ogino, A.; Kurogi, K.; Uchiyama, K.; Yasumori, T.; Adachi, K.; Togashi, K.; Iwata, H. Genetic analysis of semen production traits of Japanese Black and Holstein bulls: Genome-wide marker-based estimation of genetic parameters and environmental effect trends. J. Anim. Sci. 2017, 95, 1900–1912. [Google Scholar]
- Cornelissen, M.A.M.; Mullaart, E.; Van der Linde, C.; Mulder, H.A. Estimating variance components and breeding values for number of oocytes and number of embryos in dairy cattle using a single-step genomic evaluation. J. Dairy Sci. 2017, 100, 4698–4705. [Google Scholar] [CrossRef] [PubMed]
- Zoda, A.; Ogawa, S.; Matsuda, H.; Taniguchi, Y.; Watanabe, T.; Sugimoto, Y.; Iwaisaki, H. Genomic prediction for carcass traits in Japanese Black cattle considering mixed structure of subpopulations. J. Anim. Genet. 2022, 50, 31–38. [Google Scholar] [CrossRef]
- Fujii, T.; Naito, A.; Hirayama, H.; Kashima, M.; Yoshino, H.; Hanamure, T.; Domon, Y.; Hayakawa, H.; Watanabe, T.; Moriyasu, S.; et al. Potential of preimplantation genomic selection for carcass traits in Japanese Black cattle. J. Reprod. Dev. 2019, 65, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Scott, B.A.; Haile-Mariam, M.; Cocks, B.G.; Pryce, J.E. How genomic selection has increased rates of genetic gain and inbreeding in the Australian national herd, genomic information nucleus, and bulls. J. Dairy Sci. 2021, 104, 11832–11849. [Google Scholar] [CrossRef] [PubMed]
- Ablondi, M.; Sabbioni, A.; Stocco, G.; Cipolat-Gotet, C.; Dadousis, C.; van Kaam, J.-T.; Finocchiaro, R.; Summer, A. Genetic diversity in the Italian Holstein dairy cattle based on pedigree and SNP data prior and after genomic selection. Front. Vet. Sci. 2022, 13, 773985. [Google Scholar] [CrossRef]
- Lozada-Soto, E.A.; Tiezzi, F.; Jiang, J.; Cole, J.B.; VanRaden, P.M. Genomic characterization of autozygosity and recent inbreeding trends in all major breeds of US dairy cattle. J. Dairy Sci. 2022, 105, 8956–8971. [Google Scholar] [CrossRef]
- Leroy, G. Genetic diversity, inbreeding and breeding practices in dogs: Results from pedigree analyses. J. Vet. Med. 2011, 189, 177–182. [Google Scholar] [CrossRef]
- Eynard, S.E.; Windig, J.J.; Hulsegge, I.; Hiemstra, S.-J.; Calus, M.P.L. The impact of using old germplasm on genetic merit and diversity—A cattle breed case study. J. Anim. Breed. Genet. 2018, 135, 311–322. [Google Scholar] [CrossRef]
- Obšteter, J.; Jenko, J.; Hickey, J.M.; Gorjanc, G. Efficient use of genomic information for sustainable genetic improvement in small cattle populations. J. Dairy Sci. 2019, 102, 9971–9982. [Google Scholar] [CrossRef]
- Nomura, T.; Honda, T.; Mukai, F. Inbreeding and effective population size of Japanese Black cattle. J. Anim. Sci. 2001, 79, 366–370. [Google Scholar] [CrossRef]
- Suezawa, R.; Nikadori, H.; Sasaki, S. Genetic diversity and genomic inbreeding in Japanese Black cows in the islands of Okinawa Prefecture evaluated using single-nucleotide polymorphism array. Anim. Sci. J. 2021, 92, e13525. [Google Scholar] [CrossRef]
- Kawaguchi, F.; Nakamura, M.; Kobayashi, E.; Yonezawa, T.; Sasazaki, S.; Mannen, H. Comprehensive assessment of genetic diversity, structure, and relationship in four Japanese cattle breeds by Illumina 50 K SNP array analysis. Anim. Sci. J. 2022, 93, e13770. [Google Scholar] [CrossRef]
- Gowane, G.R.; Alex, R.; Mukherjee, A.; Vohra, V. Impact and utility of shallow pedigree using single-step genomic BLUP for prediction of unbiased genomic breeding values. Trop. Anim. Health Prod. 2022, 54, 339. [Google Scholar] [CrossRef]
- Kim, E.-H.; Kang, H.-C.; Sun, D.-W.; Myung, C.-H.; Kim, J.-Y.; Lee, D.-H.; Lee, S.-H.; Lim, H.-T. Estimation of breeding value and accuracy using pedigree and genotype of Hanwoo cows (Korean cattle). J. Anim. Breed. Genet. 2022, 139, 281–291. [Google Scholar] [CrossRef]
- Meyer, K. Impact of missing pedigrees in single-step genomic evaluation. Anim. Prod. Sci. 2021, 61, 1761–1773. [Google Scholar] [CrossRef]
- Legarra, A.; Christensen, O.F.; Vitezica, Z.G.; Aguilar, I.; Misztal, I. Ancestral relationships using metafounders: Finite ancestral populations and across population relationships. Genetics 2015, 200, 455–468. [Google Scholar] [CrossRef]
- Bradford, H.L.; Masuda, Y.; VanRaden, P.M.; Legarra, A.; Misztal, I. Modeling missing pedigree in single-step genomic BLUP. J. Dairy Sci. 2019, 102, 2336–2346. [Google Scholar] [CrossRef]
- Masuda, Y.; Tsuruta, S.; Bermann, M.; Bradford, H.L.; Misztal, I. Comparison of models for missing pedigree in single-step genomic prediction. J. Anim. Sci. 2021, 99, skab019. [Google Scholar] [CrossRef]
- Jaton, C.; Koeck, A.; Sargolzaei, M.; Malchiodi, F.; Price, C.A.; Schenkel, F.S.; Miglior, F. Genetic analysis of superovulatory response of Holstein cows in Canada. J. Dairy Sci. 2016, 99, 3612–3623. [Google Scholar] [CrossRef]
- Parker Gaddis, K.L.; Dikmen, S.; Null, D.J.; Cole, J.B.; Hansen, P.J. Evaluation of genetic components in traits related to superovulation, in vitro fertilization, and embryo transfer in Holstein cattle. J. Dairy Sci. 2017, 100, 2877–2891. [Google Scholar] [CrossRef]
- Nawaz, M.Y.; Jimenez-Krassel, F.; Steibel, J.P.; Lu, Y.; Baktula, A.; Vukasinovic, N.; Neuder, L.; Ireland, J.L.H.; Ireland, J.J.; Tempelman, R.J. Genomic heritability and genome-wide association analysis of anti-Müllerian hormone in Holstein dairy heifers. J. Dairy Sci. 2018, 101, 8063–8075. [Google Scholar] [CrossRef]
- Sasaki, S.; Ibi, T.; Watanabe, T.; Matsuhashi, T.; Ikeda, S.; Sugimoto, Y. Variants in the 3’ UTR of General Transcription Factor IIF, polypeptide 2 affect female calving efficiency in Japanese Black cattle. BMC Genet. 2013, 14, 41. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, S.; Ibi, T.; Ikeda, S.; Sugimoto, Y. A genome-wide association study reveals a quantitative trait locus for age at first calving in delta/notch-like EGF repeat containing on chromosome 2 in Japanese Black cattle. Anim. Genet. 2014, 45, 285–287. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, S.; Ibi, T.; Kojima, T.; Sugimoto, Y. A genome-wide association study reveals a quantitative trait locus for days open on chromosome 2 in Japanese Black cattle. Anim. Genet. 2016, 47, 102–105. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, S.; Ibi, T.; Matsuhashi, T.; Takeda, K.; Ikeda, S.; Sugimoto, M.; Sugimoto, Y. Genetic variants in the upstream region of activin receptor IIA are associated with female fertility in Japanese Black cattle. BMC Genet. 2015, 16, 123. [Google Scholar] [CrossRef]
- Sasaki, S.; Ibi, T. A genome-wide association study reveals a quantitative trait locus for calf mortality on chromosome 9 in Japanese Black cattle. Anim. Genet. 2021, 52, 214–216. [Google Scholar] [CrossRef]
- Hirayama, H.; Naito, A.; Fujii, T.; Sugimoto, M.; Takedomi, T.; Moriyasu, S.; Sakai, H.; Kageyama, S. Effects of genetic background on responses to superovulation in Japanese Black cattle. J. Vet. Med. Sci. 2019, 81, 373–378. [Google Scholar] [CrossRef]

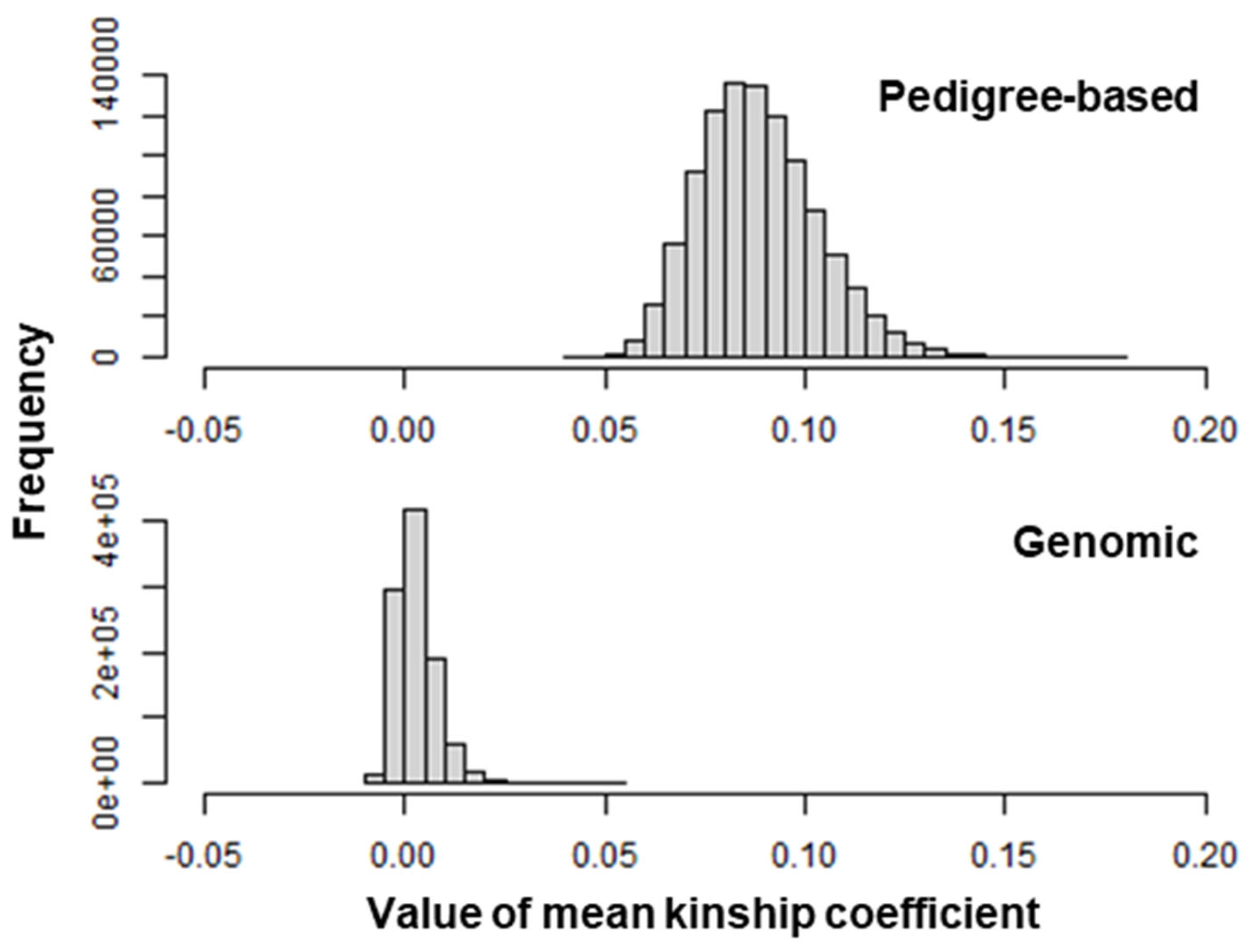
| Trait Name | Abbreviation | Mean | Standard Deviation |
|---|---|---|---|
| Total number of embryos and oocytes | TNE | 16.3 | 10.4 |
| Number of good embryos | NGE | 6.7 | 6.0 |
| Coefficient | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|
| Pedigree-based inbreeding | 0.014 | 0.032 | 0 | 0.172 |
| Genomic inbreeding | –0.033 | 0.080 | –0.215 | 0.189 |
| Pedigree-based kinship | 0.087 | 0.089 | 0 | 0.574 |
| Genomic kinship | 0.003 | 0.090 | –0.222 | 0.584 |
| Item | H Matrix | A Matrix | ||
|---|---|---|---|---|
| TNE | NGE | TNE | NGE | |
| Additive genetic variance | 19.19 ± 3.20 | 3.99 ± 0.79 | 28.07 ± 4.15 | 5.57 ± 1.05 |
| Permanent environmental variance | 17.49 ± 2.23 | 4.93 ± 0.58 | 10.87 ± 2.78 | 3.63 ± 0.73 |
| Error variance | 68.16 ± 0.63 | 26.32 ± 0.24 | 68.15 ± 0.63 | 26.32 ± 0.24 |
| Heritability | 0.18 ± 0.03 | 0.11 ± 0.02 | 0.26 ± 0.03 | 0.16 ± 0.03 |
| Repeatability | 0.35 ± 0.01 | 0.25 ± 0.01 | 0.36 ± 0.01 | 0.26 ± 0.01 |
| Genetic correlation | 0.61 ± 0.08 | 0.66 ± 0.07 | ||
| Matrix for BLUP | Matrix for REML | TNE | NGE | ||
|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | ||
| H matrix | H matrix | 0.592 | 0.002 | 0.523 | 0.002 |
| H matrix | A matrix | 0.713 | 0.002 | 0.623 | 0.002 |
| A matrix | H matrix | 0.566 | 0.002 | 0.498 | 0.003 |
| A matrix | A matrix | 0.692 | 0.002 | 0.597 | 0.003 |
| Matrix for BLUP | Matrix for REML | Matrix for BLUP | |||
|---|---|---|---|---|---|
| H Matrix | A Matrix | ||||
| Matrix for REML | |||||
| H Matrix | A Matrix | H Matrix | A Matrix | ||
| TNE | |||||
| H matrix | H matrix | -- | 0.990 | 0.972 | 0.959 |
| H matrix | A matrix | 0.990 | -- | 0.974 | 0.979 |
| A matrix | H matrix | 0.970 | 0.971 | -- | 0.990 |
| A matrix | A matrix | 0.956 | 0.976 | 0.989 | -- |
| NGE | |||||
| H matrix | H matrix | -- | 0.990 | 0.966 | 0.954 |
| H matrix | A matrix | 0.989 | -- | 0.964 | 0.971 |
| A matrix | H matrix | 0.961 | 0.958 | -- | 0.989 |
| A matrix | A matrix | 0.950 | 0.967 | 0.988 | -- |
| Matrix for BLUP | Matrix for REML | Matrix for BLUP | |||
| H Matrix | A Matrix | ||||
| Matrix for REML | |||||
| H Matrix | A Matrix | H Matrix | A Matrix | ||
| H matrix | H matrix | -- | 88% | 92% | 88% |
| H matrix | A matrix | 88% | -- | 84% | 84% |
| A matrix | H matrix | 80% | 68% | -- | 96% |
| A matrix | A matrix | 76% | 72% | 80% | -- |
| Matrix for BLUP | Matrix for REML | Mean Kinship Coefficient | p-Value Based on Empirical Distribution | ||
|---|---|---|---|---|---|
| Pedigree-Based | Genomic | Pedigree-Based | Genomic | ||
| H matrix | H matrix | 0.109 | 0.006 | 0.009 | 0.225 |
| H matrix | A matrix | 0.110 | 0.009 | 0.008 | 0.113 |
| A matrix | H matrix | 0.105 | 0.006 | 0.135 | 0.237 |
| A matrix | A matrix | 0.105 | 0.006 | 0.130 | 0.199 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zoda, A.; Ogawa, S.; Kagawa, R.; Tsukahara, H.; Obinata, R.; Urakawa, M.; Oono, Y. Single-Step Genomic Prediction of Superovulatory Response Traits in Japanese Black Donor Cows. Biology 2023, 12, 718. https://doi.org/10.3390/biology12050718
Zoda A, Ogawa S, Kagawa R, Tsukahara H, Obinata R, Urakawa M, Oono Y. Single-Step Genomic Prediction of Superovulatory Response Traits in Japanese Black Donor Cows. Biology. 2023; 12(5):718. https://doi.org/10.3390/biology12050718
Chicago/Turabian StyleZoda, Atsushi, Shinichiro Ogawa, Rino Kagawa, Hayato Tsukahara, Rui Obinata, Manami Urakawa, and Yoshio Oono. 2023. "Single-Step Genomic Prediction of Superovulatory Response Traits in Japanese Black Donor Cows" Biology 12, no. 5: 718. https://doi.org/10.3390/biology12050718
APA StyleZoda, A., Ogawa, S., Kagawa, R., Tsukahara, H., Obinata, R., Urakawa, M., & Oono, Y. (2023). Single-Step Genomic Prediction of Superovulatory Response Traits in Japanese Black Donor Cows. Biology, 12(5), 718. https://doi.org/10.3390/biology12050718






