The Structure of Evolutionary Model Space for Proteins across the Tree of Life
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Estimating Clade-Specific Models
2.2. Analyzing Model Space and Assessing the Performance of Model Fit as a Classifier
3. Results and Discussion
3.1. The Structure of Protein Model Space Resembles the Tree of Life
3.2. Models of Protein Sequence Evolution Can Sometimes Be Used as Domain-Level Classifiers
3.3. Genomic Base Composition Affects Amino Acid Frequencies and Relative Exchangeabilities
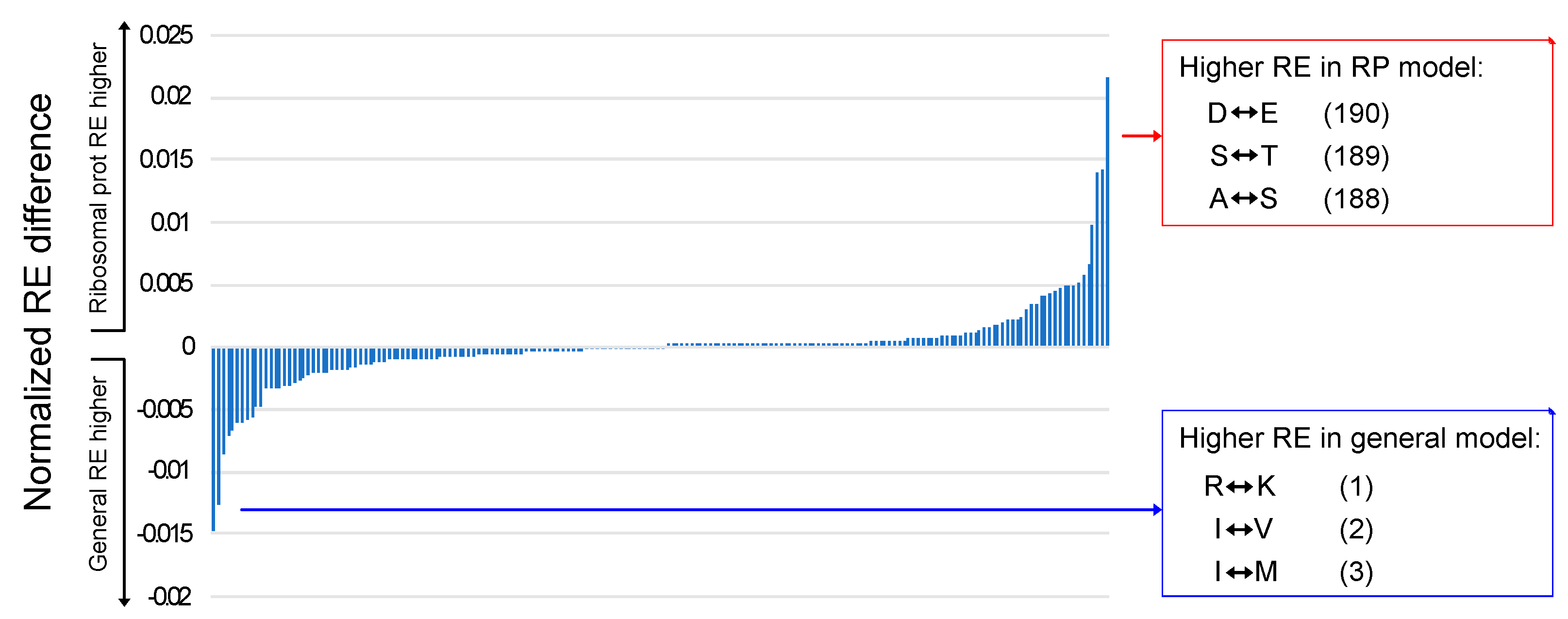
3.4. Generalized Models and Ribosomal Protein Models Exhibit Specific Differences
3.5. Aromatic–Aromatic REs Differentiate Bacterial versus Archaeal/Eukaryotic Models
3.6. Models Trained Using Methanomicrobia MSAs Are Outliers within Archaea
3.7. Does Our Approach Provide an Accurate Picture of Protein Evolutionary Model Space?
3.8. What Is the Biological Basis for the Structure of Model Space That We Observed?
3.9. Can Our Clade-Specific Models Improve Estimates of the Tree of Life?
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zuckerkandl, E.; Pauling, L. Evolutionary divergence and convergence in proteins. In Evolving Genes and Proteins; Bryson, V., Vogel, H.J., Eds.; Academic Press: New York, NY, USA, 1965; pp. 97–166. [Google Scholar] [CrossRef]
- Dayhoff, M.O.; Eck, R.V. The chemical meaning of amino acid mutations. In Atlas of Protein Sequence and Structure; Dayhoff, M.O., Ed.; National Biomedical Research Foundation: Silver Springs, MD, USA, 1969; Volume 4, pp. 85–87. [Google Scholar]
- Kimura, M.; Ohta, T. On some principles governing molecular evolution. Proc. Natl. Acad. Sci. USA 1974, 71, 2848–2852. [Google Scholar] [CrossRef] [PubMed]
- Sayers, E.W.; Cavanaugh, M.; Clark, K.; Pruitt, K.D.; Schoch, C.L.; Sherry, S.T.; Karsch-Mizrachi, I. GenBank. Nucleic Acids Res. 2021, 49, D92–D96. [Google Scholar] [CrossRef] [PubMed]
- UniProt Consortium. UniProt: The universal protein knowledgebase in 2021. Nucleic Acids Res. 2021, 49, D480–D489. [Google Scholar] [CrossRef] [PubMed]
- Zou, Z.; Zhang, J. Amino acid exchangeabilities vary across the tree of life. Sci. Adv. 2019, 5, eaax3124. [Google Scholar] [CrossRef]
- Pandey, A.; Braun, E.L. Protein evolution is structure dependent and non-homogeneous across the tree of life. In Proceedings of the 11th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Virtual Event, 21–24 September 2020; ACM: New York, NY, USA, 2020; pp. 1–11. [Google Scholar] [CrossRef]
- Minh, B.Q.; Dang, C.C.; Vinh, L.S.; Lanfear, R. Qmaker: Fast and accurate method to estimate empirical models of protein evolution. Syst. Biol. 2021, 70, 1046–1060. [Google Scholar] [CrossRef]
- Dang, C.C.; Minh, B.Q.; McShea, H.; Masel, J.; James, J.E.; Vinh, L.S.; Lanfear, R. nQMaker: Estimating time non-reversible amino acid substitution models. Syst. Biol. 2022, 71, 1110–1123. [Google Scholar] [CrossRef]
- Arenas, M. Trends in substitution models of molecular evolution. Front. Genet. 2015, 6, 319. [Google Scholar] [CrossRef]
- Tavaré, S. Some probabilistic and statistical problems in the analysis of DNA sequences. In Lectures on Mathematics in the Life Sciences; Miura, R.M., Ed.; The American Mathematical Society: Providence, RI, USA, 1986; Volume 17, pp. 57–86. [Google Scholar]
- Yang, Z. Estimating the pattern of nucleotide substitution. J. Mol. Evol. 1994, 39, 105–111. [Google Scholar] [CrossRef]
- Whelan, S.; Goldman, N. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol. Biol. Evol. 2001, 18, 691–699. [Google Scholar] [CrossRef]
- Braun, E.L. An evolutionary model motivated by physicochemical properties of amino acids reveals variation among proteins. Bioinformatics 2018, 34, i350–i356. [Google Scholar] [CrossRef]
- Tiessen, A.; Pérez-Rodríguez, P.; Delaye-Arredondo, L.J. Mathematical modeling and comparison of protein size distribution in different plant, animal, fungal and microbial species reveals a negative correlation between protein size and protein number, thus providing insight into the evolution of proteomes. BMC Res. Notes 2012, 5, 85. [Google Scholar] [CrossRef] [PubMed]
- Le, S.Q.; Gascuel, O. An improved general amino acid replacement matrix. Mol. Biol. Evol. 2008, 25, 1307–1320. [Google Scholar] [CrossRef] [PubMed]
- Kishino, H.; Miyata, T.; Hasegawa, M. Maximum likelihood inference of protein phylogeny and the origin of chloroplasts. J. Mol. Evol. 1990, 31, 151–160. [Google Scholar] [CrossRef]
- Dayhoff, M.O.; Schwartz, R.M.; Orcutt, B.C. A model of evolutionary change in proteins. In Atlas of Protein Sequence and Structure; Dayhoff, M.O., Ed.; National Biomedical Research Foundation: Silver Springs, MD, USA, 1978; Volume 5, pp. 345–352. [Google Scholar]
- Jones, D.T.; Taylor, W.R.; Thornton, J.M. The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci. 1992, 8, 275–282. [Google Scholar] [CrossRef]
- Müller, T.; Vingron, M. Modeling amino acid replacement. J. Comput. Biol. 2000, 7, 761–776. [Google Scholar] [CrossRef]
- Dimmic, M.W.; Rest, J.S.; Mindell, D.P.; Goldstein, R.A. rtREV: An amino acid substitution matrix for inference of retrovirus and reverse transcriptase phylogeny. J. Mol. Evol. 2002, 55, 65–73. [Google Scholar] [CrossRef]
- Nickle, D.C.; Heath, L.; Jensen, M.A.; Gilbert, P.B.; Mullins, J.I.; Kosakovsky Pond, S.L. HIV-specific probabilistic models of protein evolution. PLoS ONE 2007, 2, e503. [Google Scholar] [CrossRef]
- Dang, C.C.; Le, Q.S.; Gascuel, O.; Le, V.S. FLU, an amino acid substitution model for influenza proteins. BMC Evol. Biol. 2010, 10, 99. [Google Scholar] [CrossRef]
- Le, T.K.; Vinh, L.S. FLAVI: An amino acid substitution model for flaviviruses. J. Mol. Evol. 2020, 88, 445–452. [Google Scholar] [CrossRef]
- Adachi, J.; Waddell, P.J.; Martin, W.; Hasegawa, M. Plastid genome phylogeny and a model of amino acid substitution for proteins encoded by chloroplast DNA. J. Mol. Evol. 2000, 50, 348–358. [Google Scholar] [CrossRef]
- Rota-Stabelli, O.; Yang, Z.; Telford, M.J. MtZoa: A general mitochondrial amino acid substitutions model for animal evolutionary studies. Mol. Phylogenet. Evol. 2009, 52, 268–272. [Google Scholar] [CrossRef] [PubMed]
- Le, V.S.; Dang, C.C.; Le, Q.S. Improved mitochondrial amino acid substitution models for metazoan evolutionary studies. BMC Evol. Biol. 2017, 17, 136. [Google Scholar] [CrossRef] [PubMed]
- Gordon, E.L.; Kimball, R.T.; Braun, E.L. Protein structure, models of sequence evolution, and data type effects in phylogenetic analyses of mitochondrial data: A case study in birds. Diversity 2021, 13, 555. [Google Scholar] [CrossRef]
- Singer, G.A.C.; Hickey, D.A. Nucleotide bias causes a genomewide bias in the amino acid composition of proteins. Mol. Biol. Evol. 2000, 17, 1581–1588. [Google Scholar] [CrossRef]
- Singer, G.A.C.; Hickey, D.A. Thermophilic prokaryotes have characteristic patterns of codon usage, amino acid composition and nucleotide content. Gene 2003, 317, 39–47. [Google Scholar] [CrossRef]
- Fukuchi, S.; Yoshimune, K.; Wakayama, M.; Moriguchi, M.; Nishikawa, K. Unique amino acid composition of proteins in halophilic bacteria. J. Mol. Biol. 2003, 327, 347–357. [Google Scholar] [CrossRef]
- Schmidt, A.; Rzanny, M.; Schmidt, A.; Hagen, M.; Schütze, E.; Kothe, E. GC content-independent amino acid patterns in bacteria and archaea. J. Basic Microbiol. 2012, 52, 195–205. [Google Scholar] [CrossRef]
- Reed, C.J.; Lewis, H.; Trejo, E.; Winston, V.; Evilia, C. Protein adaptations in archaeal extremophiles. Archaea 2013, 2013, 373275. [Google Scholar] [CrossRef]
- Pasamontes, A.; Garcia-Vallve, S. Use of a multi-way method to analyze the amino acid composition of a conserved group of orthologous proteins in prokaryotes. BMC Bioinform. 2006, 7, 257. [Google Scholar] [CrossRef]
- Hug, L.A.; Baker, B.J.; Anantharaman, K.; Brown, C.T.; Probst, A.J.; Castelle, C.J.; Butterfield, C.N.; Hernsdorf, A.W.; Amano, Y.; Ise, K.; et al. A new view of the tree of life. Nat. Microbiol. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Edgar, R.C. Search and clustering orders of magnitude faster than BLAST. Bioinformatics 2010, 26, 2460–2461. [Google Scholar] [CrossRef] [PubMed]
- Dang, C.C.; Lefort, V.; Le, V.S.; Le, Q.S.; Gascuel, O. ReplacementMatrix: A web server for maximum-likelihood estimation of amino acid replacement rate matrices. Bioinformatics 2011, 27, 2758–2760. [Google Scholar] [CrossRef] [PubMed]
- Ragan, M.A.; McInerney, J.O.; Lake, J.A. The network of life: Genome beginnings and evolution. Philos. Trans. R. Soc. B 2009, 364, 2169–2175. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.-T.; Schmidt, H.A.; von Haeseler, A.; Minh, B.Q. IQ-TREE: A fast and effective stochastic algorithm for estimating maximum-likelihood phylogenies. Mol. Biol. Evol. 2015, 32, 268–274. [Google Scholar] [CrossRef]
- Saitou, N.; Nei, M. The neighbor-joining method: A new method for reconstructing phylogenetic trees. Mol. Biol. Evol. 1987, 4, 406–425. [Google Scholar] [CrossRef] [PubMed]
- Swofford, D.L. PAUP*. Phylogenetic Analysis Using Parsimony (* and Other Methods); Sinauer Associates: Sunderland, MA, USA, 2003. [Google Scholar]
- Bogdanowicz, D.; Giaro, K. Matching split distance for unrooted binary phylogenetic trees. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 9, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Rajan, V.; Moret, B.M.E. A metric for phylogenetic trees based on matching. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012, 9, 1014–1022. [Google Scholar] [CrossRef]
- Penny, D.; Foulds, L.R.; Hendy, M.D. Testing the theory of evolution by comparing phylogenetic trees constructed from five different protein sequences. Nature 1982, 297, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Pandey, A.; Braun, E.L. Phylogenetic analyses of sites in different protein structural environments result in distinct placements of the metazoan root. Biology 2020, 9, 64. [Google Scholar] [CrossRef]
- Scolaro, G.E.; Braun, E.L. Data for: The structure of evolutionary model space for proteins across the tree of life. Zenodo 2022. [Google Scholar] [CrossRef]
- Woese, C.R.; Fox, G.E. Phylogenetic structure of the prokaryotic domain: The primary kingdoms. Proc. Natl. Acad. Sci. USA 1977, 74, 5088–5090. [Google Scholar] [CrossRef] [PubMed]
- Eme, L.; Spang, A.; Lombard, J.; Stairs, C.W.; Ettema, T.J.G. Archaea and the origin of eukaryotes. Nat. Rev. Microbiol. 2017, 15, 711–723. [Google Scholar] [CrossRef]
- Castelle, C.J.; Wrighton, K.C.; Thomas, B.C.; Hug, L.A.; Brown, C.T.; Wilkins, M.J.; Frischkorn, K.R.; Tringe, S.G.; Singh, A.; Markillie, L.M.; et al. Genomic expansion of domain archaea highlights roles for organisms from new phyla in anaerobic carbon cycling. Curr. Biol. 2015, 25, 690–701. [Google Scholar] [CrossRef] [PubMed]
- Williams, T.A.; Szöllősi, G.J.; Spang, A.; Foster, P.G.; Heaps, S.E.; Boussau, B.; Ettema, T.J.G.; Embley, T.M. Integrative modeling of gene and genome evolution roots the archaeal tree of life. Proc. Natl. Acad. Sci. USA 2017, 114, E4602–E4611. [Google Scholar] [CrossRef]
- Williams, T.A.; Cox, C.J.; Foster, P.G.; Szöllősi, G.J.; Embley, T.M. Phylogenomics provides robust support for a two-domains tree of life. Nat. Ecol. Evol. 2020, 4, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Rinke, C.; Schwientek, P.; Sczyrba, A.; Ivanova, N.N.; Anderson, I.J.; Cheng, J.-F.; Darling, A.; Malfatti, S.; Swan, B.K.; Gies, E.A.; et al. Insights into the phylogeny and coding potential of microbial dark matter. Nature 2013, 499, 431–437. [Google Scholar] [CrossRef]
- Brown, C.T.; Hug, L.A.; Thomas, B.C.; Sharon, I.; Castelle, C.J.; Singh, A.; Wilkins, M.J.; Wrighton, K.C.; Williams, K.H.; Banfield, J.F. Unusual biology across a group comprising more than 15% of domain Bacteria. Nature 2015, 523, 208–211. [Google Scholar] [CrossRef]
- Oren, A. Life at high salt concentrations, intracellular KCl concentrations, and acidic proteomes. Front. Microbiol. 2013, 4, 315. [Google Scholar] [CrossRef]
- Kumar, S.; Tsai, C.J.; Nussinov, R. Factors enhancing protein thermostability. Protein Eng. Des. Sel. 2000, 13, 179–191. [Google Scholar] [CrossRef]
- Blanquart, S.; Groussin, M.; Le Roy, A.; Szöllosi, G.J.; Girard, E.; Franzetti, B.; Gouy, M.; Madern, D. Resurrection of ancestral malate dehydrogenases reveals the evolutionary history of halobacterial proteins: Deciphering gene trajectories and changes in biochemical properties. Mol. Biol. Evol. 2021, 38, 3754–3774. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Shao, Y.; Chen, F. Evolution of complete proteomes: Guanine-cytosine pressure, phylogeny and environmental influences blend the proteomic architecture. BMC Evol. Biol. 2013, 13, 219. [Google Scholar] [CrossRef] [PubMed]
- Lott, B.B.; Wang, Y.; Nakazato, T. A comparative study of ribosomal proteins: Linkage between amino acid distribution and ribosomal assembly. BMC Biophys. 2013, 6, 13. [Google Scholar] [CrossRef] [PubMed]
- Klipcan, L.; Frenkel-Morgenstern, M.; Safro, M.G. Presence of tRNA-dependent pathways correlates with high cysteine content in methanogenic Archaea. Trends Genet. 2008, 24, 59–63. [Google Scholar] [CrossRef] [PubMed]
- Thorne, J.L.; Goldman, N.; Jones, D.T. Combining protein evolution and secondary structure. Mol. Biol. Evol. 1996, 13, 666–673. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, R.A.; Pollock, D.D. The tangled bank of amino acids. Protein Sci. 2016, 25, 1354–1362. [Google Scholar] [CrossRef] [PubMed]
- Crooks, G.E.; Brenner, S.E. An alternative model of amino acid replacement. Bioinformatics 2005, 21, 975–980. [Google Scholar] [CrossRef]
- Melamed, D.; Young, D.L.; Gamble, C.E.; Miller, C.R.; Fields, S. Deep mutational scanning of an RRM domain of the Saccharomyces cerevisiae poly(A)-binding protein. RNA 2013, 19, 1537–1551. [Google Scholar] [CrossRef]
- Goldman, N.; Thorne, J.L.; Jones, D.T. Assessing the impact of secondary structure and solvent accessibility on protein evolution. Genetics 1998, 149, 445–458. [Google Scholar] [CrossRef]
- Le, S.Q.; Lartillot, N.; Gascuel, O. Phylogenetic mixture models for proteins. Philos. Trans. R. Soc. B 2008, 363, 3965–3976. [Google Scholar] [CrossRef]
- Le, S.Q.; Gascuel, O. Accounting for solvent accessibility and secondary structure in protein phylogenetics is clearly beneficial. Syst. Biol. 2010, 59, 277–287. [Google Scholar] [CrossRef] [PubMed]
- Pandey, A.; Braun, E.L. The roles of protein structure, taxon sampling, and model complexity in phylogenomics: A case study focused on early animal divergences. Biophysica 2021, 1, 8. [Google Scholar] [CrossRef]
- Lartillot, N.; Philippe, H. A Bayesian mixture model for across-site heterogeneities in the amino-acid replacement process. Mol. Biol. Evol. 2004, 21, 1095–1109. [Google Scholar] [CrossRef] [PubMed]
- Le, S.Q.; Gascuel, O.; Lartillot, N. Empirical profile mixture models for phylogenetic reconstruction. Bioinformatics 2008, 24, 2317–2323. [Google Scholar] [CrossRef]
- Wang, H.-C.; Minh, B.Q.; Susko, E.; Roger, A.J. Modeling site heterogeneity with posterior mean site frequency profiles accelerates accurate phylogenomic estimation. Syst. Biol. 2018, 67, 216–235. [Google Scholar] [CrossRef]
- Del Amparo, R.; Arenas, M. HIV protease and integrase empirical substitution models of evolution: Protein-specific models outperform generalist models. Genes 2021, 13, 61. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.; Conery, J.S. The origins of genome complexity. Science 2003, 302, 1401–1404. [Google Scholar] [CrossRef]
- Burley, S.K.; Petsko, G.A. Aromatic-aromatic interaction: A mechanism of protein structure stabilization. Science 1985, 229, 23–28. [Google Scholar] [CrossRef]
- Singh, J.; Thornton, J.M. The interaction between phenylalanine rings in proteins. FEBS Lett. 1985, 191, 1–6. [Google Scholar] [CrossRef]
- McGaughey, G.B.; Gagné, M.; Rappé, A.K. π-stacking interactions. J. Biol. Chem. 1998, 273, 15458–15463. [Google Scholar] [CrossRef]
- Chourasia, M.; Sastry, G.M.; Sastry, G.N. Aromatic-aromatic interactions database, A2ID: An analysis of aromatic π-networks in proteins. Int. J. Biol. Macromol. 2011, 48, 540–552. [Google Scholar] [CrossRef]
- Burley, S.K.; Petsko, G.A. Amino-aromatic interactions in proteins. FEBS Lett. 1986, 203, 139–143. [Google Scholar] [CrossRef] [PubMed]
- Zauhar, R.J.; Colbert, C.L.; Morgan, R.S.; Welsh, W.J. Evidence for a strong sulfur-aromatic interaction derived from crystallographic data. Biopolymers 2000, 53, 233–248. [Google Scholar] [CrossRef]
- Brooks, D.J.; Fresco, J.R.; Lesk, A.M.; Singh, M. Evolution of amino acid frequencies in proteins over deep time: Inferred order of introduction of amino acids into the genetic code. Mol. Biol. Evol. 2002, 19, 1645–1655. [Google Scholar] [CrossRef] [PubMed]
- Trifonov, E.N. The triplet code from first principles. J. Biomol. Struct. Dyn. 2004, 22, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Higgs, P.G.; Pudritz, R.E. A thermodynamic basis for prebiotic amino acid synthesis and the nature of the first genetic code. Astrobiology 2009, 9, 483–490. [Google Scholar] [CrossRef] [PubMed]
- Woese, C.R. On the evolution of cells. Proc. Natl. Acad. Sci. USA 2002, 99, 8742–8747. [Google Scholar] [CrossRef] [PubMed]
- Bowman, J.C.; Petrov, A.S.; Frenkel-Pinter, M.; Penev, P.I.; Williams, L.D. Root of the tree: The significance, evolution, and origins of the ribosome. Chem. Rev. 2020, 120, 4848–4878. [Google Scholar] [CrossRef]
- Londei, P.; Ferreira-Cerca, S. Ribosome biogenesis in archaea. Front. Microbiol. 2021, 12, 686977. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, O.B.; Hedman, R.; Marino, J.; Wickles, S.; Bischoff, L.; Johansson, M.; Müller-Lucks, A.; Trovato, F.; Puglisi, J.D.; O’Brien, E.P.; et al. Cotranslational protein folding inside the ribosome exit tunnel. Cell Rep. 2015, 12, 1533–1540. [Google Scholar] [CrossRef]
- Dao Duc, K.; Batra, S.S.; Bhattacharya, N.; Cate, J.H.D.; Song, Y.S. Differences in the path to exit the ribosome across the three domains of life. Nucleic Acids Res. 2019, 47, 4198–4210. [Google Scholar] [CrossRef] [PubMed]
- Bininda-Emonds, O.R.P.; Gittleman, J.L.; Steel, M.A. The (super)tree of life: Procedures, problems, and prospects. Annu. Rev. Ecol. Syst. 2002, 33, 265–289. [Google Scholar] [CrossRef]
- Maddison, W.P. Gene trees in species trees. Syst. Biol. 1997, 46, 523–536. [Google Scholar] [CrossRef]
- Patel, S.; Kimball, R.T.; Braun, E.L. Error in phylogenetic estimation for bushes in the tree of life. J. Phylogenet. Evol. Biol. 2013, 1, 110. [Google Scholar] [CrossRef]
- Roch, S.; Warnow, T. On the robustness to gene tree estimation error (or lack thereof) of coalescent-based species tree methods. Syst. Biol. 2015, 64, 663–676. [Google Scholar] [CrossRef]
- Zhu, Q.; Mai, U.; Pfeiffer, W.; Janssen, S.; Asnicar, F.; Sanders, J.G.; Belda-Ferre, P.; Al-Ghalith, G.A.; Kopylova, E.; McDonald, D.; et al. Phylogenomics of 10,575 genomes reveals evolutionary proximity between domains Bacteria and Archaea. Nat. Commun. 2019, 10, 5477. [Google Scholar] [CrossRef]
- Zhu, Q.; Mirarab, S. Assembling a reference phylogenomic tree of bacteria and archaea by summarizing many gene phylogenies. Methods Mol. Biol. 2022, 2569, 137–165. [Google Scholar] [CrossRef]
- Eisen, J.A. Phylogenomics: Improving functional predictions for uncharacterized genes by evolutionary analysis. Genome Res. 1998, 8, 163–167. [Google Scholar] [CrossRef]
- Eisen, J.A.; Wu, M. Phylogenetic analysis and gene functional predictions: Phylogenomics in action. Theor. Popul. Biol. 2002, 61, 481–487. [Google Scholar] [CrossRef]
- Spielman, S.J. Relative model fit does not predict topological accuracy in single-gene protein phylogenetics. Mol. Biol. Evol. 2020, 37, 2110–2123. [Google Scholar] [CrossRef]
- Lartillot, N.; Brinkmann, H.; Philippe, H. Suppression of long-branch attraction artefacts in the animal phylogeny using a site-heterogeneous model. BMC Evol. Biol. 2007, 7 (Suppl. 1), S4. [Google Scholar] [CrossRef] [PubMed]
- Berv, J.S.; Singhal, S.; Field, D.J.; Walker-Hale, N.; McHugh, S.W.; Shipley, J.R.; Miller, E.T.; Kimball, R.T.; Braun, E.L.; Dornburg, A.; et al. Molecular early burst associated with the diversification of birds at the K–Pg boundary. bioRxiv 2022. [Google Scholar] [CrossRef]



| Domain | Clade | Median GC % | % Precise Match | % Archaeal Match | % Eukaryotic Match | % Bacterial Match |
|---|---|---|---|---|---|---|
| Archaea | DPANN | 34.05 | 5.07 | 41.11 | 9.76 | 49.12 |
| Thaumarchaeota | 34.20 | 25.12 | 37.68 | 5.68 | 56.64 | |
| Methanomicrobia | 47.40 | 18.50 | 55.49 | 7.52 | 36.99 | |
| Thermoprotei 2 | 49.00 | 65.94 | 76.56 | 7.19 | 16.25 | |
| Halobacteriaceae 2 | 63.70 | 65.39 | 75.20 | 4.86 | 19.94 | |
| Eukaryotes | Coelomata | 40.72 | 10.74 | 50.93 | 15.96 | 33.11 |
| Pezizomycotina | 48.90 | 14.80 | 33.42 | 39.63 | 26.95 | |
| Bacteria | Lactobacillales | 37.70 | 18.90 | 24.56 | 12.01 | 63.43 |
| Cytophagales | 40.60 | 13.24 | 10.29 | 7.35 | 82.35 | |
| Bacillaceae | 42.15 | 11.84 | 36.93 | 11.15 | 51.92 | |
| Alteromonadaceae | 45.90 | 7.33 | 13.56 | 6.31 | 80.13 | |
| Selenomonadales | 48.90 | 14.68 | 28.67 | 9.35 | 61.82 | |
| Enterobacteriaceae | 52.18 | 18.28 | 18.52 | 6.98 | 74.50 | |
| Oceanospirillales | 54.40 | 1.52 | 17.81 | 7.47 | 74.72 | |
| Chromatiales | 62.15 | 21.06 | 21.62 | 6.50 | 71.88 | |
| Rhodospirillales | 65.03 | 29.77 | 14.91 | 7.37 | 77.72 | |
| Comamonadaceae | 65.38 | 18.29 | 9.84 | 6.71 | 83.46 | |
| Xanthomonadacae | 66.03 | 9.62 | 11.70 | 10.78 | 77.51 | |
| Micrococcineae | 69.65 | 36.26 | 15.36 | 5.32 | 79.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scolaro, G.E.; Braun, E.L. The Structure of Evolutionary Model Space for Proteins across the Tree of Life. Biology 2023, 12, 282. https://doi.org/10.3390/biology12020282
Scolaro GE, Braun EL. The Structure of Evolutionary Model Space for Proteins across the Tree of Life. Biology. 2023; 12(2):282. https://doi.org/10.3390/biology12020282
Chicago/Turabian StyleScolaro, Gabrielle E., and Edward L. Braun. 2023. "The Structure of Evolutionary Model Space for Proteins across the Tree of Life" Biology 12, no. 2: 282. https://doi.org/10.3390/biology12020282
APA StyleScolaro, G. E., & Braun, E. L. (2023). The Structure of Evolutionary Model Space for Proteins across the Tree of Life. Biology, 12(2), 282. https://doi.org/10.3390/biology12020282







