Divide-and-Attention Network for HE-Stained Pathological Image Classification
Abstract
:Simple Summary
Abstract
1. Introduction
2. Related Works
2.1. Pathological Image Classification
2.2. DCCA in Multi-Modal Fusion
2.3. Attention Mechanism
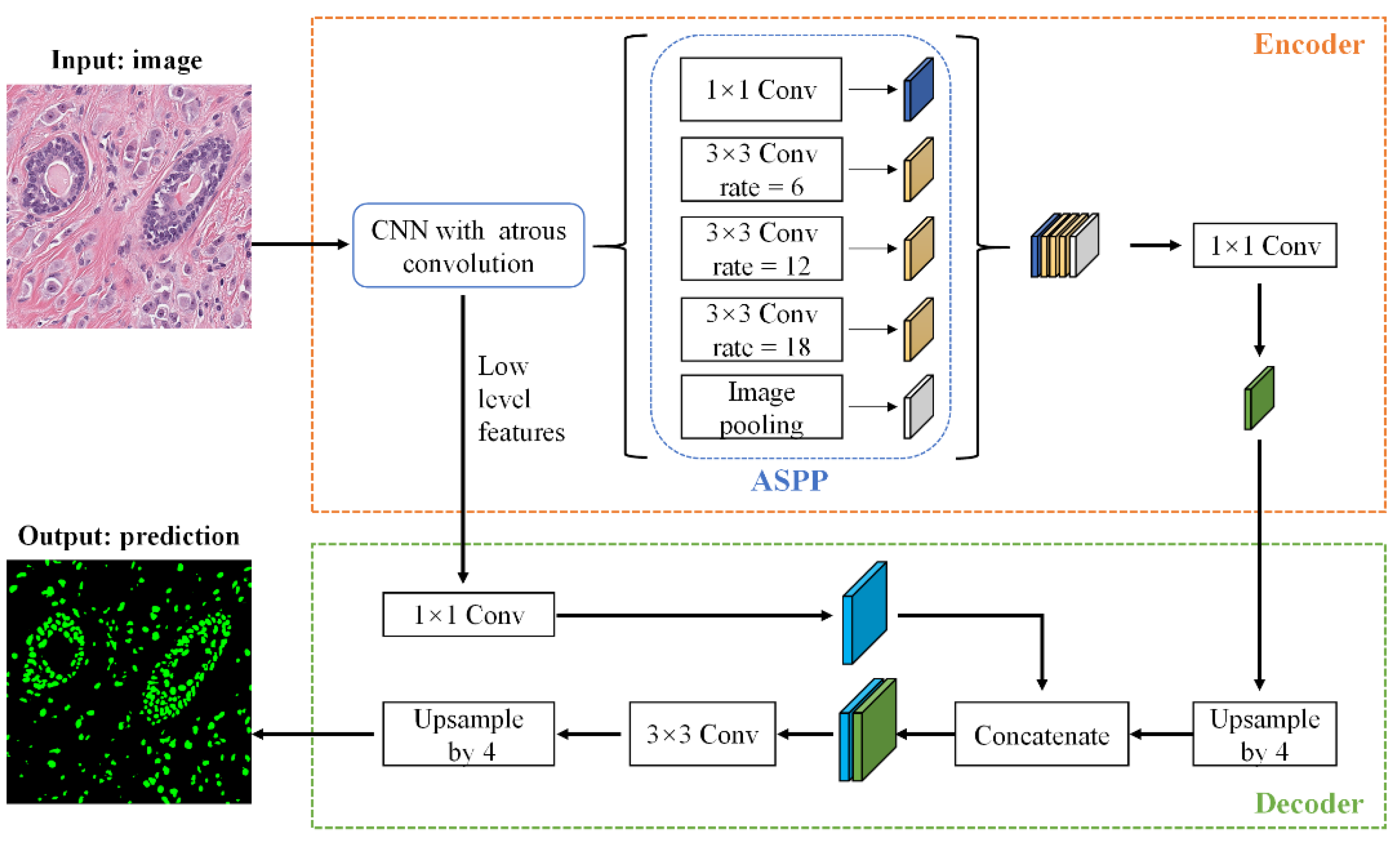
2.4. Nuclei Segmentation
3. Methods
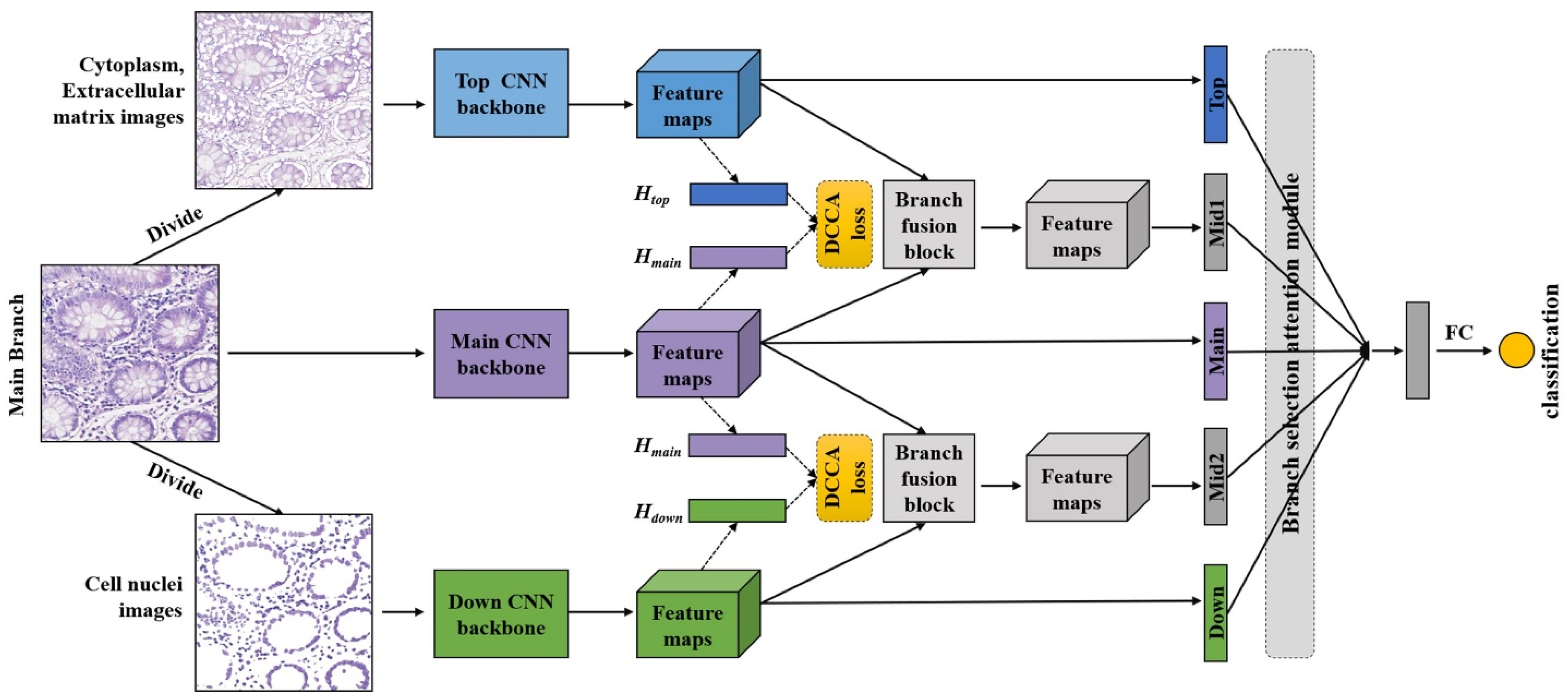
3.1. Pathological Image Decomposition Part
3.2. Pathological Image Classification Part
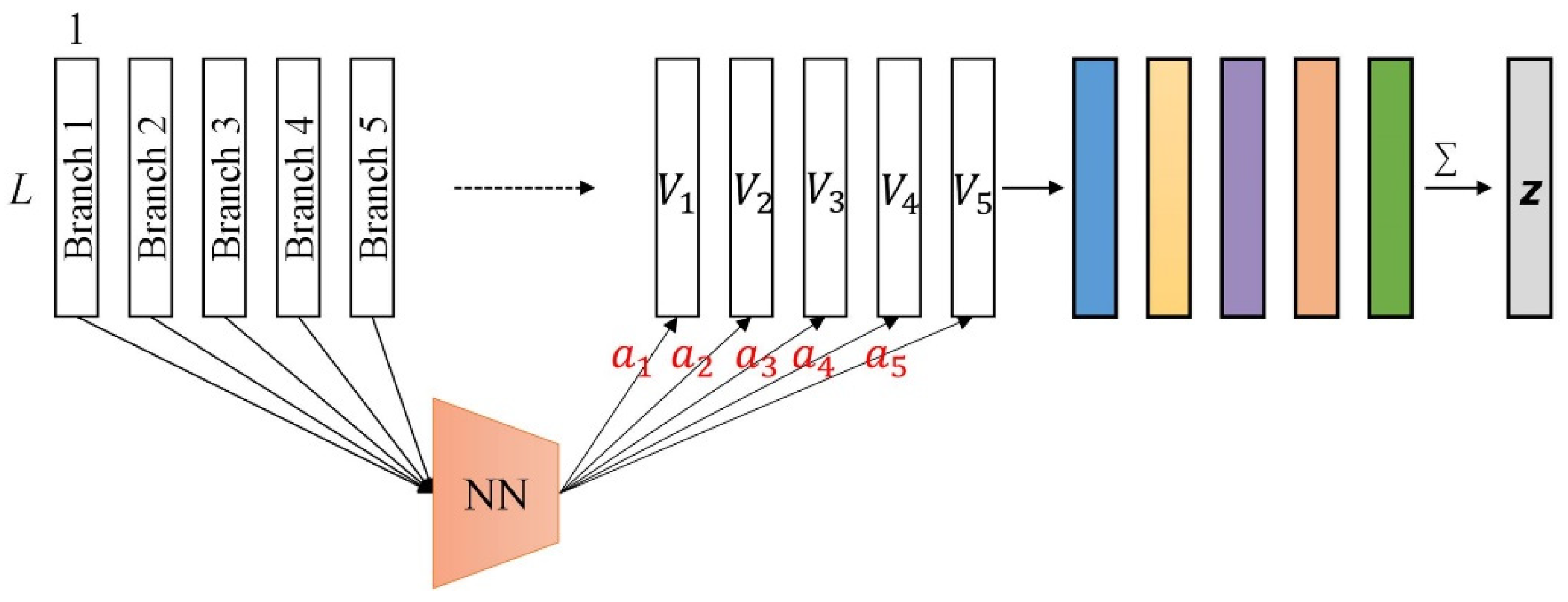
3.3. Branch Selection Attention Module
3.4. Loss Function
4. Results and Discussion
4.1. Evaluation Metrics and Training Details
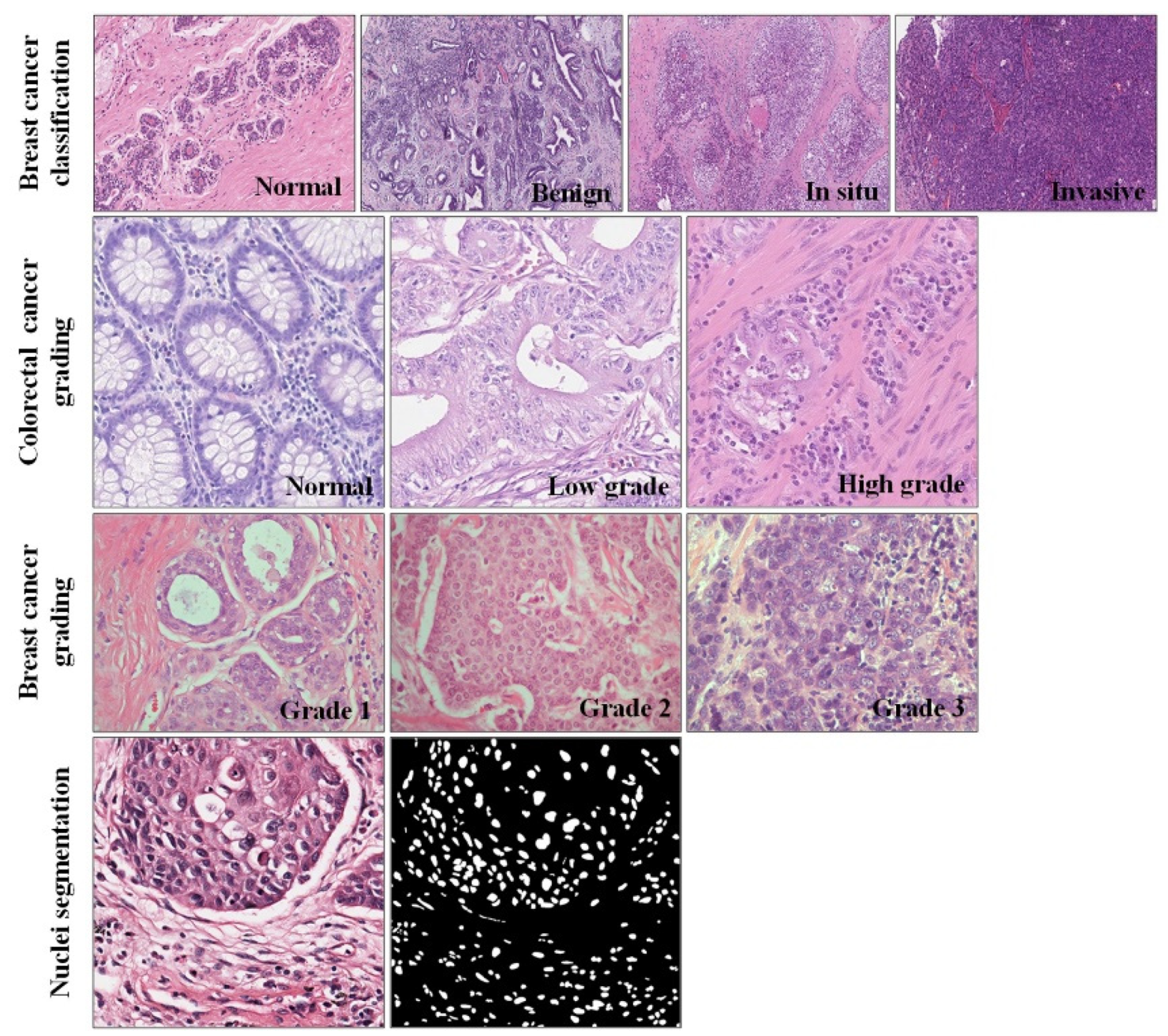
4.2. Datasets and Preprocessing
4.2.1. Breast Cancer Classification Dataset
4.2.2. Colorectal Cancer Grading Dataset
4.2.3. Breast Cancer Grading Dataset
4.2.4. Nuclei Segmentation Dataset
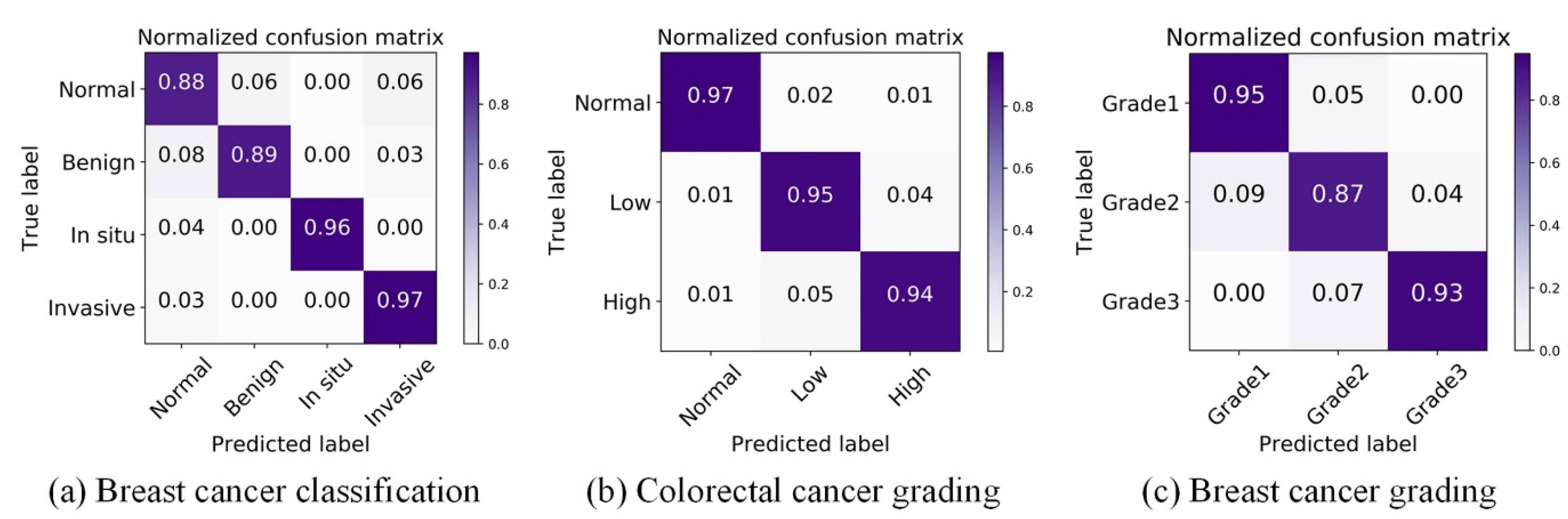
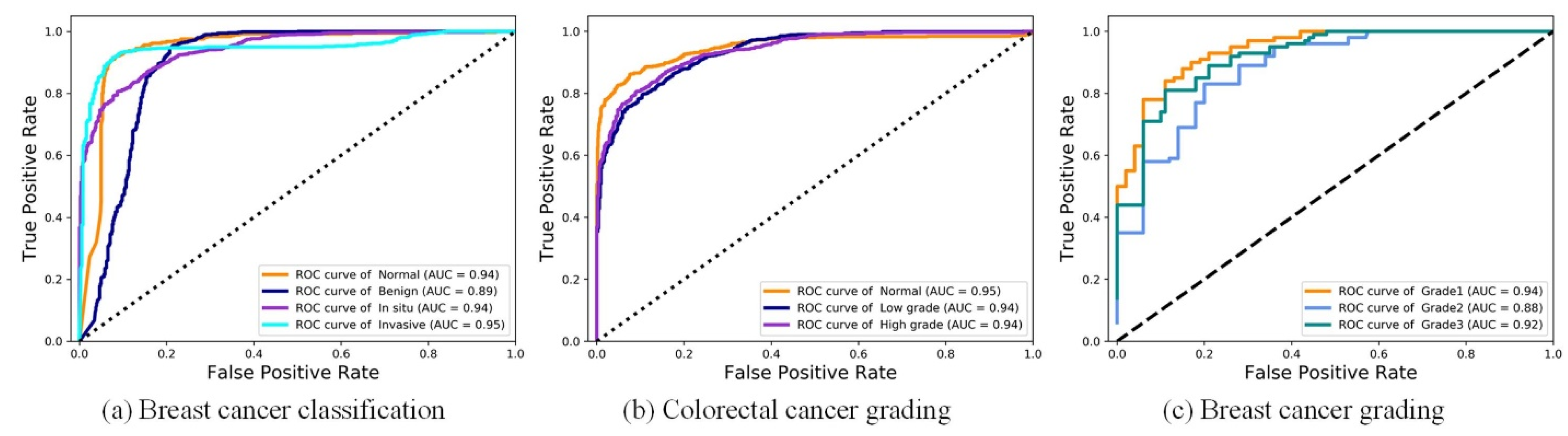
4.3. Breast Cancer Classification Results
4.4. Colorectal Cancer Grading Results
4.5. Breast Cancer Grading Results
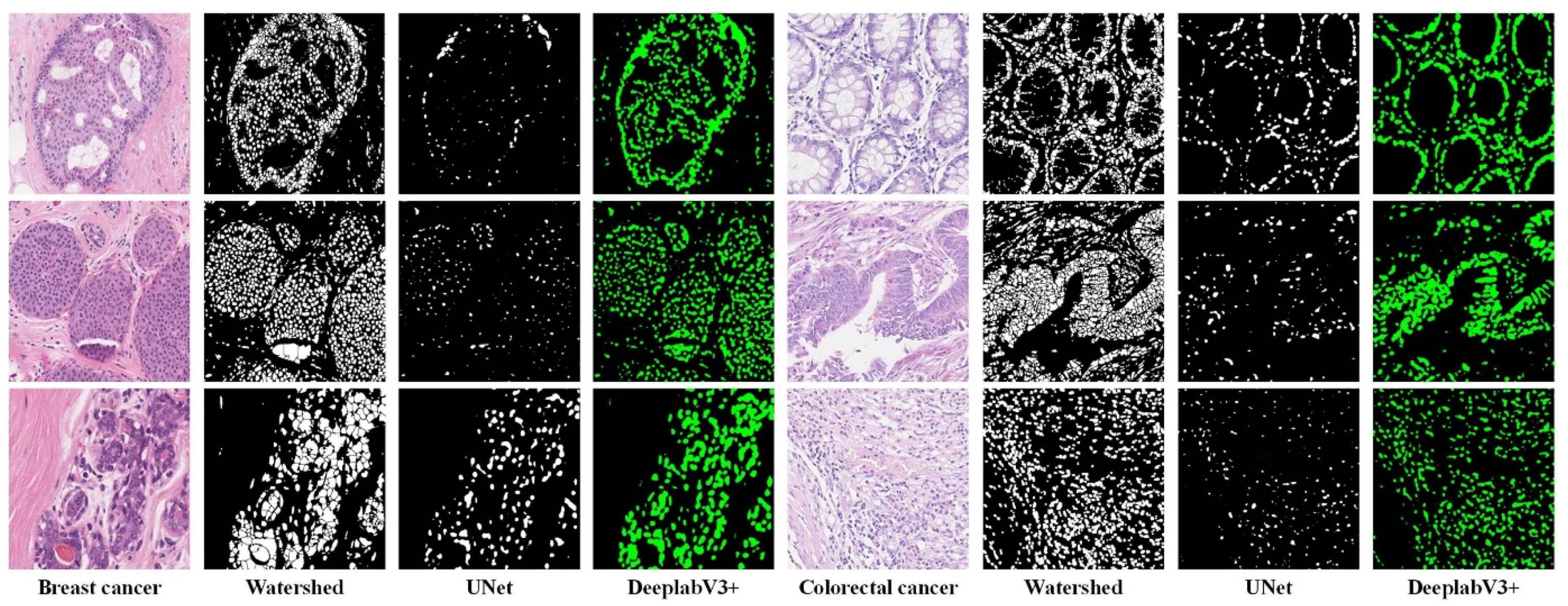
4.6. Nuclei Segmentation Results
4.7. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, S.; Zhang, X.; Yan, W.; Eric, I.; Chang, C.; Fan, Y.; Lai, M.; Xu, Y. Deep learning in digital pathology image analysis: A survey. Front. Med. 2020, 14, 470–487. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.K.; Greenspan, H.; Davatzikos, C.; Duncan, J.S.; van Ginneken, B.; Madabhushi, A.; Prince, J.L.; Rueckert, D.; Summers, R.M. A review of deep learning in medical imaging: Image traits, technology trends, case studies with progress highlights, and future promises. arXiv 2020, arXiv:200809104. [Google Scholar] [CrossRef]
- Lin, W.-A.; Liao, H.; Peng, C.; Sun, X.; Zhang, J.; Luo, J.; Chellappa, R.; Zhou, S.K. Dudonet: Dual domain network for ct metal artifact reduction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10512–10521. [Google Scholar]
- Li, Z.; Li, H.; Han, H.; Shi, G.; Wang, J.; Zhou, S.K. Encoding ct anatomy knowledge for unpaired chest X-Ray image decomposition. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2019; pp. 275–283. [Google Scholar]
- Gozes, O. Greenspan H: Lung structures enhancement in chest radiographs via ct based fcnn training. In Image Analysis for Moving Organ, Breast, and Thoracic Images; Springer: Cham, Switzerland, 2018; pp. 147–158. [Google Scholar]
- Spanhol, F.A.; Oliveira, L.S.; Petitjean, C.; Heutte, L. A dataset for breast cancer histopathological image classification. IEEE Trans. Biomed. Eng. 2016, 63, 1455–1462. [Google Scholar] [CrossRef]
- Bayramoglu, N.; Kannala, J.; Heikkilä, J. Deep learning for magnification independent breast cancer histopathology image classification. In Proceedings of the International Conference on Pattern Recognition, Cancun, Mexico, 4–8 December 2016; pp. 2440–2445. [Google Scholar]
- Araújo, T.; Aresta, G.; Castro, E.; Rouco, J.; Aguiar, P.; Eloy, C.; Polónia, A.; Campilho, A. Classification of breast cancer histology images using convolutional neural networks. PLoS ONE 2017, 12, e0177544. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Chen, L.; Zhang, H.; Xiao, X. Breast cancer histopathological image classification using convolutional neural networks with small SE-ResNet module. PLoS ONE 2019, 14, e0214587. [Google Scholar] [CrossRef] [Green Version]
- Wan, T.; Cao, J.; Chen, J.; Qin, Z. Automated grading of breast cancer histopathology using cascaded ensemble with combination of multi-level image features. Neurocomputing 2017, 229, 34–44. [Google Scholar] [CrossRef]
- Yan, R.; Li, J.; Rao, X.; Lv, Z.; Zheng, C.; Dou, J.; Wang, X.; Ren, F.; Zhang, F. NANet: Nuclei-Aware Network for Grading of Breast Cancer in HE Stained Pathological Images. In Proceedings of the 2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Seoul, Korea, 16–19 December 2020; pp. 865–870. [Google Scholar]
- Yan, R.; Ren, F.; Li, J.; Rao, X.; Lv, Z.; Zheng, C.; Zhang, F. Nuclei-Guided Network for Breast Cancer Grading in HE-Stained Pathological Images. Sensors 2022, 22, 4061. [Google Scholar] [CrossRef]
- Zhou, Y.; Graham, S.; Alemi Koohbanani, N.; Shaban, M.; Heng, P.-A.; Rajpoot, N. Cgc-net: Cell graph convolutional network for grading of colorectal cancer histology images. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Lu, C.; Ji, M.; Ma, Z.; Mandal, M. Automated image analysis of nuclear atypia in high-power field histopathological image. J. Microsc. 2015, 258, 233–240. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Liu, M.; Wang, Y.; Lai, M.; Eric, I.; Chang, C. Gland instance segmentation by deep multichannel side supervision. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2016; pp. 496–504. [Google Scholar]
- Cireşan, D.C.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J. Mitosis detection in breast cancer histology images with deep neural networks. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2013; pp. 411–418. [Google Scholar]
- Yan, R.; Li, J.; Zhou, S.K.; Lv, Z.; Zhang, X.; Rao, X.; Zheng, C.; Ren, F.; Zhang, F. Decomposition-and-Fusion Network for HE-Stained Pathological Image Classification. In International Conference on Intelligent Computing; Springer: Cham, Switzerland, 2021; pp. 198–207. [Google Scholar]
- Hotelling, H. Relations between two sets of variates. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 162–190. [Google Scholar]
- Hardoon, D.R.; Szedmak, S.; Shawe-Taylor, J. Canonical correlation analysis: An overview with application to learning methods. Neural Comput. 2004, 16, 2639–2664. [Google Scholar] [CrossRef] [Green Version]
- Andrew, G.; Arora, R.; Bilmes, J.; Livescu, K. Deep canonical correlation analysis. In International Conference on Machine Learning; PMLR: Atlanta, GA, USA, 2013; pp. 1247–1255. [Google Scholar]
- Liu, W.; Qiu, J.-L.; Zheng, W.-L.; Lu, B.-L. Multimodal emotion recognition using deep canonical correlation analysis. arXiv 2019, arXiv:190805349. [Google Scholar]
- Sun, Z.; Sarma, P.K.; Sethares, W.; Bucy, E.P. Multi-modal sentiment analysis using deep canonical correlation analysis. arXiv 2019, arXiv:190708696. [Google Scholar]
- Zhang, K.; Li, Y.; Wang, J.; Wang, Z.; Li, X. Feature Fusion for Multimodal Emotion Recognition Based on Deep Canonical Correlation Analysis. IEEE Signal Process. Lett. 2021, 28, 1898–1902. [Google Scholar] [CrossRef]
- Gao, L.; Li, D.; Yao, L.; Gao, Y. Sensor drift fault diagnosis for chiller system using deep recurrent canonical correlation analysis and k-nearest neighbor classifier. ISA Trans. 2022, 122, 232–246. [Google Scholar] [CrossRef]
- Hassanin, M.; Anwar, S.; Radwan, I.; Khan, F.S.; Mian, A. Visual Attention Methods in Deep Learning: An In-Depth Survey. arXiv 2022, arXiv:220407756. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Quader, N.; Bhuiyan, M.M.I.; Lu, J.; Dai, P.; Li, W. Weight excitation: Built-in attention mechanisms in convolutional neural networks. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 87–103. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:201011929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.-P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 568–578. [Google Scholar]
- Hassani, A.; Walton, S.; Li, J.; Li, S.; Shi, H. Neighborhood Attention Transformer. arXiv 2022, arXiv:220407143. [Google Scholar]
- Ilse, M.; Tomczak, J.; Welling, M. Attention-based deep multiple instance learning. In International Conference on Machine Learning; PMLR: Stockholm, Sweden, 2018; pp. 2127–2136. [Google Scholar]
- Hayakawa, T.; Prasath, V.; Kawanaka, H.; Aronow, B.J.; Tsuruoka, S. Computational nuclei segmentation methods in digital pathology: A survey. Arch. Comput. Methods Eng. 2021, 28, 1–13. [Google Scholar] [CrossRef]
- Chen, H.; Qi, X.; Yu, L.; Dou, Q.; Qin, J.; Heng, P.-A. DCAN: Deep contour-aware networks for object instance segmentation from histology images. Med. Image Anal. 2017, 36, 135–146. [Google Scholar] [CrossRef]
- Kumar, N.; Verma, R.; Sharma, S.; Bhargava, S.; Vahadane, A.; Sethi, A. A dataset and a technique for generalized nuclear segmentation for computational pathology. IEEE Trans. Med. Imaging 2017, 36, 1550–1560. [Google Scholar] [CrossRef]
- Graham, S.; Vu, Q.D.; Raza, S.E.A.; Azam, A.; Tsang, Y.W.; Kwak, J.T.; Rajpoot, N. Hover-net: Simultaneous segmentation and classification of nuclei in multi-tissue histology images. Med. Image Anal. 2019, 58, 101563. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in network. arXiv 2013, arXiv:13124400. [Google Scholar]
- Yan, R.; Ren, F.; Wang, Z.; Wang, L.; Zhang, T.; Liu, Y.; Rao, X.; Zheng, C.; Zhang, F. Breast cancer histopathological image classification using a hybrid deep neural network. Methods 2020, 173, 52–60. [Google Scholar] [PubMed]
- Aresta, G.; Araújo, T.; Kwok, S.; Chennamsetty, S.S.; Safwan, M.; Alex, V.; Marami, B.; Prastawa, M.; Chan, M.; Donovan, M.; et al. BACH: Grand challenge on breast cancer histology images. Med. Image Anal. 2019, 56, 122–139. [Google Scholar]
- Awan, R.; Sirinukunwattana, K.; Epstein, D.; Jefferyes, S.; Qidwai, U.; Aftab, Z.; Mujeeb, I.; Snead, D.; Rajpoot, N. Glandular morphometrics for objective grading of colorectal adenocarcinoma histology images. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Dimitropoulos, K.; Barmpoutis, P.; Zioga, C.; Kamas, A.; Patsiaoura, K.; Grammalidis, N. Grading of invasive breast carcinoma through Grassmannian VLAD encoding. PLoS ONE 2017, 12, e0185110. [Google Scholar]
- Vang, Y.S.; Chen, Z.; Xie, X. Deep learning framework for multi-class breast cancer histology image classification. In International Conference Image Analysis and Recognition; Springer: Cham, Switzerland, 2018; pp. 914–922. [Google Scholar]
- Golatkar, A.; Anand, D.; Sethi, A. Classification of breast cancer histology using deep learning. In International Conference Image Analysis and Recognition; Springer: Cham, Switzerland, 2018; pp. 837–844. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Shaban, M.; Awan, R.; Fraz, M.M.; Azam, A.; Tsang, Y.-W.; Snead, D.; Rajpoot, N.M. Context-aware convolutional neural network for grading of colorectal cancer histology images. IEEE Trans. Med. Imaging 2020, 39, 2395–2405. [Google Scholar]
- Hou, L.; Samaras, D.; Kurc, T.M.; Gao, Y.; Davis, J.E.; Saltz, J.H. Patch-Based Convolutional Neural Network for Whole Slide Tissue Image Classification. In Proceeding of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2424–2433. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [Green Version]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
| Methods (BC-Classification) | Accuracy (%) | AUC |
|---|---|---|
| Vang et al. [46] | 87.5 | - |
| Golatkar et al. [47] | 85.0 | - |
| Yan et al. [42] | 91.3 | 0.89 |
| ResNet50 [48] + MV | 84.9 | 0.85 |
| Xception [40] + MV | 85.7 | 0.86 |
| Ours (DANet + MV) | 92.5 | 0.93 |
| Methods (CRC-Grading) | Accuracy (%) | AUC |
|---|---|---|
| Awan et al. [44] | 90.66 | - |
| Hou et al. [50] | 92.12 | - |
| Shaban et al. [49] | 95.70 | - |
| ResNet50 [48] + MV | 92.08 | 0.90 |
| Xception [40] + MV | 92.09 | 0.91 |
| Ours (DANet + MV) | 95.33 | 0.94 |
| Methods (BC-Grading) | Accuracy (%) | AUC |
|---|---|---|
| Wan et al. [10] | 69.0 | - |
| Yan et al. [11] | 92.2 | 0.92 |
| ResNet50 [48] | 81.3 | 0.83 |
| Xception [40] | 81.8 | 0.85 |
| Ours (DANet) | 91.6 | 0.91 |
| Items | Accuracy (%) | Sensitivity (%) | Specificity (%) | F-Score (%) | AUC |
|---|---|---|---|---|---|
| Pathology only (Xception) | 81.8 ± 0.2 | 81.1 ± 0.2 | 82.7 ± 0.3 | 81.2 ± 0.3 | 0.85 ± 0.08 |
| Nuclei only (Xception) | 79.2 ± 0.3 | 79.4 ± 0.2 | 79.1 ± 0.3 | 79.2 ± 0.3 | 0.83 ± 0.07 |
| Non-nuclei only (Xception) | 70.1 ± 0.4 | 68.3 ± 0.3 | 70.5 ± 0.4 | 69.6 ± 0.4 | 0.72 ± 0.12 |
| DANet w/o FB and DCCA | 83.1 ± 0.2 | 82.5 ± 0.3 | 85.2 ± 0.2 | 82.0 ± 0.5 | 0.86 ± 0.06 |
| DANet w/o DCCA | 89.3 ± 0.1 | 88.3 ± 0.2 | 89.8 ± 0.1 | 88.8 ± 0.3 | 0.90 ± 0.03 |
| DANet | 91.6 ± 0.3 | 91.5 ± 0.2 | 92.1 ± 0.1 | 91.4 ± 0.3 | 0.91 ± 0.02 |
| Items | Accuracy (%) | Sensitivity (%) | Specificity (%) | F-Score (%) | AUC |
|---|---|---|---|---|---|
| Mean | 80.8 ± 0.9 | 81.5 ± 0.5 | 81.1 ± 0.5 | 81.0 ± 0.4 | 0.81 ± 0.06 |
| Max | 83.6 ± 0.6 | 82.2 ± 0.4 | 84.0 ± 0.6 | 82.5 ± 0.4 | 0.82 ± 0.08 |
| Concat | 84.5 ± 0.3 | 82.9 ± 0.4 | 85.3 ± 0.3 | 83.1 ± 0.5 | 0.84 ± 0.06 |
| Attention | 91.6 ± 0.3 | 91.5 ± 0.2 | 92.1 ± 0.1 | 91.4 ± 0.3 | 0.91 ± 0.02 |
| Items | Accuracy (%) | Sensitivity (%) | Specificity (%) | F-Score (%) | AUC |
|---|---|---|---|---|---|
| ResNet50 | 89.5 ± 0.6 | 90.9 ± 0.5 | 91.1 ± 0.6 | 89.9 ± 0.5 | 0.90 ± 0.05 |
| Inception-V3 | 89.8 ± 0.4 | 90.5 ± 0.6 | 88.5 ± 0.3 | 89.7 ± 0.5 | 0.89 ± 0.02 |
| MobileNet-V2 | 91.2 ± 0.2 | 90.4 ± 0.2 | 92.3 ± 0.1 | 91.0 ± 0.3 | 0.92 ± 0.03 |
| Xception | 91.6 ± 0.3 | 91.5 ± 0.2 | 92.1 ± 0.1 | 91.4 ± 0.3 | 0.91 ± 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, R.; Yang, Z.; Li, J.; Zheng, C.; Zhang, F. Divide-and-Attention Network for HE-Stained Pathological Image Classification. Biology 2022, 11, 982. https://doi.org/10.3390/biology11070982
Yan R, Yang Z, Li J, Zheng C, Zhang F. Divide-and-Attention Network for HE-Stained Pathological Image Classification. Biology. 2022; 11(7):982. https://doi.org/10.3390/biology11070982
Chicago/Turabian StyleYan, Rui, Zhidong Yang, Jintao Li, Chunhou Zheng, and Fa Zhang. 2022. "Divide-and-Attention Network for HE-Stained Pathological Image Classification" Biology 11, no. 7: 982. https://doi.org/10.3390/biology11070982
APA StyleYan, R., Yang, Z., Li, J., Zheng, C., & Zhang, F. (2022). Divide-and-Attention Network for HE-Stained Pathological Image Classification. Biology, 11(7), 982. https://doi.org/10.3390/biology11070982






