S Phase Duration Is Determined by Local Rate and Global Organization of Replication
Abstract
Simple Summary
Abstract
1. Introduction
2. Main
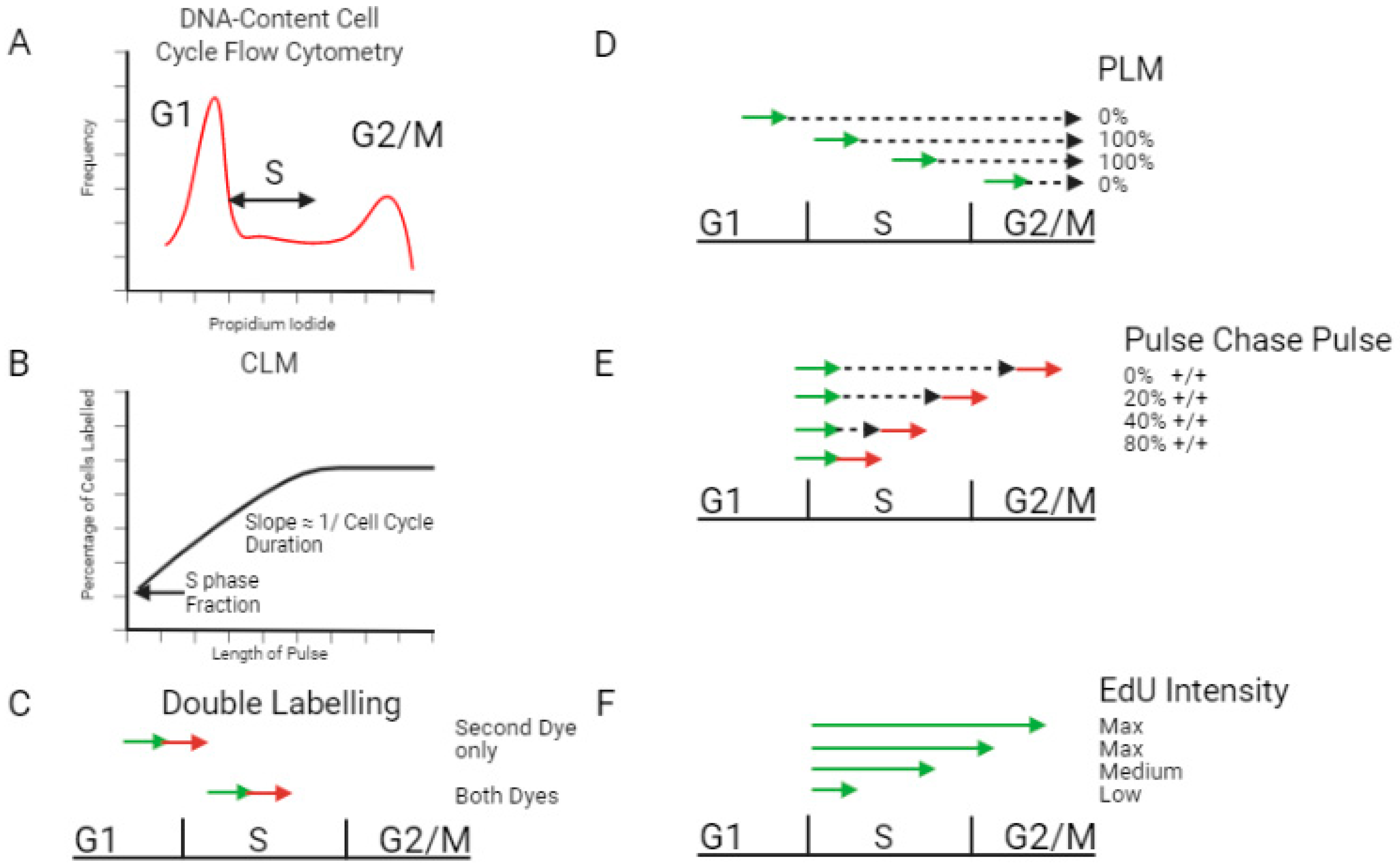
2.1. Measuring S Phase Duration
2.2. Variability in Duration of S Phase
2.3. Genome Size
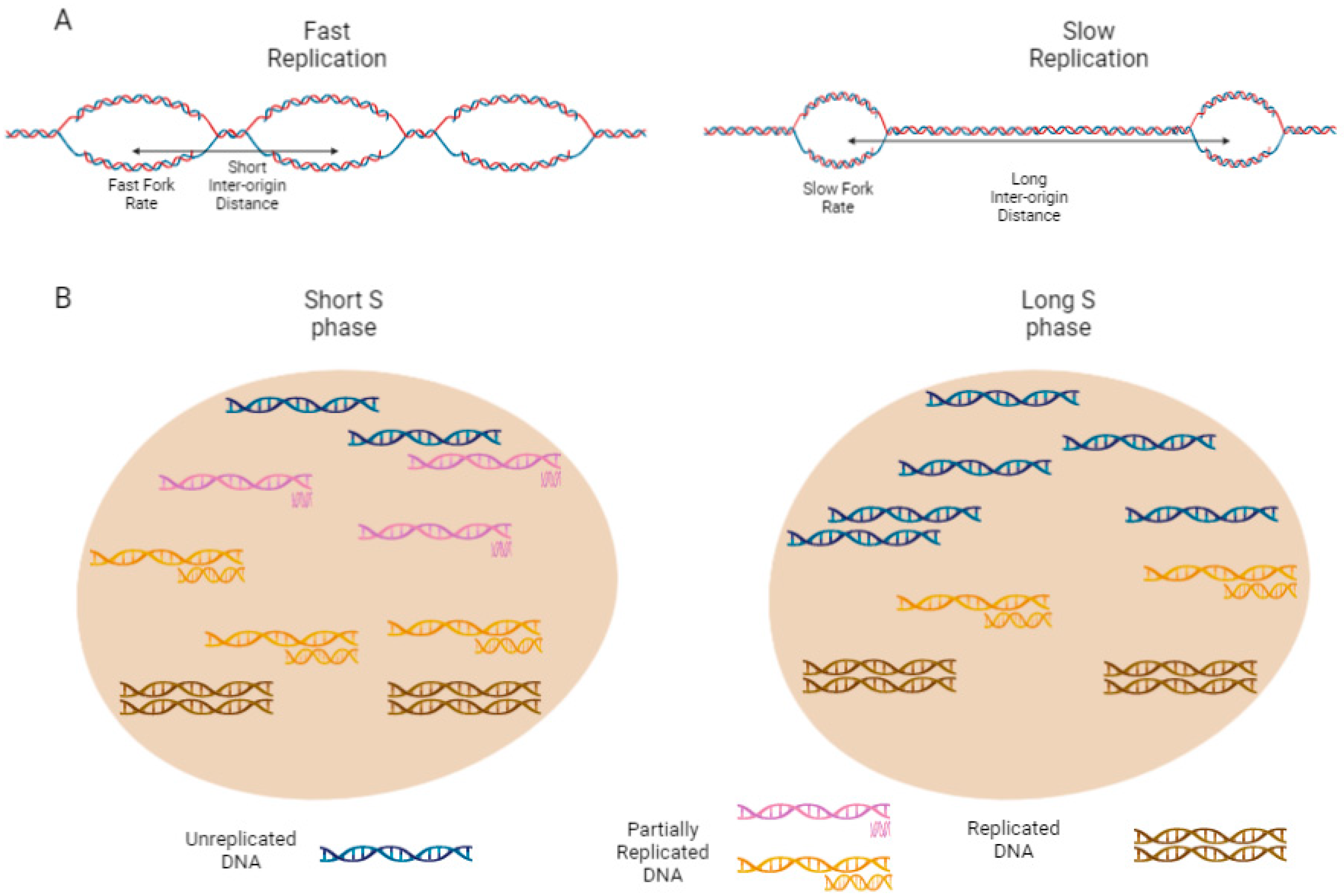
2.4. Rate of Local Replication and Replication Organization
2.5. Eukaryotic Local Replication Rate Depends on FR and the Number of Active Origins
2.6. Fork Rate
2.7. Inter-Origin Distance (IOD)
2.8. Replication Organization
2.9. Examples of S Phase Duration Regulation
3. Conclusions and Open Questions
Supplementary Materials
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dubrovsky, J.G.; Ivanov, V.B. Celebrating 50 years of the cell cycle. Nature 2003, 426, 759. [Google Scholar] [CrossRef]
- Howard, A.; Pelc, S.R. Synthesis of Nucleoprotein in Bean Root Cells. Nature 1951, 167, 599–600. [Google Scholar] [CrossRef]
- Berezney, R.; Dubey, D.D.; Huberman, J.A. Heterogeneity of eukaryotic replicons, replicon clusters, and replication foci. Chromosoma 2000, 108, 471–484. [Google Scholar] [CrossRef]
- Farkash-Amar, S.; Simon, I. Genome-wide analysis of the replication program in mammals. Chromosome Res. 2010, 18, 115–125. [Google Scholar] [CrossRef]
- Hiratani, I.; Gilbert, D.M. Replication timing as an epigenetic mark. Epigenetics 2009, 4, 93–97. [Google Scholar] [CrossRef][Green Version]
- Jackson, D.; Wang, X.; Rudner, D.Z. Spatio-temporal organization of replication in bacteria and eukaryotes (nucleoids and nuclei). Cold Spring Harb. Perspect. Biol. 2012, 4, a010389. [Google Scholar] [CrossRef][Green Version]
- Rhind, N.; Gilbert, D.M. DNA replication timing. Cold Spring Harb. Perspect. Biol. 2013, 5, a010132. [Google Scholar] [CrossRef]
- Matthes, M.; Scharpf, H. Clinical studies with a new photoelectric apparatus for determination of erythrocyte count, leukocyte count, and hemoglobin content. Klin. Wochenschr. 1951, 29, 266–267. [Google Scholar] [CrossRef]
- Texter, E.C., Jr.; Hirsch, F.G.; Horan, F.E.; Wood, L.A.; Ballard, W.C., Jr.; Wright, I.S. The electrical conductivity of blood. II. Relation to red cell count. Blood 1950, 5, 1036–1048. [Google Scholar] [CrossRef]
- Moldavan, A. Photo-Electric Technique for the Counting of Microscopical Cells. Science 1934, 80, 188–189. [Google Scholar] [CrossRef]
- Kubitschek, H.E. Electronic counting and sizing of bacteria. Nature 1958, 182, 234–235. [Google Scholar] [CrossRef]
- Rao, J.M.; Nair, P.M. Structure and mutarotation of ascorbic acid osazones. Tetrahedron 1970, 26, 3833–3838. [Google Scholar] [CrossRef]
- Scholzen, T.; Gerdes, J. The Ki-67 protein: From the known and the unknown. J. Cell. Physiol. 2000, 182, 311–322. [Google Scholar] [CrossRef]
- Nowakowski, R.S.; Lewin, S.B.; Miller, M.W. Bromodeoxyuridine immunohistochemical determination of the lengths of the cell cycle and the DNA-synthetic phase for an anatomically defined population. J. Neurocytol. 1989, 18, 311–318. [Google Scholar] [CrossRef]
- Helmstetter, C.E. Origin and sequence of chromosome replication in Escherichia coli B-r. J. Bacteriol. 1968, 95, 1634–1641. [Google Scholar] [CrossRef]
- von Waechter, R.; Jaensch, B. Generation times of the matrix cells during embryonic brain development: An autoradiographic study in rats. Brain Res. 1972, 46, 235–250. [Google Scholar] [CrossRef]
- Takahashi, T.; Nowakowski, R.S.; Caviness, V.S., Jr. Cell cycle parameters and patterns of nuclear movement in the neocortical proliferative zone of the fetal mouse. J. Neurosci. 1993, 13, 820–833. [Google Scholar] [CrossRef]
- Schorl, C.; Sedivy, J.M. Analysis of cell cycle phases and progression in cultured mammalian cells. Methods 2007, 41, 143–150. [Google Scholar] [CrossRef]
- Zatterstrom, U.K.; Johansson, M.; Kallen, A.; Baldetorp, B.; Oredsson, S.; Wennerberg, J.; Killander, D. Comparison of BrdUrd and [3H]TdR incorporation to estimate cell proliferation, cell loss, and potential doubling time in tumor xenografts. Cytometry 1992, 13, 872–879. [Google Scholar] [CrossRef]
- Quastler, H.; Sherman, F.G. Cell population kinetics in the intestinal epithelium of the mouse. Exp. Cell Res. 1959, 17, 420–438. [Google Scholar] [CrossRef]
- Wimber, D.E.; Quastler, H.; Stein, O.L.; Wimber, D.R. Analysis of tritium incorporation into individual cells by autoradiography of squash preparations. J. Biophys. Biochem. Cytol. 1960, 8, 327–331. [Google Scholar] [CrossRef] [PubMed]
- Cairnie, A.B.; Lamerton, L.F.; Steel, G.G. Cell proliferation studies in the intestinal epithelium of the rat. I. Determination of the kinetic parameters. Exp. Cell Res. 1965, 39, 528–538. [Google Scholar] [CrossRef]
- Bialic, M.; Al Ahmad Nachar, B.; Koźlak, M.; Coulon, V.; Schwob, E. Measuring S-Phase Duration from Asynchronous Cells Using Dual EdU-BrdU Pulse-Chase Labeling Flow Cytometry. Genes 2022, 13, 408. [Google Scholar] [CrossRef] [PubMed]
- Terry, N.H.; White, R.A. Flow cytometry after bromodeoxyuridine labeling to measure S and G2+M phase durations plus doubling times in vitro and in vivo. Nat. Protoc. 2006, 1, 859–869. [Google Scholar] [CrossRef] [PubMed]
- Larsson, S.; Johansson, M.; Oredsson, S.; Holst, U. A Markov model approach shows a large variation in the length of S phase in MCF-7 breast cancer cells. Cytom. A 2005, 65, 15–25. [Google Scholar] [CrossRef] [PubMed]
- Larsson, S.; Ryden, T.; Holst, U.; Oredsson, S.; Johansson, M. Estimating the total rate of DNA replication using branching processes. Bull. Math. Biol. 2008, 70, 2177–2194. [Google Scholar] [CrossRef]
- Begg, A.C.; McNally, N.J.; Shrieve, D.C.; Karcher, H. A method to measure the duration of DNA synthesis and the potential doubling time from a single sample. Cytometry 1985, 6, 620–626. [Google Scholar] [CrossRef]
- Eidukevicius, R.; Characiejus, D.; Janavicius, R.; Kazlauskaite, N.; Pasukoniene, V.; Mauricas, M.; Den Otter, W. A method to estimate cell cycle time and growth fraction using bromodeoxyuridine-flow cytometry data from a single sample. BMC Cancer 2005, 5, 122. [Google Scholar] [CrossRef]
- Pereira, P.D.; Serra-Caetano, A.; Cabrita, M.; Bekman, E.; Braga, J.; Rino, J.; Santus, R.; Filipe, P.L.; Sousa, A.E.; Ferreira, J.A. Quantification of cell cycle kinetics by EdU (5-ethynyl-2′-deoxyuridine)-coupled-fluorescence-intensity analysis. Oncotarget 2017, 8, 40514–40532. [Google Scholar] [CrossRef]
- Sakaue-Sawano, A.; Kurokawa, H.; Morimura, T.; Hanyu, A.; Hama, H.; Osawa, H.; Kashiwagi, S.; Fukami, K.; Miyata, T.; Miyoshi, H.; et al. Visualizing spatiotemporal dynamics of multicellular cell-cycle progression. Cell 2008, 132, 487–498. [Google Scholar] [CrossRef]
- Bajar, B.T.; Lam, A.J.; Badiee, R.K.; Oh, Y.H.; Chu, J.; Zhou, X.X.; Kim, N.; Kim, B.B.; Chung, M.; Yablonovitch, A.L.; et al. Fluorescent indicators for simultaneous reporting of all four cell cycle phases. Nat. Methods 2016, 13, 993–996. [Google Scholar] [CrossRef] [PubMed]
- Echevarria, C.; Gutierrez, C.; Desvoyes, B. Tools for Assessing Cell-Cycle Progression in Plants. Plant Cell Physiol. 2021, 62, 1231–1238. [Google Scholar] [CrossRef] [PubMed]
- Lamerton, L.F.; Steel, G.G. Cell population kinetics in normal and malignant tissues. Prog. Biophys. Mol. Biol. 1968, 18, 245–283. [Google Scholar] [CrossRef]
- Lala, P.K.; Patt, H.M. Cytokinetic analysis of tumor growth. Proc. Natl. Acad. Sci. USA 1966, 56, 1735–1742. [Google Scholar] [CrossRef] [PubMed]
- Cameron, I.L.; Greulich, R.C. Evidence for an essentially constant duration of DNA synthesis in renewing epithelia of the adult mouse. J. Cell Biol. 1963, 18, 31–40. [Google Scholar] [CrossRef]
- Defendi, V.; Manson, L.A. Analysis of the Life-Cycle in Mammalian Cells. Nature 1963, 198, 359–361. [Google Scholar] [CrossRef]
- Hwang, Y.; Hidalgo, D.; Socolovsky, M. The shifting shape and functional specializations of the cell cycle during lineage development. WIREs Mech. Dis. 2021, 13, e1504. [Google Scholar] [CrossRef]
- Blumenthal, A.B.; Kriegstein, H.J.; Hogness, D.S. The units of DNA replication in Drosophila melanogaster chromosomes. Cold Spring Harb. Perspect. Biol. 1974, 38, 205–223. [Google Scholar] [CrossRef]
- Newport, J.; Kirschner, M. A major developmental transition in early Xenopus embryos: I. characterization and timing of cellular changes at the midblastula stage. Cell 1982, 30, 675–686. [Google Scholar] [CrossRef]
- Bragg, A.N. Some Cytological Phenomena in Early Embryos of Bufo cognatus Say. Trans. Am. Microsc. Soc. 1939, 58, 357–370. [Google Scholar] [CrossRef]
- Su, T.T. The effect of a DNA damaging agent on embryonic cell cycles of the cnidarian Hydractinia echinata. PLoS ONE 2010, 5, e11760. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kimmel, C.B.; Ballard, W.W.; Kimmel, S.R.; Ullmann, B.; Schilling, T.F. Stages of embryonic development of the zebrafish. Dev. Dyn. 1995, 203, 253–310. [Google Scholar] [CrossRef] [PubMed]
- O’Farrell, P.H.; Stumpff, J.; Su, T.T. Embryonic cleavage cycles: How is a mouse like a fly? Curr. Biol. 2004, 14, R35–R45. [Google Scholar] [CrossRef] [PubMed]
- Snow, M.H.L. Gastrulation in the mouse: Growth and regionalization of the epiblast. Development 1977, 42, 293–303. [Google Scholar] [CrossRef]
- Mac Auley, A.; Werb, Z.; Mirkes, P.E. Characterization of the unusually rapid cell cycles during rat gastrulation. Development 1993, 117, 873–883. [Google Scholar] [CrossRef]
- Al-Saleh, A.A. Relative durations of the cell cycle phases of Xenopus cells at different temperatures. Jpn. J. Genet. 1984, 59, 601–606. [Google Scholar] [CrossRef][Green Version]
- Sugitani, N.; Vendetti, F.P.; Cipriano, A.J.; Deppas, J.J.; Moiseeva, T.N.; Schamus-Haynes, S.; Wang, Y.; Palmer, D.; Osmanbeyoglu, H.U.; Bostwick, A.; et al. ATR kinase inhibition induces thymineless death in proliferating CD8+ T cells. bioRxiv 2022. [CrossRef]
- Yoon, H.; Kim, T.S.; Braciale, T.J. The cell cycle time of CD8+ T cells responding in vivo is controlled by the type of antigenic stimulus. PLoS ONE 2010, 5, e15423. [Google Scholar] [CrossRef]
- Van’t Hof, J. Cell population kinetics of excised roots of Pisum sativum. J. Cell Biol. 1965, 27, 179–189. [Google Scholar] [CrossRef]
- Evans, M.G.; Rees, H. Mitotic cycles in dicotyledons and monocotyledons. Nature 1971, 233, 350–351. [Google Scholar] [CrossRef]
- Francis, D.; Davies, M.S.; Barlow, P.W. A strong nucleotypic effect on the cell cycle regardless of ploidy level. Ann. Bot. 2008, 101, 747–757. [Google Scholar] [CrossRef] [PubMed]
- Avanzi, S.; Deri, P.L. Duration of the Mitotic Cycle in two Cultivars of Triticum Durum as Measured by 3H-Thymidine Labelling. Caryologia 1969, 22, 187–194. [Google Scholar] [CrossRef][Green Version]
- Mickelson-Young, L.; Wear, E.; Mulvaney, P.; Lee, T.-J.; Szymanski, E.S.; Allen, G.; Hanley-Bowdoin, L.; Thompson, W. A flow cytometric method for estimating S-phase duration in plants. J. Exp. Bot. 2016, 67, 6077–6087. [Google Scholar] [CrossRef]
- Kaltsikes, P.J. Duration of the Mitotic Cycle in Triticale. Caryologia 1972, 25, 537–542. [Google Scholar] [CrossRef]
- Kaltsikes, P.J. The Mitotic Cycle in An Amphiploid (Triticale) And Its Parental Species. Can. J. Genet. Cytol. 1971, 13, 656–662. [Google Scholar] [CrossRef]
- Verma, R.S.; Lin, M.S. The duration of DNA synthetic (S) period in Zea mays: A genetic control. Theor. Appl. Genet. 1979, 54, 277–282. [Google Scholar] [CrossRef]
- Troy, R.M.; Wimber, D.E. Evidence for a constancy of the DNA synthetic period between diploid-polyploid groups in plants. Exp. Cell Res. 1968, 53, 145–154. [Google Scholar] [CrossRef]
- Yang, H.; Liu, Z.; Ma, Y.; Zhong, C.; Yin, Q.; Zhou, C.; Shi, L.; Cai, Y.; Zhao, H.; Wang, H.; et al. Generation of haploid embryonic stem cells from Macaca fascicularis monkey parthenotes. Cell Res. 2013, 23, 1187–1200. [Google Scholar] [CrossRef]
- Beach, R.R.; Ricci-Tam, C.; Brennan, C.M.; Moomau, C.A.; Hsu, P.H.; Hua, B.; Silberman, R.E.; Springer, M.; Amon, A. Aneuploidy Causes Non-genetic Individuality. Cell 2017, 169, 229–242. [Google Scholar] [CrossRef]
- Reyes-Lamothe, R.; Nicolas, E.; Sherratt, D.J. Chromosome replication and segregation in bacteria. Annu. Rev. Genet. 2012, 46, 121–143. [Google Scholar] [CrossRef]
- Lindas, A.C.; Bernander, R. The cell cycle of archaea. Nat. Rev. Microbiol. 2013, 11, 627–638. [Google Scholar] [CrossRef]
- Zhu, M.; Dai, X.; Guo, W.; Ge, Z.; Yang, M.; Wang, H.; Wang, Y.P. Manipulating the Bacterial Cell Cycle and Cell Size by Titrating the Expression of Ribonucleotide Reductase. mBio 2017, 8, e01741-17. [Google Scholar] [CrossRef]
- Chagin, V.O.; Casas-Delucchi, C.S.; Reinhart, M.; Schermelleh, L.; Markaki, Y.; Maiser, A.; Bolius, J.J.; Bensimon, A.; Fillies, M.; Domaing, P.; et al. 4D Visualization of replication foci in mammalian cells corresponding to individual replicons. Nat. Commun. 2016, 7, 11231. [Google Scholar] [CrossRef] [PubMed]
- Platel, M.; Narassimprakash, H.; Ciardo, D.; Haccard, O.; Marheineke, K. Genome wide decrease of DNA replication eye density at the midblastula transition of Xenopus laevis. Cell Cycle 2019, 18, 1458–1472. [Google Scholar] [CrossRef]
- Anglana, M.; Apiou, F.; Bensimon, A.; Debatisse, M. Dynamics of DNA replication in mammalian somatic cells: Nucleotide pool modulates origin choice and interorigin spacing. Cell 2003, 114, 385–394. [Google Scholar] [CrossRef]
- Courbet, S.; Gay, S.; Arnoult, N.; Wronka, G.; Anglana, M.; Brison, O.; Debatisse, M. Replication fork movement sets chromatin loop size and origin choice in mammalian cells. Nature 2008, 455, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.Q.; Jackson, D.A.; Blow, J.J. Dormant origins licensed by excess Mcm2-7 are required for human cells to survive replicative stress. Genes. Dev. 2007, 21, 3331–3341. [Google Scholar] [CrossRef]
- Conti, C.; Sacca, B.; Herrick, J.; Lalou, C.; Pommier, Y.; Bensimon, A. Replication fork velocities at adjacent replication origins are coordinately modified during DNA replication in human cells. Mol. Biol. Cell 2007, 18, 3059–3067. [Google Scholar] [CrossRef]
- Egger, T.; Bordignon, B.; Coquelle, A. A clinically relevant heterozygous ATR mutation sensitizes colorectal cancer cells to replication stress. Sci. Rep. 2022, 12, 5422. [Google Scholar] [CrossRef]
- Alvino, G.M.; Collingwood, D.; Murphy, J.M.; Delrow, J.; Brewer, B.J.; Raghuraman, M.K. Replication in hydroxyurea: It’s a matter of time. Mol. Cell Biol. 2007, 27, 6396–6406. [Google Scholar] [CrossRef]
- Tercero, J.A.; Diffley, J.F. Regulation of DNA replication fork progression through damaged DNA by the Mec1/Rad53 checkpoint. Nature 2001, 412, 553–557. [Google Scholar] [CrossRef]
- Krakoff, I.H.; Brown, N.C.; Reichard, P. Inhibition of ribonucleoside diphosphate reductase by hydroxyurea. Cancer Res. 1968, 28, 1559–1565. [Google Scholar]
- Ikegami, S.; Taguchi, T.; Ohashi, M.; Oguro, M.; Nagano, H.; Mano, Y. Aphidicolin prevents mitotic cell division by interfering with the activity of DNA polymerase-alpha. Nature 1978, 275, 458–460. [Google Scholar] [CrossRef]
- Sui, L.; Xin, Y.; Du, Q.; Georgieva, D.; Diedenhofen, G.; Haataja, L.; Su, Q.; Zuccaro, M.V.; Kim, J.; Fu, J.; et al. Reduced replication fork speed promotes pancreatic endocrine differentiation and controls graft size. JCI Insight 2021, 6, e141553. [Google Scholar] [CrossRef]
- Krokan, H.; Wist, E.; Krokan, R.H. Aphidicolin inhibits DNA synthesis by DNA polymerase alpha and isolated nuclei by a similar mechanism. Nucleic. Acids Res. 1981, 9, 4709–4719. [Google Scholar] [CrossRef]
- Zhong, Y.; Nellimoottil, T.; Peace, J.M.; Knott, S.R.; Villwock, S.K.; Yee, J.M.; Jancuska, J.M.; Rege, S.; Tecklenburg, M.; Sclafani, R.A.; et al. The level of origin firing inversely affects the rate of replication fork progression. J. Cell Biol. 2013, 201, 373–383. [Google Scholar] [CrossRef]
- Maya-Mendoza, A.; Moudry, P.; Merchut-Maya, J.M.; Lee, M.; Strauss, R.; Bartek, J. High speed of fork progression induces DNA replication stress and genomic instability. Nature 2018, 559, 279–284. [Google Scholar] [CrossRef]
- Poli, J.; Tsaponina, O.; Crabbé, L.; Keszthelyi, A.; Pantesco, V.; Chabes, A.; Lengronne, A.; Pasero, P. dNTP pools determine fork progression and origin usage under replication stress. EMBO J. 2012, 31, 883–894. [Google Scholar] [CrossRef]
- Rodriguez-Acebes, S.; Mouron, S.; Mendez, J. Uncoupling fork speed and origin activity to identify the primary cause of replicative stress phenotypes. J. Biol. Chem. 2018, 293, 12855–12861. [Google Scholar] [CrossRef]
- Zhuang, Z.; Ai, Y. Processivity factor of DNA polymerase and its expanding role in normal and translesion DNA synthesis. Biochim. Biophys. Acta 2010, 1804, 1081–1093. [Google Scholar] [CrossRef]
- Jiang, C.; Hwang, Y.T.; Randell, J.C.; Coen, D.M.; Hwang, C.B. Mutations that decrease DNA binding of the processivity factor of the herpes simplex virus DNA polymerase reduce viral yield, alter the kinetics of viral DNA replication, and decrease the fidelity of DNA replication. J. Virol. 2007, 81, 3495–3502. [Google Scholar] [CrossRef]
- Reha-Krantz, L.J.; Woodgate, S.; Goodman, M.F. Engineering processive DNA polymerases with maximum benefit at minimum cost. Front. Microbiol. 2014, 5, 380. [Google Scholar] [CrossRef]
- Baranovskiy, A.G.; Babayeva, N.D.; Suwa, Y.; Gu, J.; Pavlov, Y.I.; Tahirov, T.H. Structural basis for inhibition of DNA replication by aphidicolin. Nucleic. Acids Res. 2014, 42, 14013–14021. [Google Scholar] [CrossRef]
- Francis, D.; Barlow, P.W. Temperature and the cell cycle. Symp. Soc. Exp. Biol. 1988, 42, 181–201. [Google Scholar]
- Al-Saleh, A.A. Effects of temperature on the replication of chromosomal DNA of Xenopus laevis cells. J. Cell Sci. 1983, 59, 1–12. [Google Scholar] [CrossRef]
- Iurov Iu, B. Replication of chromosomal DNA in Chinese hamster cells, cultivated at different temperatures. Tsitologiia 1977, 19, 1064–1067. [Google Scholar]
- Malinsky, J.; Koberna, K.; Stanek, D.; Masata, M.; Votruba, I.; Raska, I. The supply of exogenous deoxyribonucleotides accelerates the speed of the replication fork in early S-phase. J. Cell Sci. 2001, 114, 747–750. [Google Scholar] [CrossRef]
- Chabes, A.; Georgieva, B.; Domkin, V.; Zhao, X.; Rothstein, R.; Thelander, L. Survival of DNA damage in yeast directly depends on increased dNTP levels allowed by relaxed feedback inhibition of ribonucleotide reductase. Cell 2003, 112, 391–401. [Google Scholar] [CrossRef]
- Ferraro, P.; Franzolin, E.; Pontarin, G.; Reichard, P.; Bianchi, V. Quantitation of cellular deoxynucleoside triphosphates. Nucleic. Acids Res. 2010, 38, e85. [Google Scholar] [CrossRef]
- Kumar, D.; Viberg, J.; Nilsson, A.K.; Chabes, A. Highly mutagenic and severely imbalanced dNTP pools can escape detection by the S-phase checkpoint. Nucleic. Acids Res. 2010, 38, 3975–3983. [Google Scholar] [CrossRef]
- Forey, R.; Poveda, A.; Sharma, S.; Barthe, A.; Padioleau, I.; Renard, C.; Lambert, R.; Skrzypczak, M.; Ginalski, K.; Lengronne, A.; et al. Mec1 Is Activated at the Onset of Normal S Phase by Low-dNTP Pools Impeding DNA Replication. Mol. Cell 2020, 78, 396–410. [Google Scholar] [CrossRef]
- Diehl, F.F.; Miettinen, T.P.; Elbashir, R.; Nabel, C.S.; Manalis, S.R.; Lewis, C.A.; Vander Heiden, M.G. Nucleotide imbalance decouples cell growth from cell proliferation. bioRxiv 2021. [Google Scholar] [CrossRef]
- Feeney, A.M.; Ke, N.; Beckwith, J. Mutations at several loci cause increased expression of ribonucleotide reductase in Escherichia coli. J. Bacteriol. 2012, 194, 1515–1522. [Google Scholar] [CrossRef][Green Version]
- Schmidt, T.T.; Sharma, S.; Reyes, G.X.; Gries, K.; Gross, M.; Zhao, B.; Yuan, J.-H.; Wade, R.; Chabes, A.; Hombauer, H. A genetic screen pinpoints ribonucleotide reductase residues that sustain dNTP homeostasis and specifies a highly mutagenic type of dNTP imbalance. Nucleic. Acids Res. 2019, 47, 237–252. [Google Scholar] [CrossRef]
- Zhao, X.; Chabes, A.; Domkin, V.; Thelander, L.; Rothstein, R. The ribonucleotide reductase inhibitor Sml1 is a new target of the Mec1/Rad53 kinase cascade during growth and in response to DNA damage. EMBO J. 2001, 20, 3544–3553. [Google Scholar] [CrossRef]
- Huang, M.; Zhou, Z.; Elledge, S.J. The DNA replication and damage checkpoint pathways induce transcription by inhibition of the Crt1 repressor. Cell 1998, 94, 595–605. [Google Scholar] [CrossRef]
- Pennycook, B.R.; Vesela, E.; Peripolli, S.; Singh, T.; Barr, A.R.; Bertoli, C.; de Bruin, R.A. E2F-dependent transcription determines replication capacity and S phase length. Nat. Commun. 2020, 11, 3503. [Google Scholar] [CrossRef]
- Pardee, A.B.; Li, C.J.; Reddy, G.P. Regulation in S phase by E2F. Cell Cycle 2004, 3, 1091–1094. [Google Scholar] [CrossRef][Green Version]
- Ziane, R.; Camasses, A.; Radman-Livaja, M. The asymmetric distribution of RNA polymerase II and nucleosomes on replicated daughter genomes is caused by differences in replication timing between the lagging and the leading strand. Genome Res. 2022, 32, 337–356. [Google Scholar] [CrossRef]
- Raso, M.C.; Djoric, N.; Walser, F.; Hess, S.; Schmid, F.M.; Burger, S.; Knobeloch, K.P.; Penengo, L. Interferon-stimulated gene 15 accelerates replication fork progression inducing chromosomal breakage. J. Cell Biol. 2020, 219, e202002175. [Google Scholar] [CrossRef]
- Kurat, C.F.; Yeeles, J.T.P.; Patel, H.; Early, A.; Diffley, J.F.X. Chromatin Controls DNA Replication Origin Selection, Lagging-Strand Synthesis, and Replication Fork Rates. Mol. Cell 2017, 65, 117–130. [Google Scholar] [CrossRef]
- Rivin, C.J.; Fangman, W.L. Replication fork rate and origin activation during the S phase of Saccharomyces cerevisiae. J. Cell Biol. 1980, 85, 108–115. [Google Scholar] [CrossRef]
- Myllykallio, H.; Lopez, P.; López-García, P.; Heilig, R.; Saurin, W.; Zivanovic, Y.; Philippe, H.; Forterre, P. Bacterial Mode of Replication with Eukaryotic-Like Machinery in a Hyperthermophilic Archaeon. Science 2000, 288, 2212–2215. [Google Scholar] [CrossRef]
- Voichek, Y.; Bar-Ziv, R.; Barkai, N. A role for Rtt109 in buffering gene-dosage imbalance during DNA replication. Nucleus 2016, 7, 375–381. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Frenkel, N.; Jonas, F.; Carmi, M.; Yaakov, G.; Barkai, N. Rtt109 slows replication speed by histone N-terminal acetylation. Genome Res. 2021, 31, 426–435. [Google Scholar] [CrossRef]
- Tsirkas, I.; Dovrat, D.; Lei, Y.; Kalyva, A.; Lotysh, D.; Li, Q.; Aharoni, A. Cac1 WHD and PIP domains have distinct roles in replisome progression and genomic stability. Curr. Genet. 2021, 67, 129–139. [Google Scholar] [CrossRef]
- Iyer, D.R.; Rhind, N. Replication fork slowing and stalling are distinct, checkpoint-independent consequences of replicating damaged DNA. PLoS Genet 2017, 13, e1006958. [Google Scholar] [CrossRef]
- Musiałek, M.; Rybaczek, D. Hydroxyurea-The Good, the Bad and the Ugly. Genes 2021, 12, 1096. [Google Scholar] [CrossRef]
- Vander Heiden, M.G.; Cantley, L.C.; Thompson, C.B. Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 2009, 324, 1029–1033. [Google Scholar] [CrossRef]
- Somyajit, K.; Gupta, R.; Sedlackova, H.; Neelsen, K.J.; Ochs, F.; Rask, M.B.; Choudhary, C.; Lukas, J. Redox-sensitive alteration of replisome architecture safeguards genome integrity. Science 2017, 358, 797–802. [Google Scholar] [CrossRef]
- Grallert, B.; Boye, E. The multiple facets of the intra-S checkpoint. Cell Cycle 2008, 7, 2315–2320. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nakatani, T.; Lin, J.; Ji, F.; Ettinger, A.; Pontabry, J.; Tokoro, M.; Altamirano-Pacheco, L.; Fiorentino, J.; Mahammadov, E.; Hatano, Y.; et al. DNA replication fork speed underlies cell fate changes and promotes reprogramming. Nat. Genet. 2022, 54, 318–327. [Google Scholar] [CrossRef]
- Painter, R.B.; Schaefer, A.W. Variation in the rate of DNA chain growth through the S phase in HeLa cells. J. Mol. Biol. 1971, 58, 289–295. [Google Scholar] [CrossRef]
- Housman, D.; Huberman, J.A. Changes in the rate of DNA replication fork movement during S phase in mammalian cells. J. Mol. Biol. 1975, 94, 173–181. [Google Scholar] [CrossRef]
- Van’t Hof, J. Replicon size and rate of fork movement in early S of higher plant cells (Pisum sativum). Exp. Cell Res. 1976, 103, 395–403. [Google Scholar] [CrossRef]
- Guilbaud, G.; Rappailles, A.; Baker, A.; Chen, C.L.; Arneodo, A.; Goldar, A.; d’Aubenton-Carafa, Y.; Thermes, C.; Audit, B.; Hyrien, O. Evidence for sequential and increasing activation of replication origins along replication timing gradients in the human genome. PLoS Comput. Biol. 2011, 7, e1002322. [Google Scholar] [CrossRef]
- Pillaire, M.-J.; Betous, R.; Conti, C.; Czaplicki, J.; Pasero, P.; Bensimon, A.; Cazaux, C.; Hoffmann, J.-S. Upregulation of Error-Prone DNA Polymerases Beta and Kappa Slows Down Fork Progression Without Activating the Replication Checkpoint. Cell Cycle 2007, 6, 471–477. [Google Scholar] [CrossRef][Green Version]
- Cayrou, C.; Coulombe, P.; Vigneron, A.; Stanojcic, S.; Ganier, O.; Peiffer, I.; Rivals, E.; Puy, A.; Laurent-Chabalier, S.; Desprat, R.; et al. Genome-scale analysis of metazoan replication origins reveals their organization in specific but flexible sites defined by conserved features. Genome Res. 2011, 21, 1438–1449. [Google Scholar] [CrossRef]
- Van’t Hof, J.; Bjerknes, C.A. Similar replicon properties of higher plant cells with different S periods and genome sizes. 1981, 136, 461–465. Exp. Cell Res. 1981, 136, 461–465. [Google Scholar] [CrossRef]
- Ermakova, O.V.; Nguyen, L.H.; Little, R.D.; Chevillard, C.; Riblet, R.; Ashouian, N.; Birshtein, B.K.; Schildkraut, C.L. Evidence that a single replication fork proceeds from early to late replicating domains in the IgH locus in a non-B cell line. Mol. Cell 1999, 3, 321–330. [Google Scholar] [CrossRef]
- Farkash-Amar, S.; David, Y.; Polten, A.; Hezroni, H.; Eldar, Y.C.; Meshorer, E.; Yakhini, Z.; Simon, I. Systematic determination of replication activity type highlights interconnections between replication, chromatin structure and nuclear localization. PLoS ONE 2012, 7, e48986. [Google Scholar] [CrossRef]
- Blow, J.J.; Gillespie, P.J.; Francis, D.; Jackson, D.A. Replication origins in Xenopus egg extract Are 5-15 kilobases apart and are activated in clusters that fire at different times. J. Cell Biol. 2001, 152, 15–25. [Google Scholar] [CrossRef]
- Marheineke, K.; Hyrien, O. Control of replication origin density and firing time in Xenopus egg extracts: Role of a caffeine-sensitive, ATR-dependent checkpoint. J. Biol. Chem. 2004, 279, 28071–28081. [Google Scholar] [CrossRef]
- Farrell, J.A.; Shermoen, A.W.; Yuan, K.; O’Farrell, P.H. Embryonic onset of late replication requires Cdc25 down-regulation. Genes Dev. 2012, 26, 714–725. [Google Scholar] [CrossRef]
- Williamson, D.H.; Johnston, L.H.; Fennell, D.J.; Simchen, G. The timing of the S phase and other nuclear events in yeast meiosis. Exp. Cell Res. 1983, 145, 209–217. [Google Scholar] [CrossRef]
- Collins, I.; Newlon, C.S. Chromosomal DNA replication initiates at the same origins in meiosis and mitosis. Mol. Cell Biol. 1994, 14, 3524–3534. [Google Scholar] [CrossRef]
- Callan, H.G. Replication of DNA in the chromosomes of eukaryotes. Proc. R. Soc. Lond. B Biol. Sci. 1972, 181, 19–41. [Google Scholar] [CrossRef]
- Bleiberg, H.; Galand, P. In Vitro Autoradiographic Determination of Cell Kinetic Parameters in Adenocarcinomas and Adjacent Healthy Mucosa of the Human Colon and Rectum1. Cancer Res. 1976, 36, 325–328. [Google Scholar]
- Nachar, B.A.A. Decreased Replication Potency and Extended S Phase, Due to Shortened G1 and Replication Origin under-Licensing, Are a Common Feature of Cancer Cells. Ph.D. Thesis, Université Montpellier, Montpellier, Franch, 2020. [Google Scholar]
- Hof, J. Chromosomal Replicons of Higher Plants; 1987. Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/18/085/18085305.pdf?r=1 (accessed on 5 April 2022).
- Koren, A.; Soifer, I.; Barkai, N. MRC1-dependent scaling of the budding yeast DNA replication timing program. Genome Res. 2010, 20, 781–790. [Google Scholar] [CrossRef] [PubMed]
- Goldfeder, A. Biological Properties and Radiosensitivity of Tumours: Determination of the Cell-Cycle and Time of Synthesis of Deoxyribonucleic Acid Using Tritiated Thymidine and Autoradiography. Nature 1965, 207, 612–614. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Greenberg, A.; Simon, I. S Phase Duration Is Determined by Local Rate and Global Organization of Replication. Biology 2022, 11, 718. https://doi.org/10.3390/biology11050718
Greenberg A, Simon I. S Phase Duration Is Determined by Local Rate and Global Organization of Replication. Biology. 2022; 11(5):718. https://doi.org/10.3390/biology11050718
Chicago/Turabian StyleGreenberg, Avraham, and Itamar Simon. 2022. "S Phase Duration Is Determined by Local Rate and Global Organization of Replication" Biology 11, no. 5: 718. https://doi.org/10.3390/biology11050718
APA StyleGreenberg, A., & Simon, I. (2022). S Phase Duration Is Determined by Local Rate and Global Organization of Replication. Biology, 11(5), 718. https://doi.org/10.3390/biology11050718




